Радиотехника и электроника, 2019, T. 64, № 4, стр. 361-369

ВВЕДЕНИЕ

Во многих технических приложениях, связанных с использованием моноимпульсных радиолокационных станций (РЛС), возникает потребность в увеличении разрешающей способности. Это, прежде всего, необходимо при работе по групповым целям, в условиях применения противником ложных целей, активных помех, а также при измерении угловых координат низколетящих над морской поверхностью целей [1]. Остановимся на последнем случае более детально. Отраженный от низко летящей цели эхо-сигнал может возвращаться к приемнику РЛС многими путями – непосредственно прямым путем и отраженными от подстилающей поверхности путями. Это проявляется в виде мерцания принимаемого сигнала в связи с интерференцией отраженной от цели и от подстилающей поверхности электромагнитной волны. Если пройденные пути прямого и отраженного сигнала близки и угловое расстояние между зеркальным отражением и целью невелико, то применение обычных методов моноимпульсной радиолокации для формирования измерения углового положения цели приводят к значительным ошибкам. Считается (см. [2, 3] и многие другие источники), что отраженный от морской поверхности сигнал, может быть описан как сумма двух составляющих – зеркального отражения и диффузного отражения (или резонансного рассеяния). То есть, вообще говоря, в условиях переотражения электромагнитной волны от морской поверхности, имеет место модель многолучевого распространения. Помимо этого, вследствие прямого отражения электромагнитной волны от подстилающей поверхности, принимаемый бортовой радиолокационной станцией сигнал содержит еще одну аддитивную составляющую весьма сложной природы. Однако при выполнении ряда условий, в частности, когда высота над морской поверхностью приемной антенны относительно невелика [1] и некоторых других, модель распространения электромагнитной волны может считаться двулучевой. В этом случае зеркальное отражение цели можно рассматривать как отражение радиоволны от некоторого фиктивного источника – “антипода” и задача формирования измерения координаты по углу места эквивалентна задаче разрешения двух точечных целей.

На протяжении нескольких последних десятилетий эта задача находится в центре внимания многих исследователей во всем мире. Были предложены многочисленные методы, позволяющие или в определенной степени ослабить искажения, вызываемые присутствием в принимаемом эхо сигнале сигналов от двух целей, или, при выполнении некоторых дополнительных условий, выделять эти сигналы.

В данной статье предлагается метод определения угловых координат двух неразрешенных точечных целей для произвольных величин принимаемых от них комплексных сигналов (т.е. без каких бы то ни было дополнительных предположений о функциональной зависимости принимаемых от целей сигналов). Единственно, что требуется для применения метода – возможность формирования четырех независимых диаграмм направленности, расположенных в вертикальной плоскости (“строковых” диаграмм), или, иными словами, наличия четырех одинаковых независимых приемников сигнала. Эти приемники могут быть сформированы путем соответствующих вычислительных манипуляций в практически любой линейной эквидистантной фазированной антенной решетке или могут представлять собой четыре отдельные, расположенные в вертикальной плоскости на одинаковом расстоянии друг от друга зеркальные антенны.

Следует отметить, что предлагаемый метод может с тем же успехом использоваться и для измерения курсового (азимутального) угла. Для этого требуется формирование четырех диаграмм направленности, расположенных в горизонтальной плоскости (“столбцевых” диаграмм).

С алгоритмической точки зрения предлагаемый метод сводится к решению некоторого квадратного уравнения с комплексными коэффициентами. Именно по этой причине он получил название квадратичный.

1. ОБЗОР НЕКОТОРЫХ СУЩЕСТВУЮЩИХ МЕТОДОВ ФОРМИРОВАНИЯ УГЛОВЫХ ИЗМЕРЕНИЙ БЛИЗКО РАСПОЛОЖЕННЫХ ЦЕЛЕЙ

Одним из наиболее известных алгоритмических методов формирования углового измерения близко расположенных целей является метод Уайта [4]. Метод предполагает формирование трех суммарных диаграмм направленности (ДН), одна из которых центрируется строго на среднюю точку между целями, а две оставшиеся разносятся относительно первой на некоторые равные углы в положительном и отрицательном направлениях. При таком формировании диаграмм, сигнал первой (центральной) диаграммы оказывается синфазным с суммарным сигналом двух других диаграмм, а их отношение зависит исключительно от разности углов целей. Это позволяет определить углы целей путем решения некоторого нелинейного уравнения. Понятно, что на практике направление на среднюю точку никогда не бывает известно точно. Поэтому этот метод обладает систематической ошибкой, зависящей от взаимного расположения оси центральной диаграммы и направлением на среднюю точку.

На рис. 1а и 1б представлены результаты измерений угла цели № 1 соответственно фазовым разностно-суммарным методом и методом Уайта в идеальных условиях, когда внутренние шумы антенны равны нулю. Расчеты проведены при следующих исходных данных, взятых из [5]: рабочая частота 10 ГГц, ширина ДН по половинной мощности 1 град, дальность до цели 10 км, высота цели 50 м, высота приемника 0 м. За цель № 1 принята реальная цель, за цель № 2 принят ее антипод. Угловая координата цели № 1 постоянна и равна 5 млрд. Амплитуды сигналов целей приняты равными. Угловая координата цели № 2 изменяется от 5 мрад в сторону убывания. Кривые 1, 2, 3 построены по результатам работ соответствующих алгоритмов при различных разностях фаз сигналов цели и антипода. Из рисунков видно, что систематические ошибки этих методов весьма велики.

Следует отметить одну из основополагающих работ в этой области [6], в которой показано, что с привлечением определенной априорной информации о функциональной зависимости сигналов целей (геометрического происхождения), угловые координаты целей могут быть “извлечены” (при помощи решения системы нелинейных уравнений) из типичной информации разностно-суммарного метода – измерений (комплексных) верхней и нижней диаграмм. Однако точной геометрической картины, описывающей взаимное расположение цели и антипода, не существует, а вынужденно принимаемые допущения приводят к возникновению систематических ошибок.

В ряде работ были рассмотрены различные специальные случаи, подобно методу Уайта, позволяющие решить задачу в том или ином частном случае [3, 7]. В [8] предлагается применять итерационный метод нахождения оценок углов целей. Идея метода заключается в следующем. Если бы были известны угловые положения целей ${{{\theta }}_{1}}$ и ${{{\theta }}_{2}},$ то сформировав верхнюю и нижнюю ДН таким образом, чтобы их нули находились в точке ${{{\theta }}_{1}},$ можно было бы восстановить координаты цели № 2 точно по соотношению этих диаграмм. И наоборот, если обеспечить нули диаграмм в точке ${{{\theta }}_{2}},$ то угол цели № 1 вычислялся бы точно.

Пусть выбрано начальное значение угла цели 2 – ${\theta }_{2}^{{*(k)}}$ (k = 0 – номер итерации). Формируется верхняя и нижняя ДН такие, что их нули находятся в точке ${\theta }_{2}^{{*(k)}}.$ Находим оценку угла первой цели ${\theta }_{1}^{{*(k + 1)}}.$ Затем формируются верхняя и нижняя диаграммы такие, что их нули находятся в точке ${\theta }_{1}^{{*(k + 1)}}.$ Вычисляем угол ${\theta }_{2}^{{*(k + 1)}}.$ Процесс повторяется до тех пор, пока невязка не становится меньше заданной точноcти

Приведенный метод не дает систематической погрешности. Однако быстро деградирует при сближении целей (падает точность измерения). Это вызвано тем, что нули разностной и суммарной диаграмм находятся близко друг от друга, что приводит к существенному уменьшению отношения сигнал/шум. Кроме того, как любой итерационный метод, этот метод требует привлечения дополнительных вычислительных ресурсов, что не всегда доступно.

Для решения рассматриваемой задачи можно применить метод максимального правдоподобия, что, в частности, предлагается сделать в [2]. Применение метода максимального правдоподобия приводит к задаче математического программирования без ограничений, но с невыпуклой целевой функцией, имеющей многочисленные экстремумы. Численное решение задач такого рода сопряжено с известными вычислительными трудностями [9]. Если начальное приближение итерационного метода принадлежит достаточно малой окрестности решения, то вычислительный процесс сходится за несколько итераций. В противном случае возникают проблемы – блуждание или зацикливание. Нами были предприняты попытки решения этой задачи различными численными методами – методом Ньютона, модифицированным методом Ньютона, штрафных функций, группового покоординатного спуска, различными комбинациями этих методов. При определенных соотношениях параметров удается подобрать алгоритм формирования начального приближения, но при дальнейшем численном экспериментировании, уже с другим соотношением параметров, алгоритм перестает работать. Собственно это и послужило толчком к дальнейшим исследованиям, направленным на разработку надежного и не требующего привлечения значительных вычислительных ресурсов метода расчета угловых координат двух близко расположенных целей. В завершение обсуждения метода максимального правдоподобия, следует отметить, что в тех случаях, когда удается найти численной решение экстремальной задачи метода максимального правдоподобия, это решение оказывается достаточно близким к решению, получаемому в соответствии с методом, предлагаемым в данной статье.

2. ПОСТАНОВКА ЗАДАЧИ

Обозначим через ${{{\theta }}_{1}}$ и ${{{\theta }}_{2}}$ соответственно углы целей № 1 и № 2 относительно нормали к полотну антенны. Будем считать, что в некоторый момент времени на фазовый центр диаграммы строки с номером 0 от целей поступают комплексные сигналы ${{k}_{1}}$ и ${{k}_{2}}$ соответственно. Тогда, для измерений строковых диаграмм $S_{n}^{*},$ справедливо:

где η_n – комплексный “белый шум” (внутренний шум приемной аппаратуры): – обобщенные углы целей, $F(\theta )$ – суммарная диаграмма направленности каждой из строковых диаграмм.

Задача состоит в том, чтобы на основании измерений диаграмм $S_{n}^{*}$ вычислить значения углов $\theta _{k}^{*} = \theta _{k}^{*}({\mathbf{S}}{\text{*}}),$ $k = 1,2.$

3. РЕШЕНИЕ ЗАДАЧИ

Предположим, что шумы ${{\eta }_{n}}$ в измерениях диаграмм (1) отсутствуют, ${{\eta }_{n}} = 0,$ $n = 0,1,2,3.$ Введем в рассмотрение комплексные переменные: ${{z}_{1}} = \exp (i{{\mu }_{1}}),$ ${{z}_{2}} = \exp (i{{\mu }_{2}}),$ которые будем называть комплексными углами целей. Обозначим ${{y}_{1}} = {{k}_{1}}F({{\theta }_{1}}),$ ${{y}_{2}} = {{k}_{2}}F({{\theta }_{2}}).$ Равенства (1) примут вид

Будем рассматривать равенства (4) как систему четырех нелинейных уравнений в комплексной области относительно четырех неизвестных ${{y}_{1}},$ ${{z}_{1}},$ ${{y}_{2}},$ ${{z}_{2}}.$

Утверждение 1. Комплексные углы целей ${{z}_{1}}$ и ${{z}_{2}}$ являются неподвижными точками дробно-линейного преобразования

и могут быть найдены в результате решения квадратного уравнения:

За счет этого факта можно построить весьма простой вычислительный метод формирования измерений угловых положений целей. На основании полученных измерений $S_{n}^{*}$ решаем квадратное уравнение (6), находим обобщенные углы:

и, наконец, находим оценки углов целей:

Если бы шумы ${{\eta }_{k}}$ в измерениях (1) были равны нулю, то комплексные углы целей, рассчитанные в соответствии с (7), совпадали бы с истинными и углы целей могли быть вычислены точно по формуле (9). Однако шумы ${{\eta }_{k}}$ нулю не равны, и их присутствие вносит определенный разброс в решения уравнения (6). Будем считать, что шумы достаточно малы и можно произвести линеаризацию системы уравнений (4) в окрестности решения. Влиянием вторых частных производных функций ${{G}_{n}}$ из (4) пренебрегаем.

Пусть |${{{\mathbf{x}}}^{T}} = \left\| {\begin{array}{*{20}{c}} {{{y}_{1}}}&{{{z}_{1}}}&{{{y}_{2}}}&{{{z}_{2}}} \end{array}} \right\|$ – решение системы уравнений (4). Нетрудно убедиться в том, что для матрицы частных производных комплексный вектор функции ${\mathbf{G}}({\mathbf{x}}),$ заданной уравнениями (4), будет справедливо:

Если матрица ${{\partial {\mathbf{G}}({\mathbf{x}})} \mathord{\left/ {\vphantom {{\partial {\mathbf{G}}({\mathbf{x}})} {\partial {\mathbf{x}}}}} \right. \kern-0em} {\partial {\mathbf{x}}}}$ не вырождена, то в соответствии с правилом дифференцирования неявно заданных функций для разброса вектора решений системы уравнений (4) имеем

Выполняя элементарные преобразования, нетрудно получить следующее выражение для элементов обратной матрицы ${\mathbf{H}}$:

Здесь $d = \frac{1}{{{{y}_{1}}{{y}_{2}}{{{({{z}_{2}} - {{z}_{1}})}}^{3}}}},$ ${{y}_{1}} = \frac{{S_{0}^{*}{{z}_{2}} - S_{1}^{*}}}{{({{z}_{2}} - {{z}_{1}})}},$ y₂ = $ = \frac{{S_{1}^{*} - S_{0}^{*}{{z}_{1}}}}{{({{z}_{2}} - {{z}_{1}})}}.$

Обозначим вектор разброса обобщенных углов через $\Delta {\mathbf{\mu }},$ а корреляционную матрицу этого вектора через ${{{\mathbf{K}}}_{{\Delta {\mathbf{\mu }}}}} = M\Delta {\mathbf{\mu }}\Delta {{{\mathbf{\mu }}}^{T}},$ ${{{\mathbf{K}}}_{{\Delta {\mathbf{\mu }}}}} \in {{{\text{R}}}^{{2 \times 2}}}.$

Утверждение 2. Для элементов корреляционной матрицы вектора разбросов обобщенных углов справедливо:

где ${{a}_{n}}$ и ${{b}_{n}}$ – элементы второй и четвертой строки матрицы ${\mathbf{H}}$.

Очевидно, для корреляционной матрицы вектора ошибок измерений углов $\Delta {{{\mathbf{\theta }}}^{T}} = \left\| {\begin{array}{*{20}{c}} {\Delta {{{\theta }}_{1}}}&{\Delta {{{\theta }}_{2}}} \end{array}} \right\|$ = = $\left\| {\begin{array}{*{20}{c}} {{\theta }_{1}^{*} - {{{\theta }}_{1}}}&{{\theta }_{2}^{*} - {{{\theta }}_{2}}} \end{array}} \right\|$ справедливо:

Если подставить в формулы (10), (11) истинные значения ${{z}_{1}} = \exp (i{{{\mu }}_{1}})$ и ${{z}_{2}} = \exp (i{{{\mu }}_{2}})$ и выполнить элементарные преобразования, то несложно получить формулы для расчета точности измерений обобщенных углов:

здесь ${{\delta }_{\mu }} = {{\mu }_{1}} - {{\mu }_{2}}$ – истинная разность обобщенных углов, а комплексная величина $A$ вычисляется следующим образом:

Из формул (12), (13) следует любопытный факт. Дисперсия ошибки измерения угла какой-либо одной цели не зависит от уровня сигнала другой цели. Но, конечно, зависит от разности их угловых положений.

Допустим, в соответствии с формулами (8), вычислены обобщенные углы $\mu _{1}^{*}$ и $\mu _{2}^{*}.$ Они отличаются от истинных углов на вектор разброса $\Delta {\mathbf{\mu }}$ с корреляционной матрицей (12). Поскольку $\mu _{1}^{*}$ и $\mu _{2}^{*}$ являются случайными величинами, то измерение ${\mu }_{2}^{*}$ может оказаться ближе к истинному значению ${{\mu }_{1}}$ чем $\mu _{2}^{*}.$ Если будет происходить такое “перепутывание” измерений, то это окажет негативное влияние на работу алгоритмов вторичной обработки информации, для которых измеренные углы являются входной информацией. Иными словами, измерения обобщенных углов $\mu _{1}^{*}$ и $\mu _{2}^{*}$ должны быть по возможности корректно соотнесены с номерами целей. Если предположить, что шумы измерений η являются гауссовскими, то погрешность разности измерений обобщенных углов ${{\delta }_{\mu }}$ будет также гауссовской случайной величиной с нулевым средним и дисперсией

Тогда критерий разрешения по уровню вероятности P примет вид [9]

где $F(P)$ – нормальная функция распределения вероятности. Так, например, для обеспечения вероятности 0.997 достаточно взять $F(P) = 3.$

4. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

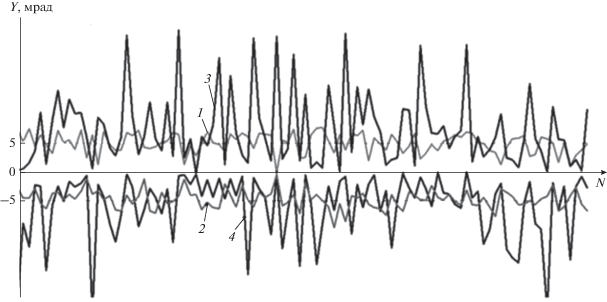
Проиллюстрируем работу предлагаемого метода на примере из работы [5]. Примем отношение сигнал/шум для каждой из целей равным 20 дБ, разность фаз сигналов, поступающих от целей на строку с номером 0, – равной нулю $\arg ({{k}_{1}}) = \arg ({{k}_{2}}).$ На рис. 2 представлены результаты статистического моделирования при уровне шума 20 и 14 дБ.

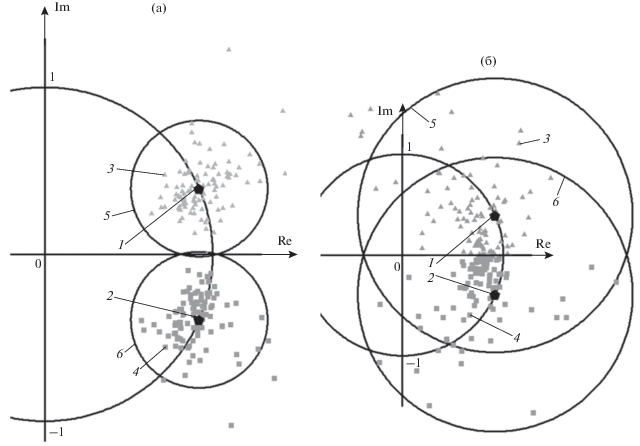
На рис. 3а и 3б представлена комплексная плоскость и измерения комплексных углов, полученные в результате статистического моделирования. Треугольниками изображены измерения цели (${{z}_{1}}$), квадратами измерения антипода (${{z}_{2}}$). Точками 1 и 2 представлены истинные комплексные углы – ${{\tilde {z}}_{1}}$ и ${{\tilde {z}}_{2}},$ окружностями 5 и 6 – эллипсы рассеяния по уровню вероятности 0.997 (окружности с центрами в ${{\tilde {z}}_{1}}$ и ${{\tilde {z}}_{2}}$ и радиусами $3\sqrt {{{K}_{{\Delta {\mathbf{\mu }}11}}}} $ и $3\sqrt {{{K}_{{\Delta {\mathbf{\mu }}22}}}} $ соответственно). Как видно из рис. 2 и 3, при уровне шума 14 дБ корректно соотнести измерения ${{z}_{1}}$ и ${{z}_{2}}$ с номерами целей невозможно и алгоритм деградирует.

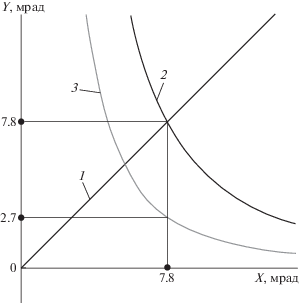
Выясним, при какой минимальной разнице в угловом положении целей при заданном уровне шума в 20 дБ алгоритм будет корректно функционировать. Ограничимся вероятностью ошибки 0.95 ($F(P) = 2$). Кривой 2 на рис. 4 представлен график изменения функции, стоящей в правой части (14) в зависимости от ${{{\theta }}_{1}} - {{{\theta }}_{2}}$. Кривая 1 изображает разность ${{\theta }_{1}} - {{\theta }_{2}}.$ Точка пересечения этих графиков определяет разрешающую способность алгоритма – это угол 7.8 мрад. Кривой 3 изображен СКО определения углов цели и антипода. При минимальном угле разрешения 7.8 мрад СКО измерения углов целей составляет 2.7 мрад.

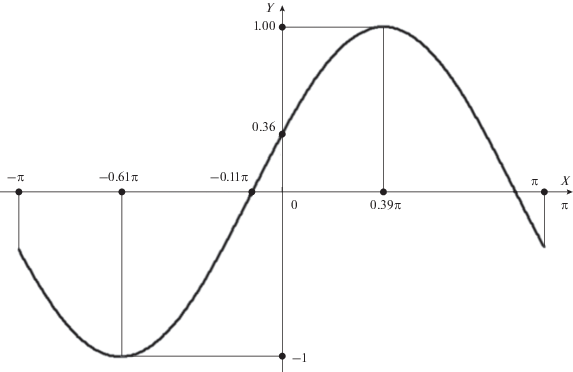
На рис. 5 представлена зависимость коэффициента корреляции ошибок измерения углов целей от разности фаз сигналов. Как следует из рисунка, коэффициент корреляции может иметь произвольное значение от –1 до 1. Поскольку разность фаз принимаемых от целей сигналов заранее не известна и может быть произвольной (в зависимости от условий переотражения и распространения электромагнитной волны), то можно предположить худший вариант, дающий наихудший угол разрешения, который будет при коэффициенте корреляции равном –1. Тогда формула для угла разрешения примет вид

ЗАКЛЮЧЕНИЕ

Рассмотрен метод получения угловых координат двух близко расположенных целей по измерениям четырех независимых одинаковых эквидистантных диаграмм направленности (суммарных). Эти диаграммы могут быть сформированы практически в любой линейной эквидистантной цифровой фазированной антенной решетке или могут быть диаграммами четырех соответствующих зеркальных антенн. Метод сводится к решению некоторого квадратного уравнения с комплексными коэффициентами. Углы целей выражаются аналитически через решения этого уравнения. Применение метода не предполагает дополнительного привлечения вычислительных ресурсов. Обоснованы формулы расчета точности угловых измерений, учитывающие внутренние шумы приемников. Сформулирован критерий углового разрешения двух целей. Показано, что точность измерения угловой координаты одной из целей зависит исключительно от отношения сигнал/шум для этой цели и не зависит от отношения сигнал/шум другой цели.

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. Из первых трех уравнений системы (4) следует, что ${{z}_{1}},$ ${{z}_{2}}$ симметричны относительно дробно-линейного преобразования [10 ] :

т.е. ${{z}_{1}} = \varsigma ({{z}_{2}}),$ ${{z}_{2}} = \varsigma ({{z}_{1}}).$ Аналогично, из последних трех уравнений (4) следует, что ${{z}_{1}},$ ${{z}_{2}}$ симметричны относительно дробно-линейного преобразования:

Поэтому точки ${{z}_{1}},$ ${{z}_{2}}$ являются неподвижными точками дробно-линейного преобразования $\rho = \omega (\varsigma (z)),$ которое, как нетрудно убедиться, приведено в (5), а уравнение (6) получается из условия $z = \rho (z)$ путем элементарных преобразований.

Доказательство утверждения 2. Прежде всего установим следующий факт. Пусть задано комплексное число $z = {{z}_{x}} + i{{z}_{y}}.$ Рассмотрим функцию $\mu (z) = \arg z.$ Зададим малое приращение $\varepsilon = {{\varepsilon }_{x}} + i{{\varepsilon }_{y}}$ числу z, ${{z}_{1}} = z + \varepsilon ,$ $\left| \varepsilon \right| \ll \left| z \right|.$ Тогда для приращения аргумента справедливо:

Рассмотрим функции ${{z}_{1}}({\mathbf{S}}{\text{*}})$ и ${{z}_{2}}({\mathbf{S}}*),$ неявно заданные системой уравнений (4) в малой окрестности решения. Дадим малое приращение по переменной $S_{j}^{*}.$ Пусть $\tilde {S}_{j}^{*} = S_{j}^{*} + {{\xi }_{j}}.$ Обозначим элементы матрицы ${\mathbf{H}}$ с номерами $(2,j)$ и $(4,j)$ через ${{a}_{j}}$ и ${{b}_{j}}\,:$

Тогда в соответствии с формулой (П.1) для приращений аргументов функций ${{z}_{1}}({\mathbf{S}}*)$ и ${{z}_{2}}({\mathbf{S}}*)$ очевидно выполнено:

Откуда следует справедливость формул (10), (11).