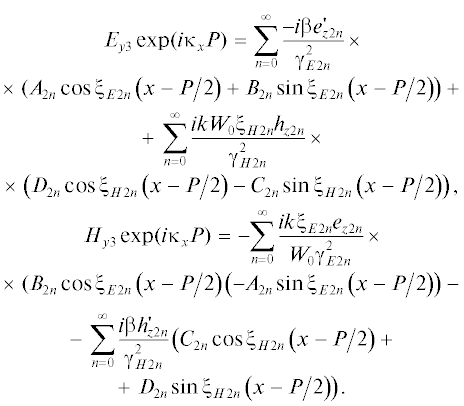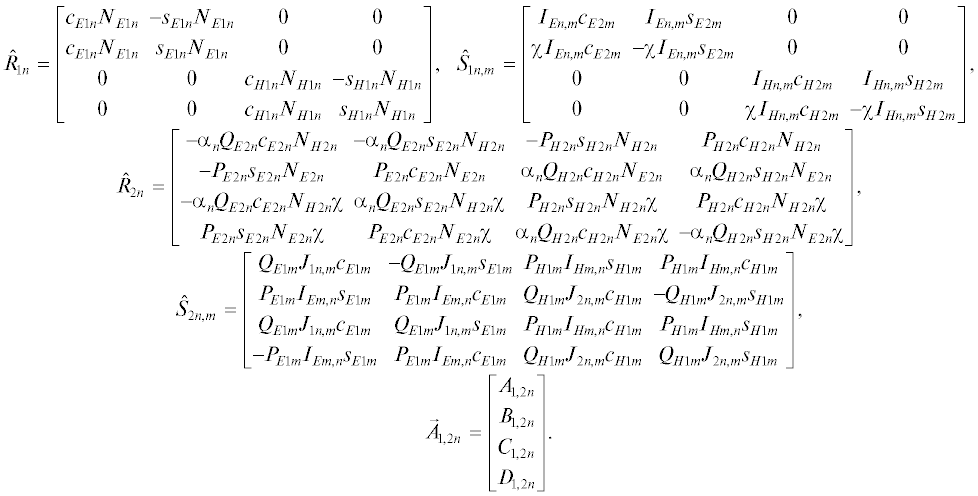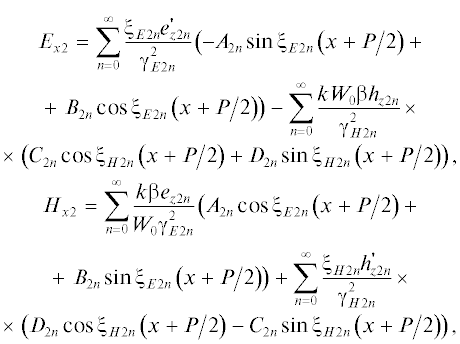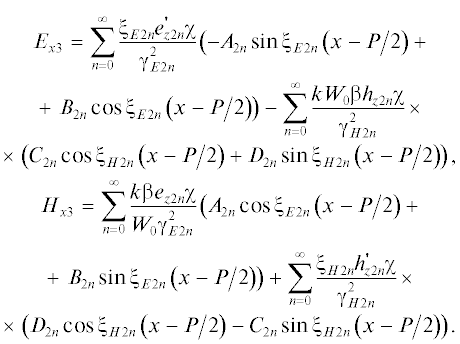1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 64, № 5, 2019

Радиотехника и электроника, 2019, T. 64, № 5, стр. 421-431

Собственные волны одномерной решетки прямоугольных диэлектрических стержней

С. Е. Банков *

Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

* E-mail: sbankov@yandex.ru

Поступила в редакцию 14.05.2018
После доработки 14.05.2018
Принята к публикации 20.06.2018

Полный текст (PDF)

Аннотация

Рассмотрена задача о собственных волнах бесконечной периодической решетки прямоугольных диэлектрических стержней, расположенных в плоском волноводе. Граничная задача решена методом частичных областей, получено дисперсионное уравнение относительно постоянной распространения собственной волны. Найдены поля собственных волн. Получено выражение для характеристического сопротивления основной волны. Представлены результаты численного исследования поведения коэффициента замедления и характеристического сопротивления основной волны решетки.

1. ПОСТАНОВКА ЗАДАЧИ

Актуальной научно-технической задачей является создание сверхширокополосных (СШП) и сверхдиапазонных (СД) антенных решеток (АР) [1, 2]. В ряде работ [3, 4], посвященных исследованию СШП АР, отмечаются факторы, препятствующие переходу от СШП АР к СД-решеткам. К ним относятся наличие в конструкции СШП излучателя частотно-зависимых элементов, таких, например, как переход от полосковой линии передачи (ЛП) к щелевой в антенне Вивальди [5].

Попытку применения в качестве элементов СШП АР антенн с выходами на двухпроводных и полосковых ЛП нельзя назвать полностью успешной, поскольку существует эффект аномального обратного излучения [6] или связанные с ним аномалии в поведении входного сопротивления АР [7].

В работе [8] была предложена так называемая двухсекционная (ДС) решетка, в которой влияние отмеченных выше негативных эффектов существенно ослаблено, что открыло возможность для создания СД АР. Идея построения ДС АР основана на результатах исследования собственных волн решеток двухпроводных, в том числе полосковых ЛП [8, 9]. В этих работах показано, что синфазная решетка эквивалентна трехпроводной ЛП, в которой существуют две основные волны, близкие по своим свойствам к T-волнам. В случае однородного диэлектрического заполнения они являются T-волнами.

Эффективное излучение из такой трехпроводной ЛП затруднительно. Поэтому необходимо предварительно преобразовать ее в двухпроводную ЛП, волна которой может быть плавно трансформирована в волну свободного пространства. Такой двухпроводной ЛП может быть щелевая линия, как в антенне Вивальди, или плоский рупор, рассмотренный в работе [8]. Независимо от вида двухпроводной ЛП, как показано в [8], переход к ней от трехпроводной ЛП сопровождается потерями мощности, обусловленными возбуждением паразитной волны трехпроводной линии. В зависимости от конструкции излучателя данный эффект приводит либо к излучению в нежелательном направлении, либо к резонансным явлениям, эквивалентным ослеплению решетки.

Способом уменьшения указанных эффектов является понижение характеристического сопротивления рабочих волн в месте сочленения ЛП. Причем потери преобразования в паразитную волну тем меньше, чем меньше сопротивление рабочих волн трех- и двухпроводной ЛП. Для понижения сопротивления ЛП в сверхширокой полосе частот в конструкции ДС АР используется плавный переход от ЛП со стандартным сопротивлением ${{Z}_{1}} = 50$ Ом на входе структуры к ЛП с пониженным сопротивлением ${{Z}_{2}}$ в месте сочленения. Далее в двухпроводной ЛП осуществляется переход от сопротивления ${{Z}_{2}}$ к сопротивлению канала Флоке с воздушным заполнением ${{Z}_{3}},$ которое в АР с одинаковыми по разным координатам периодами равно волновому сопротивлению свободного пространства ${{W}_{0}}.$

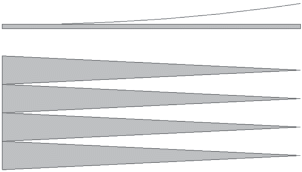
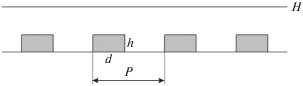
Понижение сопротивления ${{Z}_{2}}$ может быть достигнуто применением ЛП с диэлектрическим заполнением, например, широко распространенной микрополосковой линии (МПЛ). В этом случае роль двухпроводной ЛП играет плоский рупор с частичным или полным диэлектрическим заполнением. Для эффективного излучения в свободное пространство необходимо использовать дополнительный переход к рупору без диэлектрического заполнения. Такой переход можно осуществить разными способами. Технологически наиболее удобно применение диэлектрических клиньев (рис. 1), которые получаются путем фрезерования подложки МПЛ. В каждом сечении решетка из клиньев представляет собой решетку диэлектрических стержней прямоугольной формы (рис. 2). Анализ собственных волн решетки является ключевой задачей для анализа структуры в целом.

Рис. 1.

Решетка диэлектрических клиньев.

Рис. 2.

Решетка прямоугольных диэлектрических стержней.

Данная работа посвящена решению указанной ключевой задачи. Следует отметить, что решетки диэлектрических волноводов (ДВ) разного поперечного сечения вызывали интерес исследователей достаточно давно. Поэтому задача анализа собственных волн решетки прямоугольных диэлектрических стержней не является новой. Она рассматривалась в [10, 11]. В работе [10] анализируется решетка прямоугольных стержней частного вида, так называемая решетка H-образных ДВ. В работе [11] решена более сложная задача – о собственных волнах двумерной решетки круглых ДВ. Отметим также работы [12, 13], в которых анализируется излучение из решеток круглых ДВ.

При решении поставленной выше задачи мы будем использовать метод частичных областей (МЧО), который успешно применялся в [10–13]. Он основан на представлении поля в частичных областях в виде разложений по собственным функциям и их сшиванию на границах частичных областей, которое приводит к системам линейных алгебраических уравнений (СЛАУ) относительно коэффициентов указанных разложений.

2. ФОРМУЛИРОВКА ГРАНИЧНОЙ ЗАДАЧИ

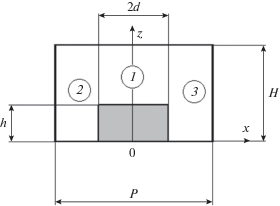
Рассмотрим период исследуемой структуры (рис. 3). Мы анализируем ее в квазипериодическом режиме, в котором поле $\vec {E}$ в разных периодах связано соотношением

(1)
$\vec {E}(x + nP) = \vec {E}(x)\exp ( - i{{\kappa }_{x}}nP),$
где $n$ – целое число, ${{\kappa }_{x}}$ – параметр периодического режима.

Рис. 3.

Период решетки диэлектрических стержней.

Благодаря соотношению (1) анализ бесконечной по оси $0x$ решетки сводится к анализу периода, который часто называют каналом Флоке [14]. При этом на ее границах при $x = {{ \pm P} \mathord{\left/ {\vphantom {{ \pm P} 2}} \right. \kern-0em} 2}$ выполняются условия периодичности:

$\vec {E}({P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}) = \vec {E}({{ - P} \mathord{\left/ {\vphantom {{ - P} 2}} \right. \kern-0em} 2})\exp ( - i{{\kappa }_{x}}nP).$

На горизонтальных металлических стенках, расположенных при $z = 0,H,$ должны выполняться условия равенства нулю тангенциальных компонент электрического поля.

Разделим период решетки на три области 1–3, как показано на рис. 3. Каждая из них представляет собой плоский волновод (ПВ) с частичным диэлектрическим заполнением (область 1) или без него. Собственные волны ПВ разделяются на E- и H-волны, у которых равны нулю соответственно компоненты ${{H}_{z}}$ и ${{E}_{z}}.$ Волны ПВ с однородным заполнением хорошо известны [15]:

(2)
${{e}_{{zn}}} = \cos {{\alpha }_{n}}z,\,\,\,\,{{h}_{{zn}}} = \sin {{\alpha }_{n}}z,$
где ${{\alpha }_{n}} = \frac{{\pi n}}{H},$ $n = 0,1,....$

Функции ${{e}_{{zn}}}$ описывают ${{E}_{z}}$-ю компоненту $E$‑волн, а функции ${{h}_{{zn}}}$ описывают ${{H}_{z}}$-ю компоненту H-волн. Волны ПВ классифицируются в соответствии с номером $n$ как En- и ${{H}_{n}}$-волны.

Соотношения (2) определяют зависимость поля волны только от координаты z. Зависимость от координат $x,y$ в общем случае не определяется. Поскольку нас интересуют собственные волны, распространяющиеся вдоль оси $0y,$ то будем искать поле с зависимостью от этой координаты в виде экспоненты $\exp ( - i\beta y),$ где β – искомая постоянная распространения волны решетки.

В этом случае зависимость поля собственной волны от координаты x имеет следующий вид:

(3)
${{f}_{n}}(x) = {{A}_{n}}\cos {{\xi }_{n}}x + {{B}_{n}}\sin {{\xi }_{n}}x,$
$\begin{gathered} {{\xi }_{n}} = \sqrt {\gamma _{n}^{2} - {{\beta }^{2}}} , \\ {{\gamma }_{n}} = \sqrt {{{k}^{2}} - \alpha _{n}^{2}} , \\ \end{gathered} $
где ${{A}_{n}},{{B}_{n}}$ – произвольные постоянные, ${{\gamma }_{n}}$ – постоянные распространения собственных волн ПВ, $k$ – волновое число свободного пространства.

Структура поля волн ПВ с диэлектриком сложнее:

(4)
$\begin{gathered} {{e}_{{zn}}} = \left\{ \begin{gathered} \cos {{q}_{n}}z,\,\,\,\,{\text{ }}z < h, \hfill \\ \frac{{\varepsilon \cos {{q}_{n}}h}}{{\operatorname{ch} {{p}_{n}}a}}\operatorname{ch} {{p}_{n}}(H - z),\,\,\,\,z > h, \hfill \\ \end{gathered} \right.{\text{ }} \\ {{h}_{{zn}}} = \left\{ \begin{gathered} \sin {{q}_{n}}z,\,\,\,\,z < h, \hfill \\ \frac{{\sin {{q}_{n}}h}}{{\operatorname{sh} {{p}_{n}}a}}\operatorname{sh} {{p}_{n}}(H - z),\,\,\,z > h, \hfill \\ \end{gathered} \right.{\text{ }} \\ \end{gathered} $
${{p}_{n}} = \sqrt {\gamma _{n}^{2} - {{k}^{2}}} ,\,\,\,\,{{q}_{n}} = \sqrt {\varepsilon {{k}^{2}} - \gamma _{n}^{2}} ,\,\,\,a = H - h.$
Здесь ε – относительная проницаемость диэлектрика, ${{\gamma }_{n}}$ имеют тот же смысл постоянных распространения собственных волн. Они определяются решением соответствующих дисперсионных уравнений:

(5)
$\varepsilon {{p}_{n}}\cos {{q}_{n}}h\operatorname{sh} {{p}_{n}}a - {{q}_{n}}\sin {{q}_{n}}h\operatorname{ch} {{p}_{n}}a = 0,$
(6)
${{p}_{n}}\sin {{q}_{n}}h\operatorname{ch} {{p}_{n}}a + {{q}_{n}}\cos {{q}_{n}}h\operatorname{sh} {{p}_{n}}a = 0.$

Соотношения (5) и (6) описывают $E$- и H-волны соответственно. Зависимость поля собственных волн ПВ с диэлектриком описывается функциями, аналогичными (3).

Отметим, что поля собственных волн удовлетворяют условиям ортогональности:

(7)
$\begin{gathered} \int\limits_0^H {{{e}_{{zn}}}{{e}_{{zm}}}\varepsilon (z)dz} = {{\delta }_{{n,m}}}{{N}_{{En}}},\,\,\,\,\int\limits_0^H {{{h}_{{zn}}}{{h}_{{zm}}}dz} = {{\delta }_{{n,m}}}{{N}_{{Hn}}}, \\ \int\limits_0^H {\frac{{{{h}_{{zn}}}e_{{zm}}^{'}}}{{\gamma _{{em}}^{2}}} + \frac{{{{e}_{{zm}}}h_{{zn}}^{'}}}{{\gamma _{{hn}}^{2}}}dz} = 0. \\ \end{gathered} $
Здесь величина со штрихом обозначает производную по координате z, а параметры ${{N}_{{E,Hn}}}$ имеют смысл норм $E$- и H-волн, ${{\delta }_{{n,m}}}$ – символ Кронекера.

Оставшиеся компоненты электромагнитного поля выражаются через ${{E}_{z}}$ и ${{H}_{z}}$ при помощи известных соотношений [16]. Запишем поле в области 1:

(8)
$\begin{gathered} {{E}_{{z1}}} = \sum\limits_{n = 0}^\infty {{{e}_{{z1n}}}\left( {{{A}_{{1n}}}\cos {{\xi }_{{E1n}}}x + {{B}_{{1n}}}\sin {{\xi }_{{E1n}}}x} \right)} , \\ {{H}_{{z1}}} = \sum\limits_{n = 0}^\infty {{{h}_{{z1n}}}\left( {{{C}_{{1n}}}\cos {{\xi }_{{H1n}}}x + {{D}_{{1n}}}\sin {{\xi }_{{H1n}}}x} \right)} , \\ \end{gathered} $
где индекс 1 показывает, что данная величина относится к области 1, а индексы $E,H$ указывают на принадлежность к E- и H-волнам, ${{A}_{{1n}}},{{B}_{{1n}}},{{C}_{{1n}}},{{D}_{{1n}}}$ – неизвестные коэффициенты. Общий для всех полей множитель $\exp ( - i\beta y)$ мы опустили.

Поле в области 2:

(9)
$\begin{gathered} {{E}_{{z2}}} = \sum\limits_{n = 0}^\infty {{{e}_{{z2n}}}({{A}_{{2n}}}\cos {{\xi }_{{E2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} + \\ \left. { + \,\,{{B}_{{2n}}}\sin {{\xi }_{{E2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right), \\ {{H}_{{z2}}} = \sum\limits_{n = 0}^\infty {{{h}_{{z2n}}}({{C}_{{2n}}}\cos {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} + \\ \left. { + \,\,{{D}_{{2n}}}\sin {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right). \\ \end{gathered} $

Поле в области 3 записываем с учетом условий (2):

(10)
$\begin{gathered} {{E}_{{z3}}} = \sum\limits_{n = 0}^\infty {{{e}_{{z2n}}}\left( {{{A}_{{2n}}}\cos {{\xi }_{{E1n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right.} + \\ \left. { + \,\,{{B}_{{2n}}}\sin {{\xi }_{{E1n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right)\exp ( - i{{\kappa }_{x}}P), \\ {{H}_{{z3}}} = \sum\limits_{n = 0}^\infty {{{h}_{{z2n}}}\left( {{{C}_{{2n}}}\cos {{\xi }_{{H2n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right.} + \\ \left. { + \,\,{{D}_{{2n}}}\sin {{\xi }_{{H2n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right)\exp ( - i{{\kappa }_{x}}P). \\ \end{gathered} $

Далее необходимо удовлетворить граничным условиям при $x = \pm d.$ В этих плоскостях должны быть непрерывны тангенциальные компоненты электрического и магнитного полей. Поэтому мы должны найти компоненты ${{E}_{y}},{{H}_{y}}.$ Сделаем это при помощи [16]:

(11)
$\begin{gathered} {{E}_{{y1}}} = \sum\limits_{n = 0}^\infty {\frac{{ - i\beta e_{{z1n}}^{'}}}{{\gamma _{{E1n}}^{2}}}\left( {{{A}_{{1n}}}\cos {{\xi }_{{E1n}}}x + {{B}_{{1n}}}\sin {{\xi }_{{E1n}}}x} \right)} + \\ + \,\,\sum\limits_{n = 0}^\infty {\frac{{ik{{W}_{0}}{{\xi }_{{H1n}}}{{h}_{{z1n}}}}}{{\gamma _{{H1n}}^{2}}}\left( {{{D}_{{1n}}}\cos {{\xi }_{{H1n}}}x - {{C}_{{1n}}}\sin {{\xi }_{{H1n}}}x} \right)} , \\ {{H}_{{y1}}} = - \sum\limits_{n = 0}^\infty {\frac{{ik\varepsilon (z){{\xi }_{{E1n}}}{{e}_{{z1n}}}}}{{{{W}_{0}}\gamma _{{E1n}}^{2}}}} \times \\ \times \,\,\left( {{{B}_{{1n}}}\cos {{\xi }_{{E1n}}}x - {{A}_{{1n}}}\sin {{\xi }_{{E1n}}}x} \right) - \\ - \,\,\sum\limits_{n = 0}^\infty {\frac{{i\beta h_{{z1n}}^{'}}}{{\gamma _{{H1n}}^{2}}}\left( {{{C}_{{1n}}}\cos {{\xi }_{{H1n}}}x + {{D}_{{1n}}}\sin {{\xi }_{{H1n}}}x} \right)} , \\ \end{gathered} $
(12)
$\begin{gathered} {{E}_{{y2}}} = \sum\limits_{n = 0}^\infty {\frac{{ - i\beta e_{{z2n}}^{'}}}{{\gamma _{{E2n}}^{2}}}} ({{A}_{{2n}}}\cos {{\xi }_{{E2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right) + \\ + \,\,{{B}_{{2n}}}\sin {{\xi }_{{E2n}}}\left. {\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right) + \sum\limits_{n = 0}^\infty {\frac{{ik{{W}_{0}}{{\xi }_{{H2n}}}{{h}_{{z2n}}}}}{{\gamma _{{H2n}}^{2}}}} \times \\ \times \,\,\left( {{{D}_{{2n}}}\cos {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right) - {{C}_{{2n}}}\sin {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right), \\ {{H}_{{y2}}} = - \sum\limits_{n = 0}^\infty {\frac{{ik{{\xi }_{{E2n}}}{{e}_{{z2n}}}}}{{{{W}_{0}}\gamma _{{E2n}}^{2}}}} ({{B}_{{2n}}}\cos {{\xi }_{{E2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right) - \\ - \,\,\left. {{{A}_{{2n}}}\sin {{\xi }_{{E2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right) - \sum\limits_{n = 0}^\infty {\frac{{i\beta h_{{z2n}}^{'}}}{{\gamma _{{H2n}}^{2}}}} \times \\ \times \,\,\left( {{{C}_{{2n}}}\cos {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right) + {{D}_{{2n}}}\sin {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right), \\ \end{gathered} $
(13)

Приравниваем следующие компоненты электромагнитного поля при $x = \pm d$:

Ez при x = –d

(14)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{e}_{{z1n}}}\left( {{{A}_{{1n}}}{{c}_{{E1n}}} - {{B}_{{1n}}}{{s}_{{E1n}}}} \right)} = \\ = \sum\limits_{n = 0}^\infty {{{e}_{{z2n}}}\left( {{{A}_{{2n}}}{{c}_{{E2n}}} + {{B}_{{2n}}}{{s}_{{E2n}}}} \right)} , \\ \end{gathered} $

Hz при x = –d –

(15)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{h}_{{z1n}}}\left( {{{C}_{{1n}}}{{c}_{{H1n}}} - {{D}_{{1n}}}{{s}_{{H1n}}}} \right)} = \\ = \sum\limits_{n = 0}^\infty {{{h}_{{z2n}}}\left( {{{C}_{{2n}}}{{c}_{{H2n}}} + {{D}_{{2n}}}{{s}_{{H2n}}}} \right)} , \\ \end{gathered} $

Ez при x = d –

(16)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{e}_{{z1n}}}\left( {{{A}_{{1n}}}{{c}_{{E1n}}} + {{B}_{{1n}}}{{s}_{{E1n}}}} \right)} = \\ = \chi \sum\limits_{n = 0}^\infty {{{e}_{{z2n}}}\left( {{{A}_{{2n}}}{{c}_{{E1n}}}} \right.} \left. { - {{B}_{{2n}}}{{s}_{{E1n}}}} \right), \\ \end{gathered} $

Hz при x = d –

(17)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{h}_{{z1n}}}\left( {{{C}_{{1n}}}{{c}_{{H1n}}} + {{D}_{{1n}}}{{s}_{{H1n}}}} \right)} = \\ = \chi \sum\limits_{n = 0}^\infty {{{h}_{{z2n}}}\left( {{{C}_{{2n}}}{{c}_{{H2n}}}} \right.} - \left. {{{D}_{{2n}}}{{s}_{{H2n}}}} \right), \\ \end{gathered} $

Ey при x = –d –

(18)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{Q}_{{E1n}}}e_{{z1n}}^{'}\left( {{{A}_{{1n}}}{{c}_{{E1n}}} - {{B}_{{1n}}}{{s}_{{E1n}}}} \right)} + \\ + \,\,{{P}_{{H1n}}}{{h}_{{z1n}}}\left( {{{D}_{{1n}}}{{c}_{{H1n}}} + {{C}_{{1n}}}{{s}_{{H1n}}}} \right) = \\ = \sum\limits_{n = 0}^\infty {{{Q}_{{E2n}}}e_{{z2n}}^{'}\left( {{{A}_{{2n}}}{{c}_{{E2n}}} + {{B}_{{2n}}}{{s}_{{E2n}}}} \right)} + \\ + \,\,{{P}_{{H2n}}}{{h}_{{z2n}}}\left( {{{D}_{{2n}}}{{c}_{{H2n}}} - {{C}_{{2n}}}{{s}_{{H2n}}}} \right), \\ \end{gathered} $

Hy при x = –d –

(19)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{P}_{{E1n}}}\varepsilon (z){{e}_{{z1n}}}\left( {{{B}_{{1n}}}{{c}_{{E1n}}} + {{A}_{{1n}}}{{s}_{{E1n}}}} \right)} + \\ + \,\,{{Q}_{{H1n}}}h_{{z1n}}^{'}\left( {{{C}_{{1n}}}{{c}_{{H1n}}} - {{D}_{{1n}}}{{s}_{{H1n}}}} \right) = \\ = \sum\limits_{n = 0}^\infty {{{P}_{{E2n}}}{{e}_{{z2n}}}\left( {{{B}_{{2n}}}{{c}_{{E2n}}} - {{A}_{{2n}}}{{s}_{{E2n}}}} \right)} + \\ + \,\,\,{{Q}_{{H2n}}}h_{{z2n}}^{'}\left( {{{C}_{{2n}}}{{c}_{{H2n}}} + {{D}_{{2n}}}{{s}_{{H2n}}}} \right), \\ \end{gathered} $

Ey при x = d –

(20)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{Q}_{{E1n}}}e_{{z1n}}^{'}\left( {{{A}_{{1n}}}{{c}_{{E1n}}} + {{B}_{{1n}}}{{s}_{{E1n}}}} \right)} + \\ + \,\,{{P}_{{H1n}}}{{h}_{{z1n}}}\left( {{{D}_{{1n}}}{{c}_{{H1n}}} - {{C}_{{1n}}}{{s}_{{H1n}}}} \right) = \\ = \left( {\sum\limits_{n = 0}^\infty {{{Q}_{{E2n}}}e_{{z2n}}^{'}\left( {{{A}_{{2n}}}{{c}_{{E2n}}} - {{B}_{{2n}}}{{s}_{{E2n}}}} \right)} } \right. + \\ \left. {\frac{{}}{{}} + \,\,{{P}_{{H2n}}}{{h}_{{z2n}}}\left( {{{D}_{{2n}}}{{c}_{{H2n}}} + {{C}_{{2n}}}{{s}_{{H2n}}}} \right)} \right)\chi , \\ \end{gathered} $

Hy при x = d –

(21)
$\begin{gathered} \sum\limits_{n = 0}^\infty {{{P}_{{E1n}}}\varepsilon (z){{e}_{{z1n}}}\left( {{{B}_{{1n}}}{{c}_{{E1n}}} - {{A}_{{1n}}}{{s}_{{E1n}}}} \right)} + \\ + \,\,{{Q}_{{H1n}}}h_{{z1n}}^{'}\left( {{{C}_{{1n}}}{{c}_{{H1n}}} + {{D}_{{1n}}}{{s}_{{H1n}}}} \right) = \\ = \left( {\sum\limits_{n = 0}^\infty {{{P}_{{E2n}}}{{e}_{{z2n}}}\left( {{{B}_{{2n}}}{{c}_{{E2n}}} + {{A}_{{2n}}}{{s}_{{E2n}}}} \right)} } \right. + \\ \left. {\frac{{}}{{}} + \,\,{{Q}_{{H2n}}}h_{{z2n}}^{'}\left( {{{C}_{{2n}}}{{c}_{{H2n}}} - {{D}_{{2n}}}{{s}_{{H2n}}}} \right)} \right)\chi . \\ \end{gathered} $

При записи формул (14)–(21) были использованы следующие обозначения:

(22)
$\begin{gathered} {{Q}_{{E,H,1,1n}}} = \frac{{ - i\beta }}{{\gamma _{{E,H,1,2n}}^{2}}}, \\ {{P}_{{E,H,1,2n}}} = \frac{{ik{{\xi }_{{E,H,1,2n}}}}}{{\gamma _{{E,H,1,2n}}^{2}}}\left\{ \begin{gathered} {{W}_{0}}, \hfill \\ - \frac{1}{{{{W}_{0}}}}, \hfill \\ \end{gathered} \right. \\ \chi = \exp ( - i{{\kappa }_{x}}P), \\ {{c}_{{E,H1n}}} = \cos {{\xi }_{{E,H1n}}}d,\,\,\,\,{{s}_{{E,H1n}}} = \sin {{\xi }_{{E,H1n}}}d, \\ {{c}_{{E,H2n}}} = \cos {{\xi }_{{E,H2n}}}b,\,\,\,\,{{s}_{{E,H2n}}} = \sin {{\xi }_{{E,H2n}}}b. \\ \end{gathered} $

Следующий этап преобразований – алгебраизация соотношений (14)–(21), выражающих граничные условия непрерывности тангенциальных компонент поля, путем устранения в них зависимости от координаты z. Для этого применим соотношения ортогональности (7). На первом этапе воспользуемся равенствами (14)–(17). Умножим выражения (14), (16) на ${{e}_{{z1n}}}\varepsilon (z)$ и проинтегрируем по z в пределах от нуля до H. Выражения (15), (17) умножим на ${{h}_{{z1n}}}$ и также проинтегрируем по z. С учетом ортогональности собственных волн в области 1 получаем

(23)
$\begin{gathered} \left( {{{A}_{{1n}}}{{c}_{{E1n}}} - {{B}_{{1n}}}{{s}_{{E1n}}}} \right){{N}_{{E1n}}} = \\ = \sum\limits_{m = 0}^\infty {{{I}_{{En,m}}}\left( {{{A}_{{2m}}}{{c}_{{E2m}}} + {{B}_{{2m}}}{{s}_{{E2m}}}} \right)} , \\ \left( {{{A}_{{1n}}}{{c}_{{E1n}}} + {{B}_{{1n}}}{{s}_{{E1n}}}} \right){{N}_{{E1n}}} = \\ = \chi \sum\limits_{m = 0}^\infty {{{I}_{{En,m}}}\left( {{{A}_{{2m}}}{{c}_{{E1m}}}} \right.} \left. { - {{B}_{{2n}}}{{s}_{{E1m}}}} \right), \\ \left( {{{C}_{{1n}}}{{c}_{{H1n}}} - {{D}_{{1n}}}{{s}_{{H1n}}}} \right){{N}_{{H1n}}} = \\ = \sum\limits_{m = 0}^\infty {{{I}_{{Hn,m}}}\left( {{{C}_{{2m}}}{{c}_{{H2m}}} + {{D}_{{2m}}}{{s}_{{H2m}}}} \right)} , \\ \left( {{{C}_{{1n}}}{{c}_{{H1n}}} + {{D}_{{1n}}}{{s}_{{H1n}}}} \right){{N}_{{H1n}}} = \\ = \chi \sum\limits_{m = 0}^\infty {{{I}_{{Hn,m}}}\left( {{{C}_{{2m}}}{{c}_{{H2m}}}} \right.} - \left. {{{D}_{{2m}}}{{s}_{{H2m}}}} \right), \\ \end{gathered} $
(24)
${{I}_{{En,m}}} = \int\limits_0^H {\varepsilon (z){{e}_{{z1n}}}{{e}_{{z2n}}}dz} ,\,\,\,\,{{I}_{{Hn,m}}} = \int\limits_0^H {{{h}_{{z1n}}}{{h}_{{z2n}}}dz} .$

Далее рассмотрим равенства (18)–(21). Умножим их на функции ${{e}_{{z2n}}},$ ${{h}_{{z2n}}}$ и, воспользовавшись ортогональностью, получим

$\begin{gathered} \sum\limits_{m = 0}^\infty {{{Q}_{{E1m}}}{{J}_{{1n,m}}}\left( {{{A}_{{1m}}}{{c}_{{E1m}}} - {{B}_{{1m}}}{{s}_{{E1m}}}} \right)} + \,{{P}_{{H1m}}}{{I}_{{Hm,n}}}\left( {{{D}_{{1m}}}{{c}_{{H1m}}} + {{C}_{{1m}}}{{s}_{{H1m}}}} \right) = \\ = \left( { - {{\alpha }_{n}}{{Q}_{{E2n}}}\left( {{{A}_{{2n}}}{{c}_{{E2n}}} + {{B}_{{2n}}}{{s}_{{E2n}}}} \right)} \right. + \,\left. {{{P}_{{H2n}}}\left( {{{D}_{{2n}}}{{c}_{{H2n}}} - {{C}_{{2n}}}{{s}_{{H2n}}}} \right)} \right){{N}_{{h2n}}}, \\ \end{gathered} $
(25)
$\begin{gathered} \sum\limits_{m = 0}^\infty {{{P}_{{E1m}}}{{I}_{{Em,n}}}\left( {{{B}_{{1m}}}{{c}_{{E1m}}} + {{A}_{{1m}}}{{s}_{{E1m}}}} \right)} + \,{{Q}_{{H1m}}}{{J}_{{2n,m}}}\left( {{{C}_{{1m}}}{{c}_{{H1m}}} - {{D}_{{1m}}}{{s}_{{H1m}}}} \right) = \\ = \left( {{{P}_{{E2n}}}\left( {{{B}_{{2n}}}{{c}_{{E2n}}} - {{A}_{{2n}}}{{s}_{{E2n}}}} \right)} \right. + \left. {{{Q}_{{H2n}}}{{\alpha }_{n}}\left( {{{C}_{{2n}}}{{c}_{{H2n}}} + {{D}_{{2n}}}{{s}_{{H2n}}}} \right)} \right){{N}_{{E2n}}}, \\ \sum\limits_{m = 0}^\infty {{{Q}_{{E1m}}}{{J}_{{1n,m}}}\left( {{{A}_{{1m}}}{{c}_{{E1m}}} + {{B}_{{1m}}}{{s}_{{E1m}}}} \right)} + \,{{P}_{{H1m}}}{{I}_{{hm,n}}}\left( {{{D}_{{1m}}}{{c}_{{H1m}}} - {{C}_{{1m}}}{{s}_{{H1m}}}} \right) = \\ = \left( { - {{Q}_{{E2n}}}{{\alpha }_{n}}\left( {{{A}_{{2n}}}{{c}_{{E2n}}} - {{B}_{{2n}}}{{s}_{{E2n}}}} \right)} \right. + \left. {\,{{P}_{{H2n}}}\left( {{{D}_{{2n}}}{{c}_{{H2n}}} + {{C}_{{2n}}}{{s}_{{H2n}}}} \right)} \right)\chi {{N}_{{H2n}}}, \\ \end{gathered} $
$\begin{gathered} \sum\limits_{m = 0}^\infty {{{P}_{{E1m}}}{{I}_{{Em,n}}}\left( {{{B}_{{1m}}}{{c}_{{E1m}}} - {{A}_{{1m}}}{{s}_{{E1m}}}} \right)} + \,\,{{Q}_{{H1m}}}{{J}_{{2n,m}}}\left( {{{C}_{{1m}}}{{c}_{{H1m}}} + {{D}_{{1m}}}{{s}_{{H1m}}}} \right) = \\ = \left( {{{P}_{{E2n}}}\left( {{{B}_{{2n}}}{{c}_{{E2n}}} + {{A}_{{2n}}}{{s}_{{E2n}}}} \right)} \right. + \left. {{{Q}_{{H2n}}}{{\alpha }_{n}}\left( {{{C}_{{2n}}}{{c}_{{H2n}}} - {{D}_{{2n}}}{{s}_{{H2n}}}} \right)} \right)\chi {{N}_{{E2n}}}, \\ \end{gathered} $
(26)
${{J}_{{1n,m}}} = \int\limits_0^H {{{h}_{{z2n}}}e_{{z1m}}^{'}dz} ,\,\,\,\,{{J}_{{2n,m}}} = \int\limits_0^H {{{e}_{{z2n}}}h_{{z1m}}^{'}dz} .$

Запишем полученные соотношения в компактной матричной форме:

(27)
${{\hat {R}}_{{1n}}}{{\vec {A}}_{{1n}}} = \sum\limits_{m = 0}^\infty {{{{\hat {S}}}_{{1n,m}}}{{{\vec {A}}}_{{2m}}}} ,\,\,\,\,{{\hat {R}}_{{2n}}}{{\vec {A}}_{{2n}}} = \sum\limits_{m = 0}^\infty {{{{\hat {S}}}_{{2n,m}}}{{{\vec {A}}}_{{1m}}}} ,$
(28)

Подставим второе соотношение из (27) в первое и получим искомую СЛАУ:

(29)
$\sum\limits_{p = 0}^\infty {{{{\hat {Z}}}_{{n,p}}}{{{\vec {A}}}_{{1p}}}} = 0,$

${{\hat {Z}}_{{n,p}}} = {{\hat {R}}_{{1n}}}{{\delta }_{{n,p}}} - \sum\limits_{m = 0}^\infty {{{{\hat {S}}}_{{1n,m}}}\hat {R}_{{2m}}^{{ - 1}}{{{\hat {S}}}_{{2m,p}}}} .$
Выражение (29) представляет собой однородную СЛАУ относительно коэффициентов разложений поля в области 1. Она имеет нетривиальные решения при условии равенства нулю ее определителя:

(30)
$\det \hat {Z} = 0.$

Соотношение (30) является дисперсионным уравнением относительно неизвестной постоянной распространения собственной волны решетки $\beta $. После решения дисперсионного уравнения и определения постоянной распространения мы можем с точностью до произвольного множителя найти коэффициенты разложений ${{\vec {A}}_{{1,2n}}},$ используя стандартные правила линейной алгебры.

3. ПОЛЯ СОБСТВЕННЫХ ВОЛН

Уравнение (30) имеет бесконечное множество решений ${{\beta }_{n}},$ соответствующих собственным волнам анализируемой структуры. Конечное их число является распространяющимися волнами с действительными ${{\beta }_{n}}.$ Нераспространяющиеся волны имеют мнимые постоянные распространения. Выделим основную волну решетки и присвоим ей индекс 1. Наибольший практический интерес представляет одноволновый режим, в котором существует одна основная распространяющаяся волна.

Для дальнейших исследований нам потребуются выражения для поперечных компонент электромагнитного поля. К ним относятся z-е и x-е компоненты. Компоненты ${{E}_{z}},{{H}_{z}}$ описаны соотношениями (8)–(10). Запишем компоненты ${{E}_{x}},{{H}_{x}}\,:$

(31)
$\begin{gathered} {{E}_{{x1}}} = \sum\limits_{n = 0}^\infty {\frac{{{{\xi }_{{E1n}}}e_{{z1n}}^{'}}}{{\gamma _{{E1n}}^{2}}}\left( { - {{A}_{{1n}}}\sin {{\xi }_{{E1n}}}x + {{B}_{{1n}}}\cos {{\xi }_{{E1n}}}x} \right)} - \\ - \,\,\sum\limits_{n = 0}^\infty {\frac{{k{{W}_{0}}\beta {{h}_{{z1n}}}}}{{\gamma _{{H1n}}^{2}}}\left( {{{C}_{{1n}}}\cos {{\xi }_{{H1n}}}x + {{D}_{{1n}}}\sin {{\xi }_{{H1n}}}x} \right)} , \\ {{H}_{{x1}}} = \sum\limits_{n = 0}^\infty {\frac{{k\varepsilon (z)\beta {{e}_{{z1n}}}}}{{{{W}_{0}}\gamma _{{E1n}}^{2}}}\left( {{{A}_{{1n}}}\cos {{\xi }_{{E1n}}}x + {{B}_{{1n}}}\sin {{\xi }_{{E1n}}}x} \right)} + \\ + \,\,\sum\limits_{n = 0}^\infty {\frac{{{{\xi }_{{H1n}}}h_{{z1n}}^{'}}}{{\gamma _{{H1n}}^{2}}}\left( {{{D}_{{1n}}}\cos {{\xi }_{{H1n}}}x - {{C}_{{1n}}}\sin {{\xi }_{{H1n}}}x} \right)} , \\ \end{gathered} $
(32)
(33)

Важным параметром основной волны является ее характеристическое сопротивление ${{Z}_{c}}.$ Однозначно оно вводится только для поперечных T‑волн, которые существуют в ЛП с однородным диэлектрическим заполнением. В нашем случае это условие нарушается. Тем не менее, как мы увидим ниже, основную волну анализируемой структуры можно отнести к числу квази-T-волн, которые похожи на поперечные волны. В частности, для них характерна слабая частотная дисперсия как коэффициента замедления $U = {\beta \mathord{\left/ {\vphantom {\beta k}} \right. \kern-0em} k},$ так и характеристического сопротивления. Поэтому выбор для их описания параметра ${{Z}_{c}}$ оправдан.

Используем определение характеристического сопротивления через напряжение V и мощность, переносимую волной ${{P}_{s}}\,:$

(34)
${{Z}_{c}} = {{{{V}^{2}}} \mathord{\left/ {\vphantom {{{{V}^{2}}} {2{{P}_{s}}}}} \right. \kern-0em} {2{{P}_{s}}}}.$

Определим напряжение через интеграл от электрического поля:

(35)
$V = \int\limits_0^H {{{E}_{z}}(z,0)dz} ,$

а мощность – через интеграл по поперечному сечению:

(36)
${{P}_{s}} = \frac{1}{2}\int\limits_S {\left( {{{E}_{z}}H_{x}^{ * } - {{E}_{x}}H_{z}^{ * }} \right)dzdx} .$

Подставим выражения для компонент поля в соотношения (35), (36) и получим:

(37)
$V = \sum\limits_{n = 0}^\infty {{{A}_{{1n}}}\int\limits_0^H {{{e}_{{z1n}}}dz} } ,$
(38)
${{P}_{s}} = {{P}_{{sE}}} + {{P}_{{sH}}},$
(39)
$\begin{gathered} {{P}_{{sE}}} = \frac{{k\beta }}{{2{{W}_{0}}}} \times \\ \times \,\,\sum\limits_{n = 0}^\infty {\left( {{{g}_{{E1n}}}\frac{{{{N}_{{E1n}}}}}{{\gamma _{{E1n}}^{2}}} + {{g}_{{E2n}}}\frac{{{{N}_{{E2n}}}}}{{\gamma _{{E2n}}^{2}}} + {{g}_{{E3n}}}\frac{{{{N}_{{E2n}}}}}{{\gamma _{{E2n}}^{2}}}} \right)} , \\ \end{gathered} $

где

$\begin{gathered} {{g}_{{E1n}}} = \int\limits_{ - d}^d {{{{\left| {{{A}_{{1n}}}\cos {{\xi }_{{E1n}}}x + {{B}_{{1n}}}\sin {{\xi }_{{E1n}}}x} \right|}}^{2}}dx} , \\ {{g}_{{E2n}}} = \int\limits_{{{ - P} \mathord{\left/ {\vphantom {{ - P} 2}} \right. \kern-0em} 2}}^{ - d} {\left| {{{A}_{{2n}}}\cos {{\xi }_{{E2n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right.} + \\ {{\left. { + \,\,{{B}_{{2n}}}\sin {{\xi }_{{E2n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right|}^{2}}dx, \\ {{g}_{{E3n}}} = \int\limits_d^{{P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} {\left| {{{A}_{{2n}}}\cos {{\xi }_{{E2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right.} + \\ {{\left. { + \,\,{{B}_{{2n}}}\sin {{\xi }_{{E2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right|}^{2}}dx, \\ \end{gathered} $

а также

(40)
$\begin{gathered} {{P}_{{sH}}} = \frac{{k{{W}_{0}}\beta }}{2} \times \\ \times \,\,\sum\limits_{n = 0}^\infty {\left( {{{g}_{{H1n}}}\frac{{{{N}_{{H1n}}}}}{{\gamma _{{H1n}}^{2}}} + {{g}_{{H2n}}}\frac{{{{N}_{{H2n}}}}}{{\gamma _{{H2n}}^{2}}} + {{g}_{{H3n}}}\frac{{{{N}_{{H2n}}}}}{{\gamma _{{H2n}}^{2}}}} \right)} , \\ \end{gathered} $

где

$\begin{gathered} {{g}_{{H1n}}} = \int\limits_{ - d}^d {{{{\left| {{{C}_{{1n}}}\cos {{\xi }_{{H1n}}}x + {{D}_{{1n}}}\sin {{\xi }_{{H1n}}}x} \right|}}^{2}}dx} , \\ {{g}_{{H2n}}} = \int\limits_{{{ - P} \mathord{\left/ {\vphantom {{ - P} 2}} \right. \kern-0em} 2}}^{ - d} {\left| {{{C}_{{2n}}}\cos {{\xi }_{{H2n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right.} + \\ {{\left. { + \,\,{{D}_{{2n}}}\sin {{\xi }_{{H2n}}}\left( {x - {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right|}^{2}}dx, \\ {{g}_{{H3n}}} = \int\limits_d^{{P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} {\left| {{{C}_{{2n}}}\cos {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right.} + \\ {{\left. { + \,\,{{D}_{{2n}}}\sin {{\xi }_{{H2n}}}\left( {x + {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}} \right)} \right|}^{2}}dx. \\ \end{gathered} $

Отметим, что в силу ортогональности собственных волн решетки их мощность представляется суммой мощностей ${{P}_{{sE,H}}},$ переносимых E- и H-волнами.

4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

На первом этапе рассмотрим проблему сходимости численного решения граничной задачи. При реализации алгоритма решения СЛАУ (29) на ЭВМ приходится ограничивать ее размерность конечным параметром N, который определяет число собственных волн ПВ, используемых для описания поля. При увеличении значения N определяемые численно параметры стабилизируются, что позволяет говорить о сходимости решения.

Среди параметров решения выделим, так называемые интегральные параметры, к которым относятся наиболее важные с практической точки зрения характеристики собственной волны как ее коэффициент замедления U и характеристическое сопротивление ${{Z}_{c}}.$ Термин “интегральные” показывает, что они связаны с электромагнитным полем при помощи интегральных соотношений. Относительно сопротивления такая связь непосредственно следует из выражений (34)–(36).

Применимость данного термина к коэффициенту замедления менее очевидна. Ее можно обосновать тем, что дисперсионное уравнение (30) получается путем интегрирования поля.

Наряду с интегральными параметрами результатом решения граничной задачи являются первичные параметры, к которым относится само электромагнитное поле собственной волны. Ниже мы покажем, что сходимость интегральных и первичных параметров существенно различается. Такой результат был ожидаемым. Отметим, что СЛАУ относительно коэффициентов разложений допустимо получить разными способами. Можно показать, что использованная нами схема вывода СЛАУ эквивалентна решению граничной задачи вариационным методом [17], при котором получаемое дисперсионное уравнение является функционалом, устойчивым по отношению к малым вариациям поля.

По этой причине зависимость поля от параметра N стабилизируется значительно медленнее, чем аналогичные зависимости для коэффициента замедления и характеристического сопротивления. Рассмотрим их на примере решетки со следующими параметрами: $P = 15,$ $H = 2.5,$ $h = 1,$ $2d = 8,$ $\varepsilon = 2,$ $f = 6$ ГГц, ${{\kappa }_{x}} = 0.$

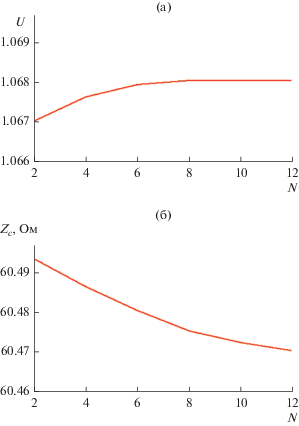
На рис. 4а показана зависимость коэффициента замедления от N, а на рис. 4б – зависимость сопротивления. Для оценки сходимости решения по полю мы использовали усредненные по координате z значения компоненты электрического поля ${{\bar {E}}_{z}}$ и ее скачка при $x = d\,:$ $\Delta {{\bar {E}}_{z}}.$ Здесь черта означает операцию усреднения. Также мы использовали средние значения компоненты магнитного поля ${{\bar {H}}_{y}}$ и ее скачка $\Delta {{\bar {H}}_{y}}.$ Отметим, что точному решению граничной задачи соответствуют нулевые скачки поля при $x = d.$

Рис. 4.

Зависимость коэффициента замедления (а) и характеристического сопротивления (б) основной волны решетки от параметра N.

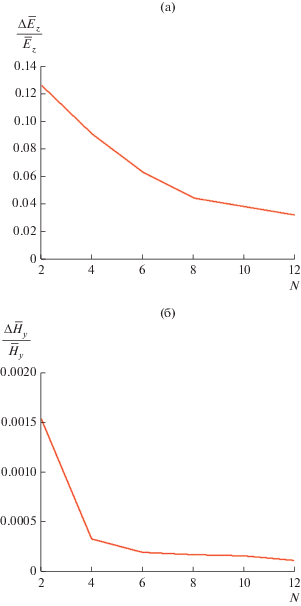
На рис. 5а, 5б показана зависимость отношений соответственно ${{\Delta {{{\bar {E}}}_{z}}} \mathord{\left/ {\vphantom {{\Delta {{{\bar {E}}}_{z}}} {{{{\bar {E}}}_{z}}}}} \right. \kern-0em} {{{{\bar {E}}}_{z}}}}$ и ${{\Delta {{{\bar {H}}}_{y}}} \mathord{\left/ {\vphantom {{\Delta {{{\bar {H}}}_{y}}} {{{{\bar {H}}}_{y}}}}} \right. \kern-0em} {{{{\bar {H}}}_{y}}}}$ от параметра N. Данные величины можно рассматривать в качестве относительной погрешности численного решения по полю. Как видно из рис. 4, сходимость по интегральным параметрам намного более быстрая, чем по полю. Они весьма слабо меняются при существенном изменении значения N, поэтому приемлемую точность решения можно получить уже при $N = 2.$ Иначе ведут себя связанные с полем первичные параметры, представленные на рис. 5а, 5б.

Рис. 5.

Сходимость численного решения по электрическому (а) и магнитному полю (б).

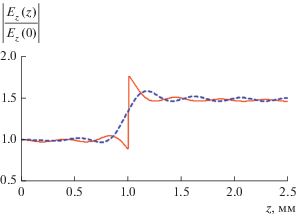
Следует отметить, что сходимость по электрическому полю более медленная, чем по магнитному полю. Причина этого поясняется на рис. 6. На нем показано нормированное распределение модуля указанной компоненты по оси $0z,$ рассчитанное при $N = 8.$ Нормировка проводится на значение поля при $z = 0.$ Сплошная кривая получена для $x = d - \delta ,$ а пунктирная для $x = d + \delta ,$ где δ – малое смещение. Точка $x = d - \delta $ расположена в области 1, в которой мы имеем неоднородное диэлектрическое заполнение. По этой причине компонента электрического поля ${{E}_{z}},$ нормальная к границе раздела двух сред при $z = h,$ имеет скачок в ε раз, а сплошная кривая в этой точке разрывается.

Рис. 6.

Распределение модуля электрического поля.

Учет скачка электрического поля при помощи собственных волн области 1 не составляет труда, так как они тоже имеют необходимые разрывы. Иная ситуация при описании скачка собственными волнами областей 2, 3, которые непрерывны при $z = h.$ В этом случае разрыв может быть описан только при использовании бесконечного числа функций, что невозможно в рамках численного решения. Поэтому при $x = d + \delta $ видим появление области быстрого изменения поля, но оно все равно остается непрерывным, что служит источником относительно большой погрешности.

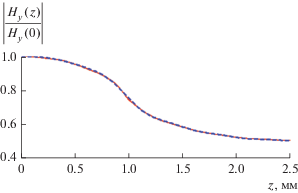
Иная ситуация наблюдается при анализе распределения магнитного поля (рис. 7), также полученного при $N = 8.$ Компонента ${{H}_{y}}$ непрерывна при $z = h.$ Поэтому сплошная и пунктирная кривые, полученные для $x = d \mp \delta ,$ практически сливаются, что указывает на высокую точность выполнения граничного условия для магнитного поля.

Рис. 7.

Распределение модуля магнитного поля.

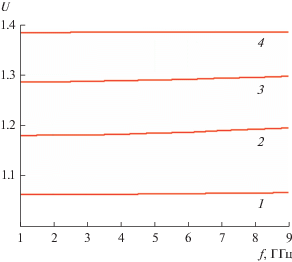
На рис. 8 показана зависимость коэффициента замедления основной волны решетки от частоты. Видно, что коэффициент замедления слабо изменяется при весьма значительном изменении частоты. При этом его абсолютное значение приближается к единице, когда область, занятая диэлектриком, стремится к нулю. Также он стремится к $\sqrt \varepsilon ,$ когда пространство между металлическими плоскостями полностью заполнено диэлектрической средой.

Рис. 8.

Частотная зависимость коэффициента замедления волны решетки получена при $h = H = 1,$ $\varepsilon = 2,$ $P = 15,$ ${{\kappa }_{x}} = 0$ и разных значениях параметра 2d = = 2 (кривая 1), 6 (2), 10 (3) и 12 (4).

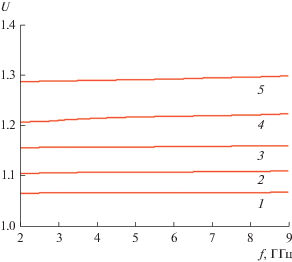
На рис. 9 также представлена частотная зависимость коэффициента замедления основной волны. Обращает на себя внимание резкое изменение замедления при увеличении расстояния между границей диэлектрика и верхним металлическим экраном. Причина сильного влияния параметра $a$ на характеристики основной волны – в концентрации электрического поля в зазоре между металлом и диэлектриком. Выше мы уже говорили, что в силу граничных условий нормальная компонента электрического поля увеличивается в ε раз на границе воздух–диэлектрик. Поэтому появление даже относительно небольшого зазора между стержнем и экраном приводит к концентрации поля в зазоре, что обусловливает его непропорционально сильное влияние на параметры волны.

Рис. 9.

Частотная зависимость коэффициента замедления волны решетки получена при $h = 1,$ $\varepsilon = 2,$ $P = 15,$ ${{\kappa }_{x}} = 0,$ $2d = 10$ и значениях параметра $H$ = = 1 (кривая 1), 1.2 (2), 1.5 (3), 2 (4) и 3 (5).

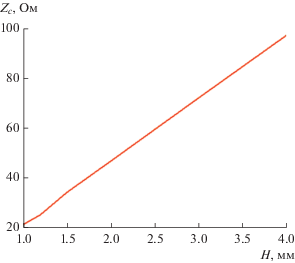
Характеристическое сопротивление меняется в зависимости от расстояние между экранами H практически линейно (рис. 10). Кривая получена при $h = 1,$ $\varepsilon = 2,$ $P = 15,$ ${{\kappa }_{x}} = 0,$ $2d = 10,$ $f = 6$ ГГц.

Рис. 10.

Зависимость характеристического сопротивления от расстояния между экранами H.

Рассмотрим зависимость характеристик основной волны от параметра сканирования ${{\kappa }_{x}}.$ Отметим, что он изменяется от нуля до значения ${\pi \mathord{\left/ {\vphantom {\pi P}} \right. \kern-0em} P}.$ Анализируемая решетка диэлектрических стержней представляет собой частный случай решетки связанных ДВ. В работе [10] рассматривалась аналогичная система и было показано, что в режиме слабой связи влияние параметра ${{\kappa }_{x}}$ описывается тригонометрической функцией $\cos {{\kappa }_{x}}P.$ На рис. 11а представлена зависимость коэффициента замедления от произведения ${{\kappa }_{x}}P$ при $h = H = 1,$ $\varepsilon = 4,$ $P = 15,$ $2d = 10.$ Видно, что она с хорошей точностью описывается следующей функцией:

(41)
$U = U(0) + \Delta U\cos {{\kappa }_{x}}P.$
Рис. 11.

Зависимость коэффициента замедления (а) и характеристического сопротивления (б) от параметра ${{\kappa }_{x}}P.$

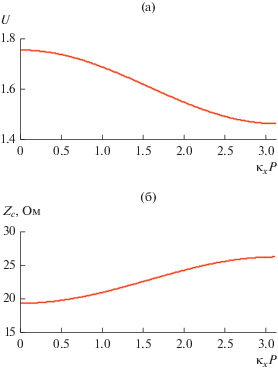
Аналогичная аппроксимация может быть предложена для зависимости характеристического сопротивления от переменной ${{\kappa }_{x}}P$ (см. рис. 11б). Кривая на рис. 11б рассчитана для параметров, приведенных для рис. 11а.

Отметим, что такая простая аппроксимация зависимостей параметров U и ${{Z}_{c}}$ от ${{\kappa }_{x}}P$ справедлива только в режиме слабой связи, который реализуется при достаточной большой диэлектрической проницаемости $\varepsilon $ и большом расстоянии между стержнями. Если указанные условия нарушены, то указанные зависимости имеют более сложный вид. Однако качественно они не сильно отличаются от показанных на рис. 11а, 11б.

ЗАКЛЮЧЕНИЕ

В работе представлено решение граничной задачи о собственных волнах бесконечной периодической решетки прямоугольных диэлектрических стержней, расположенных внутри ПВ, которое является необходимым этапом исследования ДС СШП АР. Оно открывает возможность для решения задачи синтеза параметров второй секции ДС АР. Применение для этой цели стандартных систем электродинамического моделирования не всегда целесообразно, так как задача синтеза требует перебора большого числа вариантов, что, в свою очередь, связано с большими затратами компьютерных ресурсов. В то же время описанный выше алгоритм решения поставленной задачи о собственных волнах достаточно просто реализуется на ЭВМ и его можно использовать для синтеза параметров АР с высокой эффективностью.

Работа выполнена за счет бюджетного финансирования в рамках государственного задания по теме 0030-2019-0014 и при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-07-00655а).

Список литературы

  1. Schaubert D., Kasturi S., Elsallal M.W., van Cappellen W. // Proc. EuCAP-2006. Nice. France. Nov. 2006. P. 1.

  2. Воскресенский Д.И., Котов Ю.В., Овчинникова Е.В. // Антенны. 2005. № 11. С. 7.

  3. Holter H., Chio T., Schaubert D.H. // IEEE Trans. 2000. V. AP-48. № 1. P. 122.

  4. Банков С.Е. // Труды 4-й Всерос. микроволновой конф. Москва, ноябрь 2016. С. 265.

  5. Holter H., Chio T.-H., Schaubert D.H. // IEEE Trans. 2000. V. AP-48. № 11. P. 1707.

  6. Банков С.Е., Калошин В.А., Нгуен К.З. // Труды 4-й Всерос. микроволновой конф. Москва, ноябрь 2016. С. 410.

  7. Acedo E., Garcia E., González-Posadas V. et al. // IEEE Trans. V. AP-58. № 1. P. 68.

  8. Бaнкoв C.E. // PЭ. 2018. T. 63. № 6. C. 524.

  9. Банков С.Е. // Журн. радиоэлектроники. 2017. № 11. http://jre.cplire.ru/jre/nov17/12/text.pdf.

  10. Банков С.Е., Грачев Г.Г. // РЭ. 2014. Т. 59. № 2. С. 132.

  11. Винниченко Ю.П., Захарьев Л.Н., Леманский А.А. и др. // РЭ. 1974. Т. 19. № 8. С. 1583.

  12. Винниченко Ю.П., Захарьев Л.Н., Леманский А.А. и др. // РЭ. 1975. Т. 20. № 9. С. 1804.

  13. Крехтунов В.М., Тютин В.А. // РЭ. 1983. Т. 28. № 2. С. 209.

  14. Банков С.Е., Курушин А.А., Гутцайт Э.М. Решение оптических и СВЧ задач с помощью HFSS. М.: Оркада, 2012.

  15. Банков С.Е. Антенные решетки с последовательным питанием. М.: Физматлит, 2013.

  16. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь, 1983.

  17. Никольский В.В. Вариационные методы для внутренних задач электродинамики. М.: Наука, 1967.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал