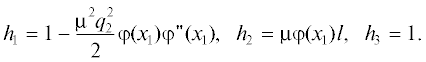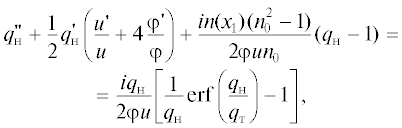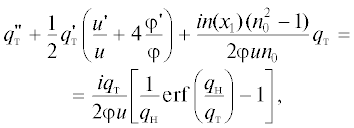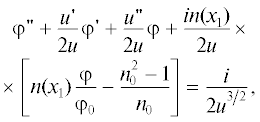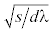Радиотехника и электроника, 2019, T. 64, № 5, стр. 498-505
О моделировании ленточных электронных пучков с учетом начальных поперечных тепловых скоростей электронов
Ю. Г. Гамаюнов 1, *, Е. В. Патрушева 1
1 Саратовский национальный исследовательский государственный университет им. Н.Г. Чернышевского
410012 Саратов, ул. Астраханская, 83, Российская Федерация
* E-mail: GamaunovYG@info.sgu.ru
Поступила в редакцию 29.06.2018
После доработки 29.06.2018
Принята к публикации 31.07.2018
Аннотация
Развит метод учета начальных поперечных тепловых скоростей электронов в сходящихся ленточных электронных пучках. Метод позволяет в параксиальном приближении через выбранные характерные траектории электронов определить основные интегральные характеристики теплового пучка как в области пушки, так и в области транспортировки. Получены уравнения движения характерных электронов, начальные условия для решения уравнений, формулы для распределения плотности тока в сечении теплового пучка, а также доли тока в его условной границе. Полученные уравнения и формулы могут быть использованы при моделировании электронно-оптических систем и выборе их параметров, при которых влияние теплового движения электронов на характеристики пучка будут в допустимых пределах.
ВВЕДЕНИЕ
В источниках излучения О-типа по мере укорочения длины волны поперечные размеры электронного пучка уменьшаются, возрастает плотность тока до десятков-сотен ампер с квадратного сантиметра, а также удельная мощность пучка. Это накладывает жесткие требования на величину токопрохождения пучка в пролетных каналах и его конфигурацию. Среди факторов, определяющих структуру таких пучков и уровень его токопрохождения, следует отметить влияние поперечных начальных тепловых скоростей электронов. Хотя средняя тепловая энергия электронов составляет доли электрон-вольта, а ускоряющее напряжение соответствует энергии электронов, превосходящей на несколько порядков тепловую, тепловое движение электронов приводит к возмущению конфигурации пучка, перераспределению плотности тока по сечению, ограничению по предельному сжатию пучка. Уже в ранних работах (см., например, [1, 2] и ссылки в них) были получены соотношения и зависимости, позволяющие судить о характеристиках ленточного теплового пучка с максвелловским распределением начальных скоростей электронов на катоде. Для электростатических пушек Пирса проведены расчеты, иллюстрирующие влияние начальных скоростей электронов в таких пучках [2], но в них не учитывается магнитное поле в пушках, что представляется важным для электронно-оптических систем (ЭОС) источников излучения коротковолнового диапазона. Имеются также строгие расчеты для некоторых ЭОС приборов О-типа этого диапазона с учетом влияния тепловых скоростей электронов в пучке, проведенные с использованием программ анализа [3]. Однако из представленных результатов в [3] неясно, в какой мере тепловое движение электронов возмущает пучок. Следует также отметить, что, хотя расчеты ЭОС по программам анализа и являются наиболее строгими, они имеют существенный недостаток – трудоемкость в подготовке данных и неоперативность. Поэтому актуальным является развитие методов, которые позволяют устранить отмеченные выше ограничения, но при этом получать в целом достоверную информацию о тепловом пучке. Как представляется, это может быть реализовано на основе изложенного в работе [1] метода учета влияния тепловых скоростей электронов в модели ленточного пучка с максвелловским распределением начальных скоростей на катоде. Метод позволяет в параксиальном приближении через выбранные характерные траектории электронов определить основные интегральные характеристики теплового пучка.
Цель данной работы – обобщить этот метод. Было учтено изменение осевой плотности заряда теплового пучка в уравнениях движения, записанных в криволинейной системе координат, получены уравнения для моделирования электронно-оптических систем и расчета основных интегральных характеристик теплового пучка, в том числе при его фокусировке магнитным полем. Проведенное обобщение расширяет возможности метода [1] при исследовании влияния поперечных тепловых скоростей электронов в сходящихся ленточных электронных пучках.
1. ОСНОВНЫЕ УРАВНЕНИЯ
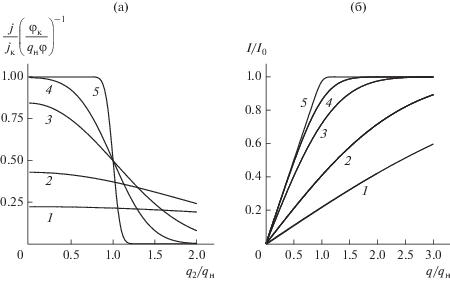
Для исследования влияния поперечных тепловых скоростей электронов в ленточных электронных пучках будем использовать криволинейную систему координат q1, q2, q3. Полагаем, что q2 является параметром семейства траекторий ламинарного пучка, т.е. семейства, в котором электроны не имеют начальных тепловых скоростей. При этом если граничная траектория ламинарного пучка описывается в декартовой системе координат функцией Ф(х), то все внутренние траектории описываются функцией у(х) = q2Ф(х), в которой значения q2 в верхней полуплоскости изменяются в пределах 0 ≤ q2 ≤ 1. Таким образом, траектории электронов ламинарного пучка лежат на поверхностях q2 = const. Другая криволинейная координата q1 является продольной координатой и выбирается так, чтобы поверхности q1 = const были ортогональны поверхностям q2 = const. Координата q3, совпадает с декартовой координатой z по ширине пучка. Координатам q1, q2, q3 соответствуют координаты х, у, z декартовой системы координат. Введенная система координат аналогична системе координат, используемой в теории формирования осесимметричных пучков, развитой В.Т. Овчаровым (см., например, [4]). Введем также нормировочные величины продольных и поперечных размеров l и Ф0 соответственно, параметр параксиальности μ = Ф0/l $ \ll $ 1, нормированную продольную криволинейную координату х1 = q1/l и нормированную функцию φ(x1) = Ф(х1)/Ф0. Для выбранной системы координат коэффициенты Ламе в параксиальном приближении с точностью до μ2 имеют вид
Связь криволинейных координат с декартовыми координатами дается формулами
Примем, что ширина электронного пучка много больше его толщины (модель бесконечно широкого ленточного пучка). Это позволяет использовать условие $(\partial {\text{/}}\partial {{q}_{3}}) \equiv 0$ в уравнениях движения [5, с. 80], записанных в криволинейных координатах. Полагая, что в реальном, тепловом пучке известны осевые распределения плотности пространственного заряда ${{\rho }_{{\text{т }}}}({{x}_{1}}),$ потенциала U(x1), магнитного поля В(x1), и, учитывая выражения (1) для коэффициентов Ламе, получим в параксиальном приближении уравнение поперечного движения электрона, стартующего на катоде из точки x1 = 0, q2 = q2к:
(2)
$\ddot {\omega } + \omega {{\psi }_{{\text{т }}}} + 4\omega \omega _{L}^{2} = 4{{q}_{{{\text{2к }}}}}{{\varphi }_{{\text{к }}}}{{\omega }_{{L{\text{к }}}}}{{\omega }_{L}},$где $\omega = {{q}_{2}}{\text{(}}t{\text{)}}\varphi ,$ 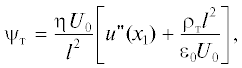 ${{\omega }_{L}} = $ $ = \frac{{\eta B{\text{(}}{{x}_{1}}{\text{)}}}}{2},$ ${{\omega }_{{L{\text{к
}}}}} = \frac{{\eta {{В
}_{{\text{к
}}}}}}{2},$ ${{\varphi }_{{\text{к
}}}} = \varphi {\text{(}}0{\text{),}}$ Вк – магнитное поле на катоде, η – удельный заряд электрона, U0 – нормировочная величина для потенциала, u(x1) – нормированный потенциал, ε0 – электрическая постоянная. При выводе (2) удерживали члены, пропорциональные µ2, не учитывали продольную вдоль оси q1 и поперечную вдоль оси q3 начальные скорости электронов на катоде, а величину текущей продольной скорости электрона
определяли через осевой потенциал. Выполняя дифференцирование в (2), получим уравнение
относительно функции q2(t), которая определяет траекторию электрона теплового пучка в криволинейной системе
координат:
${{\omega }_{L}} = $ $ = \frac{{\eta B{\text{(}}{{x}_{1}}{\text{)}}}}{2},$ ${{\omega }_{{L{\text{к
}}}}} = \frac{{\eta {{В
}_{{\text{к
}}}}}}{2},$ ${{\varphi }_{{\text{к
}}}} = \varphi {\text{(}}0{\text{),}}$ Вк – магнитное поле на катоде, η – удельный заряд электрона, U0 – нормировочная величина для потенциала, u(x1) – нормированный потенциал, ε0 – электрическая постоянная. При выводе (2) удерживали члены, пропорциональные µ2, не учитывали продольную вдоль оси q1 и поперечную вдоль оси q3 начальные скорости электронов на катоде, а величину текущей продольной скорости электрона
определяли через осевой потенциал. Выполняя дифференцирование в (2), получим уравнение
относительно функции q2(t), которая определяет траекторию электрона теплового пучка в криволинейной системе
координат:
(3)
$\begin{gathered} {{{\ddot {q}}}_{2}} + 2{{{\dot {q}}}_{2}}\frac{{\dot {\varphi }}}{\varphi } + {{q}_{2}}\frac{{\ddot {\varphi }}}{\varphi } + {{q}_{2}}{\text{(}}{{\psi }_{{\text{т }}}} + 4\omega _{L}^{2}{\text{)}} = \\ = 4{{q}_{{2{\text{к }}}}}\frac{{{{\varphi }_{{\text{к }}}}}}{\varphi }{{\omega }_{{L{\text{к }}}}}{{\omega }_{L}}. \\ \end{gathered} $Для функции φ(х1), описывающую граничную траекторию ламинарного (холодного) пучка, уравнение получается из (3), если принять q2к = = q2(t) = 1:
(4)
$\ddot {\varphi } + \varphi {\text{(}}{{\psi }_{{{\text{х о л }}}}} + 4\omega _{L}^{2}{\text{)}} = 4{{\varphi }_{{\text{к }}}}{{\omega }_{{L{\text{к }}}}}{{\omega }_{L}}.$Здесь функция ψхол(х1) определена уже через плотность пространственного заряда ${{\rho }_{{{\text{х о л }}}}}{\text{(}}{{x}_{1}}{\text{)}}$ ламинарного пучка. При этом полагаем, что распределение осевого потенциала в ламинарном и тепловом пучках различаются незначительно и описываются единой функцией u(х1). Поэтому функции ${{\psi }_{{\text{т }}}}{\text{(}}{{x}_{1}}{\text{)}}$ и ${{\psi }_{{{\text{х о л }}}}}{\text{(}}{{x}_{{\text{1}}}}{\text{) }}$ отличаются только осевой плотностью пространственного заряда.
Уравнение (3) – линейное неоднородное уравнение. Его общим решением является сумма общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. В качестве фундаментальных решений однородного уравнения выберем функции ${{q}_{{{\text{к р }}}}}(t)$ и $\mu l{{\varphi }_{{\text{к }}}}\sqrt {\frac{m}{{2\kappa T}}} {{q}_{{\text{т }}}}{\text{(}}t{\text{)}}$ (κ – постоянная Больцмана, m – масса электрона, Т – температура, К), подчинив ${{q}_{{{\text{к р }}}}}(t)$ и ${{q}_{{\text{т }}}}{\text{(}}t)$ следующим условиям:
Функция ${{q}_{{{\text{к р }}}}}(t)$ описывает движение электрона, вылетающего с кромки катода (q2к = 1) с нулевой скоростью, а функция ${{q}_{{\text{т }}}}{\text{(}}t{\text{)}}$ описывает движение электрона, вылетающего из центра катода с тепловой скоростью
(5)
${{q}_{2}}{\text{(}}t{\text{)}} = {{q}_{{\text{н }}}}{\text{(}}t{\text{)}}{{q}_{{2{\text{к }}}}} + \mu l{{\varphi }_{{\text{к }}}}\sqrt {\frac{m}{{2\kappa T}}} {{q}_{{\text{т }}}}{\text{(}}t{\text{)}}{{\dot {q}}_{{2{\text{к }}}}},$(6)
$\begin{gathered} {{{\ddot {q}}}_{{\text{н }}}} + 2{{{\dot {q}}}_{{\text{н }}}}\frac{{\dot {\varphi }}}{\varphi } + {{q}_{{\text{н }}}}\left[ {\left( {{{\psi }_{{\text{т }}}} - {{\psi }_{{{\text{х о л }}}}}} \right) + 4\frac{{{{\varphi }_{{\text{к }}}}}}{\varphi }{{\omega }_{{L{\text{к }}}}}{{\omega }_{L}}} \right] = \\ = 4\frac{{{{\varphi }_{{\text{к }}}}}}{\varphi }{{\omega }_{{L{\text{к }}}}}{{\omega }_{L}}, \\ \end{gathered} $(7)
${{\ddot {q}}_{{\text{т }}}} + 2{{\dot {q}}_{{\text{т }}}}\frac{{\dot {\varphi }}}{\varphi } + {{q}_{{\text{т }}}}\left[ {\left( {{{\psi }_{{\text{т }}}} - {{\psi }_{{{\text{х о л }}}}}} \right) + 4\frac{{{{\varphi }_{{\text{к }}}}}}{\varphi }{{\omega }_{{L{\text{к }}}}}{{\omega }_{L}}} \right] = 0.$Чтобы достичь точки x1, ${{q}_{2}},$ электрон, покидающий катод из точки q2к, должен иметь, согласно (5), начальную скорость h2к${{\dot {q}}_{{2{\text{к }}}}},$ равную
(8)
${{h}_{{{\text{2к }}}}}{{\dot {q}}_{{2{\text{к }}}}} = \frac{{{{q}_{2}} - {{q}_{{\text{н }}}}(t){{q}_{{2{\text{к }}}}}}}{{{{q}_{{\text{т }}}}(t)}}\sqrt {\frac{{2\kappa T}}{m}} .$Это является решающим при вычислении распределения плотности тока по сечению теплового пучка. Действительно, принимая максвелловский закон распределения начальных тепловых скоростей электронов на катоде и пренебрегая, как было указано выше, продольными и поперечными вдоль осей q1, ${{q}_{3}}$ начальными скоростями электронов, плотность тока $j({{x}_{1}},{{q}_{2}})$ в произвольной точке ${{x}_{1}},{{q}_{2}}$ можно выразить в виде
(9)
$j({{x}_{1}},{{q}_{2}}) = {{j}_{{\text{к }}}}\sqrt {\frac{m}{{2\kappa T}}} \int {\exp \left[ { - \frac{m}{{2\kappa T}}{{{\left( {{{h}_{{2{\text{к }}}}}{{{\dot {q}}}_{{2{\text{к }}}}}} \right)}}^{2}}} \right]} d({{h}_{2}}{{\dot {q}}_{2}}),$(10)
$\begin{gathered} j({{x}_{1}},{{q}_{2}}) = {{j}_{к }}\mu \varphi l\sqrt {\frac{m}{{2\kappa T}}} \times \\ \times \,\,\int {\exp \left[ { - {{{\left( {\frac{{{{q}_{2}} - {{q}_{{\text{т }}}}(t){{q}_{{2к }}}}}{{{{q}_{т }}(t)}}} \right)}}^{2}}} \right]} d{{{\dot {q}}}_{2}}. \\ \end{gathered} $Величину ${{\dot {q}}_{2}},$ которая в точке 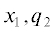 определяет скорость электрона, покидающего катод из точки ${{q}_{{2{\text{к
}}}}},$ представим в виде ${{\dot {q}}_{2}} = P(t)\,{{q}_{{2{\text{к
}}}}}$ или $d{{\dot {q}}_{2}} = P(t)d{{q}_{{2{\text{к
}}}}},$ где функция P(t) пока неизвестна. Это позволяет интегрирование в (10) по ${{\dot {q}}_{2}}$ заменить интегрированием по поверхности катода в пределах $ - 1 \leqslant {{q}_{{2{\text{к
}}}}} \leqslant 1.$ Выполняя интегрирование, получим формулу для плотности тока теплового пучка, содержащую
введенную функцию $P(t).$
определяет скорость электрона, покидающего катод из точки ${{q}_{{2{\text{к
}}}}},$ представим в виде ${{\dot {q}}_{2}} = P(t)\,{{q}_{{2{\text{к
}}}}}$ или $d{{\dot {q}}_{2}} = P(t)d{{q}_{{2{\text{к
}}}}},$ где функция P(t) пока неизвестна. Это позволяет интегрирование в (10) по ${{\dot {q}}_{2}}$ заменить интегрированием по поверхности катода в пределах $ - 1 \leqslant {{q}_{{2{\text{к
}}}}} \leqslant 1.$ Выполняя интегрирование, получим формулу для плотности тока теплового пучка, содержащую
введенную функцию $P(t).$
Если затем проинтегрировать выражение для плотности тока по координате ${{q}_{2}},$ для определения доли тока11 ${I \mathord{\left/ {\vphantom {I {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}$ в пределах условной границы q2 = ±q теплового пучка и устремить $q \to \infty $ в полученном выражении, то, очевидно, должны получить ${I \mathord{\left/ {\vphantom {I {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}} = 1.$ Это позволяет определить функцию $P(t).$ В итоге выражения для плотности тока теплового пучка в произвольной точке 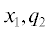 и для доли тока в пределах его условной границы примут вид
и для доли тока в пределах его условной границы примут вид
(11)
$\begin{gathered} j({{x}_{1}},{{q}_{2}}) = \frac{1}{2}{{j}_{{\text{к }}}}\frac{{{{\varphi }_{{\text{к }}}}}}{{{{q}_{{\text{н }}}}\varphi }} \times \\ \times \,\,\left[ {{\text{erf}}\left( {\frac{{{{q}_{{\text{н }}}}}}{{{{q}_{{\text{т }}}}}}\left( {\frac{{{{q}_{2}}}}{{{{q}_{{\text{н }}}}}} + 1} \right)} \right) - {\text{erf}}\left( {\frac{{{{q}_{{\text{н }}}}}}{{{{q}_{{\text{т }}}}}}\left( {\frac{{{{q}_{2}}}}{{{{q}_{{\text{н }}}}}} - 1} \right)} \right)} \right], \\ \end{gathered} $(12)
$\begin{gathered} \frac{I}{{{{I}_{0}}}} = \frac{1}{2}\left( {\frac{q}{{{{q}_{{\text{н }}}}}} + 1} \right){\text{erf}}\left( {\frac{{{{q}_{{\text{н }}}}}}{{q{}_{{\text{т }}}}}\left( {\frac{q}{{{{q}_{{\text{н }}}}}} + 1} \right)} \right) - \\ - \,\,\frac{1}{2}\left( {\frac{q}{{{{q}_{{\text{н }}}}}} - 1} \right){\text{erf}}\left( {\frac{{{{q}_{{\text{н }}}}}}{{q{}_{{\text{т }}}}}\left( {\frac{q}{{{{q}_{{\text{н }}}}}} - 1} \right)} \right) + \\ + \,\,\frac{{{{q}_{{\text{т }}}}}}{{2\sqrt \pi {{q}_{{\text{н }}}}}}{\text{exp}}\left( { - \frac{{q_{{\text{н }}}^{2}}}{{q_{{\text{т }}}^{{\text{2}}}}}{{{\left( {\frac{q}{{{{q}_{{\text{н }}}}}} + 1)} \right)}}^{2}}} \right) - \\ - \,\,\frac{{{{q}_{{\text{т }}}}}}{{2\sqrt \pi {{q}_{{\text{н }}}}}}{\text{exp}}\left( { - \frac{{q_{{\text{н }}}^{2}}}{{q_{{\text{т }}}^{{\text{2}}}}}{{{\left( {\frac{q}{{{{q}_{{\text{н }}}}}} - 1)} \right)}}^{2}}} \right), \\ \end{gathered} $Рис. 1.
Распределение плотности тока в тепловом пучке (а) и доля тока (б) в границах пучка, отстоящих симметрично от плоскости q2 = 0 на величину q для значений $({{{{q}_{{\text{н }}}}} \mathord{\left/ {\vphantom {{{{q}_{{\text{н }}}}} {{{q}_{{\text{т }}}})}}} \right. \kern-0em} {{{q}_{{\text{т }}}})}}$ = 0.2 (1), 0.4 (2), 1 (3), 2 (4), 10 (5).
Полученные формулы (11), (12) и зависимости, представленные на рис. 1, по виду аналогичны таковым в [1, 2], но отличаются тем, что в них учтено влияние магнитного поля на характеристики теплового пучка через значения функций ${{q}_{{\text{н }}}}(t),{{q}_{{\text{т }}}}(t),$ которые определены уравнениями (6), (7).
Для объемной плотности пространственного заряда на оси теплового пучка (q2 = 0) из выражения (11) имеем
Аналогично объемная плотность пространственного заряда на оси ламинарного пучка будет:
Подставляя полученные выражения для ${{\rho }_{{\text{т }}}}{\text{(}}{{x}_{1}}{\text{)}}$ и ${{\rho }_{{{\text{х о л }}}}}{\text{(}}x{}_{1}{\text{)}}$ в уравнения (6), (7), получим самосогласованную систему уравнений, в которой учтено взаимное влияние двух факторов: пространственного заряда ${{\rho }_{{\text{т }}}}{\text{(}}{{x}_{1}}{\text{)}}$ на движение электронов в тепловом пучке и движение электронов на плотность пространственного заряда. В этих уравнениях, а также в уравнении (4) удобно перейти к дифференцированию по координате x1 и вместо магнитных полей B(x1) и Bк ввести, как это сделано в [6], величины их превышения над бриллюэновским полем для ламинарного пучка с нормированной в кроссовере полутолщиной ${{\varphi }_{0}} = {d \mathord{\left/ {\vphantom {d {2{{\Phi }_{0}}}}} \right. \kern-0em} {2{{\Phi }_{0}}}}$ (d – толщина пучка). Уравнения примут вид
где n0 – превышение рабочего магнитного поля над бриллюэновским полем, ${{B}_{{{\text{Б р }}}}} = 1.04 \times {{10}^{{ - 3}}}\sqrt {\frac{{{{р }_{\mu }}{{U}_{0}}}}{{sd}}} $ (тесла, вольт, миллиметр), ${{р }_{\mu }}$ – микропервеанс пучка, s – ширина пучка, n(x1) – текущее превышение, $i = 0.0952{{{{p}_{\mu }}} \mathord{\left/ {\vphantom {{{{p}_{\mu }}} {\mu {{\mu }_{1}}}}} \right. \kern-0em} {\mu {{\mu }_{1}}}},$ ${{\mu }_{1}} = {s \mathord{\left/ {\vphantom {s l}} \right. \kern-0em} l}.$ Уравнение (16) совпадает с уравнением внутренней задачи синтеза сходящихся ленточных электронных пучков и описывает формирование ламинарных пучков при частичной магнитной экранировке катода. Решение этого уравнения, включающее определение распределения осевого потенциала $u({{x}_{1}})$ и магнитного поля $n({{x}_{1}}),$ обеспечивающих формирование ламинарного электронного пучка с заданными параметрами, согласованно входящего в область рабочего магнитного поля, представлено в [6]. Там же представлено и решение внешней задачи синтеза для определения конфигурации электродов формирующей системы. Результаты решения уравнения (16) необходимо использовать при интегрировании уравнений (14), (15) для нахождения функций ${{q}_{{\text{н }}}}({{x}_{1}}),{{q}_{{\text{т }}}}({{x}_{{\text{1}}}}),$ через которые по формулам (11)–(13) определены основные интегральные характеристики теплового пучка.Таким образом, решение системы уравнений (14)–(16) позволяет получить достаточно полную информацию о том, в какой мере реальный тепловой пучок, в котором учтены начальные скорости электронов, будет отличаться от ламинарного электронного пучка с граничной траекторией в области пушки, описываемой функцией $\varphi {\text{(}}{{x}_{1}}{\text{)}}$ и имеющий в кроссовере и регулярной области магнитного поля нормированную полутолщину φ0. Уравнения (14)–(16) могут быть использованы для исследования эффектов тепловых скоростей и при формировании пучка пушками с экранированным от магнитного поля катодом и пушками с сопровождением пучка магнитным полем. В первом случае в уравнениях сомножитель ${{(n_{0}^{2} - 1)} \mathord{\left/ {\vphantom {{(n_{0}^{2} - 1)} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ следует принять равным нулю (рабочее магнитное поле равно бриллюэновскому полю), а во втором случае заменить его на ${{n}_{0}}$ и задать нормированное магнитное поле $n{\text{(}}{{x}_{1}}{\text{)}}$ формулой $n({{x}_{1}}) = {{{{n}_{0}}{{\varphi }_{0}}} \mathord{\left/ {\vphantom {{{{n}_{0}}{{\varphi }_{0}}} {\varphi ({{x}_{1}})}}} \right. \kern-0em} {\varphi ({{x}_{1}})}}.$ Особенности решения уравнения (16) в этих случаях представлены в работах [7, 8]. Уравнения (14), (15) упрощаются для области транспортировки, где22 $\varphi ({{x}_{1}}) = {{\varphi }_{0}}.$ Так как в этой области осевой потенциал $u({{x}_{1}}) = 1$ и нормированное осевое магнитное поле $n({{x}_{1}}) = {{n}_{0}},$ то в уравнениях (14), (15) будут отсутствовать производные от $u({{x}_{1}})$ и $\varphi ({{x}_{1}}),$ а уравнение (16) превратится в тождество.
Численное интегрирование уравнений (14)–(16) непосредственно от катода (x1 = 0) невозможно, так как u(0) = 0. Поэтому необходимо сформулировать условия для функций ${{q}_{{\text{н }}}}({{x}_{1}}),{{q}_{{\text{т }}}}({{x}_{{\text{1}}}})$ вблизи катода. Из физических соображений ясно, что вблизи катода плотности объемного пространственного заряда в тепловом и ламинарном пучках близки. В этом случае ${\text{erf}}\left( {{{{{q}_{{\text{н }}}}} \mathord{\left/ {\vphantom {{{{q}_{{\text{н }}}}} {{{q}_{{\text{т }}}}}}} \right. \kern-0em} {{{q}_{{\text{т }}}}}}} \right)$ ≈ 1. Поэтому решение уравнения (14) вблизи катода будет
Физически равенство ${{q}_{{\text{н }}}}({{x}_{1}}) = 1$ означает, что траектория нетеплового электрона вблизи катода совпадает с граничной траекторией ламинарного пучка, для которого ${{q}_{{\text{2}}}}({{x}_{1}}) = 1$. Траектории будут совпадать и в общем случае, если в области формирования или транспортировки ${\text{erf}}\left( {{{{{q}_{{\text{н }}}}} \mathord{\left/ {\vphantom {{{{q}_{{\text{н }}}}} {{{q}_{{\text{т }}}}}}} \right. \kern-0em} {{{q}_{{\text{т }}}}}}} \right) \approx 1$ (отметим, что полученная ранее формула (13) будет тогда определять долю тока в границах ламинарного пучка, т.е. при q2 = ±1).
Определение начальных условий для функции ${{q}_{{\text{т }}}}({{x}_{{\text{1}}}}),$ которая описывает траекторию теплового электрона, проведем, полагая, что вблизи катода
Первое условие следует из сопровождения ламинарного пучка магнитным полем вблизи катода в пушках с частичной магнитной экранировкой катода, а второе условие является следствием изменения осевого потенциала по закону $u({{x}_{1}}) \approx kx_{1}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}},$ который получается из уравнения (16), k = ${{\left( {{{9i} \mathord{\left/ {\vphantom {{9i} {4{{\varphi }_{{\text{к }}}}}}} \right. \kern-0em} {4{{\varphi }_{{\text{к }}}}}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$ Эти условия всегда выполняются в ЭОС в режиме ограничения тока пространственным зарядом. Кроме того, так как вблизи катода правая часть уравнения (15) оказывается равной нулю, то, как показано в Приложении, решение этого уравнения будет иметь вид
(18)
${{q}_{{\text{т }}}}({{x}_{1}}) = \frac{{0.06{{n}_{0}}}}{{n_{0}^{2} - 1}}\sqrt {\frac{s}{{d\lambda }}} {\text{sin}}\left[ {{{{\left( {18\frac{{i\varphi _{0}^{3}}}{{\varphi _{{\text{к }}}^{{\text{4}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}\frac{{{\text{(}}n_{0}^{2} - 1{\text{)}}}}{{{{n}_{0}}}}x_{1}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \right],$(19)
$\begin{gathered} q_{{\text{т }}}^{'}({{x}_{1}}) = 0.02\sqrt {\frac{s}{{d\lambda }}} {{\left( {18\frac{{i\varphi _{0}^{3}}}{{\varphi _{{\text{к }}}^{{\text{4}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}} \times \\ \times \,\,x_{1}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}{\text{cos}}\left[ {{{{\left( {18\frac{{i\varphi _{0}^{3}}}{{\varphi _{{\text{к }}}^{{\text{4}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}\frac{{{\text{(}}n_{0}^{2} - 1{\text{)}}}}{{{{n}_{0}}}}x_{1}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \right], \\ \end{gathered} $2. ПРИМЕР ИСПОЛЬЗОВАНИЯ ПОЛУЧЕННЫХ СООТНОШЕНИЙ
Рассмотрим модель ЭОС, в которой распределение потенциала в области формирования $0 \leqslant {{x}_{1}} \leqslant 1$ описывается соотношением $u{\text{(}}{{x}_{1}}{\text{)}}$ = $kx_{1}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}},$ $u(1) = 1.$ Распределение потенциала по закону 4/3 характерно для ЭОС, формирующей ламинарный пучок без компрессии, когда ${{\varphi }_{{\text{к }}}} = {{\varphi }_{0}}.$ Если положить ${{\varphi }_{{\text{к }}}} = 1,$ что всегда можно сделать выбором нормирующей величины Ф0, то значение параметра i = 4/9. В области транспортировки, т.е. при ${{x}_{1}} \geqslant 1,$ осевой потенциал $u({{x}_{1}}) = 1,$ а уровень фокусирующего магнитного поля имеет нормированную величину ${{n}_{0}}.$ Пусть в плоскости x1 = 1, т.е. на аноде, магнитное поле скачком уменьшается от величины ${{n}_{0}}$ до величины ${{n}_{{\text{к }}}} = {{(n_{0}^{2} - 1)} \mathord{\left/ {\vphantom {{(n_{0}^{2} - 1)} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}.$ Это обеспечивает согласованный ввод ламинарного пучка постоянного сечения из области формирования (пушки) в область транспортировки при условии сопровождения пучка магнитным полем с уровнем nк в области пушки. Будем также полагать, что тепловые скорости электронов слабо возмущают тепловой пучок. Поэтому движение электронов теплового пучка будет происходить на фоне пространственного заряда ламинарного пучка. Подобное приближение использовали в [1, 2] при исследовании эффектов тепловых скоростей в электростатических пушках Пирса и в [5] при выводе формулы для плотности тока в тепловом аксиально-симметричном пучке. При сделанных предположениях формулы (17)–(19) оказываются справедливыми во всей области пушки, а не только вблизи катода, так как выполнено условие ${\text{erf}}\left( {{{{{q}_{{\text{н }}}}} \mathord{\left/ {\vphantom {{{{q}_{{\text{н }}}}} {{{q}_{{\text{т }}}}}}} \right. \kern-0em} {{{q}_{{\text{т }}}}}}} \right)$ ≈ 1. Поэтому в плоскости ${{x}_{1}} = 1$ (анода) будем иметь ${{\tilde {q}}_{{\text{н }}}} = 1,$ $\tilde {q}{{_{{\text{н }}}^{'}}_{{}}} = 0,$
(20)
${{\tilde {q}}_{{\text{т }}}} = \frac{{0.06{{n}_{0}}}}{{n_{0}^{2} - 1}}\sqrt {\frac{s}{{d\lambda }}} {\text{sin}}\left[ {{{{{\text{(}}18i{\text{)}}}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}\frac{{n_{0}^{2} - 1}}{{{{n}_{0}}}}} \right],$(21)
$\tilde {q}_{{\text{т }}}^{'} = 0.02\sqrt {\frac{s}{{d\lambda }}} {{\left( {18i} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}{\text{cos}}\left[ {{{{{\text{(}}18i{\text{)}}}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}\frac{{n_{0}^{2} - 1}}{{{{n}_{0}}}}} \right].$Полученные значения функции ${{\tilde {q}}_{{\text{т }}}}$ и ее производной являются начальными условиями для определения этой функции из уравнения (15) в области транспортировки. Решение уравнения (15) в этой области с начальными условиями (20), (21) имеет вид
(22)
$\begin{gathered} {{q}_{{\text{т }}}}({{x}_{1}}) = {{{\tilde {q}}}_{{\text{т }}}}\sqrt {1 + \frac{2}{{i{\text{(}}n_{0}^{2} - 1{\text{)}}}}{{{\left( {\frac{{\tilde {q}_{{\text{т }}}^{'}}}{{{{{\tilde {q}}}_{{\text{т }}}}}}} \right)}}^{2}}} \times \\ \times \,\,{\text{sin}}\left[ {\sqrt {\frac{{i{\text{(}}n_{0}^{2} - 1{\text{)}}}}{2}} {\text{(}}{{x}_{1}} - 1{\text{)}} + \psi } \right], \\ \end{gathered} $(23)
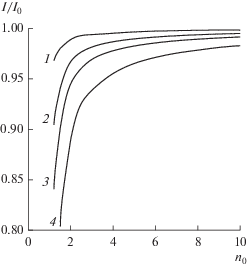
$\frac{I}{{{{I}_{0}}}} = 1 - \frac{{0.06{{n}_{0}}}}{{2\sqrt \pi {\text{(}}n_{0}^{2} - 1{\text{)}}}}\sqrt {\frac{s}{{d\lambda }}} \sqrt {{\text{si}}{{{\text{n}}}^{2}}\left[ {{{{\left( {18i} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}\frac{{{\text{(}}n_{0}^{2} - 1{\text{)}}}}{{{{n}_{0}}}}} \right] + 0.58\frac{{(n_{0}^{2} - 1)}}{{{{i}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}n_{0}^{2}}}{\text{co}}{{{\text{s}}}^{{\text{2}}}}\left[ {{{{\left( {18i} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}\frac{{{\text{(}}n_{0}^{2} - 1{\text{)}}}}{{{{n}_{0}}}}} \right]} .$Из формулы (23) видно, что доля тока в границах ламинарного пучка зависит от величины $\sqrt {{s \mathord{\left/ {\vphantom {s {d\lambda }}} \right. \kern-0em} {d\lambda }}} ,$ т.е. от электрических и геометрических параметров пучка, и от уровня фокусирующего поля. На рис. 2 представлены результаты расчета ${I \mathord{\left/ {\vphantom {I {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}$ по этой формуле в зависимости от превышения рабочего магнитного поля над бриллюэновским полем для различных значений $\sqrt {{s \mathord{\left/ {\vphantom {s {d\lambda }}} \right. \kern-0em} {d\lambda }}} .$ Эти зависимости могут быть использованы для оценки величины токопрохождения теплового пучка в пролетном канале для случая некомпрессионной оптики. Так, если параметры ЭОС, как в [3] (I0 = 0.1 А, U0 = 20000 В, Т = 1200 К, В0 = 1.12 Т, s = 0.7 мм, d = = 0.1 мм), то $\sqrt {{s \mathord{\left/ {\vphantom {s {d\lambda }}} \right. \kern-0em} {d\lambda }}} $ = 3.44, n0 = 10.8, и из зависимостей рис. 2 следует, что в такой ЭОС тепловые скорости электронов на характеристики пучка и его токопрохождение в канале практически не влияют, так как почти весь ток теплового пучка в пучностях сосредоточен в границах ламинарного пучка. Ясно, что для сходящихся электронных пучков необходимо численно интегрировать уравнения (14)–(16), а затем использовать формулы (11)–(13).
ЗАКЛЮЧЕНИЕ
Изложенный метод учета влияния начальных тепловых скоростей электронов дает возможность оперативно получать информацию об основных интегральных характеристиках тепловых электронных пучков. Его можно рассматривать как дополнение к методу синтеза при моделировании электронно-оптических систем, поскольку имеется возможность обоснованно выбирать параметры пучка, компрессию пушки, уровень фокусирующего магнитного поля, при которых влияние теплового движения электронов на характеристики пучка будут в допустимых пределах. Последнее является важным при разработке электронно-оптических систем для источников излучения О-типа коротковолнового диапазона.
Авторы признательны Д.И. Трубецкову за проявленный интерес к работе и сделанные замечания.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-02-00666).
Список литературы
Кирштейн П., Кайно Г., Уотерс У. Формирование электронных пучков. М.: Мир, 1970.
Алямовский И.В. Электронные пучки и электронные пушки. М.: Сов. радио, 1966.
Каретникова Т.А., Рожнев А.Г., Рыскин Н.М. и др. // РЭ. 2016. Т. 61. № 1. С. 54.
Невский П.В. // Обзоры по электронной технике. Сер. 1. Электроника СВЧ. 1989. Вып. 15. С. 48.
Молоковский С.И., Сушков Ф.Д. Интенсивные электронные и ионные пучки. М.: Энергоатомиздат, 1991.
Гамаюнов Ю.Г., Патрушева Е.В. // РЭ. 2017. Т. 62. № 11. С. 1126.
Гамаюнов Ю.Г., Патрушева Е.В. // Матер. Междунар. науч.-техн. конф. АПЭП-2016. Саратов. 22–23 сентября, 2016. С. 30.
Гамаюнов Ю.Г., Патрушева Е.В. // Матер. Междунар. науч.-техн. конф. АПЭП-2014. Саратов. 25–26 сентября, 2014. С. 5.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника