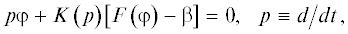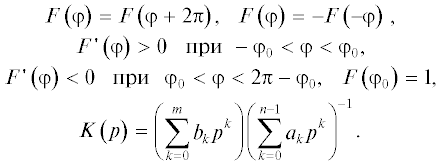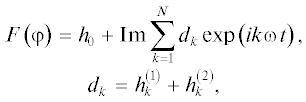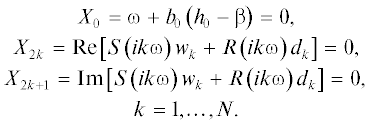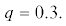Радиотехника и электроника, 2019, T. 64, № 5, стр. 470-477
Влияние высших гармоник квазигармонического метода на точность вычисления динамических характеристик фазовой автоподстройки частоты
А. Ф. Грибов 1, *, Б. И. Шахтарин 1
1 Московский государственный технический университет им. Н.Э. Баумана
105005 Москва, ул. 2-я Бауманская, 5, Российская Федерация
* E-mail: alexandr-gribov@list.ru
Поступила в редакцию 05.06.2018
После доработки 02.07.2018
Принята к публикации 10.07.2018
Аннотация
Показано влияние высших гармоник в квазигармоническом методе на точность вычисления динамических характеристик кусочно-линейной фазовой автоподстройки частоты, когда известны точные значения ее полосы захвата и частоты вращательных движений.
ВВЕДЕНИЕ
В данной работе анализируется точность приближенного метода исследования фазовых автоматических систем – квазигармонического метода (КГМ) – на примере фазовой автоподстройки частоты (ФАП), уравнение которой может быть записано в виде
где $\varphi $ – разность фаз, $F\left( \varphi \right)$ – периодическая нелинейность (нормированная характеристика фазового дискриминатора, ФД), $K\left( p \right)$ – коэффициент передачи фильтра низких частот. Функция $F\left( \varphi \right)$ удовлетворяет условиям
Квазигармонический метод удобно рассматривать, если уравнение (1) переписать в виде
или
(2)
$S\left( p \right)\varphi + R\left( p \right)\Phi \left( \varphi \right) = 0,\quad\quad\Phi \left( \varphi \right) \equiv F\left( \varphi \right) - \beta .$В основе КГМ лежит предположение о характере решения дифференциального уравнения: решение, соответствующее φ-циклам будем искать в форме
(3)
$\varphi \left( t \right) = \omega t + \operatorname{Im} \sum\limits_{k = 1}^N {{{w}_{k}}} \exp \left( {ik\omega t} \right),$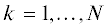
(N – число учитываемых гармоник). Представив характеристику $F\left( \varphi \right)$ частной суммой ряда Фурье
подставим $\varphi (t)$ и $F(\varphi )$ в уравнение (2). Тогда, осуществляя баланс гармонических и негармонических членов, получим систему уравнений для нахождения параметров φ-цикла:
Следует отметить, что метод дает количественные оценки параметров режимов работы ФАП.
Принцип гармонической линеаризации Е.П. Попова [1, 2] при одной гармонике предполагаемого решения дифференциального решения (ДУ) для нелинейных систем с периодической характеристикой ФД $F(x) = \sin x$ был рассмотрен в [3–5]. Однако в тех работах остались необоснованными критерии устойчивости движений, отсутствовала оценка точности принципа гармонического баланса, а также влияние высших гармоник на точность решения. Частично эти вопросы рассмотрены в [6].
Качественные оценки точности КГМ для систем второго и отчасти третьего порядков рассматривались в [6–10] при использовании, как правило, одной-двух гармоник метода и при синусоидальной характеристике ФД. В [9] была решена задача строгого обоснования метода для фазовой системы любой размерности, где показаны условия, при которых процедура квазигармонического баланса определяет решение, сходящееся при увеличении числа гармоник к точному решению. Как показали исследования, данный метод применим и для нелинейных характеристик ФД, не удовлетворяющих условиям теоремы [9], в частности при кусочно-линейной аппроксимации периодической нелинейности, в том числе разрывной. Это позволяет оценить влияние высших гармоник на точность метода, поскольку известны точные значения динамических характеристик ФАП [11, 12] при кусочно-линейной аппроксимации периодической нелинейности.
Далее рассмотрим следующие кусочно-линейные аппроксимации нелинейной функции:
1) треугольную аппроксимацию –
(5)
$F(x) = \left\{ \begin{gathered} {x \mathord{\left/ {\vphantom {x c}} \right. \kern-0em} c}\,\,\,\,{\text{п р и }}\,\,\,\,\left| x \right| \leqslant c,\,\,\,\quad\,({о б л а с т ь \;I}) \hfill \\ {{\left( {\pi - x} \right)} \mathord{\left/ {\vphantom {{\left( {\pi - x} \right)} {\left( {\pi - c} \right)\quad}}} \right. \kern-0em} {\left( {\pi - c} \right)\quad}} \hfill \\ {\text{п р и }}\,\,\,\,x \in \left( {c;2\pi - c} \right),\,\,\,\,({о б л а с т ь \;II\;}) \hfill \\ \end{gathered} \right.$2) пилообразную аппроксимацию –
(6)
$F(x) = {x \mathord{\left/ {\vphantom {x \pi }} \right. \kern-0em} \pi }\,\,\,\,{\text{п р и }}\,\,\,\,\left| x \right| \leqslant \pi .$Точность будем оценивать по полосе захвата ФАП и характеристике вращательных движений, причем последняя характеризуются частотой предельных циклов второго рода.
1. КУСОЧНО-ЛИНЕЙНАЯ СИСТЕМА ВТОРОГО ПОРЯДКА
Рассмотрим систему (1), (5) при $c = \,\quad{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и
(7)
$K\left( p \right) = {{\left( {d\alpha _{0}^{{ - 2}}p + 1} \right)} \mathord{\left/ {\vphantom {{\left( {d\alpha _{0}^{{ - 2}}p + 1} \right)} {\left( {\alpha _{0}^{{ - 2}}p + 1} \right)}}} \right. \kern-0em} {\left( {\alpha _{0}^{{ - 2}}p + 1} \right)}},\quad\,\,\,\alpha _{0}^{{ - 2}} = {c \mathord{\left/ {\vphantom {c {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}.$На рис. 1а и 1б приведены характеристики вращательных движений ${\beta }\left( {\omega } \right)$ (кривые биений) соответственно при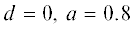 
– интегрирующий фильтр и $d = 0.1,\quad\,\,a = 0.1$ – пропорционально-интегрирующий фильтр с числом используемых гармоник одна, две и
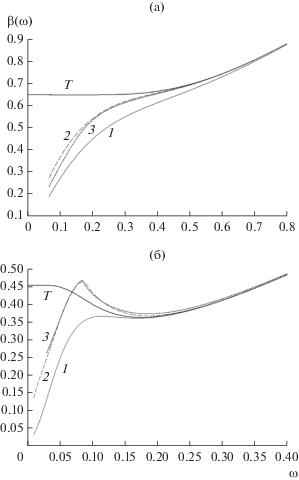
три. Точное значение полосы захвата для $d = 0;\,\,a = 0.8$ (см. рис. 1а) равно 0.6457, при учете одной гармоники – 0.6051 (ошибка 6.3%), двух гармоник –
0.6318 (ошибка 2.1%), трех гармоник – 0.6315 (ошибка 2.2%). Точное значение полосы
захвата для $d = 0.1;\,\,a = 0.1$ (см. рис. 1б) равно 0.3618. Приближенное значение полосы захвата в этом случае при учете одной
гармоники равно 0.3705 (ошибка 2.4%), двух гармоник – 0.3704 (ошибка 2.4%), трех гармоник
– 0.3750 (ошибка 3.6%). Как известно [11, 12], полоса захвата в случае интегрирующего фильтра определяется сепаратрисным циклом
и полуустойчивым предельным циклом в случае пропорционально-интегрирующего фильтра,
что в свою очередь соответствует минимуму кривой биений [6].
Рис. 1.
Кривые биения системы (1), (5), (7) при $d = 0\quad$ и $a = 0.8$ (а) и $d = 0.1\quad$ и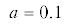 
(б) для одной (кривая 1), двух (2) и трех (3) гармоник; T – точная кривая.
На рис. 2 приведены зависимости полосы захвата ФАП от параметра ${\;\;\alpha }_{0}^{{ - 2}}$ при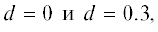 
полученные точно [7] (кривые T) и приближенно при использовании одной и трех гармоник (кривые 1 и 3).
Рис. 2.
Зависимость полосы захвата системы (1), (5), (7) от параметра $\quad{\alpha }_{0}^{{ - 2}}\,:$ номера кривых соответствуют числу гармоник, T – точная кривая.
Таким образом, как показывают вычисления полосы захвата и кривых биений, для практических приложений достаточно использовать две-три гармоники предполагаемого решения ДУ.
На рис. 3а, 3б, 4 представлены особенности применения КГМ при использовании пилообразной характеристики
ФД – система (1), (6), (7) при $d = 0,\quad\,\,a = 1.0$ (см. рис. 3а) и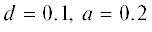 
(см. рис. 3б) и различном числе гармоник. Следует отметить, что кривые биений при 10 и 20 учитываемых
гармониках практически совпадают.
Рис. 3.
Кривые биения системы (1), (6), (7) при $d = 0$ и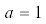 
(а) и $d = 0.1$ и 
(б): номера кривых соответствуют числу гармоник, T – точная кривая.
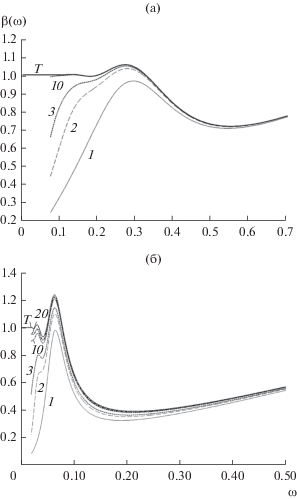
Значения оценки полосы захвата и их точные значения вместе с соответствующими частотами ω указаны при $d = 0.1$ и различных значениях a в табл. 1.
Таблица 1.
Значения полосы захвата $d = 0.1$
| Число гармоник |
Полоса захвата/частота при различном а | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 1 | $\frac{{0.2904}}{{0.1500}}$ | $\frac{{0.3230}}{{0.1990}}$ | $\frac{{0.3648}}{{0.2340}}$ | $\frac{{0.4144}}{{0.2830}}$ | $\frac{{0.4682}}{{0.3310}}$ |
| 2 | $\frac{{0.3228}}{{0.1660}}$ | $\frac{{0.3515}}{{0.2170}}$ | $\frac{{0.3906}}{{0.2620}}$ | $\frac{{0.4370}}{{0.3080}}$ | $\frac{{0.4885}}{{0.3540}}$ |
| 3 | $\frac{{0.3362}}{{0.1710}}$ | $\frac{{0.3615}}{{0.2130}}$ | $\frac{{0.3994}}{{0.2610}}$ | $\frac{{0.4451}}{{0.3090}}$ | $\frac{{0.4961}}{{0.3580}}$ |
| 10 | $\frac{{0.3578}}{{0.1820}}$ | $\frac{{0.3795}}{{0.2120}}$ | $\frac{{0.4135}}{{0.2520}}$ | $\frac{{0.4566}}{{0.2970}}$ | $\frac{{0.5059}}{{0.3440}}$ |
| 20 | $\frac{{0.3629}}{{0.1840}}$ | $\frac{{0.3839}}{{0.2120}}$ | $\frac{{0.4175}}{{0.2510}}$ | $\frac{{0.4592}}{{0.2960}}$ | $\frac{{0.5087}}{{0.3430}}$ |
| Т | $\frac{{0.3682}}{{0.1870}}$ | $\frac{{0.3886}}{{0.2140}}$ | $\frac{{0.4211}}{{0.2530}}$ | $\frac{{0.4631}}{{0.2970}}$ | $\frac{{0.5115}}{{0.3440}}$ |
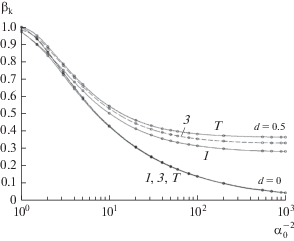
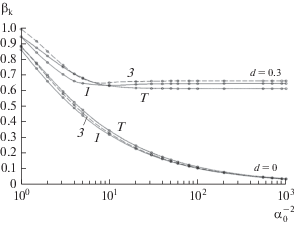
На рис. 4 изображены зависимости полосы захвата $\quad{{{\beta }}_{k}}$ ФАП от параметра $\quad\alpha _{0}^{{ - 2}}$ при $d = 0\,\,{\;и }\,\,\quad0.5.$ Отметим, что при $d = 0$ кривые 1–3 практически совпадают.
2. КУСОЧНО-ЛИНЕЙНАЯ СИСТЕМА ФАП ТРЕТЬЕГО ПОРЯДКА
Рассмотрим систему (1), (5), $c = \,\quad{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ когда передаточная функция K(p) имеет вид
(8)
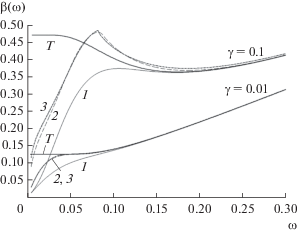
$\begin{gathered} K(p) = {{({{A}_{0}}{{p}^{2}} + {{A}_{1}}p + 1)} \mathord{\left/ {\vphantom {{({{A}_{0}}{{p}^{2}} + {{A}_{1}}p + 1)} {({{B}_{0}}{{p}^{2}} + {{B}_{1}}p + 1)}}} \right. \kern-0em} {({{B}_{0}}{{p}^{2}} + {{B}_{1}}p + 1)}}, \\ \quad{\text{г д е }}\,\,\quad{{A}_{0}} = \rho {{q}^{2}},\quad\,\,\,\,{{A}_{1}} = \gamma q\delta ,\,\,\,\,{{B}_{0}} = {{q}^{2}},\,\,\,\,\quad{{B}_{1}} = q\delta . \\ \end{gathered} $Пусть ${{A}_{0}} = {{A}_{1}} = 0\quad\,\,\left( {\gamma = 0,\,\,\quad\rho = 0} \right),$ тогда кривые биений имеют вид, представленный на рис. 5 $(\delta = 6,\quad\,\,q = 0.3).$ Характер кривых биений такой же, как в случае ФАП с интегрирующим фильтром (см. рис. 1а). Обозначение кривых по числу используемых гармоник то же, что и для ФАП второго порядка.
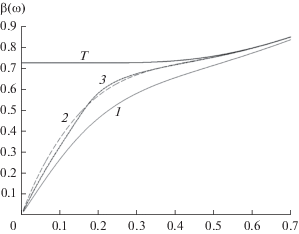
Зависимость полосы захвата от параметра δ изображена на рис. 6 при $q = 0.3,$ $q = 2.4\quad$ и $\gamma = \rho = 0.$ Из рис. 5 и 6 можно сделать вывод, что двух гармоник, а в некоторых случаях трех гармоник достаточно для обеспечения приемлемой точности вычисления полосы захвата ФАП. На рис. 7 изображены кривые биений при $\rho = 0,$ $q = 1.2,$ $\quad\delta = 150$ и ${\gamma } = 0.1\quad$ и 0.01. Значения полосы захвата при $\gamma = \,\quad0.01\,:$ для одной гармоники – 0.1169, для двух – 0.1236, для трех – 0.1224, Т – 0.1251; при $\gamma = \quad\,0.1\,:$ для одной гармоники – 0.3681, для двух – 0.3668, для трех – 0.3718, Т – 0.3616. Зависимость полосы захвата от параметра δ при $\rho = 0$ и $\quad\quad\gamma \ne 0$ при различных значениях q и γ показаны на рис. 8а, 8б.
Рис. 6.
Зависимость полосы захвата системы (1), (5), (8) от параметра δ при $\gamma = 0,\quad\,\,\rho = 0.$
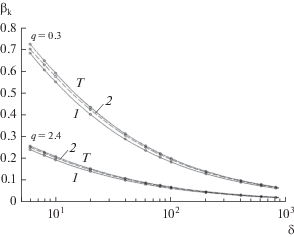
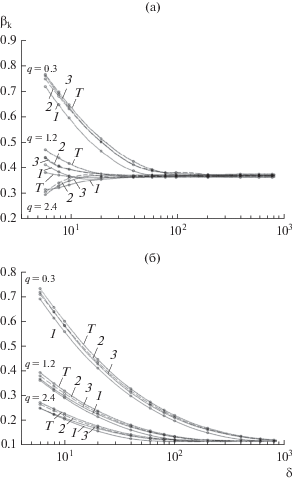
Рис. 8.
Зависимость полосы захвата системы (1), (5), (8) от параметра δ при $\quad{\rho } = 0{\;и \;\gamma } = 0.1$ (а) и 0.01 (б).
Кривые биения системы (1), (6), (8) представлены на рис. 9а $(\gamma = \rho = 0,\quad\,\,\delta = 6,\quad\,\,q = 0.3)$ и рис. 9б $(\gamma = \rho = 0.1,\,\,\quad\delta = 20,\quad\,\,q = 1.2).$ Кривые биений аналогичны кривым в системе второго порядка (см. рис. 3а и 3б). Для рис. 9а точное значение полосы захвата равно 0.8802; при учете одной гармоники – 0.8635, двух – 0.8784, трех – 0.8817, двадцати – 0.8804. Для рис. 9б точное значение полосы захвата равно 0.4434; при учете одной гармоники – 0.3930, двух – 0.4143, трех – 0.4229, двадцати – 0.4403. Зависимость полосы захвата от параметра δ при $\gamma = \quad\,\rho = 0$ и различных значениях q приведена на рис. 10а. Как видим, кривые приближенного метода практически сливаются с кривыми точного метода.
Рис. 9.
Кривые биения системы (1), (6), (8) при различных параметрах: а) $\gamma = 0,\,\,\quad\rho = 0,$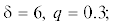 
б) $\gamma = 0.1,\quad\,\,\rho = 0.1,$ $\quad\delta = 20,\quad\,\,q = 1.2$; точные значения Т изображены сплошной кривой, номера кривых соответствует числу учитываемых гармоник.
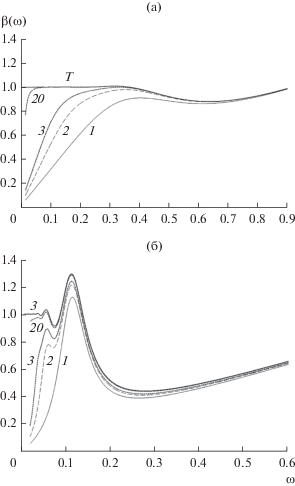
Рис. 10.
Зависимость полосы захвата системы (1), (6), (8) от параметра δ при $\gamma = 0,\quad\,\,\rho = 0$ (а), $\rho = 0$ и $\gamma = 0.3$ (б) и $\rho = 0$ и $\gamma = 0.1$ (в).
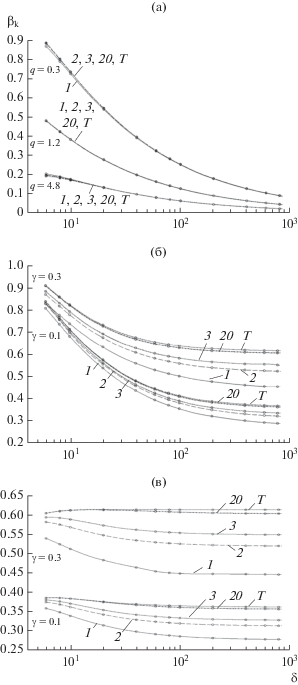
На рис. 10б и 10в иллюстрируется зависимость полосы захвата от параметра δ при $\rho = 0$ и $\quad\quad\gamma \ne 0\quad$ и различных значениях q и γ. Значения полосы захвата для $\quad\rho = 0.1$ системы (1), (6), (8) при различных значениях остальных параметров приведены в табл. 2.
Таблица 2.
Полоса захвата для пилообразной характеристики ФД при $\rho = 0.1$ и различных γ и q
| Число учитываемых гармоник | δ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 20 | Т | 1 | 2 | 3 | 20 | Т | |
| $\gamma = 0.01,\,\,\,\,q = 0.3$ | $\gamma = 0.01,\,\,\,\,q = 1.2$ | |||||||||
| 0.9579 | 0.9680 | 0.9748 | 0.9762 | 0.9772 | 0.5706 | 0.5704 | 0.5695 | 0.5716 | 0.5735 | 4 |
| 0.8633 | 0.8789 | 0.8826 | 0.8823 | 0.8832 | 0.4834 | 0.4853 | 0.4853 | 0.4869 | 0.4891 | 6 |
| 0.7236 | 0.7330 | 0.7353 | 0.7353 | 0.7360 | 0.3893 | 0.3924 | 0.3930 | 0.3945 | 0.3967 | 10 |
| 0.5424 | 0.5489 | 0.5508 | 0.5510 | 0.5516 | 0.2891 | 0.2930 | 0.2942 | 0.2961 | 0.2979 | 20 |
| 0.2657 | 0.2710 | 0.2727 | 0.2741 | 0.2746 | 0.1561 | 0.1624 | 0.1642 | 0.1678 | 0.1690 | 100 |
| 0.2000 | 0.2057 | 0.2077 | 0.2098 | 0.2105 | 0.1286 | 0.1364 | 0.1386 | 0.1430 | 0.1442 | 200 |
| $\gamma = 0.1,\,\,\,\,q = 0.3$ | $\gamma = 0.1,\,\,\,\,q = 1.2$ | |||||||||
| 0.9415 | 0.9673 | 0.9751 | 0.9853 | 0.9868 | 0.6244 | 0.6348 | 0.6380 | 0.6452 | 0.6472 | 4 |
| 0.8687 | 0.8946 | 0.9008 | 0.9087 | 0.9101 | 0.5475 | 0.5615 | 0.5665 | 0.5762 | 0.5785 | 6 |
| 0.7496 | 0.7677 | 0.7732 | 0.7819 | 0.7836 | 0.4691 | 0.4864 | 0.4931 | 0.5061 | 0.5089 | 10 |
| 0.5927 | 0.6100 | 0.6160 | 0.6267 | 0.6289 | 0.3929 | 0.4141 | 0.4227 | 0.4398 | 0.4433 | 20 |
| 0.3759 | 0.4004 | 0.4087 | 0.4264 | 0.4302 | 0.3088 | 0.3376 | 0.3497 | 0.3742 | 0.3791 | 100 |
| 0.3338 | 0.3617 | 0.3710 | 0.3923 | 0.3968 | 0.2941 | 0.3257 | 0.3388 | 0.3651 | 0.3703 | 200 |
ЗАКЛЮЧЕНИЕ
Проведенные в данной статье исследования показывают возможность получения высокой точности квазигармонического метода при использовании двух-трех гармоник предполагаемого решения ДУ при треугольной характеристике ФД, а при пилообразной характеристике ФД практически точные значения полосы захвата можно получить при числе гармоник, равном 20. Таким образом, показана возможность использования КГМ как для непрерывных кусочно-линейных характеристик ФД систем ФАП, так и для ФАП с разрывной (пилообразной) характеристикой. В случае пилообразной характеристики ФД увеличение числа гармоник в предполагаемом решении ДУ осуществляется значительно проще, чем для непрерывной кусочно-линейной характеристике ФД. Сравнение данных КГМ и точных значений динамических характеристик продемонстрировано на примерах кривых биений и полосы захвата ФАП.
Список литературы
Попов Е.П. Прикладная теория процессов управления в нелинейных системах М.: Наука, 1973.
Нелинейные системы автоматического управления // Метод гармонической линеаризации в проектировании нелинейных систем автоматического управления / Под общ. ред. Попова Е.П. М.: Машиностроение, 1970.
Урман Е.Л. // Вестник электропромышленности. 1957. № 4. С. 54.
Niawiadomski T. // Archiwum Elektrotechniki. 1960. T. 9. № 42. C. 53.
Rey T.J. Automatic phase control: theory and design Proc. IRE. 1960. V. 48. № 10. P. 1760.
Шахтарин Б.И. Квазигармонический метод и его применение к анализу нелинейных фазовых систем. М.: Энергоатомиздат, 1987.
Шахтарин Б.И. // Изв. АН СССР. Техническая кибернетика. 1977. № 5. С. 174.
Грибов А.Ф., Шахтарин Б.И. // Автоматика и телемеханика. 1981. № 10. С. 183.
Грибов А.Ф., Шахтарин Б.И. // Вестник МГТУ им. Н.Э. Баумана. Естественные науки. 2014. № 1. С. 3.
Грибов А.Ф., Шахтарин Б.И. // РЭ. 2013. Т. 58. № 11. С. 1107.
Губарь Н.А. // Прикл. математика и механика. 1961. Т. 25. № 6. С. 1011.
Шaxтapин Б.И. // PЭ. 1969. T. 14. № 8. C. 1315.
Грибов А.Ф., Крищенко А.П. // РЭ. 1982. Т. 27. № 2. С. 321.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника
Пн.-пт.: 10.00-19.00