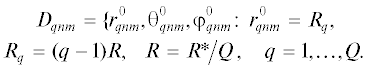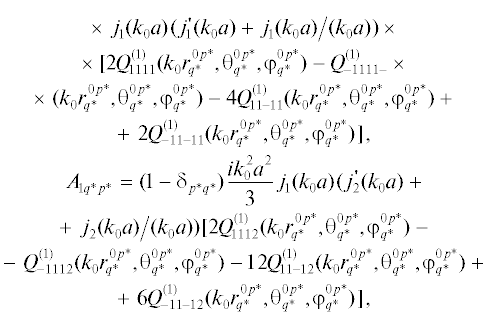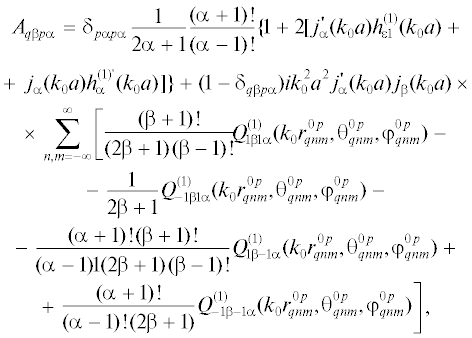Радиотехника и электроника, 2019, T. 64, № 5, стр. 432-439

ВВЕДЕНИЕ

С точки зрения теории распространения электромагнитного поля наличие большого количества частиц в среде может привести не только к ослаблению этого поля через механизм рассеяния, но и изменению скорости распространения поля в среде с частицами, что необходимо учитывать, например, при анализе сдвига спектра частот излучения из-за эффекта Доплера. Процесс распространения монохроматического звукового и электромагнитного поля в среде с частицами описывается скалярным и векторным уравнениями Гельмгольца соответственно. Теоретические исследования и эксперименты показывают, что скорость распространения звука в жидкости с пузырьками газа или пара, которая описывается скалярным уравнением Гельмгольца, может меняться на один-два порядка в зависимости от концентрации и размера пузырьков [1–5]. Следовательно, скорость распространения электромагнитных волн в среде с частицами также должна зависеть от свойств, концентрации и размера частиц. В предлагаемой статье в развитие работ [3‒5] для электромагнитных волн предложен следующий способ вычисления скорости распространения возмущений. В пространстве с заданной скоростью распространения поля (в вакууме это скорость света) выделяется область D, заполненная частицами сферической формы, и исследуется задача дифракции стороннего поля на этом множестве частиц. Далее предполагается, что область D без частиц представляет собой прозрачное тело с произвольной скоростью распространения поля, и решается задача дифракции того же стороннего поля на прозрачном теле D. Из условия равенства вне области D поля, рассеянного на частицах и на прозрачном теле, находится величина скорости распространения поля в прозрачном теле D, и эта скорость полагается равной эффективной скорости распространения поля в среде с частицами.

При произвольном расположении частиц в пространстве анализ физического механизма изменения скорости распространения электромагнитного поля затруднен из-за сложного поведения дифракционного поля на совокупности частиц. Поэтому механизм изменения скорости света за счет многократного рассеяния на частицах будем исследовать в средах, в которых частицы расположены регулярно, а именно, в виде соответствующих решеток. Рассмотрим две модели многократного рассеяния. В первой модели в качестве области D рассматривается шар D_R и для обеспечения механизма многократного рассеяния исследуется задача дифракции плоской волны на сферической Q-слойной решетке элементов сферической формы малых волновых размеров, погруженной в шар D_R. Расстояние между центрами элементов решетки порядка двух-трех диаметров элементов. Полученное решение сравнивается с решением задачи дифракции плоской волны на прозрачном шаре D_R, заполненным средой с другими параметрами распространения.

1. ПОСТАНОВКА ЗАДАЧИ ДИФРАКЦИИ НА СФЕРИЧЕСКОЙ РЕШЕТКЕ

Рассмотрим задачу дифракции плоской волны $E_{x}^{0} = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} H_{y}^{0}$ = Eexp(ik₀z), $k_{0}^{2}$ = (ω/c)²ε₀μ₀ – волновое число, ω – круговая частота, $c$ – скорость света, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} $ – вектор напряженности электрического поля, ε₀, μ₀ – относительная диэлектрическая и магнитная проницаемости среды, на сферической Q-слойной решетке. В сферической системе координат с полюсом в О координаты центра шара D_qnm задаются соотношениями:

При q > 1 углы $\theta _{{qnm}}^{0}$ = $\theta _{{qn}}^{0}$ = π(n – 1)/2q, n = 1, …, 2q + 1, $\varphi _{{qnm}}^{0}$ = 2π(m – 1)/M_qn, m = 1, …, M_qn.

Если n ≤ q + 1, то M_qn = 2n – 1, если n ≥ q + 1, то M_qn = 2(2q + 1 – n) + 1, волновой радиус k₀R* не мал. Для q = 1 в точке O располагается центр шара D₁₁₁. Множество сфер S_q радиусом R_q с элементами D_qnm будем называть сферической Q-слойной решеткой элементов D_qnm с центром в О. При такой геометрии расстояние между центрами элементов в сферической Q-слойной решетке порядка R, а число элементов равно

поэтому при конечной величине k₀R* эффект взаимного рассеяния поля на частицах в Q-слойной сферической решетке должен быть конечным.

Обозначим через DR внешность элементов Q‑слойной решетки 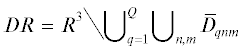(${{\bar {D}}_{{qnm}}}$ – замыкание области D_qnm). Введем локальную декартову систему координат с началом в центре шара D_qnm, оси которой одинаково ориентированы и параллельны осям основной декартовой системы координат с центром в О_c. Введем также согласованную локальную сферическую систему координат (r_qnm, θ_qnm, φ_qnm) с полюсом в центре шара D_qnm, полярной осью, совпадающей с осью z локальной декартовой системы и одинаково ориентированными полярным расстоянием и долготой основной и локальной сферических координатных систем. Пусть на сферическую Q‑слойную решетку из пространства DR падает плоская электромагнитная волна, имеющая отличную от нуля декартову компоненту

где $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} ,\vec {H}$ – векторы напряженности электрического и магнитного поля, ε₀, μ₀ – относительная диэлектрическая и магнитная проницаемости среды в области DR.

Если среда в области DR-вакуум, то ε₀ = μ₀ = 1. Для упрощения решения исследуем задачу дифракции плоской волны на частицах D_qnm сферической формы с абсолютно проводящей поверхностью в предположении, что все частицы одного размера. Поверхность шара D_qnm обозначим S_qnm. Будем исследовать электромагнитное поле в диапазоне частот, для которого волновой размер k₀a мал, а отношение расстояния между центрами частиц к диаметру частицы конечно. Представим векторы $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} ,\vec {H}$ в виде суммы падающего и рассеянного поля:

где ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} }_{0}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} }_{1}}$ – падающая и рассеянная части напряженности электрического поля, ${{\vec {H}}_{0}},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} }_{1}}$ – падающая и рассеянная части напряженности магнитного поля. Векторы напряженности электрического и магнитного поля в области DR удовлетворяют уравнениям Максвелла

Рассеянная составляющая векторов $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} $ и $\vec {H}$ должна быть ограничена по модулю в области DR при Imk₀ > 0. На поверхности сферы S_qnm должны выполняться условия сопряжения

где [ , ] – векторное произведение, $\vec {n}$ – внешняя нормаль к сфере S_qnm. Ищется дважды непрерывно дифференцируемое внутри области DR и непрерывное вплоть до границы области решение задачи (1), (2).

Будем искать решение задачи (1), (2) в области DR с помощью потенциалов Дебая электрического U и магнитного V типов, которые удовлетворяют скалярному уравнению Гельмгольца

Представим потенциалы Дебая U и V в виде сумм U= U₀ + U₁ и V= V₀ + V₁, где U₀ и V₀ – потенциалы, отвечающие падающему полю. Рассеянная составляющая потенциалов U₁ и V₁ должна быть ограничена по модулю в области D при Im k₀ > 0. На поверхности сферы S_qnm должны выполняться условия равенства нулю касательных составляющих электромагнитного поля, выписанные на границе S_qnm, через потенциалы Дебая:

где ∂/∂n – производная по нормали к поверхности S_qnm, направленная из области D_qnm, r_qnm – расстояние во вспомогательной сферической системе координат. Соотношения, связывающие потенциалы Дебая с проекциями электромагнитного поля внутри D в сферической системе координат (r, θ, φ), связанной с центром O_c, задаются по формулам

В соотношениях (7) вне шара D волновое число k заменяется на k₀.

Решение задачи для потенциала Дебая U₁ следует искать в виде потенциалов для уравнения Гельмгольца простого слоя

где через ${{G}_{0}}_{{}}$ обозначено фундаментальное решение уравнения Гельмгольца, отвечающее волновому числу k₀, R_qnm – расстояние от точки интегрирования до точки наблюдения в локальной сферической системе координат, ${{\nu }_{{qnm}}}$ – неизвестные плотности потенциалов. Потенциал Дебая V₁ будем искать в виде суммы потенциалов двойного слоя для уравнения Гельмгольца

где w_qnm – неизвестные плотности потенциалов, ∂/∂n – производная по нормали в точке интегрирования. Из теории дифракции на шаре малого волнового диаметра известно, что плотности ${{\nu }_{{qnm}}}$ и ${{w}_{{qnm}}}$ можно искать в виде

где a_1qn, a_2qnm, c_1qnm, c_2qnm – неопределенные коэффициенты, $P_{n}^{m}(x)$ –присоединенные полиномы Лежандра, (θ_qnm, φ_qnm) – сферические координаты в локальной системе.

Воспользуемся свойствами потенциалов для уравнения Гельмгольца простого и двойного слоя. Подставим представления (8), (9) в краевые условия на поверхности S_qnm. В результате получим систему интегральных уравнений для вычисления плотностей ${{\nu }_{{qnm}}}$ и ${{w}_{{qnm}}}.$ Далее используем представления (10) и представления сферических функций в разных системах координат –

Здесь $({{r}_{i}},{{\theta }_{i}},{{\phi }_{i}})$ и $({{r}_{j}},{{\theta }_{j}},{{\phi }_{j}}) - $ сферические координаты в i-й и j-й системах координат соответственно, $(r_{j}^{i},\theta _{j}^{i},\varphi _{j}^{i})$ – координаты j-го центра в i-й системе координат, j_n(x), h_n⁽¹⁾(x) – сферические функции Бесселя и Ганкеля, коэффициенты Клебша–Гордана $b_{i}^{{(qjnm)}}.$ Коэффициенты Клебша–Гордана $b_{i}^{{(qjnm)}}$ определены в [6]. Применяя представления (10), (12) в совокупности с методом Галеркина, получаем систему алгебраических уравнений для вычисления коэффициентов a_1qn, a_2qnm :

В уравнениях (13) введены обозначения

где $(r_{{q*}}^{{0p*}},\theta _{{q*}}^{{0p*}},\varphi _{{q*}}^{{0p*}})$ – координаты центра сферы S_qnm в системе координат, связанной с центром сферы S_p00; ${{j}_{i}}^{'}(ka),$ $h_{i}^{{(1)'}}(ka),$ $i = 1,2$ – соответственно производные сферических функций Бесселя и Ганкеля по аргументу, ${{\delta }_{{p*p*}}} = 1,$ ${{\delta }_{{p*q*}}} = 0,$ p* → (pjl), q* → (qnm).

Решая алгебраическую систему (13), (14), определяем амплитуды асимптотик неизвестных плотностей ${{\nu }_{{qnm}}},$ а по формуле (8) вычисляем поле U₁. Поступая аналогичным образом для вычисления коэффициентов c_1qnm, c_2qnm, получим следующую систему алгебраических уравнений:

В уравнениях (15) введены следующие обозначения:

Решая алгебраическую систему (15), определяем амплитуды асимптотик неизвестных плотностей w_q, а по формуле (9) вычисляем поле V₁.

Внутри прозрачного шара D_R для произвольных значений параметров среды шара ε*, μ*, σ* решение задачи дифракции на прозрачном шаре можно выписать в явном виде. Оно приведено во многих работах, например, в [6]. Решение ищется в виде потенциалов Дебая электрического U ^j и магнитного V ^j (j = 0, 1) типов. Вне шара D_R потенциалы удовлетворяют уравнениям

(причем потенциалы должны быть ограничены по модулю при Imk₀ > 0 в области вне шара D), а внутри D – уравнениям

На поверхности S шара D_R для потенциалов Дебая, удовлетворяющих (16), (17), выполняются условия сшивания:

где ∂/∂n – производная по нормали к поверхности S, направленная вне области D, r – расстояние в сферической системе координат. Для рассеянной составляющей потенциала Дебая $U_{0}^{1}$ электрического типа и $V_{0}^{1}$ магнитного типа в сферической системе координат, приведем взятые из работы [6] формулы

Здесь ${{\psi }_{n}}(x) = x{{j}_{n}}(x),$ ${{\zeta }_{n}}(x) = xh_{n}^{{(1)}}(x),\,\,{{\chi }_{n}}(x) = $ $ = {{\psi _{n}^{'}(x)} \mathord{\left/ {\vphantom {{\psi _{n}^{'}(x)} {{{\psi }_{n}}(x)}}} \right. \kern-0em} {{{\psi }_{n}}(x)}},$ ${{j}_{n}}(x),$ $h_{n}^{{(1)}}(x)$ – сферические функции Бесселя и Ганкеля, $\psi _{n}^{'}(x),$ $\zeta _{n}^{'}(x)$ – производная по аргументу, $P_{n}^{m}(x)$ – присоединенные полиномы Лежандра.

Обозначим через ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} }_{m}},$ ${{\vec {H}}_{m}}$ электромагнитное поле дифракции на прозрачном шаре, через ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} }_{p}},$ ${{\vec {H}}_{p}}$ электромагнитное поле дифракции на Q‑слойной решетке и потребуем, чтобы поля и их касательные составляющие были равны в замкнутой области r ≥ R*

Считая поле дифракции на решетке известным, подставим в (20) соотношения (18). Путем интегрирования по сфере r = R* получаем нелинейные уравнения для вычисления параметров ε*, μ*, σ*. Если среды не ферромагнетики, то магнитная проницаемость в приведенных выше задачах известна и равна 1.0. В этом случае достаточно решить задачу определения потенциала Дебая электрического или магнитного типа для Q-слойной решетки и прозрачного шара и сравнить эти потенциалы по первому соотношению формулы (20).

2. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ВОЛНОВОДЕ

Во второй модели для обеспечения механизма многократного рассеяния исследуется распространение электромагнитного поля через плоскую многослойную решетку. Она представляет собой Q плоскостей (слоев) z_c = const. На слоях периодически вдоль осей x,y расположены центры элементов сферической формы, волновой радиус ka элементов не мал. Решетка погружена в слой толщиной (Q + 1)L, 2a/L ≤ 0.5, L – расстояние между плоскостями, на которых расположены центры элементов двоякопериодической решетки. Для магнитной составляющей поля такая задача эквивалентна задаче распространения нормальной волны в направляющей системе вида бесконечного волновода прямоугольного поперечного сечения, на оси которого на отрезке длиной (Q + 1)L располагаются центры Q-частиц сферической формы, волновой диаметр которых не мал, а расстояние между центрами конечно. В качестве области D рассматривается расположенный внутри волновода конечный слой толщиной (Q + 1)L с другими параметрами распространения. Для вычисления скорости распространения поля при z > (Q + 1)L сравнивается распространяющаяся составляющая поля дифракции на Q-частицах с полем в волноводе, прошедшим через слой длиной (Q + 1)L.

Для волновода с частицами рассмотрим спектр излучения, для которого волновой размер частиц ka ≤ 0.5. Пространство внутри волновода W будем характеризовать параметрами ε и μ (ε –диэлектрическая, μ – магнитная проницаемости). Для вакуума параметры ε = μ = 1. На оси волновода размещены частицы сферической формы D_q, q = 1, …, Q. Радиус частицы D_q равен а, ее центр расположен в точке с координатами (0,0,(q – 1)L), так что начало декартовой системы совпадает с центром первой частицы. Для упрощения решения будем считать поверхность частицы D_q идеально проводящей. Обозначим через 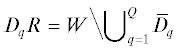(${{\bar {D}}_{q}}$ – замыкание области D_q). В области D_qR из полупространства z < 0 на конечное множество частиц D_q падает электромагнитное поле. Представим полное поле в виде суммы падающего поля и рассеянной части. Векторы напряженности полного электрического $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} $-поля и магнитного $\vec {H}$-поля в области D_qR удовлетворяют уравнениям Максвелла

где ω – круговая частота, с – скорость распространения света в вакууме. Из уравнений (21) следует, что в кусочно-однородной изотропной среде без локальных источников векторы $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} $ и $\vec {H}$ удовлетворяют векторным уравнениям Гельмгольца

где k – волновое число поля в области D_qR. На стенке волновода и на поверхностях S_q шаров D_q (q = 1, …, Q) должно выполняться условие обращения в нуль касательной составляющей электрического поля $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} $. Если в волноводе распространяется электромагнитное поле, то рассеянная часть векторов $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} $ и $\vec {H}$ должна быть ограничена по модулю в области D_qR при Im k > 0. Особенность распространения электромагнитных волн в волноводах заключается в том, что существует критическая длина волны, и волна с большей длиной в волноводе не распространяется. Если μ*, ε* – произвольные константы, характеризующие среду с включениями, то для вычисления этих констант среды нужно исследовать задачу распространения как электрической волны в волноводе (H_z-компонента равна нулю), так и задачу распространения магнитной волны (Е_z-компонента равна нулю). Если материал среды и частиц не ферромагнетик, то с высокой точностью можно положить µ* = 1.0. В этом случае достаточно исследовать задачу дифракции в волноводе или электрических, или магнитных волн.

Далее исследуем магнитные волны, для которых E_z-компонента электромагнитного поля равна нулю. Пусть распространяющаяся из бесконечности при z < 0 в области D магнитная волна имеет вид

где ${{h}_{{10}}} = \sqrt {k_{{}}^{2} - g_{{10}}^{2}} > 0,$ $E_{z}^{0} = 0,$ множитель exp(–iωt) далее опускаем. Параметр $h = {{h}_{{nm}}} = \sqrt {{{k}^{2}} - g_{{nm}}^{2}} ,$ где g_nm – собственные значения задачи Дирихле или Неймана для уравнения Лапласа в поперечном сечении волновода, называется продольным волновым числом. Потребуем, чтобы поперечный волновой размер волновода лежал в диапазоне ${{g}_{{10}}}{{l}_{1}} < k{{l}_{1}} < {{g}_{{20}}}{{l}_{1}},$ где g₁₀, g₂₀ – первое и второе в порядке возрастания отличные от нуля собственные значения задачи Неймана уравнения Лапласа, определенные в поперечном сечении волновода. В этом случае тип волны, распространяющейся в волноводе при z < –L, сохранится при z > QL, т.е. новых нормальных волн в волноводе в процессе дифракции на частицах не возникнет. Обозначим H_z-компоненту полного магнитного поля в волноводе через U и примем U = U₀+ U₁, где U₀ = $H_{z}^{0},$ U₁ – рассеянная на частицах часть магнитного поля. Поле U₁ внутри волновода удовлетворяет скалярному однородному уравнению Гельмгольца

где k – волновое число в области П, ${{\left. {{{\partial {{U}_{1}}} \mathord{\left/ {\vphantom {{\partial {{U}_{1}}} {\partial n}}} \right. \kern-0em} {\partial n}}} \right|}_{\Gamma }} = 0,$ Г – боковая поверхность волновода, n – нормаль к боковой поверхности, направленная внутрь области определения поля. Поле U₁ ограничено в области D_qR при Imk > 0. На поверхности сфер D_q должны выполняться условия

Здесь ∂/∂n – производная по нормали к сфере S_q, направленная из шара D_q.

Решение задачи (22), (23) можно представить в виде суммы потенциалов простого слоя для уравнения Гельмгольца со специальным ядром $G(\bar {x},{{\bar {\xi }}_{q}})$ в виде функции Грина для бесконечного волновода квадратного поперечного сечения с идеально проводящими стенками

Подставляя представление (24) в краевые условия (23) и пользуясь свойствами потенциала простого слоя для уравнения Гельмгольца, получим систему интегральных уравнений для вычисления плотностей ν_q:

∂/∂n₁ – производная по внешней к поверхности S_p нормали в точке ${{\bar {\xi }}_{{1p}}}$. При решении системы уравнений (25) удобно представление функции G, построенное методом отражения от стенок волновода

При условии ka, h₁₀a ≤ 0.5 плотность ν_p можно искать в виде

где a_pβ, β = 1, В, p = 1, ..., Q – неопределенные коэффициенты, (θ_p, φ_p) – сферические координаты с полюсом в центре сферы S_p. При вычислении с точностью до четвертого знака параметр В = 5. Подставим в систему (25) представление (26) и представление сферических функций в разных системах координат (12).

Применяя метод Галеркина, получаем систему алгебраических уравнений для вычисления неизвестных x_qβ =a_qβh₁₀/(2H):

где

δ_pαpα =1, δ_qβpα = 0; q, p = 1,…, Q; α, β = 1, …, B; J_n(x) – функция Бесселя. $(r_{{qnm}}^{{0p}},\theta _{{qnm}}^{{0p}},\varphi _{{qnm}}^{{0p}})$ – координаты центра qnm – элемента двоякопериодической решетки в системе координат, связанной с центром элемента p = p00.

Решая алгебраическую систему (27), (28) определяем амплитуды асимптотик неизвестных плотностей ν_q, а по формуле (24) вычисляем поле U₁. В процессе рассеяния поля на частицах образуется не только дифракционное поле U₁, но и так называемая эффективная скорость распространения волн в среде с частицами. Эту скорость определим следующим образом. Пусть внутри волновода с параметрами среды ε, μ размещен слой S = = {(x, y, z): –l₁ ≤ x, y ≤ l₁, –L ≤ z ≤ QL} диэлектрика с параметрами среды $\varepsilon _{s}^{'} = {{\varepsilon }_{s}} + {{4\pi i{{\sigma }_{s}}} \mathord{\left/ {\vphantom {{4\pi i{{\sigma }_{s}}} \omega }} \right. \kern-0em} \omega },\quad$ μ_s = 1, где σ_s – проводимость среды слоя. Материал среды слоя будем считать не ферромагнетиком. Из полупространства z < 0 на слой S падает стороннее поле в виде магнитной волны

Требуется найти амплитуду прошедшей через слой волны при z > QL. Будем считать, что поперечный волновой размер волновода, содержащего диэлектрический слой, также лежит в диапазоне ${{g}_{{10}}}{{l}_{1}} < k{{l}_{1}} < {{g}_{{20}}}{{l}_{1}}.$ Магнитное поле удовлетворяет: вне S однородному уравнению Гельмгольца (22); внутри S тому же уравнению (22), в котором ε и µ надо заменить на $\varepsilon _{s}^{'},$ μ_s, – и однородным условиям Неймана на границе поперечного сечения. В процессе распространения волны $H_{z}^{0}$ в волноводе со слоем диэлектрика при z < 0 образуется отраженная волна, внутри слоя – стоячая волна с волновым числом $k_{s}^{2} = k_{0}^{2}\varepsilon _{s}^{'}{{\mu }_{s}},$ а вне слоя при z > QL возбуждается прошедшая волна. Амплитуды этих волн вычисляются из условий равенства касательных составляющих магнитного поля H_z на границах слоя при z = –L и z = QL. Решение этой задачи известно [7]. Прошедшая через слой волна имеет вид

где

Если потребовать, чтобы в волноводе при z > QL амплитуда H_zs прошедшего через слой S поля равнялась амплитуде H_zd падающего поля плюс амплитуде распространяющейся части поля дифракции на конечном множестве частиц D_q,

то при известных параметрах задачи ω, ε, μ = μ_s =1.0, равенство (29) с учетом соотношений (28) есть нелинейное уравнение для вычисления электрической проницаемости $\varepsilon _{s}^{'} = \varepsilon {*\;}$ или скорости распространения электромагнитного поля c_s = ${c \mathord{\left/ {\vphantom {c {\sqrt {\varepsilon {\text{*}}} }}} \right. \kern-0em} {\sqrt {\varepsilon {\text{*}}} }},$ которая, вообще говоря, комплексна. Скорость распространения поля c_s в слое S назовем эффективной скоростью распространения электромагнитного поля в среде волновода, содержащей включения.

ЗАКЛЮЧЕНИЕ

Предложены два способа вычисления скорости распространения электромагнитного поля в среде с включениями. Очевидно, что эффект многократного рассеяния возрастает с ростом числа слоев решеток. Если аналогия изменения скорости звука и света с ростом концентрации частиц справедлива, то скорость электромагнитного поля должна убывать с ростом концентрации от скорости света при нулевой концентрации, а затем возрастать. С точки зрения вычислений второй способ предпочтительнее первого, поскольку размерность матриц системы алгебраических уравнений (13), (15) существенно выше размерности матрицы системы (27), так как дифракционное взаимодействие между элементами в плоскости решетки учитывается специально выбранной функцией Грина в представлении (24). Например, при числе слоев сферической и плоской решетки, равной 50, и точности вычисления до четвертого знака размерность матрицы коэффициентов систем (13), (15) равна (500 292 × × 500 292), а размерность матрицы коэффициентов (27) равна (250 × 250).