Радиотехника и электроника, 2019, T. 64, № 6, стр. 525-534
Формирование амплитудных и поляризационных характеристик коротких волн при распространении в ионосфере
В. Е. Захаров *
Балтийский федеральный университет имени Иммануила Канта
236041 Калининград, ул. Александра Невского, 14, Российская Федерация
* E-mail: VEZakharov@kantiana.ru
Поступила в редакцию 19.09.2017
После доработки 18.09.2018
Принята к публикации 11.12.2018
Аннотация
Исследовано изменение параметров вектора комплексной амплитуды узкополосных сигналов вдоль лучевых траекторий применительно к коротким волнам в трехмерно неоднородной анизотропной плазме ионосферы. Проведены численные эксперименты, а также анализ поляризационных и амплитудных характеристик обыкновенных и необыкновенных волн в зависимости от положения источника, несущей частоты сигнала, угловых координат излучения и геофизических условий.
ВВЕДЕНИЕ
Радиоволны декаметрового диапазона широко применяют в радиосвязи, радиолокации, радионавигации и при изучении структуры и динамики ионосферы. Обработка сигналов на приеме требует понимания закономерностей их преобразования при распространении в ионосфере. Актуально исследование формирования характеристик поля радиоизлучения в трехмерно неоднородной анизотропной ионосфере под действием комплекса геофизических факторов. Действие факторов может быть разнонаправленным и проявляться в разной степени в зависимости от выбора радиотрассы и геофизических условий.
В [1] предложен метод бихарактеристической системы исследования распространения радиоволн в неоднородной магнитоактивной ионосфере. Построение расширенной бихарактеристической системы уравнений позволяет найти фазовые и групповые траектории лучей, а затем поглощение, амплитудные и поляризационные характеристики сигналов вдоль них [2]. Разработаны алгоритмы расчета расходимости лучевого потока, фазы волны и вращения вектора поляризации [3].
В работе [4] моделировали распространение обыкновенной и необыкновенной волн в анизотропной однослойной и двуслойной моделях плазмы при наличии локальных неоднородностей. В [5] метод бихарактеристик применен к решению задач распространения радиоволн с использованием глобальной экспериментальной модели ионосферы IRI-2012 [6]. В [7] вариационный принцип применен для построения лучевых траекторий в ионосфере при заданном положении начала и конца каждой лучевой траектории. В [8] представлен комплекс вычислительных программ для проведения расчетов лучевых траекторий коротких волн в ионосфере.
В [9] сравнивали результаты численных расчетов лучевых траекторий и поглощения коротких волн, полученных для условий магнитной бури 26–29 сентября 2011 г. с использованием глобальной самосогласованной модели термосферы, ионосферы и протоносферы (ГСМ ТИП) [10] и IRI-2012 [6]. Там же [9] проведено сопряжение численной модели распространения коротких волн в ионосфере [11] с моделью ГСМ ТИП [10]. В [12] исследовано формирование лучевых траекторий на низких и высоких широтах в условиях геомагнитной бури.
В [13] применен метод бихарактеристик в рамках пространственно-временной геометрической оптики к исследованию распространения частотно модулированных сигналов обыкновенной и необыкновенной мод с учетом влияния геомагнитного поля и отклоняющего поглощения. Использована одномерная модель ионосферы в дневных и ночных условиях. Отмечено, что влияние поглощения на лучевые траектории – слабое. В [14] моделировали распространение частотно модулированных сигналов в зависимости от высоты источника излучения и угла выхода сигнала. Исследован эффект запирания излучения в канале для определенных частот источника излучения.
Цель данной работы – исследование формирования амплитудных и поляризационных характеристик коротких волн в трехмерно неоднородной анизотропной ионосфере посредством интегрирования уравнений переноса параметров вектора комплексной амплитуды волны вдоль лучевых трубок [15].
1. МОДЕЛЬ РАСПРОСТРАНЕНИЯ РАДИОВОЛН
Ограничимся стационарными каналами коротковолновой связи в ионосфере. Сигналы могут быть как широкополосными, так и узкополосными. Каждый узкополосный сигнал представляет собой волновой пакет с определенной несущей частотой. Широкополосные сигналы по сравнению с узкополосными испытывают большие дисперсионные искажения в ионосфере, особенно на частотах, близких к критической частоте плазмы.
Излучаемый антенной широкополосный сигнал можно представить последовательностью волновых пакетов. Такой подход использован в [16] для представления линейной частотной модуляции (ЛЧМ) импульсов. Энергия каждого волнового пакета распространяется с групповой скоростью вдоль выделенной лучевой траектории, соответствующей приближенно гармоническому сигналу на несущей частоте ω волнового пакета. В [17] численно исследованы дисперсионные искажения ЛЧМ-импульсов в трехмерно неоднородной анизотропной ионосфере для обеих нормальных мод в зависимости от геофизических условий.
Комплексная геометрическая оптика позволяет учесть согласованный характер формирования лучевых траекторий и поглощения волн в плавно неоднородной среде [15].
Пусть поле гармонического сигнала частоты ω изменяется со временем по закону ~exp(–jωt). Введем обозначения: $n\left( {\vec {r},\vec {\ell }} \right)$ – комплексный показатель преломления среды для выделенной нормальной моды, $\vec {r}$ – радиус-вектор точки наблюдения, $\vec {\ell }$ – единичный вектор в направлении вектора комплексного импульса $\vec {p} = p\vec {\ell }$ (p – комплексная величина импульса), 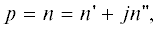 где n' и n" – вещественная и мнимая часть величины n соответственно. Мнимая часть показателя преломления обусловлена наличием поглощения
в среде. Столкновения частиц в плазме влияют на обе величины n' и n"
где n' и n" – вещественная и мнимая часть величины n соответственно. Мнимая часть показателя преломления обусловлена наличием поглощения
в среде. Столкновения частиц в плазме влияют на обе величины n' и n"
Для лучей в “освещенной” области, без перехода в область каустической тени, радиус-вектор $\vec {r}$ принимает вещественные значения ($\operatorname{Im} \vec {r} = 0$). Интегрируя уравнение эйконала методом характеристик в фазовом пространстве {pi, qi}, i = 1, 2, 3, импульса и обобщенных координат были получены [18] лучевые уравнения
(1)
$\begin{gathered} \frac{{d{{q}_{i}}}}{{d\tau }} = \operatorname{Re} \left( {\frac{{\partial H}}{{\partial {{p}_{i}}}}} \right)\left( {1 + {{{\left( {\frac{{\operatorname{Im} \left( {{{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial {{p}_{i}}}}} \right. \kern-0em} {\partial {{p}_{i}}}}} \right)}}{{\operatorname{Re} \left( {{{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial {{p}_{i}}}}} \right. \kern-0em} {\partial {{p}_{i}}}}} \right)}}} \right)}}^{2}}} \right), \\ \frac{{d{{p}_{i}}}}{{d\tau }} = - \left( {1 - j\frac{{\operatorname{Im} \left( {{{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial {{p}_{i}}}}} \right. \kern-0em} {\partial {{p}_{i}}}}} \right)}}{{\operatorname{Re} \left( {{{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial {{p}_{i}}}}} \right. \kern-0em} {\partial {{p}_{i}}}}} \right)}}} \right)\frac{{\partial H}}{{\partial {{q}_{i}}}}, \\ \end{gathered} $Система (1) применима для плавно неоднородных сред как в случае слабого, так и сильного
поглощения и учитывает влияние столкновений частиц в среде на лучевые траектории.
Используя (1), в [19] численно исследовали влияние поглощения на формирование лучевых траекторий для одномерной
модели слоя ионосферы без учета анизотропии плазмы. Для наклонного падения лучей на
слой получено, что по мере роста поглощения (увеличения отношения 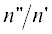 ) усиливается проникновение лучей в слой. При этом отражение луча от слоя может даже
смениться на прохождение луча через слой.
) усиливается проникновение лучей в слой. При этом отражение луча от слоя может даже
смениться на прохождение луча через слой.
Для среды со слабым поглощением величина 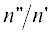 – малый параметр.
– малый параметр.
Модуль величины комплексного импульса
можно разложить в ряд по малому параметру 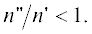 Нулевое приближение соответствует бесстолкновительной среде. Разложение с точностью
до величин второго порядка малости дает
Нулевое приближение соответствует бесстолкновительной среде. Разложение с точностью
до величин второго порядка малости дает
а до первого порядка малости – $\left| p \right| \approx n{\text{'}}$ и $\vec {p} \approx n{\text{'}}\vec {\ell },$ где $n{\text{'}}$ зависит от частоты столкновений частиц в среде. В этом приближении вместо (1) для каждой из двух нормальных волн следует система лучевых уравнений
(2)
$\frac{{d\vec {r}}}{{d\tau }} = \vec {p} - n{\text{'}}\frac{{\partial n{\text{'}}}}{{\partial{ \vec {p}}}} = \vec {d}\left( {\vec {r},\vec {p}} \right),\,\,\,\,\frac{{d\vec {p}}}{{d\tau }} = n{\text{'}}\frac{{\partial n{\text{'}}}}{{\partial{ \vec {r}}}},$где τ – параметр интегрирования вдоль каждой лучевой траектории, $\vec {p}$ и $\vec {d}$ – векторы импульса и луча соответственно.
В слабонеоднородной среде независимое распространение нормальных волн можно рассматривать лишь приближенно. Геомагнитное поле в ионосфере и нейтральной атмосфере принято дипольным, учтены эффекты мирового времени. Напряженность электрического $\vec {E}$ и магнитного $\vec {H}$ полей нормальной волны выражается [15] в виде
(3)
$\vec {E} = \Phi \vec {f},\,\,\,\,\vec {H} = \sqrt {\frac{{{{\varepsilon }_{0}}}}{{{{\mu }_{0}}}}} \vec {p} \times \vec {E},$где Φ и $\vec {f}$ – комплексные амплитуда и вектор поляризации поля волны, ε0 и ${{\mu }_{0}}$ – диэлектрическая и магнитная проницаемости вакуума соответственно.
Используя условие нормировки, получим
где знак “*” означает операцию комплексного сопряжения.
С учетом (3) из (4) найдем
Компоненты вектора поляризации $\vec {f}$ в каждой точке наблюдения в ионосфере удовлетворяют системе однородных уравнений
(6)
$\left( {{{p}^{2}}{{\delta }_{{im}}} - {{p}_{i}}{{p}_{m}} - {{\varepsilon }_{{im}}}} \right){{f}_{m}} = 0,\,\,\,\,i = 1,2,3,$где ε – тензор комплексной относительной диэлектрической проницаемости плазмы ионосферы, m = 1, 2, 3, и δim – символ Кронекера.
Система (6) имеет нетривиальные решения, если ее определитель равен нулю, откуда следуют дисперсионные соотношения для нормальных волн:
(7)
${{H}_{k}}\left( {\vec {p},\vec {r}} \right) = \frac{1}{2}\left( {{{p}^{2}} - n_{k}^{2}\left( {\vec {r},\vec {\ell }} \right)} \right) = 0,\,\,\,\,k = 1,2,$где n1 и n2 – комплексные показатели преломления обыкновенной и необыкновенной волн в анизотропной плазме.
Для радиоволн, применяемых в радиосвязи, существенно взаимодействие с электронами, а не с ионами плазмы ионосферы. Тогда имеем [20]:
(8)
$\begin{gathered} n_{{1,2}}^{2}\left( {\vec {r},\vec {\ell }} \right) = \frac{{ - D \pm \sqrt {{{D}^{2}} - 4AC} }}{{2A}}, \\ A = \varepsilon - \left( {\varepsilon - \eta } \right){{\cos }^{2}}\alpha , \\ D = \left( {{{\varepsilon }^{2}} - \varepsilon \eta - {{g}^{2}}} \right){{\cos }^{2}}\alpha - \left( {{{\varepsilon }^{2}} + \varepsilon \eta - {{g}^{2}}} \right), \\ C = \eta \left( {{{\varepsilon }^{2}} - {{g}^{2}}} \right),\,\,\,\,\eta = 1 - \frac{{\omega _{e}^{2}}}{{\omega \omega _{e}^{'}}}, \\ \varepsilon = 1 - \frac{{\omega _{e}^{2}}}{{2\omega }}\left( {\frac{1}{{\omega _{e}^{'} - {{\Omega }_{e}}}} + \frac{1}{{\omega _{e}^{'} + {{\Omega }_{e}}}}} \right), \\ g = \frac{{\omega _{e}^{2}}}{{2\omega }}\left( {\frac{1}{{\omega _{e}^{'} - {{\Omega }_{e}}}} - \frac{1}{{\omega _{e}^{'} + {{\Omega }_{e}}}}} \right), \\ \end{gathered} $где ${{\omega }_{e}} = \sqrt {{{{{n}_{e}}{{e}^{2}}} \mathord{\left/ {\vphantom {{{{n}_{e}}{{e}^{2}}} {\left( {{{m}_{e}}{{\varepsilon }_{0}}} \right)}}} \right. \kern-0em} {\left( {{{m}_{e}}{{\varepsilon }_{0}}} \right)}}} $ – плазменная частота (частота собственных колебаний каждого электрона в плазме),
Ωe = |e|B/me – ларморовская частота электрона, B – индукция геомагнитного поля, me и e – заряд и масса электрона, соответственно, $\omega _{e}^{'} = \omega + j{{\nu }_{e}}$ – комплексная частота, (${{\nu }_{e}}$ – эффективная частота столкновений каждого электрона с ионами и молекулами нейтральной
атмосферы), 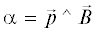 – угол между направлением вектора импульса и вектором индукции геомагнитного поля.
– угол между направлением вектора импульса и вектором индукции геомагнитного поля.
Выражения для частот столкновений электронов с ионами и молекулами нейтрального газа приведены в работе [20].
Среднее за период колебаний значение вектора плотности потока энергии поля электромагнитной волны в плазме равно
(9)
$\vec {S} = \frac{1}{2}\operatorname{Re} \left( {\vec {E} \times \vec {H}{\text{*}}} \right) = \vec {\sigma }{{\left| \Phi \right|}^{2}},$где
(10)
$\vec {\sigma } = \frac{1}{4}\sqrt {\frac{{{{\varepsilon }_{0}}}}{{{{\mu }_{0}}}}} \left[ {\vec {f} \times \left( {\vec {p} \times \vec {f}{\text{*}}} \right) + \vec {f}{\text{*}} \times \left( {\vec {p} \times \vec {f}} \right)} \right].$Среднее за период колебаний значение плотности энергии поля равно
(11)
$\begin{gathered} w = \frac{1}{4}\left( {{{\varepsilon }_{0}}\frac{{\partial \left( {\omega \varepsilon _{{im}}^{e}} \right)}}{{\partial \omega }}{{E}_{i}}E_{m}^{*} + {{\mu }_{0}}{{H}_{i}}H_{m}^{*}} \right) = \\ = \frac{{{{\varepsilon }_{0}}}}{4}\frac{{\partial \left( {{{\omega }^{2}}\varepsilon _{{im}}^{e}} \right)}}{{\omega \partial \omega }}{{f}_{i}}f_{m}^{*}{{\left| \Phi \right|}^{2}}, \\ \end{gathered} $где ${{{\mathbf{\varepsilon }}}^{e}}$ – эрмитова часть тензора ε, причем $\varepsilon _{{im}}^{e} = {{\left( {{{\varepsilon }_{{im}}} + \varepsilon _{{mi}}^{ * }} \right)} \mathord{\left/ {\vphantom {{\left( {{{\varepsilon }_{{im}}} + \varepsilon _{{mi}}^{ * }} \right)} 2}} \right. \kern-0em} 2}$ (i, m = 1, 2, 3).
Наличие не эрмитовой части ${{{\mathbf{\varepsilon }}}^{a}},$ где $\varepsilon _{{im}}^{a} = {{\left( {{{\varepsilon }_{{im}}} - \varepsilon _{{mi}}^{ * }} \right)} \mathord{\left/ {\vphantom {{\left( {{{\varepsilon }_{{im}}} - \varepsilon _{{mi}}^{ * }} \right)} 2}} \right. \kern-0em} 2},$ у тензора $\varepsilon _{{im}}^{e}$ обусловлено диссипативными свойствами среды распространения волн.
Имеем: $\vec {S} = w\vec {g},$ где $\vec {g}$ – вектор групповой скорости. С учетом (9) и (11) выразим
(12)
$\vec {g} = {{\vec {\sigma }} \mathord{\left/ {\vphantom {{\vec {\sigma }} {\left( {\frac{{{{\varepsilon }_{0}}}}{4}\frac{{\partial \left( {{{\omega }^{2}}\varepsilon _{{im}}^{e}} \right)}}{{\omega \partial \omega }}{{f}_{i}}f_{m}^{*}} \right)}}} \right. \kern-0em} {\left( {\frac{{{{\varepsilon }_{0}}}}{4}\frac{{\partial \left( {{{\omega }^{2}}\varepsilon _{{im}}^{e}} \right)}}{{\omega \partial \omega }}{{f}_{i}}f_{m}^{*}} \right)}}.$В приближении геометрической оптики уравнение переноса энергии волны с учетом поглощения в среде [15] имеет вид
(13)
$div\left( {\vec {\sigma }{{{\left| \Phi \right|}}^{2}}} \right) - \frac{1}{2}j\omega {{\varepsilon }_{0}}\varepsilon _{{im}}^{a}{{f}_{i}}f_{m}^{*}{{\left| \Phi \right|}^{2}} = 0.$В нормализованной форме комплексная амплитуда имеет вид $\Phi = \left| \Phi \right|\exp \left( {ju} \right),$ где u – фаза амплитуды. Запишем уравнение, описывающее изменение фазы вдоль выделенной лучевой траектории:
2. ЧИСЛЕННЫЙ АЛГОРИТМ
Положение точечного излучателя на поверхности Земли задано значениями географической широты φ и долготы λ. Заданы угол места β и азимут γ опорного луча в точке излучения. В окрестности опорного луча выделим пучок лучей с узким угловым раствором (Δβ, Δγ). Простая аппроксимация пучка лучей получается дополнением опорного луча еще четырьмя лучами с угловыми координатами излучения (β ± Δβ, γ ± Δγ).
Каждый из пяти лучей находится интегрированием уравнений (2) методом Рунге–Кутты с применением численного алгоритма [11]. Ограничимся моделированием либо односкачковых трасс, либо проходящих до верхней границы ионосферы на высоте h = 1000 км. Численное интегрирование уравнений (2) с учетом (8) проводится в сферической геомагнитной системе координат.
Комплексные показатели преломления обыкновенной и необыкновенной волн на ионосферных высотах от 60 до 1000 км рассчитаны по формуле (8) на основе экспериментальных моделей ионосферы IRI2012 [8] и нейтральной атмосферы MSIS86 [21].
Точки наблюдения совпадают с узлами координатной сетки, найденной при интегрировании системы (1) вдоль выделенных пяти лучей. Выразим тензор ε в каждой такой точке в локальной декартовой системе координат, где ось z направлена вдоль вектора импульса $\vec {p},$ а ось y расположена в плоскости векторов $\vec {p}$ и индукции геомагнитного поля $\vec {B}\,:$
(15)
${\mathbf{\varepsilon }} = \left( {\begin{array}{*{20}{c}} \varepsilon &{jg\cos \alpha }&{ - jg\sin \alpha } \\ { - jg\cos \alpha }&{\eta - \left( {\eta - \varepsilon } \right){{{\cos }}^{2}}\alpha }&{\left( {\eta - \varepsilon } \right)\sin \alpha \cos \alpha } \\ {jg\sin \alpha }&{\left( {\eta - \varepsilon } \right)\sin \alpha \cos \alpha }&{\eta - \left( {\eta - \varepsilon } \right){{{\sin }}^{2}}\alpha } \end{array}} \right).$В той же системе координат в каждой точке наблюдения выражается и вектор поляризации $\vec {f}$ из системы (4), (6), вектор групповой скорости $\vec {g}$ из (12) и скалярные величины $\varepsilon _{{im}}^{a}{{f}_{i}}f_{m}^{*}.$ Значения векторов $\vec {f}$ и $\vec {g}$ преобразуются в сферическую геомагнитную систему координат для нахождения вектора $\vec {\sigma }$ из (10) в каждой точке.
На высотах 0< h< 60 км концентрация электронов и ионов плазмы полагается равной нулю. В выражении (15) поляризацией молекул нейтрального газа в электрическом поле волны пренебрегается. Тогда в (15), для любого значения высоты из интервала 0< h< 60 км матрица тензора ε становится единичной, а показатель преломления среды в (8) равным единице. Это происходит независимо от выбора модели нейтральной атмосферы на интервале высот 0 < h < 60 км. Рефракцией и поглощением ионосферных волн на тех же высотах пренебрегаем.
Численным интегрированием уравнений (2) находим также и векторы импульса и поляризации, как и показатель преломления.
Для каждого узла на опорном луче находится время группового запаздывания сигнала от источника излучения до этого узла. Элемент волновой поверхности, пересекающий трубку лучей, аппроксимируется для каждого значения такого времени кусочно-плоской поверхностью из треугольных элементов. Поперечное сечение S = S(s), где s – длина вдоль опорного луча, находится как проекция вектора площади поверхности из треугольных элементов на направление вектора групповой скорости волны в узле опорного луча.
Далее проводится расчет полевых характеристик в точках разностной сетки опорного луча с учетом данных, полученных на первом этапе для всех лучей выделенного пучка. Интегрируя уравнение (13) вдоль опорного луча, найдем множитель ослабления амплитуды волны в ионосфере: ${{V}_{3}} = 20\lg \left( {{{\left| \Phi \right|} \mathord{\left/ {\vphantom {{\left| \Phi \right|} {\left| {{{\Phi }_{0}}} \right|}}} \right. \kern-0em} {\left| {{{\Phi }_{0}}} \right|}}} \right),$ где $\left| {{{\Phi }_{0}}} \right|$ – значение амплитуды волны при входе луча в ионосферу при h = 60 км. Получим
где ${{V}_{1}}$ и ${{V}_{2}}$ – вклады в множитель ослабления от затухания волны и от расходимости лучей в выделенном пучке соответственно,
(17)
${{V}_{1}} = - 2.17j\omega {{\varepsilon }_{0}}\int\limits_{{{s}_{0}}}^s {\frac{1}{{\left| {\vec {\sigma }} \right|}}} \varepsilon _{{im}}^{a}{{f}_{i}}f_{m}^{*}ds,$ds – элемент длины вдоль опорного луча, s0 и s – начальное (при входе луча в ионосферу) и текущее (в ионосфере) значения длины опорного луча,
(18)
${{V}_{2}} = - 4.34\int\limits_{{{s}_{0}}}^s {\frac{{{\text{div}}\vec {\sigma }}}{{\left| {\vec {\sigma }} \right|}}} ds.$Для узкого пучка учтем ${\text{div}}\vec {\sigma } \approx \left( {{1 \mathord{\left/ {\vphantom {1 S}} \right. \kern-0em} S}} \right){{\partial \left( {S\left| {\vec {\sigma }} \right|} \right)} \mathord{\left/ {\vphantom {{\partial \left( {S\left| {\vec {\sigma }} \right|} \right)} {\partial s}}} \right. \kern-0em} {\partial s}}$ и подставим это выражение в (18). Проинтегрируем и найдем
(19)
${{V}_{2}} = - 10\lg \frac{{\left| {\vec {\sigma }} \right|S}}{{\left| {{{{\vec {\sigma }}}_{0}}} \right|{{S}_{0}}}}.$Множитель ослабления от расходимости лучей (17) является обобщенным. Представим 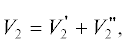 где $V_{2}^{'} = - 10\lg \left( {{S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}}} \right),$ и
где $V_{2}^{'} = - 10\lg \left( {{S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}}} \right),$ и 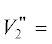 $ = - 10\lg \left( {{{\left| {\vec {\sigma }} \right|} \mathord{\left/ {\vphantom {{\left| {\vec {\sigma }} \right|} {\left| {{{{\vec {\sigma }}}_{0}}} \right|}}} \right. \kern-0em} {\left| {{{{\vec {\sigma }}}_{0}}} \right|}}} \right),$ где $V_{2}^{'}$ – геометрический фактор, а
$ = - 10\lg \left( {{{\left| {\vec {\sigma }} \right|} \mathord{\left/ {\vphantom {{\left| {\vec {\sigma }} \right|} {\left| {{{{\vec {\sigma }}}_{0}}} \right|}}} \right. \kern-0em} {\left| {{{{\vec {\sigma }}}_{0}}} \right|}}} \right),$ где $V_{2}^{'}$ – геометрический фактор, а 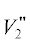 – фактор, учитывающий влияние как поляризации волны, так и показателя преломления
среды.
– фактор, учитывающий влияние как поляризации волны, так и показателя преломления
среды.
Интегрируя уравнение (14) вдоль опорного луча, найдем
(20)
$\begin{gathered} u = \frac{1}{4}\sqrt {\frac{{{{\varepsilon }_{0}}}}{{{{\mu }_{0}}}}} \int\limits_{{{s}_{0}}}^s {\frac{1}{{\left| {\vec {\sigma }} \right|}}} \times \\ \times \,\,\operatorname{Im} \left( {\vec {f}{\text{*}}rot\left( {\vec {p} \times \vec {f}} \right) + \vec {p} \times \vec {f}rot\vec {f}{\text{*}}} \right)ds. \\ \end{gathered} $Численный расчет значений величин $rot\left( {\vec {p} \times \vec {f}} \right)$ и $rot\vec {f}{\text{*}}$ в узлах разностной сетки на опорном луче основан на применении конечно-разностной аппроксимации формулы Стокса
где вектор $\vec {A}$ может обозначать $rot\left( {\vec {p} \times \vec {f}} \right)$ и $rot\vec {f}{\text{*}}.$
Векторное равенство (21) проектируется на координатные плоскости декартовой геомагнитной системы координат и применяется для нахождения декартовых проекций векторов $rot\left( {\vec {p} \times \vec {f}} \right)$ и $rot\vec {f}{\text{*}}$ в каждом узле опорного луча.
Точность представления поля волны можно повысить, увеличив число лучей в узком пучке. Широкий по угловому раствору пучок лучей можно представить совокупностью узких пучков. Численное интегрирование выражения (17), например методом трапеций, проводится в сферической геомагнитной системе координат вдоль опорного луча.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Расчеты проведены для условий солнцестояния при высокой солнечной активности (F10.7= = 150), номер дня в году задан N = 172. Географические координаты передатчика на поверхности Земли: широта φ = 15° и долгота λ = 290°.
На рис. 1а представлены результаты численных расчетов лучевых траекторий для обыкновенной волны. Задано мировое время UT = 16.65 ч. Для опорного луча передатчика были заданы угол места β = 30° и азимут γ = 90° излучения. Рассмотрено излучение передатчика в пучке с узким угловым раствором (Δβ = 2°, Δγ = 2°) в окрестности опорного луча. Выбор значений Δβ и Δγ обоснован численными экспериментами. Уменьшение этих значений способствует повышению точности вычислений, но ограничено разрешающей способностью используемых моделей ионосферы и нейтральной атмосферы. Видно, что лучи на частотах f = 5 и 10 МГц испытывают отражение от ионосферы, а луч на частоте f = 15 МГц проникает сквозь ионосферу.
Рис. 1.
Лучевые траектории для обыкновенной волны (а) и изменение отношения скорости света к групповой скорости волны (б) на трех частотах: f = 5 (1), 10 (2) и 15 МГц (3) при UT = 16.65 ч. Координатная сетка: h – высота над поверхностью Земли, s – длина вдоль луча.
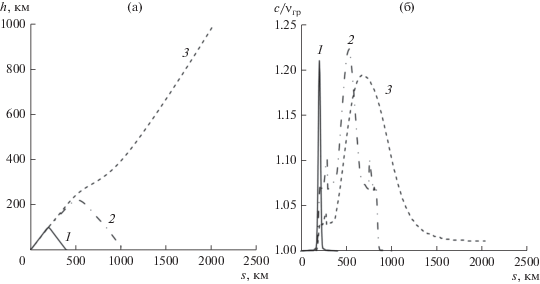
Рис. 1б описывает изменение параметров среды и волны вдоль каждого луча на рис. 1а. Так, на рис. 1б показана зависимость отношения скорости света к групповой скорости волны от s. Видно, что по мере проникновения лучей вглубь ионосферы в целом происходит замедление скорости распространения лучевой энергии.
На рис. 2а представлена зависимость величины угла между вектором импульса и вектором индукции
геомагнитного поля (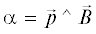 ) от s. Направление распространения каждого из лучей по отношению к геомагнитному полю изменяется
в процессе распространения. Режим распространения остается ближе к поперечному, чем
к продольному.
) от s. Направление распространения каждого из лучей по отношению к геомагнитному полю изменяется
в процессе распространения. Режим распространения остается ближе к поперечному, чем
к продольному.
Рис. 2.
Изменение угла между вектором импульса и вектором индукции геомагнитного поля (а) и лучевым вектором (б) вдоль лучей на частотах: f = 5 (1), 10 (2) и 15 МГц (3) при UT = 16.65 ч.
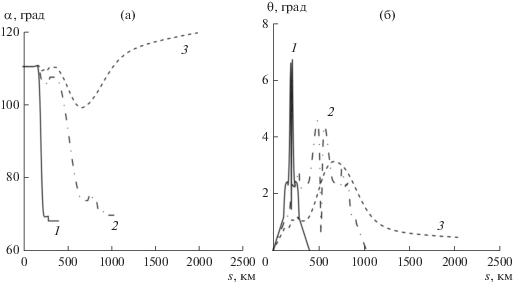
На рис. 2б показана зависимость величины угла между вектором импульса и лучевым вектором (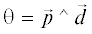 ) от s. Величина угла θ служит мерой развития неоднородности в структуре волны. По мере погружения
луча в ионосферный слой значение угла θ растет. При переходе через поперечный режим
распространения волны по отношению к геомагнитному полю образуется локальный минимум
величины угла θ. Теоретически в момент перехода через поперечный режим обыкновенная
волна превращается в линейно поляризованную однородную волну [20].
) от s. Величина угла θ служит мерой развития неоднородности в структуре волны. По мере погружения
луча в ионосферный слой значение угла θ растет. При переходе через поперечный режим
распространения волны по отношению к геомагнитному полю образуется локальный минимум
величины угла θ. Теоретически в момент перехода через поперечный режим обыкновенная
волна превращается в линейно поляризованную однородную волну [20].
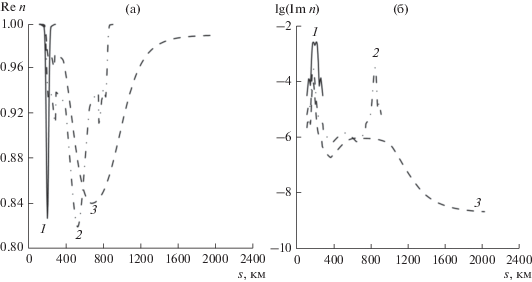
На рис. 3 показано изменение вещественной $\operatorname{Re} n = n{\text{'}}$ (а) и мнимой 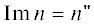 (б) части показателя преломления для обыкновенной волны вдоль лучей. Коэффициент дифференциального
поглощения (в дБ) выражается величиной, равной $ - 8.68\left( {{\omega \mathord{\left/ {\vphantom {\omega с
}} \right. \kern-0em} с
}} \right)\operatorname{Im} n,$ где с – скорость света. Для частоты 5 МГц в дневных условиях отмечается большее развитие
области отклоняющего поглощения, чем двух областей не отклоняющего поглощения на восходящем
и нисходящем участках лучевой траектории. Поглощение падает с ростом частоты. Для
частот 10 и 15 МГц отмечается большее развитие не отклоняющего поглощения, чем отклоняющего.
Если пренебречь наличием столкновений электронов плазмы с ионами и молекулами нейтрального
газа, то численные расчеты в отсутствие поглощения показывают, что лучевые траектории
на рис. 3 изменятся слабо по сравнению с рис. 1а.
(б) части показателя преломления для обыкновенной волны вдоль лучей. Коэффициент дифференциального
поглощения (в дБ) выражается величиной, равной $ - 8.68\left( {{\omega \mathord{\left/ {\vphantom {\omega с
}} \right. \kern-0em} с
}} \right)\operatorname{Im} n,$ где с – скорость света. Для частоты 5 МГц в дневных условиях отмечается большее развитие
области отклоняющего поглощения, чем двух областей не отклоняющего поглощения на восходящем
и нисходящем участках лучевой траектории. Поглощение падает с ростом частоты. Для
частот 10 и 15 МГц отмечается большее развитие не отклоняющего поглощения, чем отклоняющего.
Если пренебречь наличием столкновений электронов плазмы с ионами и молекулами нейтрального
газа, то численные расчеты в отсутствие поглощения показывают, что лучевые траектории
на рис. 3 изменятся слабо по сравнению с рис. 1а.
Рис. 3.
Изменение вещественной $\operatorname{Re} \,n = n{\text{'}}$ (а) и мнимой 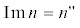 (б) части показателя преломления для обыкновенной волны вдоль лучей на частотах:
f = 5 (1), 10 (2) и 15 МГц (3) при UT = 16.65 ч.
(б) части показателя преломления для обыкновенной волны вдоль лучей на частотах:
f = 5 (1), 10 (2) и 15 МГц (3) при UT = 16.65 ч.
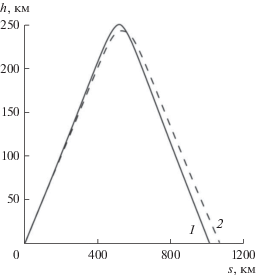
На рис. 4 отражены лучевые траектории для обыкновенной и необыкновенной волн на частоте f = 10 МГц. В отличие от рис. 1а здесь задано UT = 4.65 ч. Лучевая траектория имеет начальный прямолинейный участок длиной около 118 км в сферическом слое на высотах 0< h < 60 км. Как видно из рис. 4, при переходе из нейтральной атмосферы в ионосферу луч испытывает двойное лучепреломление. Точка поворота луча для обыкновенной волны (сплошная линия) в ионосфере расположена выше, чем в случае необыкновенной волны (пунктир).
Рис. 4.
Лучевые траектории для обыкновенной (1) и необыкновенной (2) волн на частоте f = 10 МГц при UT = 4.65 ч.
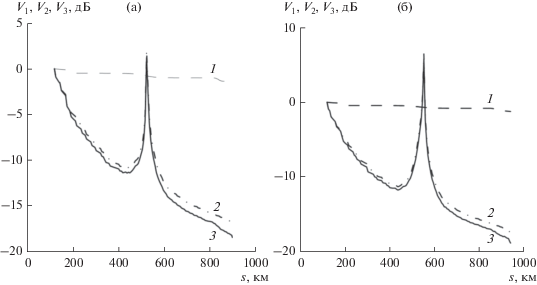
На рис. 5 показаны результаты расчетов множителя ослабления V3, и вклады в него от затухания V1 и расходимости лучей в трубке V2. Рис. 5а получен для обыкновенной волны, а рис. 5б – для необыкновенной волны вдоль лучей рис. 4. Видны локальные максимумы множителей ослабления в окрестности точек поворота лучей. Уменьшение ослабления обусловлено падением поперечного сечения выделенной лучевой трубки в окрестности точек поворота лучей. Здесь лучевая структура в трубке перестраивается: верхний по высоте луч переходит в нижний, а нижний – в верхний.
Рис. 5.
Множитель ослабления (V3, кривая 3) и вклады в него от затухания (V1, кривая 1) и расходимости лучей в трубке (V2, кривая 2) для обыкновенной (а) и необыкновенной (б) волн на частоте f = 10 МГц при UT = 4.65 ч.
На рис. 5 геометрический фактор $V_{2}^{'}$ дает основной вклад в величину ${{V}_{2}}.$ На пологих траекториях уменьшение величины $\left| {\vec {\sigma }} \right|$ в точке поворота луча по сравнению с $\left| {{{{\vec {\sigma }}}_{0}}} \right|$ при входе луча в ионосферу не превышает нескольких десятков процентов. Величина $\left| {\vec {\sigma }} \right|$ падает прямо пропорционально вещественной части показателя преломления среды по мере
погружения луча в каждый ионосферный слой. По мере приближения точки поворота луча
к максимуму слоя F2 ионосферы вклад от 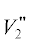 в величину ${{V}_{2}}$ будет расти.
в величину ${{V}_{2}}$ будет расти.
На начальном участке траектории вне ионосферы напряженность поля точечного источника убывает обратно пропорционально расстоянию от источника. В дальней по отношению к источнику области вклад начального участка траектории в множитель ослабления амплитуды, по оценкам, составляет порядка –40 дБ. По данным, представленным на рис. 5, можно определить вклад в ослабление на остальной части лучевой траектории, после входа в ионосферу. Видно, что в ночных условиях, в отличие от дневных, поглощение слабо влияет на множитель ослабления.
На рис. 6 представлены модули декартовых проекций вектора поляризации обыкновенной (а) и необыкновенной (б) волн, рассчитанные вдоль опорных лучей на частоте f = 10 МГц (см. рис. 1а). Выбор локальной декартовой системы координат в каждой точке выделенного опорного луча обсуждался выше. Основными по величине являются модули проекций |fx| (кривая 1) и |fy| (кривая 2). Появление третьей компоненты |fz| (кривая 3) обусловлено развитием неоднородной структуры эллиптически поляризованной нормальной волны при распространении в ионосфере (см. рис. 2б). По мере проникновения вглубь ионосферы эксцентриситет эллипса поляризации как обыкновенной, так и необыкновенной волны растет. Для обыкновенной волны (левой поляризации) эллипс вытягивается вдоль оси y, а для необыкновенной (правой поляризации) – вдоль оси x. Наиболее сильная перестройка эллипса поляризации происходит при прохождении волны через режим поперечного распространения к геомагнитному полю в согласии с рис. 2а. Причем обыкновенная волна в этом режиме становится однородной и линейно поляризованной, а необыкновенная волна остается неоднородной и эллиптически поляризованной.
Рис. 6.
Модули декартовых проекций (|fx| (1), |fy| (2) и |fz| (3)) вектора поляризации обыкновенной (а) и необыкновенной (б) волн на частоте f = 10 МГц при UT = 16.65 ч.
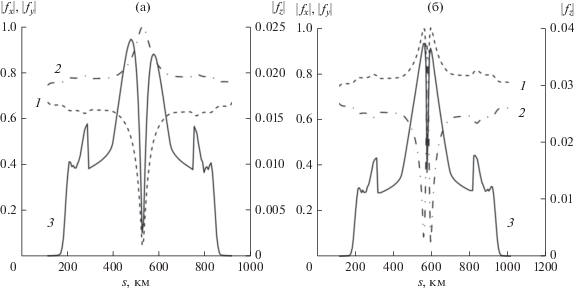
Рис. 7а получен для тех же условий, что и рис. 6а, но отражает результаты расчетов сдвига фазы между декартовыми проекциями вектора поляризации. Видно, что фазовые сдвиги имеют величину около 90° на участке луча в глубине ионосферы и уменьшаются по мере приближения к нижней границе ионосферы на высоте h = 60 км. Такие фазовые сдвиги характерны для волны левой поляризации (обыкновенной волны) и также проявляются в результатах расчетов для частот f = 5 и 15 МГц.
Рис. 7.
Сдвиги фазы arg(fy) – arg(fx) (1) и arg(fz) – arg(fx) (2) между декартовыми проекциями вектора поляризации обыкновенной волны (а) вдоль опорного луча на частоте f = 10 МГц (3); изменение фазы комплексной амплитуды обыкновенной волны (б) вдоль лучей рис. 1 на частотах 5 (1), 10 (2) и 15 МГц (3) при UT = 16.65 ч.
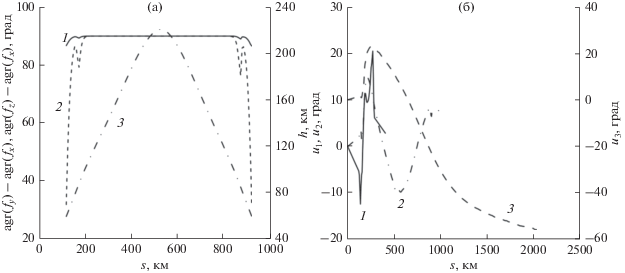
На рис. 7б показана зависимость величины фазы комплексной амплитуды волны от s. Кривые описывают знакопеременные зависимости. Режим распространения (см. рис. 2б) остается ближе к поперечному, чем к продольному.
При изменении азимута γ = 90° излучения для опорного луча передатчика (см. рис. 1а) на γ = 0° на лучевых траекториях обыкновенной и необыкновенной волны появляются участки не только с квазипоперечным, но и с квазипродольным распространением. Скорость изменения фазы на участках лучевой траектории с квазипродольным распространением как в дневных, так и в ночных условиях существенно больше, чем на участках квазипоперечного распространения. Максимальное изменение фазы, по сравнению с рис. 7б, уже составит по порядку величины 103 град.
На масштабе длины волны изменение фазы комплексной амплитуды оказывается много меньше изменения в 360° полной фазы волны, что соответствует приближению геометрической оптики. Оценки изменения фазы комплексной амплитуды сигнала вдоль радиотрассы можно использовать для синхронизации радиоаппаратуры на приеме и передаче.
ЗАКЛЮЧЕНИЕ
Основными результатами работы являются следующие.
Разработана численная модель, описывающая изменение векторов комплексной амплитуды нормальных мод коротких волн вдоль лучевых траекторий в трехмерно неоднородной анизотропной ионосфере.
Получено выражение для обобщенного множителя ослабления нормальных мод для анизотропной неоднородной плазмы.
Исследовано численно развитие неоднородной структуры волн, а также изменение модуля и фазы вектора комплексной амплитуды волн, вектора поляризации при распространении в ионосфере в зависимости от частоты, выбора радиотрассы и геофизических условий.
Список литературы
Казанцев А.Н., Лукин Д.С., Спиридонов Ю.Г. // Космич. исслед. 1967. Т. 5. № 4. С. 593.
Лукин Д.С., Спиридонов Ю.Г. // РЭ. 1969. Т. 14. № 9. С.1673.
Лукин Д.С., Палкин Е.А. Численный канонический метод в задачах дифракции и распространения электромагнитных волн в неоднородных средах. М.: МФТИ, 1982.
Крюковский А.С., Лукин Д.С., Кирьянова К.С. // РЭ. 2012. Т. 57. № 9. С. 1028.
Ипатов Е.Б., Крюковский А.С., Лукин Д.С. и др. // РЭ. 2014. Т. 59. № 12. С. 1180.
Bilitza D., Altadill D., Zhang Y. et al. // J. Space Weather Clim. 2014. V. 4. № A07. http://dx.doi.org/https://doi.org/10.1051/ swsc/2014004.
Coleman C.J. // Radio Sci. 2011. V. 46. RS5016. http://dx.doi.org/https://doi.org/10.1029/2011RS004748.
Azzarone A., Bianchi C., Pezzopane M. et al. // Comput. Geosci. 2012. V. 42. P. 57. http://dx.doi.org/https://doi.org/10.1016/ j.cageo.2012.02.008.
Kotova D.S., Klimenko M.V., Klimenko V.V., Zakharov V.E. // Adv. Space Res. 2015. V. 56. P. 2012.
Korenkov Yu.N., Klimenko V.V., Fӧrster M. et al. // J. Geophys. Res. 1990. V. 103. № A7. P. 14697.
Захаров В.Е., Черняк А.А. // Вестн. РГУ им. И. Канта. Серия “Физико-математические науки”. Калининград: РГУ им. И. Канта. 2007. Вып. 3. С. 36.
Котова Д.С., Клименко М.В., Клименко В.В., Захаров В.Е. // Геомагнетизм и аэрономия. 2017. Т. 57. № 3. С. 1.
Бова Ю.И., Крюковский А.С., Лукин Д.С. // Вестн. Рос. нового ун-та. Серия: Сложные системы: модели, анализ и управление. 2017. № 3. С. 5.
Бова Ю.И., Крюковский А.С., Лукин Д.С. // Электромагнитные волны и электронные системы. 2017. Т. 22. № 5. С. 4–11.
Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных средств. М.: Наука, 1980.
Захаров В.Е., Котова Д.С. // Радиотехника. 2013. № 2. С. 87.
Захаров В.Е., Котова Д.С. // Труды XXIV Всероссийской научной конференции “Распространение радиоволн”. Иркутск: ИСЗФ СО РАН, 2014. Т. 4. С. 97.
Захаров В.Е., Котова Д.С. // Труды XXIII Всероссийской научной конференции “Распространение радиоволн”. Йошкар-Ола: МарГТУ, 2011. Т. 3. С. 340.
Захаров В.Е., Котова Д.С. // Труды XXIII Всероссийской научной конференции “Распространение радиоволн”. Йошкар-Ола: МарГТУ, 2011. Т. 3. С. 336.
Брюнелли Б.Е., Намгаладзе А.А. Физика ионосферы. М.: Наука, 1988.
Hedin A.E. // J. Geophys. Res. 1991. V. 96. № A1. P. 1159.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника