Радиотехника и электроника, 2019, T. 64, № 7, стр. 666-677
Рассеяние электромагнитных волн на субволновой решетке квадратных полосковых проводников
Б. А. Беляев 1, 2, *, В. В. Тюрнев 1, 2, Н. В. Волков 1, 3
1 Институт физики им. Л.В. Киренского ФИЦ КНЦ СО РАН
660036 Красноярск, Академгородок, 50/38, Российская Федерация
2 Сибирский федеральный университет
660041 Красноярск, просп. Свободный, 79, Российская Федерация
3 Сибирский государственный университет науки и технологий им. академика М.Ф. Решетнева
660014 Красноярск, просп. им. Газеты “Красноярский рабочий”, 31, Российская Федерация
* E-mail: belyaev@iph.krasn.ru
Поступила в редакцию 13.06.2018
После доработки 05.10.2018
Принята к публикации 05.10.2018
Аннотация
Получены простые формулы для расчета матрицы рассеяния плоской электромагнитной волны, падающей нормально на безграничную 2D-решетку, образованную квадратными полосковыми проводниками и расположенную на границе раздела двух диэлектрических сред. Впервые учтено вихревое поведение электрического поля решетки, что позволило многократно уменьшить погрешность вычислений на высоких частотах. Это подтверждается хорошим согласием рассчитанных по формулам амплитудно-частотных характеристик структуры с характеристиками, полученными численным электродинамическим анализом 3D-модели, когда период решетки меньше половины длины волны.
ВВЕДЕНИЕ
Как известно, многослойные тонкопленочные диэлектрические зеркала широко применяются в оптике благодаря их высокому коэффициенту отражения. При этом возможность варьирования отражательной способности таких зеркал изменением контраста диэлектрической проницаемости и количеством слоев [1] позволяет использовать их в полосно-пропускающих фильтрах (ППФ) в качестве элементов связи между резонаторами, формирующими полосу пропускания, а также элементов связи оконечных резонаторов с окружающим пространством [2]. Однако такие фильтры сложны в изготовлении и, как правило, имеют большую неравномерность амплитудно-частотной характеристики (АЧХ) в полосе пропускания, когда порядок фильтра выше второго. Известные методы уменьшения неравномерности АЧХ в полосе пропускания многослойных диэлектрических фильтров [3–5] не снижают сложности их изготовления. Поэтому поиск и исследование новых подходов конструирования ППФ на слоистых структурах является важной и актуальной задачей.
В настоящее время для создания фильтров многими исследователями используются конструкции на основе диэлектрических слоев, на поверхности которых сформированы резонансные 2D структуры из металлических проводников, так называемые частотно-селективные поверхности. Такие конструкции служат ППФ и полосно-заграждающими фильтрами в диапазонах от микронных [6–8] до дециметровых [9–11] длин волн. Отметим важную особенность частотно-селективных поверхностей, которая заключается в том, что их частотные характеристики зависят от угла падения и поляризации электромагнитной волны [12].
Первые частотно-селективные поверхности представляли собой плоские двумерно-периодические металлические решетки, элементарные ячейки которых выполнялись как в виде прямоугольных отверстий в тонком металлическом экране (сеток), так и в виде тонких плоских прямоугольных проводников, расположенных на диэлектрической подложке [13]. При этом размер элементарной ячейки решетки равен приблизительно длине волны на резонансной частоте. Каскадирование нескольких таких металлических резонансных решеток позволяет создавать многослойные структуры, АЧХ которых соответствуют ППФ высокого порядка [12]. Однако плоские металлические решетки, содержащие резонансные элементарные ячейки, обладают низкой собственной добротностью из-за высоких омических потерь в проводниках.
Поэтому более перспективными являются конструкции частотно-селективных поверхностей, в которых, как и в традиционных оптических фильтрах [12], резонаторами являются полуволновые диэлектрические слои. Однако вместо многослойных диэлектрических зеркал в них используются нерезонансные субволновые решетки полосковых проводников, расположенные на границах раздела диэлектрических слоев-резонаторов. Такими решетками, в частности, могут служить 1D-решетки из ленточных полосковых проводников с периодом много меньше длины волны, имеющих параллельное направление осей симметрии на всех слоях [14, 15]. Электродинамический анализ таких ленточных полосковых структур представлен в работах [16, 17]. Фильтры на диэлектрических слоях, зеркала которых представляют собой ленточные полосковые структуры с параллельными осями, обладают частотно-селективными свойствами только для электромагнитных волн с линейной поляризацией и направлением вектора электрического поля вдоль полосковых проводников. Волны ортогональной поляризации такие фильтры пропускают с малыми потерями в диапазоне частот от нуля и выше.
Резонаторы в конструкциях рассматриваемых фильтров могут состоять не из одного, а из двух диэлектрических слоев, разделенных также субволновой 1D-решеткой полосковых проводников, но с ортогональной осью по отношению к 1D-решеткам на границах двухслойных резонаторов [18]. Такой фильтр одновременно является поляризатором. В заданной полосе частот он пропускает волны линейной поляризации с направлением вектора электрического поля вдоль наружных полосковых проводников, но практически не пропускает волны ортогональной поляризации [18].
Фильтр, в котором в качестве зеркал на границах диэлектрических слоев-резонаторов использованы субволновые металлические сетки с квадратными окнами, уже не проявляет поляризационных свойств. В работе [19] исследован экспериментальный образец фильтра третьего порядка с сетками между диэлектрическими слоями, обладающий не только высокими характеристиками, но и хорошим согласием АЧХ измеренных и АЧХ рассчитанных численным электродинамическим анализом 3D-модели устройства. Однако программы электродинамического анализа таких сложных конструкций требуют большого машинного времени, поэтому параметрический синтез фильтра проводился скоростным матричным методом с использованием формул, полученных в работе [20], которые достаточно хорошо описывают отражательные свойства металлических сеток. Найденные в результате синтеза конструктивные параметры были использованы в качестве начальных параметров при параметрическом синтезе с использованием электродинамического анализа 3D-модели.
Для решеток из квадратных полосковых проводников, которые также могут служить зеркалами в фильтрах на диэлектрических слоях-резонаторах, подобные формулы, описывающие их отражательные свойства, до сих пор не были получены. В расчетах решетки из полосковых проводников обычно используют формулы для матрицы рассеяния электромагнитных волн линейной поляризации на соответствующей решетке параллельных ленточных проводников [13, 21] с тем же периодом и шириной, когда вектор электрического поля ортогонален направлению проводников. Очевидно, что при таком подходе элементы матрицы рассеяния описывают только емкостные взаимодействия полосковых проводников, но полностью игнорируются индуктивные взаимодействия, относительный вклад которых растет пропорционально квадрату частоты.
В данной работе выполнен расчет матрицы рассеяния электромагнитных волн, падающих ортогонально на плоскую 2D-решетку квадратных полосковых проводников, расположенных на границе раздела двух диэлектрических сред. При расчете используется метод решений уравнений Максвелла для определенных выделенных областей рассматриваемой структуры, который был применен в работе [20]. В этом расчете наряду с потенциальной частью электрического поля рассматривается и вихревая часть, что существенно повышает точность расчета в высокочастотной области.
1. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ РЕШЕТКИ ИЗ КВАДРАТНЫХ ПОЛОСКОВЫХ ПРОВОДНИКОВ
Рассчитаем электромагнитные поля вблизи решетки квадратных полосковых проводников на границе раздела двух диэлектрических сред (рис. 1). Поля возбуждаются нормально падающими на решетку с обеих сторон линейно поляризованными волнами с компонентами
(1)
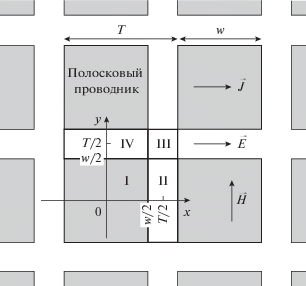
$\begin{gathered} E_{x}^{{{\text{п а д }}}} = \left\{ {\begin{array}{*{20}{l}} {E_{1}^{{{\text{п а д }}}}\exp (i{{k}_{1}}z - i\omega t),} \\ {E_{2}^{{{\text{п а д }}}}\exp ( - i{{k}_{2}}z - i\omega t),} \end{array}{\text{ }}\begin{array}{*{20}{c}} {\,{\text{е с л и }}z < 0,} \\ {\,{\text{е с л и }}z > 0,} \end{array}} \right. \\ H_{y}^{{{\text{п а д }}}} = \left\{ {\begin{array}{*{20}{l}} {Z_{1}^{{ - 1}}E_{1}^{{{\text{п а д }}}}\exp (i{{k}_{1}}z - i\omega t),} \\ { - Z_{2}^{{ - 1}}E_{2}^{{{\text{п а д }}}}\exp ( - i{{k}_{2}}z - i\omega t),} \end{array}{\text{ }}\begin{array}{*{20}{c}} {\,{\text{е с л и }}z < 0,} \\ {\,{\text{е с л и }}z > 0,} \end{array}} \right. \\ \end{gathered} $Рис. 1.
Решетка полосковых проводников; I, II, III и IV – рассматриваемые участки ее элементарной ячейки.
где
– волновые числа, а
(3)
${{Z}_{{1,2}}} = {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {\sqrt {{{\varepsilon }_{{1,2}}}} }}} \right. \kern-0em} {\sqrt {{{\varepsilon }_{{1,2}}}} }}{\text{,}}\,\,\,\,{{Z}_{0}} = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} $– характеристические сопротивления, нижние индексы 1 и 2 указывают на стороны решетки, соприкасающиеся соответственно со средой с диэлектрической проницаемостью ε1 и со средой с диэлектрической проницаемостью ε2. Начало отсчета координаты z выбрано на поверхности решетки.
Так как компоненты поля падающих волн (1) однородны в плоскости решетки, то возбуждаемые ими компоненты поля решетки ${{\vec {E}}^{{{\text{р е ш }}}}}$ и ${{\vec {H}}^{{{\text{р е ш }}}}}$ будут в общем случае периодическими функциями координат x и y с периодом, равным периоду решетки T. Это значит, что любая из компонент электромагнитного поля может быть разложена в двойной ряд Фурье по аргументам x и y. Учитывая симметрию компонент полей относительно плоскостей симметрии решетки, можно записать следующие разложения:
(4)
$\begin{gathered} E_{x}^{{{\text{р е ш }}}}(x,y,z) = \sum\limits_{n\, = \,0}^\infty {\sum\limits_{m\, = \,0}^\infty {E_{x}^{{nm}}(z)\cos \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)} } , \\ H_{y}^{{{\text{р е ш }}}}(x,y,z) = \sum\limits_{n\, = \,0}^\infty {\sum\limits_{m\, = \,0}^\infty {H_{y}^{{nm}}(z)\cos \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)} } , \\ E_{z}^{{{\text{р е ш }}}}(x,y,z) = \sum\limits_{n\, = \,0}^\infty {\sum\limits_{m\, = \,0}^\infty {E_{z}^{{nm}}(z)\sin \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)} } , \\ H_{z}^{{{\text{р е ш }}}}(x,y,z) = \sum\limits_{n\, = \,0}^\infty {\sum\limits_{m\, = \,0}^\infty {H_{z}^{{nm}}(z)\cos \left( {{{k}_{n}}x} \right)\sin \left( {{{k}_{m}}y} \right)} } , \\ \end{gathered} $где kn = 2πn/T, km = 2πm/T. Потребуем, чтобы каждый член двойного ряда Фурье в выражениях (4) удовлетворял уравнениям Гельмгольца
(5)
$\left( {{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{y}^{2}}}}} \right. \kern-0em} {\partial {{y}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}} + k_{{1,2}}^{2}}}} \right. \kern-0em} {\partial {{z}^{2}} + k_{{1,2}}^{2}}}} \right){{\vec {E}}^{{{\text{р е ш }}}}} = 0,$(6)
$\left( {{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{y}^{2}}}}} \right. \kern-0em} {\partial {{y}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}} + k_{{1,2}}^{2}}}} \right. \kern-0em} {\partial {{z}^{2}} + k_{{1,2}}^{2}}}} \right){{\vec {H}}^{{{\text{р е ш }}}}} = 0.$В этом случае формулы (4) принимают вид:
при z < 0 –
(7)
$\begin{gathered} E_{x}^{{{\text{р е ш }}}} = E_{x}^{{00}}\exp \left( {i{{k}_{1}}\left| z \right|} \right) + \\ + \,\,\sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {E_{x}^{{nm}}\cos \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)\exp \left( { - k_{1}^{{nm}}\left| z \right|} \right),} } \\ H_{y}^{{{\text{р е ш }}}} = H_{{1y}}^{{00}}\exp \left( {i{{k}_{1}}\left| z \right|} \right) + \\ + \,\,\sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {H_{{1y}}^{{nm}}\cos \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)\exp \left( { - k_{1}^{{nm}}\left| z \right|} \right),} } \\ E_{z}^{{{\text{р е ш }}}} = \sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {E_{{1z}}^{{nm}}\sin \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)\exp \left( { - k_{1}^{{nm}}\left| z \right|} \right),} } \\ H_{z}^{{{\text{р е ш }}}} = \sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {H_{z}^{{nm}}\cos \left( {{{k}_{n}}x} \right)\sin \left( {{{k}_{m}}y} \right)\exp \left( { - k_{1}^{{nm}}\left| z \right|} \right)} } \\ \end{gathered} $и при z > 0 –
(8)
$\begin{gathered} E_{x}^{{{\text{р е ш }}}} = E_{x}^{{00}}\exp \left( {i{{k}_{2}}\left| z \right|} \right) + \\ + \,\,\sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {E_{x}^{{nm}}\cos \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)\exp \left( { - k_{2}^{{nm}}\left| z \right|} \right),} } \\ H_{y}^{{{\text{р е ш }}}} = H_{{2y}}^{{00}}\exp \left( {i{{k}_{2}}\left| z \right|} \right) + \\ + \,\,\sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {H_{{2y}}^{{nm}}\cos \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)\exp \left( { - k_{2}^{{nm}}\left| z \right|} \right),} } \\ E_{z}^{{{\text{р е ш }}}} = \sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {E_{{2z}}^{{nm}}\sin \left( {{{k}_{n}}x} \right)\cos \left( {{{k}_{m}}y} \right)\exp \left( { - k_{2}^{{nm}}\left| z \right|} \right)} } , \\ H_{z}^{{{\text{р е ш }}}} = \sum\limits_{n\, = \,1}^\infty {\sum\limits_{m\, = \,1}^\infty {H_{z}^{{nm}}\cos \left( {{{k}_{n}}x} \right)\sin \left( {{{k}_{m}}y} \right)\exp \left( { - k_{2}^{{nm}}\left| z \right|} \right)} } , \\ \end{gathered} $где
Здесь мы учли, что компоненты поля $E_{x}^{{{\text{р е ш }}}}$ и $H_{z}^{{{\text{р е ш }}}}$ непрерывны при z = 0. Формулы (7) и (8) можно рассматривать как разложение компонент поля решетки ${{\vec {E}}^{{{\text{р е ш }}}}},{\text{ }}{{\vec {H}}^{{{\text{р е ш }}}}}$ в ряд по всем модам, отвечающим симметрии решетки и поляризации падающих волн.
Будем предполагать, что период решетки T много меньше длины волны, т.е. k1,2T $ \ll $ 2π. Это позволяет нам выполнять электродинамический расчет в квазистатическом приближении и вместо уравнений Гельмгольца (5) и (6) решать уравнения Лапласа
(10)
$\left( {{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{y}^{2}}}}} \right. \kern-0em} {\partial {{y}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}}}}} \right. \kern-0em} {\partial {{z}^{2}}}}} \right){{\vec {E}}^{{{\text{р е ш }}}}} = 0,$(11)
$\left( {{{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{y}^{2}}}}} \right. \kern-0em} {\partial {{y}^{2}}}} + {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}}}}} \right. \kern-0em} {\partial {{z}^{2}}}}} \right){{\vec {H}}^{{{\text{р е ш }}}}} = 0.$В этом случае в разложениях (7) и (8) все члены рядов Фурье, кроме основных членов с n = m = 0, быстро убывают с ростом |z|. Поэтому формулы (7) и (8) в дальней зоне при k1,2|z| $ \gg $ 1 упрощаются и принимают вид
(12)
$\begin{gathered} E_{x}^{{{\text{р е ш }}}}(x,y,z) = E_{x}^{{00}}\exp \left( {i{{k}_{1}}\left| z \right|} \right) \\ H_{y}^{{{\text{р е ш }}}}(x,y,z) = \left\{ {\begin{array}{*{20}{c}} {H_{{1y}}^{{00}}\exp \left( {i{{k}_{1}}\left| z \right|} \right)}&{{\text{п р и }}z < 0} \\ {H_{{2y}}^{{00}}\exp \left( {i{{k}_{2}}\left| z \right|} \right)}&{{\text{п р и }}z > 0,} \end{array}} \right. \\ E_{z}^{{{\text{р е ш }}}}(x,y,z) = 0, \\ H_{z}^{{{\text{р е ш }}}}(x,y,z) = 0, \\ \end{gathered} $где амплитуды компонент поля выражаются интегралами
(13)
$E_{x}^{{00}} = \frac{1}{{{{T}^{2}}}}\int\limits_{x\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {\int\limits_{y\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {E_{x}^{{{\text{р е ш }}}}(x,y,0)dxdy} } ,$(14)
$\begin{array}{*{20}{c}} {H_{{1y}}^{{00}} = \frac{1}{{{{T}^{2}}}}\int\limits_{x\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {\int\limits_{y\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {H_{y}^{{{\text{р е ш }}}}(x,y,0)dxdy} } }&{{\text{п р и }}z < 0,} \\ {H_{{2y}}^{{00}} = \frac{1}{{{{T}^{2}}}}\int\limits_{x\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {\int\limits_{y\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {H_{y}^{{{\text{р е ш }}}}(x,y,0)dxdy} } }&{{\text{п р и }}z > 0.} \end{array}$Здесь w – размер стороны квадратного полоскового проводника в решетке. Очевидно, найдя величины $E_{x}^{{00}},{\text{ }}H_{{1y}}^{{00}}$ и $H_{{2y}}^{{00}},$ мы сможем вычислить элементы искомой матрицы рассеяния S для дальней зоны рассматриваемой решетки.
Для нахождения амплитуд $E_{x}^{{00}},{\text{ }}H_{{1y}}^{{00}}$ и $H_{{2y}}^{{00}}$ по формулам (13) и (14) нам достаточно получить решения уравнений Максвелла только вблизи поверхности проводников решетки. Запишем граничные условия, которым эти решения должны удовлетворять. Для этого поверхность элементарной ячейки решетки удобно разбить на четыре прямоугольные области I–IV (рис. 1). Тогда в области I, занимающей четверть площади полоскового проводника, граничные условия имеют вид
(15)
$\begin{gathered} E_{x}^{{{\text{р е ш }}}}(x,y,0) = 0,\,\,\,\,E_{y}^{{{\text{р е ш }}}}(x,y,0) = 0, \\ {\text{ }}H_{z}^{{{\text{р е ш }}}}(x,y,0) = 0, \\ \end{gathered} $а в областях II, III и IV, свободных от металлизации, кроме условий непрерывности никаких других ограничений на компоненты электромагнитного поля нет.
Уравнения Максвелла для электромагнитного поля в приповерхностной области решетки имеют два решения, удовлетворяющие граничным условиям (15). Первое квазистатическое решение тривиально. В статическом пределе оно имеет единственную магнитную компоненту H0, не зависящую от координат и направленную вдоль вектора магнитного поля падающей волны, т.е. вдоль оси y. Электрическое поле ${{\vec {E}}^{{{\text{р е ш }}}}}$ у первого решения существует только в динамике, оно является вихревым и обращается в нуль на всей поверхности решетки.
Второе квазистатическое решение имеет в статическом пределе только компоненты электрического поля ${{\vec {E}}^{{{\text{р е ш }}}}}.$ Оно содержит лишь потенциальную часть ${{\vec {E}}^{{{\text{п о т }}}}}.$ Магнитное поле ${{\vec {H}}^{{{\text{р е ш }}}}}$ у второго решения появляется только в динамике. Оно является вихревым, так как связано с электрическим полем ${{\vec {E}}^{{{\text{р е ш }}}}}$ уравнением Максвелла
(16)
$\operatorname{rot} \vec {H}_{{1,2}}^{{{\text{р е ш }}}} = - i{\kern 1pt} \omega {{\varepsilon }_{0}}{{\varepsilon }_{{1,2}}}\vec {E}_{{1,2}}^{{{\text{р е ш }}}}.$Поэтому в дальнейшем магнитное поле второго решения будем обозначать как $\vec {H}_{{1,2}}^{{{\text{в и х }}}}.$ Электрическое же поле в этом случае следует представить суммой
(17)
${{\vec {E}}^{{{\text{р е ш }}}}} = {{\vec {E}}^{{{\text{п о т }}}}} + {{\vec {E}}^{{{\text{в и х }}}}},$где ${{\vec {E}}^{{{\text{п о т }}}}}$ – потенциальная часть электрического поля, а ${{\vec {E}}^{{{\text{в и х }}}}}$ – вихревая часть. Потенциальную часть электрического поля удобно описывать скалярным потенциалом φ, используя уравнение
Поверхность каждого полоскового проводника вместе с пересекающей его плоскостью симметрии, ортогональной оси x, эквипотенциальна. Это следует из граничных условий (15) и из симметрии задачи. Полагая, что разность потенциалов φ между соседними проводниками равна U, по формуле (13) находим величину вклада в амплитуду $E_{x}^{{00}}$ от потенциальной части электрического поля$E_{x}^{{{\text{п о т }}}}$
(19)
${{\left\langle {E_{x}^{{{\text{п о т }}}}} \right\rangle }_{{T\,T}}} = {U \mathord{\left/ {\vphantom {U T}} \right. \kern-0em} T}.$Здесь нижний индекс TT указывает на то, что усреднение $E_{x}^{{{\text{п о т }}}}$ произведено по площади элементарной ячейки решетки с периодом T.
Потенциальная часть ${{\vec {E}}^{{{\text{п о т }}}}}$ электрического поля связана с поверхностными зарядами ρ на полосковых проводниках граничным условием
(20)
${{\varepsilon }_{0}}{{\varepsilon }_{2}}E_{{2z}}^{{{\text{п о т }}}} - {{\varepsilon }_{0}}{{\varepsilon }_{1}}E_{{1z}}^{{{\text{п о т }}}} = \rho .$В свою очередь, заряды ρ связаны с поверхностными токами $\vec {J}$ законом сохранения
а сами поверхностные токи $\vec {J}$ связаны с вихревым магнитным полем ${{\vec {H}}^{{{\text{в и х }}}}}$ на обеих сторонах решетки граничным условием
(22)
$H_{{2x}}^{{{\text{в и х }}}} - H_{{1x}}^{{{\text{в и х }}}} = {{J}_{y}},\,\,\,\,H_{{2y}}^{{{\text{в и х }}}} - H_{{1y}}^{{{\text{в и х }}}} = - {{J}_{x}}.$Так как магнитное поле ${{\vec {H}}^{{{\text{в и х }}}}}$ является вихревым, то его тангенциальные компоненты меняют знак при переходе с одной стороны полоскового проводника на другую сторону. Поэтому граничные условия (22) можно переписать в виде
(23)
$2H_{{2x}}^{{{\text{в и х }}}} = {{J}_{y}},\,\,\,\,{\text{2}}H_{{2y}}^{{{\text{в и х }}}} = - {{J}_{x}}.$Найдем амплитуду магнитного поля $H_{{2y}}^{{00}}.$ Из формул (14) и (23) получаем
(24)
$H_{{2y}}^{{00}} = - \frac{1}{{{\text{2}}T}}\int\limits_{x\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {{{{\left\langle {{{J}_{x}}(x)} \right\rangle }}_{T}}dx} ,$где
(25)
${{\left\langle {{{J}_{x}}(x)} \right\rangle }_{T}} = \frac{1}{T}\int\limits_{y\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {{{J}_{x}}(x,y)dy} $– усредненная по координате y функция плотности продольного поверхностного тока. Эта функция, согласно уравнению (21), связана с усредненной функцией плотности поверхностных зарядов
(26)
${{\left\langle {\rho (x)} \right\rangle }_{T}} = \frac{1}{T}\int\limits_{y\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {\rho (x,y)dy} $равенством
(27)
$\frac{\partial }{{\partial x}}{{\left\langle {{{J}_{x}}(x)} \right\rangle }_{T}} = i\omega {{\left\langle {\rho (x)} \right\rangle }_{T}}.$Здесь было учтено, что усредненная функция плотности поперечного тока равна ${{\left\langle {{{J}_{y}}(x)} \right\rangle }_{T}} = 0.$ При расчете усредненной функции плотности зарядов ${{\left\langle {\rho (x)} \right\rangle }_{T}}$ следует учитывать то обстоятельство, что поверхностные электрические заряды ρ(x, y) концентрируются не только вблизи края полоскового проводника, обращенного к области II, но и вблизи другого края, обращенного к области IV. Те заряды, которые концентрируются на краю проводника, обращенном к области IV, порождают компоненту $E_{x}^{{{\text{п о т }}}}$ не только в областях I и II, но и в областях IV и III. Именно поэтому усреднение ρ(x, y) по координате y следует производить в областях I и IV, т.е. по всему периоду T.
Потенциал φ(x, z), отвечающий усредненной функции ${{\left\langle {\rho (x)} \right\rangle }_{T}}$ и разности потенциалов U, выражается формулой
(28)
$\varphi (x,z) = \frac{U}{\pi }\operatorname{Im} \operatorname{arch} \left( {{{\cos (\pi \frac{{x + iz}}{T})} \mathord{\left/ {\vphantom {{\cos (\pi \frac{{x + iz}}{T})} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right. \kern-0em} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right).$Формула (28) является точным решением 2D-уравнения Лапласа для квазистатического потенциала решетки полосковых проводников [16]. Этот потенциал постоянен на поверхности решетки при |x| < w/2 и при |x–T| < w/2.
По формулам (18) и (28) находим нормальную компоненту потенциальной части электрического поля на верхней стороне решетки
(29)
$\begin{gathered} {{\left\langle {E_{{2z}}^{{{\text{п о т }}}}(x,0)} \right\rangle }_{T}} = \\ = - \frac{U}{\pi }\operatorname{Re} \frac{\partial }{{\partial x}}\operatorname{arch} \left( {{{\cos \left( {\frac{{\pi x}}{T}} \right)} \mathord{\left/ {\vphantom {{\cos \left( {\frac{{\pi x}}{T}} \right)} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right. \kern-0em} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right). \\ \end{gathered} $Так как потенциал φ является четной функцией координаты z, то компонента $E_{{1z}}^{{{\text{п о т }}}}$ на нижней стороне полоскового проводника отличается от компоненты $E_{{2z}}^{{{\text{п о т }}}}$ только знаком. Тогда из формул (20) и (29) получаем
(30)
$\begin{gathered} {{\left\langle {\rho (x)} \right\rangle }_{T}} = - {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{\pi }U \times \\ \times \,\,\operatorname{Re} \frac{\partial }{{\partial x}}\operatorname{arch} \left( {{{\cos \left( {\frac{{\pi x}}{T}} \right)} \mathord{\left/ {\vphantom {{\cos \left( {\frac{{\pi x}}{T}} \right)} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right. \kern-0em} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right). \\ \end{gathered} $Отсюда по формуле (27) находим усредненный продольный ток
(31)
$\begin{gathered} {{\left\langle {{{J}_{x}}(x)} \right\rangle }_{T}} = - i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{\pi }U \times \\ \times \,\,\operatorname{Re} \operatorname{arch} \left( {{{\cos \left( {\frac{{\pi x}}{T}} \right)} \mathord{\left/ {\vphantom {{\cos \left( {\frac{{\pi x}}{T}} \right)} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right. \kern-0em} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right), \\ \end{gathered} $а по формуле (23) – усредненное магнитное поле
(32)
$\begin{gathered} {{\left\langle {H_{{2y}}^{{{\text{в и х }}}}(x,0)} \right\rangle }_{T}} = \\ = i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2\pi }}U\operatorname{Re} \operatorname{arch} \left( {{{\cos \left( {\frac{{\pi x}}{T}} \right)} \mathord{\left/ {\vphantom {{\cos \left( {\frac{{\pi x}}{T}} \right)} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right. \kern-0em} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right). \\ \end{gathered} $Подставляя выражение (31) в интеграл (24), находим амплитуду магнитного поля
(33)
$H_{{2y}}^{{00}} = i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{{\text{2}}\pi }}U\ln \left( {\sec \left( {\frac{{\pi w}}{{2T}}} \right)} \right),$где было учтено значение интеграла
(34)
$\int\limits_{\xi \, = \, - a}^a {\operatorname{arch} \left( {\frac{{\cos \xi }}{{\cos a}}} \right)d\xi } = \pi \ln \left( {\sec a} \right).$Для нахождения вклада вихревой части электрического поля $E_{x}^{{{\text{в и х }}}}$ в среднее значение ${{\left\langle {E_{x}^{{{\text{в и х }}}}} \right\rangle }_{{T\,T}}}$ необходимо знать компоненту магнитного поля $Н _{z}^{{{\text{в и х }}}},$ с которой $E_{x}^{{{\text{в и х }}}}$ связана уравнением Максвелла
(35)
${{(\operatorname{rot} {{\vec {E}}^{{{\text{в и х }}}}})}_{z}} = i\omega {{\mu }_{0}}H_{z}^{{{\text{в и х }}}}.$Для этого запишем формулы усреднения для тока Jx(x, y) и магнитной компоненты $H_{{2y}}^{{{\text{в и х }}}}(x,y,z)$ по координате x:
(36)
${{\left\langle {{{J}_{x}}(y)} \right\rangle }_{T}} = \frac{1}{T}\int\limits_{x\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {{{J}_{x}}(x,y)dx} ,$(37)
${{\left\langle {H_{{2y}}^{{{\text{в и х }}}}(y,z)} \right\rangle }_{T}} = \frac{1}{T}\int\limits_{x\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {H_{{2y}}^{{{\text{в и х }}}}(x,y,z)dx} .$Эти величины, согласно граничному условию (23), связаны на поверхности решетки равенством
(38)
${{\left\langle {{{J}_{x}}(y)} \right\rangle }_{T}} = - 2{{\left\langle {H_{{2y}}^{{{\text{в и х }}}}(y,0)} \right\rangle }_{T}}.$Так как усредненная компонента ${{\left\langle {H_{{2y}}^{{{\text{в и х }}}}(y,z)} \right\rangle }_{T}}$ не зависит от координаты x, то решение 2D-уравнения Лапласа (11) для усредненных компонент может быть получено методом конформных отображений [16]. Это решение имеет вид
(39)
$\begin{gathered} {{\left\langle {H_{{2y}}^{{{\text{в и х }}}}(y,z)} \right\rangle }_{T}} = i{\kern 1pt} \omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{{\text{2}}{{\pi }^{2}}}}TU \times \\ \times \,\,\ln \left( {\sec (\frac{{\pi w}}{{2T}})} \right)\operatorname{Re} \frac{\partial }{{\partial y}}\arcsin \left( {\frac{{\sin \left( {\pi \frac{{y + iz}}{T}} \right)}}{{\sin \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right). \\ \end{gathered} $Оно отвечает значению амплитуды $H_{{2y}}^{{00}},$ выражаемому формулой (33). Сравнение формул (32) и (39) позволяет построить функцию
(40)
$\begin{gathered} H_{{2y}}^{{{\text{в и х }}}}(x,y,0) = i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}TU \times \\ \times \,\,\operatorname{Re} \operatorname{arch} \left( {\frac{{\cos ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} T}} \right. \kern-0em} T})}}{{\cos ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right)\operatorname{Re} \frac{\partial }{{\partial y}}\arcsin \left( {\frac{{\sin ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} T}} \right. \kern-0em} T})}}{{\sin ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right), \\ \end{gathered} $которая описывает зависимость компоненты $H_{{2y}}^{{{\text{в и х }}}}$ от координат x и y на всей поверхности решетки. Видно, что компонента $H_{{2y}}^{{{\text{в и х }}}}$ отлична от нуля только на поверхности полоскового проводника. Полученной компоненте $H_{{2y}}^{{{\text{в и х }}}}(x,y,0),$ согласно граничному условию (23), соответствует продольный ток
(41)
$\begin{gathered} {{J}_{x}}(x,y) = - i{\text{2}}\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}TU \times \\ \times \,\,\operatorname{Re} \operatorname{arch} \left( {\frac{{\cos ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} T}} \right. \kern-0em} T})}}{{\cos ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right)\operatorname{Re} \frac{\partial }{{\partial y}}\arcsin \left( {\frac{{\sin ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} T}} \right. \kern-0em} T})}}{{\sin ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right). \\ \end{gathered} $Поперечный же ток ${{J}_{y}}(x,y)$ может быть рассчитан из закона сохранения заряда (21), но для этого необходимо знать кроме продольного тока Jx(x, y) еще и плотность поверхностных зарядов ρ(x, y). Поэтому неизвестную функцию ρ(x, y) аппроксимируем функцией ${{\left\langle {\rho (x)} \right\rangle }_{w}},$ получаемой усреднением ρ(x, y) по координате y. В отличие от функции ${{\left\langle {\rho (x)} \right\rangle }_{T}},$ заданной формулой (26), усреднение произведем не по периоду решетки T, а по ширине полоскового w. Из формулы (30) получаем
(42)
$\begin{gathered} {{\left\langle {\rho (x)} \right\rangle }_{w}} = - \frac{T}{w}{{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{\pi }\,\, \times \\ \times \,\,U\operatorname{Re} \frac{\partial }{{\partial x}}\operatorname{arch} \left( {{{\cos \left( {\frac{{\pi x}}{T}} \right)} \mathord{\left/ {\vphantom {{\cos \left( {\frac{{\pi x}}{T}} \right)} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right. \kern-0em} {\cos \left( {\frac{{\pi w}}{{2T}}} \right)}}} \right). \\ \end{gathered} $Подставляя формулы (41) и (42) в уравнение (21), находим поперечный ток
(43)
$\begin{gathered} {{J}_{y}}(x,y) = i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{{{\pi }^{2}}}}TU \times \\ \times \,\,\operatorname{Re} \frac{\partial }{{\partial x}}\operatorname{arch} \left( {\frac{{\cos ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} T}} \right. \kern-0em} T})}}{{\cos ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right) \times \\ \times \,\,\operatorname{Re} \left[ {\arcsin \left( {\frac{{\sin ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} T}} \right. \kern-0em} T})}}{{\sin ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right) - \frac{{\pi y}}{w}} \right]. \\ \end{gathered} $Здесь константа интегрирования выбрана равной нулю для того, чтобы ток Jy обращался в нуль на краю полоскового проводника при y = w/2. Согласно граничному условию (23), току Jy соответствует компонента магнитного поля
(44)
$\begin{gathered} H_{{2x}}^{{{\text{в и х }}}}(x,y,0) = i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}TU \times \\ \times \,\,\operatorname{Re} \frac{\partial }{{\partial x}}\operatorname{arch} \left( {\frac{{\cos ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} T}} \right. \kern-0em} T})}}{{\cos ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right) \times \\ \times \,\,\operatorname{Re} \left[ {\arcsin \left( {\frac{{\sin ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} T}} \right. \kern-0em} T})}}{{\sin ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right) - \frac{{\pi y}}{w}} \right]. \\ \end{gathered} $Она отвечает условиям Мейкснера на ребре [22]
(45)
$\begin{gathered} {{\left. {{{H}_{x}}} \right|}_{{\left| x \right|\, \leqslant \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2},{\text{ }}y\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}\, - \,r}}} \propto {{r}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{\left. {{{H}_{x}}} \right|}_{{x\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}\, - \,r,{\text{ }}\left| y \right|\, \leqslant \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}}} \propto {{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}, \\ {{\left. {{{H}_{y}}} \right|}_{{\left| x \right|\, \leqslant \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2},{\text{ }}y\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}\, - \,r}}} \propto {{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{\left. {{{H}_{y}}} \right|}_{{x\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}\, - \,\rho ,{\text{ }}\left| y \right|\, \leqslant \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}}} \propto {{r}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{\left. {{{H}_{z}}} \right|}_{{\left| x \right|\, \leqslant \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2},{\text{ }}y\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2} - r}}} \propto {{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}, \\ {{\left. {{{H}_{z}}} \right|}_{{x\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}\, - \,r,{\text{ }}\left| y \right|\, \leqslant \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}}} \propto {{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{\text{ }}(r \to 0). \\ \end{gathered} $Видно, что две компоненты магнитного поля $H_{{2x}}^{{{\text{в и х }}}}$ и $H_{z}^{{{\text{в и х }}}}$ на краю полоскового проводника между областями I и II имеют сингулярность. Это значит, что вблизи этого края можно пренебречь третьей компонентой $H_{{2y}}^{{{\text{в и х }}}},$ а в уравнении Лапласа (11) пренебречь производными компонент $H_{{2x}}^{{{\text{в и х }}}}$ и $H_{z}^{{{\text{в и х }}}}$ по координате y по сравнению с производными этих же компонент по координате x. Тогда из формулы (44) следует, что компоненту $H_{z}^{{{\text{в и х }}}}$ в области II можно аппроксимировать функцией
(46)
$\begin{gathered} H_{z}^{{{\text{II}}}}(x,y,0) = - i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}TU \times \\ \times \,\,\frac{\partial }{{\partial x}}\arccos \left( {\frac{{\cos ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} T}} \right. \kern-0em} T})}}{{\cos ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right) \times \\ \times \,\,\left[ {\arcsin \left( {\frac{{\sin ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} T}} \right. \kern-0em} T})}}{{\sin ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right) - \frac{{\pi y}}{w}} \right]. \\ \end{gathered} $Очевидно, что такая аппроксимация $H_{z}^{{{\text{в и х }}}}$ в области II правомерна только в случае, когда ширина этой области (T–w) меньше ее высоты w. Но именно этот случай и является интересным с точки зрения практических применений решетки из полосковых проводников.
На другом краю проводника между областями I и IV, согласно условиям (45), сингулярность имеют уже компоненты $H_{{2y}}^{{{\text{в и х }}}}$ и $H_{z}^{{{\text{в и х }}}}.$ Поэтому в области IV из формулы (40) и уравнения Максвелла
находим нормальную компоненту
(48)
$\begin{gathered} H_{z}^{{{\text{IV}}}}(x,y,0) = - i\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}TU \times \\ \times \,\,\operatorname{arch} \left( {\frac{{\cos ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} T}} \right. \kern-0em} T})}}{{\cos ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right)\operatorname{Im} \frac{\partial }{{\partial y}}\arcsin \left( {\frac{{\sin ({{\pi y} \mathord{\left/ {\vphantom {{\pi y} T}} \right. \kern-0em} T})}}{{\sin ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right). \\ \end{gathered} $Для нахождения вихревого поля ${{\vec {E}}^{{{\text{в и х }}}}}$ в областях II, III и IV обратимся к уравнению Максвелла (35).
В области III, согласно формулам (40) и (44), отсутствуют магнитные компоненты $H_{{2y}}^{{{\text{в и х }}}}$ и $H_{{2x}}^{{{\text{в и х }}}},$ поэтому будет отсутствовать и третья компонента $H_{z}^{{{\text{в и х }}}},$ связанная с первыми двумя компонентами уравнением (47). Следовательно, в области III вихревое электрическое поле равно $E_{x}^{{{\text{III}}}} = 0.$
В области II выполним интегрирование уравнения (35) по площади, ограниченной неравенствами w/2 < x < T–w/2 и y' < y < w/2. Используя теорему Стокса о роторе, получаем
(49)
$\begin{gathered} \int\limits_{x\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T{{ - w} \mathord{\left/ {\vphantom {{ - w} 2}} \right. \kern-0em} 2}} {E_{x}^{{{\text{II}}}}(x,y{\text{'}},0)dx} = \\ = i{\kern 1pt} \omega {{\mu }_{0}}\int\limits_{x\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T{{ - w} \mathord{\left/ {\vphantom {{ - w} 2}} \right. \kern-0em} 2}} {\int\limits_{y\, = \,y{\text{'}}}^{{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {H_{z}^{{{\text{II}}}}(x,y,0)dy} dx} , \\ \end{gathered} $где мы учли, что на краях проводников, т.е. при x = w/2 и x = T – w/2, компонента $E_{y}^{{{\text{II}}}} = 0,$ а на границе областей II и III компонента $E_{x}^{{{\text{II}}}} = 0.$ Уравнение (49) после подстановки в него выражения (46) принимает вид
(50)
$\begin{gathered} \int\limits_{x\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{T{{ - w} \mathord{\left/ {\vphantom {{ - w} 2}} \right. \kern-0em} 2}} {E_{x}^{{{\text{II}}}}(x,y,0)dx} = \\ = {{\omega }^{2}}{{\varepsilon }_{0}}{{\mu }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}{{T}^{2}}U\left[ {I\left( {\frac{{\pi y}}{T},\frac{{\pi w}}{{2T}}} \right) + {{\pi }^{2}}\frac{{4{{y}^{2}} - {{w}^{2}}}}{{8wT}}} \right], \\ \end{gathered} $где функция I(ζ, a) обозначает интеграл
(51)
$I(\zeta ,a) = \int\limits_{\xi \, = \,\zeta }^a {\arcsin \left( {\frac{{\sin \xi }}{{\sin a}}} \right)d\xi } .$Для нахождения вклада ${{\left\langle {E_{x}^{{{\text{II}}}}} \right\rangle }_{{T\,T}}}$ в амплитуду $E_{x}^{{00}}$ от компоненты $E_{x}^{{{\text{в и х }}}}$ на участке II подставляем выражение (50) в формулу (13). После интегрирования имеем
(52)
${{\left\langle {E_{x}^{{{\text{II}}}}} \right\rangle }_{{TT}}} = {{\omega }^{2}}{{\varepsilon }_{0}}{{\mu }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{{{\pi }^{3}}}}TU\left[ {X\left( {\frac{{\pi w}}{{2T}}} \right) - \frac{{{{\pi }^{3}}{{w}^{2}}}}{{24{{T}^{2}}}}} \right],$где функция Х(a) обозначает двойной интеграл
(53)
$X(a) = \int\limits_{\zeta = \,0}^a {\left[ {\int\limits_{\xi = \,\zeta }^a {\arcsin \left( {\frac{{\sin \xi }}{{\sin a}}} \right)d\xi } } \right]d\zeta } .$В области IV выполним интегрирование уравнения (35) по площади, ограниченной неравенствами |x| < w/2 и w/2 < y < y'. Используя теорему Стокса о роторе, получаем
(54)
$\begin{gathered} - \int\limits_{x\, = \,{{ - w} \mathord{\left/ {\vphantom {{ - w} 2}} \right. \kern-0em} 2}}^{{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {E_{x}^{{{\text{IV}}}}(x,y{\text{'}},0)dx} = \\ = i\omega {{\mu }_{0}}\int\limits_{x\, = \, - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}}^{{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {\int\limits_{y\, = \,{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}\,}^{y{\text{'}}} {H_{z}^{{{\text{IV}}}}(x,y,0)dy} dx} , \\ \end{gathered} $где мы учли, что на краю полоскового проводника, т.е. при y = w/2, компонента $E_{y}^{{{\text{IV}}}} = 0,$ а на границе областей III и IV также и компонента $E_{x}^{{{\text{IV}}}} = 0.$ Уравнение (54) после подстановки в него выражения (48) принимает вид
(55)
$\begin{gathered} - \int\limits_{x\, = \,{{ - w} \mathord{\left/ {\vphantom {{ - w} 2}} \right. \kern-0em} 2}}^{{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {E_{x}^{{{\text{IV}}}}(x,y{\text{'}},0)dx} = {{\omega }^{2}}{{\varepsilon }_{0}}{{\mu }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}{{T}^{2}}U \times \\ \times \,\,\ln \left( {\sec \left( {\frac{{\pi w}}{{2T}}} \right)} \right)\operatorname{arch} \left( {\frac{{\sin ({{\pi y{\text{'}}} \mathord{\left/ {\vphantom {{\pi y{\text{'}}} T}} \right. \kern-0em} T})}}{{\sin ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}} \right). \\ \end{gathered} $Для нахождения вклада ${{\left\langle {E_{x}^{{{\text{IV}}}}} \right\rangle }_{{T\,T}}}$ в амплитуду $E_{x}^{{00}}$ от компоненты $E_{x}^{{{\text{в и х }}}}$ на участке IV подставим выражение (55) в формулу (13). После интегрирования получим
(56)
$\begin{gathered} {{\left\langle {E_{x}^{{{\text{IV}}}}} \right\rangle }_{{TT}}} = - {{\omega }^{2}}{{\varepsilon }_{0}}{{\mu }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}} \times \\ \times \,\,TU\ln \left( {\sec \left( {\frac{{\pi w}}{{2T}}} \right)} \right)\ln \left( {\operatorname{cosec} \left( {\frac{{\pi w}}{{2T}}} \right)} \right), \\ \end{gathered} $где было учтено значение интеграла
(57)
$\int\limits_{\xi = a}^{\pi \, - a} {\operatorname{arch} \left( {\frac{{\sin \xi }}{{\sin a}}} \right)d\xi } = \pi \ln (\operatorname{cosec} a).$Суммируя вклады ${{\left\langle {E_{x}^{{{\text{п о т }}}}} \right\rangle }_{{TT}}},$ ${{\left\langle {E_{x}^{{{\text{II}}}}} \right\rangle }_{{TT}}}$ и ${{\left\langle {E_{x}^{{{\text{IV}}}}} \right\rangle }_{{TT}}},$ выражаемые формулами (19), (52) и (56), находим
(58)
$\begin{gathered} E_{x}^{{00}} = \frac{U}{T}\left[ {1 - {{\omega }^{2}}{{\varepsilon }_{0}}{{\mu }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{{2{{\pi }^{2}}}}{{T}^{2}} \times } \right. \\ \times \,\,\left[ {\ln \left( {\sec \left( {\frac{{\pi w}}{{2T}}} \right)} \right)\ln \left( {\operatorname{cosec} \left( {\frac{{\pi w}}{{2T}}} \right)} \right)} \right. + \\ \left. {\left. { + \,\,\frac{{{{\pi }^{2}}{{w}^{2}}}}{{12{{T}^{2}}}} - \frac{2}{\pi }X} \right]\left( {\frac{{\pi w}}{{2T}}} \right)} \right]. \\ \end{gathered} $Полученные формулы (33) и (58) для амплитуд $H_{{2y}}^{{00}}$ и $E_{x}^{{00}}$ позволяют приступить к непосредственному расчету матрицы рассеяния.
2. ФОРМУЛЫ ДЛЯ МАТРИЦЫ РАССЕЯНИЯ
Рассчитаем матрицу рассеяния S, рассматривая поверхности по обе стороны решетки как два порта четырехполюсника. Эта матрица связывает нормированные амплитуды рассеянных волн b1 и b2, исходящих из первого и второго порта, с нормированными амплитудами падающих волн a1 и a2 уравнением [23]
(59)
$\left( {\begin{array}{*{20}{c}} {{{b}_{1}}} \\ {{{b}_{2}}} \end{array}} \right) = {\mathbf{S}}\left( {\begin{array}{*{20}{c}} {{{a}_{1}}} \\ {{{a}_{2}}} \end{array}} \right).$Сами нормированные амплитуды определяются формулами [23]
(60)
${{a}_{{1,2}}} = {{E_{{1,2}}^{{{\text{п а д }}}}} \mathord{\left/ {\vphantom {{E_{{1,2}}^{{{\text{п а д }}}}} {\sqrt {{{Z}_{{1,2}}}} }}} \right. \kern-0em} {\sqrt {{{Z}_{{1,2}}}} }},\,\,\,\,{{b}_{{1,2}}} = {{E_{{1,2}}^{{{\text{р а с }}}}} \mathord{\left/ {\vphantom {{E_{{1,2}}^{{{\text{р а с }}}}} {\sqrt {{{Z}_{{1,2}}}} }}} \right. \kern-0em} {\sqrt {{{Z}_{{1,2}}}} }},$где $E_{{1,2}}^{{{\text{п а д }}}}$ – амплитуды падающих волн в формуле (1), а $E_{{1,2}}^{{{\text{р а с }}}}$ – амплитуды рассеянных волн.
Запишем граничные условия для электрического поля Ex и магнитного поля Hy в первом порте
(61)
$\begin{gathered} {{a}_{1}}\sqrt {{{Z}_{1}}} {\text{ }} + {{b}_{1}}\sqrt {{{Z}_{1}}} {\text{ }} = E_{x}^{{00}}, \\ {{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} {\sqrt {{{Z}_{1}}} }}} \right. \kern-0em} {\sqrt {{{Z}_{1}}} }} - {{{{b}_{1}}} \mathord{\left/ {\vphantom {{{{b}_{1}}} {\sqrt {{{Z}_{1}}} }}} \right. \kern-0em} {\sqrt {{{Z}_{1}}} }} = H_{{1y}}^{{00}} + {{H}_{0}}. \\ \end{gathered} $В уравнении (61) учтено, что волна с амплитудой b1 распространяется против направления оси z, и поэтому магнитное поле этой волны отличается знаком.
Аналогичные уравнения записываем для электрического и магнитного поля на втором порте
(62)
$\begin{gathered} {{b}_{2}}\sqrt {{{Z}_{2}}} {\text{ }} + {{a}_{2}}\sqrt {{{Z}_{2}}} = E_{x}^{{00}}, \\ {{{{b}_{2}}} \mathord{\left/ {\vphantom {{{{b}_{2}}} {\sqrt {{{Z}_{2}}} }}} \right. \kern-0em} {\sqrt {{{Z}_{2}}} }} - {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {\sqrt {{{Z}_{2}}} }}} \right. \kern-0em} {\sqrt {{{Z}_{2}}} }} = H_{{2y}}^{{00}} + {{H}_{0}}. \\ \end{gathered} $Отметим, что волна с амплитудой a2 распространяется против направления оси z, поэтому напряженность ее магнитного поля имеет противоположный знак, как и для волны с амплитудой b1 в формуле (61).
Совместно решая уравнения (61), (62) и учитывая, что амплитуды $H_{{1y}}^{{00}}$ и $H_{{2y}}^{{00}}$ различаются только знаком, находим нормированные амплитуды рассеянных волн
(63)
$\begin{gathered} {{b}_{1}} = \frac{{\sqrt {{{\varepsilon }_{1}}} - \sqrt {{{\varepsilon }_{2}}} - {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{a}_{1}} + \\ + \,\,\frac{{2\sqrt[4]{{{{\varepsilon }_{1}}{{\varepsilon }_{2}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{a}_{2}}, \\ {{b}_{2}} = \frac{{2\sqrt[4]{{{{\varepsilon }_{1}}{{\varepsilon }_{2}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{a}_{1}} + \\ + \,\,\frac{{\sqrt {{{\varepsilon }_{2}}} - \sqrt {{{\varepsilon }_{1}}} - {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{a}_{2}}, \\ \end{gathered} $где введена величина ${{Z}^{{{\text{р е ш }}}}} = {{E_{x}^{{00}}} \mathord{\left/ {\vphantom {{E_{x}^{{00}}} {\left( {2H_{{1y}}^{{00}}} \right)}}} \right. \kern-0em} {\left( {2H_{{1y}}^{{00}}} \right)}},$ которая согласно формулам (33) и (58) принимает значение
(64)
$\begin{gathered} {{Z}^{{{\text{р е ш }}}}} = \frac{i}{{\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{\pi }T\ln \left( {\sec (\frac{{\pi w}}{{2T}})} \right)}} - \\ - \,\,i\omega {{\mu }_{0}}T\left[ {\frac{1}{{{\text{2}}\pi }}\ln \left( {\operatorname{cosec} ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})} \right)} \right. + \\ + \,\,\left. {\frac{{{{\pi {{w}^{2}}} \mathord{\left/ {\vphantom {{\pi {{w}^{2}}} {24{{T}^{2}}}}} \right. \kern-0em} {24{{T}^{2}}}} - {{\pi }^{{ - 2}}}X({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}{{\ln \left( {\sec ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})} \right)}}} \right]. \\ \end{gathered} $Из уравнений (63) получаем искомую матрицу рассеяния
(65)
$\begin{gathered} {\mathbf{S}} = \\ = \left( {\begin{array}{*{20}{c}} {\frac{{\sqrt {{{\varepsilon }_{1}}} - \sqrt {{{\varepsilon }_{2}}} - {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}}&{\frac{{2\sqrt[4]{{{{\varepsilon }_{1}}{{\varepsilon }_{2}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}} \\ {\frac{{2\sqrt[4]{{{{\varepsilon }_{1}}{{\varepsilon }_{2}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}}&{\frac{{\sqrt {{{\varepsilon }_{2}}} - \sqrt {{{\varepsilon }_{1}}} - {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}{{\sqrt {{{\varepsilon }_{1}}} + \sqrt {{{\varepsilon }_{2}}} + {{{{Z}_{0}}} \mathord{\left/ {\vphantom {{{{Z}_{0}}} {{{Z}^{{{\text{р е ш }}}}}}}} \right. \kern-0em} {{{Z}^{{{\text{р е ш }}}}}}}}}} \end{array}} \right). \\ \end{gathered} $Заметим, что величина Zреш является импедансом элементарной ячейки решетки. Первое слагаемое в формуле (64), которое обратно пропорционально частоте ω, описывает емкостную составляющую импеданса. Второе слагаемое, пропорциональное ω, описывает индуктивную составляющую импеданса. При этом первый член индуктивной части импеданса обусловлен продольными токами Jx, а второй член – поперечными токами Jy.
Элементы матрицы S связаны равенствами S12 = = S21, |S11| = |S22|. Первое равенство свидетельствует о том, что рассматриваемая решетка является взаимным четырехполюсником. Формула (65) точно совпадает с формулой для матрицы рассеяния волн на стыке линий передачи с волновыми сопротивлениями Z1 и Z2, выражаемыми формулой (3), когда этот стык нагружен на параллельный колебательный контур с импедансом Z реш.
3. АНАЛИЗ ПОЛУЧЕННЫХ ФОРМУЛ
Проанализируем подробнее формулу (64). В соответствии со сказанным выше ее можно записать в виде
(66)
${{Z}^{{{\text{р е ш }}}}} = \frac{i}{{\omega C}} - i\omega \left( {{{L}_{x}} + {{L}_{y}}} \right),$где
(67)
$C = {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{\pi }T\ln \left( {\sec \left( {\frac{{\pi w}}{{2T}}} \right)} \right)$– емкость элементарной ячейки решетки,
(68)
${{L}_{x}} = \frac{{{{\mu }_{0}}T}}{{2\pi }}\ln \left( {\operatorname{cosec} \left( {\frac{{\pi w}}{{2T}}} \right)} \right)$– первая часть индуктивности элементарной ячейки, связанная с продольным током Jx,
(69)
${{L}_{y}} = {{\mu }_{0}}T\frac{{{{\pi {{w}^{2}}} \mathord{\left/ {\vphantom {{\pi {{w}^{2}}} {24{{T}^{2}}}}} \right. \kern-0em} {24{{T}^{2}}}} - \frac{1}{{{{\pi }^{2}}}}X({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}})}}{{\ln (\sec ({{\pi w} \mathord{\left/ {\vphantom {{\pi w} {2T}}} \right. \kern-0em} {2T}}))}}$– вторая часть индуктивности элементарной ячейки, связанная с поперечным током Jy.
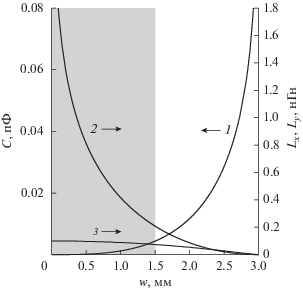
На рис. 2 построены зависимости емкости C и индуктивностей Lx и Ly элементарной ячейки решетки от ширины w ее полосковых проводников. Расчет этих зависимостей выполнен по формулам (65)–(69) для решетки с периодом T = 3 мм, расположенной на границе сред с диэлектрическими проницаемостями ε1 = 1 и ε2 = 2. Видно, что с увеличением ширины w проводников от нуля до T емкость C растет от нуля до бесконечности, индуктивность Lx, отвечающая продольным токам, убывает от бесконечности до нуля, а индуктивность Ly, отвечающая поперечным токам, убывает до нуля от некоторого конечного значения. Однако, как уже отмечалось, правомерность используемого в расчете приближения определяется условием: ширина области II (см. рис. 1) (T – w) должна быть меньше ее высоты w. Зона, где не выполняется это условие, обозначена на рис. 2 серым тоном.
Рис. 2.
Зависимости емкости C (1), “продольной” Lx (2) и “поперечной” Ly (3) индуктивностей элементарной ячейки решетки от ширины ее проводников при периоде решетки T = 3 мм.
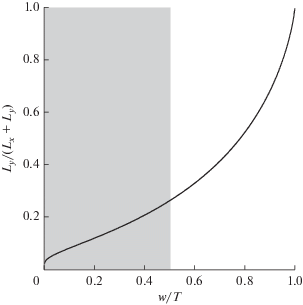
Зависимость отношения “поперечной” части индуктивности Ly к полной индуктивности Lx + Ly от относительной ширины проводников w/T представлена на рис. 3. Это отношение не зависит ни от периода T, ни от диэлектрических проницаемостей сред, между которыми решетка расположена. Видно, что оно всегда растет с увеличением ширины полоскового проводника и приближается к единице при w → T. Зона, где не выполняется условие правомерности используемого в расчете приближения, также отмечена серым фоном.
Рис. 3.
Зависимость отношения поперечной части индуктивности к полной индуктивности от относительной ширины полосковых проводников решетки.
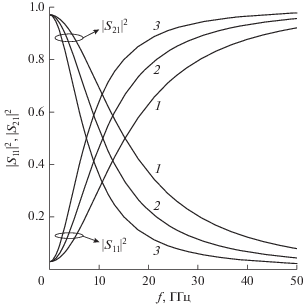
По формулам (53), (64) и (65) были построены частотные зависимости коэффициента отражения |S11|2 и коэффициента прохождения |S21|2 электромагнитной волны через решетку на границе раздела сред с диэлектрическими проницаемостями ε1 = 1 и ε2 = 2 (рис. 4). Эти зависимости рассчитаны для нескольких значений ширины проводников w при фиксированном периоде решетки T = 3 мм. Видно, что коэффициент отражения |S11|2 растет как с увеличением частоты, так и с увеличением ширины полосковых проводников.
Рис. 4.
Частотные зависимости коэффициентов отражения |S11|2 и прохождения |S21|2 для решетки с периодом T = 3 мм и шириной проводников w = 2.85 (1), 2.95 (2), 2.99 мм (3).
Для оценки погрешности полученных формул нами был выполнен численный электродинамический расчет 3D-модели решетки квадратных полосковых проводников в пакете программ CST Microwave Studio. Предполагалось, что проводники имеют бесконечную проводимость и нулевую толщину. Сравнение матричных элементов, рассчитанных по формулам и полученных с помощью пакета программ, производилось для решетки проводников, расположенной на границе раздела сред с диэлектрическими проницаемостями ε1 = 1 и ε2 = 2, имеющей период T = 3 мм. Численные расчеты 3D-модели показали, что для рассмотренных решеток самая низкая резонансная частота, на которой коэффициент прохождения |S21|2 обращается в нуль, приблизительно равна 70 ГГц. Однако в области столь высоких частот не выполняются условия квазистатического приближения, поэтому полученные формулы здесь уже не могут быть использованы.
На рис. 5 для трех значений ширины полосковых проводников w представлены частотные зависимости относительных погрешностей расчета элементов матрицы рассеяния. Пунктирные линии изображают погрешность расчета по полученным формулам (65)–(69). Штриховые линии изображают погрешность расчета по известной формуле [12, 24]
(70)
${{Z}^{{{\text{р е ш }}}}} = \frac{i}{{\omega {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{1}} + {{\varepsilon }_{2}}}}{\pi }T\ln \left( {\sec \left( {\frac{{\pi w}}{{2T}}} \right)} \right)}},$Рис. 5.
Частотные зависимости относительной погрешности расчета элементов матрицы рассеяния S11 (а) и S21 (б) для трех значений ширины полоскового проводника, w = 2.85 (1), 2.95 (2), 2.99 мм (3); штриховые линии – расчет по известным формулам, пунктирные линии – расчет по полученным формулам (65)–(69), сплошные линии – использование усредненной формулы (71).
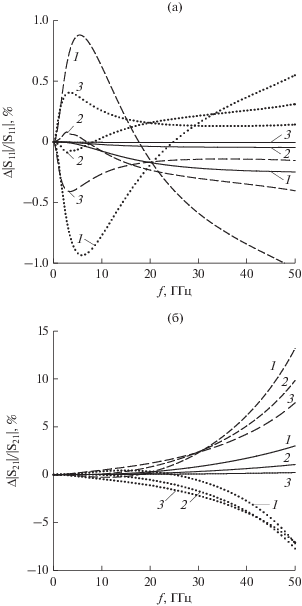
если ее подставить в формулу (65) для расчета матрицы рассеяния электромагнитных волн на емкостной решетке полосковых проводников. Эта формула отличается от полученной формулы (66) только отсутствием индуктивностей Lx и Ly. Как видим, различие между пунктирными и штриховыми линиями заключается прежде всего в противоположности знаков отображаемых ими погрешностей. Поэтому вместо полученной формулы (66) мы предлагаем использовать усредненную формулу
(71)
${{Z}^{{{\text{р е ш }}}}} = \frac{i}{{{\kern 1pt} \omega C}} - i\omega \frac{{{{L}_{x}} + {{L}_{y}}}}{2}$с прежними значениями электрических параметров C, Lx и Ly. Погрешность расчета матрицы рассеяния при использовании усредненной формулы (71) также приведена на рис. 5. Эта погрешность оказывается многократно меньше погрешности, получающейся при использовании формул (66) или (70).
ЗАКЛЮЧЕНИЕ
Решение уравнений Максвелла, полученное в работе в квазистатическом приближении, подтверждает тот факт, что решетка полосковых проводников на границе раздела двух сред эквивалентна последовательному колебательному контуру, подключенному параллельно к точкам каскадного соединения двух линий передачи. Значения элементов матрицы рассеяния такой решетки зависят только от импеданса Zреш ее элементарной ячейки, который определяется топологией полосковых проводников и диэлектрических проницаемостей сред ε1 и ε2. Импеданс Zреш, согласно формуле (66), является суммой двух частей, различающихся частотной зависимостью. Его емкостная часть убывает по абсолютной величине обратно пропорционально частоте ω, а индуктивная часть растет по абсолютной величине прямо пропорционально ω. Это значит, что на низких частотах емкостная часть Zреш преобладает по абсолютной величине над индуктивной частью. Поэтому на достаточно низких частотах можно пренебречь индуктивностью элементарной ячейки по сравнению с ее емкостью, выражаемой формулой (67).
Формула (67) подтверждает эмпирическое предположение [13, 21] о совпадении на низких частотах отражательных свойств субволновой решетки квадратных полосковых проводников и решетки ленточных полосковых проводников в случае падения на нее линейно поляризованной электромагнитной волны с направлением вектора электрического поля ортогонально полосковым проводникам. При этом обе решетки должны иметь один и тот же период, а ширина ленточных полосковых проводников должна быть равна размеру стороны квадратных проводников.
Однако с увеличением частоты необходимо учитывать не только емкостную, но и индуктивную часть импеданса Zреш, обусловленную как продольной Jx, так и поперечной Jy компонентами тока в квадратных полосковых проводниках. Индуктивная часть импеданса характеризуется суммой соответствующих индуктивностей Lx и Ly, описываемых формулами (68) и (69), которые были получены впервые. Сравнение частотных характеристик, рассчитанных по формулам и полученных численным электродинамическим расчетом 3D-модели рассматриваемой структуры, показало, что учет индуктивной части импеданса позволяет многократно повысить точность расчета на высоких частотах.
Важно отметить, что исследованная структура может использоваться для создания зеркал, обладающих заданной отражательной способностью, на границах раздела диэлектрических слоев. Такие зеркала необходимы при конструировании оптических и СВЧ многослойных полосно-пропускающих фильтров или радиопрозрачных в заданном диапазоне частот поверхностей для укрытия антенн. При этом решетки из квадратных полосковых проводников на границах диэлектрических слоев-резонаторов позволяют обеспечить оптимальные связи резонаторов друг с другом, а крайних резонаторов с пространством. Перспективность таких фильтров демонстрируют аналогичные многослойные конструкции, но с решетками в виде металлических сеток на границах раздела диэлектрических слоев [19]. Использование формул, полученных в [20] для металлических сеток, и формул, полученных в данной работе для решеток квадратных металлических проводников, позволит многократно сократить время конструирования частотно-селективных устройств на многослойных диэлектрических структурах.
Список литературы
Belyaev B.A., Tyurnev V.V. // Microw. Opt. Technol. Lett. 2013. V. 55. № 7. P. 1613.
Macleod H.A. Thin-film Optical Filters. Boca Raton: CRC Press, 2010.
Беляев Б.А., Тюрнев В.В., Шабанов В.Ф. // ДАН. 2014. Т. 454. № 6. С. 551.
Беляев Б.А., Тюрнев В.В., Шабанов В.Ф. // ДАН. 2014. Т. 456. № 4. С. 413.
Belyaev B.A., Tyurnev V.V., Shabanov V.F. // Opt. Lett. 2014. V. 39. № 12. P. 3512.
Ade P.A.R., Pisano G., Tucker C., Weaver S. // Proc. SPIE. 2006. V. 6275. P. 62750U-1.
Melo A.M., Kornberg M.A., Kaufmann P. et al. // Appl. Opt. 2008. V. 47. № 32. P. 6064.
Garcia-Vidal F.J., Martin-Moreno L., Ebbesen T.W., Kuipers L. // Rev. Modern Phys. 2010. V. 82. P. 729.
Munk B. Frequency Selective Surfaces: Theory and Design. N.Y.: John Wiley & Sons, Inc., 2000.
Tomasek P. // Int. J. Circuits, Systems and Signal Processing. 2014. V. 8. P. 594.
Oh S., Lee H., Jung J.-H., Lee G.-Y. // Int. J. Microwave Sci. Technol. 2014. V. 2014. Article number 857582.
Al-Joumayly M.A., Behdad N. // IEEE Trans. 2010. V. AP-58. № 12. P. 4030.
Ulrich R. // Infrared Phys. 1967. V. 7. P. 37.
Belyaev B.A., Tyurnev V.V. // Opt. Lett. 2015. V. 40. № 18. P. 4333.
Belyaev B.A., Tyurnev V.V. // Opt. Lett. 2016. V. 41. № 3. P. 536.
Беляев Б.А., Тюрнев В.В. // Известия вузов. Физика. 2015. Т. 58. № 5. С. 57.
Банков С.Е., Левченко И.В. // РЭ. 1988. Т. 33. № 10. С. 2045.
Belyaev B.A., Tyurnev V.V. // Microw. Opt. Technol. Lett. 2018. V. 60. № 3. P. 630.
Беляев Б.А., Тюрнев В.В., Волошин А.С., Галеев Р.Г. // Письма в ЖТФ. 2018. Т. 44. № 10. С. 3.
Беляев Б.А, Тюрнев В.В. // РЭ. 2017. Т. 62. № 7. С. 642.
Whitbourn L.B., Compton R.C. // Appl. Opt. 1985. V. 24. № 2. P. 217.
Meixner J. // IEEE Trans. 1972. V. AP-20. № 4. P. 442.
Гупта К., Гардж Р., Чадха Р. Машинное Проектирование СВЧ устройств. М.: Радио и связь, 1987.
Luukkonen O., Simovski C., Granet G. et al. // IEEE Trans. 2008. V. AP-56. № 6. P. 1624.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


