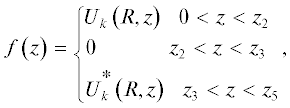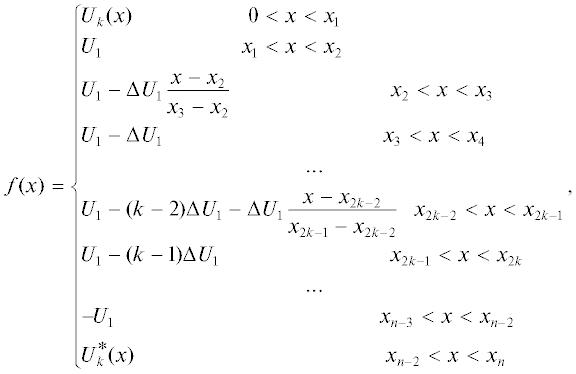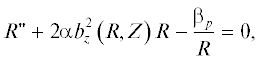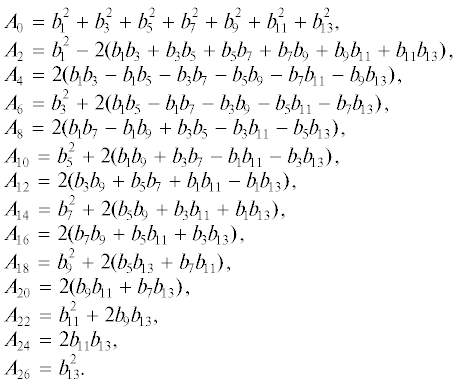Радиотехника и электроника, 2019, T. 64, № 7, стр. 719-727

ВВЕДЕНИЕ

Одним из существенных факторов, ограничивающих продвижение в получении больших мощностей в вакуумных СВЧ-приборах (клистронах или лампах бегущей волны (ЛБВ)) с магнитными периодическими фокусирующими системами (МПФС) в коротковолновой части сантиметрового и миллиметрового диапазонов, является оседание электронного потока на элементы замедляющей или резонаторной системы. Для ЛБВ сантиметрового диапазона с замедляющей системой (ЗС) из цепочки связанных резонаторов (ЦСР) для повышения амплитуды магнитного поля применяют МПФС, в которых полюсные наконечники пространственно совмещены с элементами ЗС [1]. В этом случае период МПФС определяется требуемыми электродинамическими характеристиками ЗС и, по сути, является заданным. Однако при всех достоинствах (по сравнению с системами фокусировки однородным полем) фокусировка с помощью МПФС обладает одним весьма неприятным свойством. При переходе в коротковолновую часть СВЧ-диапазона и миниатюризации ЗС период “совмещенной” МПФС становится кратным периоду ЗС и величина так называемого параметра магнитного поля α¹¹ из-за требуемых высоких значений фокусирующего магнитного поля может стать больше критических значений. Это приводит к неустойчивой фокусировке пучка и неограниченному возрастанию амплитуды пульсаций потока по мере его продвижения вдоль оси пролетного канала, вследствие чего существенная часть электронного потока оседает на элементы замедляющей системы [2]. За счет ввода в распределение осевой компоненты индукции магнитного поля высших гармонических составляющих удается сдвинуть область параметрического резонанса в сторону более высоких значений параметра магнитного поля [3]. Исследованное в [3] влияние гармонического состава распределения магнитного поля на устойчивость фокусировки пучка при повышенных значениях параметра магнитного поля α, позволило сформулировать требования, накладываемые на амплитуды высших гармонических составляющих, при которых зоны устойчивой фокусировки смещаются в сторону больших значениях параметра магнитного поля α.

В работе [4] найдены приближенные аналитические выражения для гармоник магнитного поля, формируемого МПФС с магнитомягкими вставками, внутренний диаметр отверстий в которых равен диаметру отверстий в наконечниках.

В данной работе приведено приближенное аналитическое решение задачи о нахождении распределения магнитного поля, формируемого МПФС с магнитомягкими вставками, внутренний диаметр отверстий в которых существенно отличается от диаметра отверстий в наконечниках.

Проведено исследование устойчивости фокусировки электронного потока при повышенных значениях параметра магнитного поля.

1. ПОСТАНОВКА ЗАДАЧИ

В большинстве случаев для фокусировки протяженных электронных потоков в ЛБВ длинноволновой части СВЧ-диапазона применяются МПФС, в которых знакопеременное распределение осевой компоненты индукции магнитного поля создается с помощью чередующихся магнитов и полюсных наконечников (рис. 1а). В таких МПФС структура осевой компоненты магнитного поля является практически синусоидальной. Для ЛБВ коротковолновой части СВЧ-диапазона с МПФС, совмещенной с замедляющей системой в виде ЦСР (рис. 1б), структура магнитного поля может несколько искажаться за счет высших гармонических составляющих. В случаях, когда из-за связи периодов ЗС и совмещенной с ней МПФС параметр магнитного поля α принимает значения, при которых фокусировка пучка становится неустойчивой, между полюсными наконечниками размещают одну или несколько вставок из магнитомягкого материала с диаметром отверстия для прохождения пучка, равным диаметру пролетного канала (рис. 1в).

Рис. 1.

МПФС с гармоническим распределением осевой компоненты индукции магнитного поля (а), МПФС, пространственно совмещенная с элементами ЗС (б), совмещенная МПФС со вставками из магнитомягкого материала (в).

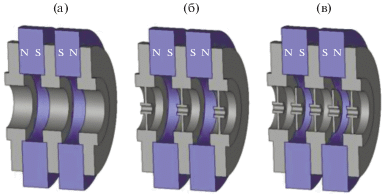
При продвижении в область СВЧ-колебаний миллиметрового диапазона из-за роста требуемой для фокусировки амплитуды магнитного поля и уменьшения размеров элементов, обеспечивающих необходимые электродинамические параметры ЗС, материал полюсных наконечников, образующих МПФС, насыщается. Это приводит к увеличению поперечных составляющих магнитного поля под наконечниками и к нарушению необходимой структуры распределения осевой компоненты индукции магнитного поля для устойчивой фокусировки пучка.

Для нахождения гармонического состава в ячейках МПФС с полюсными наконечниками, диаметр отверстий в которых существенно больше диаметра магнитомягких вставок, можно воспользоваться аналитическим методом решения уравнения Лапласа для нахождения магнитостатического потенциала в виде ряда [4, 5], а затем, взяв соответствующие производные, определить продольные и радиальные компоненты индукции магнитного поля. После определения спектрального состава распределения магнитного поля в ячейках рассмотренной МПФС, определить зоны устойчивой фокусировки и амплитуду пульсаций пучка при оптимальном вводе его в МПФС можно, как и в [3], с помощью параксиального уравнения колебаний границы электронного потока.

2. РАСЧЕТ РАСПРЕДЕЛЕНИЯ МАГНИТНОГО ПОЛЯ В МПФС С МАГНИТОМЯГКИМИ ВСТАВКАМИ

А. Распределение магнитного поля в МПФС с одной магнитомягкой вставкой

Схематическое изображение ячейки бесконечной МПФС с магнитомягкой вставкой, симметрично расположенной на расстоянии Δ относительно полюсных наконечников, представлено на рис. 2а. Ширина вставки d, ширина наконечников b, их внутренний диаметр 2R₁ больше внутреннего диаметра вставки 2R . Решение задачи о нахождении распределения продольной и радиальной компоненты индукции магнитного поля B_z(r, z) при отсутствии в области решения источников магнитного поля может быть сведено к решению уравнения Лапласа для магнитного скалярного потенциала U в приосевой области, ограниченной внутренним радиусом отверстий в полюсных наконечниках МПФС и магнитомягкой вставке.

Рис. 2.

Схематическое изображение МПФС: 1 – магниты, 2 – полюсные наконечники, 3 – магнитомягкая вставка (а); распределения скалярного магнитного потенциала U(x) (х = 2πz/L) на границе области, ограниченной внутренним радиусом R₁ отверстия в наконечнике (сплошная линия) и радиусом канала R (штриховая) (б); фрагмент ячейки МПФС (в); распределение скалярного магнитного потенциала U(x) (х = 2πz/L₁) на верхней границе левой кольцевой области, ограниченной внутренним радиусом наконечника R₁ (г).

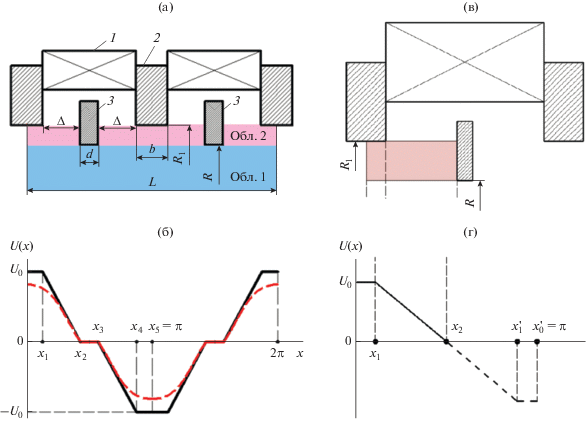
Как и в [4], общее решение уравнения Лапласа, искали в виде ряда

(1а)

$\begin{gathered} U\left( {r,z} \right) = \sum\limits_k {\left( {{{A}_{k}}\cos \left( {\gamma kz} \right) + {{B}_{k}}\sin \left( {\gamma kz} \right)} \right)} \times \\ \times \,\,\left( {{{C}_{k}}{{I}_{0}}\left( {\gamma kr} \right) + {{D}_{k}}{{K}_{0}}\left( {\gamma kr} \right)} \right)\quad.\quad \\ \end{gathered} $

Рассмотрим связанные области: цилиндрическую область, ограниченную внутренним радиусом отверстия во вставке, и кольцевые области, ограниченные внутренними радиусами отверстий в полюсных наконечниках и вставках.

Пусть на границе цилиндрической области распределение магнитного скалярного потенциала задано функцией (рис. 2б)

(2)

где U_k(R, z) и $U_{k}^{*}\left( {R,z} \right)$ – решения уравнения Лапласа для кольцевых областей, ограниченных внутренними радиусами отверстий в вставках и полюсных наконечниках, а z₂ = b/2 + Δ, z₃ = b/2 + + Δ + d, z₅ = L/2.

Так как потенциал U(z) является четной функцией аргумента z и решения должны быть конечны во всей рассматриваемой области, в том числе и на оси системы, то в выражении (1а) все коэффициенты при слагаемых, содержащих синусы, равны нулю, а коэффициент D_1n = 0. Тогда решение уравнения Лапласа для цилиндрической области 1 (см. рис. 2а) может быть записано в виде

(1б)

$U\left( {r,z} \right) = \sum\limits_n {{{A}_{n}}\cos \left( {\gamma nz} \right){{I}_{0}}\left( {\gamma nr} \right)} ,\quad$

где ${{A}_{n}} = {{A}_{{1n}}}{{C}_{{1n}}},$ γ = 2π/L, а с учетом выражения для границы цилиндрической области (2) решение (1б) принимает вид

(3а)

$U\left( {r,z} \right) = \sum\limits_n {{{A}_{n}}} \cos \left( {\gamma nz} \right)\frac{{{{I}_{0}}\left( {\gamma nr} \right)}}{{{{I}_{0}}\left( {\gamma nR} \right)}}\quad,$

где

(3б)

${{A}_{n}} = \frac{4}{L}\int\limits_0^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {f\left( z \right)} \cos \left( {\gamma nz} \right)dz.$

Для определения функции f(z) рассмотрим кольцевую область 2 (рис. 2а), ограниченную внутренними радиусами отверстий в полюсном наконечнике R₁ и во вставке R (рис. 2в).

Достроим функцию распределения скалярного потенциала f₁(x), заданную на границе кольцевой области от 0 до π, как показано на рис. 2г (штриховая линия).

Распределение магнитного скалярного потенциала на внешней границе имеет вид

${{f}_{1}}(x) = \left\{ \begin{gathered} {{U}_{0}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 < x < {{x}_{1}} \hfill \\ {{U}_{0}} - {{U}_{0}}\frac{{x - {{x}_{1}}}}{{{{x}_{2}} - {{x}_{1}}}}\,\,\,\,\,{{x}_{1}} < x < {{x}_{2}} \hfill \\ - {{U}_{0}}\frac{{x - {{x}_{2}}}}{{x_{1}^{'} - {{x}_{2}}}}\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{2}} < x < x_{1}^{'} \hfill \\ - {{U}_{0}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{x}_{2}} < x < x_{0}^{'} \hfill \\ \end{gathered} \right.,$

где с учетом нормировки x = 2πz/L₁ получаем z₁= = b/2, z₂= b/2 + Δ, $z_{1}^{'} = {b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0em} 2} + 2\Delta ,$ $z_{0}^{'} = b + 2\Delta $ = L₁/2 (L₁– период кольцевой области).

Поскольку для внешней границы кольцевой области радиусом R₁ функция f₁(z) вычисляется по формуле

(5а)

$\begin{gathered} {{f}_{1}}\left( z \right) = \sum\limits_k {{{A}_{{2k}}}\cos \left( {{{\gamma }_{1}}kz} \right)} \times \\ \times \,\,\left( {{{C}_{{2k}}}{{I}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right) + {{D}_{{2k}}}{{K}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right)} \right) \\ \end{gathered} $

(γ₁ =2π/L₁), то решение уравнения Лапласа для кольцевой области с учетом заданного распределения скалярного магнитного потенциала на внешней границе области может быть записано в следующем виде:

(5б)

$\begin{gathered} {{U}_{k}}\left( {r,z} \right) = \sum\limits_k {{{A}_{{2k}}}} \cos \left( {{{\gamma }_{1}}kz} \right) \times \\ \times \,\,\frac{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}kr} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}kr} \right)}}{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right)}}\quad, \\ \end{gathered} $

где

${{A}_{{2k}}} = \frac{2}{\pi }\int\limits_0^\pi {{{f}_{1}}\left( x \right)} \cos \left( {kx} \right)dx\quad\quad$

или, после проведения необходимого интегрирования, –

$\begin{gathered} {{A}_{{2k}}} = \frac{2}{\pi }\left( {\int\limits_0^{{{x}_{1}}} {{{U}_{0}}\cos \left( {kx} \right)dx\quad} + \int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\left( {{{U}_{0}} - {{U}_{0}}\frac{{x - {{x}_{1}}}}{{{{x}_{2}} - {{x}_{1}}}}} \right)} } \right. \times \\ \times \,\,\cos \left( {kx} \right)dx - \int\limits_{{{x}_{2}}}^{x_{1}^{'}} {{{U}_{0}}} \frac{{x - {{x}_{2}}}}{{x_{1}^{'} - {{x}_{2}}}}\cos \left( {kx} \right)dx - \\ - \,\left. {\,\int\limits_{x_{1}^{'}}^\pi {{{U}_{0}}} \cos \left( {kx} \right)dx\quad} \right) = \frac{{8{{U}_{0}}\left( {{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0em} 2} + \Delta } \right)}}{{\Delta {{k}^{2}}{{\pi }^{2}}}}\sin \frac{{\pi k}}{2}\sin {{\gamma }_{1}}k\Delta . \\ \end{gathered} $

Коэффициенты C₂ и D₂ могут быть найдены из граничных условий для связанных областей²²:

(6)

$\begin{gathered} \quad{{C}_{{2k}}}{{I}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right) + {{D}_{{2k}}}{{K}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right) = 1, \\ {{C}_{{2k}}}{{I}_{0}}\left( {{{\gamma }_{1}}R} \right) + {{D}_{{2k}}}{{K}_{0}}\left( {{{\gamma }_{1}}R} \right) = {{C}_{{1k}}}{{I}_{0}}\left( {\gamma R} \right), \\ {{C}_{{2k}}}{{I}_{1}}\left( {{{\gamma }_{1}}R} \right) - {{D}_{{2k}}}{{K}_{1}}\left( {{{\gamma }_{1}}R} \right) = \frac{\gamma }{{{{\gamma }_{1}}}}{{C}_{{1k}}}{{I}_{1}}\left( {\gamma R} \right)\quad, \\ \end{gathered} $

и имеют вид

(7)

$\begin{gathered} \quad{{C}_{2}} = \frac{{1 - {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right)}}{{{{I}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right)}}, \\ {{D}_{2}} = \frac{{\left( {{{I}_{0}}\left( {\gamma R} \right){{I}_{1}}\left( {{{\gamma }_{1}}R} \right) - {{I}_{0}}\left( {{{\gamma }_{1}}R} \right){{I}_{1}}\left( {\gamma R} \right)\left( {{\gamma \mathord{\left/ {\vphantom {\gamma {\gamma 1}}} \right. \kern-0em} {\gamma 1}}} \right)} \right)}}{{\left\{ {\left[ {{{I}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right){{K}_{1}}\left( {{{\gamma }_{1}}R} \right) + {{K}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right){{I}_{1}}\left( {{{\gamma }_{1}}R} \right)} \right]\quad{{I}_{0}}\left( {\gamma R} \right) + \left[ {{{K}_{0}}\left( {{{\gamma }_{1}}R} \right){{I}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right) - {{I}_{0}}\left( {{{\gamma }_{1}}R} \right){{K}_{0}}\left( {{{\gamma }_{1}}{{R}_{1}}} \right)} \right]{{I}_{1}}\left( {\gamma R} \right)\left( {{\gamma \mathord{\left/ {\vphantom {\gamma {\gamma 1}}} \right. \kern-0em} {\gamma 1}}} \right)} \right\}}}{\;}. \\ \end{gathered} $

Решение уравнения Лапласа для кольцевой области, расположенной слева от вставки (рис. 2в), получаем из выражения

${{U}_{k}}\left( {r,z} \right) = \sum\limits_k {{{A}_{{2k}}}} \cos \left( {{{\gamma }_{1}}kz} \right)\,\frac{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}kr} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}kr} \right)}}{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right)}},$

а для кольцевой области, расположенной справа от вставки, – из выражения

$\begin{gathered} U_{k}^{*}\left( {r,z} \right) = \sum\limits_k {{{A}_{{2k}}}} \cos \left( {{{\gamma }_{1}}k\left( {z - d} \right)} \right) \times \\ \times \,\,\frac{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}kr} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}kr} \right)}}{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right)}}. \\ \end{gathered} $

Коэффициент A_n, входящий в решение уравнения Лапласа для цилиндрической области, находим интегрированием выражения

$\begin{gathered} {{A}_{n}} = \frac{4}{L}\left( {\int\limits_0^{{{z}_{2}}} {\sum\limits_k {A_{{2k}}^{*}} } \cos \left( {{{\gamma }_{1}}kz} \right)\cos \left( {\gamma nz} \right)dz} \right. + \\ \left. { + \,\,\int\limits_{{{z}_{3}}}^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {\sum\limits_k {A_{{2k}}^{*}} } \cos \left( {{{\gamma }_{1}}k\left( {z - d} \right)} \right)\cos \left( {\gamma nz} \right)dz} \right), \\ \end{gathered} $

где

$A_{{2k}}^{*} = {{A}_{{2k}}}\frac{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}kR} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}kR} \right)}}{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right)}}\quad.$

Окончательно выражение для магнитного скалярного потенциала в цилиндрической области имеет вид

$\begin{gathered} U\left( {r,z} \right) = \sum\limits_n {\frac{4}{L}} \sum\limits_k {\left( {A_{{2k}}^{*}\sin \left( {\frac{{n\pi d}}{L}} \right)\left( {\frac{{\cos \left( {\frac{{\pi \left( {k - n} \right)}}{2}} \right)}}{{{{\gamma }_{1}}k - \gamma n}}} \right.} \right.} + \\ \left. {\left. { + \frac{{ - \cos \left( {\frac{{\pi \left( {k + n} \right)}}{2}} \right)}}{{{{\gamma }_{1}}k + \gamma n}}} \right)} \right)\cos \left( {\gamma nz} \right)\frac{{{{I}_{0}}\left( {\gamma nr} \right)}}{{{{I}_{0}}\left( {\gamma nR} \right)}}. \\ \end{gathered} $

Распределения продольной и радиальной компонент индукции магнитного поля имеют следующий вид:

(8)

$\begin{gathered} {{B}_{z}}\left( {r,z} \right) = \sum\limits_n {\frac{{4\gamma n}}{L}} \sin \left( {\frac{{n\pi d}}{L}} \right) \times \\ \times \,\,\sum\limits_k {\left( {A_{{2k}}^{*}\left( {\frac{{\cos \left( {\frac{{\pi \left( {k - n} \right)}}{2}} \right)}}{{{{\gamma }_{1}}k - \gamma n}} + \left. {\left. {\frac{{ - \cos \left( {\frac{{\pi \left( {k + n} \right)}}{2}} \right)}}{{{{\gamma }_{1}}k + \gamma n}}} \right)} \right)} \right.} \right.} \times \\ \times \,\,\sin \left( {\gamma nz} \right)\frac{{{{I}_{0}}\left( {\gamma nr} \right)}}{{{{I}_{0}}\left( {\gamma nR} \right)}}\quad, \\ {{B}_{r}}\left( {r,z} \right) = \sum\limits_n {\frac{{4\gamma n}}{L}} \sin \left( {\frac{{n\pi d}}{L}} \right) \times \\ \times \,\,\sum\limits_k {\left( {A_{{2k}}^{*}\left( {\frac{{\cos \left( {\frac{{\pi \left( {k - n} \right)}}{2}} \right)}}{{{{\gamma }_{1}}k - \gamma n}} + \left. {\left. {\frac{{ - \cos \left( {\frac{{\pi \left( {k + n} \right)}}{2}} \right)}}{{{{\gamma }_{1}}k + \gamma n}}} \right)} \right)} \right.} \right.} \times \\ \times \,\,\cos \left( {\gamma nz} \right)\frac{{{{I}_{1}}\left( {\gamma nr} \right)}}{{{{I}_{0}}\left( {\gamma nR} \right)}}\quad. \\ \end{gathered} $

Б. Распределение магнитного поля в МПФС с произвольным количеством магнитомягких вставок

Рассмотрим МПФС (рис. 3а), образованную полюсными наконечниками диаметром 2R₁ и одинаковыми N вставками, расположенными на одном и том же расстоянии друг от друга, внутренний диаметр вставок 2R меньше диаметра полюсных наконечников.

Рис. 3.

Ячейка МПФС с произвольным количеством вставок (а) и распределение магнитного потенциала U(x) на границе области (б).

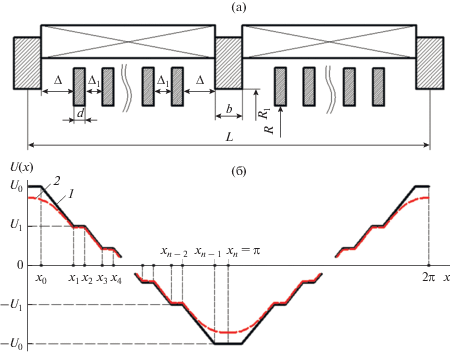
Для нахождения распределения магнитного поля в приосевой области МПФС, так же как и для случая МПФС с одной вставкой, рассматривались три связанные области: две кольцевые с периодом L₁= 2(2b + 2Δ₁) в промежутках от 0 до х₁ и от х_{n – 2} до х_n и одна цилиндрическая область с периодом L = 2(2b + 2Δ₁+ Nd + (N – 1)Δ).

Распределение магнитного скалярного потенциала на границе цилиндрической области радиусом R_k (рис. 3б кривая 2) имеет вид

(9)

где ΔU₁ = 2U₁/(N – 1) – разность потенциалов между вставками, N – количество вставок, k – порядковый номер вставки.

Разность потенциалов между полюсным наконечником и вставкой можно определить по формуле $\Delta {{U}_{0}} = {{\left( {\Delta {{U}_{1}}\Delta } \right)} \mathord{\left/ {\vphantom {{\left( {\Delta {{U}_{1}}\Delta } \right)} {\Delta 1}}} \right. \kern-0em} {\Delta 1}},$ тогда U₀= U₁+ ΔU₀.

Распределения продольной и радиальной компонент индукции магнитного поля имеют следующий вид:

(10)

$\begin{gathered} {{B}_{z}}\left( {r,z} \right) = \sum\limits_n {\left\{ {{{A}_{n}} + \sin \left( {\frac{{n\pi \left( {Nd + \left( {N - 1} \right)\Delta 1} \right)}}{L}} \right) \times \frac{{^{{^{{_{{_{{_{{_{{}}}}}}}}}}}}}}{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}} \right.} \\ \times \,\,\sum\limits_k {{{A}_{k}}\left. {\left( {\frac{{\cos \left( {\frac{{\pi \left[ {k - n} \right]}}{2}} \right)}}{{{{\gamma }_{1}}k - \gamma n}} + \frac{{ - \cos \left( {\frac{{\pi \left[ {k + n} \right]}}{2}} \right)}}{{{{\gamma }_{1}}k + \gamma n}}} \right)} \right\}} \times \\ \times \,\,\sin \left( {\gamma nz} \right)\frac{{{{I}_{0}}\left( {\gamma nr} \right)}}{{{{I}_{0}}\left( {\gamma nR} \right)}}, \\ {{B}_{r}}\left( {r,z} \right) = \sum\limits_n {\left\{ {{{A}_{n}} + \sin \left( {\frac{{n\pi \left( {Nd + \left( {N - 1} \right)\Delta 1} \right)}}{L}} \right) \times \frac{{^{{^{{_{{_{{_{{_{{}}}}}}}}}}}}}}{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}} \right.} \\ \times \,\,\sum\limits_k {{{A}_{k}}\left. {\left( {\frac{{\cos \left( {\frac{{\pi \left[ {k - n} \right]}}{2}} \right)}}{{{{\gamma }_{1}}k - \gamma n}} + \frac{{ - \cos \left( {\frac{{\pi \left[ {k + n} \right]}}{2}} \right)}}{{{{\gamma }_{1}}k + \gamma n}}} \right)} \right\}} \times \\ \times \,\,\cos \left( {\gamma nz} \right)\frac{{{{I}_{1}}\left( {\gamma nr} \right)}}{{{{I}_{0}}\left( {\gamma nR} \right)}}, \\ \end{gathered} $

где

$\begin{gathered} {{A}_{n}} = \frac{{8{{U}_{1}}}}{{\Delta 1\pi n(N - 1)}}\sin \left( {\frac{{\pi n\Delta 1}}{L}} \right) \times \\ \times \,\,\sum\limits_{l = 2}^N {\sin \left( {\frac{{\pi n}}{L}\left( {b + 2\Delta + \left( {2l - 2} \right)d + \left( {2l - 3} \right)\Delta 1} \right)} \right)} , \\ \end{gathered} $

$\begin{gathered} {{A}_{k}} = \frac{{64n\Delta {{U}_{0}}\left( {{b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0em} 2} + \Delta } \right)}}{{{{L}^{2}}{{k}^{2}}\Delta \pi }}\sin \left( {\frac{{k\pi }}{2}} \right)\sin \left( {{{\gamma }_{1}}k\Delta } \right) \times \\ \times \,\,\frac{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}kR} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}kR} \right)}}{{{{C}_{2}}{{I}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right) + {{D}_{2}}{{K}_{0}}\left( {{{\gamma }_{1}}k{{R}_{1}}} \right)}}. \\ \end{gathered} $

3. РАСЧЕТ ФОКУСИРОВКИ ЭЛЕКТРОННОГО ПОТОКА В МПФС И ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Решение задачи о распределении магнитного поля в МПФС с магнитомягкими вставками, внутренний диаметр отверстий которых существенно меньше внутреннего диаметра полюсных наконечников, позволяет поставить в соответствие “идеальные” распределения [6] и реально получающиеся распределения магнитного поля, а также оценить влияние полученного спектрального состава высших гармонических составляющих на пульсации потока в пролетном канале.

Были рассмотрены МПФС с одной, двумя и тремя магнитомягкими вставками со следующими параметрами: b = 1.9 мм; d = 0.85 мм; Δ = 1.725 мм; R₁ = 2.0 мм; R = 0.45 мм, периоды МПФС составили L₁ = 12.4 мм, L₂ = 17.55 мм и L₃ = 22.7 мм соответственно. Как и в [3], для расчета оптимального радиуса R_опт и амплитуды пульсаций Δ потока использовалось параксиальное уравнение

где R = r/a_p, Z = 2πz/L – нормированные значения координат (L – период МПФС), $\alpha = \frac{{\eta В _{а }^{2}{{L}^{2}}}}{{64{{\pi }^{2}}U}}$ – параметр магнитного поля, ${{\beta }_{p}}{\text{ = }}\frac{P}{{4{{\pi }^{3}}{{\varepsilon }_{0}}\sqrt {2\eta } }}{{\left( {\frac{L}{{2{{a}_{p}}}}} \right)}^{2}}$ – параметр пространственного заряда, $a_{p}^{2} = \frac{{\sqrt 2 PU}}{{\pi {{\varepsilon }_{0}}{{\eta }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}B_{{{\text{э ф }}}}^{2}}}$ – бриллюэновский радиус пучка, $В _{{{\text{э ф }}}}^{2}$ = $\frac{{В _{а }^{2}}}{2}\sum\nolimits_n {b_{{2n - 1}}^{2}} - $ эффективное значение магнитного поля, Р –первеанс пучка, U – ускоряющий потенциал.

Распределение осевой компоненты индукции магнитного поля в МПФС³³

тогда

Коэффициент А₀ пропорционален величине эффективного магнитного поля, а коэффициенты А_2k – амплитуды при соответствующих резонансных слагаемых:

Величины b_{2n– 1} представлены в табл. 1.

Сопоставление результатов расчета структуры магнитного поля по полученным аналитическим соотношениям и по строгим численным моделям приведено на рис. 4.

Рис. 4.

Распределения осевой компоненты индукции магнитного поля в ячейках МПФС с одной (а), двумя (б) и тремя (в) вставками: расчет по аналитическим формулам (сплошная кривая) и по строгим моделям (пунктирная).

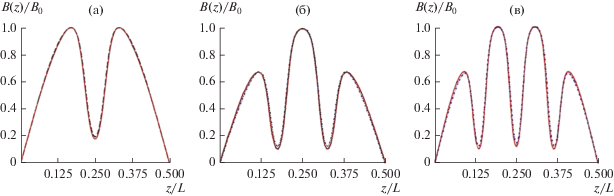
На рис. 5 представлены результаты расчетов ближайших зон неустойчивой фокусировки пучка в зависимости от величины параметра магнитного поля α для структур магнитного поля в МПФС с одной, двумя и тремя вставками. Следует отметить, что при значениях α > 0.9 (для одной вставки) начинается “зона непропускания” для любого электрона пучка.

Рис. 5.

Зависимость амплитуды пульсаций Δ границы электронного потока (2) и оптимальных величин радиуса потока R_опт на входе в регулярную часть МПФС (1) от параметра магнитного поля α для распределения осевой компоненты индукции магнитного поля в ячейках МПФС с одной (а), двумя (б) и тремя (в) вставками; 3 – зона “непропускания” при β_p = 0.

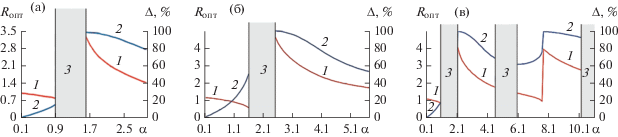
Как следует из анализа результатов, представленных на рис. 5, полученные структуры распределений магнитного поля позволили сместить зоны неустойчивой фокусировки в сторону более высоких значений параметра магнитного поля, хотя и в меньшей степени, чем при оптимальном соотношении высших гармонических составляющих для МПФС [6]. Так, при оптимальном вводе электронного потока в МПФС со вставками (см. рис. 5 кривые 2) пульсации границы пучка Δ в МПФС не превосходили величины 20% (кривые 1) вплоть до значений параметра магнитного поля, равного 0.9.

В качестве примера использования рассмотренных структур магнитного поля на рис. 6а и 6б представлен расчет фокусировки электронного пучка в обычной МПФС с синусоидальным распределением магнитного поля и в МПФС с одной магнитомягкой вставкой.

Рис. 6.

Зависимость радиуса границы электронного потока (1) и его фазового портрета (R', R) от продольной координаты z в МПФС (2) без вставок (а) и с одной (б) вставкой; режим фокусировки: α = β_p, α = 0.45.

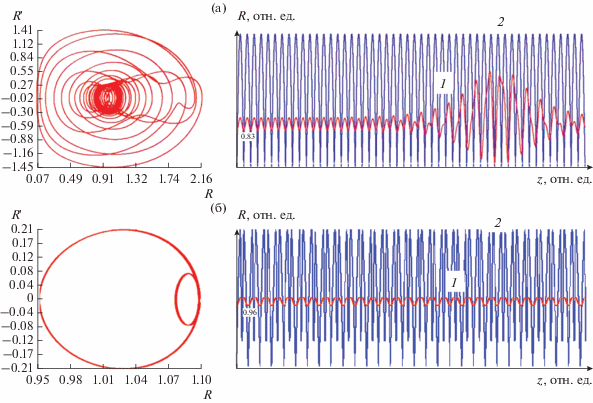
При синусоидальном распределении магнитного поля в регулярной части МПФС и значении параметра α = 0.45 транспортировка электронного потока затруднительна из-за возникающего параметрического резонанса, приводящего к “раскачке” пучка (см. рис. 6а). Введение вставки позволяет добиться транспортировки потока с малыми пульсациями границы пучка (см. рис. 6б).

ЗАКЛЮЧЕНИЕ

Найдено легко реализуемое в совмещенных МПФС распределение магнитного поля, которое существенно смещает положение зоны неустойчивой фокусировки пучка в сторону более высоких значений параметра магнитного поля и позволяет повысить величину параметра магнитного поля с 0.2 до 0.9, т.е. более чем в четыре раза.

Представленные результаты исследований свидетельствуют о возможности применения полученных структур распределений магнитного поля и связанных с этими распределениями конструкциями совмещенных МПФС для фокусировки интенсивного электронного потока в мощных ЛБВ, включая ЛБВ миллиметрового диапазона.