Радиотехника и электроника, 2019, T. 64, № 8, стр. 796-799

ВВЕДЕНИЕ

При измерении координат источника радиоизлучений (ИРИ) пеленгационным методом важным параметром при объединении пеленгов является погрешность их измерения. Эта погрешность влияет на “вес” линии положения, который учитывается при вынесении решения о координатах ИРИ. Учитывая плотность сигнальной загрузки радиоэфира и все возрастающие требования к скорости измерения координат ИРИ средствами радиоконтроля, можно полагать, что использование предложенного решения существенно повысит эффективность измерения координат за счет значительного сокращения времени, затрачиваемого на оценку среднеквадратической ошибки (СКО) измерений пеленгов.

1. ОЦЕНКА КООРДИНАТ ИРИ МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

Оценивание координат излучателя методом максимального правдоподобия (МП) можно представить в виде (см. [1], выражение (122))

где ${\mathbf{\hat {r}}}$ – оцениваемые координаты ИРИ; ${{{\mathbf{r}}}_{0}}$ – координаты опорной точки (приближенное решение, полученное неким эвристическим способом, например, по пересечению двух пеленгов); θ(r₀) = = ||α₁, …, α_N||^Т – вектор азимутов с N позиций на опорную точку; $\hat {\theta }$ = ||${{\hat {\alpha }}_{1}},$ …, ${{\hat {\alpha }}_{N}}$||^Т – вектор измеренных пеленгов с N позиций; Ф = diag($\sigma _{{\alpha n}}^{2}$) – матрица, описывающая погрешности измерений пеленгов, размером N × N; $\sigma _{{\alpha n}}^{2}$ – дисперсия измерения пеленга с n-й позиции; – матрица частных производных, рассчитанная для опорной точки; ^T – знак транспонирования. Из всех параметров в (1) неизвестным является Ф – матрица дисперсий пеленга.

В пеленгационных комплексах, построенных на основе цифровых антенных решеток, сигнал, принятый каждой точкой приема (ТП), усиливается, оцифровывается и поступает на специальный вычислитель. Здесь и далее под ТП будем понимать антенну с круговой диаграммой направленности. При этом оценка азимута на излучатель осуществляется методом максимального правдоподобия (см. [2], выражение (24))

где

μ = m – 1; λ = $\ell $ – 1; $\tau _{0}^{\varphi }$ ≡ 0; ${{A}_{m}}_{\ell } = \int_{{{f}_{1}}}^{{{f}_{2}}} {{{{\tilde {u}}}_{m}}(f)\tilde {u}_{\ell }^{*}(f)df;} $ ${{\Phi }_{{m\ell }}}$ = ${arctg\{ Im}[{{A}_{{m\ell }}}],$ ${\text{Re}}[{{A}_{{m\ell }}}]\} $ – разность псевдофаз между сигналами ${{\tilde {u}}_{m}}(f)$ и $\tilde {u}_{\ell }^{*}(f),$ принятыми m‑й и $\ell $-й ТП соответственно; arctg(b, c) = arctg(b/c) при c > 0; arctg(b, c) = arctg(b/c) + sign(b)π при c < 0; sign(b) = 1(–1) при b > 0 (b < 0); arctg(b, 0) = = sign(b)π/2 (b ≠ 0); arctg(0,0) = 0; f₀ – центральная частота сигнала; f₁ = f₀ – Δ_f и f₂ = f₀ + Δ_f – соответственно нижняя и верхняя границы сигнала; 2Δ_f – ширина полосы сигнала.

Оценку дисперсии измерения пеленга проведем в соответствии с классической процедурой [3, с. 291] (далее речь будет идти об одной n-й позиции, и поэтому индекс n в последующих выражениях указывать не будем)

где $\hat {\alpha } = \frac{1}{K}\sum\nolimits_{k = 1}^K {{{\alpha }_{k}}} $– оценка среднего значения измерения пеленга; K – число измерений пеленга; ${{\alpha }_{k}}$ – измеренное значение пеленга на k-м интервале наблюдения.

Точность оценки СКО по формуле (4) оценим с помощью выражения [3, c. 298]

Таким образом, чтобы получить оценку СКО с 10%-ной точностью необходимо провести 50 измерений, что в ряде случаев является неприемлемым (например, при ограниченном времени наблюдения, перемещающемся ИРИ и т.д.).

Существенно сократить время, необходимое на оценивание СКО, можно путем использования соотношения (см. [2], выражение (25))

где B(μ) = ${{\partial \tau _{\mu }^{\varphi }} \mathord{\left/ {\vphantom {{\partial \tau _{\mu }^{\varphi }} {\partial \alpha }}} \right. \kern-0em} {\partial \alpha }}$ = (–X_μsinα + Y_μcosα)/c; X_μ = X_m – – X₁; Y_μ = Y_m – Y₁ (μ = m – 1, m = $\overline {2,M} $) – составляющие матрицы B; $\tau _{\mu }^{\varphi }$ = (X_μ cos α + Y_μ sin α)/c – время прохождения сигнала от ТП₁ до ТП_m (от ТП_m до ТП₁, если $\tau _{\mu }^{\varphi }$ < 0); c – скорость света; α – пеленг на излучатель; M – число ТП в комплексе пеленгования; X_m, Y_m – координаты ТП; X₁, Y₁ – координаты первой (опорной) ТП.

Матрица ${{{\mathbf{Ф }}}_{{{{{\mathbf{T}}}_{\varphi }}}}}$ = (E + 1)/(PM) описывает погрешность измерений фазовых (т.е. соизмеримых с длиной волны) задержек $\tau _{\mu }^{\varphi },$ причем ее диагональные элементы описывают дисперсию их измерений $\sigma _{{{{\tau }_{\varphi }}}}^{2} = {2 \mathord{\left/ {\vphantom {2 {(PM)}}} \right. \kern-0em} {(PM)}}$. Здесь E – единичная матрица размером (М – 1) × (М – 1), 1 – матрица того же размера у которой все элементы равны 1; Р = = $16{{p}^{2}}{{Т }_{{\text{н }}}}f_{0}^{2}{{\Delta _{f}^{2}} \mathord{\left/ {\vphantom {{\Delta _{f}^{2}} {(1 + Mq)}}} \right. \kern-0em} {(1 + Mq)}};$ Т_н – время наблюдения; $q$ – отношение сигнал/шум. Легко видеть, что ${\mathbf{Ф }}_{{{{{\mathbf{T}}}_{\varphi }}}}^{{ - 1}}$ = Р(МЕ – 1). Отметим, что здесь мы не учитываем составляющие оценок по углу места β.

Учитывая пояснения к (6) представим это выражение в виде

2. ОЦЕНКА СКО ИЗМЕРЕНИЯ ПЕЛЕНГА

Как следует из соотношения (7) для оценки $\sigma _{\alpha }^{{}}$ необходимо произвести оценку СКО измерений фазовых задержек ${{\sigma }_{{{{\tau }_{\varphi }}}}}.$ Для этого используем следующий алгоритм, основанный на измерении невязок фаз. В соотношении (3) $\tau _{\mu }^{\varphi }$ и $\tau _{\lambda }^{\varphi }$ жестко связаны с параметром α, в то время как введенные в (3) разности псевдофаз между сигналами ${{\Phi }_{{m\ell }}}$ за счет шумов, налагающихся на входной сигнал, не имеют жесткой взаимной привязанности (т.е., не соблюдается линейная зависимость ${{\Phi }_{{m\ell }}}$ = Ф_mk – – ${{\Phi }_{{\ell k}}}$). Поэтому мы имеем M = М(М – 1)/2 независимых измерений псевдофаз (здесь учтено, что ${{\Phi }_{{m\ell }}}$ ≡ $ - {{\Phi }_{{\ell m}}}$).

Таким образом, если составить следующий набор невязок фаз

где комбинация $m\ell $ принимает значения 21; 31; …; М1; 32; 42; …; М2; …; М(М – 1); m = $\sum\nolimits_{i = 1}^\ell {\sum\nolimits_{j = i + 1}^m 1 } ;$ μ = m – 1; λ = $\ell - 1;$ $\tau _{0}^{\varphi }$ ≡ 0, то можно сформировать оценку СКО на основании следующего правила

Теоретическое значение ${{\sigma }_{\varphi }}$ получим из выражения для $\sigma _{{{{\tau }_{\varphi }}}}^{2},$ приняв во внимание, что в этом случае M = 2 и ${{\sigma }_{\varphi }}$ = $\frac{{2\pi {{f}_{0}}}}{{\sqrt {{{P}_{{(M = 2)}}}} }}.$

Таким образом,

и

При q $ \gg $ 1 соотношение (11) представим в виде

Для кольцевых антенных решеток нетрудно получить достаточно компактный вариант формулы, описывающий СКО измерения пеленга. Если учесть, что [см. 4, выражение (2)]

где М_Σ = $\sum\nolimits_{j = 1}^J {{{M}_{j}}} $ – общее количество антенн в АР; M_r = $\sum\nolimits_{j = 1}^J {{{M}_{j}}r_{j}^{2}} $; r_j – радиус j-го кольца; М_j – количество антенн в j-м кольце; J – количество колец в антенной решетке, то выражение (13) можно переписать в виде

где λ₀ = с/f₀ – длина волны сигнала.

Для q $ \gg $ 1 выражение (14) представим в виде

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

При выводе выражений для оценки дисперсий использовался ряд приближений и допущений. Для их подтверждения целесообразно провести дополнительную проверку путем имитационного моделирования.

В качестве исходных данных выберем следующие значения. Антенная решетка – кольцевая, 2Δ_f = 3 кГц, Т_н = 0.1 с, J = 1, М_Σ =М = 32, λ₀ =30 м, r_j = r = 150 м.

Таким образом, выражение (13), описывающее теоретическую СКО, преобразуется к виду

где $\ell $ = 2πr – длина окружности, на которой расставлены антенны.

На основании соотношений (9) и (14) на k-м измерении (k = $\overline {1,K} $, K – количество измерений) проведем оценку СКО измерения пеленга

Из (15) следует приближенное равенство

На рис. 1 представлены результаты измерений следующих значений: кривая 1 – теоретическое значение ${{\sigma }_{\alpha }},$ вычисленное по формуле (16); кривая 2 – оценка СКО ${{\hat {\sigma }}_{\alpha }},$ вычисленная в соответствии с соотношением (4); кривые 3 и 4 – оценка СКО ${{\hat {\sigma }}_{\alpha }},$ полученная путем усреднения значений, вычисленных по формулам (17) и (18) соответственно, с учетом следующего правила

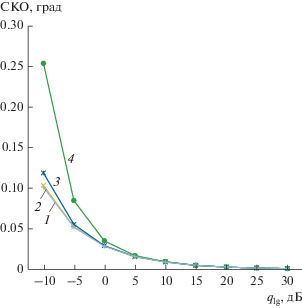
Отметим, что, начиная с отношения сигнал/шум q_lg = 10 lg(q) = 0 дБ выражение (18) вполне точно описывает СКО измерения пеленга.

Необходимо также ответить на вопрос – насколько точно оценивается СКО измерения пеленга ${{\hat {\sigma }}_{\alpha }}(k)$ на каждом k-м цикле измерений. Как видим из выражений (17) и (18), точность оценки СКО определяется погрешностью оценки ${{\hat {\sigma }}_{\varphi }}.$ Если предположить, что на k-м цикле измерений в соответствии с (9) оценивается ${{\hat {\sigma }}_{\varphi }}(k),$ то ошибку ее измерения можно оценить по формуле

где ${{\hat {\sigma }}_{\varphi }}$ – усредненная СКО, вычисленная в соответствии с выражением

Гистограмма распределения случайной величины (СВ) ${{\hat {\sigma }}_{\varphi }}(k)$ представлена на рис. 2. Ее распределение может быть аппроксимировано в виде нормального с оценкой математического ожидания (МО) по формуле (21) и СКО в соответствии с формулой (20).

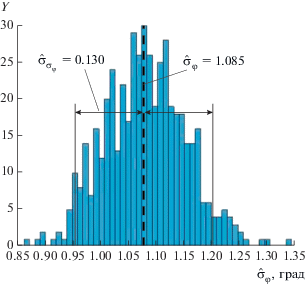
Для гауссовской СВ точность оценки СКО определяется количеством независимых измерений в соответствии с выражением (5). В процессе оценки СКО по формуле (9) участвуют М = М(М – 1)/2 измерений. Для М = 32 общее количество М = 496. Однако в этот объем входят зависимые друг от друга измерения. Для определения правильного числа воспользуемся следующей аналогией. Если имеется набор независимых друг от друга гауссовских СВ δ_i с одинаковой дисперсией и нулевым средним, то из комбинаций (δ₂ – δ₁); (δ₃ – δ₁); …; (δ_М – δ₁); (δ₃ – δ₂); (δ₄ – δ₂); …; (δ_М – δ₂); …; (δ_М – δ_М – 1) можно оценить дисперсию СВ по формуле

Как видно из (22), в процессе оценки дисперсии реальный вклад дает только первое слагаемое, состоящее из суммы квадратов М независимых СВ, поскольку второе слагаемое в силу независимости СВ стремится к нулю. Следовательно, погрешность измерения дисперсии будет примерно равна

На рис. 3 приведены результаты моделирования, в ходе которого оценивали величины ${{\hat {\sigma }}_{\varphi }},$ ${{\hat {\sigma }}_{{{{\sigma }_{\varphi }}}}}.$ Приведенные на рисунке кривые отображают значения ${{{{{\hat {\sigma }}}_{{{{\sigma }_{\varphi }}}}}} \mathord{\left/ {\vphantom {{{{{\hat {\sigma }}}_{{{{\sigma }_{\varphi }}}}}} {{{{\hat {\sigma }}}_{\varphi }}}}} \right. \kern-0em} {{{{\hat {\sigma }}}_{\varphi }}}}$ и ${1 \mathord{\left/ {\vphantom {1 {\sqrt {2М } }}} \right. \kern-0em} {\sqrt {2М } }}$ для различных отношений сигнал/шум (от –10 до +30 дБ) и разного количества антенн (М = 32, 64, 128).

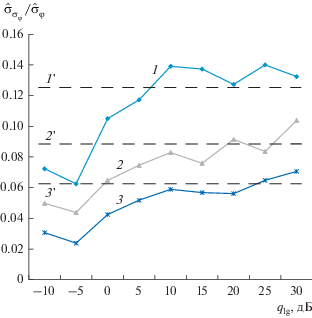
ЗАКЛЮЧЕНИЕ

Предложен способ оценки СКО измерения пеленга по однократной выборке сигнала. Получено компактное выражение, описывающее СКО оценки пеленга в явном виде через измеренные невязки фаз для кольцевой антенной решетки. Показано, что погрешность оценки СКО обратно пропорциональна количеству антенн в решетке, и что результаты моделирования хорошо согласуются с теоретическим предсказанием.