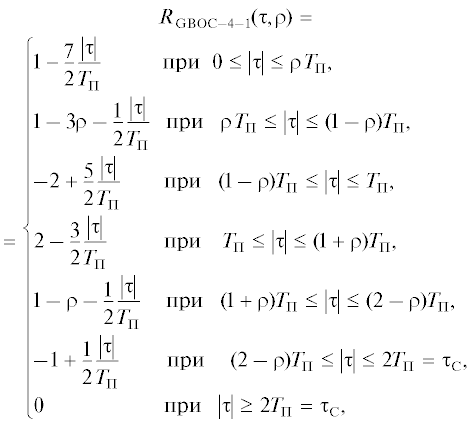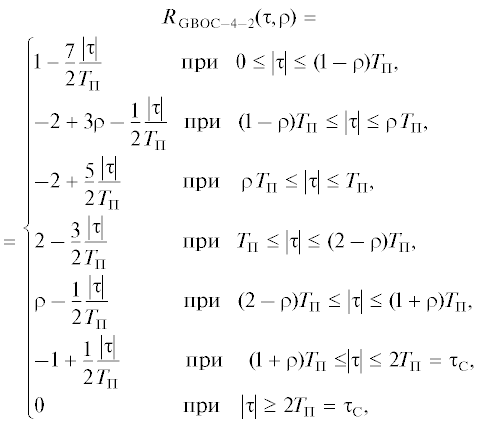Радиотехника и электроника, 2019, T. 64, № 8, стр. 775-786

Корреляционные функции навигационных GBOC-сигналов как обратное преобразование Фурье энергетических спектров

М. С. Ярлыков^*

Редакция журнала “Радиотехника и электроника”
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

Поступила в редакцию 31.01.2019
После доработки 31.01.2019
Принята к публикации 15.02.2019

DOI: 10.1134/S0033849419080187

Аннотация

Рассмотрены модулирующие функции (МФ) GBOC-сигналов (обобщенных BOC-сигналов) перспективных спутниковых радионавигационных систем, таких, например, как Galileo (ЕС), GPS (США) и BeiDou (Китай). Предложена методика вычисления корреляционных функций (КФ) одиночных элементов МФ GBOC-сигналов на основе обратного преобразования Фурье (ПФ) их энергетических спектров. В основе методики лежит представление энергетического спектра в виде взвешенной алгебраической суммы косинусов углов, определяемых характерными точками синусного символа МФ GBOC-сигналов (точками излома КФ). Согласно методике, получены аналитические выражения КФ одиночных элементов МФ GBOC-сигналов как обратное ПФ энергетических спектров при коэффициенте кратности импульсов ${{N}_{{\text{П }}}}$ = 2 и 4 для различных значений коэффициента заполнения ρ, где $\rho $ $ \in $ [0, 1]. В ряде случаев вычисление КФ GBOC-сигналов на основе обратного ПФ энергетических спектров предпочтительнее (в частности, по трудоемкости) при сравнении со способом получения КФ на основе ее общего определения.

ВВЕДЕНИЕ

Все большую привлекательность для применения в глобальных спутниковых радионавигационных системах (СРНС), таких как GPS (США), Galileo (Европейский союз), ГЛОНАСС (Россия) и BeiDou (Китай), приобретают навигационные BOC-сигналы (binary offset carrier modulated signals), их разновидности и обобщения [1–4]. В этой связи для перспективных глобальных СРНС заметным событием является разработка GBOC-сигналов (Generalized binary offset carrier modulated signals) – обобщенных BOC-сигналов [5–9].

Отличительная особенность GBOC-сигналов (по сравнению с BOC-сигналами) заключается в том, что у них поднесущее колебание (ПК) представляет собой прямоугольный сигнал, т.е. периодическую биполярную последовательность прямоугольных видеоимпульсов, с произвольным значением коэффициента заполнения ρ, где ρ ∈ [0, 1]. Такое ПК навигационных GBOC-сигналов называют прямоугольным ПК (ППК) [7–9].

Если у ППК коэффициент заполнения ρ = 0.5, то оно является меандровым ПК (МПК), а сам GBOC-сигнал в этом важном частном случае представляет собой традиционный BOC-сигнал.

Иными словами, GBOC-сигналы – это шумоподобные сигналы с ППК, а BOC-сигналы – это шумоподобные сигналы с МПК.

В другом частном случае, когда ρ = 0 или ρ = 1, GBOC-сигналы вырождаются в двоичные фазоманипулированные сигналы (binary phase shift keying signals – BPSK-сигналы) [10]. Этот случай является вырожденным, так как при этом утрачивается зависимость сигналов от значения коэффициента кратности импульсов ${{N}_{{\text{П }}}}$.

Поскольку у GBOC-сигналов коэффициент заполнения ρ может иметь то или иное заданное значение в пределах от 0 до 1, то за счет выбора значения ρ предоставляется дополнительная возможность изменять форму и параметры корреляционных функций и энергетических спектров таких сигналов. Это обстоятельство обусловливает определенные преимущества (в частности, по электромагнитной совместимости) при использовании в перспективных СРНС навигационных GBOC-сигналов по сравнению с BOC-сигналами или BPSK-сигналами.

Так, например, для СРНС BeiDou применительно к третьей фазе ее развития рассматривается возможность использования GBOC-сигналов с модуляцией типа GBOC(2,2,ρ). При этом обсуждаются следующие значения параметров таких GBOC-сигналов: несущая частота GBOC-сигнала ${{f}_{{\text{Н }}}}$ = 1561.098 МГц, коэффициент заполнения ρ = = 0.3, частота следования символов псевдослучайной последовательности (ПСП) дальномерного кода ${{f}_{{\text{С }}}}$ = 2.046 МГц, частота ППК ${{f}_{{\text{П }}}}$ = 2.046 МГц, базовая (опорная) частота (ОП) ${{f}_{{{\text{О }}{\kern 1pt} {\text{П }}}}}$ = 1.023 МГц [5, 6].

Навигационные GBOC-сигналы (аналогично BOC-сигналам) в зависимости от относительного сдвига по времени между ПСП дальномерного кода и ППК делятся на sinGBOC-сигналы (sine Generalized BOC-signals) – синусные обобщенные BOC-сигналы, и cosGBOC-сигналы (cosine Generalized BOC-signals) – косинусные обобщенные BOC-сигналы [5–9].

Далее ограничимся рассмотрением sinGBOC-сигналов, а приставку sin там, где это не затрудняет понимание, не применяем.

Свойства и возможности GBOC-сигналов во многом определяются их корреляционными характеристиками. Знание аналитических выражений и графиков их корреляционных функций (КФ) позволяет в принципе количественно рассчитать для приемников СРНС потенциальные характеристики точности слежения за ПСП дальномерного кода и оценить разрешающую способность сигналов в условиях многолучевости и при действии помех. Располагая формулами КФ GBOC-сигналов, можем разрабатывать дискриминаторы приемников, близкие к оптимальным, которые обеспечивали бы, по возможности, однозначное слежение за основным пиком КФ и минимизировали бы вероятность захвата ее боковых (ложных) пиков.

Получение явных формул КФ GBOC-сигналов (особенно при больших значениях коэффициента кратности импульсов ${{N}_{{\text{П }}}}$) представляет собой довольно трудоемкую задачу [8].

В ряде случаев аналитические выражения КФ GBOC-сигналов (аналогично BOC-сигналам [11, 12]) предпочтительнее получать как обратное преобразование Фурье (ПФ) их энергетических спектров. Помимо этого, вычисление КФ GBOC-сигналов другим методом (на основе энергетических спектров, а не прямым методом, в котором используется общее определение КФ) позволяет дополнительно подтвердить правильность полученных формул КФ.

Цель работы – предложить методику и в соответствии с ней получить аналитические выражения КФ одиночных элементов модулирующей функции (МФ) GBOC-сигналов путем обратного ПФ энергетических спектров при различных значениях коэффициента заполнения ρ, где ρ $ \in $ [0, 1], для коэффициента кратности импульсов ${{N}_{{\text{П }}}}$ = 2 и 4. Предложенная методика является обобщением методики для BOC-сигналов [4, 11, 12] на случай различных значений коэффициента заполнения ρ.

В основе методики лежит представление энергетического спектра GBOC-сигналов в виде взвешенной алгебраической суммы косинусов углов, определяемых характерными точками синусного символа МФ ${{\mu }_{{\sin {\text{GBOC}}}}}(t)$ GBOC-сигнала (т.е. точками излома КФ $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho )$). В частном случае, когда ρ = 0.5, т.е. рассматриваются BOC-сигналы, предложенная методика трансформируется в известную [4, 11, 12].

Рассматриваемые ПСП дальномерного кода и ППК имеют единичные амплитуды, поэтому полученные выражения характеризуют нормированные КФ.

Термин типа “одиночный элемент МФ GBOC-сигнала” означает, что рассматривается математическое выражение, описывающее один элемент МФ GBOC-сигнала.

1. СТРУКТУРА И ХАРАКТЕРИСТИКИ ИЗЛУЧАЕМЫХ GBOC-СИГНАЛОВ

Излучаемый бортовым передатчиком какого-либо одного спутника из состава орбитальной группировки GBOC-сигнал $s(t)$ среднеорбитальных СРНС характеризуется известным выражением [2, 4, 7, 13]

(1)

$s(t - {{t}_{0}}) = A{\kern 1pt} d(t - {{t}_{0}})\cos [{{\omega }_{{\text{Н }}}}(t - {{t}_{0}}) + \varphi (t)],$

где $A = \sqrt {2{{P}_{{{\text{с }}{\kern 1pt} {\text{р }}}}}} $ – амплитуда GBOC-сигнала на выходе передатчика; ${{P}_{{{\text{с }}{\kern 1pt} {\text{р }}{\kern 1pt} }}}$ – средняя мощность GBOC-сигнала на выходе передатчика; $d(t)$ – МФ GBOC-сигнала, $\,{{\omega }_{{\text{Н }}}} = 2\pi {\kern 1pt} {{f}_{{\text{Н }}}}$ – круговая несущая частота радиосигнала; ${{f}_{{\text{Н }}}}$ – несущая частота GBOC-сигнала; $\varphi (t)$ – фаза радиосигнала; ${{t}_{0}}$ – начало отсчета.

Как следует из (1), вся сложность и специфика GBOC-сигналов $s(t)$ полностью определяется структурой и характеристиками МФ $d(t).$ Формирование, структура и свойства МФ $d(t),$ а также ее статистические характеристики в случаях sinGBOC- и cosGBOC-сигналов достаточно детально рассмотрены в [7–9].

Далее, когда это не влияет на суть изложения, при выкладках для краткости полагаем, что МФ $d(t)$ GBOC-сигнала $s(t)$ обусловлена собственно ПСП дальномерного кода и ППК. В таком случае МФ $d(t)$ GBOC-сигнала $s(t)$ описывается следующим выражением [7–9]:

(2)

$d(t - {{t}_{0}}) = g(t - {{t}_{0}})r(t - {{t}_{0}}),$

где g(t) – собственно ПСП дальномерного кода; $r(t)$ – синусное ППК, отражающее специфику GBOC-сигналов $s(t)$.

Как видно из формулы (2), МФ ${\kern 1pt} d{\kern 1pt} (t)$ формируется путем перемножения взаимно синхронизированных последовательностей $g(t)$ и $r(t)$, каждая из которых состоит из чередующихся единичных видеоимпульсов соответствующей длительности, меняющих свою полярность по определенным законам согласно кодовым коэффициентам, значения которых на каждом такте равны +1 или –1.

Выражение, определяющее ПСП дальномерного кода $g(t)$ на одном ее периоде, имеет традиционный вид [4, 7, 10, 13]

(3)

$g(t - {{t}_{0}}) = \sum\limits_{k = 0}^{L - 1} {\nu {{{\kern 1pt} }_{k}}{\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{C}}}}}}}} [t - k{{\tau }_{{\text{С }}}} - {{t}_{0}}],$

где ${{\tau }_{{\text{С }}}}$ – длительность элемента ПСП $g(t)$; L – коэффициент расширения спектра, т.е. число элементов на периоде ПСП $g(t)$; k = 0, 1, 2, … , (L – 1) – номер элемента ПСП на периоде.

Функция ${\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{C}}}}}}}[ \cdot ]$ в (3) представляет собой импульс единичной амплитуды длительностью ${{\tau }_{{\text{С }}}}$:

(4)

${\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{C}}}}}}}[t - k{{\tau }_{{\text{С }}}}] = \left\{ \begin{gathered} 1\,\,\,\,{\text{п р и }}k{{\tau }_{{\text{С }}}} \leqslant t < (k + 1){{\tau }_{{\text{С }}}}, \hfill \\ 0\,\,\,\,{\text{п р и }}k{{\tau }_{{\text{С }}}} > t \geqslant (k + 1){{\tau }_{{\text{С }}}}, \hfill \\ \end{gathered} \right.$

где $k = 0,1,2, \cdots ,(L - 1).$

Длительность периода ПСП $g(t)$ (3) равна

(5)

${{T}_{L}} = L{{\tau }_{{\text{C}}}}.$

Кодовые коэффициенты ${{\nu }_{k}} = \nu ({{t}_{k}}),$ где ${{t}_{k}} = k{\kern 1pt} {{\tau }_{{\text{С }}}}$ – дискретное время, формируют ПСП дальномерного кода $g(t)$ (3). Они принимают на каждом элементе ПСП длительностью ${{\tau }_{{\text{С }}}}$ значения +1 или –1 согласно закону чередования элементов на периоде.

Так, например, в СРНС типа ГЛОНАСС дальномерный код стандартной точности представляет собой периодическую последовательность максимальной длины (М – последовательность, или последовательность Хаффмена) с периодом $T{}_{L}$ = 1 мс и частотой следования символов ${{f}_{{\text{С }}}}$ = = 511 кГц. В СРНС типа GPS дальномерный C/A код является периодической последовательностью Голда с периодом ${{T}_{L}}$ = 1 мс и частотой следования символов ${{f}_{{\text{С }}}}$ = 1.023 МГц [13, 14].

Графики, входящих в соотношение (2) синусного ППК $r(t)$, МФ $d(t)$ и ПСП $g(t)$ (при произвольно заданной в примере реализации), представлены на рис. 1.

Рис. 1.

Формирование модулирующей функции GBOC-сигнала: ${{T}_{{\text{П }}}}$ – длительность периода синусного ППК $r(t),$ ${{\tau }_{{\text{1}}}}$ и ${{\tau }_{2}}$ – длительности положительного и отрицательного импульсов синусного ППК $r(t),$ ${{\tau }_{{\text{С }}}}$ – длительность элемента ПСП $g(t)$.

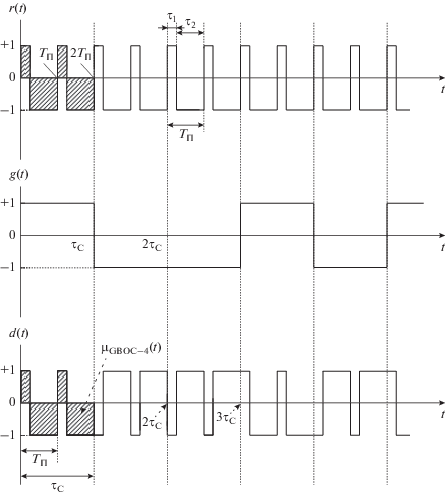
График МФ $d(t)$ на рис. 1 характеризует GBOC-сигналы с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 4. На рис. 1 принято, что начало отсчета ${{t}_{0}}$ = 0.

Рис. 2.

Синусные символы модулирующей функции GBOC-сигналов.

Как следует из рис. 1, для синусного ППК $r(t)$ имеют место соотношения

(6)

${{T}_{{\text{П }}}} = {{\tau }_{{\text{1}}}} + {{\tau }_{2}},$

(7)

${{f}_{{\text{П }}}} = \frac{1}{{{{T}_{{\text{П }}}}}} = \frac{1}{{{{\tau }_{{\text{1}}}} + {{\tau }_{2}}}},$

где ${{f}_{{\text{П }}}}$ – частота ППК $r(t).$

Применительно к GBOC-сигналам важным параметром является коэффициент заполнения прямоугольного сигнала ρ, который определяется как [6–9]

(8)

$\rho \triangleq {{{{\tau }_{{\text{1}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{1}}}}} {{{T}_{{\text{П }}}}}}} \right. \kern-0em} {{{T}_{{\text{П }}}}}},$

где ρ $ \in $ [0, 1].

Согласно (6) и (8) для коэффициента заполнения ρ можно записать (см. рис. 1):

(9)

${{\tau }_{{\text{1}}}} = \rho {{T}_{{\text{П }}}},\,\,\,\,{{\tau }_{2}} = (1 - \rho ){{T}_{{\text{П }}}}.$

В качестве примера на рис. 1 коэффициент заполнения синусного ППК $r(t)$ принят равным ρ = 0.25.

Частным случаем синусного ППК $r(t)$, когда коэффициент заполнения ρ = 0.5, является меандровый сигнал, у которого длительности положительного и отрицательного импульсов одинаковы, т.е.

(10)

${{\tau }_{{\text{1}}}} = {{\tau }_{2}} \triangleq {{\tau }_{{\text{М }}}},$

где ${{\tau }_{{\text{М }}}}$ – длительность меандрового импульса. При этом длительность периода ПК равна

${{T}_{{\text{П }}}} \triangleq {{T}_{{\text{М }}}} = 2{{\tau }_{{\text{М }}}},$

где ${{T}_{{\text{М }}}}$ – период МПК [1, 2, 4].

Таким образом, если коэффициент заполнения ρ = 0.5, то ППК $r(t)$ представляет собой МПК, а GBOC-сигнал (1) является традиционным BOC-сигналом.

При сопоставлении различных типов модуляции GBOC-сигналов (по аналогии с BOC-сигналами) используется следующее обозначение: GBOC (${{f}_{{\text{П }}}}$, ${{f}_{{\text{С }}}}$, $\rho $) [5–9]. Поскольку у СРНС частоты ${{f}_{{\text{П }}}}$ и ${{f}_{{\text{С }}}}$ обычно кратны ОП частоте ${{f}_{{{\text{О }}{\kern 1pt} {\text{П }}}}}$ (в частности, для систем GPS и Galileo ${{f}_{{{\text{О }}{\kern 1pt} {\text{П }}}}}$ = 1.023 МГц), то часто применяется и иная форма записи для обозначения типа модуляции GBOC-сигналов: GBOC($\alpha ,\,\beta \,,\rho $), где $\alpha = {{{{f}_{{\text{П }}}}} \mathord{\left/ {\vphantom {{{{f}_{{\text{П }}}}} {{{f}_{{{\text{О }}{\kern 1pt} {\text{П }}}}}}}} \right. \kern-0em} {{{f}_{{{\text{О }}{\kern 1pt} {\text{П }}}}}}}$ и $\beta = {{{{f}_{{\text{С }}}}} \mathord{\left/ {\vphantom {{{{f}_{{\text{С }}}}} {{{f}_{{{\text{О }}{\kern 1pt} {\text{П }}}}}}}} \right. \kern-0em} {{{f}_{{{\text{О }}{\kern 1pt} {\text{П }}}}}}}.$

В качестве еще одного показателя GBOC-сигналов используется либо коэффициент кратности импульсов ${{N}_{{\text{П }}}}$ ППК $r(t),$ либо эквивалентный ему параметр ${{{\text{Q}}}_{{\text{П }}}}$ – коэффициент кратности периодов ППК $r(t)$ [7–9].

Коэффициент кратности импульсов ${{N}_{{\text{П }}}}$ представляет собой число прямоугольных импульсов (положительных длительностью ${{\tau }_{{\text{1}}}}$ и отрицательных длительностью ${{\tau }_{{\text{2}}}}$) ППК $r(t),$ которые укладываются на длительности τ_C одного элемента ПСП $g(t)$ (см. рис. 1):

(11)

${{N}_{{\text{П }}}} = \frac{{2{\kern 1pt} {{\tau }_{{\text{С }}}}}}{{{{T}_{{\text{П }}}}}} = \frac{{2{\kern 1pt} {{f}_{{\text{П }}}}}}{{{{f}_{{\text{С }}}}}} = \frac{{2\alpha }}{\beta },$

где ${{N}_{{\text{П }}}}$ – положительное четное число (${{N}_{{\text{П }}}}$ = 2, 4, 6, …).

Коэффициент кратности периодов ${{{\text{Q}}}_{{\text{П }}}}$ представляет собой число периодов длительностью ${{T}_{{\text{П }}}}$ ППК $r(t)$, которые укладываются на длительности ${{\tau }_{{\text{С }}}}$ одного элемента ПСП $g(t)$ (см. рис. 1):

${{{\text{Q}}}_{{\text{П }}}} = \frac{1}{2}{{N}_{{\text{П }}}}{\text{ = }}\frac{{{{\tau }_{{\text{С }}}}}}{{{{T}_{{\text{П }}}}}} = \frac{{{{f}_{{\text{П }}}}}}{{{{f}_{{\text{С }}}}}} = \frac{\alpha }{\beta },$

где ${{{\text{Q}}}_{{\text{П }}}}$ = 1, 2, 3, …

В частном случае GBOC-сигналов при $\rho $ = 0.5, т.е. в случае BOC-сигналов, коэффициент кратности импульсов ${{N}_{{\text{П }}}}$ представляет собой применяемый при рассмотрении BOC-сигналов параметр ${{N}_{{\text{М }}}}$ – коэффициент кратности меандровых импульсов:

(12)

${{N}_{{\text{М }}}} = \frac{{{\kern 1pt} {{\tau }_{{\text{С }}}}}}{{{\kern 1pt} {{\tau }_{{\text{М }}}}}} = \frac{{2{\kern 1pt} {{f}_{{\text{М }}}}}}{{{{f}_{{\text{С }}}}}} = \frac{{2\alpha }}{\beta },$

где ${{\tau }_{{\text{М }}}}$ – длительность меандрового импульса МПК, определяемая (10).

2. ОДИНОЧНЫЕ ЭЛЕМЕНТЫ МОДУЛИРУЮЩЕЙ ФУНКЦИИ GBOC-СИГНАЛОВ

По аналогии с BOC-сигналами, согласно (2) и (3), произвольный k-й элемент МФ $d(t)$ GBOC-сигналов определяется следующим выражением [7–9]:

(13)

${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t) = {{\nu }_{k}}{{\mu }_{{{\text{GBOC}}}}}(t),$

где ${{\nu }_{k}}$ = $\nu {\kern 1pt} ({{t}_{k}})$ – кодовый коэффициент k-го элемента ПСП дальномерного кода $g(t)$, характеризуемой (3); ${{\mu }_{{{\text{GBOC}}}}}(t)$ – одиночный синусный символ МФ $d(t)$ (2) GBOC-сигналов; ${{t}_{k}} = k{\kern 1pt} {{\tau }_{{\text{С }}}}$ – дискретное время, где $k = 0,1,2, \ldots .$

В (13) и далее принято, что начало отсчета ${{t}_{0}}$ = 0. Индекс ${{\tau }_{{\text{С }}}}$ у обозначения ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - }}{\kern 1pt} {\text{GBOC}}}}}(t)$ указывает, что рассматривается одиночный элемент МФ $d(t)$ длительностью ${{\tau }_{{\text{С }}}}.$ (Далее, когда это не вызывает сомнений, слово “одиночный” в выражениях типа “одиночный символ” или “одиночный элемент” для краткости не пишем.)

В соответствии с (13) элемент МФ ${{d}_{{{{\tau }_{{\text{C}}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигнала $s(t)$ (1) представляет собой синусный символ МФ ${{\mu }_{{{\text{GBOC}}}}}(t),$ взятый со знаком “+” или “–” в зависимости от значения кодового коэффициента ${{\nu }_{k}}$ k-го элемента ПСП $g(t)$.

Рассмотрим синусный символ МФ ${{\mu }_{{{\kern 1pt} {\text{GBOC}}}}}(t)$ GBOC-сигналов $s(t)$ [7–9].

Синусный символ МФ ${{\mu }_{{{\kern 1pt} {\text{GBOC}}}}}(t)$ GBOC-сигналов $s(t)$ для различных значений коэффициента кратности импульсов ${{N}_{{\text{П }}}}$ с учетом (3), (4) и (11) характеризуется следующим выражением (см. рис. 1) [7]:

(14)

$\begin{gathered} {{\mu }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(t) = \\ = \sum\limits_{m = 0}^{0.5{{N}_{{\text{П }}}} - 1} {\left\{ {{\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{1}}}}}}}\left[ {t - m{{T}_{{\text{П }}}}} \right]--{\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{2}}}}}}}\left[ {t - \left( {m{{T}_{{\text{П }}}} + {{\tau }_{{\text{1}}}}} \right)} \right]} \right\}} , \\ \end{gathered} $

где ${{N}_{{\text{П }}}}$ = 2, 4, 6, ….

В формуле (14) и далее индекс${\kern 1pt} {\kern 1pt} {{N}_{{\text{П }}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} $ в обозначениях типа ${{\mu }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(t)$ указывает значение коэффициента кратности импульсов ${{N}_{{\text{П }}}}.$ Как видно из (14) и рис. 1, синусный символ МФ ${{\mu }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(t)$ представляет собой отрезок длительностью ${{\tau }_{{\text{С }}}}$ синусного ППК $r(t)$ при определенном значении коэффициента заполнения ρ. Длительность ${{\tau }_{{\text{С }}}}$ синусного символа ${{\mu }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(t)$ в соответствии с (11) равна

(15)

${{\tau }_{{\text{С }}}} = 0.5{{N}_{{\text{П }}}}{{T}_{{\text{П }}}}.$

Синусный символ МФ ${{\mu }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(t)$ на рис. 1 заштрихован.

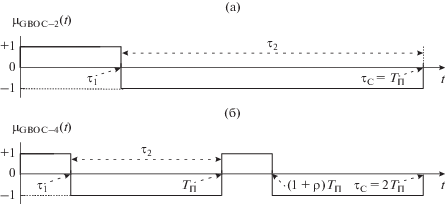
Согласно (14) на рис. 2 представлены графики синусных символов МФ ${{\mu }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(t)$ при ρ = 0.25 и одной и той же длительности ${{\tau }_{{\text{С }}}}$ элемента ПСП $g(t)$ применительно к двум типам GBOC-сигналов в случаях, когда ${{N}_{{\text{П }}}}$ = 2 и ${{N}_{{\text{П }}}}$ = 4.

График на рис. 2а представляет синусный символ ${{\mu }_{{{\text{GBOC--}}2}}}(t),$ который, согласно (14), характеризуется формулой

(16)

${{\mu }_{{{\text{GBOC--}}2}}}(t) = {\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{1}}}}}}}\left[ t \right]--{\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{2}}}}}}}\left[ {t - {{\tau }_{{\text{1}}}}} \right].$

Синусный символ МФ ${{\mu }_{{{\text{GBOC--}}2}}}(t)$ определяет GBOC-сигналы при ${{N}_{{\text{П }}}}$ = 2 с модуляцией, например, типа GBOC(1, 1, 0.2) или GBOC(2, 2, 0.3).

На рис. 2б представлен график синусного символа МФ

(17)

$\begin{gathered} {{\mu }_{{{\text{GBOC--}}4}}}(t) = {\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{1}}}}}}}\left[ t \right]--{\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{2}}}}}}}\left[ {t - {{\tau }_{{\text{1}}}}} \right] + \\ + \,\,{\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{1}}}}}}}\left[ {t--{{T}_{{\text{П }}}}} \right]--{\text{rec}}{{{\text{t}}}_{{{{\tau }_{{\text{2}}}}}}}\left[ {t - ({{T}_{{\text{П }}}} + {{\tau }_{{\text{1}}}})} \right], \\ \end{gathered} $

который определяет GBOC-сигналы при ${{N}_{{\text{П }}}}$ = 4 с модуляцией, например, типа GBOC(10, 5, 0.3).

В частном случае, когда коэффициент заполнения ρ = 0.5 (т.е. ${{\tau }_{{\text{1}}}}$ = ${{\tau }_{{\text{2}}}}$ = ${{\tau }_{{\text{М }}}}$), синусные символы МФ ${{\mu }_{{{\text{GBOC--}}\,{{N}_{{\text{П }}}}}}}(t)$ GBOC-сигналов, характеризуемые (14), представляют собой синусные символы МФ ${{\mu }_{{{\text{BOC}}}}}(t)$ BOC-сигналов [4].

Как следует из формулы (14) и рис. 2, применительно к GBOC-сигналам в зависимости от значения коэффициента заполнения ρ, где ρ $ \in $ [0, 1], при ${{N}_{{\text{П }}}}$ = 2, 4, 6, … возможен один из двух вариантов формирования синусного ППК $r(t),$ что обусловлено взаимным соотношением длительностей ${{\tau }_{{\text{1}}}}$ и ${{\tau }_{2}}$ [8].

Так, первый вариант формирования синусного ППК $r(t)$ GBOC-сигналов соответствует условию ${{\tau }_{{\text{1}}}}$ ≤ ${{\tau }_{2}}$, а второй вариант – ${{\tau }_{{\text{1}}}}$ ≥ ${{\tau }_{2}}$, т.е. соответственно

(18)

$\rho \in \left[ {0,0.5} \right],$

(19)

$\rho \in \left[ {0.5{\text{ }},1} \right].\quad$

Каждому варианту формирования синусного ППК $r(t)$ соответствует свое аналитическое выражение КФ $R{{{\kern 1pt} }_{{{\kern 1pt} {\kern 1pt} {\text{GBOC}}}}}(\tau ,{\kern 1pt} {\kern 1pt} \rho {\kern 1pt} )$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигналов [8].

3. ОСНОВНЫЕ СООТНОШЕНИЯ ПО РАСЧЕТУ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ОДИНОЧНЫХ ЭЛЕМЕНТОВ МОДУЛИРУЮЩЕЙ ФУНКЦИИ GBOC-СИГНАЛОВ

Под статистическими характеристиками одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигналов понимаем, как обычно, его спектральные и корреляционные характеристики. Спектральная плотность (спектральная функция) ${{G}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho {\kern 1pt} ){\kern 1pt} $ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигнала представляет собой прямое ПФ от этого элемента МФ [7, 9, 15–17]:

(20)

$\begin{gathered} {{G}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho ) \triangleq {\text{FT}}\left\{ {{{d}_{{{{\tau }_{{\text{С }}}}{\text{ - G}}{\kern 1pt} {\text{BOC}}}}}(t)} \right\} = \\ = \int\limits_{ - \infty }^\infty {{{d}_{{{{\tau }_{{\text{С }}}}{\text{ - G}}{\kern 1pt} {\text{BOC}}}}}(t){\text{exp}}\left\{ {{\text{--}}i\omega t} \right\}} dt,\,\,\,\,{{t}_{0}} = 0, \\ \end{gathered} $

где ${\text{FT}}\left\{ \cdot \right\}$ – символ прямого ПФ.

Энергетический спектр (спектральная плотность мощности) ${{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho {\kern 1pt} )\,$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигнала характеризуется соотношением [7, 9, 15–17]

(21)

${{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho ) \triangleq \frac{1}{{{{\tau }_{{\text{C}}}}}}\left[ {{{G}_{{{\text{GBOC}}}}}(\omega ,\rho ){\kern 1pt} G_{{{\text{GBOC}}}}^{ * }(\omega ,{\kern 1pt} \rho )} \right],$

где $G_{{{\text{GBOC}}}}^{ * }(\omega ,{\kern 1pt} \rho )$ – комплексно-сопряженная спектральная плотность от ${{G}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho ).$

Для одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигнала, характеризуемого (13) и (14), в соответствии с определением КФ можно записать [15–17]

(22)

$R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho ) \triangleq \frac{1}{{{{\tau }_{{\text{C}}}}}}\int\limits_0^{{{\tau }_{{\text{C}}}}} {{{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t){{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t--\tau )dt} ,$

где $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho )$ – КФ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигнала; ${{\tau }_{{\text{C}}}} = {1 \mathord{\left/ {\vphantom {1 {{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{f}_{{\text{С }}}}}}$ – длительность элемента ПСП $g(t);$ $\left| \tau \right| \leqslant {{\tau }_{{\text{С }}}}.$

Согласно общему положению статистической радиотехники, КФ $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho )$ и соответствующий энергетический спектр ${{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho )$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигнала представляют собой пару ПФ (оригиналы и изображения) [15–17].

В соответствии с этим выполняются следующие соотношения:

(23)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho ) = {\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {{{S}_{{{\text{GBOC}}}}}(\omega ,\rho )} \right\} = \\ = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {{{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho ){\text{exp}}\left\{ {i\omega \tau } \right\}} d\omega , \\ \end{gathered} $

(24)

$\begin{gathered} {{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho ) = {\text{FT}}\left\{ {{{R}_{{{\text{GBOC}}}}}(\tau ,{\kern 1pt} \rho )} \right\} = \\ = \int\limits_{ - \infty }^\infty {{{R}_{{{\text{GBOC}}}}}(\tau ,\rho ){\text{exp}}\left\{ {{\text{--}}i\omega \tau } \right\}} d\tau , \\ \end{gathered} $

где ${\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ \cdot \right\}$ – символ обратного ПФ.

Учитывая, что КФ $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho )$ и энергетический спектр ${{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho )$ представляют собой четные функции своих аргументов, формулы (23) и (24) принимают вид

(25)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho ) = {\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {{{S}_{{{\text{GBOC}}}}}(\omega ,\rho )} \right\} = \\ = \frac{1}{\pi }\int\limits_0^\infty {{{S}_{{{\text{GBOC}}}}}(\omega ,\rho ){\text{cos}}\omega \tau } \,d\omega \,, \\ \end{gathered} $

(26)

$\begin{gathered} {{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho ) = {\text{FT}}\left\{ {{{R}_{{{\text{GBOC}}}}}(\tau ,{\kern 1pt} \rho )} \right\} = \\ = 2\int\limits_0^\infty {{{R}_{{{\text{GBOC}}}}}(\tau ,{\kern 1pt} \rho ){\text{cos}}\omega \tau } \,d\tau . \\ \end{gathered} $

Суть методики, позволяющей получить аналитические выражения КФ $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho )$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигналов на основе обратного преобразования Фурье энергетического спектра ${{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho ),$ состоит в том, что энергетический спектр представляется в виде взвешенной алгебраической суммы косинусов углов, определяемых характерными точками (точками излома КФ) синусного символа МФ ${{\mu }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(t).$ При таком представлении энергетического спектра ${{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho )$ последующее вычисление оригиналов по изображениям затруднений не вызывает.

Пары ПФ (оригиналы и изображения), которые необходимы для получения аналитических выражений КФ $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho ),$ представлены в табл. 1 [4, 11, 16, 17].

Таблица 1.

Пары преобразований Фурье

Оригинал	Изображение
$R{\kern 1pt} (\tau ) = {\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {S(\omega )} \right\} = \frac{1}{{2\pi }} = \int\limits_{ - \infty }^\infty {S(\omega ){\text{exp}}\left\{ {i\omega \tau } \right\}} d\omega $	$S(\omega ) = {\text{FT}}\left\{ {R{\kern 1pt} (\tau )} \right\} = \int\limits_{ - \infty }^\infty {R{\kern 1pt} (\tau ){\text{exp}}\left\{ {{\text{--}}i\omega \tau } \right\}} d\tau $
$\frac{1}{2}[\delta (\tau + T) + \delta (\tau --T)]$	$\cos \omega T$
${\text{sign(}}\tau \,{\text{)}}$	$\frac{2}{{i\omega }}$
${{\tau }^{n}}$	${{i}^{n}}2\pi {{\delta }^{{(n)}}}(\omega )$
$\tau $	$i2\pi {\kern 1pt} {{\delta }^{{(1)}}}(\omega )$
$\tau \,{\text{sign(}}\tau {\text{)}}$	$ - \frac{2}{{{{\omega }^{2}}}}$
$ - \frac{1}{2}\tau \,{\text{sign(}}\tau {\text{)}}$	$\frac{1}{{{{\omega }^{2}}}}$
$ - \frac{1}{4}(\tau + bT){\text{sign(}}\tau + bT{\text{)}} - \frac{1}{4}(\tau - bT){\text{sign(}}\tau - bT{\text{)}}$	$\frac{1}{{{{\omega }^{2}}}}\cos b\omega T$

Примечание: ${{\delta }^{{(n)}}}(\omega )$ – n-я производная дельта-функции Дирака $\delta (\omega )$, ${{\delta }^{{(1)}}}(\omega )$ – 1-я производная дельта-функции Дирака $\delta (\omega )$.

Далее на основе формулы (25) получим аналитические выражения КФ $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho )$ одиночных элементов МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигналов как обратное ПФ энергетических спектров ${{S}_{{{\text{GBOC}}}}}(\omega ,{\kern 1pt} \rho )$ при коэффициенте кратности импульсов ${{N}_{{\text{П }}}}$ = 2 и 4 для различных значений коэффициента заполнения ρ, где ρ $ \in $ [0, 1].

4. КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ ОДИНОЧНЫХ ЭЛЕМЕНТОВ МОДУЛИРУЮЩЕЙ ФУНКЦИИ GBOC-СИГНАЛОВ

Энергетический спектр ${{S}_{{{\text{GBOC}}}}}(f,\rho )$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигналов при произвольном значении коэффициента кратности импульсов ${{N}_{{\text{П }}}}$ определяется следующей формулой [7]:

(27)

$\begin{gathered} {{S}_{{{\text{GBOC}}}}}(f,{\kern 1pt} \rho ) = \frac{1}{{{{f}_{{\text{С }}}}}}\frac{{{\text{si}}{{{\text{n}}}^{{\text{2}}}}\left( {{{\pi f} \mathord{\left/ {\vphantom {{\pi f} {{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{f}_{{\text{С }}}}}}} \right)}}{{{{{\left( {{{\pi f} \mathord{\left/ {\vphantom {{\pi f} {{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{f}_{{\text{С }}}}}}} \right)}}^{2}}{\text{si}}{{{\text{n}}}^{{\text{2}}}}\left( {{{2{\kern 1pt} \pi f} \mathord{\left/ {\vphantom {{2{\kern 1pt} \pi f} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right)}} \times \\ \times \,\,\left[ {{\text{si}}{{{\text{n}}}^{{\text{2}}}}\left( {{{2\pi f} \mathord{\left/ {\vphantom {{2\pi f} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right)} \right. + 4{{\cos }^{{\text{2}}}}\left( {{{2\pi f} \mathord{\left/ {\vphantom {{2\pi f} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right) \times \\ \times \,\,{\text{s}}{\kern 1pt} {\text{i}}{{{\text{n}}}^{{\text{2}}}}\left( {{{2{\kern 1pt} \pi f\rho } \mathord{\left/ {\vphantom {{2{\kern 1pt} \pi f\rho } {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right)-- \\ - \,\,\left. {{\text{s}}{\kern 1pt} {\text{in}}\left( {{{4{\kern 1pt} \pi f} \mathord{\left/ {\vphantom {{4{\kern 1pt} \pi f} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right){\text{si}}{\kern 1pt} {\text{n}}\left( {{{4\pi f\rho } \mathord{\left/ {\vphantom {{4\pi f\rho } {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{N}_{{\text{П }}}}{{f}_{{\text{С }}}}}}} \right)} \right], \\ \end{gathered} $

где ${{f}_{{\text{С }}}}$ – частота следования символов ПСП $g(t);$ ${{N}_{{\text{П }}}}$ = 2, 4, 6, … – коэффициент кратности импульсов, характеризуемый (11); ρ $ \in $ [0, 1] – коэффициент заполнения (8).

Заметим, что применительно к (27) относительно коэффициента заполнения ρ выполняется соотношение [7]

(28)

${{S}_{{{\text{GBOC}}}}}(f,{\kern 1pt} \rho ) = {{S}_{{{\text{GBOC}}}}}(f,1--\rho ).$

Согласно формуле (25) получим аналитические выражения КФ $R{{{\kern 1pt} }_{{{\text{GBOC}}}}}(\tau ,\rho )$ одиночных элементов МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC}}}}}(t)$ GBOC-сигналов как обратное ПФ энергетического спектра ${{S}_{{{\text{GBOC}}}}}(\omega ,\rho )$ (42) при ${{N}_{{\text{П }}}}$ = 2 и 4 для различных значений коэффициента заполнения ρ, где ρ $ \in $ [0, 1].

А. Корреляционная функция $R{{{\kern 1pt} }_{{{\kern 1pt} {\text{GBOC--}}\,2}}}(\tau ,{\kern 1pt} {\kern 1pt} \rho {\kern 1pt} )$ одиночного элемента модулирующей функции GBOC-сигнала с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 2

Энергетический спектр ${{S}_{{{\text{GBOC--2}}}}}(f,\rho )$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC--}}2}}}(t)$ GBOC-сигнала при коэффициенте кратности импульсов ${{N}_{{\text{П }}}}$ = 2 описывается, согласно (27), следующим выражением:

(29)

$\begin{gathered} {{S}_{{{\text{GBOC--2}}}}}(f,\rho ) = \frac{1}{{{{f}_{{\text{С }}}}}}\frac{1}{{{{{\left( {{{\pi f} \mathord{\left/ {\vphantom {{\pi f} {{{f}_{{\text{С }}}}}}} \right. \kern-0em} {{{f}_{{\text{С }}}}}}} \right)}}^{2}}}} \times \\ \times \,\,\left[ {{\text{si}}{{{\text{n}}}^{{\text{2}}}}\left( {\frac{{\pi f}}{{{{f}_{{\text{С }}}}}}} \right) + 4{{{\cos }}^{{\text{2}}}}\left( {\frac{{\pi f}}{{{{f}_{{\text{С }}}}}}} \right)} \right. \times \\ \times \,\,\left. {{\text{si}}{{{\text{n}}}^{{\text{2}}}}\left( {\rho \frac{{\pi f}}{{{{f}_{{\text{С }}}}}}} \right)--{\text{sin}}\left( {\frac{{2\pi f}}{{{{f}_{{\text{С }}}}}}} \right){\text{sin}}\left( {\rho \frac{{2\pi f}}{{{{f}_{{\text{С }}}}}}} \right)} \right], \\ \end{gathered} $

где ρ $ \in $ [0, 1], ${{N}_{{\text{П }}}}$ = 2, ${{\tau }_{{\text{C}}}}$ = ${{T}_{{\text{П }}}}.$

Чтобы получить аналитическое выражение КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,{\kern 1pt} \rho )$ (22) одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC--2}}}}}(t)$ GBOC-сигналов при ${{N}_{{\text{П }}}}$ = 2, представим, согласно методике, энергетический спектр ${{S}_{{{\text{GBOC--2}}}}}(f,\rho )$ (29) в виде взвешенной алгебраической суммы косинусов углов, определяемых характерными точками синусного символа МФ ${{\mu }_{{{\text{GBOC--2}}}}}(t)$ (16) GBOC-сигнала. В этом случае формула (29) принимает вид

(30)

$\begin{gathered} {{S}_{{{\text{GBOC--2}}}}}(\omega ,\rho ) = \frac{2}{{{{\omega }^{2}}{{\tau }_{{\text{C}}}}}} \times \\ \times \,\,\left[ {3 + {\text{cos}}\omega {{\tau }_{{\text{C}}}}--2\cos \rho \omega {{\tau }_{{\text{C}}}}--2{\text{cos(1--}}\rho )\omega {{\tau }_{{\text{C}}}}} \right], \\ \end{gathered} $

где ρ $ \in $ [0, 1], ${{N}_{{\text{П }}}}$ = 2, ${{\tau }_{{\text{C}}}}$ = ${{T}_{{\text{П }}}},$ ${{\tau }_{{\text{C}}}}$ = $\frac{1}{{{{f}_{{\text{С }}}}}},$ $\omega = 2\pi f.$

Найдем КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,{\kern 1pt} \rho )$ (22) при ${{N}_{{\text{П }}}}$ = 2 как обратное ПФ энергетического спектра ${{S}_{{{\text{GBOC--2}}}}}(\omega ,\rho )$ (30). Подставив (30) в (25), получим

(31)

$\begin{gathered} {{R}_{{{\text{GBOC--2}}}}}(\tau ,\rho ) = {\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {{{S}_{{{\text{GBOC--2}}}}}(\omega ,\rho ))} \right\} = \\ = \frac{1}{\pi }\int\limits_0^\infty {{{S}_{{{\text{GBOC--2}}}}}(\omega ,\rho ){\text{cos}}\omega \tau } \,d\omega = \frac{1}{\pi }\int\limits_0^\infty {\frac{2}{{{{\omega }^{2}}{{\tau }_{{\text{C}}}}}}} \times \\ \times \,\,\left[ {3 + {\text{cos}}\omega {{\tau }_{{\text{C}}}}--2\cos \rho \omega {{\tau }_{{\text{C}}}}--2{\text{cos(1--}}\rho )\omega {{\tau }_{{\text{C}}}}} \right] \times \\ \times \,\,{\text{cos}}\omega \tau \,d\omega \,. \\ \end{gathered} $

В соответствии с (25) выражение (31) можем записать в виде

(32)

$\begin{gathered} {{R}_{{{\text{GBOC--2}}}}}(\tau ,\rho ) = \frac{6}{{{{\tau }_{{\text{C}}}}}}{\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {\frac{1}{{{{\omega }^{2}}}}} \right\} + \\ + \,\,\frac{2}{{{{\tau }_{{\text{C}}}}}}{\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {\frac{1}{{{{\omega }^{2}}}}{\text{cos}}\omega {{\tau }_{{\text{C}}}}} \right\} - \frac{4}{{{{\tau }_{{\text{C}}}}}}{\text{F}}{{{\text{T}}}^{{{\text{--1}}}}} \times \\ \times \,\,\left\{ {\frac{1}{{{{\omega }^{2}}}}{\text{cos}}\rho \omega {{\tau }_{{\text{C}}}}} \right\}--\frac{4}{{{{\tau }_{{\text{C}}}}}}{\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {\frac{1}{{{{\omega }^{2}}}}{\text{cos}}(1--\rho )\omega {{\tau }_{{\text{C}}}}} \right\}. \\ \end{gathered} $

Оригиналы, входящие в формулу (32), представлены в табл. 1. Подставив их в (32), находим, что КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,{\kern 1pt} \rho )$ описывается следующим выражением:

(33)

$\begin{gathered} {{R}_{{{\text{GBOC--2}}}}}(\tau ,\rho ) = - 3\frac{\tau }{{{{\tau }_{{\text{C}}}}}}{\text{sign(}}\tau {\text{)}}--\frac{1}{2}\frac{\tau }{{{{\tau }_{{\text{C}}}}}} \times \\ \times \,\,\left[ {{\text{sign(}}\tau + {{\tau }_{{\text{C}}}}{\text{)}} + {\text{sign(}}\tau --{{\tau }_{{\text{C}}}}{\text{)}}} \right]-- \\ - \,\,\frac{1}{2}\left[ {{\text{sign(}}\tau + {{\tau }_{{\text{C}}}}{\text{)}}--{\text{sign(}}\tau --{{\tau }_{{\text{C}}}}{\text{)}}} \right] + \\ + \,\,\frac{\tau }{{{{\tau }_{{\text{C}}}}}}\left[ {{\text{sign(}}\tau + \rho {{\tau }_{{\text{C}}}}{\text{)}} + {\text{sign(}}\tau --\rho {{\tau }_{{\text{C}}}}{\text{)}}} \right] + \\ + \,\,\rho \left[ {{\text{sign(}}\tau + \rho {{\tau }_{{\text{C}}}}{\text{)}}--{\text{sign(}}\tau --\rho {{\tau }_{{\text{C}}}}{\text{)}}} \right] + \\ + \,\,\frac{\tau }{{{{\tau }_{{\text{C}}}}}}\left[ {{\text{sign(}}\tau + \left( {1--\rho } \right){{\tau }_{{\text{C}}}}{\text{)}} + {\text{sign(}}\tau --\left( {1--\rho } \right){{\tau }_{{\text{C}}}}{\text{)}}} \right] + \\ + \,\,\left( {1--\rho } \right)\left[ {{\text{sign(}}\tau + \left( {1--\rho } \right){{\tau }_{{\text{C}}}}{\text{)}}--{\text{sign(}}\tau --\left( {1--\rho } \right){{\tau }_{{\text{C}}}}{\text{)}}} \right], \\ \end{gathered} $

где ρ $ \in $ [0, 1], ${{N}_{{\text{П }}}}$ = 2, ${{\tau }_{{\text{C}}}}$ = ${{T}_{{\text{П }}}}$.

Входящая в формулу (33) функция “сигнум” z имеет вид [4, 17, 18 ]

(34)

${\text{sign}}{\kern 1pt} z = \left\{ \begin{gathered} 1\,\,\,\,\,\,{\text{п р и }}\,\,\,\,z > 0; \hfill \\ 0\,\,\,\,\,\,{\text{п р и }}\,\,\,\,z = 0; \hfill \\ - 1\,\,\,\,{\text{п р и }}\,\,\,\,z < 0. \hfill \\ \end{gathered} \right.$

Видно, что для формулы (33) выполняется условие

$R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho ) = {{R}_{{{\text{GBOC--2}}}}}(\tau ,1--\rho ).$

Как отмечали (см. (18) и (19)), для GBOC-сигналов в зависимости от значения коэффициента заполнения ρ, где ρ $ \in $ [0, 1], при ${{N}_{{\text{П }}}}$ = 2, 4, 6, … возможен один из двух вариантов формирования синусного ППК $r(t),$ что обусловлено взаимным соотношением длительностей ${{\tau }_{{\text{1}}}}$ и ${{\tau }_{2}}.$

Так, первый вариант формирования синусного ППК $r(t)$ GBOC-сигналов характерен тем, что ${{\tau }_{{\text{1}}}}$ ≤ ${{\tau }_{2}}$, т.е. ρ $ \in $ [0, 0.5], и второй вариант – тем, что ${{\tau }_{{\text{1}}}}$ ≥ ${{\tau }_{2}}$, т.е. ρ $ \in $ [0.5 , 1].

Каждому варианту формирования синусного ППК $r(t)$ соответствует своя последовательность чередования характерных точек КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ на оси времени смещения τ (т.е. точек излома КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$).

Произведем вычисления в (33) с учетом значений функции “сигнум” (34) отдельно для каждого вариантов формирования синусного ППК $r(t).$ Как обычно, для каждого варианта используем следующую методику: сначала находим КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ при $\tau $ ≥ $0$, т.е. все преобразования и вычисления выполняем в пределах $0 \leqslant \tau \leqslant {{\tau }_{{\text{C}}}}{\kern 1pt} .$ Затем, используя свойства четности КФ ($R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ = $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(--\tau ,\rho )$), распространяем результат на область, где $\tau \leqslant 0{\kern 1pt} .$

Выполнив преобразования и произведя вычисления в (33), находим, что КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC--2}}}}}(t)$ GBOC-сигналов с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 2 имеет вид

(35)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho ) = \\ = \left\{ {\begin{array}{*{20}{c}} {{{R}_{{{\text{GBOC--2--1}}}}}(\tau ,\rho )\,\,{\text{п р и }}\,\,0 \leqslant \rho \leqslant 0.5,} \\ {{{R}_{{{\text{GBOC--2--2}}}}}(\tau ,\rho )\,\,{\text{п р и }}\,\,0.5 \leqslant \rho \leqslant 1.} \end{array}} \right. \\ \end{gathered} $

Входящие в формулу (35) КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2--1}}}}}(\tau ,\rho )$ и $R{{{\kern 1pt} }_{{{\text{GBOC--2--2}}}}}(\tau ,\rho )$ описываются следующими выражениями:

(36)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--2--1}}}}}(\tau ,\rho ) = \\ = \left\{ \begin{gathered} 1 - \frac{{3\left| \tau \right|}}{{{{\tau }_{{\text{С }}}}}}\,\,\,\,\,\,\,\,\,\,\,\,{\text{п р и }}\,\,\,\,0 \leqslant \left| \tau \right| \leqslant \rho {{\tau }_{{\text{С }}}}, \hfill \\ 1--2\rho - \frac{{\left| \tau \right|}}{{{{\tau }_{{\text{С }}}}}}\,\,\,{\text{п р и }}\,\,\,\,\rho {{\tau }_{{\text{С }}}} \leqslant \left| \tau \right| \leqslant (1--\rho ){{\tau }_{{\text{С }}}}, \hfill \\ --1 + \frac{{\left| \tau \right|}}{{{{\tau }_{{\text{С }}}}}}\,\,\,\,\,\,\,\,\,\,{\text{п р и }}\,\,\,\,(1--\rho ){{\tau }_{{\text{С }}}} \leqslant \left| \tau \right| \leqslant {{\tau }_{{\text{С }}}}, \hfill \\ {\text{0}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{п р и }}\,\,\,\,\left| \tau \right| \geqslant {{\tau }_{{\text{С }}}}, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

где ρ $ \in $ [0, 0.5], ${{N}_{{\text{П }}}}$ = 2,${{\tau }_{{\text{C}}}}$ = ${{T}_{{\text{П }}}}$;

(37)

$\begin{gathered} {{R}_{{{\text{GBOC--2--2}}}}}(\tau ,\rho ) = \\ = \left\{ \begin{gathered} 1 - \frac{{3\left| \tau \right|}}{{{{\tau }_{{\text{С }}}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{п р и }}\,\,\,\,0 \leqslant \left| \tau \right| \leqslant (1--\rho ){{\tau }_{{\text{С }}}}, \hfill \\ 2\rho --1 - \frac{{\left| \tau \right|}}{{{{\tau }_{{\text{С }}}}}}\,\,\,\,{\text{п р и }}\,\,\,\,(1--\rho ){{\tau }_{{\text{С }}}} \leqslant \left| \tau \right| \leqslant \rho {{\tau }_{{\text{С }}}}, \hfill \\ --1 + \frac{{\left| \tau \right|}}{{{{\tau }_{{\text{С }}}}}}\,\,\,\,\,\,\,\,\,\,\,{\text{п р и }}\,\,\,\,\rho {{\tau }_{{\text{С }}}} \leqslant \left| \tau \right| \leqslant {{\tau }_{{\text{С }}}}, \hfill \\ {\text{0}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{п р и }}\,\,\,\,\left| \tau \right| \geqslant {{\tau }_{{\text{С }}}}, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

где ρ $ \in $ [0.5, 1], ${{N}_{{\text{П }}}}$ = 2 ,${{\tau }_{{\text{C}}}}$ = ${{T}_{{\text{П }}}}$.

Вторые индексы 1 или 2 в формулах (35)–(37) и далее, характеризующих КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ и $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho ),$ означают, что рассматривается первый или второй варианты формирования синусного ППК $r(t)$ GBOC-сигналов.

Из рассмотрения (36) и (37) следует, что применительно к КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2--1}}}}}(\tau ,\rho )$ и $R{{{\kern 1pt} }_{{{\text{GBOC--2--2}}}}}(\tau ,\rho )$ выполняются соотношения

(38)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--2--1}}}}}(\tau ,\rho ) = R{{{\kern 1pt} }_{{{\text{GBOC--2--2}}}}}(\tau ,1--\rho ), \\ R{{{\kern 1pt} }_{{{\text{GBOC--2--2}}}}}(\tau ,\rho ) = {{R}_{{{\text{GBOC--2--1}}}}}(\tau ,1--\rho ). \\ \end{gathered} $

В соответствии с (38) имеем, что для КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ справедливы равенства, например, в случаях

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,0.1) = R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,{\kern 1pt} \,0.9)\,\,\,\,{\text{и }} \\ {{R}_{{{\text{GBOC--2}}}}}(\tau ,0.2) = R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,{\kern 1pt} \,0.8). \\ \end{gathered} $

Видно, что формулы (35)–(37) совпадают с соответствующими выражениями для КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ из [8, ф-лы (23)–(25)], которые получены другим методом (на основе общего определения КФ и без использования энергетического спектра).

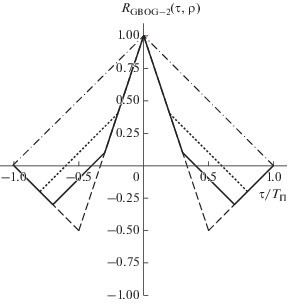
На рис. 3 представлены графики КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho ),$ построенные согласно (35)–(37), для одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC--2}}}}}(t)$ GBOC-сигналов с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 2 при ρ = 0.3 и 0.2. На этом же рисунке изображены графики КФ $R{{{\kern 1pt} }_{{{\text{BOC--2}}}}}(\tau )$ и $R{{{\kern 1pt} }_{{{\text{BPSK}}}}}(\tau )$ соответствующих BOC- и BPSK-сигналов. Все КФ на рис. 3 являются нормированными. Особенности КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ обсуждаются в [8].

Рис. 3.

Корреляционные функции $R{{{\kern 1pt} }_{{{\text{GBOC--}}2}}}(\tau ,\rho )$ одиночного элемента модулирующей функции GBOC-сигнала с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 2 при ρ = 0.3 (сплошная линия), ρ = 0.2 (пунктирная линия); также изображены графики КФ $R{{{\kern 1pt} }_{{{\text{BOC--2}}}}}(\tau )$ (штриховая линия) и $R{{{\kern 1pt} }_{{{\text{BPSK}}}}}(\tau )$ (штрихпунктирная линия) соответствующих BOC- и BPSK-сигналов.

Б. Корреляционная функция $R{{{\kern 1pt} }_{{{\kern 1pt} {\text{GBOC--}}\,4}}}(\tau ,{\kern 1pt} {\kern 1pt} \rho {\kern 1pt} )$ одиночного элемента модулирующей функции GBOC-сигнала с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 4

Согласно (27) энергетический спектр ${{S}_{{{\text{GBOC--4}}}}}(f,\rho )$ (21) одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC--}}4}}}(t)$ (13) и (17) GBOC-сигналов с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 4 описывается следующим выражением:

(39)

$\begin{gathered} {{S}_{{{\text{GBOC--4}}}}}(f,\rho ) = \frac{4}{{{{f}_{{\text{С }}}}}}\frac{{{{{\cos }}^{{\text{2}}}}\left( {\frac{{\pi f}}{{2{{f}_{{\text{С }}}}}}} \right)}}{{{{{\left( {\frac{{\pi f}}{{{{f}_{{\text{С }}}}}}} \right)}}^{2}}}}\left[ {{\text{s}}{\kern 1pt} {\text{i}}{{{\text{n}}}^{{\text{2}}}}\left( {\frac{{\pi f}}{{2{{f}_{{\text{С }}}}}}} \right)} \right. + \\ + \,\,4{{\cos }^{{\text{2}}}}\left( {\frac{{\pi f}}{{2{{f}_{{\text{С }}}}}}} \right){\text{si}}{{{\text{n}}}^{{\text{2}}}}\left( {\rho {\kern 1pt} \frac{{\pi f}}{{2{{f}_{{\text{С }}}}}}} \right)--{\text{si}}{\kern 1pt} {\text{n}}\left( {\frac{{\pi f}}{{{{f}_{{\text{С }}}}}}} \right){\text{sin}}\left( {\rho \frac{{\pi f}}{{{{f}_{{\text{С }}}}}}} \right), \\ \end{gathered} $

где ρ $ \in $ [0, 1], ${{N}_{{\text{П }}}}$ = 4, ${{\tau }_{{\text{C}}}}$ = $2{{T}_{{\text{П }}}}.$

В соответствии с предложенной методикой (по аналогии с GBOC-сигналами при ${{N}_{{\text{П }}}}$ = 2) представим энергетический спектр ${{S}_{{{\text{GBOC--4}}}}}(f,\rho )$ (39) при ${{N}_{{\text{П }}}}$ = 4 в виде взвешенной алгебраической суммы косинусов углов, определяемых характерными точками синусного символа МФ ${{\mu }_{{{\text{GBOC--}}4}}}(t)$ (т.е. точками излома КФ $R{{{\kern 1pt} }_{{\sin {\text{GBOC--4}}}}}(\tau ,\rho )$).

В таком случае формула (39) принимает следующий вид:

(40)

${{S}_{{{\text{GBOC--4}}}}}(\omega ,\rho ) = \frac{1}{{{{\omega }^{2}}{{T}_{{\text{П }}}}}}\sum\limits_{i = 0}^6 {{{h}_{i}}{\text{cos}}{{g}_{i}}\omega {{T}_{{\text{П }}}}} ,$

где $\omega = 2\pi f,$ ρ $ \in $ [0, 1], ${{N}_{{\text{П }}}}$ = 4, ${{\tau }_{{\text{C}}}}$ = $2{{T}_{{\text{П }}}},$ коэффициенты $h{{{\kern 1pt} }_{i}}{\kern 1pt} $ и ${{g}_{{{\kern 1pt} i}}}$ (i = $\overline {0,6} $) приведены в табл. 2.

Таблица 2.

Коэффициенты h_i и g_i формулы энергетического спектра S_GBOC–4(ω, ρ) при различных значениях i

$i$	${{h}_{{{\kern 1pt} i}}}$	${{g}_{i}}$
0	7	0
1	8	1
2	– 6	$\rho $
3	– 6	1 – $\rho $
4	– 2	1 + $\rho $
5	– 2	2 – $\rho $
6	1	2

Видно, что (40) совпадает с соответствующим выражением для энергетического спектра ${{S}_{{{\text{GBOC--4}}}}}(\omega ,\rho )$ из [8, ф-ла (44)].

Согласно (25) найдем КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ (22) при ${{N}_{{\text{П }}}}$ = 4 как обратное ПФ энергетического спектра ${{S}_{{{\text{GBOC--4}}}}}(\omega ,\rho )$ (40).

Подставив (40) в (25), получим

(41)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,{\kern 1pt} \rho ) = {\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {{{S}_{{{\text{GBOC--4}}}}}(\omega ,\rho )} \right\} = \\ = \frac{1}{\pi }\int\limits_0^\infty {{{S}_{{{\text{GBOC--4}}}}}(\omega ,\rho ){\text{cos}}\omega \tau } \,d\omega = \\ = {\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {\frac{1}{{{{\omega }^{2}}{{T}_{{\text{П }}}}}}\sum\limits_{i{\kern 1pt} = 0}^6 {{{h}_{i}}{\text{cos}}{{g}_{i}}\omega {{T}_{{\text{П }}}}} } \right\} = \\ = \frac{1}{{{{T}_{{\text{П }}}}}}\sum\limits_{i = 0}^6 {{{h}_{i}}{\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {\frac{1}{{{{\omega }^{2}}}}{\text{cos}}{{g}_{i}}\omega {{T}_{{\text{П }}}}} \right\}} . \\ \end{gathered} $

Оригиналы ${\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {\frac{1}{{{{\omega }^{2}}}}{\text{cos}}{{g}_{i}}\omega {{T}_{{\text{П }}}}} \right\},$ где i = $\overline {0,6} ,$ приведены в табл. 1 и имеют вид

(42)

$\begin{gathered} {\text{F}}{{{\text{T}}}^{{{\text{--1}}}}}\left\{ {\frac{1}{{{{\omega }^{2}}}}{\text{cos}}{{g}_{i}}\omega {\kern 1pt} {{T}_{{\text{П }}}}} \right\} = --\frac{1}{4}(\tau + {{g}_{{{\kern 1pt} i}}}{{T}_{{\text{П }}}}) \times \\ \times \,\,{\text{sign(}}\tau + {{g}_{i}}{{T}_{{\text{П }}}}{\text{)}} - \frac{1}{4}(\tau - {{g}_{i}}{{T}_{{\text{П }}}}){\text{sign(}}\tau - {{g}_{i}}{{T}_{{\text{П }}}}{\text{),}} \\ \end{gathered} $

коэффициенты ${{g}_{{{\kern 1pt} i}}}$ (i = $\overline {0,6} $) приведены в табл. 2.

Подставив (42) в (41), находим, что КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ описывается следующим выражением:

(43)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho ) = \\ = --\frac{1}{4}\sum\limits_{i = 0}^6 {{\kern 1pt} {{h}_{i}}\left\{ {\frac{\tau }{{{{T}_{{\text{П }}}}}}\left[ {{\text{sign(}}\tau + {{g}_{i}}{{T}_{{\text{П }}}}{\text{)}} + {\text{sign(}}\tau --{{g}_{i}}{{T}_{{\text{П }}}}{\text{)}}} \right]} \right.} + \\ \left. {\frac{{}}{{}} + \,\,{{g}_{i}}\left[ {{\text{sign(}}\tau + {{g}_{i}}{{T}_{{\text{П }}}}{\text{)}}--{\text{sign(}}\tau --{{g}_{i}}{{T}_{{\text{П }}}}{\text{)}}} \right]} \right\}, \\ \end{gathered} $

где ρ $ \in $ [0, 1], ${{N}_{{\text{П }}}}$ = 4, ${{\tau }_{{\text{C}}}}$ = $2{{T}_{{\text{П }}}},$ коэффициенты $h{{{\kern 1pt} }_{i}}{\kern 1pt} $ и ${{g}_{{{\kern 1pt} i}}}$ (i = $\overline {0,6} $) приведены в табл. 2.

Как следует из (43), для КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ выполняется соотношение $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ = $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,{\kern 1pt} 1--\rho ).$

Применительно к GBOC-сигналам с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 4 (аналогично GBOC-сигналам при ${{N}_{{\text{П }}}}$ = 2) в зависимости от значения коэффициента заполнения ρ возможен один из двух вариантов формирования синусного ППК $r(t).$ Так, первый вариант формирования синусного ППК $r(t)$ GBOC-сигналов характерен тем, что ${{\tau }_{{\text{1}}}}$ ≤ ${{\tau }_{2}}$, т.е. ρ $ \in $ [0, 0.5], второй вариант характерен тем, что ${{\tau }_{{\text{1}}}}$ ≥ ${{\tau }_{2}}$, т.е. ρ $ \in $ [0.5, 1]. Каждому варианту формирования синусного ППК ${{r}_{{{\kern 1pt} \sin }}}(t)$ соответствует свое аналитическое выражение КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho ).$

Согласно предложенной методике (по аналогии с GBOC-сигналами при ${{N}_{{\text{П }}}}$ = 2) произведем вычисления в формуле (43) с учетом значений функции “сигнум” (34) отдельно для каждого варианта формирования синусного ППК $r(t).$

В результате находим, что КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC--4}}}}}(t)$ GBOC-сигналов с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 4 определяется следующим соотношением:

(44)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho ) = \\ = \left\{ {\begin{array}{*{20}{c}} {{{R}_{{{\text{GBOC--4--1}}}}}(\tau ,\rho )\,\,\,\,{\text{п р и }}\,\,\,\,0 \leqslant \rho \leqslant 0.5,} \\ {{{R}_{{{\text{GBOC--4--2}}}}}(\tau ,\rho )\,\,\,\,{\text{п р и }}\,\,\,\,0.5 \leqslant \rho \leqslant 1.} \end{array}} \right. \\ \end{gathered} $

Входящие в (44) КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4--1}}}}}(\tau ,\rho )$ и $R{{{\kern 1pt} }_{{{\text{GBOC--4--2}}}}}(\tau ,\rho )$ соответственно равны

(45)

где ρ $ \in $ [0, 0.5], ${{N}_{{\text{П }}}}$ = 4, ${{\tau }_{{\text{C}}}}$ = $2{{T}_{{\text{П }}}}$;

(46)

где ρ $ \in $ [$0.5$, 1], ${{N}_{{\text{П }}}}$ = 4, ${{\tau }_{{\text{C}}}}$ = $2{{T}_{{\text{П }}}}.$

Из рассмотрения (45) и (46) следует, что применительно к КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4--1}}}}}(\tau ,\rho )$ и $R{{{\kern 1pt} }_{{{\text{GBOC--4--2}}}}}(\tau ,\rho )$ выполняются следующие соотношения:

(47)

$\begin{gathered} R{{{\kern 1pt} }_{{{\text{GBOC--4--1}}}}}(\tau ,\rho ) = {{R}_{{{\text{GBOC--4--2}}}}}(\tau ,1--\rho )\,\,\,\,{\text{и }} \\ R{{{\kern 1pt} }_{{{\text{GBOC--4--2}}}}}(\tau ,\rho ) = {{R}_{{{\text{GBOC--4--1}}}}}(\tau ,1--\rho ). \\ \end{gathered} $

Согласно (47) для КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ (аналогично КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$) выполняются такие равенства, как, например, $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,0.1)$ = $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,0.9)$ и $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,0.2)$ = $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,0.8).$

Как и следовало ожидать, формулы (44)–(46) совпадают с соответствующими выражениями для КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ из [8, ф-лы (36)–(38)], которые получены другим способом (на основе общего определения КФ и без использования энергетического спектра).

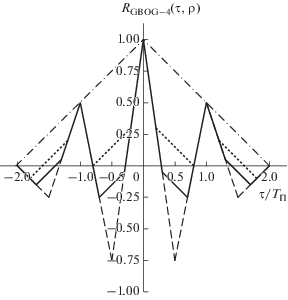
На рис. 4 изображены графики КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho ),$ построенные согласно (44)–(46), для одиночного элемента МФ ${{d}_{{{{\tau }_{{\text{С }}}}{\text{ - GBOC--4}}}}}(t)$ GBOC-сигналов с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 4 и при различных значениях коэффициента заполнения ρ = 0.3 и 0.2. На этом же рисунке показаны графики КФ $R{{{\kern 1pt} }_{{{\text{BOC--4}}}}}(\tau {\kern 1pt} )$ (штриховая линия) и $R{{{\kern 1pt} }_{{{\text{BPSK}}}}}(\tau )$ (штрихпунктирная линия) соответствующих BOC- и BPSK-сигналов. Все КФ на рис. 4 являются нормированными. Особенности КФ $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ рассматриваются в [8].

Рис. 4.

Корреляционные функции $R{{{\kern 1pt} }_{{{\text{GBOC--}}4}}}(\tau ,\rho )$ одиночного элемента модулирующей функции GBOC-сигнала с коэффициентом кратности импульсов ${{N}_{{\text{П }}}}$ = 4 при различных значениях коэффициента заполнения: ρ = 0.3 (сплошная линия) и ρ= 0.2 (пунктирная линия); также показаны графики КФ $R{{{\kern 1pt} }_{{{\text{BOC--4}}}}}(\tau )$ (штриховая линия) и $R{{{\kern 1pt} }_{{{\kern 1pt} {\text{BPSK}}}}}(\tau {\kern 1pt} {\kern 1pt} )$ (штрихпунктирная линия) соответствующих BOC- и BPSK-сигналов.

ЗАКЛЮЧЕНИЕ

Рассмотрены GBOC-сигналы, предназначенные для применения в перспективных глобальных СРНС), таких как, например, GPS (США), Galileo (ЕС), ГЛОНАСС (Россия) и BeiDou (Китай).

Предложена методика вычисления КФ одиночных элементов МФ таких GBOC-сигналов на основе обратного ПФ энергетических спектров, и этим способом получены аналитические выражения КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ и $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ при коэффициенте кратности импульсов ${{N}_{{\text{П }}}}$ = 2 и 4 для различных значений коэффициента заполнения ρ, где ρ $ \in $ [0, 1]. В основе методики лежит представление энергетического спектра GBOC-сигналов в виде взвешенной алгебраической суммы косинусов углов, определяемых характерными точками синусного символа МФ ${{\mu }_{{{\text{GBOC}}}}}(t)$ (т.е. точками излома КФ).

В ряде случаев вычисление КФ $R{{{\kern 1pt} }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(\tau ,\rho )$ путем обратного ПФ энергетических спектров оказывается более предпочтительным при сравнении со способом получения КФ на основе их общего определения.

Как и следовало ожидать, полученные аналитические выражения КФ $R{{{\kern 1pt} }_{{{\text{GBOC--2}}}}}(\tau ,\rho )$ и $R{{{\kern 1pt} }_{{{\text{GBOC--4}}}}}(\tau ,\rho )$ совпадают с соответствующими формулами из [8], найденными другим методом (на основе общего определения КФ и без использования энергетических спектров).

По изложенной методике аналогичным образом можно получить аналитические выражения КФ $R{{{\kern 1pt} }_{{{\text{GBOC--}}{{N}_{{\text{П }}}}}}}(\tau ,\rho )$ одиночных элементов МФ GBOC-сигналов при любом другом значении коэффициента кратности импульсов ${{N}_{{\text{П }}}},$ где ${{N}_{{\text{П }}}}$ = = 2, 4, 6, …..

Знание аналитических выражений КФ одиночных элементов МФ GBOC-сигналов позволяет осознанно преодолевать трудности при разработке навигационной аппаратуры потребителей (в частности, дискриминаторов) с целью обеспечения, по возможности, однозначного слежения за основным пиком КФ и минимизации вероятности захвата ее боковых (ложных) пиков. На этой же основе для СРНС грядущего поколения можно количественно рассчитать потенциальные характеристики точности слежения за ПСП дальномерного кода и оценить разрешающую способность сигналов при действии помех и в условиях многолучевости.

Список литературы

Betz J.W. // Proc. National Technical Meeting of the Institute of Navigation (ION – NTM’99), January 1999, P. 639.
Betz J.W. // Binary Offset Carrier Modulations for Radionavigation. – Navigation, J. ION. 2001. V. 48. № 4. P. 227.
Hein G.W., Godet J., Issler J.-L. et al. // Status of Galileo Frequency and Signal Design. – Proc. Institute of Navigation Global Positioning System Meeting (ION GPS 2002). Portland. USA. 24–27 Sep. 2002. Fairfax: ION, 2002. P. 266.
Ярлыков М.С. Меандровые шумоподобные сигналы (ВОС-сигналы) и их разновидности в спутниковых радионавигационных системах. М.: Радиотехника, 2017.
Liu W., Hu Y., Zhan X.Q. // Electron. Lett. 2012. V. 48. № 5. P. 284.
Liu W., Hu Y. // J. Comm. Technology and Electronics. 2014. V. 59. № 11. P. 1206.
Яpлыкoв M.C. // PЭ. 2017. T. 62. № 10. C. 964.
Ярлыков М.С., Ярлыкова С.М. // РЭ. 2018. Т. 63. № 2. С. 157.
Яpлыкoв M.C. // PЭ. 2018. T. 63. № 8. C. 808.
Варакин Л.Е. Системы связи с шумоподобными сигналами. М.: Радио и связь, 1985.
Яpлыкoв M.C. // PЭ. 2016. T. 61. № 8. C. 725.
Ярлыков М.С., Ярлыкова С.М. // РЭ. 2017. Т. 62. № 2. С. 126.
Шебшаевич В.С., Дмитриев П.П., Иванцевич Н.В. и др. Сетевые спутниковые радионавигационные системы. 2-е изд. М.: Радио и связь, 1993.
Interface Specification IS – GPS – 200. Navstar GPS Space Segment/Navigation User Interface. Los Angeles: Global Positioning Systems Directorate, 2012. 226 p. https://www.gps.gov/technical/icwg/IS-GPS-200H.pdf
Тихонов В.И. Статистическая радиотехника. 2-е изд. М.: Сов. радио, 1982.
Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высш. школа, 2005.
Стеценко О.А. Радиотехнические цепи и сигналы. М.: Высш. школа, 2007.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал