Радиотехника и электроника, 2019, T. 64, № 9, стр. 887-890
Синтез трехзеркальной системы с заданной формой главного зеркала по фазовому фронту и закону отображения
В. А. Калошин 1, *, Е. В. Фролова 1
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, Моховая, 11, стр. 7, Российская Федерация
* E-mail: vak@cplire.ru
Поступила в редакцию 13.07.2018
После доработки 13.07.2018
Принята к публикации 23.07.2018
Аннотация
В приближении геометрической оптики получено аналитическое решение задачи синтеза образующих зеркал осесимметричной трехзеркальной системы с заданным главным зеркалом, которая преобразует сферический фронт источника в произвольный выходной фронт с заданным законом отображения, при этом образующая одного из вспомогательных зеркал выражена в виде полинома по четным степеням угла. Полученное решение обеспечивает точную реализацию выходного фронта и заданную ошибку закона отображения. Рассмотрены задачи синтеза апланатического трехзеркального телескопа, в котором в качестве главного зеркала используется либо параболическое, либо сферическое зеркало.
В различных приложениях возникает задача построения трехзеркальных систем [1–4]. В данной работе рассматривается задача синтеза трехзеркальной системы с заданной формой главного зеркала. Синтез двухзеркальной системы с заданным главным зеркалом позволяет реализовать заданную форму выходного фронта и, соответственно, диаграммы направленности [5]. Однако этого часто оказывается недостаточно, и необходимо дополнительно реализовать заданный закон отображения фронтов. Этот закон определяет многие важные характеристики системы: КИП, уровень боковых лепестков, сканирующие свойства. Реализация заданной формы выходного фронта и закона отображения в системе с заданным главным зеркалом возможна, если число зеркал системы не менее трех.
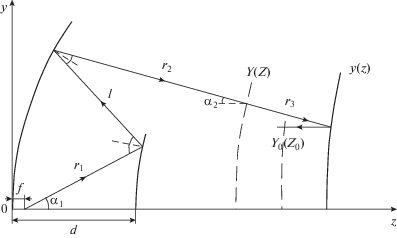
Рассмотрим геометрию формирования лучей в трехзеркальной системе с цилиндрической или осевой симметрией и произвольным выходным фронтом ${{Y}_{0}}({{Z}_{0}})$ (рис. 1).
Ось трехзеркальной системы совпадает с осью 0z декартовой системы координат, начало координат находится в вершине второго вспомогательного зеркала, образующая которого описывается функцией ${{r}_{2}}({{\alpha }_{2}}),$ где ${{r}_{2}}$ – расстояние вдоль луча между вторым вспомогательным зеркалом и фронтом Y(Z), ${{\alpha }_{2}}$ – угол, отсчитываемый от оси, параллельной оси 0z. Источник сферической волны расположен в фокусе системы на расстоянии f от начала координат, осевое расстояние между вспомогательными зеркалами системы равно d.
Образующая первого вспомогательного зеркала описывается зависимостью ${{r}_{1}}({{\alpha }_{1}})$, где ${{r}_{1}}$ – радиус в полярной системе координат с центром в фокусе $f$, ${{\alpha }_{1}}$ – угол, отсчитываемый от оси 0z, $l$ – расстояние между точками на вспомогательных зеркалах вдоль луча. Образующая главного зеркала характеризуется декартовыми координатами y(z).
Необходимо, чтобы все лучи, выходящие из первого фокуса и отраженные зеркалами, формировали выходной фронт ${{Y}_{0}}({{Z}_{0}}),$ при этом должен выполняться заданный закон отображения ${{\alpha }_{2}} = {{\alpha }_{2}}({{\alpha }_{1}}).$
Требуя, чтобы система зеркал удовлетворяла условию равенства проекций лучей на оси координат и оптических путей при прохождении лучей между двумя фронтами, нетрудно получить линейное дифференциальное уравнение для образующей первого вспомогательного зеркала:
(1)
$\left( {{1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r}} \right){\text{'}} = - Q(\alpha )\left( {{1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r}} \right) - P(\alpha ),$(2)
$P({{\alpha }_{1}},{{\alpha }_{2}}) = \frac{{2\sin \frac{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{2}}}{{\Delta Z\cos \frac{{{{\alpha }_{1}} - {{\alpha }_{2}}}}{2} + \Delta Y\sin \frac{{{{\alpha }_{1}} - {{\alpha }_{2}}}}{2} - {{L}_{0}}\cos \frac{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{2}}},$(3)
$Q({{\alpha }_{1}},{{\alpha }_{2}}) = \frac{{\Delta Z\sin \frac{{{{\alpha }_{1}} - {{\alpha }_{2}}}}{2} - \Delta Y\cos \frac{{{{\alpha }_{1}} - {{\alpha }_{2}}}}{2} - {{L}_{0}}\sin \frac{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{2}}}{{\Delta Z\cos \frac{{{{\alpha }_{1}} - {{\alpha }_{2}}}}{2} + \Delta Y\sin \frac{{{{\alpha }_{1}} - {{\alpha }_{2}}}}{2} - {{L}_{0}}\cos \frac{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{2}}},$L0 = r01 + d + r02, ΔZ = r01 + r02 – d – S, S и ΔY определяются формой главного зеркала, r01 = r1(0), r02 = r2(0).
Ранее дифференциальное уравнение для синтеза двухзеркальной системы по заданному волновому фронту было получено в работе [6].
Уравнение (2) является уравнением Бернулли, а его решение выражается через двукратный интеграл
(4)
$r(\alpha ) = - \frac{{\exp \left( { - \int {Q(\alpha )} d\alpha } \right)}}{{\int {(P(\alpha )\exp \left( { - \int {Q(\alpha )} d\alpha )} \right)d\alpha } }}.$Для телескопической трехзеркальной системы с параболической формой главного зеркала решение (4) сводится к однократному интегралу [6]. При этом решение в явном виде удается получить только для нескольких частных случаев. Например, для апланатической системы, характеризующейся законом отображения $y = {{f}_{1}}\sin ({{\alpha }_{1}}),$ с параболическим главным зеркалом решение имеет вид [6]
(5)
$\begin{gathered} \frac{1}{r} = \left[ {\frac{1}{{2({{r}_{{01}}} - {{\rho }_{{02}}})}} + \frac{1}{{2d}}} \right] + \,\,\left[ {\frac{1}{{2({{r}_{{01}}} - {{\rho }_{{02}}})}} - \frac{1}{{2d}}} \right]\cos \alpha - \\ - \,\,\frac{{{{\rho }_{{02}}}}}{{{{r}_{{01}}}({{r}_{{01}}} - {{\rho }_{{02}}})}}{{\left[ {\frac{{1 + \cos \alpha }}{2}} \right]}^{{{\eta \mathord{\left/ {\vphantom {\eta {(2 + \eta )}}} \right. \kern-0em} {(2 + \eta )}}}}}\,{{\left[ {\frac{{\eta + 1 - \cos \alpha }}{\eta }} \right]}^{{{2 \mathord{\left/ {\vphantom {2 {(2 + \eta )}}} \right. \kern-0em} {(2 + \eta )}}}}}, \\ \end{gathered} $Для нахождения решения в общем случае воспользуемся методикой, предложенной в работе [4]. Будем искать решение уравнения (1) в виде полинома степени 2n:
(6)
${1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r} = {{b}_{0}} + {{b}_{2}}{{\alpha }^{2}} + {{b}_{4}}{{\alpha }^{4}} + {{b}_{6}}{{\alpha }^{6}} + ... + {{b}_{{2n}}}{{a}^{{2n}}}.$При этом производная $\left( {{1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r}} \right)'$ также выражается в виде полинома:
(7)
$\left( {{1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-0em} r}} \right){\text{'}} = 2{{b}_{2}}\alpha + 4{{b}_{4}}{{\alpha }^{3}} + 6{{b}_{6}}{{\alpha }^{5}} + ... + 2n{{b}_{n}}{{a}^{{2n - 1}}},$где
(8)
${{b}_{0}} = \frac{1}{{{{r}_{{01}}}}},\,\,\,\,{{b}_{2}} = - \frac{1}{{4{{r}_{{01}}}d}}\left( {d - {{r}_{{01}}} + 2m{{\rho }_{{02}}}} \right).$Используя разложение функции отображения в ряд Тэйлора по степеням $\alpha $, нетрудно получить явные выражения для величины $m$. После подстановки (6), (7) в (1), считая ${{b}_{0}}$ и ${{b}_{2}}$ известными, получим следующее равенство:
(9)
$\begin{gathered} \sum\limits_{n = 2}^{2N} {{{b}_{{2n}}}} \left[ {{{\alpha }^{{2n - 1}}}\left[ {Q(\alpha )\alpha + 2n} \right]} \right] = \\ = - {{b}_{0}}Q(\alpha ) - \left[ {2\alpha + Q(\alpha ){{\alpha }^{2}}} \right]{{b}_{2}} - P(\alpha ), \\ \end{gathered} $которое должно выполняться для любого $\alpha $, т.е. для любой точки образующей зеркала. Выбирая число таких точек (узлов), равное количеству неизвестных коэффициентов полинома (n – 1), получим систему линейных уравнений для определения ${{b}_{4}},{{b}_{6}},...,{{b}_{{2n}}}.$
Ограничимся случаем N = 3 и, выбрав две узловые точки, получим систему двух уравнений с двумя неизвестными коэффициентами полинома 6-го порядка. Решение этой системы имеет вид
(10)
${{b}_{4}} = \frac{{{{C}_{1}}{{D}_{{22}}} - {{C}_{2}}{{D}_{{12}}}}}{{{{D}_{{11}}}{{D}_{{22}}} - {{D}_{{21}}}{{D}_{{12}}}}},\,\,\,\,{{b}_{6}} = \frac{{{{C}_{1}}{{D}_{{11}}} - {{C}_{2}}{{D}_{{21}}}}}{{{{D}_{{11}}}{{D}_{{12}}} - {{D}_{{22}}}{{D}_{{21}}}}},$где
(11)
$\begin{gathered} {{D}_{{11}}} = \alpha _{{01}}^{3}\left[ {{{\alpha }_{{01}}}Q({{\alpha }_{{01}}}) + 4} \right], \\ {{D}_{{21}}} = \alpha _{{02}}^{3}\left[ {{{\alpha }_{{02}}}Q({{\alpha }_{{02}}}) + 4} \right], \\ {{D}_{{22}}} = \alpha _{{02}}^{5}\left[ {{{\alpha }_{{02}}}Q({{\alpha }_{{02}}}) + 6} \right], \\ {{D}_{{12}}} = \alpha _{{01}}^{5}\left[ {{{\alpha }_{{01}}}Q({{\alpha }_{{01}}}) + 6} \right], \\ {{C}_{1}} = - {{b}_{0}}Q({{\alpha }_{{01}}}) - {{\alpha }_{{01}}}\left[ {{{\alpha }_{{01}}}Q({{\alpha }_{{01}}}) + 2} \right] - P({{\alpha }_{{01}}}), \\ {{C}_{2}} = - {{b}_{0}}Q({{\alpha }_{{02}}}) - {{\alpha }_{{02}}}\left[ {{{\alpha }_{{02}}}Q({{\alpha }_{{02}}}) + 2} \right] - P({{\alpha }_{{02}}}), \\ \end{gathered} $${{\alpha }_{{01}}}$ и ${{\alpha }_{{02}}}$ – узловые точки.
Анализ точности аппроксимации решения дифференциального уравнения (2) для образующей малого вспомогательного зеркала полиномом 6-го порядка с коэффициентами, определяемыми соотношениями (7), (8) и (10), (11), был проведен для трехзеркального апланатического телескопа, в котором использовали два вида главного зеркала: параболическое или сферическое.
Нетрудно показать, что для параболического зеркала:
(12)
$\begin{gathered} \Delta Y = - {{f}_{p}}\sin ({{\alpha }_{2}}),\,\,\,\,S = 2{{f}_{p}}{{\sin }^{2}}\frac{{{{\alpha }_{2}}}}{2}, \\ {{\alpha }_{2}} = 2arctg(m\sin {{\alpha }_{1}}),\,\,\,\,m = \frac{{{{f}_{1}}}}{{2{{f}_{p}}}}, \\ \end{gathered} $а для сферического зеркала:
(13)
$\Delta Y = - R\sin \frac{{{{\alpha }_{2}}}}{2}\left( {1 - 4\cos \frac{{{{\alpha }_{2}}}}{2}{{{\sin }}^{2}}\frac{{{{\alpha }_{2}}}}{4}} \right)$, $S = 4R{{\sin }^{2}}\frac{{{{\alpha }_{2}}}}{4}{{\cos }^{2}}\frac{{{{\alpha }_{2}}}}{2}$,где ${{\alpha }_{2}} = 2\arcsin (m\sin {{\alpha }_{1}}),$ $m = {{{{f}_{1}}} \mathord{\left/ {\vphantom {{{{f}_{1}}} R}} \right. \kern-0em} R},$ $R$ – радиус сферы.
Для примера были выбраны следующие значения параметров системы: фокальный радиус $f{}_{1}$ = = 1 м, расстояние между вспомогательными зеркалами d = 0.1 м, положение источника сферического фронта f = 0, угловой размер первого вспомогательного зеркала $2{{\alpha }_{m}}$ = 60°.
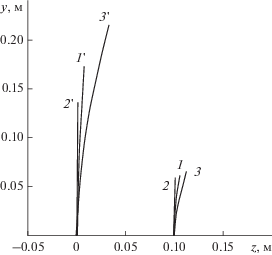
Точность аппроксимации решения для образующей вспомогательного зеркала полиномом и реализации закона отображения зависит от выбора узлов при заданной целевой функции. При минимизации ошибки закона отображения ${{\delta }_{m}}$ были получены значения ${{\alpha }_{{01}}} = 0.69{{\alpha }_{m}}$ и ${{\alpha }_{{02}}} = 0.97{{\alpha }_{m}}.$ Образующие вспомогательных зеркал, рассчитанные для этих случаев с помощью разложения (6), приведены на рис. 2. Фокальное расстояние параболического зеркала равно${{f}_{p}}$ = 0.7 м, радиусы сферического зеркала R = 1.4 и 1.6 м. Образующая второго вспомогательного зеркала при этом определялась из условия точного формирования заданного выходного фронта.
Рис. 2.
Образующие первого (кривые 1–3) и второго (1 '–3 ') вспомогательных зеркал трехзеркального апланатического телескопа с главным зеркалом: параболическим, ${{f}_{p}}$ = 0.7 (кривые 1, 1 ') и сферическим, R = 1.4 (2, 2 ') и 1.6 м (3, 3 ').
На рис. 3 изображены зависимости ошибки аппроксимации образующей вспомогательного зеркала полиномом шестого порядка с выбранными узловыми точками от нормированного угла. На рис. 4 приведены соответствующие зависимости ошибки реализации закона отображения δm = $ = \left[ {(\operatorname{tg} {{({{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} 2}} \right. \kern-0em} 2}))} \mathord{\left/ {\vphantom {{({{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} 2}} \right. \kern-0em} 2}))} {\sin ({{\alpha }_{1}})}}} \right. \kern-0em} {\sin ({{\alpha }_{1}})}} - m} \right]$ – для параболического главного зеркала, ${{\delta }_{m}} = \left[ {(\sin {{({{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} 2}} \right. \kern-0em} 2}))} \mathord{\left/ {\vphantom {{({{{{\alpha }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}} 2}} \right. \kern-0em} 2}))} {\sin ({{\alpha }_{1}})}}} \right. \kern-0em} {\sin ({{\alpha }_{1}})}} - m} \right]$ – для сферического.
Рис. 3.
Зависимости ошибки образующей первого вспомогательного зеркала от нормированного угла для параболического (1) и сферического главного зеркала с разными диаметрами (2, 3).
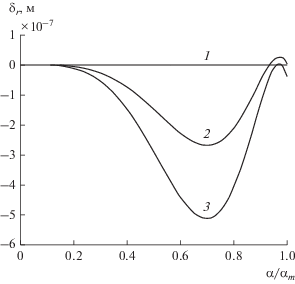
Рис. 4.
Зависимости ошибки закона отображения от нормированного угла для параболического (1) и сферического главного зеркала с разными диаметрами (2, 3).
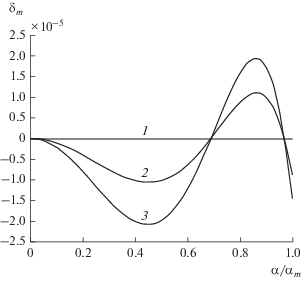
Как видно на рис. 3, 4, использование четырехчленного полинома позволяет обеспечить точность аппроксимации образующей малого вспомогательного зеркала не хуже 5 × 10–7 м и точность реализации закона отображения порядка 2 × 10–5.
Таким образом, полученные в работе формулы описывают решение задачи синтеза образующих трехзеркальной системы с произвольной формой образующей главного зеркала, реализующей заданный выходной фронт и, с заданной точностью, закон отображения. Форму образующей главного зеркала при этом можно выбирать из технологических соображений либо использовать как степень свободы для оптимизации трехзеркальной системы.
Список литературы
Михельсон Н.Н. Оптика астрономических телескопов и методы ее расчета. М.: Физматлит, 1995.
Бодров С.В., Батшев В.И. // Труды РНТОРЭС им. А.С. Попова. Сер: Акустооптические и радиолокационные методы измерений и обработки информации. Москва; Суздаль. 2015. Вып. 8. С. 252.
Венецкий А.С., Калошин В.А., Нгуен К.Т., Фролова Е.В. // Журн. радиоэлектроники. 2018. № 1. http://jre.cplire.ru/jre/jan18/4/text.pdf
Венецкий А.С. // Журн. радиоэлектроники. 2018. № 3. http://jre.cplire.ru/jre/mar18/13/text.pdf
Калошин В.А., Попов А.П. // РЭ. 1982. Т. 27. № 6. С. 1110.
Head A. // Proc. Phys. Soc. 1958. V. 71. № 4. P. 546.
Калошин В.А., Фролова Е.В. // РЭ. 2012. Т. 57. № 2. С. 52.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника