Радиотехника и электроника, 2019, T. 64, № 9, стр. 932-940
Предельные характеристики классического джозефсоновского детектора
В. В. Павловский 1, *, Ю. Я. Дивин 1, **
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая 11, стр. 7, Российская Федерация
* E-mail: pvv@cplire.ru
** E-mail: yyd@cplire.ru
Поступила в редакцию 26.12.2018
После доработки 25.02.2019
Принята к публикации 07.03.2019
Аннотация
Проведены аналитические и численные расчеты предельных характеристик детекторов электромагнитного излучения на основе джозефсоновских переходoв, которые описываются простой резистивной моделью и имеют джозефсоновскую энергию, сравнимую с энергией тепловых флуктуаций. Установлены режимы работы таких переходов в качестве классического детектора, использующего выпрямление переменного тока на статической нелинейной вольт-амперной характеристике. Проведено сравнение результатов численных и аналитических расчетов и показано, что анализ и оптимизацию классического режима детектирования можно проводить на основе выведенных аналитических выражений для основных предельных характеристик. Указано на возможность достижения предельной чувствительности до 2 × 10–15 Вт/Гц1/2, динамического диапазона по мощности 105…106, и спектрального диапазона до 1.4 ТГц, в температурном интервале (50…77) К при использовании новых джозефсоновских тонкопленочных переходов, состоящих из высокотемпературных сверхпроводников YBa2Cu3O7– x со взаимно наклоненными осями c.
ВВЕДЕНИЕ
Терагерцовый (ТГц) диапазон в спектре электромагнитного излучения расположен между СВЧ- и ИК-диапазонами и в сравнении с ними существенно менее насыщен эффективными генераторами и детекторами электромагнитного излучения. ТГц-технологии, инициированные ранее фундаментальными исследованиями в радиоастрономии и физике твердого тела, в настоящее время становятся все более востребованными в новых, весьма важных областях науки и практических применениях, таких как физика и техника высоких энергий, биология и медицина, информационные и коммуникационные технологии, обеспечение безопасности в общественных местах, глобальный контроль окружающей среды и сверхбыстрые вычислительные устройства [1]. Многие из этих перспективных применений связаны со регистрацией слабого ТГц-излучения в реальном времени при повышенных температурах фонового излучения и требуют ТГц-детекторов, обладающих одновременно высокими быстродействием, чувствительностью и динамическим диапазоном по мощности.
Большинство разработок ТГц-детекторов проводится на основе полупроводниковых устройств из соседних СВЧ- и ИК-диапазонов, например, таких как диоды Шоттки или фотодетекторы с квантовыми ямами [2]. Однако, в ТГц-диапазоне эффективность традиционных электронных СВЧ- и фотонных ИК-устройств падает, поскольку либо период ТГц-колебаний становится меньше характерных времен носителей заряда, либо энергия кванта фотона в ТГц-диапазоне оказывается меньше, чем тепловая энергия при комнатной и даже азотной температурах [2]. Продвижение полупроводниковых электронных и фотонных детекторов в ТГц-диапазон часто сопровождается их охлаждением до весьма низких температур. Последнее обстоятельство позволяет равноправно рассматривать применимость в ТГц-диапазоне и сверхпроводниковых приемных устройств.
Квантовая природа когерентного сверхпроводящего состояния дает уникальную возможность реализовывать устройства с функциональностью и параметрами, недостижимыми в традиционной полупроводниковой электронике [3]. Например, детекторы, использующие сильную нелинейность квазичастичного тока в переходах сверхпроводник–изолятор–сверхпроводник (СИС), имеют при частотах, меньших частот 2Δ/h (2Δ – энергетическая щель сверхпроводника), предельную чувствительность, близкую к квантовой [4, 5]. Другим примером являются джозефсоновские переходы, у которых имеется сильная динамическая нелинейность сверхпроводящего туннельного тока [6]. Традиционно для целей детектирования используется режим, когда джозефсоновские энергии Ej = hIc/4πe (Ic – критический ток перехода, h – постоянная Планка; e – заряд электрона) гораздо больше тепловых энергий kT (k – постоянная Больцмана, T – температура). В этом случае спектр колебаний на переходе состоит из узких линий на основной частоте fj = 2eV/h и ее гармониках, где V – среднее напряжение на переходе.
При воздействии слабого электромагнитного монохроматического излучения происходит затягивание джозефсоновской частоты fj к частоте внешнего излучения f1 и соответствующее изменение ΔV среднего напряжения на переходе. Это изменение напряжения ΔV(V) пропорционально мощности внешнего излучения и имеет нечетно-резонансную форму около V1 = hf1/2e [7], что является основой для частотно-селективного детектирования и гильберт-спектроскопии [8].
Менее изучено детектирование с помощью джозефсоновских переходов, у которых джозефсоновские энергии Ej сравнимы с тепловыми энергиями kT. В таком случае спектр колебаний уже сплошной, не спадающий до частот около характерной частоты ωc = 4πeIcRn/h (Rn – сопротивление перехода в нормальном состоянии), а вольт-амперная характеристика (ВАХ) перехода все еще имеет нелинейный вид [6, с. 78, 82]. Из качественных соображений следует, что на такой нелинейности возможно классическое выпрямление токов, наведенных излучением при достаточно низких частотах ω $ \ll $ ωc. Для джозефсоновских переходов, изготовленных из традиционных низкотемпературных сверхпроводников, такие детекторные отклики уже наблюдались при частотах, меньших 150 [9] или 290 ГГц [10], что масштабировалось с величинами характерных напряжений IcRn у использовавшихся переходов. При этом в условиях ограничения чувствительности тепловым фоном были измерены величины NEP порядка 10–14 Вт/Гц1/2 [11].
Значительного увеличения характерных джозефсоновских частот и продвижения их в терагерцовый диапазон можно достичь при использовании высокотемпературных сверхпроводников (ВТСП) для таких переходов. К настоящему времени, на основе эпитаксиальных пленок из ВТСП YBa2Cu3O7 – x с взаимнонаклоненными осями с уже получены бикристаллические джозефсоновские переходы с величинами IcRn(5 К) = = 7 ± 1 мВ в диапазоне сопротивлений Rn переходов от десятых долей ома до 350 Ом [12]. Экспериментально показано, что для переходов при температуре 50 К возможна реализация классического детектора с широкополосным частотным диапазоном до 1 ТГц [13]. Предварительные оценки предельной чувствительности NEP дали величины не хуже 10–14 Вт/Гц1/2 при Т = 50 К [13], что значительно лучше NEP-детекторов на основе традиционных неохлаждаемых диодов Шоттки [14] или болометров из InSb, охлаждаемых жидким гелием [15].
Оптимизация режимов работы классического детектора на основе джозефсоновского перехода осложняется из-за того, что отсутствуют аналитические выражения для всех предельных характеристик детектора в этом режиме. Имеются лишь численные расчеты отклика ΔV(V) джозефсоновских детекторов на монохроматическое излучение с частотой ω/ωc = 3 для нескольких величин γ, от 0.1 до 10, и частотная зависимость ΔV(ω) для γ = 0.4 и нескольких напряжений смещения [6, с. 185]. Также получены оценки величин NEP [16, с. 347] при промежуточных частотах, откуда следует квадратичное ухудшение предельной чувствительности при повышении частоты. Последнее обстоятельство указывает на то, что случай малых частот, где возможно классическое детектирование и, соответственно, не зависящая от частоты предельная чувствительность, ранее отдельно не рассматривался. Также отсутствуют расчеты таких характеристик, как динамический диапазон по мощности и частотный диапазон.
В более поздней работе [17] был исследован обширный класс детекторов на основе сверхпроводящих переходов, использующих различные механизмы детектирования. При этом для джозефсоновского квадратичного видеодетектора был проанализирован только режим самоселекции в приближении узкополосного входного сигнала. А в качестве широкополосного квадратичного видеодетектора рассматривался лишь туннельный переход “сверхпроводник–изолятор–сверхпроводник”, работающий на квазичастичной нелинейности. Широкополосный квадратичный видеодетектор на основе джозефсоновского перехода остался за рамками работы [17].
Цель данной работы – провести аналитический расчет и оптимизацию основных предельных характеристик классического джозефсоновского детектора, сравнить полученные результаты с результатами численных расчетов. Такой подход позволяет создать основу для оптимизации режимов джозефсоновского детектора как с наилучшей чувствительностью, так и максимальным динамическим диапазоном, а также режимов с максимальной полосой классического детектирования.
1. ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДЖОЗЕФСОНОВСКОГО ПЕРЕХОДА ПРИ γ ≥ 1
Динамика джозефсоновского перехода в рамках резистивной модели при доминировании тепловых флуктуаций тока If(t) описывается уравнением Смолуховского (см. [6, с. 76]):
(1)
$\omega _{c}^{{ - 1}}\frac{{\partial \sigma }}{{\partial t}} + \frac{\partial }{{\partial \varphi }}\left[ {f\left( \varphi \right)\sigma } \right] = \gamma \frac{{{{\partial }^{2}}\sigma }}{{\partial {{\varphi }^{2}}}},$Ранее для нахождения основных характеристик джозефсоновсокого перехода при произвольных величинах γ были предложены решения стохастических уравнений (1), как при отсутствии внешнего излучения, так и при его наличии, в виде рядов Фурье, а также получены цепочки уравнений для коэффициентов рядов Фурье для произвольных величин γ [6]. Оказалось, что для искомого случая с γ ≥ 1 можно существенно упростить решения цепочек уравнений и ограничиться первыми уравнениями в цепочках.
Вольт-амперные характеристики V(I) джозефсоновского перехода для случая γ ≥ 1 в безразмерных переменных $v$ = V/IcRn, i = I/Ic описываются следующим выражением [6, с. 79]:
(2)
$v\left( i \right) = i + {\text{Re}}{{\sigma }_{{1,0}}} = i - \frac{i}{{2\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}},$(3)
$\begin{gathered} 2(i - jk\gamma ){{\sigma }_{{k,0}}} + {{\sigma }_{{k - 1,0}}} + {{\sigma }_{{k + 1,0}}} = 0,~ \\ {{\sigma }_{{0,0}}} = 1,\,\,\,\,k > 1,~ \\ \end{gathered} $а σ20 полагается равным нулю. Первая dV/dI и вторая d2V/dI2 производные были определены по формулам
(4)
$\begin{gathered} \frac{1}{{{{R}_{n}}}}\frac{{{\text{d}}V}}{{{\text{d}}I}} = \frac{{{\text{d}}v}}{{{\text{d}}i}} = 1 + \frac{{{{i}^{2}} - {{\gamma }^{2}}}}{{2{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{2}}}}; \\ \frac{{{{I}_{c}}}}{{{{R}_{n}}}}{\kern 1pt} {\kern 1pt} ~\frac{{{{{\text{d}}}^{2}}V}}{{{\text{d}}{{I}^{2}}}} = \frac{{{{{\text{d}}}^{2}}v}}{{{\text{d}}{{i}^{2}}}} = ~\frac{{3i{{\gamma }^{2}} - {{i}^{3}}}}{{{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{3}}}}, \\ \end{gathered} $и имеют максимумы, равные 1 + 1/16γ2 при i1m = = 1.73γ и 0.73/γ3 при i2m = 0.41γ.
Величина спектральной плотности SV(f) флуктуаций напряжения в пределе низких частот f → 0 рассчитывается из уравнений, приведенных в [6, с. 81] и равна
(5)
$\begin{gathered} \frac{{{{S}_{V}}\left( {f = 0} \right)}}{{2kT{{R}_{n}}}} = \frac{{{{s}_{v}}\left( {f = 0} \right)}}{{2\gamma }} = \\ = 1 + 2{\text{Re}}\left[ {{{c}_{1}}\left( 0 \right)} \right] = 1 + \frac{{3{{i}^{2}} - {{\gamma }^{2}}}}{{2{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{2}}}}, \\ \end{gathered} $где с1(0) находится из первого уравнения цепочки
(6)
$\begin{gathered} 2[i - {\text{ }}jk\gamma ]{{с}_{k}} + {{с}_{k}}_{{ - 1}} + {{с}_{k}}_{{ + 1}} + (1 - {{ji} \mathord{\left/ {\vphantom {{ji} {k\gamma }}} \right. \kern-0em} {k\gamma }}){{\sigma }_{k}}_{{,0}} = 0, \\ k > 0,\,\,\,\,{{с}_{0}}~\, = 0~, \\ \end{gathered} $а с2(0) считается равной нулю.
Основные электрические характеристики $v$, dv/di, d2v/di2 и sv(0) джозефсоновского перехода как функции тока i были получены согласно приближенным формулам (2), (4) и (5), а также было проведено их сравнение с аналогичными характеристиками, полученными численным счетом из полных цепочек уравнений (3) и (6) для одинаковых величин γ ≥ 1. При этом наибольшие расхождения оказались у максимальных величин d2v/di2 (35%), и в величинах токов (23%), где этот максимум наблюдается, при γ = 1. При увеличении γ эти расхождения резко уменьшались. Обнаружено, что для γ порядка 1 и γ ≥ 1 расхождения у характеристик, вычисленных по приближенным формулам и по полным цепочкам уравнений, можно существенно снизить до единиц процентов, если в формулах (2), (4) и (5) использовать эффективное γe, которое хорошо описывается выражением
(7)
${{\gamma }_{e}} = \gamma + {{0.18} \mathord{\left/ {\vphantom {{0.18} \gamma }} \right. \kern-0em} \gamma }.$Результаты расчетов основных электрических характеристик переходов v; dv/di; d2v/di2; sv(0)/2γ (кривые 1, 4, 5, 6), выполненных численным образом по полным цепочкам уравнений (3) и (6) при γ =1, в сравнении с соответствующими характеристиками, выполненным по приближенным формулам (2), (4), (5) с эффективным γe = 1.18 из (7), приведены на рис. 1. ВАХ из (3) при γ = 1 занимает промежуточное место между сильно нелинейной ВАХ при γ = 0, состоящей из сверхпроводящего участка с v = 0 при i ≤ 1 и резистивного участка с v = (i2 – 1)1/2 при i ≥ 1, и ВАХ при γ → ∞, описываемой законом Ома. ВАХ из (2) при γ = 1.18 практически совпадает с ВАХ из (3) при γ = 1. Токовые зависимости первой dv/di и второй d2v/di2 производных, которые вычислены из (2) при γe = = 1.18 и из (3) при γ = 1, весьма близки другу к другу. В частности, максимальная величина d2v/di2 и положение максимума i2m второй производной, полученной из точного расчета по (3) при γ = 1, отличаются лишь на 2% и 4% соответственно от аналогичных величин, полученных из приближенной формулы (2) при γe = 1.18. Аналогичные расчеты, проведенные для других величин γ в диапазоне 0.5…3, показали, что отличия в максимальных величинах d2v/di2 и положениях максимума i2m второй производной между точным и приближенным расчетами составляют около 10% при γ = 0.7 и уменьшаются до 1% при повышении γ до 3.
Рис. 1.
Результаты полного численного расчета цепочки уравнений (3) и (5) при γ = 1 (сплошные кривые) и расчета по приближенным аналитическим формулам (2), (4), (5) при γe = 1.18 (штриховые) следующих величин: среднее напряжение v(i) (кривые 1, 1 '), первые dv/di (кривые 4, 4 ') и вторая d2v/di2 (кривые 5, 5 ') производные, а также спектральная плотность флуктуаций напряжения sv(0)/2γ (кривые 6, 6 ') как функции тока i = I/Ic через джозефоновский переход. Для сравнения с кривой 1 приведены ВАХ при γ → 0 (кривая 2, точки) и ВАХ при γ → ∞ (3, точки).
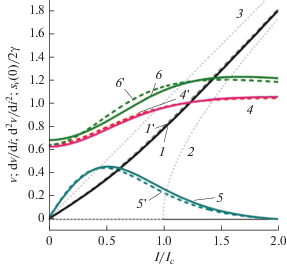
Спектральная плотность флуктуаций напряжения sv(0)/2γ (см. рис. 1, кривые 6, 6 ') как функция тока i изменяется незначительно: сначала растет, начиная от величин, меньших 1, а затем после достижения максимума, большего 1, падает до 1. Такая зависимость с sv(0)/2γ >1 при промежуточных смещениях обусловлена, по-видимому, преобразованием шума к нулевым частотам из-за его взаимодействия с широкополосной джозефсоновской генерацией, в данном случае при γ ≈ 1. Сплошные кривые, рассчитанные из (6) при γ = 1, с точностью до единиц процентов согласуются с таковыми, рассчитанными из (5) при γe = 1.18. Полученное описание простыми аналитическими выражениями электрических характеристик для джозефсоновского детектора значительно упрощает выяснение режимов его работы и оптимизацию в режиме классического детектора.
2. РАСЧЕТ ХАРАКТЕРИСТИК ДЖОЗЕФСОНОВСКОГО ДЕТЕКТОРА
Линейный отклик джозефсоновского перехода на воздействие переменных токов, наведенных внешним излучением, т.е. импеданс перехода Z(ω), при γ ≥1 можно найти, используя следующее уравнение из [6, ф-ла (10.19)]:
где коэффициенты $c_{1}^{ \pm }$ определяются из первых уравнений в цепочке уравнений
(9)
$\begin{gathered} 2\left[ {\left( {i \pm \frac{\omega }{{{{\omega }_{c}}}}} \right) - jk\gamma } \right]c_{k}^{ \pm } + c_{{k - 1}}^{ \pm } + c_{{k + 1}}^{ \pm } + {{\sigma }_{{k,0}}} = 0 \\ {\text{при}}\,\,\,\,~k \ne 0,\,\,\,\,c_{0}^{ \pm } = 0, \\ \end{gathered} $а $c_{2}^{ \pm }$ полагаются равными 0. Тогда для ReZ(ω) получаем
(10)
$\begin{gathered} \frac{{{\text{Re}}Z\left( \omega \right)}}{{{{R}_{n}}}} = 1 + \left[ {\frac{1}{{2\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}} \right] \times \\ \times \,\,\left\{ {\frac{{{{i}^{2}}\left( {{{i}^{2}} - {{{\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)}}^{2}}} \right) - {{\gamma }^{2}}({{{\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)}}^{2}} + {{\gamma }^{2}})}}{{\left[ {{{{\left( {i + \left( {{\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)} \right)}}^{2}} + {{\gamma }^{2}}} \right]\left[ {{{{\left( {i - \left( {{\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)} \right)}}^{2}} + {{\gamma }^{2}}} \right]}}} \right\}. \\ \end{gathered} $При малых частотах ω/ωc$ \ll $ i и γ ≥ 1 имеем
(11)
$\frac{{{\text{Re}}Z\left( \omega \right)}}{{{{R}_{n}}}} \to \,\,~1 + \frac{{{{i}^{2}} - {{\gamma }^{2}}}}{{2{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{2}}}} = \frac{{dv}}{{di}}~,$т.е. действительная часть ReZ(ω) импеданса становится равной дифференциальному сопротивлению перехода, которое даже при γ = 1 близко к Rn. При увеличении частоты ω/ωc > i и γ значение ReZ(ω) в (10) быстро стремится к сопротивлению Rn.
Детекторные отклики ΔV джозефсоновского перехода на наведенные переменные токи Iω рассматриваются в два этапа. Сначала рассматривается приближение малого сигнала iω$ \ll $ Iω/Ic и вычисляются квадратичные отклики δv =ΔV/IcRn на малый сигнал iω, как в [6]. Затем из полного уравнения (1) вычисляются отклики δv на сигнал произвольной величины. Коэффициент пропорциональности ρV в зависимости отклика ΔV джозефсоновского перехода от квадрата Iω рассчитывается из уравнения
(12)
${{\rho }_{V}} = \frac{{\Delta V}}{{I_{\omega }^{2}}} = \left( {\frac{{{{R}_{n}}}}{{{{I}_{c}}}}} \right)\frac{{\delta v}}{{i_{\omega }^{2}}} = \left( {\frac{{{{R}_{n}}}}{{{{I}_{c}}}}} \right){\text{Re}}{{d}_{1}},$где коэффициент d1 для нашего случая γ ≥ 1 определяется из первого уравнения в цепочке уравнений из работы [6, ф-ла (10.63)]:
(13)
$2\left( {i - jk\gamma } \right){{d}_{k}} + {{d}_{{k - 1}}} + {{d}_{{k + 1}}} + c_{k}^{ + } + c_{k}^{ - } = 0,\,\,\,~{{d}_{0}} = 0,~$причем коэффициенты $c_{1}^{ \pm }$ находятся из цепочек уравнений (9), а d2 полагается равным нулю. В результате имеем выражение
(14)
$\begin{gathered} \frac{{\delta v}}{{i_{\omega }^{2}}} = \left( {\frac{1}{4}} \right)\left[ {\frac{{i\left( {3{{\gamma }^{2}} - {{i}^{2}}} \right)}}{{{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{3}}}}} \right] \times \\ \times \,\,\left\{ {\frac{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)\left( {{{i}^{2}} + {{{\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)}}^{2}} + {{\gamma }^{2}}} \right)}}{{\left( {{{{\left( {i + {\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)}}^{2}} + {{\gamma }^{2}}} \right)\left( {{{{\left( {i - {\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)}}^{2}} + {{\gamma }^{2}}} \right)}}} \right\}, \\ \end{gathered} $где сомножитель в квадратных скобках есть не что иное, как вторая производная статической ВАХ, что указывает на близость отклика к таковому из теории классического выпрямления (см., например, [18].) При ω/ωc$ \ll $ i квадратичный отклик δv действительно стремится к классическому значению δv0, а именно
и достигает максимума в 0.18/γ3 при токе i2m = = 0.41γ.
Частотная зависимость отклика δv определяется сомножителем в фигурных скобках (14), который дает плавное снижение в два раза при частоте ω0
(16)
${{\left( {{{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} {{{\omega }_{c}}}}} \right. \kern-0em} {{{\omega }_{c}}}}} \right)}^{2}} = 2{{i}^{2}} + {{\left[ {4{{i}^{4}} + {{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$и квадратичное спадание при дальнейшем увеличении частоты. Таким образом, из выражения (16) для эффективной частотной полосы ω0 классического детектора следует ее прямая пропорциональность характерной джозефсоновской частоте ωc и зависимость от тока смещения i на переходе. Например, для максимального отклика δv при i2m = 0.41γ полоса ω0/ωc джозефсоновского классического детектора достигает 1.23γ. Из (14), (16) также следует, что при повышении тока i > 0.41γ может происходить увеличение полосы ω0/ωc. Так, например, при i = 1 и γ = 1 из (16) следует, что полоса ω0/ωc повышается до 2.2, причем d2v/di2 понижается менее чем в два раза относительно максимума (см. рис. 1).
Таким образом, в пределе малых частот ω < ω0, джозефсоновский переход при γ ≈ 1 и γ ≥ 1 ведет себя как классический квадратичный детектор переменных сигналов, и можно получить основные предельные характеристики исходя из подходов, развитых ранее для других детекторов с нелинейной ВАХ (см., например, [18]). Из (10) и (15) следует, что вольт-ваттная чувствительность ΔV/P0= 2ρV/ReZ(ω) при ω/ωc$ \ll $ i будет равна
(17)
$\frac{{\Delta V}}{{{{P}_{0}}}} = \frac{{2{{\rho }_{V}}}}{{{{R}_{n}}{{dv} \mathord{\left/ {\vphantom {{dv} {di}}} \right. \kern-0em} {di}}}} = \frac{1}{{2{{I}_{c}}}}\left[ {\frac{{{{{{d}^{2}}v} \mathord{\left/ {\vphantom {{{{d}^{2}}v} {d{{i}^{2}}}}} \right. \kern-0em} {d{{i}^{2}}}}}}{{{{dv} \mathord{\left/ {\vphantom {{dv} {di}}} \right. \kern-0em} {di}}}}} \right] = \frac{{{\text{resp}}}}{{{{I}_{c}}}}.$В физике детекторов в качестве Pmin принята мощность, эквивалентная шуму, NEP, которая определяется как входная мощность, необходимая для создания отклика ΔV0, равного среднеквадратичному значению шумового напряжения ${{\left\langle {V_{n}^{2}} \right\rangle }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = S_{V}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}(f = 0){{B}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ на детекторе в частотной полосе B = 1 Гц, т.е.
(18)
${\text{NEP}} = \frac{{{{{\left\langle {{{S}_{V}}\left( {f = 0} \right)} \right\rangle }}^{{\frac{1}{2}}}}}}{{{{\Delta V} \mathord{\left/ {\vphantom {{\Delta V} P}} \right. \kern-0em} P}}} = {\text{nep}}{{\left( {\frac{{hI_{c}^{3}{{R}_{n}}}}{{4\pi e}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$где из (5) и (17) следует
(19)
${\text{nep}} = \frac{{s_{v}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\left( {f = 0} \right)}}{{{\text{resp}}}} = \frac{{{{{\left( {2\gamma } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{{\left[ {2{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{2}} + 3{{i}^{2}} - {{\gamma }^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left[ {2{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{2}} + {{i}^{2}} - {{\gamma }^{2}}} \right]}}{{i\left( {3{{\gamma }^{2}} - {{i}^{2}}} \right)}}.$Зависимости вольт-ваттной (resp) и предельной (nep) чувствительностей классического джозефсоновского детектора от тока i представлены на рис. 2а как результат расчета по приближенным аналитическим формулам (2), (4), (5), (17), (19) при γe = γ + 0.18/γ =1.18 и по полным цепочкам уравнений (3), (6), (9), (13) при γ = 1. Из рис. 2а следует, что предельные характеристики, вычисленные по приближенным аналитическим формулам, хорошо согласуются c результатами точного расчета при γ = 1. При γ, больших 1, согласие между приближенными и точными результатами только улучшалось, а при γ < 1 ошибка в приближенных результатах не превосходила 10% до γ = 0.7.
Рис. 2.
Результаты вычислений (а) на основе полных цепочек уравнений (3), (6), (9), (13) при γ = 1 и f/fc = 0.01 (сплошные) и расчет по приближенным аналитическим формулам (2), (4), (5), (17), (19) при γe = γ +0.18/γ = 1.18 (штриховые) следующих величин: вторая d2v/di2 = (d2V/dI2)(Ic/Rn) производная ВАХ (кривые 1, 1 '), вольт-ваттная чувствительность resp = IcΔV/P (кривые 2, 2 '), предельная чувствительность nep = NEP/($hI_{c}^{3}{{{{R}_{n}}} \mathord{\left/ {\vphantom {{{{R}_{n}}} {4\pi e}}} \right. \kern-0em} {4\pi e}}$)1/2 (кривые 3, 3 ') как функции тока i = I/Ic через переход при тепловых флуктуациях с γ = 1, а также двумерное распределение (б) величин предельной чувствительности nep = NEP/($hI_{c}^{3}{{{{R}_{n}}} \mathord{\left/ {\vphantom {{{{R}_{n}}} {4\pi e}}} \right. \kern-0em} {4\pi e}}$)1/2 в координатах – частота f/fc наведенных токов и постоянный ток i = I/Ic – для джозефсоновского перехода с γ = 1. Величины nep представлены ступенчатыми градациями серого (шкала справа от рисунка), различающимися в последовательности 1 : 2 : 5 : 10 : … Числами на рисунке представлены соответствующие граничные значения nep.
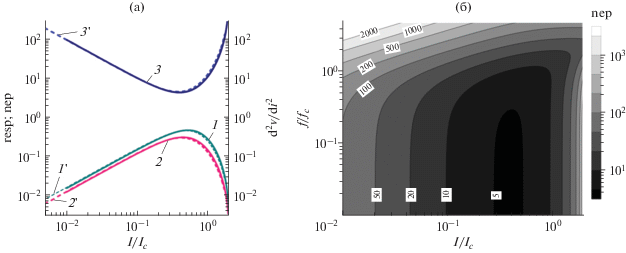
При сравнении с зависимостью второй d2v/di2 производной ВАХ от тока i (кривая 1) видно, что максимум resp (кривая 2) и минимум nep (кривая 3) достигаются при более низких токах, чем максимум d2v/di2. Величины nep = NEP/($hI_{c}^{3}{{{{R}_{n}}} \mathord{\left/ {\vphantom {{{{R}_{n}}} {4\pi e}}} \right. \kern-0em} {4\pi e}}$)1/2 достигают 4.2 при токе 0.4, а в широкой полосе токов от 0.12 до 0.9 не превосходят эту минимальную величину более чем в два раза. Вольт-ваттная чувствительность resp = IcΔV/P при токе 0.44 имеет максимум, равный 0.3, и не падает более чем в два раза в диапазоне токов 0.13…0.95.
Полный анализ детекторных характеристик джозефсоновского перехода очень удобно проводить по их двумерным распределениям в координатах частота f/fc = ω0/ωc и ток i = I/Ic через переход. На рис. 2б представлено такое распределение для величин nep =NEP/($hI_{c}^{3}{{{{R}_{n}}} \mathord{\left/ {\vphantom {{{{R}_{n}}} {4\pi e}}} \right. \kern-0em} {4\pi e}}$)1/2, полученное с помощью точного численного расчета по полным цепочкам уравнений (6), (9), (13) при γ = 1. Сечение распределения на рис. 2б при малой частоте 0.01 фактически является представлением кривой 3 из рис. 2а. И такое представление nep с минимумом при i = 0.4 cохраняется при увеличении частоты до f/fc ≅ 0.2, после чего происходит плавное ухудшение nep и смещение минимума в область больших токов i. При токе i = 0.4 минимальный nep имеет величину около 5 и не увеличивается более чем в два раза при повышении частоты дo f/fc ≅ 1, что согласуется с результатами приближенного расчета частотной полосы (16) при использовании той же величины γ = 1. Из рис. 2б также следует, что если взять допустимую величину nep, равную 10, то при постоянном токе 1 можно достигнуть и большей частотной полосы f/fc ≅ 2 даже для того же перехода с γ = 1.
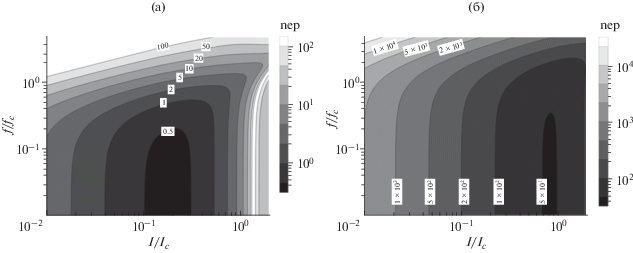
Изменением частотной полосы можно также управлять при использовании других величин γ, но при этом происходит резкое изменение величин nep. На рис. 3 приведены два двумерных распределения величин предельной чувствительности nep = NEP/($hI_{c}^{3}{{{{R}_{n}}} \mathord{\left/ {\vphantom {{{{R}_{n}}} {4\pi e}}} \right. \kern-0em} {4\pi e}}$)1/2 в координатах частота f/fc наведенных токов и постоянный ток i = I/Ic для джозефсоновских переходов с γ = 0.5 и 2.0. Минимальные величины nep наблюдаются при низких частотах и при токах i ≅ 0.4γ. При γ = 0.5 величины минимальных nep ≅ 0.5 почти на порядок меньше (см. рис. 3а), чем величины минимальных nep у перехода с γ = 1 (см. рис. 2б). Однако это улучшение минимальной предельной чувствительности при уменьшении γ до 0.5 сопровождается уменьшением частотного диапазона f/fc классического детектора почти до 0.5. Вместе с тем увеличение γ до 2 приводит к ухудшению минимальных nep до 50, и при этом полоса f/fc увеличивается до 2 (рис. 3б). Здесь, так же как и в случае перехода с γ = 1, увеличивая ток i > 0.4γ, можно увеличивать полосу детектора почти вдвое (при i ≈ γ) при ухудшении вдвое же величин nep.
Рис. 3.
Двумерные распределения величин предельной чувствительности nep =NEP/($hI_{c}^{3}{{{{R}_{n}}} \mathord{\left/ {\vphantom {{{{R}_{n}}} {4\pi e}}} \right. \kern-0em} {4\pi e}}$)1/2 в координатах – частота f/fc наведенных токов и постоянный ток i = I/Ic – для джозефсоновских переходов с γ = 0.5 (а) и 2.0 (б). Величины nep представлены ступенчатыми градациями серого (шкала справа от рисунка), различающимися в последовательности 1 : 2 : 5 : 10 : … . Числами на рисунке представлены соответствующие граничные значения nep.
Весьма важным является вопрос о динамическом диапазоне по мощности сигнала у классического джозефсоновского детектора. Для традиционных квадратичных детекторов с достаточно слабыми нелинейными электрическими характеристиками в [18] вычисляются основные детекторные характеристики с учетом высших степеней по амплитуде наведенного тока Iω, что позволяет находить малые отклонения от квадратичного отклика и приписывать к заданным отклонениям величину максимально допустимой мощности сигнала. Оказалось, что такой подход в случае сильных нелинейностей электрических характеристик у джозефсоновских переходов в ряде случаев приводит к вычислению максимальных откликов, превосходящих характерные напряжения IcRn. Поэтому в нашем случае численным образом находили решение полного уравнения из [6, ф-ла (10.17)], справедливого для произвольных величин наведенных токов, и определяли величины отклика δv = ΔV/IcRn как функции наведенных токов iω= Iω/Ic с малой частотой ω/ωc$ \ll $ 1 (рис. 4). Отклики δv для каждой величины γ были рассчитаны при токе i2m, при котором вторая производная d2v/di2 имела максимальную величину.
Рис. 4.
Зависимость нормированного отклика δv = = ΔV/IcRn от амплитуды наведенных токов iω для джозефсоновских переходов с величинами γ = 0.01 (1), 0.1 (2), 0.4 (3), 1.0 (4, 4 ', 4 "), 2.0 (5, 5 ', 5 "): сплошные кривые (1–5) – результат решения полного уравнения (1) для токов i2m, соответствующих максимумам вторых производных d2v/di2; штриховые прямые (4 ', 5') – отклики δv = (${{i_{\omega }^{2}} \mathord{\left/ {\vphantom {{i_{\omega }^{2}} 4}} \right. \kern-0em} 4}$)d2v/di2 при токах i2m; пунктирные (4 ", 5 ") – максимальные отклики δvm = i – v, вычисленные из приближенной аналитической формулы (2), (4) при γe = γ +0.18/γ.
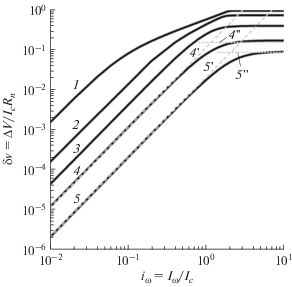
Оказалось, что при всех величинах γ отклики δv при малых iω пропорциональны квадрату наведенного тока iω, а при iω ≥ 1 выходят на насыщение. При малых γ ≤ 0.1 на зависимостях δv (iω) имеется еще и промежуточный участок – от квадратичной зависимости к насыщению с протяженностью, увеличивающейся при понижении γ (сплошные кривые 1 и 2). С повышением γ ≥ 0.4 этот промежуточный участок сужается и наблюдается достаточно локализованный при iω ≈ 1 переход квадратичной зависимости к насыщению (сплошные кривые 3–5).
Полученные зависимости δv(iω) при γ ≥ 1 (сплошные кривые 4 и 5) в области квадратичного отклика сопоставлены с аналогичными зависимостями δv(iω) = (${{i_{\omega }^{2}} \mathord{\left/ {\vphantom {{i_{\omega }^{2}} 4}} \right. \kern-0em} 4}$)d2v/di2, вычисленными из приближенных аналитических формул (2), (4) и (15) (штриховые прямые 4 ' и 5 '). При этом в аналитических формулах для d2v/di2 (4) использовалось эффективное значение γe = γ + 0.18/γ. Как следует из сопоставления, в широком интервале наведенных токов iω < 1 зависимоcти δv(iω) = = (${{i_{\omega }^{2}} \mathord{\left/ {\vphantom {{i_{\omega }^{2}} 4}} \right. \kern-0em} 4}$)d2v/di2 (4 ' и 5 '), полученные из аналитических формул (4), с высокой точностью согласуются с результатами точного расчета (4 и 5).
Прямые 4 " и 5 " представляют собой максимальные отклики δvs = i – v(i), вычисленные согласно (2) при i = i2m для γe = γ + 0.18/γ при значениях γ, равных 1 и 2 соответственно. Из рис. 4 видно, что эти прямые для γ = 1 и 2 хорошо описывают насыщение откликов δv(iω) (кривые 4 и 5), полученных точным расчетом, при iω$ \gg $ 1. Таким образом, насыщение откликов δv(iω) джозефсоновского детектора при больших iω обусловлено разницей постоянных напряжений на переходе в нормальном (v = i) и сверхпроводящем (v = v(i)) состояниях. Из (2) и (4) следует, что при токе i2m = 0.41γ, при котором вторая производная имеет максимум, отклик равен δvs = 0.175/γ. Максимальная величина δvs = 0.25/γ достигается при i = γ.
Можно также определить величину наведенного тока iωс, при котором наступает кроссовер между квадратичной зависимостью отклика и его насыщением, из равенства δv = (${{i_{\omega }^{4}} \mathord{\left/ {\vphantom {{i_{\omega }^{4}} 4}} \right. \kern-0em} 4}$)d2v/di2= δvs, что при i = i2m = 0.41γ дает iωс= 0.98γ. Как видно из рис. 4, положение кроссовера iωс ≈ γ, полученное оценкой из приближенных формул для отклика (кривые 4 ', 5 ' и 4 ", 5 " ) хорошо согласуется с положениями кроссовера, полученными из точных расчетов (кривые 4, 5), для γ = 1 и 2 соответственно, если в оценках используется эффективная величина γe = γ + 0.18/γ. Для кривых 1 и 2, полученных при γ, меньших 0.4, положения кроссовера уже существенно выше, чем iωс ≈ γ из приближенных формул.
Используя выражения для отклика в режиме насыщения, δVs = IcRni/2(i2 + γ2), и шумового ограничения для отклика снизу,
получим для динамического диапазона D = δVs/δVmin джозефсоновского детектора по сигналу (а также и по мощности наведенных токов) следующее выражение:
(20)
$D = {{\left( {\frac{\pi }{{2\gamma }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{i}{{{{{\left[ {2{{{\left( {{{i}^{2}} + {{\gamma }^{2}}} \right)}}^{2}} + \left( {3{{i}^{2}} - {{\gamma }^{2}}} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\frac{{f_{c}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}{{{{B}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$Таким образом, при i2m = 0.41γ мы получим D ≅ ≅ $0.3{{f_{c}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \mathord{\left/ {\vphantom {{f_{c}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} {{{\gamma }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{B}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{\gamma }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{B}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$ А при токах i ≅ γ можно получить и большую величину динамического диапазона D ≅ $0.45{{f_{c}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \mathord{\left/ {\vphantom {{f_{c}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} {{{\gamma }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{B}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{\gamma }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{B}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$
3. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Джозефсоновский переход, описываемый простой резистивной моделью, при джозефсоновских энергиях, сравнимых с энергией тепловых флуктуаций, может служить основой для создания классического детектора электромагнитного излучения. Используя результаты, полученные в разделах 2 и 3, оценим возможные предельные детекторные характеристики для переходов, недавно реализованных на основе эпитаксиальных пленок из высокотемпературного сверхпроводника YBa2Cu3O7– x [12]. При оценках будут использоваться следующие достигнутые параметры переходов: средние характерные напряжения IcRn (50 K) = 2.5 мВ и IcRn (77 K) = 1 мВ. Для того чтобы отношения γ = = 4πekT/hIc у этих переходов были равны заданной величине при температуре T, необходимо, чтобы сопротивление Rn = IcRn (T)/(4πekT/hγ). Оценки основных параметров классического детектора были проведены при токах через переходы, соответствующих минимальным величинам NEP (cм. таблицу).
Оценки предельных характеристик классических джозефсоновских детекторов при использовании переходов [12] из высокотемпературных сверхпроводников
| Т, К | IcRn, мВ | γ | Rn, кОм | NEP, Вт/Гц1/2 | f0 , ТГц | DB1/2, Гц1/2 |
|---|---|---|---|---|---|---|
| 50 | 2.5 | 0.5 | 0.6 | 2 × 10–15 | 0.7 | 9 × 105 |
| 77 | 1 | 0.5 | 0.15 | 2 × 10–15 | 0.3 | 6 × 105 |
| 50 | 2.5 | 1 | 1.2 | 8 × 10–15 | 1.4 | 3 × 105 |
| 77 | 1 | 1 | 0.31 | 7 × 10–15 | 0.6 | 2 × 105 |
| 50 | 2.5 | 2 | 2.4 | 5 × 10–14 | 2.8 | 1 × 105 |
| 77 | 1 | 2 | 0.62 | 5 × 10–14 | 1.2 | 7 × 104 |
В таблице приведены характеристики джозефсоновских детекторов, работающих в режиме классического детектора в области температур 50…77 К, поскольку этот диапазон температур детекторов легко достигается при охлаждении жидким азотом, а также с помощью электрических охладителей. Даже в этом достаточно ограниченном диапазоне температур можно реализовать режимы классического детектирования в ВТСП-переходах с величинами γ от 0.5 до 2 при сопротивлениях переходов от 0.15 до 2.4 кОм. Малые величины, до 2 × 10–15 Вт/Гц1/2, предельных чувствительностей NEP могут иметь детекторы c γ= 0.5 при сопротивлениях Rn от 600 до 150 Ом. Сравнительно низкие величины сопротивлений Rn в этом случае перспективны для согласования с широкополосными антеннами. Дополнительным преимуществом этого режима детектирования является высокий динамический диапазон по мощности до величин порядка 106. Недостатком этого режима с γ = 0.5 является невысокая частотная полоса f0, не превышающая 0.7 ТГц при 50 К.
Для γ = 2 можно существенно повысить полосу классического детектирования до 1.2 ТГц даже при температуре детектора Т = 77 К, но при этом необходимы переходы с большими сопротивлениями, величины NEP = 5 × 10–14 Вт/Гц1/2 существенно хуже, а динамический диапазон по мощности на порядок меньше, чем для случая с γ = 0.5. Реализация режима классического детектирования при γ = 1 может оказаться разумным компромиссом между требуемыми величинами сопротивлений Rn и достижимыми величинами NEP, f0, DB1/2.
Условия реализации конкретных режимов классического джозефсоновского детектора могут существенно различаться, но приведенные оценки различных комбинаций параметров этих детекторов показывают их высокий потенциал для целого ряда перспективных применений в ТГц-технологиях. Оцененная предельная чувствительность порядка 10–14 Вт/Гц1/2 в полосе от 0 до 1.4 ТГц существенно, на два порядка меньше аналогичных величин у традиционных полупроводниковых приемников [14, 15]. Также эти детекторы имеют ряд особенностей, которые могут облегчить реализацию тех применений, где требуется сочетание высокой чувствительности и быстродействия. Наличие динамического диапазона DB1/2 по мощности порядка 105…106 Гц1/2 означает возможность работать с отношением сигнал/шум в детекторе до 10…102 при частотной полосе B = 100 МГц. При этом ограничения сигнала собственной постоянной времени τ в данном детекторе не будет, так как постоянная времени весьма мала и составляет τ ≅ 1/f0 ≅ 10–12 c. Сохранение предельных значений чувствительностей в широкой полосе задаваемых токов является весьма полезной особенностью джозефсоновского классического детектора, особенно привлекательной для создания одномерных или двумерных решеток из этих детекторов.
Список литературы
Tonouchi M. // Nature Photon. 2007. V. 1. P. 97.
Rogalski A., Sizov F. // Opto-Electron. Rev. 2011. V. 19. P. 346.
Anders S., Blamire M.G., Buchholz F.-Im. et al. // Physica C. 2010. V. 470. P. 2079. 2010.
Zmuidzinas J., Richards P. // Proc. IEEE. 2004. V. 92. P. 1597.
Ariyoshi S., Otani C., Dobroiuet A. et al. // Appl. Phys. Lett. 2006. V. 88. P. 203503.
Лихарев К.К. Введение в динамику джозефсоновских переходов. М.: Наука, 1985.
Kanter H., Vernon F.L. // J. Appl. Phys. 1972. V. 43. № 7. P. 3174.
Дивин Ю.Я., Полянский О.Ю., Шульман А.Я. // Письма в ЖТФ. 1980. Т. 6. Вып. 17. С. 1056.
Tolner H. // J. Appl. Phys. 1977. V. 48. P. 691.
Дивин Ю.Я., Малов А.Д., Надь Ф.Я. // РЭ. 1978. Т. 23. № 9. С. 1875.
Divin Yu.Ya., Nad’ F.Ya. // IEEE Trans. 1979. V. MAG-15. № 1. P. 450.
Gundareva I., Divin Y. // IEEE Trans. 2016. V. AS-26. № 3. P. 1100204.
Gundareva I., Pavlovskiy V., Divin Y. // IEEE Trans. 2018. V. AS-28. № 4. 1800105.
Hesler J.L., Crowe T.W. // Proc.18th Int. Symp. Space Terahertz Technol. 2007. P. 89. http://vadiodes.com/ images/pdfs/VDI_Detector_Char_ISSTT2007.pdf.
Induim antimonide (InSb) hot electron bolometer. QMC Instruments Ltd. 2017. http://www.terahertz.co.uk/ qmc-instruments-ltd/thz-detector-systems/ insb-heb
Лихарев К.К., Ульрих Б.Т. Системы с джозефсоновскими контактами. М.: МГУ, 1978.
Devyatov I.A., Kuzmin L.S., Likharev K.K. et al. // J. Appl. Phys. 1986. V. 60. P. 1808.
Cowley A.M., Sorensen H.O. // IEEE Trans. 1966. V. MTT-14. № 12. P. 588.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


