Радиотехника и электроника, 2020, T. 65, № 1, стр. 31-48
Анализ антенных решеток щелевых и ленточных излучателей методом обобщенной матрицы рассеяния
С. Е. Банков *
Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация
* E-mail: sbankov@yandex.ru
Поступила в редакцию 06.03.2019
После доработки 06.03.2019
Принята к публикации 20.04.2019
Аннотация
Рассмотрено применение метода обобщенной матрицы рассеяния для анализа антенных решеток щелевых и ленточных излучателей конечных размеров. Изложена схема метода, основанная на разложении электромагнитного поля по векторным сферическим волнам в локальной системе координат, связанной с выделенным элементом решетки. Численно реализован алгоритм разложения полей сферических волн, заданных в одной локальной системе координат по волнам в других локальных системах координат. Показано, что полученные коэффициенты разложений инвариантны к типу элемента решетки и ее конфигурации. Анализируются алгоритмы решения задач возбуждения щелевых и ленточных излучателей векторными сферическими волнами. Приведены примеры применения развитого в работе метода для анализа решеток разных типов: решетки ленточных вибраторов, решетки щелевых излучателей, возбуждаемых волноводными резонаторами, волноводно-щелевой решетки. Приведены результаты сравнения с расчетами в стандартных системах электродинамического моделирования. Показано, что предложенный алгоритм решения граничной задачи для решетки с большими электрическими размерами обладает вычислительной эффективностью, которая многократно превосходит эффективность стандартных систем электродинамического моделирования.
1. ПОСТАНОВКА ЗАДАЧИ
Интерес к фазированным антенным решеткам (ФАР) с большим коэффициентом усиления (КУ) обусловлен их широким использованием в различных системах локации, связи, диагностики, научных исследованиях и т.д. Реализация высокого КУ неизбежно связана с увеличением числа элементарных излучателей (ЭИ) и, следовательно, электрических размеров ФАР. Несмотря на бурное развитие вычислительной техники и программного обеспечения, электродинамический анализ таких структур представляет сложную задачу, требующую больших затрат компьютерных ресурсов.
По этой причине широко используется приближение бесконечной решетки, в рамках которого ищется решение граничной задачи для одного периода структуры, так называемого канала Флоке [1]. Основанием для замены конечного объекта бесконечным является допущение о том, что ЭИ конечной решетки, достаточно удаленные от ее краев, функционируют в режиме, близком к режиму работы ЭИ бесконечной решетки. Такое допущение неоднократно проверялось и можно считать достаточно обоснованным.
При всех достоинствах данного подхода нельзя не отметить его недостатки. К их числу относятся:
— невозможность расчета диаграммы направленности (ДН) ФАР, которая для бесконечной структуры вырождается в дельта функцию;
— невозможность оценки влияния краевых эффектов на параметры решетки;
— невозможность анализа чувствительности характеристик ФАР по отношению к отклонениям ее параметров от номинальных значений;
— невозможность статистического анализа характеристик ФАР.
Говоря о недостатках, мы имеем в виду возможность выполнения разных видов анализа на электродинамическом уровне строгости в рамках модели бесконечной решетки. Безусловно, используя разные приближенные методы, можно оценить ДН структуры и, например, влияние краевых эффектов. Однако, подобные оценки всегда будут приближенными и их использование для оценки таких “тонких” эффектов как уровень дальних боковых лепестков вызывает оправданные опасения.
Поэтому, не ставя под сомнение полезность модели ФАР в виде канала Флоке, мы должны отметить ограниченность области ее применения. В связи с этим актуальной задачей остается электродинамический анализ решеток с большим КУ. Как отмечалось выше, непосредственное применение таких методов электродинамического моделирования, как метод конечных элементов [2], метод интегральных уравнений [3], метод конечных элементов во временной области, не является оптимальным подходом, так как получаемые при их помощи вычислительные алгоритмы требуют чрезмерно больших затрат компьютерных ресурсов. Увеличение времени решения граничной задачи делает проблематичным или, как минимум, весьма затратным выполнение этапов инженерного проектирования, связанных с перебором большого числа вариантов.
В связи с ситуацией, описанной выше, в начале ХХ столетия был предложен ряд новых методов моделирования многоэлементных структур больших электрических размеров. Можно отметить ряд подходов, основанных на методе моментов [3]. Основным из них является метод быстрых мультиполей [4] и его развитие – многоуровневый быстрый мультипольный алгоритм [5, 6]. Этот эффективный метод расчета матричных форм используется во многих других методах, таких как метод сложных мультиполей [6], метод локализации матрицы импеданса [7], адаптивный метод [8], многоуровневый алгоритм матричной декомпозиции [8] и метод интегральных уравнений в сочетании с быстрым преобразованием Фурье [10].
Существуют методы, направленные на сокращение числа неизвестных без значительной потери точности. Концепция сокращения размерности матричных уравнений преобладает в недавно разработанных итерационных алгоритмах, например, в методе характеристических базисных функций [11], методе синтетических базисных функций [12], методе базисных функций подобластей [13], методе собственных токов [14] и многоуровневом методе подобластей [15]. Эти методы имеют общую основу в виде применения обобщенных базисных функций для представления поверхностных электрических и/или магнитных токов. Разница между ними прежде всего в способах определения базисных функций.
В ряде методов электродинамического анализа ФАР больших электрических размеров используется в качестве основы решение для бесконечной ФАР, которое затем разными приближенными способами адаптируется таким образом, чтобы новое решение учитывало конечные размеры структуры. Так, в работе [16] коэффициенты связи между элементами ФАР рассчитываются для бесконечной решетки, а затем их используют для анализа конечной структуры. Более строгий подход аналогичного типа предложен в работе [17]. Он может быть эффективно использован для определения ДН элемента ФАР ограниченных размеров. Однако возможность определения коэффициентов связи в рамках данного метода остается неопределенной.
Метод обобщенной матрицы передачи предложен в работе [18]. В рамках этого метода каждый элемент решетки окружается поверхностью, на которой поле представляется в виде суммы возбуждающего и рассеянного полей. Далее поле на поверхности заменяется эквивалентными электрическими и магнитными поверхностными токами. Специально разработанные численные процедуры [19] связывают эквивалентные токи с параметрами ЭИ, расположенного внутри поверхности, а также с токами на поверхностях, окружающих разные элементы решетки. Указанные связи представляются в виде матричного уравнения, для которого может быть получено эффективное численное решение.
Отмеченные выше методы объединяет общая идея, которая состоит в том, чтобы разделить поле в окрестности ЭИ на возбуждающее его поле, источником которого являются другие элементы решетки и рассеянное им поле. Кроме того, в рассеянное поле входит поле излучения ЭИ при возбуждении его со стороны входа излучателя, а также волны, отраженные от входа. Далее тем или иным образом вводится оператор рассеяния, связывающий два вида полей. Наиболее удобными являются матричные операторы, связывающие амплитуды возбуждающих и рассеянных волн. Такие операторы близки к известным в технике СВЧ обобщенным матрицам рассеяния (ОМР). Определение ОМР ЭИ является важным этапом для данной группы методов. Другим важным этапом является определение оператора связи между амплитудами волн на разных элементах решетки, поскольку волны, рассеянные некоторым ЭИ, являются одновременно падающими волнами для других ЭИ. Такой оператор имеет вид матрицы связи, или матрицы взаимодействия. Применение операторов двух видов дает возможность формулировки матричной системы уравнений, которая полностью описывает волновые процессы в многоэлементной антенной системе.
Важно отметить, что в силу идентичности ЭИ ФАР оператор рассеяния ищется однократно. При этом решается электродинамическая задача для структуры с относительно малыми электрическими размерами. Решение системы матричных уравнений, описывающей всю решетку в целом не требует таких затрат ресурсов как прямое решение граничной задачи. Таким образом, в применении разных методов достигается их рациональное распределение, когда электродинамические методы используются для анализа малоразмерной структуры (ЭИ), а структура больших размеров анализируется при помощи намного более эффективных матричных методов. Результатом указанной рационализации оказывается существенное снижение затрат вычислительных ресурсов, необходимых для анализа ФАР с высоким КУ.
Назовем группу методов, реализующих описанную выше схему решения граничной задачи методами ОМР (МОМР). Наиболее близким подходом к данной работе является вариант МОМР, в котором в качестве возбуждающих и рассеянных волн используются векторные сферические гармоники (ВСГ). Идея разложения по ВСГ (РВСГ) антенных полей была использована в работах [20–23]. При этом необходимо отметить, что развитые в них методы использовались не только для анализа ФАР, но и для решения задач рассеяния на апериодически расположенных одинаковых объектах. Подходы, использованные в [23], наиболее близки к данной работе. Отметим эффективное применение дополнительной теоремы сложения для сферических функций при решении задачи представления полей в смещенных друг относительно друга сферических системах координат.
Нашей задачей является развитие МОМР – РВСГ применительно к важному классу объектов – щелевым и ленточным антенным решеткам с большими электрическими размерами. В первую очередь, с практической точки зрения нас интересуют щелевые решетки. Ленточные структуры представляют методический интерес, так как их удобно использовать в качестве тестовых объектов для сравнения результатов, полученных разными методами.
Отметим, что щелевые решетки активно развиваются, в том числе и в настоящее время [24, 25]. Интерес к ним обусловлен простотой конструкции и технологичностью. В последнее десятилетие дополнительный интерес к щелевым решеткам связан с созданием антенн, сфокусированных в ближней зоне, которые находят применение в разных областях науки и техники. Сфокусированные волноводно-щелевые решетки [26, 27] относятся к числу апериодических решеток. Их электродинамический анализ особенно сложен, поскольку использование модели бесконечной решетки в данном случае невозможно. Единственным средством моделирования в такой ситуации оказывается численное решение граничной задачи для всей решетки со всеми отмеченными выше недостатками. Поэтому разработка новых эффективных методов анализа щелевых ФАР является актуальной задачей.
2. ВЕКТОРНЫЕ СФЕРИЧЕСКИЕ ГАРМОНИКИ
Определение ВСГ следует из общего решения уравнения Максвелла в сферических координатах $r,\theta ,\varphi $ [28]:
(1)
$\begin{gathered} \left[ \begin{gathered} {\rm E}_{{rn,m}}^{e} \hfill \\ {\rm H}_{{rn,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{1}{\rho }n(n + 1){{U}_{{n,m}}},\,\,\,\,\left[ \begin{gathered} {\rm E}_{{\theta n,m}}^{e} \hfill \\ {\rm H}_{{\theta n,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{1}{\rho }\frac{{{{\partial }^{2}}(\rho {{U}_{{n,m}}})}}{{\partial \theta \partial \rho }}, \\ \left[ \begin{gathered} {\rm E}_{{\varphi n,m}}^{e} \hfill \\ {\rm H}_{{\varphi n,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{1}{{\rho \sin \theta }}\frac{{{{\partial }^{2}}(\rho {{U}_{{n,m}}})}}{{\partial \varphi \partial \rho }}, \\ \left[ \begin{gathered} {\rm H}_{{\theta n,m}}^{e} \hfill \\ - {\rm E}_{{\theta n,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{i}{{\rho \sin \theta }}\frac{{\partial (\rho {{U}_{{n,m}}})}}{{\partial \varphi }}, \\ \left[ \begin{gathered} {\rm H}_{{\varphi n,m}}^{e} \hfill \\ - {\rm E}_{{\varphi n,m}}^{m} \hfill \\ \end{gathered} \right] = - \frac{i}{\rho }\frac{{\partial (\rho {{U}_{{n,m}}});}}{{\partial \theta }} \\ \end{gathered} $(2)
$\begin{gathered} {{U}_{{n,m}}} = P_{n}^{m}(\cos \theta )\exp ( - im\varphi )\left\{ \begin{gathered} \xi _{n}^{{(2)}}(\rho ) \hfill \\ {{\psi }_{n}}(\rho ) \hfill \\ \end{gathered} \right., \\ {{\psi }_{n}}(\rho ) = \sqrt {\frac{\pi }{{2\rho }}} {{J}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(\rho ),\,\,\,\,\xi _{n}^{{(2)}}(\rho ) = \sqrt {\frac{\pi }{{2\rho }}} H_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{(2)}}(\rho ), \\ \rho = kr, \\ \end{gathered} $Назовем ВСФ в верхней формуле (2) рассеянными волнами, а в нижней – возбуждающими. Рассеянные волны описывают поле при радиусах бóльших радиальных координат создающих их источников, а возбуждающие волны соответственно при меньших радиусах. Для обозначения возбуждающих и рассеянных волн мы будем использовать нижние индексы $i,s$ от английских терминов incident и scattered.
Соотношения (1) записаны для нормированных компонент поля ${\rm E},{\rm H}$. Они связаны с компонентами векторов $E,H$ следующим образом:
(3)
$\begin{gathered} \left[ \begin{gathered} {\rm E}_{{rn,m}}^{e} \hfill \\ {\rm H}_{{rn,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{1}{k}\left[ \begin{gathered} E_{{rn,m}}^{e} \hfill \\ H_{{rn,m}}^{m} \hfill \\ \end{gathered} \right],\,\,\,\,\left[ \begin{gathered} {\rm E}_{{\theta n,m}}^{e} \hfill \\ {\rm H}_{{\theta n,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{1}{k}\left[ \begin{gathered} E_{{\theta n,m}}^{e} \hfill \\ H_{{\theta n,m}}^{m} \hfill \\ \end{gathered} \right], \\ \left[ \begin{gathered} {\rm E}_{{\varphi n,m}}^{e} \hfill \\ {\rm H}_{{\varphi n,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{1}{k}\left[ \begin{gathered} E_{{\varphi n,m}}^{e} \hfill \\ H_{{\varphi n,m}}^{m} \hfill \\ \end{gathered} \right],\,\,\,\,\left[ \begin{gathered} {\rm H}_{{\theta n,m}}^{e} \hfill \\ - {\rm E}_{{\theta n,m}}^{e} \hfill \\ \end{gathered} \right] = \frac{1}{k}\left[ \begin{gathered} H_{{\theta n,m}}^{e}{{W}_{0}} \hfill \\ {{ - E_{{\theta n,m}}^{e}} \mathord{\left/ {\vphantom {{ - E_{{\theta n,m}}^{e}} {{{W}_{0}}}}} \right. \kern-0em} {{{W}_{0}}}} \hfill \\ \end{gathered} \right], \\ \left[ \begin{gathered} {\rm H}_{{\varphi n,m}}^{e} \hfill \\ - {\rm E}_{{\varphi n,m}}^{m} \hfill \\ \end{gathered} \right] = \frac{1}{k}\left[ \begin{gathered} H_{{\varphi n,m}}^{e}{{W}_{0}} \hfill \\ {{ - E_{{\varphi n,m}}^{m}} \mathord{\left/ {\vphantom {{ - E_{{\varphi n,m}}^{m}} {{{W}_{0}}}}} \right. \kern-0em} {{{W}_{0}}}} \hfill \\ \end{gathered} \right], \\ \end{gathered} $Отметим, что нормированные ВСГ не имеют размерности и зависят только от угловых координат и электрического радиуса. Кроме того, важно указать, что у электрических волн равна нулю компонента поля ${{H}_{r}}$, а у магнитных – ${{E}_{r}}$.
Сферические гармоники удовлетворяют соотношениям ортогональности:
(4)
$\int\limits_0^\pi {\int\limits_0^{2\pi } {\left[ \begin{gathered} {\rm E}_{{rn,m}}^{e} \hfill \\ {\rm H}_{{rn,m}}^{m} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {\rm E}_{{rp,q}}^{e} \hfill \\ {\rm H}_{{rp,q}}^{m} \hfill \\ \end{gathered} \right]\sin \theta d\varphi d\theta } } = N_{{rn,m}}^{{e,m}}{{\delta }_{{n,p}}}{{\delta }_{{ - m,q}}},$При анализе щелевых и ленточных решеток при $\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ нам будет удобно разместить плоскость симметрии, которая для щелевых структур является идеальной электрической стенкой, а для ленточных идеальной магнитной стенкой. Поэтому целесообразно разделить ВСФ на четные и нечетные относительно указанной плоскости:
(5)
${\rm E}_{{rn,m}}^{e} = {\rm E}_{{rn,m}}^{{ee}} + {\rm E}_{{rn,m}}^{{eo}},\,\,\,\,{\rm H}_{{rn,m}}^{e} = {\rm H}_{{rn,m}}^{{ee}} + {\rm H}_{{rn,m}}^{{eo}}.$Четным электрическим и магнитным волнам соответствуют нечетные и четные значения $n + \left| m \right|\,:$ $n + \left| m \right| = 2l + 1,$ $n + \left| m \right| = 2l,$ а нечетным электрическим и магнитным волнам соответствуют четные и нечетные значения $n + \left| m \right|$: $n + \left| m \right| = 2l,$ $n + \left| m \right| = 2l + 1,$ $l = 0,1,....$ Данные соотношения следуют из свойств присоединенных функций Лежандра [29].
3. СХЕМА МОМР–РВСГ
Рассмотрим некоторую решетку (рис. 1), состоящую из ЭИ, которые в общем случае могут отличаться друг от друга. Также они могут быть расположены апериодически. На рис. 1 изображен фрагмент щелевой решетки. Однако на данном этапе тип излучателя неважен, так как он не влияет на общую схему метода.
Положение ЭИ в решетке обычно описывают при помощи двух индексов, например, $n,m.$ Такая нумерация удобна в случае периодической структуры. Мы будем использовать сквозную нумерацию ЭИ при помощи индекса $\nu $, который меняется от единицы до ${{M}_{R}}$, где ${{M}_{R}}$ – общее число ЭИ в решетке. Также используем один индекс $N$для задания типа ВСГ вместо двух индексов $n,m,$ которые применялись в формулах (1)–(5).
Введем в пространстве ВСГ следующие векторы:
(6)
$\begin{gathered} {\mathbf{\vec {E}}}_{{i,s\nu }}^{{e,m}} = \left[ \begin{gathered} {\text{ }}..... \hfill \\ \vec {E}_{{i,s\nu ,N - 1}}^{{e,m}} \hfill \\ \vec {E}_{{i,s\nu ,N}}^{{e,m}} \hfill \\ \vec {E}_{{i,s\nu ,N + 1}}^{{e,m}} \hfill \\ {\text{ }}..... \hfill \\ \end{gathered} \right],\,\,\,\,{\mathbf{\vec {H}}}_{{i,s\nu }}^{{e,m}} = \left[ \begin{gathered} {\text{ }}..... \hfill \\ \vec {H}_{{i,s\nu ,N - 1}}^{{e,m}} \hfill \\ \vec {H}_{{i,s\nu ,N}}^{{e,m}} \hfill \\ \vec {H}_{{i,s\nu ,N + 1}}^{{e,m}} \hfill \\ {\text{ }}..... \hfill \\ \end{gathered} \right], \\ {\mathbf{A}}_{{i,s\nu }}^{{e,m}} = \left[ \begin{gathered} {\text{ }}..... \hfill \\ A_{{i,s\nu ,N - 1}}^{{e,m}} \hfill \\ A_{{i,s\nu ,N}}^{{e,m}} \hfill \\ A_{{i,s\nu ,N + 1}}^{{e,m}} \hfill \\ {\text{ }}..... \hfill \\ \end{gathered} \right]. \\ \end{gathered} $Каждый ЭИ окружен сферой с электрическим радиусом $R$, которая не пересекает ни выделенный ЭИ, ни соседние с ним ЭИ. В случае щелевых излучателей сферы заменяются полусферами, что не вносит принципиальных изменений в схему метода. Источником возбуждающих волн для $\mu $-го ЭИ являются волны, рассеянные всеми элементами решетки, за исключением μ-го. Источником рассеянных волн этого излучателя является дифракция возбуждающих волн на нем, а также падающие волны на его входы. Мы предполагаем, что таких входов может быть не один, а несколько. Объединяя амплитуды падающих волн ${{U}_{{i\mu ,j}}}$ ($j$ – номер входа), мы получаем вектор падающих волн μ-го ЭИ: ${{{\mathbf{U}}}_{{i\mu }}}$. Аналогично можно получить вектор отраженных волн ${\mathbf{U}}_{{r\mu }}^{{}}$.
Отметим, что при отсутствии пересечений сфер, окружающих ЭИ, они оказываются расположенными вне областей, занятых источниками, что позволяет нам представить поля на них в виде разложений по ВСГ:
(7)
$\begin{gathered} {{{\vec {E}}}_{\nu }} = {{{\vec {E}}}_{{i\nu }}} + {{{\vec {E}}}_{{s\nu }}},\,\,\,\,{{{\vec {H}}}_{\nu }} = {{{\vec {H}}}_{{i\nu }}} + {{{\vec {H}}}_{{s\nu }}}, \\ {{{\vec {E}}}_{{i\nu }}} = {\mathbf{A}}_{{i\nu }}^{e}{\mathbf{\vec {E}}}_{{i\nu }}^{e} + {\mathbf{A}}_{{i\nu }}^{m}{\mathbf{\vec {E}}}_{{i\nu }}^{m},\,\,\,\,{{{\vec {E}}}_{{s\nu }}} = {\mathbf{A}}_{{s\nu }}^{e}{\mathbf{\vec {E}}}_{{s\nu }}^{e} + {\mathbf{A}}_{{s\nu }}^{m}{\mathbf{\vec {E}}}_{{s\nu }}^{m}, \\ {{{\vec {H}}}_{{i\nu }}} = {\mathbf{A}}_{{i\nu }}^{e}{\mathbf{\vec {H}}}_{{i\nu }}^{e} + {\mathbf{A}}_{{i\nu }}^{m}{\mathbf{\vec {H}}}_{{i\nu }}^{m},\,\,\,\,{{{\vec {H}}}_{{s\nu }}} = {\mathbf{A}}_{{s\nu }}^{e}{\mathbf{\vec {H}}}_{{s\nu }}^{e} + {\mathbf{A}}_{{s\nu }}^{m}{\mathbf{\vec {H}}}_{{s\nu }}^{m}. \\ \end{gathered} $Следующий этап – определение связи между амплитудами волн, рассеянных ν-м ЭИ, и амплитудами волн, падающих на μ-й ЭИ. Для определения указанной связи нам необходимо осуществить разложение поля рассеянной волны ν-го ЭИ в системе координат μ-го ЭИ. Воспользуемся следующими соотношениями, связывающими координаты двух систем:
(8)
$\begin{gathered} {{\varphi }_{\nu }} = {\text{arctg}}\left( {\frac{{R\sin {{\theta }_{\mu }}\sin {{\varphi }_{\mu }} - \Delta {{y}_{{\mu ,\nu }}}}}{{R\sin {{\theta }_{\mu }}\cos {{\varphi }_{\mu }} - \Delta {{x}_{{\mu ,\nu }}}}}} \right), \\ {{\rho }_{\nu }} = \sqrt {{{R}^{2}}{{{\cos }}^{2}}{{\theta }_{\mu }} + {{{\left( {R\sin {{\theta }_{\mu }}\cos {{\varphi }_{\mu }} - \Delta {{x}_{{\mu ,\nu }}}} \right)}}^{2}} + {{{\left( {R\sin {{\theta }_{\mu }}\sin {{\varphi }_{\mu }} - \Delta {{y}_{{\mu ,\nu }}}} \right)}}^{2}}} , \\ {{\theta }_{\nu }} = \arcsin \left( {\frac{{\sqrt {{{{\left( {R\sin {{\theta }_{\mu }}\cos {{\varphi }_{\mu }} - \Delta {{x}_{{\mu ,\nu }}}} \right)}}^{2}} + {{{\left( {R\sin {{\theta }_{\mu }}\sin {{\varphi }_{\mu }} - \Delta {{y}_{{\mu ,\nu }}}} \right)}}^{2}}} }}{{{{\rho }_{\mu }}}}} \right). \\ \end{gathered} $(9)
$\Delta {{x}_{{\mu ,\nu }}} = \Delta {{r}_{{\mu ,\nu }}}\cos \Delta {{\varphi }_{{\mu ,\nu }}},\,\,\,\,\Delta {{y}_{{\mu ,\nu }}} = \Delta {{r}_{{\mu ,\nu }}}\sin \Delta {{\varphi }_{{\mu ,\nu }}}.$Также нам необходимо учесть поворот векторов при переходе от одной системы к другой. Матрица ${{\hat {M}}_{\nu }}$ связывает компоненты вектора в декартовой системе координат с компонентами в сферической системе ν-го ЭИ:
(10)
${{\hat {M}}_{\nu }} = \left[ {\begin{array}{*{20}{c}} {\cos {{\varphi }_{\nu }}\sin {{\theta }_{\nu }}}&{\sin {{\varphi }_{\nu }}\sin {{\theta }_{\nu }}}&{\cos {{\theta }_{\nu }}} \\ {\cos {{\varphi }_{\nu }}\cos {{\theta }_{\nu }}}&{\sin {{\varphi }_{\nu }}\cos {{\theta }_{\nu }}}&{ - \sin {{\theta }_{\nu }}} \\ { - \sin {{\varphi }_{\nu }}}&{\cos {{\varphi }_{\nu }}}&0 \end{array}} \right].$Поскольку переход от одной декартовой системы координат к другой состоит в ее параллельном переносе, который не меняет ориентацию вектора, то при помощи соотношения (10) можно получить матрицу ${{\hat {M}}_{{\mu ,\nu }}},$ связывающую компоненты векторов в двух сферических системах координат:
Полученные выше соотношения позволяют нам записать падающее на μ-й ЭИ поле:
(12)
$\begin{gathered} \vec {E}_{{ir\mu }}^{e} = \sum\limits_\nu {^{{(\mu )}}\left( {{\mathbf{A}}_{{s\nu }}^{e}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {E}}}_{{s\nu }}^{e}} \right)}}_{r}} + {\mathbf{A}}_{{s\nu }}^{m}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {E}}}_{{s\nu }}^{m}} \right)}}_{r}}} \right)} , \\ \vec {H}_{{ir\mu }}^{m} = \sum\limits_\nu {^{{(\mu )}}\left( {{\mathbf{A}}_{{s\nu }}^{e}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {H}}}_{{s\nu }}^{e}} \right)}}_{r}} + {\mathbf{A}}_{{s\nu }}^{m}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {H}}}_{{s\nu }}^{m}} \right)}}_{r}}} \right)} . \\ \end{gathered} $Суммирование в (12) ведется по всем элементам кроме μ-го. Соотношения (12) описывают радиальные компоненты электрического и магнитного полей. Они являются функциями сферических координат ${{r}_{\mu }},{{\theta }_{\mu }},{{\varphi }_{\mu }}$ согласно выражениям (8). Вместе с тем радиальные компоненты можно представить в виде разложений по возбуждающим волнам μ-го ЭИ:
(13)
$E_{{ir\mu }}^{e} = {\mathbf{A}}_{{i\mu }}^{e}{\mathbf{E}}_{{ir\mu }}^{e},\,\,\,\,H_{{ir\mu }}^{m} = {\mathbf{A}}_{{i\mu }}^{m}{\mathbf{H}}_{{ir\mu }}^{m}.$Приравнивая (12) и (13) и используя ортогональность ВСГ, находим векторы ${\mathbf{A}}_{{i\mu }}^{{e,m}}$:
(14)
$\begin{gathered} {\mathbf{A}}_{{i\mu }}^{e} = \int\limits_{{{\Omega }_{\mu }}} {\sum\limits_\nu {^{{(\mu )}}{{{\left( {{{{\mathbf{N}}}^{e}}} \right)}}^{{ - 1}}}\left( {{\mathbf{A}}_{{s\nu }}^{e}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {E}}}_{{s\nu }}^{e}} \right)}}_{r}}} \right.} } + \\ \left. { + \,\,{\mathbf{A}}_{{s\nu }}^{m}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {E}}}_{{s\nu }}^{m}} \right)}}_{r}}} \right){\mathbf{\vec {E}}}_{{ir\mu }}^{e}d{{\Omega }_{\mu }}, \\ {\mathbf{A}}_{{i\mu }}^{m} = \int\limits_{{{\Omega }_{\mu }}} {\sum\limits_\nu {^{{(\mu )}}{{{\left( {{{{\mathbf{N}}}^{m}}} \right)}}^{{ - 1}}}\left( {{\mathbf{A}}_{{s\nu }}^{e}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {H}}}_{{s\nu }}^{e}} \right)}}_{r}}} \right.} } + \\ + \,\,{\mathbf{A}}_{{s\nu }}^{m}{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {H}}}_{{s\nu }}^{m}} \right)}_{r}}{\mathbf{\vec {H}}}_{{ir\mu }}^{m}d{{\Omega }_{\mu }}, \\ N_{{iM}}^{e} = \int\limits_{{{\Omega }_{\mu }}} {{{{\left| {E_{{ir\mu ,M}}^{e}} \right|}}^{2}}d{{\Omega }_{\mu }}} ,\,\,\,\,N_{{iM}}^{m} = \int\limits_{{{\Omega }_{\mu }}} {{{{\left| {H_{{ir\mu ,M}}^{m}} \right|}}^{2}}d{{\Omega }_{\mu }}} . \\ \end{gathered} $Введем обозначения:
(15)
$\begin{gathered} {\mathbf{K}}_{{\mu ,\nu }}^{{ee}} = \int\limits_{{{\Omega }_{\mu }}} {{{{\left( {{{{\mathbf{N}}}^{e}}} \right)}}^{{ - 1}}}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {E}}}_{{s\nu }}^{e}} \right)}}_{r}}{\mathbf{\vec {E}}}_{{ir\mu }}^{e}d{{\Omega }_{\mu }}} , \\ {\mathbf{K}}_{{\mu ,\nu }}^{{em}} = \int\limits_{{{\Omega }_{\mu }}} {{{{\left( {{{{\mathbf{N}}}^{e}}} \right)}}^{{ - 1}}}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {E}}}_{{s\nu }}^{m}} \right)}}_{r}}{\mathbf{\vec {E}}}_{{ir\mu }}^{e}d{{\Omega }_{\mu }}} , \\ {\mathbf{K}}_{{\mu ,\nu }}^{{me}} = \int\limits_{{{\Omega }_{\mu }}} {{{{\left( {{{{\mathbf{N}}}^{m}}} \right)}}^{{ - 1}}}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {H}}}_{{s\nu }}^{e}} \right)}}_{r}}{\mathbf{\vec {H}}}_{{ir\mu }}^{m}d{{\Omega }_{\mu }}} , \\ {\mathbf{K}}_{{\mu ,\nu }}^{{mm}} = \int\limits_{{{\Omega }_{\mu }}} {{{{\left( {{{{\mathbf{N}}}^{m}}} \right)}}^{{ - 1}}}{{{\left( {{{{\hat {M}}}_{{\mu ,\nu }}}{\mathbf{\vec {H}}}_{{s\nu }}^{m}} \right)}}_{r}}{\mathbf{\vec {H}}}_{{ir\mu }}^{m}d{{\Omega }_{\mu }}} . \\ \end{gathered} $С учетом соотношений (15) запишем выражения (14) в компактном виде
(16)
$\begin{gathered} {\mathbf{A}}_{{i\mu }}^{e} = \sum\limits_\nu {^{{(\mu )}}\left( {{\mathbf{K}}_{{\mu ,\nu }}^{{ee}}{\mathbf{A}}_{{s\nu }}^{e} + {\mathbf{K}}_{{\mu ,\nu }}^{{em}}{\mathbf{A}}_{{s\nu }}^{m}} \right)} , \\ {\mathbf{A}}_{{i\mu }}^{m} = \sum\limits_\nu {^{{(\mu )}}\left( {{\mathbf{K}}_{{\mu ,\nu }}^{{me}}{\mathbf{A}}_{{s\nu }}^{e} + {\mathbf{K}}_{{\mu ,\nu }}^{{mm}}{\mathbf{A}}_{{s\nu }}^{m}} \right)} . \\ \end{gathered} $Матрицы ${\mathbf{K}}$ описывают искомую связь между амплитудами рассеянных на ν-м и возбуждающих на μ-м элементах волн. Назовем их матрицами связи.
Далее нам необходимо ввести оператор рассеяния ЭИ. Этот оператор связывает амплитуды возбуждающих и рассеянных волн ЭИ. Отметим, что наряду с ВСГ он может возбуждаться волноводными волнами со стороны своих портов. Оператор рассеяния находится в результате решения электродинамической граничной задачи. Ее решение для щелевого и ленточного излучателей будет представлено ниже, а сейчас будем полагать, что оно известно и может быть записано в следующей форме:
(17)
$\begin{gathered} {\mathbf{A}}_{{s\mu }}^{e} = {\mathbf{L}}_{{^{{ss\mu }}}}^{{ee}}{\mathbf{A}}_{{i\mu }}^{e} + {\mathbf{L}}_{{ss\mu }}^{{em}}{\mathbf{A}}_{{i\mu }}^{m} + {\mathbf{L}}_{{sw\mu }}^{e}{{{\mathbf{U}}}_{{i\mu }}}, \\ {\mathbf{A}}_{{s\mu }}^{m} = {\mathbf{L}}_{{ss\mu }}^{{me}}{\mathbf{A}}_{{i\mu }}^{e} + {\mathbf{L}}_{{ss\mu }}^{{mm}}{\mathbf{A}}_{{i\mu }}^{m} + {\mathbf{L}}_{{sw\mu }}^{m}{\mathbf{U}}_{{i\mu }}^{{}}, \\ {\mathbf{U}}_{{r\mu }}^{{}} = {\mathbf{L}}_{{ws\mu }}^{e}{\mathbf{A}}_{{i\mu }}^{e} + {\mathbf{L}}_{{ws\mu }}^{m}{\mathbf{A}}_{{i\mu }}^{m} + {\mathbf{L}}_{{ww\mu }}^{{}}{\mathbf{U}}_{{i\mu }}^{{}}, \\ \end{gathered} $Введем обозначения:
(18)
$\begin{gathered} {{{\mathbf{L}}}_{{ss\mu }}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{L}}_{{^{{ss\mu }}}}^{{ee}}}&{{\mathbf{L}}_{{^{{ss\mu }}}}^{{em}}} \\ {{\mathbf{L}}_{{^{{ss\mu }}}}^{{me}}}&{{\mathbf{L}}_{{^{{ss\mu }}}}^{{mm}}} \end{array}} \right],\,\,\,\,{{{\mathbf{K}}}_{{\mu ,\nu }}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{K}}_{{\mu ,\nu }}^{{ee}}}&{{\mathbf{K}}_{{\mu ,\nu }}^{{em}}} \\ {{\mathbf{K}}_{{\mu ,\nu }}^{{me}}}&{{\mathbf{K}}_{{\mu ,\nu }}^{{mm}}} \end{array}} \right], \\ {\mathbf{L}}_{{sw\mu }}^{{}} = \left[ \begin{gathered} {\mathbf{L}}_{{sw\mu }}^{e} \hfill \\ {\mathbf{L}}_{{sw\mu }}^{m} \hfill \\ \end{gathered} \right],\,\,\,\,{\mathbf{L}}_{{ws\mu }}^{{}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{L}}_{{ws\mu }}^{e}}&{{\mathbf{L}}_{{ws\mu }}^{m}} \end{array}} \right], \\ {{{\mathbf{A}}}_{s}} = \left[ \begin{gathered} {\mathbf{A}}_{s}^{e} \hfill \\ {\mathbf{A}}_{s}^{m} \hfill \\ \end{gathered} \right], \\ \end{gathered} $(19)
$\begin{gathered} {{{\mathbf{A}}}_{{s\mu }}} = \sum\limits_\nu {^{{(\mu )}}{{{\mathbf{L}}}_{{ss\mu }}}{\mathbf{K}}_{{\mu ,\nu }}^{{}}{\mathbf{A}}_{{s\nu }}^{{}}} + {{{\mathbf{L}}}_{{sw\mu }}}{{{\mathbf{U}}}_{{i\mu }}}, \\ {\mathbf{U}}_{{r\mu }}^{{}} = \sum\limits_\nu {^{{(\mu )}}{{{\mathbf{L}}}_{{ws\mu }}}{{{\mathbf{K}}}_{{\mu ,\nu }}}{{{\mathbf{A}}}_{{s\nu }}}} + {{{\mathbf{L}}}_{{ww\mu }}}{{{\mathbf{U}}}_{{i\mu }}}. \\ \end{gathered} $Уравнения (19) представляют собой систему линейных алгебраических уравнений (СЛАУ), которую можно решать численно любым из известных методов. Если векторы ${{{\mathbf{U}}}_{{i\mu }}}$ известны, то достаточно решить первое из уравнений (19). Решение будет иметь вид линейной комбинации векторов ${{{\mathbf{U}}}_{{i\mu }}}$:
(20)
${{{\mathbf{A}}}_{{s\nu }}} = \sum\limits_\xi {{{{\mathbf{Q}}}_{{\nu ,\xi }}}{{{\mathbf{U}}}_{{i\xi }}}} .$Подставим соотношение (20) во второе уравнение (19) и найдем векторы отраженных волн ${\mathbf{U}}_{{r\mu }}^{{}}$:
(21)
${\mathbf{U}}_{{r\mu }}^{{}} = {{{\mathbf{L}}}_{{ws\mu }}}\sum\limits_\nu {\sum\limits_\xi {^{{(\mu )}}{\mathbf{K}}_{{\mu ,\xi }}^{{}}} {{{\mathbf{Q}}}_{{\xi ,\nu }}}{{{\mathbf{U}}}_{{i\nu }}}} + {\mathbf{L}}_{{ww\mu }}^{{}}{\mathbf{U}}_{{i\mu }}^{{}}.$Из соотношения (21) несложно найти матрицу рассеяния всей решетки:
(22)
${{{\mathbf{S}}}_{{a\mu ,\nu }}} = {{{\mathbf{L}}}_{{ws\mu }}}\sum\limits_\xi {^{{(\mu )}}{\mathbf{K}}_{{\mu ,\xi }}^{{}}} {{{\mathbf{Q}}}_{{\xi ,\nu }}} + {\mathbf{L}}_{{ww\mu }}^{{}}{{\delta }_{{\mu ,\nu }}}.$Матрица рассеяния ${{{\mathbf{S}}}_{a}}$ имеет блочную структуру. Ее размерность равна ${{M}_{R}} \times {{M}_{R}},$ а элементами являются матрицы размерностью $J \times J,$ где $J$ – число входов ЭИ.
Система (19) может быть решена итерационно по следующей схеме:
(23)
$\begin{gathered} {\mathbf{A}}_{{s\mu }}^{{q + 1}} = \sum\limits_\nu {^{{(\mu )}}{{{\mathbf{L}}}_{{ss\mu }}}{\mathbf{K}}_{{\mu ,\nu }}^{{}}{\mathbf{A}}_{{s\nu }}^{q}} + {{{\mathbf{L}}}_{{sw\mu }}}{{{\mathbf{U}}}_{{i\mu }}}, \\ {\mathbf{A}}_{{s\nu }}^{0} = {{{\mathbf{L}}}_{{sw\mu }}}{{{\mathbf{U}}}_{{i\mu }}}, \\ \end{gathered} $Для определения поля в дальней зоне при $\rho \to \infty $ воспользуемся асимптотическим представлением сферической функции Ганкеля:
Также отметим, что в дальней зоне нас интересуют главные члены асимптотических представлений поля. В рамках такого приближения производная по координате $\rho $ в выражениях (1) эквивалентна умножению на $ - i$. С учетом этих замечаний получаем асимптотические выражения для полей ВСГ в дальней зоне:
(25)
$\begin{gathered} \left[ \begin{gathered} {\rm E}_{{rn,m}}^{{ea}} \hfill \\ {\rm H}_{{rn,m}}^{{ma}} \hfill \\ \end{gathered} \right] = 0,\,\,\,\left[ \begin{gathered} {\rm E}_{{\theta n,m}}^{{ea}} \hfill \\ {\rm H}_{{\theta n,m}}^{{ma}} \hfill \\ \end{gathered} \right] = - i\frac{{\partial U_{{n,m}}^{a}}}{{\partial \theta }}, \\ \left[ \begin{gathered} {\rm E}_{{\varphi n,m}}^{{ea}} \hfill \\ {\rm H}_{{\varphi n,m}}^{{ma}} \hfill \\ \end{gathered} \right] = - \frac{i}{{\sin \theta }}\frac{{\partial U_{{n,m}}^{a}}}{{\partial \varphi }}, \\ \left[ \begin{gathered} {\rm H}_{{\theta n,m}}^{{ea}} \hfill \\ - {\rm E}_{{\theta n,m}}^{{ma}} \hfill \\ \end{gathered} \right] = \frac{i}{{\sin \theta }}\frac{{\partial U_{{n,m}}^{a}}}{{\partial \varphi }}, \\ \left[ \begin{gathered} {\rm H}_{{\varphi n,m}}^{{ea}} \hfill \\ - {\rm E}_{{\varphi n,m}}^{{ma}} \hfill \\ \end{gathered} \right] = - i\frac{{\partial U_{{n,m}}^{a}}}{{\partial \theta }},\,\,\,U_{{n,m}}^{a} = P_{n}^{m}(\cos \theta )\exp ( - im\varphi ){{i}^{{n + 1}}}. \\ \end{gathered} $В выражениях (25) опущен общий множитель ${{\exp ( - i\rho )} \mathord{\left/ {\vphantom {{\exp ( - i\rho )} \rho }} \right. \kern-0em} \rho }.$
Далее аналогично формуле (6) формируем векторы ${\mathbf{\vec {E}}}_{{s\nu }}^{a},$ ${\mathbf{\vec {H}}}_{{s\nu }}^{a},$ являющиеся функциями угловых координат $\theta ,\varphi $:
(26)
${\mathbf{\vec {E}}}_{{s\nu }}^{a} = \left[ \begin{gathered} {\mathbf{\vec {E}}}_{{s\nu }}^{{ea}} \hfill \\ {\mathbf{\vec {E}}}_{{s\nu }}^{{ma}} \hfill \\ \end{gathered} \right],\,\,\,\,{\mathbf{\vec {H}}}_{{s\nu }}^{a} = \left[ \begin{gathered} {\mathbf{\vec {H}}}_{{s\nu }}^{{ea}} \hfill \\ {\mathbf{\vec {H}}}_{{s\nu }}^{{ma}} \hfill \\ \end{gathered} \right].$Используя выражения (26), запишем поле излучения решетки в дальней зоне:
(27)
$\begin{gathered} {\mathbf{\vec {E}}}_{s}^{a} = \sum\limits_\nu {{{{\mathbf{A}}}_{{s\nu }}}{\mathbf{\vec {E}}}_{{s\nu }}^{a}} \exp (ik\sin \theta ({{x}_{\nu }}\cos \varphi + {{y}_{\nu }}\sin \varphi )), \\ {\mathbf{\vec {H}}}_{s}^{a} = \sum\limits_\nu {{{{\mathbf{A}}}_{{s\nu }}}{\mathbf{\vec {H}}}_{{s\nu }}^{a}} \exp (ik\sin \theta ({{x}_{\nu }}\cos \varphi + {{y}_{\nu }}\sin \varphi )). \\ \end{gathered} $Соотношения (27) будут использованы нами для определения ДН решетки.
Результаты данного раздела инвариантны по отношению к виду ФАР. Смена типа излучателя приводит только к изменению вида оператора рассеяния ${\mathbf{L}}$, не меняя общей схемы решения. Видно, что МОМР-РВСГ включает два основных этапа: определение матрицы связи и определение оператора рассеяния. Рассмотрим их подробнее.
4. ВЫЧИСЛЕНИЕ МАТРИЦЫ СВЯЗИ
Алгоритм вычисления матрицы связи описан в разд. 3 и в таком виде он был использован для решения конкретных задач. Рассмотрим ряд важных его особенностей, которые существенно повышают вычислительную эффективность метода МОМР-РВСГ.
Во-первых, необходимо отметить, что на этапе вычисления матриц ${\mathbf{K}}_{{\mu ,\nu }}^{{}}$ удобно использовать нормированные ВСГ (1), так как они не зависят от частоты, что позволяет уменьшить число свободных параметров. Все расчеты можно проводить для электрических расстояний. Переход к ненормированным гармоникам с помощью соотношений (3) не составляет труда.
Во-вторых, следует отметить, что элементы матриц ${\mathbf{K}}_{{\mu ,\nu }}^{{}}$ зависят от угла смещения $\Delta {{\varphi }_{{\mu ,\nu }}}$ (10) тривиальным образом. Допустим мы нашли при $\Delta {{\varphi }_{{\mu ,\nu }}} = 0$ и некотором радиусе смещения $\Delta {{r}_{{\mu ,\nu }}}$ элемент ${{{\mathbf{K}}}_{{\mu ,\nu ,M,N}}}(0),$ где $N$ – номер рассеянной гармоники, а $M$ – номер падающей гармоники. Тогда тот же элемент при произвольном угле и том же значении $\Delta {{r}_{{\mu ,\nu }}}$ можно найти следующим образом:
(28)
${{{\mathbf{K}}}_{{\mu ,\nu ,M,N}}}(\Delta \varphi ) = {{{\mathbf{K}}}_{{\mu ,\nu ,M,N}}}(0)\exp ( - i\Delta \varphi ({{m}_{N}} - {{m}_{M}})),$Таким образом, матрицы ${{{\mathbf{K}}}_{{\mu ,\nu }}},$ по существу, являются функциями одной переменной – электрического расстояния. Такое положение служит основанием для использования следующего алгоритма вычисления матрицы связи. Отметим, что расчет матриц ${{{\mathbf{K}}}_{{\mu ,\nu }}}$ привязан к конкретной решетке, геометрия которой задает значения расстояний между элементами. При большом их числе приходится многократно проводить вычисление матриц связи. Важно также иметь в виду, что выполнение расчетов по формулам (15) является достаточно трудоемким процессом, требующим значительных затрат компьютерных ресурсов. Поэтому необходимо максимально его оптимизировать.
Для этого вместо множества матриц ${\mathbf{K}}_{{\mu ,\nu }}^{{}}$ мы рассматривали матричную функцию ${\mathbf{K}}(\Delta r),$ которая находится при $\Delta \varphi = 0.$ Ее рассчитывали при фиксированных значениях электрического расстояния $\Delta {{r}_{s}}$ с шагом, достаточным для построения с приемлемой точностью аппроксимации функции ${\mathbf{K}}(\Delta r)$:
(29)
$\Delta {{r}_{s}} = \pi \left\{ \begin{gathered} 1,{\text{ }}s = 0, \hfill \\ 1.125,{\text{ }}s = 1, \hfill \\ 1.25,{\text{ }}s = 2, \hfill \\ 1.5,{\text{ }}s = 3, \hfill \\ 1.75,{\text{ }}s = 4, \hfill \\ 2 + 0.5(s - 5),{\text{ 5}} \leqslant s \leqslant 41. \hfill \\ \end{gathered} \right..$При малых расстояниях между ЭИ элементы матричной функции быстро меняются при изменении аргумента, поэтому на участке $\Delta {{r}_{s}} \leqslant 2\pi $ шаг изменения расстояния уменьшен: при $\Delta {{r}_{s}} > 2\pi $ он равен ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Максимальное значение электрического расстояния равно $20\pi .$ Для вычисления матричной функции ${\mathbf{K}}(\Delta r)$ при больших расстояниях удобно воспользоваться ее асимптотическим представлением при $\Delta r \gg 1$:
(30)
${\mathbf{K}}_{{M,N}}^{a}(\Delta r) = {{a}_{{M,N}}}\frac{{\exp ( - i\rho )}}{\rho } + {{b}_{{M,N}}}\frac{{\exp ( - i\rho )}}{{{{\rho }^{2}}}}.$Коэффициенты ${{\left( {a,b} \right)}_{{M,N}}}$ можно найти аналитически, применяя асимптотические представления сферических функций Ганкеля. На практике удобнее оказался численный вариант, при котором указанные постоянные определяли из условий совпадения асимптотических ${\mathbf{K}}_{{M,N}}^{a}(\Delta r)$ и точных функций ${\mathbf{K}}_{{M,N}}^{{}}(\Delta r)$ при $\Delta r = 10,20\pi .$
Если решетка составлена из одинаковых ЭИ с одинаковыми операторами рассеяния ${{{\mathbf{L}}}_{\mu }},$ то лучшие результаты с точки зрения скорости вычислительного процесса дает аппроксимация не матрицы связи, а матриц взаимодействий ${\mathbf{W}}$, являющихся произведением матрицы связи и операторов рассеяния:
(31)
${{{\mathbf{W}}}_{{ss}}} = {{{\mathbf{L}}}_{{ss}}}{\mathbf{K}},\,\,\,\,{{{\mathbf{W}}}_{{ws}}} = {{{\mathbf{L}}}_{{ws}}}{\mathbf{K}}.$Матрицы взаимодействий напрямую входят в СЛАУ (19), описывающую решетку. При анализе решеток щелевых и ленточных излучателей использовалась сплайн-аппроксимация элементов матриц (31).
Независимо от способа аппроксимации переход к матричной функции ${\mathbf{K}}(\Delta r)$ дает существенное повышение эффективности метода. Массивы значений матричной функции рассчитываются однократно и сохраняются в виде файлов данных. Как отмечалось выше, эти данные инвариантны к типу излучателя и конфигурации решетки. При расчетах частных структур файлы считываются, преобразуются, и на их основе строятся те или иные аппроксимации, по которым определяются матрицы ${\mathbf{W}}_{{\mu ,\nu }}^{{}}$, входящие в СЛАУ (19). Таким образом, матричная функция K(Δr) играет роль специальной функции метода МОМР-РВСГ, которая однократно вычисляется и далее без существенных затрат ресурсов многократно используется при анализе ФАР.
Важным вопросом является выбор числа ВСГ. При этом следует иметь в виду, что число рассеянных и возбуждающих гармоник может быть различным. Число возбуждающих волн выбираем так, чтобы обеспечить необходимую точность представления поля на сфере, окружающей ЭИ. Наибольшее число гармоник необходимо для минимального расстояния $\Delta r$, которое в нашем случае равно π.
Число рассеянных волн существенно зависит от вида излучателя. Оно определяется из условия достижения приемлемой точности описания поля на сфере ЭИ суммой ВСГ при его возбуждении по входу. Числом учитываемых угломестных гармоник ${{N}_{\theta }}$ определяется общее число ВСГ ${{N}_{h}}\,:$
Были приняты следующие количественные критерии точности представления поля:
(33)
$\begin{gathered} {{\delta }^{e}} = \frac{1}{{4\pi \max \left| {{{E}_{r}}} \right|}}\int\limits_0^{2\pi } {\int\limits_0^\pi {\left| {E_{r}^{a} - {{E}_{r}}} \right|d\Omega } } , \\ {{\delta }^{m}} = \frac{1}{{4\pi \max \left| {{{H}_{r}}} \right|}}\int\limits_0^{2\pi } {\int\limits_0^\pi {\left| {H_{r}^{a} - {{H}_{r}}} \right|d\Omega } \,} . \\ \end{gathered} $Поля в соотношениях (33) брались на сфере, окружающей ЭИ с радиусом ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Индекс a соответствует приближенным аппроксимациям. Было принято условие, что погрешности ${{\delta }^{{e,m}}}$ не должны превышать 10–3 ни при каких условиях, т.е. при минимальном расстоянии $\Delta r$ для любой из рассеянных волн. Эти условия удовлетворялись при ${{N}_{{\theta s}}} = 5,$ ${{N}_{{\theta i}}} = 12$ (${{N}_{{\theta i,s}}}$ – число учитываемых угломестных гармоник возбуждающих и рассеянных волн). Таким образом, мы видим, что параметры ${{N}_{{\theta i,s}}}$ неодинаковые и, следовательно, матрицы ${\mathbf{K}},{\mathbf{L}}$ прямоугольные. При этом, однако, матрица ${\mathbf{W}}$ оказывается квадратной.
5. ОПЕРАТОР РАССЕЯНИЯ
Определение оператора рассеяния – следующий этап МОМР-РВСГ. На этом этапе учитывается конструкция ЭИ. Рассматривается одиночный ЭИ, который многократно возбуждается со стороны своих входов, а также со стороны свободного пространства ВСГ. В работе были исследованы три типа излучателей: щель в волноводе, щель в резонаторе, ленточный вибратор. Они показаны на рис. 2а–2в. Щель и лента имеют длину $L$ и ширину w. Ширина волновода a, а высота b. Волновод и волноводный резонатор (см. рис. 2а, 2б) заполнены диэлектриком с относительной проницаемостью ε. Щелевые излучатели имеют бесконечный бесконечно тонкий экран, в котором выполнена щель. Все металлические элементы конструкций идеально проводящие.
Волноводно-щелевой ЭИ предназначен для использования в составе волноводно-щелевой решетки бегущей волны, поэтому он имеет два входа 1, 2, роль которых выполняют полубесконечные волноводы, расположенные слева и справа от щели соответственно. Резонаторно-щелевой ЭИ возбуждается при помощи коаксиальной линии передачи, которая моделируется цилиндром, радиус которого ${{R}_{{\text{ц}}}}$. Цилиндр имеет контакт с верхней стенкой резонатора. В зазор между нижней стенкой и цилиндром включен источник напряжения с внутренним сопротивлением ${{R}_{{\text{г}}}}$, которое равно характеристическому сопротивлению коаксиальной линии. Данный источник выполняет функцию единственного входа 1 излучателя.
Рассмотрим процедуру определения оператора рассеяния в простейшем случае ленточного ЭИ. Решение для всех рассмотренных структур было получено с помощью стандартной методики, которая неоднократно описывалась в литературе. Она основана на записи интегральных уравнений (ИУ) относительно электрических токов на ленте или магнитных на щели и последующем решении ИУ методом Галеркина [30]. Поэтому подробно излагать ее не имеет смысла, остановимся только на некоторых существенных для нас моментах решения.
Излучатель имеет один вход 1 в виде сосредоточенного источника с сопротивлением ${{R}_{{\text{г}}}}$. Мы решаем граничную задачу в приближении узкой ленты, полагая, что
где $\lambda $ – длина волны в свободном пространстве.
Условия (34) позволяют нам учитывать только продольные компоненты электрических токов, текущих по ленте $I_{y}^{e}$ и пренебречь поперечными токами. Для записи ИУ воспользуемся представлением функции Грина свободного пространства в виде интеграла Фурье [28]:
(35)
$\begin{gathered} - ik{{W}_{0}}\int\limits_S {I_{y}^{e}(s{\kern 1pt} ')\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\frac{{\exp ( - i(x - x{\kern 1pt} '){{\kappa }_{1}} - i(y - y{\kern 1pt} '){{\kappa }_{2}})}}{\gamma }} } } \times \\ \times \,\,d{{\kappa }_{1}}d{{\kappa }_{2}}ds{\kern 1pt} ' = \delta (y)({{e}_{0}} + J{{R}_{{\text{г}}}}), \\ \gamma = \sqrt {\kappa _{1}^{2} + \kappa _{2}^{2} - {{k}^{2}}} . \\ \end{gathered} $Здесь ${{e}_{0}}$ – электродвижущая сила (ЭДС) источника напряжения, а $J$ – текущий через него полный ток:
(36)
$J = \int\limits_{{{ - w} \mathord{\left/ {\vphantom {{ - w} 2}} \right. \kern-0em} 2}}^{{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {I_{y}^{e}(x,0)dx} .$В соответствии с методом Галеркина представляем ток в виде ряда по базисным функциям ${{f}_{{bn}}}(x,y)$:
(37)
$\begin{gathered} I_{y}^{e}(x,y) = \sum\limits_p {{{X}_{p}}\frac{{{{f}_{{bp}}}(y)}}{{\sqrt {{{{\left( {{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} \right)}}^{2}} - {{x}^{2}}} }}} , \\ {{f}_{{bp}}}(x,y) = \sin ({{\alpha }_{p}}(y + {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2})),\,\,\,\,{{\alpha }_{p}} = {{\pi p} \mathord{\left/ {\vphantom {{\pi p} L}} \right. \kern-0em} L}, \\ \end{gathered} $Алгебраизация ИУ (35) проводится в соответствии с методом Галеркина:
(38)
$\begin{gathered} - ik{{W}_{0}}{{\pi }^{2}}\sum\limits_{p = 1}^P {{{X}_{p}}} \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {J_{0}^{2}\left( {{{\kappa }_{1}}\frac{w}{2}} \right)\frac{{{{\psi }_{p}}({{\kappa }_{2}})\psi _{q}^{ * }({{\kappa }_{2}})}}{\gamma }d{{\kappa }_{1}}d{{\kappa }_{2}}} } = \\ = \pi {{f}_{{bq}}}(0)\left( {{{e}_{0}} + \pi {{R}_{{\text{г}}}}\sum\limits_{n = 1}^N {{{X}_{p}}{{f}_{{bp}}}(0)} } \right), \\ q = 1,...P,\,\,\,\,{{\psi }_{p}}({{\kappa }_{2}}) = \int\limits_{ - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}}^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {{{f}_{{bp}}}(y)\exp (i{{\kappa }_{2}}y)dy} . \\ \end{gathered} $Соотношение (38) представляет собой СЛАУ относительно коэффициентов ${{X}_{p}}.$ ЭДС источника ${{e}_{0}}$ может быть выражена через параметры рассеяния:
где ${{U}_{i}}$ – амплитуда падающей на вход волны. Считаем, что она равна единице, ${{e}_{0}} = 2$. Тогда амплитуда отраженной волны ${{U}_{r}}$ представляется следующим образом:Отметим, что система (39) и соотношение (40) получены для случая возбуждения вибратора со стороны его входа. В выражении (40) мы использовали индекс $w$, чтобы подчеркнуть, что данный параметр соответствует возбуждению ЭИ со стороны его входа.
Полученный результат позволяет нам найти оператор ${{{\mathbf{L}}}_{{ww}}}$ (см. разд. 3), который в данном случае является скалярной величиной из-за наличия у ЭИ одного входа. Поскольку амплитуда падающей волны равна единице, то ${{{\mathbf{L}}}_{{ww}}} = {{U}_{r}}.$
Также мы теперь можем определить оператор ${{{\mathbf{L}}}_{{sw}}}.$ Для этого необходимо найти амплитуды ВСГ, возбуждаемых электрическим током на вибраторе. Для этого воспользуемся результатами [28]. При решении данной задачи был принят ряд упрощающих допущений.
Воспользуемся еще раз условиями (34). Если лента узкая, то мы можем приближенно заменить ток, распределенный по координате $x$ нитью тока:
Представление тока (41) нельзя использовать при решении интегрального уравнения, однако его применение для вычисления полей пространственных гармоник допустимо, так как поля ВСГ достаточно низкого порядка сравнительно слабо меняются по ширине ленты. Поэтому при интегрировании по координате $x$ допустимо поля ВСГ положить равными постоянной, например, значению при x = 0. Такое приближение соответствует представлению (41). Отметим, что при решении интегрального уравнения замена листка тока нитью недопустима, так как поле, возбужденное листком тока может существенно меняться в области, занятой током, т.е. на поверхности ленты.
Выражение (41) можно без труда записать в сферических координатах:
(42)
$\begin{gathered} I_{r}^{e}(r,\varphi ) = \pi \delta (\varphi - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2})\sum\limits_{p = 1}^P {{{X}_{p}}{{f}_{{bp}}}(r)} - \\ - \,\,\pi \delta (\varphi - {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2})\sum\limits_{p = 1}^P {{{X}_{p}}{{f}_{{bp}}}( - r)} . \\ \end{gathered} $При записи формулы (42) учтены соотношения
(43)
$\begin{gathered} r = y,\,\,\,\,\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},\,\,\,\,I_{r}^{e} = I_{y}^{e}\,\,\,\,{\text{при}}\,\,\,\,y > 0, \\ r = - y,\,\,\,\,\varphi = {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2},\,\,\,\,I_{r}^{e} = - I_{y}^{e}\,\,\,\,{\text{при}}\,\,\,\,y < 0. \\ \end{gathered} $Теперь для определения амплитуд рассеянных волн можем воспользоваться соотношением из [28, ф-ла (2.108)]:
(44)
$\begin{gathered} A_{{sn,m}}^{e} = - \frac{{{{W}_{0}}(2n + 1)(n - m)!P_{n}^{m}(0)}}{{4\pi (n + m)!}} \times \\ \times \,\,\int\limits_S {I_{r}^{e}(r{\kern 1pt} ',\varphi {\kern 1pt} ')r{\kern 1pt} '{{\psi }_{n}}(kr{\kern 1pt} ')\exp ( - im\varphi {\kern 1pt} ')dr{\kern 1pt} 'd\varphi {\kern 1pt} '} , \\ \end{gathered} $Для того чтобы найти оператор ${{{\mathbf{L}}}_{{sw}}}$, достаточно разделить выражение (44) на амплитуду падающей волны ${{U}_{i}}$ (но в силу того, что ток пропорционален ${{U}_{i}}$, она не войдет в соотношение для оператора).
Для того чтобы найти операторы ${{{\mathbf{L}}}_{{ws}}},{{{\mathbf{L}}}_{{ss}}},$ нам необходимо возбудить вибраторы полями ВСГ. Интегральное уравнение в этом случае приобретает вид
(45)
$\begin{gathered} - ik{{W}_{0}}\int\limits_S {I_{y}^{e}(s{\kern 1pt} ')\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\frac{{\exp ( - i(x - x{\kern 1pt} '){{\kappa }_{1}} - i(y - y{\kern 1pt} '){{\kappa }_{2}})}}{\gamma }} } } \times \\ \times \,\,d{{\kappa }_{1}}d{{\kappa }_{2}}ds{\kern 1pt} ' = \delta (y)J{{R}_{{\text{г}}}} + E_{{iyn,m}}^{e}(x,y). \\ \end{gathered} $Здесь $E_{{iyn,m}}^{e}(x,y)$ – поле возбуждающей ВСГ электрического типа на ленте. Уравнение (45) записано для случая единичной амплитуды ВСГ.
Алгебраизация уравнения (45) приводит к необходимости вычисления интегралов ${{i}_{{n,m,q}}},$ в которые входит функция $E_{{iyn,m}}^{e}(x,y)\,:$
(46)
${{i}_{{n,m,q}}} = \int\limits_{{{ - w} \mathord{\left/ {\vphantom {{ - w} 2}} \right. \kern-0em} 2}}^{{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. \kern-0em} 2}}^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {\frac{{{{f}_{{bq}}}(y)E_{{iyn,m}}^{e}(x,y)}}{{\sqrt {{{{\left( {{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0em} 2}} \right)}}^{2}} - {{x}^{2}}} }}} } dxdy.$Применим для вычисления параметров ${{i}_{{n,m,q}}}$ прием, аналогичный приему, использованному выше (см. формулу (41)):
(47)
$\begin{gathered} {{i}_{{n,m,q}}} = \pi \int\limits_{{{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. \kern-0em} 2}}^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {{{f}_{{bq}}}(y)E_{{iyn,m}}^{e}(0,y)dy} = \\ = \pi \int\limits_0^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {{{f}_{{bq}}}(r)E_{{irn,m}}^{e}(r,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2})dr} - \\ - \,\,\pi \int\limits_0^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {{{f}_{{bq}}}( - r)E_{{irn,m}}^{e}(r,{{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2})dr} . \\ \end{gathered} $Поскольку компонента поля $E_{{irn,m}}^{e}$ выражается с помощью соотношений (1), (2), то для определения параметров ${{i}_{{n,m,q}}}$ необходимо взять интегралы, аналогичные интегралам, стоящим в формуле (44). Их определяли численно. После этого СЛАУ для коэффициентов ${{X}_{p}}$ при возбуждении ВСГ полностью определена и может быть решена. В результате решения находим параметры ${{X}_{{sp}}}$, где индекс $s$ показывает, что они получены при возбуждении вибратора ВСГ.
Для определения оператора ${{{\mathbf{L}}}_{{ss}}}$ мы должны воспользоваться соотношением (44), заменив в нем ${{X}_{{wp}}}$ на ${{X}_{{sp}}}$. Для оператора ${{{\mathbf{L}}}_{{ws}}}$ имеется следующее соотношение:
(48)
${{{\mathbf{L}}}_{{ws}}} = \pi {{R}_{{\text{г}}}}\sum\limits_{p = 1}^P {{{X}_{{sp}}}{{f}_{{bp}}}(0)} .$Таким образом, оператор рассеяния полностью определен. Отметим, что в рамках принятых приближений удалось уменьшить число учитываемых пространственных гармоник за счет исключения магнитных волн, а также за счет учета только четных волн. Нечетные волны не возбуждаются вибраторами в силу симметрии структуры относительно плоскости XOY.
6. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
На рис. 3 представлена зависимость модуля элемента матрицы взаимодействия $\left| {{{{\mathbf{W}}}_{{6,6}}}} \right|$ от электрического расстояния ρ. Матрица взаимодействия получена для щелевой решетки. Она не зависит от типа щелевого излучателя (см. рис. 2а, 2б). Как отмечено выше, для обозначения ВСГ была использована сквозная нумерация с индексом N. Номеру $N = 6$ соответствуют индексы ВСГ в двойной нумерации: $n = 1,$ $m = - 1.$
Рис. 3.
Зависимость модуля (а) и фазы (б) элемента матрицы взаимодействия ${{{\mathbf{W}}}_{{6,6}}},$ а также модуля элемента матрицы взаимодействия ${{{\mathbf{W}}}_{{2,2}}}$ (в) от электрического расстояния: точки – расчет по формуле (30), сплошная кривая – сплайн аппроксимация.

Отметим, что учет конкретного типа излучателя позволяет дополнительно уменьшить размерность матрицы взаимодействия, так как многие из ВСГ возбуждаются щелью или лентой с нулевыми или пренебрежимо малыми амплитудами. Выше было отмечено, что при описании рассеянных полей мы ограничились пятью угломестными гармониками ${{N}_{{\theta s}}} = 5.$ При этом в соответствии с формулой (32) общее число гармоник равно 35. Из них существенные амплитуды имеют волны с номерами N в сквозной нумерации, представленными в таблице 1.
Таблица 1.
Номера, ВСГ с существенными амплитудами в сквозной и двойной нумерациях
| N | n | m |
|---|---|---|
| 2 | 3 | –3 |
| 6 | 1 | –1 |
| 7 | 3 | –1 |
| 12 | 1 | 1 |
| 13 | 3 | 1 |
| 17 | 3 | 3 |
Как следует из таблицы, для достижения приемлемой точности расчетов нам достаточно учитывать шесть ВСГ.
Представленные на рис. 3а–3в зависимости получены при $L = 10,$ $w = 1,$ $f = 9.15$ ГГц. Все размеры на рис. 3 и далее приведены в миллиметрах. Сплошная кривая рассчитана с использованием сплайн-аппроксимации матричной функции ${\mathbf{W}}(\rho )$. Точки соответствуют расчету по формуле (30). Как видно из рис. 3а, аппроксимация при больших ρ описывает функцию $\left| {{{{\mathbf{W}}}_{{6,6}}}} \right|$ с достаточно высокой точностью уже при $\rho > 2\pi $. На рис. 3б показана зависимость фазы функции ${{{\mathbf{W}}}_{{6,6}}}$ от электрического расстояния $\rho $. Видно, что для фазы совпадение между ними еще лучше, чем для амплитуды. На рис. 3в показана зависимость модуля функции ${{{\mathbf{W}}}_{{2,2}}}$ также от параметра $\rho $. В данном случае асимптотическая формула хуже описывает исходную функцию. Причина в том, что номеру $N = 2$ соответствует ВСГ с большим угломестным индексом $n = 3$, для которого условия дальней зоны начинают выполнять при больших ρ. Очевидно, что расхождение асимптотики и точной функции будет увеличиваться с ростом индекса $n$.
Из рис. 3а–3в может показаться, что вклады ВСГ с номерами $N = 2,6$ в матрицу взаимодействия сильно отличаются друг от друга. Однако это не совсем так, поскольку при изменении индекса существенно меняются сами пространственные гармоники (см. соотношение (2)). Поэтому изменения в амплитудах не дают полного представления об изменении вклада ВСГ в рассеянное поле.
Рассмотрим далее результаты численного решения граничной задачи для ленточного ЭИ. На рис. 4 показана частотная зависимость модуля коэффициента отражения от входа вибратора ${{S}_{{11}}}$ при $L = 13.85$, $w = 1$, ${{R}_{{\text{г}}}} = 70$ Ом. Для представления тока на ленте мы использовали три базисные функции (37). Число базисных функций выбиралось из условия сходимости решения. При этом использовался следующий критерий сходимости:
(49)
$\left| {\left| {S_{{11}}^{{(n + 1)}}} \right| - \left| {S_{{11}}^{{(n)}}} \right|} \right| < {{10}^{{ - 3}}},$Рис. 4.
Частотная зависимость модуля коэффициента отражения одиночного ленточного излучателя: сплошная кривая – расчет по МОМР-РВСГ, точки – расчет по методу ИУ.
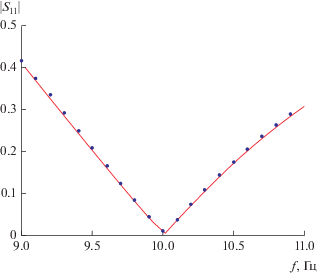
Зависимости получены методом МОМР-РВСГ и с помощью стандартной системы электродинамического моделирования. При решении в такой системе (см. рис. 4, точки) нами использовался метод ИУ. Расхождение решений, полученных двумя способами по модулю коэффициента отражения не превышает 0.01.
Важным параметром, характеризующим точность решения, является выполнение закона сохранения энергии. Для одиночного вибратора он формулируется следующим образом:
(50)
$\begin{gathered} {{\left| {{{S}_{{11}}}} \right|}^{2}} + \frac{\pi }{{{{P}_{i}}{{W}_{0}}}}\sum\limits_{n,m} {{{{\left| {{{A}_{{sn,m}}}} \right|}}^{2}} \times } \\ \times \,\,\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\left( {{{{\left( {\frac{{mP_{n}^{m}(\cos \theta )}}{{\sin \theta }}} \right)}}^{2}} + {{{\left( {\frac{{dP_{n}^{m}(\cos \theta )}}{{d\theta }}} \right)}}^{2}}} \right)\sin \theta d\theta } = 1, \\ \end{gathered} $(51)
${{P}_{i}} = {{U_{i}^{2}} \mathord{\left/ {\vphantom {{U_{i}^{2}} {2{{R}_{{\text{г}}}}}}} \right. \kern-0em} {2{{R}_{{\text{г}}}}}}.$– мощность, падающая на вход вибратора.
В формуле (50) ${{A}_{{sn,m}}}$ – амплитуды четных рассеянных ВСГ электрического типа. При выводе уравнения (51) принято во внимание асимптотическое поведение сферических функций Ганкеля (24).
На рис. 5 показана частотная зависимость параметра $\Delta $, показывающего точность выполнения закона сохранения энергии ($\Delta $ – модуль разницы между выражением в левой части (51) и единицей). Видно, что энергетический дисбаланс весьма мал, что является свидетельством корректности использованного метода решения.
Точность решения проверялась также путем сравнения с результатами, полученными при помощи стандартной системы. Расчеты в ней, как и в случае одиночного вибратора, проводили методом ИУ. На рис. 6 показана решетка из пяти вибраторов, рассчитанная в режиме синфазного возбуждения, расстояние между вибраторами равно 17.
На рис. 7а–7в показаны частотные зависимости модулей коэффициентов отражения от входов вибраторов с номерами 1–3 (см. рис. 6). Под коэффициентом отражения вибратора в составе решетки ${{R}_{j}}$ ($j = 1,...5$) мы понимаем отношение амплитуды отраженной волны к амплитуде падающей волны при условии возбуждения всех элементов решетки. Параметры вибраторов: $L = 13.85,$ $w = 1,$ ${{R}_{{\text{г}}}} = 70$ Ом. Сплошные кривые получены методом МОМР-РВСГ, а точки – методом ИУ. Расхождение в параметрах рассеяния не превышает 0.01.
Рис. 7.
Частотная зависимость модулей коэффициентов отражения первого–третьего (а)–(в) ленточных излучателей в составе решетки, сплошные кривые – расчет по МОМР-РВСГ, точки – расчет по методу ИУ.

На рис. 8 показана частотная зависимость погрешности $\Delta $ выполнения закона сохранения энергии для пятиэлементной решетки. На рис. 9 показана нормированная ДН решетки по вектору Пойнтинга в плоскости $ZOY$.
Рис. 9.
Диаграмма направленности решетки ленточных излучателей: сплошная кривая – расчет по МОМР-РВСГ, точки – расчет по методу ИУ.

В целом следует отметить достаточно хорошее совпадение результатов, полученных методом МОМР-РВСГ, с расчетами с помощью стандартной системы моделирования. Исключение составляет только уровень дальних боковых лепестков ДН, который в случае МОМР-РВСГ на 2.5 дБ выше, чем при использовании метода ИУ. При этом наблюдается хорошее совпадение ДН в области главного и первого бокового лепестков.
Рассмотрим далее применение МОМР-РВСГ для анализа решетки щелевых ЭИ, изображенных на рис. 2б. Мы рассматривали ЭИ со следующими параметрами: $a = 14,$ $b = 5,$ $L = 10,$ $w = 1.2,$ ${{R}_{{\text{ц}}}} = 0.62,$ ${{L}_{c}} = 4,$ ${{L}_{1}} = 7.06,$ ${{L}_{2}} = 1,$ $\varepsilon = 2.5.$ Решетка состояла из 26 излучателей (${{N}_{x}} = 26$) расположенных вдоль оси 0х с периодом ${{P}_{x}} = 17.$
Параметры ЭИ выбраны из условия его согласования на частоте 10 ГГц. Частотная характеристика модуля коэффициента отражения ${{S}_{{11}}}$ излучателя приведена на рис. 10.
Рис. 10.
Частотная зависимость модуля коэффициента отражения одиночного резонаторно – щелевого излучателя: сплошная кривая – расчет по МОМР-РВСГ, точки – расчет по методу ИУ.

Контроль точности решения для щелевого излучателя также осуществлялся путем расчета погрешности выполнения закона сохранения энергии $\Delta $. Ее зависимость от частоты показана на рис. 11. Из кривых на рис. 10, 11 видно, что решение по МОМР-РВСГ имеет достаточно высокую точность и в случае щелевого ЭИ.
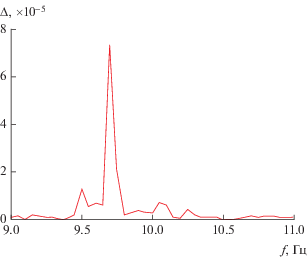
Рис. 11.
Погрешность выполнения закона сохранения энергии для одиночного резонаторно – щелевого излучателя.
На рис. 12 представлена частотная зависимость модуля коэффициента отражения. Кривая 2 соответствует одиночному ЭИ (см. также рис. 10), а кривая 1 соответствует коэффициенту отражения от решетки. Отметим, что решетка работает в режиме синфазного возбуждения. При этом каждый из ее элементов может быть описан при помощи коэффициента отражения излучателя в составе решетки ${{R}_{j}},$ $j = 1,...,{{N}_{x}}.$ Под коэффициентом отражения всей решетки в целом мы понимаем корень из отношения суммарной мощности всех волн, отраженных от входов ЭИ, к мощности всех падающих волн. Из рис. 12 видно, что резонансная частота, соответствующая минимуму ${{S}_{{11}}}$ сместилась вверх, а минимальное значение коэффициента отражения увеличилось, что является следствием взаимодействия излучателей в решетке.
Рис. 12.
Частотная зависимость модуля коэффициента отражения решетки резонаторно-щелевых излучателей (кривая 1) в сравнении с коэффициентом отражения одиночного резонаторно-щелевого излучателя (кривая 2).

На рис. 13 представлено распределение коэффициентов ${{R}_{j}}$ вдоль решетки на частоте 10 ГГц. Видно, что на границах структуры наблюдаются достаточно резкие изменения параметров ${{R}_{j}},$ являющиеся следствием краевых эффектов. При смещении к центру вариации коэффициента отражения уменьшаются, а его значение стремится к коэффициенту отражения в составе бесконечной решетки.
Рис. 13.
Распределение модулей коэффициентов отражения резонаторно-щелевых излучателей в составе 26-элементной решетки вдоль решетки.

На рис. 14 представлена нормированная ДН структуры на частоте 10 ГГц в плоскости $XOZ$. Она соответствует ДН линейной антенны с равномерным амплитудно-фазовым распределением источников. Таким образом, мы видим, что влияние краевых эффектов на ДН незначительно.
В заключение рассмотрим применение МОМР-РВСГ для анализа волноводно-щелевой линейной решетки. Ее излучатель показан на рис. 2в. Особенностью данной структуры является схема возбуждения ЭИ. Если раньше каждый из них возбуждался индивидуально, то теперь все они возбуждаются последовательно общим волноводом. Таким образом, в составе решетки появляется дополнительный блок, выполняющий функцию связи ЭИ.
Для анализа решетки целесообразно рассмотреть схему двух многополюсников (рис. 15). Первый из них с матрицей рассеяния ${{S}_{a}}$ является решеткой, состоящей из ${{N}_{x}}$ щелевых ЭИ. Входы ЭИ не связаны между собой. Матрицу ${{S}_{a}}$ мы можем найти в соответствии с методикой, изложенной в разд. 3, последовательно возбуждая решетку со стороны всех ее входов. Второй многополюсник с матрицей рассеяния ${{S}_{c}}$ состоит из отрезков волноводов длиной ${{P}_{x}}$. Определение матрицы ${{S}_{c}}$ не составляет труда, и мы не будем останавливаться на этом вопросе. Из рис. 15 видно, что два входа решетки с номерами $1,2{{N}_{x}}$ остаются свободными. Они являются входами интересующей нас волноводно-щелевой решетки. Присвоим им соответственно номера $1,2$.
Найти результирующую матрицу рассеяния волноводно-щелевой решетки по заданным матрицам ${{S}_{{a,c}}}$ можно любым из известных способов. Мы использовали методику анализа сложных составных многополюсников описанную в книге [31].
На рис. 16 показана частотная зависимость параметров рассеяния волноводно-щелевой решетки от частоты. Здесь $R$ – модуль коэффициента отражения от входа 1, а $T$ – модуль коэффициента передачи со входа 1 на вход $2{{N}_{x}}.$ Кривые получены при следующих параметрах структуры: ${{N}_{x}} = 30,$ ${{P}_{x}} = 17,$ $a = 16,$ $b = 5,$ $L = 9,$ $w = 1,$ $\varepsilon = 2.5.$
Видно, что коэффициент передачи падает с ростом частоты, а коэффициент отражения растет. Причем на частотах, близких к 11 ГГц, в некоторой полосе наблюдается резкий рост коэффициента отражения. Данный эффект часто называют эффектом нормали, поскольку в указанной полосе максимум ДН направлен по нормали к плоскости решетки.
Эволюцию ДН анализируемой структуры можно понять из рис. 17а–17в, на котором показаны нормированные ДН в плоскости XOZ, рассчитанные соответственно на частотах 9, 10 и 10.5 ГГц. Положительные углы $\theta $ соответствуют полуплоскости $x > 0,$ а отрицательные $x < 0.$ Видно, что максимум ДН находится в области отрицательных углов. Если учесть, что возбуждение решетки ведется со входа 1, т.е. в положительном направлении по оси 0х, то можно сделать вывод, что излучение происходит на минус первой пространственной гармонике, что возможно благодаря диэлектрическому заполнению волновода.
Рис. 17.
Диаграммы направленности волноводно-щелевой решетки на частотах 9.5 (а), 10 (б), 10.5 ГГц (в).
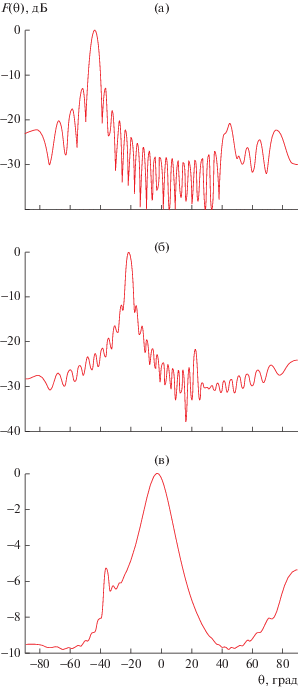
Главный луч ДН смещается при повышении частоты в направлении угла $\theta = 0,$ т.е. к нормали к плоскости, в которой расположена структура. При этом изменяется амплитудное распределение источников в апертуре решетки. На рис. 18 показано распределение нормированного модуля амплитуды доминирующей рассеянной пространственной гармоники ${{A}_{{s6,j}}}$ ($j$ – номер щели). Номер гармоники в сквозной нумерации соответствует индексам двойной нумерации $n = 1,$ $m = - 1$ (см. таблицу). Нормировка осуществлялась на максимальную амплитуду гармоники.
Рис. 18.
Распределение модуля амплитуды пространственной гармоники ${{A}_{{s,6}}}$ вдоль решетки на частотах 9.5 (1), 10 (2), 10.5 ГГц (3).

Видно, что распределение имеет экспоненциальный характер, что соответствует элементарной теории решеток бегущей волны [32] с одинаковыми ЭИ. Скорость затухания волны в решетке сильно зависит от частоты. Кривые 1–3 рассчитаны при $f = 9.5,10,10.5$ ГГц. Амплитудное распределение определяет форму ДН. В частности, на частоте 10.5 ГГц скорость затухания столь велика, что практически работает лишь небольшой участок структуры, расположенный в ее левой части. При этом ДН сильно искажается (см. рис. 17в).
Программа расчета щелевых и ленточных решеток была реализована в среде Маткад. Полный расчет характеристик решетки из 30 элементов на 10 частотных точках занимает 20…30 с при использовании компьютера со средней производительностью. При этом существенная часть времени расходуется на вычисление ДН. Если анализ не связан с изменением параметров ЭИ, то оператор рассеяния определяется однократно.
ЗАКЛЮЧЕНИЕ
Из представленных результатов видно, что алгоритм на основе МОМР-РВСГ обеспечивает при анализе решеток щелевых ЭИ существенно более высокую вычислительную эффективность, чем стандартные системы электродинамического моделирования и при этом дает близкие к ним результаты, что является подтверждением его точности.
Одним из ключевых этапов метода является решение граничной задачи для одиночного ЭИ и определение его оператора рассеяния. В рассмотренном нами случае несложная геометрия щели или ленты позволяет решить эту задачу достаточно простыми средствами. Однако, если рассматривать возможность применения МОМР-РВСГ к решеткам ЭИ произвольного вида, то нетрудно увидеть, что ее решение требует создания специальной системы электродинамического моделирования, которая будет мало отличаться от уже существующих универсальных систем типа HFSS. Поэтому целесообразно было бы рассмотреть возможность их использования для решения указанной задачи.
Современные системы электродинамического моделирования предусматривают решение задач возбуждения сложных структур заданными источниками. Особенностью МОМР-РВСГ является то, что источником служит поле ВСГ. Напрямую современные системы моделирования таких источников не имеют, что заставляет искать те или иные обходные пути решения данной задачи.
В заключение имеет смысл остановиться на ограничениях на конструкцию ЭИ и параметры решетки, которые накладывает МОМР-РВСГ. Главным из них является то, что излучатели должны быть вписаны в сферы некоторого радиуса и эти сферы не должны пересекаться. Несложно увидеть, что выполнить данное условие не всегда возможно даже для таких структур как щели. Например, если они расположены достаточно близко.
Требование на отсутствие пересечений сфер соседних ЭИ является следствием представления поля в виде разложения по сферическим гармоникам. Его можно ослабить, если в качестве базиса использовать решения уравнений Максвелла в координатных системах более общего вида, например в сфероидальной системе координат. В этом случае поверхность, окружающая ЭИ будет иметь форму эллипсоида вращения, вытянутого вдоль оси 0z, что ослабит ограничения на соответствующий габаритный размер ЭИ.
Список литературы
Банков С.Е., Курушин А.А. Электродинамика для пользователей САПР СВЧ. М.: Солон–Пресс. 2017.
Jian-Ming Jin. The Finite Element Method in Electromagnetics. 3rd ed. N-Y.: Wiley-IEEE Press, 2014.
Harrington R.F. Field Computation by Moment Methods. N-Y. USA: Macmillan, 1968.
Engheta N., Murphy W.D., Rokhlin V., Vassilion M.S. // IEEE Trans. 1992. V. AP-40. № 6. P. 634.
Song J.M., Chew W.C. // Microwave and Optical Technology Letters. 1995. V. 10. № 1. P. 14.
Song J.M., Lu C.C., Chew W.C. // IEEE Trans. 1997. V. AP-45. № 10. P. 1488.
Boag A., Mittra R. // IEEE Trans. 2007. V. 42. № 4. P. 366.
Canning F.X. // IEEE Antennas and Propagation Magazine. 1990. V. 42. № 5. P. 18.
Bleszynski E., Jaroszewicz T. // Radio Sci. 1996. V. 31. № 5. P. 1225.
Michielssen E., Boag A. // Microwave and Optical Technology Letters. 1994. V. 7. № 12. P. 790.
Seo S.M., Lee J.-F. // IEEE Trans. 1997. V. M-41. № 9. P. 1476.
Prakash V., Mittra R. // Microwave Opt. Technol. Lett. 2003. V. 36. № 1. P. 95.
Matekovits L., Laza V.A., Vecchi G. // IEEE Trans. 2007. V. AP-55. № 9. P. 2509.
Lu W.B., Cui T.J., Qian Z.G., Yin X.X., Hong W. // IEEE Trans. 2004. V. AP-52. № 11. P. 3078.
Bekers D.J., Van Eijndhoven S.J.L., Van de Ven A.A.F. et al. // IEEE Trans. 2006. V. MTT-54. № 6. P. 2821.
Roscoe A.J., Perrott R.A. // IEEE Trans. 1994. V. AP-42. № 7. P. 983.
Bhattacharyya A.K. // IEEE Trans. 2015. V. AP-63. № 3. P. 1040.
Xiao G.B., Mao J.F., Yuan B. // IEEE Trans. 2008. V. AP-56. № 12. P. 3723.
Xiang S., Xiao G., Tian X., Mao J. // IEEE Trans. 2013. V. AP-61. № 11. P. 5453.
Roblin C., Sibille A. // Proc. of 29th URSI General Assembly. Chicago. USA. 10–16 August 2008.
Кузикова. Н.И. // Антенны. 2004. Вып. 1(81). С. 79.
Кузикова Н.И. // Тез. докл. Всерос. науч.-техн. конф. ИСТ-2001. Н. Новгород. 2001. С. 49.
Mohammad A., Homayoon O. // IEEE Trans. 2018. V. AP-66. № 11. P. 6233.
Ettorre M., Sauleau R., Le Coq L. // IEEE Trans. 2011. V. AP-59. № 4. P. 1093.
Akiyama A., Yamamoto T., Hirokawa J. et al. // IEE Proc. Microwaves, Antennas and Propagation. 2000. V. 147. № 2. P. 134.
Банков С.Е., Калошин В.А., Фролова Е.В. // Журнал радиоэлектроники. 2017. № 5. http://jre.cplire.ru/jre/may17/9/text.pdf.
Бaнкoв C.E. // PЭ. 2018. T. 63. № 9. C. 902.
Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь, 1983.
Янке Е., Эмде Ф., Леш Ф. Специальные функции. М.: Наука, 1964.
Никольский В.В. Вариационные методы для внутренних задач электродинамики. М.: Наука, 1967.
Гупта К., Гардж Р., Чадха Р. Машинное проектирование СВЧ устройств. М.: Радио и связь, 1987.
Банков С.Е. Антенные решетки с последовательным питанием. М.: Физматлит, 2013.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника










