Радиотехника и электроника, 2020, T. 65, № 10, стр. 967-978

ВВЕДЕНИЕ

Антенные решетки (АР), располагаемые на конической поверхности летательного аппарата, позволяют существенно уменьшить объем носовой части, занимаемой непосредственно антенной, и отказаться от использования дорогостоящего обтекателя. Проведенные ранее исследования таких антенн (см., например, [1–5]), с одной стороны, продемонстрировали возможности их практической реализации, а с другой – поставили ряд задач, связанных с необходимостью разработки более адекватных алгоритмов моделирования, учета дифракционных эффектов на криволинейной поверхности конуса и определения оптимальной структуры излучателей и их возбуждения, обеспечивающих получение требуемых характеристик антенны. Так, до сих пор неясен вопрос о максимальном коэффициенте направленного действия (КНД) конической антенны и его зависимости от геометрии конуса и структуры излучателей. В частности, в [2] отмечалось, что максимальный КНД конической антенны не превышает КНД эквивалентного плоского раскрыва. Однако это заключение было сделано на основе приближенных методов анализа и требует дальнейшего изучения характеристик направленности конических антенн.

Современные численные методы решения электродинамических задач позволяют с высокой степенью точности ответить на поставленные выше вопросы. В данной работе приводится один из наиболее удобных алгоритмов анализа характеристик конической АР, позволяющий не только определить оптимальные характеристики антенны, но и сформировать требования, предъявляемые к отдельным излучателям и их взаимному расположению.

Наиболее целесообразным типом излучателей для рассматриваемой антенны являются щелевые излучатели, расположенные на поверхности конуса. Такие излучатели обладают хорошей механической прочностью, хорошей аэродинамикой и возможностью работать в значительных интервалах перепада температуры. Поэтому нами были исследованы возможности антенных решеток, состоящих из щелевых излучателей и расположенных на проводящей конической поверхности, и проведено электродинамическое моделирование характеристик направленности таких антенн.

Рассмотрены предельные возможности по параметрам конической антенны с квазинепрерывным распределением возбуждения за счет использования элементарных щелевых излучателей и проведена оптимизация их расположения и возбуждения. Также исследованы возможности реализации этого оптимального возбуждения с помощью волноводно-щелевых антенных решеток (ВЩАР) различной конфигурации.

1. ПОЛЕ ИЗЛУЧЕНИЯ И ДИАГРАММА НАПРАВЛЕННОСТИ АР, СОСТОЯЩЕЙ ИЗ ЩЕЛЕВЫХ ИЗЛУЧАТЕЛЕЙ И РАСПОЛОЖЕННОЙ НА ПРОВОДЯЩЕЙ КОНИЧЕСКОЙ ПОВЕРХНОСТИ

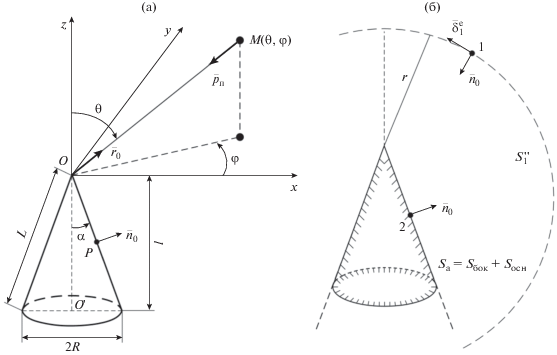
Рассмотрим дифракцию плоской волны, падающей на проводящую коническую поверхность (бесконечную или конечную с высотой конуса l и углом при вершине α (рис. 1а)). Пусть с направления (θ, φ ) вдоль вектора ${{\vec {p}}_{п}} = - {{\vec {r}}_{0}}$ на эту поверхность падает плоская волна с частотой ω и с вектором электрического поля на поверхности конуса:

где ${{\vec {r}}_{0}}$, ${{\vec {\theta }}_{0}}$, ${{\vec {\varphi }}_{0}}$ – единичные векторы сферической системы координат; ${{E}_{п}} = \left| {{{{\vec {E}}}_{п}}({{{\vec {r}}}_{0}})} \right|$ – комплексная амплитуда напряженности падающего электрического поля; ${{\alpha }_{\theta }}$, ${{\alpha }_{\varphi }}$ – в общем случае комплексные коэффициенты, определяющие поляризацию падающего поля.

При дифракции падающего поля на конусе на его поверхности в произвольной точке P, совпадающей с точкой 2, возникает магнитное поле ${{\vec {H}}_{п}}(P,{{\vec {r}}_{0}})$ вида

где ${{\vec {H}}_{{п1}}}(P,{{\vec {r}}_{0}})$ – составляющая напряженности полного магнитного поля в точке P при падении на конус только волны с направления ${{\vec {r}}_{0}}$ с напряженностью ${{\vec {E}}_{{п1}}}$, а ${{\vec {H}}_{{п2}}}(P,{{\vec {r}}_{0}})$ – аналогичная составляющая поля только при падении волны с напряженностью ${{\vec {E}}_{{п2}}}$.

Наличие магнитного поля на поверхности конуса эквивалентно возбуждению на его поверхности поверхностных электрических токов ${{\vec {\delta }}^{e}}(P)$ вида

где ${{\vec {n}}_{0}}$ – единичный вектор внешней к поверхности конуса нормали (рис. 1б).

Рассмотрим теперь излучение конической антенны в режиме возбуждения. Пусть на поверхности конуса в произвольной точке 2 расположены щелевые излучатели, которые в режиме активного возбуждения создают на частоте ω в точке 2 напряженность электрического поля ${{\vec {E}}_{2}}(2)$ (см. рис. 1б).

Предполагая, что источники – элементарные с линейным током ${{I}_{1}}$ вида

(${{\vec {r}}_{1}}$ – радиус-вектор точки источника 1), а также используя условие взаимности, в соответствии с интегральной формулировкой леммы Лоренца при r → ∞ поле ${{\vec {E}}_{2}}$ источника 2 в точке 1 определяем по соотношению где ${{\vec {\tau }}_{{01}}}$ – единичный вектор ориентации поля ${{\vec {E}}_{2}}(1)$.

Соответственно, поле ${{\vec {\tau }}_{{01}}}$ составляющей находим следующим образом:

В соотношениях (5), (6) $\vec {\delta }_{1}^{e}(2)$ – поверхностная плотность электрического тока, возникающего на поверхности конуса при падении на конус поля от источника 1; ${{\vec {E}}_{2}}(2)$ – напряженность электрического поля источников, расположенных на конусе, в режиме возбуждения; ${{\vec {E}}_{2}}(1)$ – напряженность электрического поля в точке 1, излучаемого источниками, расположенными на конусе при r → ∞.

Соотношения (5), (6) позволяют найти поле излучения и диаграммы направленности (ДН) произвольной антенны или АР, расположенных на поверхности конуса, с учетом дифракционных эффектов, если известно решение соответствующей дифракционной задачи, приведенное, например, в [6, 7] или полученное методами численного моделирования¹¹. Подобный подход рассмотрен в [8, 9] и может быть использован для определения поля излучения как одиночной щели, так и системы щелей, расположенных на проводящей поверхности.

В первом приближении напряженность магнитного поля, а следовательно, и распределение поверхностных токов на проводящей конической поверхности можно найти как

где ${{\vec {H}}_{{пад}}}(P,{{\vec {r}}_{0}})$ – напряженность магнитного поля падающей плоской волны в точке P.

2. ОПТИМИЗАЦИЯ СТРУКТУРЫ И ХАРАКТЕРИСТИК НАПРАВЛЕННОСТИ АР, РАСПОЛОЖЕННОЙ НА ПОВЕРХНОСТИ ПРОВОДЯЩЕГО КОНУСА

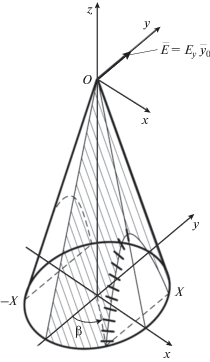
Воспользуемся приведенными выше соотношениями для оптимизации структуры АР и ее характеристик направленности применительно к следующей задаче: АР должна обладать максимальным КНД в направлении оси конуса с возможностью формирования суммарно-разностной ДН в двух взаимно-ортогональных плоскостях. Пусть поляризация АР в направлении оси конуса выбирается линейной с вектором излучаемого поля $\vec {E}(0,0)$, направленным вдоль оси Oy.

Для решения задачи по выбору оптимальной структуры и оптимального возбуждения рассмотрим случай дифракции плоской волны, падающей на конус вдоль оси Oz, с вектором электрического поля ${{\vec {\tau }}_{{01}}} = {{\vec {y}}_{0}}$, т.е. ${{\alpha }_{\theta }} = 0$, ${{\alpha }_{\varphi }} = 1$ в соотношении (1). Тогда напряженность электрического поля излучения конической антенны в направлении оси Oz определяется соотношением (5), и с учетом (6) получаем соотношение для поля основной поляризации:

Максимальное значение $\left| {{{{\vec {E}}}_{2}}(r,0,0)} \right|$ достигается при возбуждении антенны по закону

где c – произвольная константа.

Соответственно,

Максимальный КНД антенны в направлении оси Oz $D_{{макс}}^{{кон}}$ рассчитывается по соотношению

где ${{W}_{0}} = 120\pi $ – волновое сопротивление свободного пространства; ${{W}_{S}}$ – поверхностное (на конусе) волновое сопротивление.

Учитывая, что для щелевых излучателей ${{W}_{S}} = {{W}_{0}}$ [4], получаем

Входящее в (11) соотношение ${{{{{\left| {\vec {\delta }_{{10}}^{e}(2)} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {\vec {\delta }_{{10}}^{e}(2)} \right|}}^{2}}} {E_{п}^{2}}}} \right. \kern-0em} {E_{п}^{2}}}$ можно определить на модельной задаче, когда конус переходит в плоскость (α = 90°), а боковая поверхность конуса в апертуру с круглым раскрывом. При этом при r → ∞ амплитуду тока на апертуре можно полагать постоянной:

Кроме того, в соответствии с (11) для круглой апертуры максимальный КНД $D_{{макс}}^{{апер}}$ может быть записан в виде

Вместе с тем $D_{{макс}}^{{апер}}$ можно найти как

Из сравнения (13) и (14) получаем

Подставляя (15) в (11), находим

Величина $\vec {\delta }_{{10}}^{{\operatorname{const} }}$ зависит от вида и значений напряженности электрического поля, падающего на конус или плоскую апертуру. Для рассматриваемого частного случая падения поля плоской волны, распространяющейся вдоль оси Oz с напряженностью электрического поля ${{\vec {E}}_{п}} = {{E}_{п}}{{\vec {y}}_{0}}$, имеем

Сравним значение $D_{{макс}}^{{кон}}$ с максимальным значением КНД круглой синфазной апертуры с радиусом R, равным $D_{{макс}}^{{апер}} = {{(kR)}^{2}}$:

Величина ${{\nu }_{{кон}}}$ показывает возможное увеличение максимального КНД конической антенны по сравнению с максимальным КНД эквивалентной плоской апертуры.

При условии (9), т.е. при возбуждении антенны из условия максимизации КНД в направлении оси Oz, поле излучения антенны по основной τ-й составляющей в соответствии с (6) определяется по выражению

С учетом (15) запишем

Соответственно, нормированная ДН по основной поляризации ${{F}^{{осн}}}(\theta ,\varphi )$ представляется следующим образом:

ДН по кроссполяризации ${{F}^{{кр}}}(\theta ,\varphi )$, нормированная к ${{F}^{{осн}}}(0,0)$, рассчитывается по соотношению

где $\vec {\delta }_{1}^{{e \bot }}(r,\theta ,\varphi )$ – распределение тока при падении на конус волны с ориентацией вектора напряженности электрического поля вдоль вектора ${{\vec {\tau }}_{{01}}}$, причем

Токи $\vec {\delta }_{1}^{e}$, $\vec {\delta }_{1}^{{e \bot }}$ на поверхности конечного конуса в строгом варианте должны определяться при дифракции как на боковой поверхности конуса, так и на поверхности проводящего дна. Однако для рассматриваемой задачи без существенной потери точности можно полагать, что при падении плоской волны вдоль оси конуса токи на поверхности дна конуса значительно меньше, чем на боковой поверхности ${{S}_{{бок}}}$, и влияют лишь на уровень дальних боковых лепестков. Поэтому при интегрировании везде вместо ${{S}_{а}}$ можно использовать только боковую поверхность конуса ${{S}_{{бок}}}$.

Обратимся снова к соотношению (9), определяющему закон оптимального возбуждения антенны. Это соотношение, по сути, решает три задачи, а именно: показывает закон требуемой поляризации отдельных излучателей на конусе в зависимости от их координат, характеризует оптимальное амплитудное возбуждение излучателей, а также оптимальное фазовое возбуждение излучателей.

В самом деле, представим комплексный вектор тока ${{\vec {\delta }}_{{10}}}(2)$ в виде произведения

где ${{\vec {e}}_{0}}(2)$ – единичный вектор, показывающий ориентацию тока ${{\vec {\delta }}_{{10}}}$ в точке 2; $\left| {{{{\vec {\delta }}}_{{10}}}(2)} \right|$ – амплитуда тока в точке 2; ${{\Phi }_{{прм}}}(2)$ – фаза тока в точке 2 в режиме приема в результате дифракции.

Из (9) получаем, что оптимальное распределение излучателей в произвольной точке 2 должно быть таким, при котором ориентация напряженности электрического поля в режиме активного возбуждения должна совпадать с ориентацией вектора ${{\vec {e}}_{0}}(2)$, т.е.

амплитуда этого поля $\left| {{{{\vec {E}}}_{2}}(2)} \right|$ должна быть пропорциональна амплитуде тока $\vec {\delta }_{{10}}^{ * }(2)$: а фаза поля ${{\Phi }_{{прд}}}(2)$ должна быть комплексно сопряженной по отношению к фазе тока ${{\Phi }_{{прм}}}(2)$, т.е.

Только при точном выполнении каждого из условий (25)–(27) антенна, расположенная на поверхности проводящего конуса, будет иметь максимально возможный КНД (16).

Отметим, что при реализации конической антенны в виде решетки реальных излучателей, расположенных на проводящей поверхности, интегрирование в приведенных выше соотношениях заменяется на суммирование.

3. ОПТИМАЛЬНЫЙ И ЦЕЛЕСООБРАЗНЫЙ ЗАКОНЫ РАЗМЕЩЕНИЯ И ВОЗБУЖДЕНИЯ ЩЕЛЕВЫХ ИЗЛУЧАТЕЛЕЙ АР НА КОНИЧЕСКОЙ ПОВЕРХНОСТИ

Рассмотрим сначала случай, когда в качестве отдельных излучателей используются элементарные щелевые диполи. Для определения наиболее целесообразного варианта размещения излучателей АР на конической поверхности проанализируем особенности структуры и распределения тока, наводимого на этой поверхности при дифракции волны от источника 2.

На рис. 2 и 3 представлены структура и законы распределения тока ${{\vec {\delta }}_{{10}}}(2)$ на поверхности конечного проводящего конуса (l = 12.5λ, R = 2.5λ) с металлическим дном при дифракции поля плоской волны, падающей вдоль оси Oz с $\left| {{{{\vec {E}}}_{п}}} \right| = 1$ и ${{\vec {\tau }}_{{01}}} = {{\vec {y}}_{0}}$. На рис. 2 различным тоном показан закон амплитудного распределения тока на всей боковой поверхности конуса, а на рис. 3 изображены законы нормированного амплитудного и фазового распределений вдоль образующей конуса, лежащей в плоскости yOz.

Как видно, особенностью распределения тока является, во-первых, существенное различие (на два-три порядка) уровня амплитуды тока на верхней (в плоскости yOz) и боковой (в плоскости xOz) образующих, а во-вторых, наличие периодических максимумов и минимумов в амплитудном распределении тока вдоль образующей конуса с периодом примерно λ/2. Это обстоятельство позволяет определить наиболее целесообразные области размещения щелевых излучателей как в азимутальном, так и в меридиональном направлениях на конусе и, в частности, определить целесообразные азимутальные секторы размещения щелевых излучателей, а также координаты их расположения вдоль образующих в местах расположения гребней “стоячей волны” тока на поверхности конуса, а более конкретно – в местах пересечения линий тока с гребнями “стоячей волны”. Для конусов с длиной образующей L $ \gg $ λ распределение тока в режиме приема в результате дифракции и в режиме передачи можно определить соотношением (24).

Для элементарных щелевых диполей оптимальный закон их размещения и возбуждения определяется соотношением (25). Для получения аналитических соотношений по зависимости ориентации поверхностного тока в каждой точке конической поверхности рассмотрим более детально оптимальное расположение щелевых излучателей на конической поверхности с точки зрения минимизации уровня кроссполяризационного излучения. При этом будем предполагать, что поляризация излучаемого поля линейная с вектором электрического поля ${{\vec {E}}_{{изл}}} = {{E}_{{изл}}}{{\vec {y}}_{0}}$ в направлении оси Oz (рис. 4).

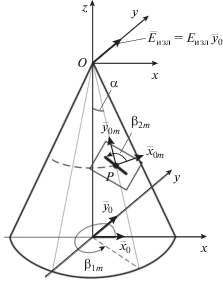
Пусть в произвольной точке P, расположенной на поверхности конуса, ориентация продольной оси m-й щели, расположенной в этой точке, ${{\vec {\delta }}_{m}}(P)$ в системе координат O_mx_my_mz_m имеет вид

где ${{\beta }_{{2m}}}$ – угол, характеризующий положение продольной оси m-й щели в точке P и отсчитываемый от оси O_mx_m.

Запишем единичные векторы ${{\bar {x}}_{{0m}}}$, ${{\bar {y}}_{{0m}}}$ в системе координат Oxyz:

Тогда с учетом (28), (29) выражение для вектора ${{\vec {\delta }}_{m}}(P)$ в системе координат Oxyz может быть представлено следующим образом:

Из соотношения (30) следует, что оптимальное размещение продольной оси щели в точке P, при котором кроссполяризационная составляющая равна нулю, должно удовлетворять условию

Тогда оптимальная ориентация продольной оси m-й щели в точке P на конической поверхности определяется из выражения

или

Соотношение (33) показывает, что ориентация оптимально расположенной продольной оси m‑й щели зависит от угловой координаты ${{\beta }_{{1m}}}$ образующей конуса, проходящей через точку P, и угла α при вершине конуса.

В частности, при размещении щелей вдоль образующей конуса оптимальная ориентация всех щелей характеризуется одинаковым значением угла ${{\beta }_{{2m}}}$. При размещении щелей вдоль продольной оси ВЩАР оптимальная ориентация каждой щели своя и определяется угловым положением ${{\beta }_{{1m}}}$ образующей конуса в этой точке. На рис. 5 показан оптимальный вариант ориентации щелей, направление продольной оси которых обозначено короткими полужирными отрезками, вдоль продольных осей трех ВЩАР, расположенных в пределах четверти конической поверхности.

4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ХАРАКТЕРИСТИК НАПРАВЛЕННОСТИ КОНИЧЕСКОЙ АНТЕННЫ

Все результаты, приведенные в данном разделе, получены в предположении дифракции на конусе поля плоской волны, падающей вдоль оси Oz с вектором электрического поля, ориентированным вдоль оси Oy.

Проанализируем величину максимального КНД конической антенны и сравним $D_{{макс}}^{{кон}}$ с величиной КНД эквивалентной апертуры $D_{{макс}}^{{апер}}$. При этом предполагается, что на части конической поверхности возбуждаются токи по закону (9), а сама часть конической поверхности представляет часть боковой поверхности конуса, ограниченной двумя плоскостями X = const и –X = const (половина этой поверхности заштрихована на рис. 5).

Расчеты проводились для конуса с параметрами R = 2.5λ, l = 12.5λ, α = 11°20′. Зависимость ${{\nu }_{{кон}}}$ от величины X/R, рассчитанная по соотношению (18), представлена на рис. 6 сплошной линией 2. При этом максимальное значение КНД ${{D}_{{макс}}}$ = = 896.3 достигается при X/R = 1, что в 3.63 раза больше, чем максимальный КНД круглой апертуры, являющейся основанием конуса.

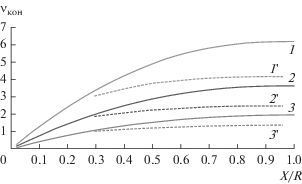
Как следует из рис. 6, уже при X/R ≥ 0.2 максимальный КНД конической антенны превышает максимальный КНД круглой апертуры примерно в 1.4 раза, а при X/R = 0.6 в 3.2 раза. При дальнейшем увеличении X/R рост КНД конической антенны существенно замедляется, и поэтому расположение излучателей на поверхности конуса в области X/R > 0.6 (β > 37°…40°) с точки зрения КНД нецелесообразно.

Кроме того, на рис. 6 представлены зависимости ${{\nu }_{{кон}}}$ от X/R для конусов с другим значением угла при вершине α = 6.8° и 21.8°. Как видно, с уменьшением α выигрыш в КНД конической антенны увеличивается, а целесообразный сектор расположения излучателей практически не меняется.

На рис. 7 показаны суммарные ДН конической антенны (размеры конуса l = 12.5λ, R = 2.5λ) по основной и кроссполяризационной составляющим, рассчитанные при возбуждении (24) для значения X/R = 1. Сравнение ширины этой ДН по уровню –3 дБ с шириной ДН эквивалентного раскрыва при X/R = 1 показывает, что в плоскости φ = 0° ширина ДН обеих антенн примерно одинакова, а в плоскости φ = 90° ДН конической антенны существенно (более чем в 1.5 раза) уже, чем ДН эквивалентного раскрыва. Кроме того, уровень дальних боковых лепестков у конической антенны меньше, чем у эквивалентного раскрыва.

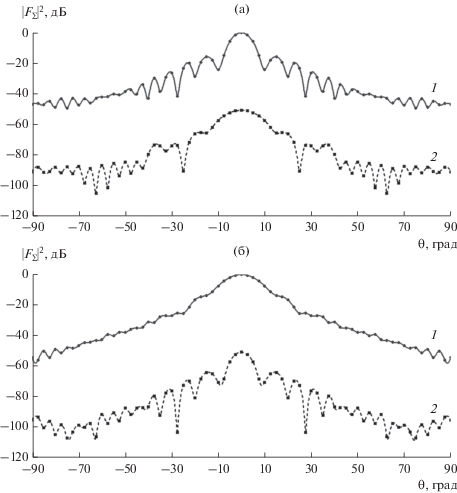
Уровень кроссполяризационной составляющей при оптимальной ориентации щелевых диполей примерно на 50 дБ ниже уровня основной поляризации.

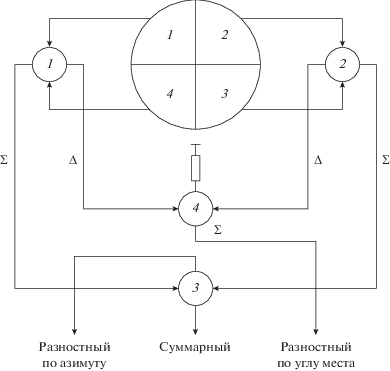
Также были рассчитаны ДН конической антенны по разностным каналам, построенным в соответствии со схемой, показанной на рис. 8. Важнейшей характеристикой разностной ДН является ее крутизна. В литературе [10] крутизна разностной ДН μ в сечении φ = φ₀ определяется по соотношению

где ${{F}_{\Delta }}(\theta ,{{\varphi }_{0}})$ – разностная ДН в сечении φ = φ₀; ${{F}_{\Sigma }}(\theta ,\varphi )$ – суммарная ДН по полю; $\theta = 0,\,\,\varphi = 0$ – направление максимума суммарной ДН ${{F}_{\Sigma }}(\theta ,\varphi )$.

На рис. 9 показаны значения крутизны ДН по разностным каналам в двух ортогональных плоскостях, рассчитанные для восьми конусов с различными углами при вершине α = 4.5°…63°. Представленная зависимость крутизны нормирована относительно крутизны разностной ДН эквивалентного плоского раскрыва (α = 90°).

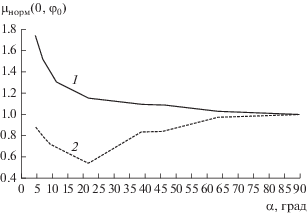
Как видно из рис. 9, крутизна разностной ДН конической антенны (при условии достижения максимума КНД в направлении оси Oz) в E-плоскости превышает крутизну эквивалентного плоского раскрыва и возрастает при уменьшении угла при вершине конуса, а в H-плоскости оказывается меньше крутизны эквивалентного раскрыва и немонотонно зависит от угла α.

Рассмотрим теперь случай, когда в качестве отдельного излучателя используется криволинейная щель, расположенная на боковой поверхности конуса. Понятно, что замена элементарного излучателя на щель с шириной d приводит к падению КНД конической антенны, так как условие оптимальности (9) уже не удается обеспечить на всей конической поверхности. Будем полагать, что каждая m-я щель расположена на конической поверхности таким образом, что продольная ось щели перпендикулярна линии тока $\vec {\delta }_{{10}}^{e}({{\rho }_{m}},{{\beta }_{{1m}}})$ в точке 2, совпадающей с центром m-й щели $({{\rho }_{m}},{{\beta }_{{1m}}})$, где ${{\rho }_{m}}$ – расстояние от вершины конуса до центра m-й щели. Поэтому распределение вектора напряженности в щели ${{E}_{щ}}(\rho ,{{\beta }_{1}})$ имеет вид

где $(\rho ,{{\beta }_{1}})$ – текущие координаты точки на боковой поверхности конуса; $({{\rho }_{m}},{{\beta }_{{1m}}})$ – координаты центра m-й щели; $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$; $2{{l}_{m}}$ – продольный размер m‑й щели; ${{x}_{m}}$ – продольная координата m-й щели в локальной системе координат ${{O}_{m}}{{x}_{m}}{{y}_{m}}$ (рис. 10); ${{\vec {y}}_{{0m}}}$ – единичный вектор, направление которого совпадает с направлением тока $\vec {\delta }_{{10}}^{e}({{\rho }_{m}},{{\beta }_{{1m}}})$; ${{E}_{{щмакс}}}({{\rho }_{m}},{{\beta }_{{1m}}})$ – максимальное значение напряженности электрического поля в центре m-й щели.

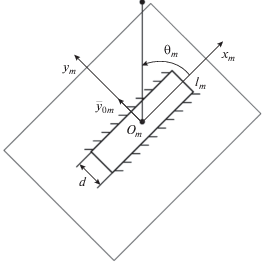
Подставляя (35) в (8) и полагая, что ДН криволинейной щели мало отличается от ДН щели, расположенной на плоскости, касательной в точке P к боковой поверхности конуса, получаем

где ${{f}_{m}}({{\theta }_{m}})$ – множитель направленности m‑го симметричного щелевого излучателя в меридиональной плоскости в собственной системе координат ${{O}_{m}}{{x}_{m}}{{y}_{m}}$, ось ${{O}_{m}}{{x}_{m}}$ которой совпадает с продольной осью m-й щели: ${{u}_{{щмакс}}}({{\rho }_{m}},{{\beta }_{{1m}}})$ – разность потенциалов в центре m‑й щели:

Величину ${{E}_{{щмакс}}}({{\rho }_{m}},{{\beta }_{{1m}}})$ выбираем из условия

Здесь ${{\theta }_{{0m}}}$ – угол, который соответствует направлению вдоль продольной оси конуса O и определяется по формуле где ${{\beta }_{{2m}}} = \operatorname{arctg} {{\left( {\sin \alpha \operatorname{tg} {{\beta }_{{1m}}}} \right)}^{{ - 1}}}$.

С учетом (39) из (36) находим

Соответственно, мощность излучения M односторонних щелей рассчитывается следующим образом:

Для щелей с сопротивлением излучения R_Σп, отнесенным к току в пучности, при оптимальном возбуждении щелей из условия (39) находим

Используя (41) и (43), получаем выражение для максимального КНД системы из рассматриваемых щелей на конусе $D_{{макс}}^{{АРкон}}$:

Подставляя в (44) выражение для ${{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {E_{п}^{2}}}} \right. \kern-0em} {E_{п}^{2}}}$ из (15), окончательно получаем

Соответственно,

В частном случае конуса при α = 90° и полуволновых щелей ($k{{l}_{m}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$) имеем

Учитывая, что число полуволновых щелей $M$ на поверхности апертуры при размерах ячейки $\frac{\lambda }{2} \times \frac{\lambda }{2}$ равно

из (47) получаем, что $\nu _{{апер}}^{{АР}}$ = 1.047, т.е. близок к 1.

Проанализируем величину максимального КНД конической антенной решетки из полуволновых излучателей и ее зависимость от степени заполнения поверхности конуса излучателями. При этом предполагается, что каждая из щелей имеет независимое возбуждение в соответствии с (39), а структуры всех щелевых АР подобны структуре АР, показанных на рис. 5. Расчеты, проведенные по соотношению (46), представлены на рис. 6 пунктирными линиями для конусов с различными углами при вершине конуса: 6.8°, 11.3° и 21.8°.

Из полученных результатов следует, что при выборе полуволновых щелей, расположенных на поверхности конуса с α = 6.8°…21.8° с шагом λ/2 по обеим координатам, максимальное значение КНД АР снижается примерно в 1.4…1.5 раза по сравнению с максимальным значением КНД антенны с непрерывным возбуждением.

ЗАКЛЮЧЕНИЕ

Представленные в работе выражения позволяют определить оптимальное возбуждение как элементарных щелевых излучателей, так и реальных полуволновых излучателей в конической антенной решетке, обеспечивающее максимальный КНД по суммарному каналу, а также оптимальную конфигурацию расположения щелей в зависимости от координат каждой щели. Установлено, что величина максимального КНД зависит от угла при вершине конуса α и при уменьшении α с сохранением неизменным размера эквивалентной апертуры возрастает, при этом целесообразный сектор размещения излучателей меняется незначительно. Крутизна разностной ДН в E-плоскости конической антенны (при условии достижения максимума КНД в направлении оси Oz) превышает крутизну эквивалентного плоского раскрыва и возрастает при уменьшении угла при вершине конуса.

В частном случае конуса с углом при вершине α = 11°20′ максимальный КНД конической антенны при возбуждении элементарных щелевых излучателей на боковой поверхности конуса по закону (9) превышает максимальный КНД эквивалентной плоской апертуры в 3.6 раза. При этом целесообразный сектор β достигает величины примерно 40°, при котором КНД конической антенны приблизительно в три раза выше КНД эквивалентной плоской апертуры. При использовании полуволновых излучателей, расположенных на конической поверхности с шагом λ/2 и возбуждаемых в соответствии с (39), КНД конической антенны примерно в 2.4 раза выше КНД эквивалентной плоской апертуры.