Радиотехника и электроника, 2020, T. 65, № 11, стр. 1116-1121

ВВЕДЕНИЕ

Потребители современных систем цифровой связи проявляют особую требовательность в вопросе энергетической эффективности используемых устройств. Известно, что одной из наиболее энергозатратных частей передающего устройства является аналоговый радиотракт, который в силу неидеальности характеристик своих составных частей – усилителя мощности, фильтрующих цепей, квадратурного модулятора – становится источником различного рода нелинейно-динамических искажений. Наличие внутрисистемных помех в тракте приводит к увеличению уровня внеполосного излучения и внутриполосного шума передаваемого сигнала. В настоящее время одним из основных методов борьбы с сигнальными искажениями в передающем тракте является процедура линеаризации его передаточной характеристики, основанная на применении корректора, который еще на стадии формирования сигнала осуществляет ввод цифровых предыскажений [1]. Цифровой корректор осуществляет такое нелинейно-динамическое преобразование передаваемого сигнала, при котором нелинейно-динамические искажения аналогового устройства естественным образом компенсируют введенные предыскажения.

Если передающий тракт представляет собой последовательное соединение аналогового квадратурного модулятора и усилителя мощности, то его внутреннюю структуру можно считать двух-блочной системой, первый блок которой вносит дисбаланс квадратур, а второй – нелинейные искажения. В работах [2–4] предложены решения задачи цифровой линеаризации подобной структуры радиотракта с помощью обобщенной модели цифрового корректора. Выбор такой модели вслед за ростом числа коэффициентов корректора ведет к увеличению вычислительной сложности процесса ввода предыскажений в сравнении с традиционными методами выравнивания характеристик усилителя мощности [5] и квадратурного модулятора [6] по отдельности. Поэтому в данной работе предлагается алгоритм построения и способы идентификации двухблочной модели цифрового корректора для линеаризации радиотракта с аналоговым квадратурным модулятором и усилителем мощности, оперирующей меньшим, чем одноблочный аналог, числом параметров.

1. СИНТЕЗ ДВУХБЛОЧНОЙ МОДЕЛИ КОРРЕКТОРА

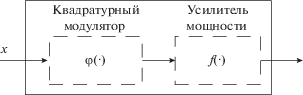
На рис. 1 представлена бесструктурная модель рассматриваемого аналогового радиотракта, состоящая из двух независимых поведенческих моделей.

Поведение квадратурного модулятора может быть описано с помощью математической модели [7], реализующей передаточную характеристику $\varphi (\cdot)$ вида:

где x(n) – отсчеты входного сигнала модели; ${\text{*}}$ – оператор комплексного сопряжения; $\vec {h} = \left[ {{{h}_{1}}, \ldots ,{{h}_{{\tilde {Q}}}}} \right]$ – вектор коэффициентов модели длиной $\tilde {Q} = 2Q;$ Q – параметр глубины памяти модели. Такая модель позволяет достаточно точно описывать частотно-зависимый квадратурный дисбаланс, характерной особенностью которого является расщепление амплитудной характеристики модулятора на две разнесенные составляющие. Подобная деформация передаточной характеристики приводит к смещению сигнального созвездия и, как итог, снижению достоверности передачи данных системы беспроводной связи.

Другим источником сигнальных искажений в передающем радиотракте является аналоговый усилитель мощности, нелинейно-динамические свойства которого приводят к росту внеполосного излучения и, как следствие, к снижению энергетической эффективности устройства. В рамках данной работы будем полагать, что инерционные свойства усилителя мощности незначительны, а нелинейный вид его передаточной характеристики может быть аппроксимирован с помощью полиномиальной функции. Тогда математическое описание его передаточной характеристики $f(x(n))$ можно представить в виде полиномиальной модели без памяти [8]:

где x(n) – отсчеты входного сигнала модели; $\vec {d} = \left[ {{{d}_{1}}, \ldots ,{{d}_{P}}} \right]$ – вектор коэффициентов модели, P – степень нелинейности модели.

Основным способом выравнивания амплитудной и амплитудно-фазовой характеристик аналоговых компонент радиотракта является метод ввода в сигнал цифровых предыскажений, зеркальных к обозначенным характеристикам $f(\cdot)$ и $\varphi (\cdot).$ Устройства ввода соответствующих предыскажений называют цифровыми корректорами. Метод ввода цифровых предыскажений сводится к построению цифрового корректора, который преобразует сигнал таким образом, чтобы источник аналоговых искажений выступал в роли естественного компенсатора искусственно введенных в передаваемый сигнал цифровых предыскажений.

Перейдем теперь к задаче построения корректора для радиотракта, в котором и усилитель мощности, и квадратурный модулятор одновременно становятся значимыми источниками искажений. В работе [2] для линеаризации такого тракта предложена одноблочная модель цифрового корректора (рис. 2), сигнал на выходе которой $z$ (без учета тока смещения) записывается в следующем виде:

где x(n) – отсчеты входного сигнала корректора; $\vec {c} = \left[ {{{c}_{1}} \ldots {{c}_{{P\tilde {Q}}}}} \right]$ – вектор коэффициентов одноблочной модели корректора. Одноблочный корректор синтезирует совместную обратную характеристику для квадратурного модулятора и усилителя мощности с помощью свертки $\bar {f} \times \bar {\varphi }(x(n)),$ где $\bar {f}(\cdot)$ и $\bar {\varphi }(\cdot)$ – обратные функции для $f(\cdot)$ и $\varphi (\cdot)$ соответственно. Результатом подобного обобщения нелинейных и динамических свойств аналогового радиотракта становятся, с одной стороны, удобство расчета коэффициентов модели (единый вектор параметров предыскажений), а с другой – рост совокупного числа параметров предыскажений.

Для того чтобы снизить количество коэффициентов модели корректора, рассмотрим решение аналогичной задачи с помощью двухблочной структуры, предложенной в работе [9], где аналоговый тракт представлен в виде последовательного соединения фильтрующей цепи (источника инерционных искажений) и усилителя мощности (источника нелинейных искажений). В рассматриваемом случае построение двухблочной модели корректора потребует внесения поправок в блок, отвечающий за динамическую составляющую модели, путем замены корректора фильтра на корректор квадратурного модулятора (рис. 3). Выходной z и промежуточный y сигналы двухблочного корректора в таком случае имеют вид

где вектор $\vec {a} = \left[ {{{a}_{1}}, \ldots ,{{a}_{P}}} \right]$ содержит коэффициенты предыскажений первого блока модели корректора (корректор усилителя мощности), а вектор $\vec {b} = \left[ {{{b}_{1}}, \ldots ,{{b}_{{\tilde {Q}}}}} \right]$ длиной $\tilde {Q} = 2Q$ содержит коэффициенты предыскажений второго блока модели корректора (корректор квадратурного модулятора). Совокупное число параметров двухблочного корректора составляет${{N}_{2}} = 2Q + P,$ в то время как для одноблочного варианта имеем ${{N}_{1}} = 2QP.$ Таким образом, в силу замены операции свертки на операцию сложения с ростом степени нелинейности P и/или динамики Q рассматриваемых моделей разница числа параметров одноблочной ${{N}_{1}}$ и двух-блочной ${{N}_{2}}$ структур будет расти в пользу второй.

Следует отметить, что предлагаемая модель позволяет осуществить более гибкий подход к практической реализации адаптивного обновления параметров предыскажений. В процессе работы аналоговые части радиотракта по-разному реагируют на изменение внешних и внутренних факторов системы, к которым можно отнести колебание температуры или смену рабочей частоты. Если, к примеру, с ростом температуры скорость изменения характеристики усилителя мощности оказывается существеннее скорости изменения свойств квадратурного модулятора, то двухблочная модель корректора позволяет адаптивно подстраивать только коэффициенты корректора усилителя мощности при фиксированных параметрах корректора модулятора. Это ведет к снижению вычислительной нагрузки на решающее устройство, реализующее алгоритмы оптимизации искомых параметров предыскажений.

2. ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ ДВУХБЛОЧНОЙ МОДЕЛИ КОРРЕКТОРА

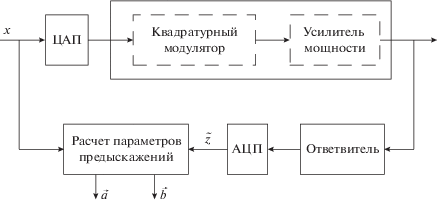
Для расчета параметров синтезированной модели корректора в работе используется обратный метод обучения [10], подразумевающий построение обратной модели объекта линеаризации (рис. 4). В основе большиства алгоритмов оптимизации лежит минимизация некоторой целевой функции J, которая определяется сигналом мгновенной ошибки e, в нашем случае принимающим вид

где $x(n)$ и $\tilde {z}(n)$ – отсчеты сигнала на входе и выходе аналогового тракта.

Простейшим алгоритмом многопараметрической оптимизации выступает метод стохастического градиента (МСГ) [11], который оперирует целевой функцией $J = e(n)e{\text{*}}(n).$ Обновление параметров предыскажений на основе алгоритма МСГ для предлагаемой модели сводится к системе уравнений:

где ${{{\mu }}_{1}},{{{\mu }}_{2}}$ – константы метода стохастического градиента; n – номер итерации адаптивного алгоритма. Таким образом, рассчитав необходимые производные, удается получить следующее итерационное правило расчета коэффициентов предыскажений:

Более качественным адаптивным методом многопараметрической оптимизации является рекурсивный метод наименьших квадратов (РМНК). Для него целевая функция определяется не только текущим значением сигнала ошибки, но и рядом его предшествующих состояний с учетом весового коэффициента $\lambda {\text{:}}$

Коэффициенты двухблочной модели также определяются из условия минимизации данной целевой функции. Таким образом, удается получить следующие соотношения для итерационного расчета искомых параметров предыскажений двухблочного корректора:

Векторы коэффициентов Калмана ${{\vec {g}}_{a}}(n)$ длиной P и ${{\vec {g}}_{b}}(n)$ длиной $\tilde {Q}$ согласно алгоритму РМНК в общем случае определяются следующим образом:

где $\sigma _{{\tilde {z}}}^{2}$ – дисперсия выходного сигнала, $I$ – единичная матрица; $^{H}$ – оператор эрмитова сопряжения. При этом для расчета коэффициентов первого блока корректора мгновенное значение вектора $\vec {M}(n)$ длиной P вычисляется согласно следующему выражению: а для второго блока корректора вектор $\vec {M}(n)$ длиной $\tilde {Q}$ принимает вид

3. КРИТЕРИИ ОЦЕНКИ

Оценку эффективности работы цифрового корректора будем проводить с помощью параметров EVM (Error Vector Magnitude) и ACPR (Adjacent Channel Power Ratio). Первый показывает деформацию сигнального созвездия (в процентном соотношении):

где ${{I}_{{{\text{вх}}}}},{{I}_{{{\text{вых}}}}},{{Q}_{{{\text{вх}}}}},{{Q}_{{{\text{вых}}}}}$ – квадратуры сигнального созвездия на входе и выходе устройства. Второй критерий характеризует внеполосное излучение сигнала:

где под ${{P}_{{{\text{о}}{\text{.к}}{\text{.}}}}}$ подразумевается мощность сигнала в эффективно передаваемой полосе, а под ${{P}_{{{\text{с}}{\text{.к}}{\text{.}}}}}$ – мощность сигнала в соседних каналах.

4. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА

Для проверки работоспособности синтезированной двухблочной модели цифрового корректора, а также выведенных соотношений для идентификации ее параметров была проведена практическая линеаризация передающего тракта, работающего на частоте 3 ГГц. В качестве источника сигнала использовался векторный генератор Rohde&Schwarz серии SMJ с встроенной функцией управления дисбалансом квадратур. В качестве ответвителя и петли обратной связи использовался анализатор спектра Rohde&Schwarz серии FSW. Квадратурный дисбаланс (10 градусов разности фаз и 1 дБм рассогласования) задавался внутра передатчика SMJ. В роли лабораторного усилителя мощности использовался усилитель Keysight 87405c. Решающим устройством, ответственным за расчет параметров предыскажений в лабораторных условиях, выступал компьютер, поэтому математическая обработка сигнала проводилась отдельно в среде Matlab.

В качестве тестового был выбран сигнал с модуляцией КАМ-16 и полосой 4 МГц (частота дискретизации 32 МГц). Эксперимент состоял из двух этапов: расчета параметров предыскажений по экспериментально измеренным данным и их применения. На первом этапе исходный сигнал загружался в векторный генератор, где претерпевал квадратурные искажения, а затем подавался на усилитель мощности, с выхода которого записывался векторным анализатором. Затем на базе отсчетов исходного и измеренного сигналов проводился расчет коэффициентов моделей корректоров. При этом начальные условия адаптивных алгоритомов были определены так: первый коэффициент параметров оптимизации принимался за единицу, остальные – нули. Второй этап повторял первый, однако вместо исходного сигнала в генератор загружались квадратуры с учетом внесения предыскажений, рассчитанных на первом этапе.

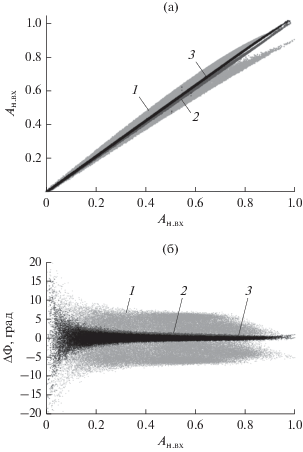
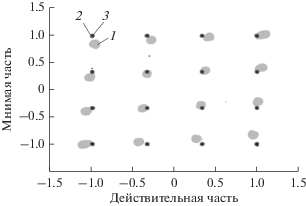
Общие результаты работы различных цифровых корректоров приведены в табл. 1. Оценка параметра ACPR проводилась для интермодуляционных зон третьего и пятого порядков, которые в таблице обозначены соседним и дополнительным каналами соответственно. Из полученных данных видно, что применение двухблочной модели корректора позволило вдвое меньшим числом параметров достичь сопоставимых одноблочной модели результатов линеаризации. На рис. 5, 6 приведены соответственно амплитудно-амплитудные (зависимость нормированной выходной амплитуды А_н. вых от нормированной входной амплитуды А_н. вх) и амплитудно-фазовые (зависимость сдвига фаз ΔФ на выходе тракта от нормированной входной амплитуды А_{н. вх}) характеристики исследуемой системы до и после линеаризации с помощью одноблочной и предлагаемой двухблочной моделей цифрового корректора (с помощью алгоритма РМНК). На рис. 7 показана деформация сигнального созвездия на выходе радиотракта до и после введения предыскажений, рассчитанных с помощью алгоритма РМНК.

ЗАКЛЮЧЕНИЕ

В работе рассмотрена задача цифровой линеаризации аналогового радиотракта, представленного в виде последовательного соединения аналогового квадратурного модулятора и усилителя мощности. На основе метода стохастического градиента и рекурсивного метода наименьших квадратов были выведены соотношения для идентификации двухблочной модели цифрового корректора для выравнивания дисбаланса квадратур модулятора и нелинейности усилителя мощности. Проведен экспериментальный сравнительный анализ корректоров, построенных на базе одноблочной и предлагаемой двухблочной моделей. Результаты проведенных исследований показали, что двухблочный корректор при сопоставимых одноблочному аналогу результатах линеаризации позволяет сократить число целевых параметров и, следовательно, снизить вычислительную нагрузку алгоритма расчета параметров предыскажений аналогового радиотракта.