Радиотехника и электроника, 2020, T. 65, № 11, стр. 1074-1078

Энергетические потери при сращивании двух оптических волокон, одно из которых эллиптически деформировано в месте соединения

В. А. Гладких^a, В. Д. Власенко^a, *

^a Вычислительный центр Дальневосточного отделения РАН
680000 Хабаровск, ул. Ким Ю Чена, 65, Российская Федерация

Поступила в редакцию 18.03.2020
После доработки 18.03.2020
Принята к публикации 27.03.2020

DOI: 10.31857/S0033849420110066

Аннотация

Рассмотрены круглый и эллиптический (в месте соединения) в поперечном сечении два фрагмента волоконно-оптической линии передачи информации. Для одномодового режима работы получены аналитические выражения для потерь энергии при соединении двух таких фрагментов. Показано, что потери энергии возрастают при увеличении эксцентриситета и одновременно уменьшаются при увеличении волноводного числа.

ВВЕДЕНИЕ

Конструирование и практическое построение волоконно-оптических линий связи должно учитывать максимально возможную безопасность от внешних воздействий (механических, электромагнитного поля и окружающей среды) для получения и передачи информации с возможно меньшими потерями [1–6]. Потери энергии связаны также с материалом оптоволокна [7]. Поскольку оптоволоконные линии связи ввиду большой протяженности составляются из отдельных фрагментов, то также следует учитывать потери, возникающие при сращивании отдельных фрагментов [4, 8]. Все это в полной мере относится и к широко применяемым в современных исследованиях волоконно-оптическим датчикам. В частности, некоторые фрагменты волокна могут быть деформированы [9, 10].

Цель данной работы – анализ потерь, возникающих при сращивании двух волокон (в одномодовом режиме), одно из которых круглое в поперечном сечении, другое – эллиптически деформировано (только практически в торце для упрощения анализа).

1. ПОЛЕ В ОДНОМОДОВОМ ВОЛОКНЕ СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ

При соединении волокон потери a_пот можно рассчитать по следующей формуле (см., например, [11]):

${{a}_{{{\text{пот}}(NA)}}} = 10\lg ({{N{{A}_{r}}} \mathord{\left/ {\vphantom {{N{{A}_{r}}} {N{{A}_{c}})}}} \right. \kern-0em} {N{{A}_{c}})}}$

при рассогласовании апертур (см. далее формулу (6) и следующие) передающего и принимающего волокна, где NA_r, NA_c – числовые апертуры передающего и принимающего волокна, соответственно, или по [11]:

${{a}_{{{\text{пот}}({\rho })}}} = 10\lg \left( {{{{\left[ {{{{{\rho }_{r}}} \mathord{\left/ {\vphantom {{{{\rho }_{r}}} {{{\rho }_{c}}}}} \right. \kern-0em} {{{\rho }_{c}}}}} \right]}}^{2}}} \right),$

если радиус сердцевины ρ_r передающего волокна больше радиуса сердцевины ρ_c принимающего.

При стыковке маломодовых оптических волокон также существует довольно точный расчет вносимых потерь a_пот [12]:

${{a}_{{{\text{пот}}}}} = 10\lg \left\{ {\frac{{\sqrt {\sum\limits_{i = 1}^{{{M}_{{{\text{вх}}}}}} {{{{\left[ {P_{{lm}}^{{\left( {{\text{вх}}} \right)}}} \right]}}^{2}}} } }}{{\sum\limits_{i = 1}^{{{M}_{{{\text{вх}}}}}} {\sum\limits_{j = 1}^{{{M}_{{{\text{вых}}}}}} {{\eta }_{{mn}}^{2}{{{\left[ {P_{{lm}}^{{\left( {{\text{вх}}} \right)}}} \right]}}^{2}}} } }}} \right\},$

где $P_{{lm}}^{{({\text{вх}})}}$ – мощность модовой компоненты LP_lm оптического сигнала, поступающего с выхода “передающего” волокна “слева” на вход “принимающего” волокна “справа”, M_вх – общее число модовых компонентов оптического сигнала, поступающего на вход волокна “справа”, M_вых – общее число мод, возбуждаемых в волокне “справа” модовой составляющей сигнала LP_lm заданного порядка, η_mn – коэффициент связи вводимой и возбуждаемой моды соответствующего порядка. Предлагаемая методика дает хорошее совпадение с экспериментом, но сложна практически.

В данной статье предложен алгоритм, построенный на простых основах электродинамики и гауссовом приближении для поля, позволяющий рассчитать потери в обобщенном виде – в зависимости от эксцентриситета деформированного торца одного из стыкуемых волокон и от волноводного числа.

При механическом соединении двух фрагментов оптоволокна (с одинаковым показателем преломления при нормальном падении волны на поперечное сечение) для коэффициента прохождения D_1 → 2 из фрагмента 1 во фрагмент 2 (аналогично для D₂ _→ ₁ в обратном направлении) имеем (во избежание отражения на границе соединения фрагментов применяется технологический прием – контакт происходит по возможности точечно и по центру):

(1)

${{D}_{{1 \to 2}}} = {{{{P}_{2}}} \mathord{\left/ {\vphantom {{{{P}_{2}}} {{{P}_{1}}}}} \right. \kern-0em} {{{P}_{1}}}},\,\,\,\,\left( {{{D}_{{2 \to 1}}} = {{{{P}_{1}}} \mathord{\left/ {\vphantom {{{{P}_{1}}} {{{P}_{2}}}}} \right. \kern-0em} {{{P}_{2}}}}} \right),$

где P₁, P₂ (P₂, P₁) – соответственно передаваемая и получаемая фрагментами мощность энергии:

(2)

$\begin{gathered} {{P}_{2}} = {{\left( {\oint\limits_{\vec {f}} {\vec {S}d\vec {f}} } \right)}_{2}} = \int\limits_{{{f}_{2}}} {\left| {{{S}_{2}}} \right|d{{f}_{2}}} {\text{,}} \hfill \\ {{P}_{1}} = {{\left( {\oint\limits_{\vec {f}} {\vec {S}d\vec {f}} } \right)}_{1}} = \int\limits_{{{f}_{1}}} {\left| {{{S}_{1}}} \right|d{{f}_{1}}} {\text{,}} \hfill \\ \end{gathered} $

где ${{f}_{1}}{\text{,}}{{f}_{2}}$ – площади поперечного сечения соответственно 1-го и 2-го соединяемых фрагментов, ${{S}_{1}}{\text{,}}{{S}_{2}}$ – значения векторов Умова–Пойнтинга в соответствующих фрагментах. При этом соответствующие потери энергии a_пот (в децибелах) вычисляются по следующим формулам [8, 11]:

(3)

${{a}_{{{\text{пот}}\left( {1 \to 2} \right)}}} = - 10{\text{lg}}{{D}_{{1 \to 2}}}{\text{,}}\,\,\,\,\left( {{{a}_{{{\text{пот}}\left( {2 \to 1} \right)}}} = - 10{\text{lg}}{{D}_{{2 \to 1}}}} \right){\text{.}}$

Для поля рассматриваемого волновода в одномодовом режиме достаточно хорошей моделью может служить гауссово приближение [11] (r² = x² + y², ось z – вдоль распространения волны):

(4)

$\begin{gathered} {{E}_{{{\text{круг}}}}} \equiv {{E}_{{{\text{эл}}}}}\sim C\exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {2r_{0}^{2}}}} \right. \kern-0em} {2r_{0}^{2}}}} \right) \to {{D}_{{1 \to 2}}} = \\ = \frac{{{{P}_{2}}}}{{{{P}_{1}}}} = \frac{{\int\limits_{{{f}_{2}}} {\exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}} \right)d{{f}_{2}}} }}{{\int\limits_{{{f}_{1}}} {\exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}} \right)d{{f}_{1}}} }}; \\ {{D}_{{2 \to 1}}} = \frac{{{{P}_{1}}}}{{{{P}_{2}}}} = \frac{{\int\limits_{{{f}_{1}}} {\exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}} \right)d{{f}_{1}}} }}{{\int\limits_{{{f}_{2}}} {\exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}} \right)d{{f}_{2}}} }}, \\ \end{gathered} $

где r₀ – радиус модового пятна волокна, E_круг, E_эл – круговая (циркулярная) и эллиптическая поляризации. Поскольку соединяемые фрагменты по всей длине круглые в поперечном сечении, кроме эллиптически деформированного торца одного из соединяемых фрагментов, то внутри этих фрагментов поля совпадают – E_круг, E_эл, что и отражено в формуле (4).

2. РАСЧЕТ МОЩНОСТИ ЭНЕРГИИ

2.1. Мощность энергии, проходящей через поперечное круговое сечение первого фрагмента

Пусть при соединении фрагмент 2 эллиптически деформирован в поперечнике и, таким образом, в месте соединения поперечное сечение фрагмента 1 – круг, а фрагмента 2 – эллипс. Тогда можно записать (С – постоянная):

(5)

где ρ – радиус круга (радиус поперечного сечения 1-го волокна).

Как известно, волновод со ступенчатым профилем показателем преломления является одномодовым, если [5, 13]:

(6)

$\begin{gathered} 0 < V \equiv \left( {{{2\pi \rho } \mathord{\left/ {\vphantom {{2\pi \rho } \lambda }} \right. \kern-0em} \lambda }} \right)NA = \\ = \left( {{{2\pi \rho } \mathord{\left/ {\vphantom {{2\pi \rho } \lambda }} \right. \kern-0em} \lambda }} \right)\sqrt {n_{{{\text{вол}}}}^{{\text{2}}} - n_{{{\text{обл}}}}^{2}} < 2.405{\text{,}} \\ \end{gathered} $

где n_вол, n_обл – показатели преломления волокна и оболочки соответственно, V – волноводное число (нормализованная частота), NA – числовая апертура, λ – длина волны. В соответствии с этой формулой для радиуса модового пятна можем воспользоваться выражением, справедливым при V < 2.5 [13, 14]:

(7)

${{r}_{0}} \cong {{0.4{\lambda }} \mathord{\left/ {\vphantom {{0.4{\lambda }} {\sqrt {n_{{{\text{вол}}}}^{2} - n_{{{\text{обл}}}}^{{\text{2}}}} }}} \right. \kern-0em} {\sqrt {n_{{{\text{вол}}}}^{2} - n_{{{\text{обл}}}}^{{\text{2}}}} }} \to {\gamma } = \frac{{{{\rho }^{2}}}}{{r_{0}^{2}}} = 0.16{{V}^{2}},$

и результат запишется в виде

(8)

${{P}_{{1\left( {{\text{круг}}} \right)}}}\left( V \right) = С{\pi }r_{0}^{2}\left\{ {1 - {\text{exp}}( - 0.16{{V}^{2}})} \right\}.$

2.2. Мощность энергии, проходящей через поперечное эллиптическое сечение второго фрагмента

Согласно уравнению эллипса

(9)

$\frac{{{{x}^{2}}}}{{{{a}^{2}}}} + \frac{{{{y}^{2}}}}{{{{b}^{2}}}} = 1,\,\,\,\,\varepsilon \equiv \sqrt {1 - \frac{{{{b}^{2}}}}{{{{a}^{2}}}}} \,\,\,\,\left( {b \leqslant \rho \leqslant a,\,\,\varepsilon \in \left( {0,1} \right)} \right)$

(a, b – соответственно большая и малая полуоси, ε – эксцентриситет) в этом случае, переходя к полярным координатам x = r cos φ, y = r sin φ, запишем

(10)

$\begin{gathered} {{P}_{{2\left( {{\text{эл}}} \right)}}} = C\int\limits_{{{{{x}^{2}}} \mathord{\left/ {\vphantom {{{{x}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}} + {{{{y}^{2}}} \mathord{\left/ {\vphantom {{{{y}^{2}}} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}} \leqslant 1} {\exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}} \right)rdrd{\varphi }} = \\ = \left\{ {r \leqslant \frac{1}{{\sqrt {{{{{{\cos }}^{2}}{\varphi }} \mathord{\left/ {\vphantom {{{{{\cos }}^{2}}{\varphi }} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}} + {{{{{\sin }}^{2}}{\varphi }} \mathord{\left/ {\vphantom {{{{{\sin }}^{2}}{\varphi }} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} }}} \right\} = \\ = С\int\limits_0^{2\pi } {d\varphi \left( {\int\limits_0^{{1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{{{\cos }}^{2}}\varphi } \mathord{\left/ {\vphantom {{{{{\cos }}^{2}}\varphi } {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}} + {{{{{\sin }}^{2}}\varphi } \mathord{\left/ {\vphantom {{{{{\sin }}^{2}}\varphi } {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} }}} \right. \kern-0em} {\sqrt {{{{{{\cos }}^{2}}\varphi } \mathord{\left/ {\vphantom {{{{{\cos }}^{2}}\varphi } {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}} + {{{{{\sin }}^{2}}\varphi } \mathord{\left/ {\vphantom {{{{{\sin }}^{2}}\varphi } {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} }}} {\exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}} \right)rdr} )} \right) = } \\ = \left\{ {1 - \frac{2}{\pi }\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\exp \left\{ { - \frac{{{{b}^{2}}\left( {1 + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)}}{{r_{0}^{2}\left( {{{{{b}^{2}}} \mathord{\left/ {\vphantom {{{{b}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}} + {\text{t}}{{{\text{g}}}^{2}}\varphi } \right)}}} \right\}d\varphi } } \right\} \times \\ \times \,\,С\pi r_{0}^{2} = \left( {z = {\text{tg}}\varphi } \right) = \\ = С\pi r_{0}^{2}\left\{ {1 - \frac{2}{\pi }\int\limits_0^\infty {{\text{exp}}\left\{ { - \frac{{{{b}^{2}}\left( {1 + {{z}^{2}}} \right)}}{{r_{0}^{2}\left( {\frac{{{{b}^{2}}}}{{{{a}^{2}}}} + {{z}^{2}}} \right)}}} \right\}\frac{{dz}}{{1 + {{z}^{2}}}}} } \right\}. \\ \end{gathered} $

Полагая равными объемы профилей, запишем

(11)

$\begin{gathered} \pi ab = \pi {{\rho }^{2}} \to ab = {{\rho }^{2}} \to {{\varepsilon }^{2}} = \\ = \left\{ {\begin{array}{*{20}{c}} {1 - \frac{{{{\rho }^{4}}}}{{{{a}^{4}}}}} \\ {1 - \frac{{{{b}^{4}}}}{{{{\rho }^{4}}}}} \end{array}} \right. \to \left\{ {\begin{array}{*{20}{c}} {a = \rho {{{\left( {1 - {{\varepsilon }^{2}}} \right)}}^{{ - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}} \\ {b = \rho {{{\left( {1 - {{\varepsilon }^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}} \end{array}} \right., \\ \end{gathered} $

и с учетом (7) формула принимает вид

(12)

$\begin{gathered} {{P}_{{2\left( {{\text{эл}}} \right)}}}\left( {\varepsilon ,V} \right) = C\pi r_{0}^{2} \times \\ \times \,\,\left\{ {1 - \frac{2}{\pi }\exp ( - 0.16{{V}^{2}}\sqrt {1 - {{\varepsilon }^{2}}} )I\left( {\varepsilon ,V} \right)} \right\}{\text{,}} \\ I\left( {{\varepsilon ,}V} \right) \equiv \\ \equiv \int\limits_0^\infty {\exp \left\{ { - 0.16{{V}^{2}}\frac{{{{\varepsilon }^{2}}\sqrt {1 - {{\varepsilon }^{2}}} }}{{(1 - {{\varepsilon }^{2}} + {{z}^{2}})}}} \right\}\frac{{dz}}{{1 + {{z}^{2}}}}} {\text{.}} \\ \end{gathered} $

Легко видеть, что

(13)

${{P}_{{2\left( {{\text{эл}}} \right)}}}\left( {0{\text{,}}V} \right) = {{P}_{{1\left( {{\text{круг}}} \right)}}}\left( V \right){\text{,}}\,\,\,\,{{P}_{{2\left( {{\text{эл}}} \right)}}}\left( {1{\text{,}}V} \right) = 0{\text{,}}$

как и следовало ожидать.

2.3. Мощность энергии, проходящей через пересечение эллиптического сечения с круговым

Решим систему уравнений для определения точек пересечения соосных эллипса и окружности:

(14)

$\begin{gathered} \left\{ {\begin{array}{*{20}{c}} {{{x}^{2}} + {{y}^{2}} = {{r}^{2}}} \\ {\frac{{{{x}^{2}}}}{{{{a}^{2}}}} + \frac{{{{y}^{2}}}}{{{{b}^{2}}}} = 1} \end{array}} \right. \to {{x}_{1}} = - {{x}_{2}} \equiv {{x}_{0}} = \rho \frac{{\sqrt {1 - \sqrt {1 - {{\varepsilon }^{2}}} } }}{\varepsilon }, \\ {{y}_{1}} = - {{y}_{2}} \equiv {{y}_{0}} = \sqrt {{{\rho }^{2}} - x_{0}^{2}} . \\ \end{gathered} $

Определим угол α – угол между радиусом, проведенным в точку пересечения с координатами (x₀, y₀), и осью x:

(15)

$\begin{gathered} \cos \alpha \equiv \frac{{{{x}_{0}}}}{\rho } = \frac{{\sqrt {1 - \sqrt {1 - {{\varepsilon }^{2}}} } }}{\varepsilon } \to \alpha = \\ = \arccos \left\{ {\frac{{\sqrt {1 - \sqrt {1 - {{\varepsilon }^{2}}} } }}{\varepsilon }} \right\}. \\ \end{gathered} $

Площадь пересечения рассматриваемых соосных эллипса и окружности равна площади эллипса минус площади эллиптических сегментов при x ≥ x₀, x ≤ –x₀ (начало сегмента x ≥ x₀ при x > 0, прямая x = x₀, находится под углом 2α из центра) и плюс площади круговых сегментов (также при x ≥ x₀, x ≤ –x₀ и под тем же углом из центра). Поскольку

(16)

$\begin{gathered} x \geqslant {{x}_{0}} \to r\cos \varphi \geqslant \rho \cos \alpha \to \\ \to r \geqslant \rho \left( {{{\cos \alpha } \mathord{\left/ {\vphantom {{\cos \alpha } {\cos \varphi }}} \right. \kern-0em} {\cos \varphi }}} \right), \\ \end{gathered} $

то получим (tg α = (1 – ε²)^1/4):

(17)

$\begin{gathered} {{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}} = {{P}_{{2\left( {ell} \right)}}} - 2C \times \\ \times \,\,\int\limits_{ - \alpha }^\alpha {d{\varphi }\left\{ {\int\limits_{\rho \frac{{\cos \alpha }}{{\cos \varphi }}}^{{1 \mathord{\left/ {\vphantom {1 {\sqrt {\frac{{{{{\cos }}^{2}}\varphi }}{{{{a}^{2}}}} + \frac{{{{{\sin }}^{2}}\varphi }}{{{{b}^{2}}}}} }}} \right. \kern-0em} {\sqrt {\frac{{{{{\cos }}^{2}}\varphi }}{{{{a}^{2}}}} + \frac{{{{{\sin }}^{2}}\varphi }}{{{{b}^{2}}}}} }}} {\exp \left( { - \frac{{{{r}^{2}}}}{{r_{0}^{2}}}} \right)rdr} } \right\}} + \\ + \,\,\,\,2C\int\limits_{ - \alpha }^\alpha {d{\varphi }\left\{ {\int\limits_{{{\rho \cos \alpha } \mathord{\left/ {\vphantom {{\rho \cos \alpha } {\cos \varphi }}} \right. \kern-0em} {\cos \varphi }}}^\rho {\exp \left( { - \frac{{{{r}^{2}}}}{{r_{0}^{2}}}} \right)rdr} } \right\}} . \\ \end{gathered} $

Путем несложных вычислений и с учетом (7) окончательно получим (где I взято из (12)):

(18)

$\begin{gathered} {{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}} = С\pi r_{0}^{2} \times \\ \times \,\,\left\{ {1 - \frac{2}{\pi }\exp \left\{ { - 0.16{{V}^{2}}\sqrt {1 - {{\varepsilon }^{2}}} } \right\}I\left( {\varepsilon ,V} \right) + } \right. \\ + \,\,\frac{2}{\pi }\exp \left\{ { - 0.16{{V}^{2}}\sqrt {1 - {{\varepsilon }^{2}}} } \right\}{{I}_{1}}\left( {\varepsilon ,V} \right) - \\ - \,\,\frac{2}{\pi }\exp ( - 0.16{{V}^{2}})\left. {\arccos \left[ {\frac{{\sqrt {1 - \sqrt {1 - {{\varepsilon }^{2}}} } }}{\varepsilon }} \right]} \right\}, \\ {{I}_{1}} = {{I}_{1}}\left( {\varepsilon ,V} \right) \equiv \\ \equiv \int\limits_0^{{{{\left( {1 - {{\varepsilon }^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}} {\exp \left\{ { - 0.16{{V}^{2}}\frac{{{{\varepsilon }^{2}}\sqrt {1 - {{\varepsilon }^{2}}} }}{{(1 - {{\varepsilon }^{2}} + {{z}^{2}})}}} \right\}\frac{{dz}}{{1 + {{z}^{2}}}}} . \\ \end{gathered} $

Легко видеть, что

(19)

$\begin{gathered} \mathop {\lim }\limits_{{\varepsilon } \to 0} \left\{ {{{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}\left( {{\varepsilon },V} \right)} \right\} = {{P}_{{1\left( {{\text{круг}}} \right)}}}\left( V \right), \\ {{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}\left( {1,V} \right) = 0, \\ \end{gathered} $

как и следовало ожидать.

2.4. Влияние деформации поперечного сечения волокна на передачу энергии

Влияние деформации поперечного сечения волокна на передачу энергии, согласно (8) и (12), можно описать относительной величиной η(ε, V):

(20)

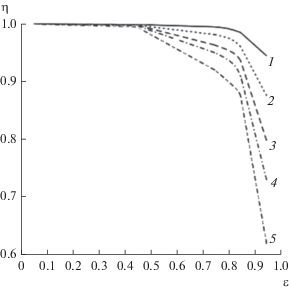
$\begin{gathered} \eta \left( {\varepsilon ,V} \right) \equiv \frac{{{{P}_{{2\left( {{\text{эл}}} \right)}}}\left( {\varepsilon ,V} \right)}}{{{{P}_{{1\left( {{\text{круг}}} \right)}}}\left( V \right)}} = \\ = \frac{{\left\{ {1 - \frac{2}{\pi }\exp \left\{ { - {\text{0}}{\text{.16}}{{V}^{2}}\sqrt {1 - {{{\varepsilon }}^{2}}} } \right\}I\left( {\varepsilon ,V} \right)} \right\}}}{{\left\{ {1 - \exp ( - 0.16{{V}^{2}})} \right\}}}{\text{,}} \\ \end{gathered} $

которая при изменении эксцентриситета ε от 0 до 1 убывает от 1 до 0 согласно (13). Численные расчеты дают следующую графическую зависимость. Из рис. 1 видно, что величина η быстрее убывает при возрастании волноводного параметра V. Для расчетов выбраны следующие значения параметра V: V₁ = 0.5; V₂ = 1; V₃ = 1.5; V₄ = 2; V₅ = 2.4.

Рис. 1.

Зависимость величины η от эксцентриситета ε при различных значениях волноводного параметра V = 0.5 (1), 1 (2), 1.5 (3), 2 (4), 2.4 (5).

3. РАСЧЕТ ПОТЕРЬ ЭНЕРГИИ

3.1. Часть потерь энергии при передаче из фрагмента 1 во фрагмент 2

Согласно (3), (8) и (18) имеем

(21)

$\begin{gathered} {{a}_{{{\text{пот}}\left( {{\text{1}} \to {\text{2}}} \right)}}}\left( {{\varepsilon },V} \right) = - 10{\text{lg}}\left\{ {\frac{{{{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}\left( {{\varepsilon },V} \right)}}{{{{P}_{{1\left( {{\text{круг}}} \right)}}}\left( V \right)}}} \right\} = \\ = - 10{\text{lg}}\left\{ {\frac{{{{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}\left( {{\varepsilon },V} \right)}}{{\left[ {1 - \exp ( - {\text{0}}{\text{.16}}{{V}^{2}})} \right]}}} \right\}{\text{;}} \\ {{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}\left( {{\varepsilon },V} \right) = \left\{ {1 - \frac{2}{\pi }\exp \left\{ { - 0.16{{V}^{2}}\sqrt {1 - {{\varepsilon }^{2}}} } \right\}} \right.I + \\ \end{gathered} $

$\begin{gathered} + \,\,\frac{2}{\pi }\exp \left\{ { - 0.16{{V}^{2}}\sqrt {1 - {{\varepsilon }^{2}}} } \right\}{{I}_{1}} - \\ \left. { - \,\,\frac{2}{\pi }\exp ( - 0.16{{V}^{2}})\arccos \left[ {\frac{{\sqrt {1 - \sqrt {1 - {{\varepsilon }^{2}}} } }}{\varepsilon }} \right]} \right\}{\text{,}} \\ {{I}_{1}} = {{I}_{1}}\left( {\varepsilon ,V} \right) \equiv \\ \equiv \int\limits_0^{{{{\left( {1 - {{\varepsilon }^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}} {\exp \left\{ { - 0.16{{V}^{2}}\frac{{{{\varepsilon }^{2}}\sqrt {1 - {{\varepsilon }^{2}}} }}{{(1 - {{\varepsilon }^{2}} + {{z}^{2}})}}} \right\}\frac{{dz}}{{1 + {{z}^{2}}}}} , \\ \end{gathered} $

где I = I(ε, V) определено в (12).

3.2. Часть потерь энергии при передаче из фрагмента 2 во фрагмент 1

Согласно (3), (12) и (18) имеем

(22)

$\begin{gathered} {{a}_{{{\text{пот}}\left( {{\text{2}} \to {\text{1}}} \right)}}}\left( {\varepsilon {\text{,}}V} \right) = - 10{\text{lg}}\left\{ {\frac{{{{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}\left( {\varepsilon {\text{,}}V} \right)}}{{{{P}_{{2\left( {{\text{эл}}} \right)}}}\left( {\varepsilon {\text{,}}V} \right)}}} \right\} = \\ = - 10{\text{lg}}\left\{ {\frac{{{{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}\left( {\varepsilon {\text{,}}V} \right)}}{{\left[ {1 - {\text{exp}}\left\{ { - 0.16{{V}^{2}}\sqrt {1 - {{\varepsilon }^{2}}} } \right\}I\left( {\varepsilon {\text{,}}V} \right)} \right]}}} \right\}{\text{,}} \\ \end{gathered} $

где I = I(ε, V) также определено в (12), а P_{1(круг)∩2(эл)} берется из (21).

3.3. Полные потери энергии при соединении фрагментов 1 и 2 волоконной линии

Выражения для потерь энергии, рассчитанные на основах электродинамики, в направлениях 1 → 2 и 2 → 1 не совпадают, и это связано с тем, что на самом деле выражения (21), (22) являются составляющими полных потерь. Действительно, для стыкуемых фрагментов волноводной линии справедлива формула для потерь энергии a_пот [15, 16]:

(23)

${{a}_{{{\text{пот}}}}} = - 10\lg \left\{ {\frac{{{{{\left| {\iint {{{E}_{{{\text{круг}}}}}{{E}_{{{\text{эл}}}}}rdrd{\varphi }}} \right|}}^{2}}}}{{\iint {{{{\left| {{{E}_{{{\text{круг}}}}}} \right|}}^{2}}rdrd{\varphi }\iint {{{{\left| {{{E}_{{{\text{эл}}}}}} \right|}}^{2}}rdrd{\varphi }}}}}} \right\}.$

В нашем случае согласно (4), (5), (12) и (18) имеем

${{a}_{{{\text{пот}}}}} = - 10\lg \left\{ {\frac{{{{{\left| {{{P}_{{1\left( {{\text{круг}}} \right) \cap 2\left( {{\text{эл}}} \right)}}}} \right|}}^{2}}}}{{{{P}_{{1\left( {{\text{круг}}} \right)}}}{{P}_{{2\left( {{\text{эл}}} \right)}}}}}} \right\},$

так что в соответствии с (21), (22) окончательно получаем

(24)

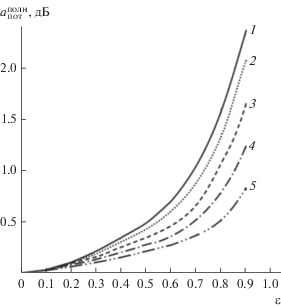
$a_{{{\text{пот}}}}^{{{\text{полн}}}}\left( {{\varepsilon },V} \right) = {{a}_{{{\text{пот}}\left( {1 \to 2} \right)}}}\left( {\varepsilon ,V} \right) + {{a}_{{{\text{пот}}\left( {2 \to 1} \right)}}}\left( {\varepsilon ,V} \right).$

Численные расчеты дают графическую зависимость, представленную на рис. 2.

Рис. 2.

Зависимость полных потерь энергии $a_{{{\text{пот}}}}^{{{\text{полн}}}}$ от эксцентриситета ε при различных значениях волноводного параметра V = 0.5 (1), 1 (2), 1.5 (3), 2 (4), 2.4 (5).

ЗАКЛЮЧЕНИЕ

Таким образом, можно сделать выводы, что в результате эллиптической деформации торца одного из двух сращиваемых фрагментов:

– величина η(ε, V) убывает при возрастании эксцентриситета и одновременно быстрее убывает при возрастании параметра V;

– полные потери энергии $a_{{{\text{пот}}}}^{{{\text{полн}}}}$ увеличиваются при возрастании эксцентриситета и при этом одновременно уменьшаются при возрастании волноводного параметра.

При большой деформации полные потери увеличиваются с уменьшением волноводного числа V. Это может быть связано с тем, что в инфракрасной области с увеличением λ возрастают потери и согласно (6) возрастает волноводное число V. Это также может быть связано с тем, что в одномодовом волокне с уменьшением ρ площадь пятна моды уменьшается вместе с волноводным числом V, что приводит на выходе из волокна к увеличению расхождения пучка и тем самым к увеличению потерь.

Приведенные данные помогут выбрать подходящий одномодовый режим для практических применений.

Список литературы

Мидвинтер Дж. Волоконные световоды для передачи информации. М.: Радио и связь, 1983.
Окоси Т., Окамото К., Оцу М. и др. Волоконно-оптические датчики. Л.: Энергоатомиздат, 1990.
Чео П.К. Волоконная оптика: Приборы и системы. М.: Энергоатомиздат, 1988.
Семенов Н.А. Оптические кабели связи: Теория и расчет. М.: Радио и связь, 1981.
Убайдуллаев Р.Р. Волоконно-оптические сети. М.: ИТЦ Эко-Трендз, 2000.
Маркузе Д. Оптические волноводы. М.: Мир, 1974.
Дмитриев А.Л. Оптические системы передачи информации. Учебное пособие. СПб: СПбГУИТМО, 2007.
Унгерн Х.Г. Планарные и волоконные оптические волноводы. М.: Мир, 1980.
Адамс М. Введение в теорию оптических волноводов. М.: Мир, 1984.
Снайдер А., Лав Дж. Теория оптических волноводов. М.: Радио и связь, 1987.
Воронин В.Г., Наний О.Е., Туркин А.Н. и др. Интегральные потери в элементах волоконно-оптических линий связи. М.: МАКС Пресс, 2012.
Бурдин А.В., Жуков А.Е., Прапорщиков Д.Е. // T‑Comm: Телекоммуникации и транспорт. 2015. Т. 9. № 4. С. 60.
Листвин В.Н., Трещиков В.Н. // Фотон – экспресс. 2012. № 7. С. 30.
Гладких В.А. // Компьютерная оптика. 2019. Т. 43. № 4. С. 557.
Franco M.A.R., Vasconcellos L.C., Machado J.M. // Revista Científica Periódica – Telecomunicações. 2004. V. 7. № 1. P. 54.
Буров Н.В, Лин Дж., Ромашова В.Б. // Фотоника. 2018. Т. 12. № 1. С. 16.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал