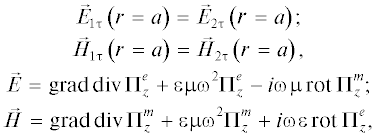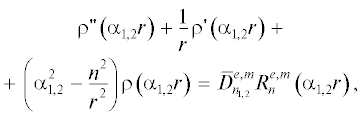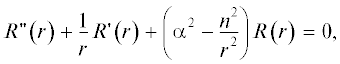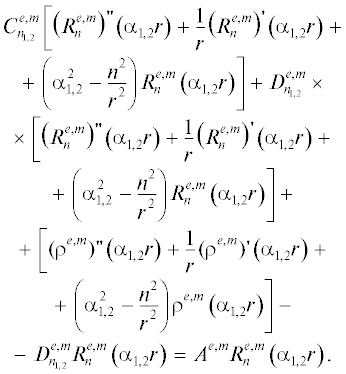Радиотехника и электроника, 2020, T. 65, № 11, стр. 1068-1073

ВВЕДЕНИЕ

Наиболее общим решениям несамосопряженных краевых задач соответствуют [1] комплексные собственные значения, которые значительно расширяют спектры волн направляющих структур. Комплексность собственных значений определяет комплексность волновых чисел. Комплексные волновые числа в направляющих структурах без диссипации энергии соответствуют [2–4] комплексным волнам (КВ). Наглядная классификация волн открытых направляющих структур дана в [5]. Классификация волн в неоднородных экранированных направляющих структурах [2] требует дополнений.

Понятие “несобственные волны” в направляющих структурах как описываемые решениями краевых задач с неоднородными граничными условиями, по-видимому, было впервые введено В.В. Шевченко [5]. В работах [6–9] показано, что в экранированных волноводах с неоднородным заполнением наряду с собственными волнами могут существовать присоединенные к источнику несобственные волны, описываемые краевыми задачами на присоединенном уравнении Гельмгольца, под которым понимается уравнение с правой частью, являющейся решением однородной краевой задачи на том же самом уравнении, но с нулевой правой частью. Такие краевые задачи являются самосогласованными, поскольку в них учитывается обратное влияние возбуждаемого поля на первичный источник, и волновые числа в функциях поля и источника совпадают. Источники указанного вида можно классифицировать как источники типа антенны бегущей волны, находящейся в синхронизме с возбуждаемым ей полем, либо как источники, включенные граничными условиями в замкнутую колебательную систему. Постоянная “подпитка” поля распределенным (бегущим) источником приводит к его (поля) линейному нарастанию в направлении распространения. Возникает эффект, подобный взаимодействию волноводного поля с полем пространственного заряда, наблюдаемый в лампе бегущей волны.

При парном возбуждении КВ, имеющих комплексную сопряженность по волновым числам и амплитудам, образуется колебание [6–9], “присоединенное” к источнику, которое описывается самосогласованной краевой задачей на присоединенном уравнении Гельмгольца, то есть на уравнении, в правой части которого стоит решение однородной краевой задачи. Особенность комплексного резонанса заключается в том, что он существует во всем диапазоне комплексных волн при обязательном присутствии источника. Колебания, соответствующие комплексному резонансу (КР), будучи присоединенными к источнику, являются несобственными. Данная работа является продолжением работы [9]. В ней даются дополнительные пояснения по формулировке присоединенных самосогласованных краевых задач, по представлению их решений, соответствующих присоединенными функциями. Дается развернутая запись этих функций. Отмечается, что присоединенная краевая задача в предлагаемой формулировке является самосогласованной и (в силу наличия у уравнения Гельмгольца правой части) неоднородной, вследствие чего присоединенные волны и колебания являются несобственными.

1. САМОСОГЛАСОВАННЫЕ ПРИСОЕДИНЕННЫЕ КРАЕВЫЕ ЗАДАЧИ

Поля в направляющих структурах описываются векторами Герца во взаимных структурах, как правило, их продольными компонентами, удовлетворяющими уравнению Гельмгольца. После разделения переменных получаются задачи на собственные значения вида:

(${{U}_{\nu }} = 0$ – граничные условия), в которых коэффициенты дифференциальных уравнений и уравнений ${{U}_{\nu }}\left( y \right) = 0$ являются аналитическими функциями параметра ${{\lambda }_{0}}.$

Когда ${{\lambda }_{0}}$ – собственное значение, а $\varphi \left( x \right)$ – собственная функция, ему соответствующая, функция ${{\varphi }_{1}}$ будет [1] присоединенной к функции $\varphi \left( x \right),$ если она удовлетворяет уравнению:

где ${{\varphi }_{0}} = \varphi \left( x \right).$

Отсюда следует, что каждой собственной функции можно поставить в соответствие присоединенную функцию, которая вместе с ${{\varphi }_{0}}$ будет описывать присоединенную волну.

В работах [6–9] обсуждались вопросы теории присоединенных волн в двухслойных изотропных направляющих структурах. Рассмотрим краевую задачу для присоединенных к источнику (существующих только в его присутствии) бегущих волн и колебаний круглого двухслойного экранированного волновода (КДЭВ). Радиус внутреннего слоя a (область 1), радиус экрана b. Области 2 соответствует интервал [a, b]. Она (задача) состоит из уравнения:

которое называем присоединенным уравнением Гельмгольца, и граничных условий где ${\text{П}}_{z}^{{e,m}}$ – продольные компоненты электрического и магнитного векторов Герца; a и b – радиусы внутреннего слоя и экрана; $\beta $ и $\beta = {{\beta }_{1}} + i{{\beta }_{2}}$ – продольные волновые числа присоединенной волны [6, 7] и комплексных волн (КВ) [10, 11], соответственно.

Функции $R_{n}^{{e,m}}$ в правой части уравнения (1) имеют [8] вид:

$R_{n}^{{e,m}}\left( {{{\alpha }_{1}}r} \right) = {{J}_{n}}\left( {{{\alpha }_{1}}r} \right)$ при r ∈ [0, a];

при r ∈ [a, b] где ${{J}_{n}}\left( {{{\alpha }_{{1.2}}}r} \right),$ ${{Y}_{n}}\left( {{{\alpha }_{2}}r} \right)$ – цилиндрические функции первого и второго рода; ${{\alpha }_{{1,2}}}$ – поперечные волновые числа.

Правую часть уравнения (1) можно рассматривать либо как функцию распределенного источника типа бегущей волны, а присоединенную краевую задачу (1), (2) – как задачу о возбуждении волн, “присоединенных” к указанному источнику, либо как функцию источника (нижняя действительная функция координаты z), создающего КР.

Решения сформулированных краевых задач записываем [9] в виде:

где функции ${{\rho }^{{e,m}}}\left( {{{\alpha }_{{1,2}}}r} \right)$ удовлетворяют [6–9] уравнениям (штрих означает производную по радиальной координате) которые получаются, после разделения в (1) переменных, и граничным условиям Дирихле и Неймана при $r = b{\text{:}}$

Уравнения (4) можно рассматривать как присоединенные уравнения Бесселя.

Функции ${{\rho }^{{e,m}}}\left( {{{\alpha }_{2}}r} \right)$ в интервале $r \in \left[ {0,...,a} \right]$ записываются как:

В интервале r ∈ [0, а] решения уравнения (4), полученные методом Лагранжа, имеют вид:

где $R\left( {\alpha r} \right) = {{R}^{{e,m}}}\left( {\alpha r} \right)$ – решения уравнения

соответствующие краевым задачам Дирихле и Неймана; $W\left( {\alpha r} \right)$ – вронскиан, записываемый как 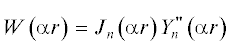– $J_{n}^{'}\left( {\alpha r} \right){{Y}_{n}}\left( {\alpha r} \right) = \frac{2}{{\pi \alpha r}};$ ${{Y}_{n}}\left( {\alpha r} \right)$ – функция Неймана.

Из граничных условий (2б) получаем систему функциональных уравнений, зависящих от продольной координаты. Приравнивая в них члены, имеющие линейную зависимость от координаты z, получаем систему линейных однородных алгебраических уравнений относительно коэффициентов $D_{{{{n}_{{1,2}}}}}^{{e,m}}.$ Условие нетривиальности решений этой системы дает уравнение, совпадающее с дисперсионным уравнением собственных волн круглого двухслойного экранированного волновода.

Члены в вышеуказанных функциональных уравнениях, не имеющие координатной зависимости, при условии (4) дают систему линейных неоднородных алгебраических уравнений относительно коэффициентов: $C_{{{{n}_{{1,2}}}}}^{{e,m}}.$ Главные определители двух систем (однородной и неоднородной) совпадают. Будучи приравненными нулю, они дают дисперсионные уравнения собственных волн КДЭВ.

Нетривиальные решения системы линейных однородных алгебраических уравнений (коэффициенты $D_{{{{n}_{{1,2}}}}}^{{e,m}}$) подставляются в систему неоднородных уравнений, которая решается относительно коэффициентов $C_{{{{n}_{{1,2}}}}}^{{e,m}}.$

Поскольку для волн, описываемых решениями (3) должны выполнятся граничные условия (2б), необходимо, чтобы системы однородных и неоднородных линейных алгебраических уравнений имели совместные решения. Система однородных уравнений имеет нетривиальные решения только при равенстве нулю ее определителя. Поскольку главный определитель системы неоднородных уравнений совпадает с определителем системы однородных уравнений, система неоднородных уравнений может иметь решения только при равенстве нулю ее дополнительных определителей. Таким образом, собственные значения краевой задачи, определяющие волновые числа волн, описываемых этой задачей, находятся [6–9] как совместные решения трех трансцендентных уравнений.

Каждое из этих уравнений решается совместно с уравнениями:

Волнам, описываемым рассматриваемой присоединенной краевой задачей, соответствуют решения, удовлетворяющие одновременно всем трем указанным уравнениям совместно с уравнениями (8), связывающими волновые числа. Численное решение указанных уравнений [6, 7] показало существование их совместных решений, соответствующих волнам, которые можно назвать присоединенными к источнику, поскольку они описываются уравнением (1), в правой части которого стоит функция (описывающая источник), являющаяся решением соответствующей краевой задачи на однородном уравнении Гельмгольца.

Объединяя математическую и физическую идеологии, можем заключить, что, решая краевую задачу на присоединенном уравнении Гельмгольца, получаем волны, существующие только при наличии источника, присоединенные (привязанные) к нему, то есть присоединенная краевая задача является самосогласованной и в то же время имеющей нетривиальные решения только при наличии источника. Специфика записи правой части уравнения (1) говорит о самосогласованности решаемой задачи. В постановке (1), (2) присоединенная краевая задача фактически является задачей о возбуждении поля согласованным с ним источником.

2. ПРИСОЕДИНЕННЫЕ ВОЛНЫ И КОЛЕБАНИЯ

Таким образом, присоединенную задачу в предлагаемой формулировке можно рассматривать как особый вариант задачи о возбуждении. Подставляя решение (3) в уравнение (1), получаем:

Из (9) видно, что решение (3) удовлетворяет с учетом уравнения (4) присоединенному уравнению Гельмгольца (1) при условии:

Как и должно быть, характер возбуждаемой заданным источником волны определяется амплитудой ${{A}^{{e,m}}}$ этого источника – условием, накладываемым на эту амплитуду.

В том случае, когда

решения (3) удовлетворяют обычному (однородному) уравнению Гельмгольца и соответствуют точкам жордановой кратности волновых чисел [12], обеспечивая полноту системы волн направляющей структуры [12–14].

Условия (10), (11) являются естественными дополнительными условиями, накладываемыми на источник, поскольку от последнего зависит вид возбуждаемого им поля: несобственного колебания, в частности, соответствующего (при возбуждении пары сопряженных КВ) комплексному резонансу. В [15–18] показано, что для возбуждения сопряженной пары КВ необходимо брать источник, описываемый действительной функцией координат. В этом случае возбуждается присоединенное колебание, дающее КР. Для возбуждения индивидуальных КВ нужен источник типа антенны бегущей волны. Это учитывается в представлении (3). Таким образом, задача о существовании присоединенной волны (колебания) есть задача одномодового возбуждения.

Сформулированная задача о возбуждении КР является самосогласованной, а колебание, соответствующее КР, следует называть колебанием, присоединенным к источнику. Самосогласовнность задачи следует из совпадения волновых чисел в правых частях уравнений (1), (4) с волновыми числами КВ, образующих колебание, соответствующее КВ.

Таким образом, источники, описываемые действительными функциями координат, возбуждают в КДЭВ по обе стороны от себя по две комплексных волны с противоположно направленными фазовыми скоростями. Это приводит к возникновению стоячей волны, поле которой локализовано вблизи источника. При этом отрезок волновода, включаемый “на проход” или “на отражение” (в первом случае в плоскости симметрии, перпендикулярной оси волновода, располагаются возбуждающий и воспринимающий электроды, во втором – лишь один возбуждающий электрод), во всем диапазоне комплексных волн ведет себя как резонатор и обладает при этом фильтрующими свойствами. Поскольку в отличие от обычного резонанса отмеченное явление, возникающее в двухслойном экранированном волноводе, обнаруживает резонансные свойства (возрастание выходного сигнала в схеме “на проход” и резкое падение коэффициентов стоячей волны ${{K}_{{{\text{ст}}U}}}$ в схеме “на отражение”) во всем частотном диапазоне комплексных волн, оно классифицировано [15, 16] как “комплексный резонанс”.

Резонансным признаком рассматриваемого явления служит факт увеличения запасенной энергии в указанной выше полосе частот, что позволяет ввести понятие добротности (в энергетической формулировке), вычислить ее и измерить косвенным методом. Поскольку КР существует только в присутствии источника, возбуждающего пару КВ, и описывается присоединенной краевой задачей, соответствующее ему колебание следует называть присоединенным, а краевую задачу полагать самосогласованной.

Поскольку в правой части уравнения (1) стоит действительная функция (нижняя строка), источник создает [12, 13] сопряженную пару КВ, образующих КР. Поскольку указанные КВ связаны через источник, образуемое ими колебание, соответствующее КР, можно называть присоединенным к источнику, а краевую задачу, описывающую КР, следует считать самосогласованной. КВ, описываемые уравнением (1) с нижней правой частью, возбуждаются независимо и являются присоединенными к источнику волнам. В этом случае распределенное взаимодействие с источником.

Заменой функций $R_{n}^{{e,m}}\left( {{{\alpha }_{2}}r} \right),$ описывающих поля во внешней области двухслойной структуры, на функции Ганкеля $H_{n}^{{(2)}}\left( {{{\alpha }_{2}}r} \right)$ можно перейти от краевой присоединенной задачи для круглого двухслойного экранированного волновода к задаче для открытого ДВ. Поскольку в этом случае формулировать граничные условия задач Дирихле и Неймана на внешней границе нет необходимости, решение уравнения (4) можно записать непосредственно в виде (6). Присоединенным волнам (колебаниям), описываемыми краевыми задачами на обычном уравнении Гельмгольца соответствуют решения дисперсионных уравнений в точках жордановой кратности волновых чисел [16–18].

3. РАСЧЕТ ДОБРОТНОСТИ КР

Теоретически собственная добротность комплексного резонанса рассчитывалась по следующей схеме.

Выразив компоненты поля через векторы Герца:

где функции ${{\chi }_{{11}}}\left( {{{\alpha }_{2}}r} \right),$ ${{\chi }_{{21}}}\left( {{{\alpha }_{2}}r} \right)$ – комбинации цилиндрических функций, обеспечивающие выполнение на экранирующей поверхности граничных условий Дирихле и Неймана, соответственно, подставляем их и решения дисперсионного уравнения в формулу:

учитывающую потери в диэлектрике и в экранирующей поверхности волновода.

В (12) индексы “1”, “2” соответствуют внутренней и внешней областям двухслойного волновода; S – экранирующая поверхность, $\sigma $ – проводимость ее материала; f – частота комплексного резонанса. Формула (12) записана в гауссовой системе единиц.

Результаты расчета показали, что добротность комплексного резонанса в волноводных структурах рассмотренного типа имеет порядок $Q = 300...1000$ (${{Q}_{{{\text{эксп}}}}} \approx 300;$ ${{Q}_{{{\text{теор}}}}} \approx 1000$) и уменьшается с приближением к нижней частотной границе диапазона существования комплексных волн.

Значительное отличие теоретического результата от экспериментального объясняется влиянием внешних цепей резонатора (экспериментально измерялась нагруженная добротность). Кроме того, при определении добротности полагалось, что распределения полей в области, заполненной диэлектриком, при комплексном и эталонном резонансах совпадают, однако в действительности это выполняется лишь приближенно.

ЗАКЛЮЧЕНИЕ

Показано, что самосогласованные присоединенные краевые задачи фактически являются задачами одномодового возбуждения. Присоединенные колебания (волны), описываемые краевыми задачами на уравнении Гельмгольца, в правой части которого стоит решение однородной краевой задачи на этом же уравнении, могут существовать только при наличии источника, то есть являются несобственными. Это второй вид несобственных волн – несобственных из-за присутствия источника. Первый вид [5] – из-за неоднородности (в частности, на бесконечности) граничных условий. Главное – будучи несобственными, зависящими от источника, волны (колебания), присоединенные к источнику, зависят, с учетом соотношений (10), (11), от амплитуд источников.

Отмечается, что в диапазоне существования комплексных волн при условии их парного возбуждения в круглом двухслойном экранированном волноводе возникает резонансное явление, получившее [16–18] название “комплексный резонанс”. Установлено его (резонанса) соответствие самосогласованной присоединенной краевой задаче, описаны его характерные особенности. Сделана оценка добротности комплексного резонанса при реализации его в отрезке КДЭВ. Колебание, соответствующее КР предлагается классифицировать как присоединенное к источнику, поскольку теоретически оно описывается краевой задачей на присоединенном уравнении Гельмгольца, в правой части которого стоит функция, являющаяся решением однородной краевой задачи. Такая задача (на присоединенном уравнении Гельмгольца) является самосогласованной [19].