1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 65, № 11, 2020

Радиотехника и электроника, 2020, T. 65, № 11, стр. 1061-1067

Эквивалентный поверхностный импеданс бесконечной периодической решетки щелевых импедансных нагрузок, выполненных на основе полости c поперечным сечением в виде равностороннего треугольника, с диэлектрическим покрытием

В. Г. Кошкидько a, *, Э. С. Сердюк a

a Институт радиотехнических систем и управления Южного федерального университета
347922 Таганрог, Некрасовский пер., 44, Российская Федерация

* E-mail: kvg59@mail.ru

Поступила в редакцию 22.12.2019
После доработки 22.12.2019
Принята к публикации 18.01.2020

Полный текст (PDF)

Аннотация

Рассмотрена двумерная задача определения эквивалентного поверхностного импеданса бесконечной решетки щелевых импедансных нагрузок со слоем диэлектрика. Каждый элемент решетки содержит три области: первая занимает все полупространство над границей раздела и первичное поле возбуждается в этой области плоской волной; вторая область не содержит возбуждающих источников и представляет собой слой диэлектрика; третья область также не содержит возбуждающих источников и ограничена стенками полости c поперечным сечением в виде равностороннего треугольника. Вторая и третья области связаны через одну или нескольких щелей в идеально проводящем экране, расположенном на их границе. В раскрыве каждой щели расположен полосковый проводник. Решение задачи проводилось методом интегральных уравнений, для численной реализации которого использовался метод Крылова–Боголюбова. Приведены численные результаты в виде зависимостей эквивалентного поверхностного импеданса от геометрических размеров конструкции при фиксированных значениях периода решетки, угла падения электромагнитной волны и толщины слоя диэлектрика. Проведен сравнительный анализ полученных зависимостей с характеристиками аналогичной решетки без диэлектрического слоя.

ВВЕДЕНИЕ

Проблема реализации реактивного поверхностного импеданса является актуальной при решении задач управления рассеянными полями проводящих тел в радиолокации [1–8], в антенной технике при создании антенн поверхностных волн и в задачах обеспечения развязки антенн [9–11], а также при разработке так называемых “текстурированных электромагнитных поверхностей” (textured electromagnetic surface) и “искусственных импедансных поверхностей” (artificial impedance surfaces) [12, 13].

В большинстве случаев, в качестве конструкции, реализующей реактивный поверхностный импеданс, используется, как правило, либо одиночные прямоугольные канавки, либо ребристые структуры на их основе. Кроме этого, для этой цели нашли применение щелевые импедансные нагрузки (ЩИН), построенные на основе отверстия в идеально проводящем экране, нагруженного полостью.

В работах [14–43 ] исследованы характеристики различных конструкций ЩИН, позволяющих реализовать реактивный поверхностный импеданс, как в одиночном исполнении [14–28], так и в составе бесконечных решеток [29–43].

В работе [14] решена задача о возбуждении плоской волной одиночной ЩИН на основе полости c поперечным сечением в виде равностороннего треугольника, а в работах [37, 43] приведены результаты для такой конструкции в составе бесконечной решетки.

Для защиты подобных структур от воздействия внешней среды применяют диэлектрические покрытия – обтекатели. Поэтому в данной статье рассмотрено влияние диэлектрического слоя на характеристики этой же конструкция ЩИН в составе бесконечной решетки.

1. ПОСТАНОВКА ЗАДАЧИ

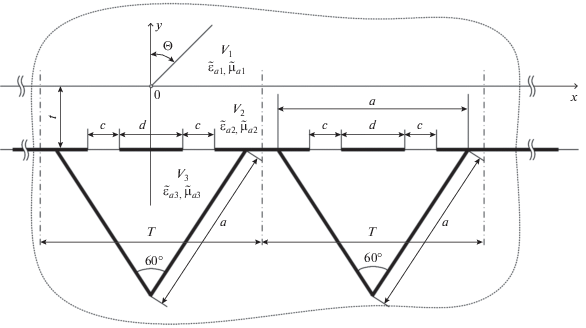
Имеется бесконечная периодическая решетка ЩИН со слоем диэлектрика (рис. 1), размещенных с периодом $T.$ Каждый элемент решетки содержит три области – ${{V}_{1}},$ ${{V}_{2}}$ и ${{V}_{3}}.$

Рис. 1.

К постановке задачи.

Область ${{V}_{1}}$ с параметрами ${{\tilde {\varepsilon }}_{{a1}}},{{\tilde {\mu }}_{{a1}}}$ занимает все полупространство над границей раздела, лежащей в плоскости $x0z.$ Первичное поле возбуждается в области ${{V}_{1}}$ плоской волной, падающей под углом $\theta ,$ отсчитываемым от нормали к плоскости $x0z.$ Область ${{V}_{2}}$ с параметрами ${{\tilde {\varepsilon }}_{{a2}}},{{\tilde {\mu }}_{{a2}}}$ не содержит возбуждающих источников и представляет собой слой диэлектрика толщиной $t,$ расположенный между плоскостями $y = 0$ и $y = - t.$ Область ${{V}_{3}}$ с параметрами ${{\tilde {\varepsilon }}_{{a3}}},{{\tilde {\mu }}_{{a3}}}$ также не содержит возбуждающих источников и ограничена стенками полости с поперечным сечением в виде равностороннего треугольника со стороной $a$ (${{\tilde {\varepsilon }}_{{a1,2,3}}},$ ${{\tilde {\mu }}_{{a1,2,3}}}$ – абсолютные комплексные диэлектрическая и магнитная проницаемости сред соответствующих областей). Область ${{V}_{2}}$ связана с областью ${{V}_{3}}$ через одну или нескольких щелей в идеально проводящем экране, расположенном на границе областей ${{V}_{2}}$ и ${{V}_{3}}$ ($y = - t$). В раскрыве каждой щели, имеющей ширину $c,$ расположен полосковый проводник шириной $d.$

Возбуждающие источники имеют составляющие полей ${{H}_{z}}, {{E}_{x}}, {{E}_{y}}$ ($H$ – поляризация), а параметры конструкции будем считать независимыми от координаты $z$ (двумерная задача). Требуется найти усредненный по периоду решетки $T$ эквивалентный поверхностный импеданс.

2. РЕШЕНИЕ ЗАДАЧИ

Поля в области ${{V}_{1}}.$ Выражения для полей в области ${{V}_{1}}$ были получены в [29] в виде разложения по пространственным гармоникам Флоке

(1)
$\begin{gathered} {{H}_{z}}(x,y) = \sum\limits_{m = - \infty }^\infty {I_{m}^{{(1)}}{{\psi }_{m}}(x)\exp \left( { - i\Gamma _{m}^{{(1)}}y} \right)} + \\ + \,\,{{\psi }_{0}}(x)\exp \left( {i\Gamma _{0}^{{(1)}}y} \right), \\ \end{gathered} $
(2)
$\begin{gathered} {{E}_{x}}(x,y) = - \sum\limits_{m = - \infty }^\infty {Z_{m}^{{(1)}}I_{m}^{{(1)}}{{\psi }_{m}}(x)\exp \left( { - i\Gamma _{m}^{{(1)}}y} \right)} + \\ + \,\,Z_{0}^{{(1)}}{{\psi }_{0}}(x)\exp \left( {i\Gamma _{0}^{{(1)}}y} \right), \\ \end{gathered} $
где $T$ – период решетки, $I_{m}^{{(1)}}$ – коэффициенты разложения тока, $\Gamma _{m}^{{(1)}}$ – постоянная распространения, ${{\psi }_{m}}(x)$ – функции, определяющие изменение поля в поперечном направлении [44]:

$\begin{gathered} {{\psi }_{m}}(x) = \sqrt {\frac{1}{T}} \exp \left( { - i\left( {\frac{{2m\pi }}{T} - {{k}_{1}}\sin \theta } \right)x} \right), \\ m = 0, \pm 1, \pm 2,..., \\ \Gamma _{m}^{{(1)}} = \sqrt {k_{1}^{2} - {{{\left( {\frac{{2m\pi }}{{\rm T}} - {{k}_{1}}\sin \theta } \right)}}^{2}}} ,\,\,\,\,Z_{m}^{{(1)}} = {{\Gamma _{m}^{{(1)}}} \mathord{\left/ {\vphantom {{\Gamma _{m}^{{(1)}}} {\omega {{{\tilde {\varepsilon }}}_{{a1}}}}}} \right. \kern-0em} {\omega {{{\tilde {\varepsilon }}}_{{a1}}}}}, \\ {{k}_{1}} = \omega \sqrt {{{{\tilde {\varepsilon }}}_{{a1}}}{{{\tilde {\mu }}}_{{a1}}}} . \\ \end{gathered} $

Используя ортогональность гармоник Флоке, из (2) найдем коэффициенты разложения тока $I_{m}^{{(1)}}$ и, подставляя их в (1), получим выражение для магнитного поля на границе областей ${{V}_{1}}$ и ${{V}_{2}}$ со стороны области ${{V}_{1}},$ т.е. в плоскости x0z при $y = 0$

(3)
$\begin{gathered} {{H}_{z}}(x,0) = - \int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {\left\{ {\sum\limits_{m = - \infty }^\infty {\Upsilon _{m}^{{(1)}}{{\psi }_{m}}(x)\psi _{m}^{*}(x{\kern 1pt} ')} } \right\}} \times \\ \times \,\,{{E}_{x}}(x{\kern 1pt} ',0)dx{\kern 1pt} ' + 2{{\psi }_{0}}(x), \\ \end{gathered} $

где $Y_{m}^{{(1)}} = {1 \mathord{\left/ {\vphantom {1 {Z_{m}^{{(1)}}}}} \right. \kern-0em} {Z_{m}^{{(1)}}}}.$

Поля в области ${{V}_{2}}.$ Выражения для полей в области ${{V}_{2}}$ запишем также в виде разложения по гармоникам Флоке

(4)
$\begin{gathered} {{H}_{z}}(x,y) = \\ = \sum\limits_{m = - \infty }^\infty {\left( {I_{m}^{ - }\exp \left( {i\Gamma _{m}^{{(2)}}y} \right) + I_{m}^{ + }\exp \left( { - i\Gamma _{m}^{{(2)}}y} \right)} \right)} {{\psi }_{m}}(x), \\ \end{gathered} $
(5)
$\begin{gathered} {{E}_{x}}(x,y) = \\ = \sum\limits_{m = - \infty }^\infty {\left( {I_{m}^{ - }\exp \left( {i\Gamma _{m}^{{(2)}}y} \right) - I_{m}^{ + }\exp \left( { - i\Gamma _{m}^{{(2)}}y} \right)} \right)} Z_{m}^{{(2)}}{{\psi }_{m}}(x), \\ \Gamma _{m}^{{(2)}} = \sqrt {k_{2}^{2} - {{{\left( {\frac{{2m\pi }}{{\rm T}} - {{k}_{1}}\sin \theta } \right)}}^{2}}} ,\,\,\,\,Z_{m}^{{(2)}} = {{\Gamma _{m}^{{(2)}}} \mathord{\left/ {\vphantom {{\Gamma _{m}^{{(2)}}} {\omega {{{\tilde {\varepsilon }}}_{{a2}}}}}} \right. \kern-0em} {\omega {{{\tilde {\varepsilon }}}_{{a2}}}}}, \\ {{k}_{2}} = \omega \sqrt {{{{\tilde {\varepsilon }}}_{{a2}}}{{{\tilde {\mu }}}_{{a2}}}} . \\ \end{gathered} $

Коэффициенты $I_{m}^{ - }$ определяют отражение от границы $y = 0$, коэффициенты $I_{m}^{ + }$ – отражение от границы $y = - t.$

На границе областей ${{V}_{1}}$ и ${{V}_{2}}$ со стороны области ${{V}_{2}},$ т.е. при $y = 0$ из выражений (4) и (5) получим

(6)
${{H}_{z}}(x,0) = \sum\limits_{m = - \infty }^\infty {\left( {I_{m}^{ - } + I_{m}^{ + }} \right){{\psi }_{m}}(x),} $
(7)
${{E}_{x}}(x,0) = \sum\limits_{m = - \infty }^\infty {Z_{m}^{{(2)}}\left( {I_{m}^{ - } - I_{m}^{ + }} \right){{\psi }_{m}}(x).} $

На границах областей ${{V}_{2}}$ и ${{V}_{3}}$ со стороны области ${{V}_{2}},$ т.е. при $y = - t$ из выражений (4) и (5) получим

(8)
$\begin{gathered} {{H}_{z}}(x, - t) = \\ = \sum\limits_{m = - \infty }^\infty {\left( {I_{m}^{ - }\exp \left( { - i\Gamma _{m}^{{(2)}}t} \right) + I_{m}^{ + }\exp \left( {i\Gamma _{m}^{{(2)}}t} \right)} \right){{\psi }_{m}}(x),} \\ \end{gathered} $
(9)
$\begin{gathered} {{E}_{x}}(x, - t) = \\ = \sum\limits_{m = - \infty }^\infty {Z_{m}^{{(2)}}\left( {I_{m}^{ - }\exp \left( { - i\Gamma _{m}^{{(2)}}t} \right) - I_{m}^{ + }\exp \left( {i\Gamma _{m}^{{(2)}}t} \right)} \right){{\psi }_{m}}(x)} . \\ \end{gathered} $

Поскольку поля в областях ${{V}_{1}}$ и ${{V}_{2}}$ разложены по одной системе функций ${{\psi }_{m}}(x),$ то можно приравнять коэффициенты с одинаковыми индексами в парах соотношений (1) и (6), (2) и (7). В результате получаем

(10)
$\left. {\begin{array}{*{20}{c}} {I_{0}^{{(1)}} = I_{0}^{ - } + I_{0}^{ + } - 1,} \\ {Z_{0}^{{(1)}}\left( {1 - I_{0}^{{(1)}}} \right) = Z_{0}^{{(2)}}\left( {I_{0}^{ - } - I_{0}^{ + }} \right),} \\ {I_{m}^{{(1)}} = I_{m}^{ - } + I_{m}^{ + },} \\ { - I_{m}^{{(1)}}Z_{m}^{{(1)}} = Z_{m}^{{(2)}}\left( {I_{m}^{ - } - I_{m}^{ + }} \right).} \end{array}} \right\}$

Исключая из (10) коэффициенты $I_{m}^{{(1)}},$ получим

(11)
$\left. {\begin{array}{*{20}{c}} {I_{0}^{ + } = \frac{{I_{0}^{ - }\left( {Y_{0}^{{(2)}} + Y_{0}^{{(1)}}} \right) - 2Y_{0}^{{(2)}}}}{{Y_{0}^{{(1)}} - Y_{0}^{{(2)}}}},} \\ {I_{m}^{ + } = I_{m}^{ - }\frac{{Y_{m}^{{(1)}} + Y_{m}^{{(2)}}}}{{Y_{m}^{{(1)}} - Y_{m}^{{(2)}}}},} \end{array}} \right\}$

где $Y_{m}^{{(2)}} = {1 \mathord{\left/ {\vphantom {1 {Z_{m}^{{(2)}}}}} \right. \kern-0em} {Z_{m}^{{(2)}}}}.$

Подставим (11) в (9) и, используя ортогональность гармоник Флоке, получим

(12)
$\begin{gathered} I_{m}^{ - } = \frac{{Y_{m}^{{(2)}}\left( {Y_{m}^{{(2)}} - Y_{m}^{{(1)}}} \right)}}{{2\left( {Y_{m}^{{(2)}}\cos \Gamma _{m}^{{(2)}}t + iY_{m}^{{(1)}}\sin \Gamma _{m}^{{(2)}}t} \right)}} \times \\ \times \,\,\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ', - t)\psi _{m}^{*}(x{\kern 1pt} ')dx{\kern 1pt} '} , \\ \end{gathered} $
(13)
$\begin{gathered} I_{0}^{ - } = \frac{{Y_{0}^{{(2)}}\exp \left( {i\Gamma _{0}^{{(2)}}t} \right)}}{{Y_{0}^{{(2)}}\cos \Gamma _{0}^{{(2)}}t + iY_{0}^{{(1)}}\sin \Gamma _{0}^{{(2)}}t}} + \\ + \,\,\frac{{Y_{0}^{{(2)}}\left( {Y_{0}^{{(2)}} - Y_{0}^{{(1)}}} \right)}}{{2\left( {Y_{0}^{{(2)}}\cos \Gamma _{0}^{{(2)}}t + iY_{0}^{{(1)}}\sin \Gamma _{0}^{{(2)}}t} \right)}} \times \\ \times \,\,\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ', - t)\psi _{0}^{*}(x{\kern 1pt} ')dx{\kern 1pt} '} . \\ \end{gathered} $

Подставим (11) в (8), получим

(14)
$\begin{gathered} {{H}_{z}}(x, - t) = \frac{{2Y_{0}^{{(2)}}\exp \left( {i\Gamma _{0}^{{(2)}}t} \right)}}{{Y_{0}^{{(2)}} - Y_{0}^{{(1)}}}} + \\ + \,\,\sum\limits_{m = - \infty }^\infty {2I_{m}^{ - }\frac{{Y_{m}^{{(1)}}\cos \Gamma _{m}^{{(2)}}t + iY_{m}^{{(2)}}\sin \Gamma _{m}^{{(2)}}t}}{{Y_{m}^{{(1)}} - Y_{m}^{{(2)}}}}{{\psi }_{m}}(x).} \\ \end{gathered} $

Подставляя (12) и (13) в (14), получим выражение для магнитного поля на границе областей ${{V}_{2}}$ и ${{V}_{3}}$ со стороны области ${{V}_{2}}$ ($y = - t$)

(15)
$\begin{gathered} {{H}_{z}}(x, - t) = - \sum\limits_{m = - \infty }^\infty {Y_{m}^{{(2)}}\frac{{Y_{m}^{{(1)}} + iY_{m}^{{(2)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}}{{Y_{m}^{{(2)}} + iY_{m}^{{(1)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}} \times } \\ \times \,\,\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ', - t){{\psi }_{m}}(x)\psi _{m}^{*}(x{\kern 1pt} ')dx{\kern 1pt} '} + \\ + \,\,\frac{{2{{\psi }_{0}}(x)}}{{\cos \left( {\Gamma _{0}^{{(2)}}t} \right) + i\frac{{Y_{0}^{{(1)}}}}{{Y_{0}^{{(2)}}}}\sin \left( {\Gamma _{0}^{{(2)}}t} \right)}}. \\ \end{gathered} $

Поля в области ${{V}_{3}}.$ Выражения для полей в области ${{V}_{3}}$ было получено в [14] в виде разложения по собственным функциям области с поперечным сечением в виде равностороннего треугольника с использованием функции Грина такой области, приведенной в работе [45]. На границе областей ${{V}_{2}}$ и ${{V}_{3}}$ со стороны области ${{V}_{3}}$ ($y = - t$) выражение для магнитного поля примет вид:

(16)
${{H}_{z}}\left( {x,0} \right) = - \int\limits_{{{ - c} \mathord{\left/ {\vphantom {{ - c} 2}} \right. \kern-0em} 2}}^{{c \mathord{\left/ {\vphantom {c 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ')K(x,x{\kern 1pt} ')dx{\kern 1pt} '} .$

где

(17)
$\begin{gathered} K\left( {x,x{\kern 1pt} '} \right) = - i\frac{4}{{\sqrt 3 }}\frac{{{{k}_{3}}}}{{{{W}_{3}}}} \times \\ \times \,\,\sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {\frac{{{{T}_{1}}\left( x \right){{T}_{1}}\left( {x{\kern 1pt} '} \right) + {{T}_{2}}\left( x \right){{T}_{2}}\left( {x{\kern 1pt} '} \right)}}{{16{{\pi }^{2}}\left( {{{m}^{2}} + mn + {{n}^{2}}} \right) - 9{{a}^{2}}k_{3}^{2}}}} } , \\ \end{gathered} $
(18)
${{k}_{3}} = \omega \sqrt {{{{\tilde {\varepsilon }}}_{3}}{{{\tilde {\mu }}}_{3}}} ,\,\,\,\,{{W}_{3}} = \sqrt {{{{{{\tilde {\mu }}}_{3}}} \mathord{\left/ {\vphantom {{{{{\tilde {\mu }}}_{3}}} {{{{\tilde {\varepsilon }}}_{3}}}}} \right. \kern-0em} {{{{\tilde {\varepsilon }}}_{3}}}}} ,$
(19)
$\begin{gathered} {{T}_{1}}\left( x \right) = {{\left( { - 1} \right)}^{{m + n}}}\cos \left( {\frac{{2\pi \left( {m - n} \right)x}}{{3a}}} \right) + \\ + \,\,{{\left( { - 1} \right)}^{m}}\cos \left( {\frac{{2\pi \left( {2n + m} \right)x}}{{3a}}} \right) + \\ + \,\,{{\left( { - 1} \right)}^{n}}\cos \left( {\frac{{2\pi \left( {2m + n} \right)x}}{{3a}}} \right), \\ \end{gathered} $
(20)
$\begin{gathered} {{T}_{2}}\left( x \right) = {{\left( { - 1} \right)}^{{m + n}}}\sin \left( {\frac{{2\pi \left( {m - n} \right)x}}{{3a}}} \right) + \\ + \,\,{{\left( { - 1} \right)}^{m}}\sin \left( {\frac{{2\pi \left( {2n + m} \right)x}}{{3a}}} \right) - \\ - \,\,{{\left( { - 1} \right)}^{n}}\sin \left( {\frac{{2\pi \left( {2m + n} \right)x}}{{3a}}} \right). \\ \end{gathered} $

Интегральное уравнение. Удовлетворяя условию непрерывности касательных составляющих полей в раскрыве отверстий в плоскости $y = - t,$ получим интегральное уравнение относительно касательной составляющей электрического поля ${{E}_{x}}(x, - t)$ путем приравнивая правых частей (15) и (16)

(21)
$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ', - t)} } \end{array}} \end{array}\left[ {{{Q}_{1}}(x,x{\kern 1pt} ') + {{Q}_{2}}(x,x{\kern 1pt} ')} \right]dx{\kern 1pt} ' = P(x),$

где

(22)
$\begin{gathered} \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{Q}_{1}}(x,x{\kern 1pt} ') = } \end{array}} \end{array} \\ = \sum\limits_{m = - \infty }^\infty {Y_{m}^{{(2)}}\frac{{Y_{m}^{{(1)}} + iY_{m}^{{(2)}}\operatorname{tg} (\Gamma _{m}^{{(2)}}t)}}{{Y_{m}^{{(2)}} + iY_{m}^{{(1)}}\operatorname{tg} (\Gamma _{m}^{{(2)}}t)}}{{\psi }_{m}}(x)\psi _{m}^{*}(x{\kern 1pt} ')} , \\ \end{gathered} $
(23)
$\begin{gathered} \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{Q}_{2}}(x,x{\kern 1pt} ')} \end{array}} \end{array} = - i\frac{4}{{\sqrt 3 }}\frac{{{{k}_{3}}}}{{{{W}_{3}}}} \times \\ \times \,\,\sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {\frac{{{{T}_{1}}\left( x \right){{T}_{1}}\left( {x{\kern 1pt} '} \right) + {{T}_{2}}\left( x \right){{T}_{2}}\left( {x{\kern 1pt} '} \right)}}{{16{{\pi }^{2}}\left( {{{m}^{2}} + mn + {{n}^{2}}} \right) - 9{{a}^{2}}k_{3}^{2}}}} } , \\ \end{gathered} $
(24)
$P(x) = \frac{{2{{\psi }_{0}}(x)}}{{\cos \left( {\Gamma _{0}^{{(2)}}t} \right) + i\frac{{Y_{0}^{{(1)}}}}{{Y_{0}^{{(2)}}}}\sin \left( {\Gamma _{0}^{{(2)}}t} \right)}}.$

Таким образом, получено интегральное уравнение для решетки импедансных нагрузок с диэлектрическим покрытием. Из сравнения уравнения (21) и интегрального уравнения для аналогичной решетки без диэлектрического покрытия [26] видно, что эти уравнения аналогичны. Отличия обусловлены наличием диэлектрического слоя и заключены в выражениях, относящихся к областям пространства ${{V}_{1}}$ и ${{V}_{2}}.$

Эквивалентная проводимость ${{\tilde {Y}}_{m}}$ в выражении (22), определяемая соотношением

(25)
${{\tilde {Y}}_{m}} = Y_{m}^{{(2)}}\frac{{Y_{m}^{{(1)}} + iY_{m}^{{(2)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}}{{Y_{m}^{{(2)}} + iY_{m}^{{(1)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}},$

является входной проводимостью отрезка длинной линии, имеющего длину $t,$ волновую проводимость $Y_{m}^{{(2)}}$ и постоянную распространения $\Gamma _{m}^{{(2)}}$ и нагруженного на проводимость $Y_{m}^{{(1)}}.$ Кроме того, правая часть выражения (21) отличается от соответствующей правой части интегрального уравнения в [26] наличием коэффициента $\cos \left( {\Gamma _{0}^{{(2)}}t} \right) + i\frac{{Y_{0}^{{(1)}}}}{{Y_{0}^{{(2)}}}}\sin \left( {\Gamma _{0}^{{(2)}}t} \right)$ в знаменателе. Отметим, что при условии $t = 0,$ соответствующем отсутствию диэлектрического слоя, уравнение (21) полностью совпадает с интегральным уравнением [26], полученным для такой же решетки без диэлектрического слоя.

3. ЭКВИВАЛЕНТНЫЙ ПОВЕРХНОСТНЫЙ ИМПЕДАНС

Эквивалентный поверхностный импеданс (ЭПИ), определяется по следующей формуле [46, 47]

(26)
${{Z}_{{\text{э}}}} = {{\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ')H_{z}^{*}(x{\kern 1pt} ')dx{\kern 1pt} '} } \mathord{\left/ {\vphantom {{\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ')H_{z}^{*}(x{\kern 1pt} ')dx{\kern 1pt} '} } {\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{{\left| {{{H}_{z}}(x{\kern 1pt} ')} \right|}}^{2}}dx{\kern 1pt} '} }}} \right. \kern-0em} {\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{{\left| {{{H}_{z}}(x{\kern 1pt} ')} \right|}}^{2}}dx{\kern 1pt} '} }},$

где Zэ – эквивалентный поверхностный импеданс, T – интервал усреднения импеданса.

Для расчета ЭПИ по формуле (26) необходимо знать распределение касательных составляющих поля ${{E}_{x}}(x)$ и ${{H}_{z}}(x)$ в сечении $y = 0,$ в то время как в результате решения интегрального уравнения (21) были определены значения поля в сечении $y = - t.$ Конечно, можно было бы сразу записать интегральное уравнение относительно касательной составляющей электрического поля ${{E}_{x}}(x,0).$ Однако, в этом случае получалась бы система из двух интегральных уравнений, решение которой численным методом привело бы к необходимости обращения матрицы как минимум вдвое большей размерности.

Поэтому для нахождения касательных составляющих поля ${{E}_{x}}(x)$ и ${{H}_{z}}(x)$ в сечении $y = 0$ сначала решается интегральное уравнение (21), далее определяются коэффициенты $I_{m}^{ - }$ по формулам (12) и (13), после чего находятся коэффициенты $I_{m}^{ + }$ по формуле (11), что позволяет по формуле (7) пересчитать распределение поля ${{E}_{x}}(x)$ из сечения $y = - t$ в сечение $y = 0.$

В итоге полученная расчетная формула для распределения поля ${{E}_{x}}(x)$ в сечении $y = 0$ имеет вид:

$\begin{gathered} {{E}_{x}}(x,0) = \sum\limits_{m = - \infty }^\infty {\frac{{Y_{m}^{{(2)}}{{\psi }_{m}}(x)}}{{Y_{m}^{{(2)}}\cos \left( {\Gamma _{m}^{{(2)}}t} \right) + iY_{m}^{{(1)}}\sin \left( {\Gamma _{m}^{{(2)}}t} \right)}}} \times \\ \times \,\,\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ', - t)\psi _{m}^{*}(x{\kern 1pt} ')dx{\kern 1pt} ' + \frac{{2{{\psi }_{0}}(x)}}{{Y_{0}^{{(1)}} - iY_{0}^{{(2)}}\operatorname{ctg} \left( {\Gamma _{0}^{{(2)}}t} \right)}}} . \\ \end{gathered} $

Таким же образом, подставляя коэффициенты (11), (12) и (13) в формулу (6), получаем выражение для магнитного поля ${{H}_{z}}(x)$ в сечении $y = 0{\text{:}}$

$\begin{gathered} {{H}_{z}}(x,0) = - \sum\limits_{m = - \infty }^\infty {\frac{{Y_{m}^{{(1)}}Y_{m}^{{(2)}}{{\psi }_{m}}(x)}}{{Y_{m}^{{(2)}}\cos \left( {\Gamma _{m}^{{(2)}}t} \right) + iY_{m}^{{(1)}}\sin \left( {\Gamma _{m}^{{(2)}}t} \right)}}} \times \\ \times \,\,\int\limits_{{{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {{{E}_{x}}(x{\kern 1pt} ', - t)\psi _{m}^{*}(x{\kern 1pt} ')dx{\kern 1pt} ' + \frac{{2{{\psi }_{0}}(x)}}{{1 + i\frac{{Y_{0}^{{(1)}}}}{{Y_{0}^{{(2)}}}}\operatorname{tg} \left( {\Gamma _{0}^{{(2)}}t} \right)}}} . \\ \end{gathered} $

4. АЛГОРИТМИЗАЦИЯ ЗАДАЧИ

Для численной реализации полученного интегрального уравнения (21) использовался метод Крылова–Боголюбова, в результате чего указанное интегральное уравнение сводилось к системе линейных алгебраических уравнений следующего вида

$\left| {\begin{array}{*{20}{c}} {{{C}_{{11}}}{{C}_{{12}}}...{{C}_{{N1}}}} \\ {{{C}_{{21}}}{{C}_{{22}}}...{{C}_{{N2}}}} \\ \begin{gathered} . \hfill \\ . \hfill \\ . \hfill \\ \end{gathered} \\ {{{C}_{{N1}}}{{C}_{{N2}}}...{{C}_{{NN}}}} \end{array}} \right| \cdot \left| {\begin{array}{*{20}{c}} {{{E}_{{x1}}}} \\ {{{E}_{{x2}}}} \\ \begin{gathered} . \hfill \\ . \hfill \\ . \hfill \\ \end{gathered} \\ {{{E}_{{xN}}}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{{P}_{1}}} \\ {{{P}_{2}}} \\ \begin{gathered} . \hfill \\ . \hfill \\ . \hfill \\ \end{gathered} \\ {{{P}_{N}}} \end{array}} \right|,$

где

${{C}_{{ij}}} = C_{{ij}}^{{(1)}} + C_{{ij}}^{{(2)}},$
(27)
$\begin{gathered} C_{{ij}}^{{(1)}} = \int\limits_{{{x}_{j}} - \Delta x}^{{{x}_{j}} + {\Delta }x} {\sum\limits_{m = - \infty }^\infty {Y_{m}^{{(2)}}\frac{{Y_{m}^{{(1)}} + iY_{m}^{{(2)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}}{{Y_{m}^{{(2)}} + iY_{m}^{{(1)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}}} } \times \\ \times \,\,{{\psi }_{m}}({{x}_{i}})\psi _{m}^{*}(x{\kern 1pt} ')dx{\kern 1pt} ', \\ \end{gathered} $
(28)
$\begin{gathered} C_{{ij}}^{{(2)}} = - i\frac{4}{{\sqrt 3 }} \cdot \frac{{{{k}_{3}}}}{{{{W}_{3}}}} \times \\ \times \,\,\int\limits_{{{x}_{j}} - {{\Delta }_{x}}}^{{{x}_{j}} + {{{\Delta }}_{x}}} {\sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {\frac{{{{T}_{1}}\left( {{{x}_{i}}} \right){{T}_{1}}\left( {x{\kern 1pt} '} \right) + {{T}_{2}}\left( {{{x}_{i}}} \right){{T}_{2}}\left( {x{\kern 1pt} '} \right)}}{{16{{\pi }^{2}}\left( {{{m}^{2}} + mn + {{n}^{2}}} \right) - 9{{a}^{2}}k_{3}^{2}}}} } dx{\kern 1pt} ',} \\ \end{gathered} $
${{P}_{i}} = \frac{{2{{\psi }_{0}}({{x}_{i}})}}{{\cos \left( {\Gamma _{0}^{{(2)}}t} \right) + i\frac{{Y_{0}^{{(1)}}}}{{Y_{0}^{{(2)}}}}\sin \left( {\Gamma _{0}^{{(2)}}t} \right)}},$

${{x}_{j}} = {{ - T} \mathord{\left/ {\vphantom {{ - T} 2}} \right. \kern-0em} 2} + {{\Delta }_{x}}\left( {2j - 1} \right)$ – координаты точек коллокации, $N$ – количество интервалов разбиения, $2{{\Delta }_{x}} = {{x}_{{j + 1}}} - {{x}_{j}}$ – размер интервала разбиения, $i = 1, \ldots ,N,$ $j = 1, \ldots ,N.$

Расчетное соотношение для элементов матрицы $C_{{ij}}^{{(1)}}$ получается аналитическим интегрированием выражения (27) по отрезку разбиения $2{{\Delta }_{x}},$ в результате имеем

$\begin{gathered} C_{{ij}}^{{(1)}} = \frac{{2{{\Delta }_{x}}}}{T}\sum\limits_{m = - \infty }^\infty {Y_{m}^{{(2)}}\frac{{Y_{m}^{{(1)}} + iY_{m}^{{(2)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}}{{Y_{m}^{{(2)}} + iY_{m}^{{(1)}}\operatorname{tg} \left( {\Gamma _{m}^{{(2)}}t} \right)}}} \times \\ \times \,\,\frac{{\sin R{{\Delta }_{x}}}}{{R{{\Delta }_{x}}}}\exp ( - iR({{x}_{i}} - {{x}_{j}})), \\ \end{gathered} $

где $R = \frac{{2m\pi }}{T} - {{k}_{1}}\sin \theta .$

Выражение для коэффициентов матрицы $C_{{ij}}^{{(2)}}$ получено в [14] интегрированием выражения (28) по размеру участка разбиения интервала интегрирования $2{{\Delta }_{x}}$

$\begin{gathered} C_{{ij}}^{{(2)}} = - i\frac{4}{{\sqrt 3 }}\frac{{{{k}_{3}}}}{{{{W}_{3}}}} \times \\ \times \,\,\sum\limits_{m = - \infty }^\infty {\sum\limits_{n = - \infty }^\infty {\frac{{T_{1}^{{\text{S}}}\left( {{{x}_{j}}} \right){{T}_{1}}\left( {{{x}_{i}}} \right) + T_{2}^{{\text{S}}}\left( {{{x}_{j}}} \right){{T}_{2}}\left( {{{x}_{i}}} \right)}}{{16{{\pi }^{2}}\left( {{{m}^{2}} + mn + {{n}^{2}}} \right) - 9{{a}^{2}}k_{3}^{2}}}} } , \\ \end{gathered} $

где

$\begin{gathered} T_{1}^{{\text{S}}}\left( {{{x}_{j}}} \right) = \int\limits_{{{x}_{j}} - {{\Delta }_{x}}}^{{{x}_{j}} + {{\Delta }_{x}}} {{{T}_{1}}\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} = \\ = 2{{\Delta }_{x}}\left( \begin{gathered} {{\left( { - 1} \right)}^{{m + n}}}\frac{{\sin \left( {U1} \right)}}{{U1}}\cos \left( {\frac{{2\pi \left( {m - n} \right){{x}_{j}}}}{{3a}}} \right) + \hfill \\ + \,\,{{\left( { - 1} \right)}^{m}}\frac{{\sin \left( {U2} \right)}}{{U2}}\cos \left( {\frac{{2\pi \left( {2n + m} \right){{x}_{j}}}}{{3a}}} \right) + \hfill \\ + \,\,{{\left( { - 1} \right)}^{n}}\frac{{\sin \left( {U3} \right)}}{{U3}}\cos \left( {\frac{{2\pi \left( {2m + n} \right){{x}_{j}}}}{{3a}}} \right) \hfill \\ \end{gathered} \right), \\ \end{gathered} $
$\begin{gathered} T_{2}^{{\text{S}}}\left( {{{x}_{j}}} \right) = \int\limits_{{{x}_{j}} - {{\Delta }_{x}}}^{{{x}_{j}} + {{\Delta }_{x}}} {{{T}_{2}}\left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} = \\ = 2{{\Delta }_{x}}\left( \begin{gathered} {{\left( { - 1} \right)}^{{m + n}}}\frac{{\sin \left( {U1} \right)}}{{U1}}\sin \left( {\frac{{2\pi \left( {m - n} \right){{x}_{j}}}}{{3a}}} \right) + \hfill \\ + \,\,{{\left( { - 1} \right)}^{m}}\frac{{\sin \left( {U2} \right)}}{{U2}}\sin \left( {\frac{{2\pi \left( {2n + m} \right){{x}_{j}}}}{{3a}}} \right) - \hfill \\ - \,\,{{\left( { - 1} \right)}^{n}}\frac{{\sin \left( {U3} \right)}}{{U3}}\sin \left( {\frac{{2\pi \left( {2m + n} \right){{x}_{j}}}}{{3a}}} \right) \hfill \\ \end{gathered} \right), \\ U1 = \frac{{2\pi \left( {m - n} \right){{\Delta }_{x}}}}{{3a}},\,\,\,\,U2 = \frac{{2\pi \left( {2n + m} \right){{\Delta }_{x}}}}{{3a}}, \\ U3 = \frac{{2\pi \left( {2m + n} \right){{\Delta }_{x}}}}{{3a}}. \\ \end{gathered} $

5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

По изложенному алгоритму были рассчитаны зависимости комплексного ЭПИ ${{Z}_{{\text{э}}}} = {{R}_{{\text{э}}}} + i{{X}_{{\text{э}}}}$ от размера щели $c$ и от угла падения $\theta $ электромагнитной волны, причем импеданс является чисто реактивным (${{Z}_{{\text{э}}}} = i{{X}_{{\text{э}}}},$ ${{R}_{{\text{э}}}} = 0$). Все виды зависимостей приведены для реактивной составляющей ЭПИ, нормированной на сопротивление свободного пространства ${{W}_{0}} = 120\pi $ Ом. Все расчеты выполнялись для параметров сред ${{\tilde {\mu }}_{{a1}}} = {{\tilde {\mu }}_{{a2}}} = {{\tilde {\mu }}_{{a3}}} = {{\mu }_{0}},$ ${{\tilde {\varepsilon }}_{{a1}}} = $ $ = {{\tilde {\varepsilon }}_{{a2}}} = {{\tilde {\varepsilon }}_{{a3}}} = {{\varepsilon }_{0}}.$

На рис. 2 представлены зависимости реактивной составляющей ЭПИ от ширины щели $c$ при $T = a$ и отсутствии полоскового проводника ($d = 0$). Расчеты выполнены для толщины диэлектрического слоя $t = 0.2\lambda $ и нескольких фиксированных значений периода решетки $Т$ ($1{\text{ }}--T = 0.1\lambda ,$ $2{\text{ }}--T = 0.15\lambda ,$ $3{\text{ }}--T = 0.2\lambda ,$ $4{\text{ }}--T = 0.24\lambda $) при изменении ширины щели $c$ в пределах от $0.1Т$ до $1.0Т.$

Рис. 2.

Зависимость эквивалентного поверхностного импеданса от ширины щели $c{\text{/}}a$ при отсутствии полоскового проводника ($d = 0$). Кривые 1–4 соответствуют T/λ: 0.1; 0.15; 0.2; 0.24.

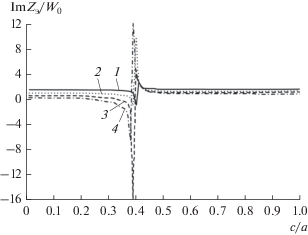
Зависимости при всех значениях периода $Т$ имеют ярко выраженный максимум, положение которого определяется величиной ширины щели $c$ и перемещается в пределах $0.35T \leqslant c \leqslant {\text{0}}.45T.$ По сравнению с аналогичной решеткой без диэлектрического слоя [43], в данном случае наличие диэлектрического слоя позволяет реализовать не только положительные, но и отрицательные значения реактивной составляющей ЭПИ в пределах от –16 до +12.

На рис. 3 представлены зависимости реактивной составляющей ЭПИ от угла падения электромагнитной волны $\theta .$ Расчеты выполнены при $T = a,$ отсутствии полоскового проводника ($d = 0$) и толщине диэлектрического слоя $t = 0.01\lambda $ для нескольких фиксированных значений периода решетки $Т$ ($1{\text{ }}--T = 0.05\lambda ,$ $2{\text{ }}--T = 0.1\lambda ,$ $3{\text{ }}--T = 0.15\lambda ,$ $4{\text{ }}--T = 0.2\lambda $) при изменении угла падения электромагнитной волны в пределах $0 \leqslant \theta \leqslant 90^\circ .$

Рис. 3.

Зависимость эквивалентного поверхностного импеданса от угла падения электромагнитной волны $\theta $ при отсутствии полоскового проводника ($d = 0$). Кривые 1–4 соответствуют T/λ: 0.05; 0.1; 0.15; 0.2.

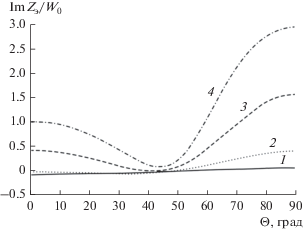
Из графиков следует, что, как и в случае аналогичной решетки без диэлектрического слоя, зависимость импеданса от угла падения электромагнитной волны является существенной, причем наличие диэлектрического слоя даже незначительной толщины делает эту зависимость более сильной.

Полученные результаты позволяют сделать следующие выводы:

1) как и в случае аналогичной решетки такой же конструкции без диэлектрического слоя, ЭПИ имеет чисто реактивный характер, причем наличие диэлектрического слоя позволяет реализовать как положительные, так и отрицательные значения реактивной составляющей ЭПИ;

2) в рассматриваемой конструкции щелевой импедансной нагрузки так же, как и в случае бесконечной решетки без диэлектрического слоя, имеется технологическая возможность эффективной регулировки величины ЭПИ за счет изменения геометрических размеров конструкции.

Список литературы

  1. Захарьев Л.И., Леманский А.А. Рассеяние волн “черными” телами. М.: Сов. радио, 1972.

  2. Schindler J.K., Mack R.B., Blacksmith P. // Proc. IEEE. 1965. V. 53. № 8. P. 993.

  3. Chen K.M., Liepa V.V. // IEEE Trans. 1964. V. AP-12. № 5. P. 576.

  4. Short J.R., Chen K.M. // IEEE Trans. 1969. V. AP-17. № 3. P. 315.

  5. Чаплин А.Ф., Кондратьев А.С. // РЭ. 1977. Т. 22. № 3. С. 505.

  6. Петров Б.М., Юханов Ю.В. // Изв. вузов. Радиоэлектроника. 1980. Т. 23. № 9. С. 79.

  7. Петров Б.М., Юханов Ю.В. // Изв. вузов. Радиоэлектроника. 1980. Т. 23. № 9. С. 59.

  8. Юxaнoв Ю.B. // PЭ. 2000. T. 45. № 4. C. 404.

  9. Kюpкчaн A.Г. // PЭ. 1977. T. 22. № 7. C. 1362.

  10. Кюркчан А.Г., Зимнов М.Х. // РЭ. 1985. Т. 30. № 12. С. 2308.

  11. Бененсон Л.С., Кюркчан А.Г., Суков А.И. // РЭ. 1992. Т. 37. № 1. С. 77.

  12. Balanis C.A. Modern Antenna Handbook. N.Y.: John Wiley & Sons, 2008.

  13. Sievenpiper D. High-Impedance Electromagnetic Surfaces. Ph.D. Dissertation. Los Angeles: Univ. California, 1999. 162 p. http://optoelectronics.eecs.berkeley.edu/ThesisDan.pdf

  14. Кошкидько В.Г., Сердюк Э.С. // РЭ. 2016. Т. 61. № 12. С. 1176.

  15. Кошкидько В.Г., Алпатова О.В. // Антенны. 2016. № 3. С. 33.

  16. Кошкидько В.Г., Алпатова О.В. // Изв. вузов. Радиоэлектроника. 2015. № 5. С. 20.

  17. Кошкидько В.Г., Алпатова О.В., Сердюк Э.С. // Изв. ЮФУ. Технические науки. 2014. № 11. С. 58.

  18. Кошкидько В.Г., Алпатова О.В. // РЭ. 2003. Т. 48. № 1. С. 57.

  19. Кошкидько В.Г., Ганжела Н.В. // РЭ. 1999. Т. 44. № 8. С. 947.

  20. Кошкидько В.Г., Алпатова О.В. // РЭ. 1999. Т. 44. № 1. С. 25.

  21. Кошкидько В.Г., Петров Б.М., Юханов Ю.В. // РЭ. 1997. Т. 42. № 6. С. 652.

  22. Кошкидько В.Г., Размазнин А.В. // Рассеяние электромагнитных волн (междувед. тем. науч. сборник). Таганрог: ТРТИ, Вып. 10, 1995. С. 109.

  23. Кошкидько В.Г., Федотов В.Г. // Рассеяние электромагнитных волн (междувед. тем. науч. сборник). Таганрог: ТРТИ, Вып. 9, 1993. С. 135.

  24. Петров Б.М., Кошкидько В.Г. // РЭ. 1988. Т. 33. № 10. С. 2060.

  25. Кошкидько В.Г. // Рассеяние электромагнитных волн (междувед. тем. науч. сборник). Таганрог: ТРТИ, Вып. 6, 1987. С. 12.

  26. Кошкидько В.Г., Петров Б.М., Юханов Ю.В. // Рассеяние электромагнитных волн (междувед. тем. науч. сборник). Таганрог: ТРТИ, Вып. 6, 1987. С. 87.

  27. Юханов Ю.В., Кошкидько В.Г. // Рассеяние электромагнитных волн (междувед. тем. науч. сборник). Таганрог: ТРТИ, Вып. 5, 1985. С. 17.

  28. Кошкидько В.Г., Шарварко В.Г. // Рассеяние электромагнитных волн (междувед. тем. науч. сборник). Таганрог: ТРТИ, Вып. 4, 1983. С. 64.

  29. Koшкидькo B.Г. // PЭ. 2000. T. 45. № 7. C. 773.

  30. Кошкидько В.Г., Алпатова О.В. // РЭ. 2014. Т. 59. № 10. С. 1003.

  31. Кошкидько В.Г., Алпатова О.В., Сердюк Э.С. // Изв. ЮФУ. Технические науки. 2015. № 11. С. 72.

  32. Кошкидько В.Г., Ганжела Н.В., Алпатова О.В., Сердюк Э.С. // РЭ. 2016. Т. 61. № 4. С. 313.

  33. Кошкидько В.Г., Алпатова О.В. // Изв. вузов. Радиоэлектроника. 2016. № 4. С. 63.

  34. Кошкидько В.Г. // Рассеяние электромагнитных волн (междувед. тем. науч. сборник). Таганрог: ТРТИ, Вып. 7, 1989. С. 134.

  35. Кошкидько В.Г., Сердюк Э.С. // РЭ. 2015. Т. 60. № 1. С. 45.

  36. Кошкидько В.Г., Алпатова О.В., Сердюк Э.С. // РЭ. 2016. Т. 61. № 5. С. 447.

  37. Koshkid’ko V.G., Alpatova O.V., Serdyuk E.S. // Conf. Proc. 2017. Radiation and Scattering of Electromagnetic Waves (RSEMW). Divnomorskoe. 26–30 June. N.Y.: IEEE, 2017. P. 168.

  38. Кошкидько В.Г., Алпатова О.В. // Антенны. 2017. № 2(234). С. 32.

  39. Кошкидько В.Г., Алпатова О.В. // Антенны. 2017. № 9(241). С. 26.

  40. Кошкидько В.Г., Алпатова О.В. // Изв. вузов. Радиоэлектроника. 2017. № 3. С. 66.

  41. Koшкидькo B.Г. // PЭ. 2018. T. 63. № 2. C. 119.

  42. Koshkid'ko V.G., Alpatova O.V. // Conf. Proc. 2019 Radiation and Scattering of Electromagnetic Waves (RSEMW). Divnomorskoe. 2–28 June. N.Y.: IEEE, 2019. P. 252.

  43. Кошкидько В.Г., Сердюк Э.С. // РЭ. 2019. Т. 64. № 3. С. 252.

  44. Амитей И., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток. М.: Мир, 1974.

  45. Chadha R., Gupta K.C. // IEEE Trans. 1980. V. MTT-28. № 10. P. 1139.

  46. Цалиев Т.А., Черенков В.С. // РЭ. 1985. Т. 30. № 9. С. 1689.

  47. Волков И.А., Черенков В.С. // Наукові праці ОНАЗ ім. О.С. Попова. 2004. № 1. С. 28.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал