Радиотехника и электроника, 2020, T. 65, № 11, стр. 1052-1060

1. ИЗВЕСТНЫЕ ЭВРИСТИЧЕСКИЕ ПОДХОДЫ

Эвристические подходы, в отличие от строгих подходов, основаны на физических представлениях о процессе дифракции. Метод геометрической оптики (ГО) [1–4] состоит в том, что рассеянное поле находят в виде совокупности лучей первичного поля, направление распространения которых было изменено рассеивателем (т.е., например, зеркально отраженных или отсутствующих в направлении “прямо вперед” – так называемого “теневого столбика”). Метод физической оптики (ФО) [5] основан на применении интеграла Кирхгофа. Рассеянное поле находят при помощи интеграла по поверхности рассеивателя от поля ГО, при этом считают, что возмущения поля вблизи кромок не происходит. Эти подходы (ГО и ФО) дают решение во всех случаях, однако оно является точным лишь в некоторых практических задачах, когда точка наблюдения находится в окрестности границы “свет–тень”. К таким задачам относятся, например, рассеяние на объектах округлой формы в направлении точек зеркального отражения, нахождение диаграммы направленности зеркальных антенн в окрестности главного лепестка и рассеяние на уголковом отражателе.

Метод ФО правильно описывает структуру поля. Рассеяние от кромок идет вдоль дифракционных конусов, при этом направление на точку наблюдения составляет такой же угол с кромкой, что и направление на источник [1, 2]. Вблизи от границ “свет–тень” метод ФО дает правильную амплитуду. Вдали от окрестности границ “свет–тень” амплитуда поля ФО нуждается в уточнении. Решение ФО можно описать при помощи “равномерного” краевого тока [5].

Метод геометрической теории дифракции (ГТД) находит рассеянное поле в виде совокупности лучей, образованных при взаимодействии первичного поля с поверхностями и кромками рассеивателя. При этом учитывают возмущение поля в окрестности кромок.

Метод краевых волн (МКВ) состоит в коррекции решения ФО при помощи добавления к “равномерной” части поля дополнительной “неравномерной” части, характеризующей возмущение поля кромкой [5].

Подходы ГТД и МКВ используют строгое решение двумерной задачи рассеяния на кромке бесконечной длины с целью учета возмущения поля кромкой в трехмерной задаче. При этом возмущение поля считается одинаковым по всей длине кромки, таким образом, учет дополнительного возмущения поля в окрестности концов трехмерной кромки отсутствует. Это обстоятельство является заложенной методической погрешностью ГТД и МКВ.

Метод краевых волн иногда называют еще физической теорией дифракции (ФТД). Этот термин можно использовать и в расширенном толковании, применяя его ко всем эвристическим подходам: ГО, ФО, ГТД, ФТД и другим, основанным на интуиции и физических представлениях о процессе дифракции. Мы будем применять термин ФТД в расширенном толковании.

2. МЕТОД БАЗОВЫХ КОМПОНЕНТОВ

Очевидно, что самые ценные и надежные формулы – строгие аналитические. К сожалению, их очень немного, поскольку они описывают решения задач дифракции на рассеивателях, поверхность которых соответствует каноническим ортогональным системам координат, а таких систем существует ограниченное число. Для получения строгих формул может потребоваться значительное время, которое бывает трудно спрогнозировать. Кроме того, строгие аналитические формулы могут иметь очень сложный вид и, например, представлять собой плохо сходящиеся бесконечные ряды по специальным функциям. Применение таких аналитических формул может само по себе представлять определенные трудности и не давать выигрыша по сравнению с численными решениями.

Описанные проблемы приводят к тому, что для построения новых решений задач дифракции на рассеивателях сложной формы применяют эвристические методы, такие, как уже упомянутые выше ГТД и МКВ, основанные на уточнении трехмерного решения ФО при помощи двумерного решения на бесконечной кромке.

Можно действовать и более сложным способом. Существующие аналитические формулы для задач дифракции, сформулированных в простейшей постановке, разбивают на составляющие с ясным физическим смыслом (базовые компоненты). Затем из этих компонентов строят эвристические решения новых задач с более сложной геометрией и граничными условиями, для которых не существует строгих аналитических решений. Подвергая эти эвристические решения процессам верификации и настройки при помощи различных численных решений, можно получать новые базовые компоненты. В результате получим расширенный набор базовых компонентов, при помощи которых можно строить относительно простые по форме аналитические решения, точность которых задана заранее в соответствии с требованиями практической задачи. Описанная последовательность действий лежит в основе метода базовых компонентов (МБК) [6].

Отличие МБК от других эвристических методов, таких как ГТД и МКВ – осуществление процедуры “настройки”. Из этого отличия вытекают все недостатки и преимущества МБК. Недостаток – необходимость проведения дополнительных работ (как численных, так и аналитических). Преимущество – увеличение точности, расширение области применимости эвристических подходов (расширение допустимой области значений параметров, уточнение решения, получение автономных формул, проведение физической интерпретации). Процедура настройки позволяет проводить тонкий физический анализ. При помощи верификационного решения можно последовательно отсеивать особенности, которые описываются известными базовыми компонентами, и обнаруживать новые физические характеристики процесса дифракции.

В данной работе мы рассмотрим две простейшие постановки задач, для которых известны аналитические решения. Это двумерная задача дифракции на идеально проводящем клине [5–7] и трехмерная задача дифракции на идеально проводящем плоском многоугольнике в приближении физической оптики и при выполнении условия дальней зоны [6–8].

3. РЕШЕНИЕ ДВУМЕРНОЙ ЗАДАЧИ ДИФРАКЦИИ НА ПОЛУБЕСКОНЕЧНОМ РАССЕИВАТЕЛЕ

Выделим из строгой математической формулы сингулярные дифракционные коэффициенты. Для этого рассмотрим интегральное представление ν(ψ), при помощи которого можно найти рассеянное поле на полубесконечном рассеивателе [6, 7]. Для случая дифракции электромагнитной волны на клине с внешним углом раствора πn:

Здесь (r₀, φ₀) и (r, φ) – координаты источника и точки наблюдения соответственно, P(w_sm) – поле источника в седловой точке w_sm. С геометрической точки зрения седловая точка соответствует ситуации, когда кромка находится на линии, соединяющей точку наблюдения с источником. Значения m = 1, 2 соответствуют границам тени падающего или отраженного поля. Входящие в формулу (1) эйконал S(ψ) и эйконал в седловой точке S(w_sm) равны:

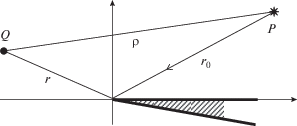
Центр координат совпадает с вершиной клина. Область, внешняя по отношению к клину, занимает пространство углов 0 < φ < πn. Геометрия задачи дифракции на клине приведена на рис. 1. Источник обозначен буквой P, точка наблюдения – буквой Q.

Для определения рассеянного поля V(φ) в случае ТН- или ТЕ-поляризованной электромагнитной волны применяем выражения:

Решение задачи дифракции на полубесконечном рассеивателе с формой кромки, более сложной, чем клин, приведено в [7].

Рассмотрим интегральное представление задачи дифракции на клине в случае двух седловых точек (1). Каждое из двух слагаемых (стоящих под знаком суммы) в правой части выражения (1) состоит из четырех сомножителей.

Первый множитель

не зависит от угловой переменной и представляет собой произведение значения поля в седловой точке (т.е. на границе тени) на фактор, определяющий зависимость решения от расстояний до источника и точки наблюдения.

Второй множитель

представляет собой половину дифракционного коэффициента. Полный дифракционный коэффициент для определенного вида поляризации получится, если сложить или вычесть значения этого сомножителя в точке наблюдения:

Произведение третьего и четвертого множителей

представляет собой частное от деления интеграла Френеля на свою асимптотику и характеризует зависимость поля от углового расстояния до границы тени. Вдали от границы “свет–тень” модуль этого произведения близок к 1. На границе “свет–тень” этот множитель равен нулю и компенсирует сингулярность половины дифракционного коэффициента (5). Эта компенсация приводит к тому, что на границе “свет–тень” у полубесконечного рассеивателя поле равно 1/2 от поля геометрической оптики.

При возбуждении плоской волной r₀ → ∞, P(w_sm) = exp(ikr), и тогда вдали от границы “свет–тень” (когда модуль произведения (7) близок к единице) из (1) получим:

Здесь f и g – сингулярные дифракционные коэффициенты строгого решения для клина (1) в случае ТН- и ТЕ-волны соответственно. Для полуплоскости n = 2, и тогда:

Данная формула, описывающая поле рассеяния полуплоскости вдали от границы “свет–тень” имеет, как и двумерное физоптическое решение, сингулярности на этой границе.

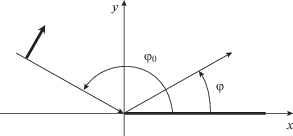
Геометрия для случая нормального падения волны с Т-поляризованным вектором $\vec {E}$ или $\vec {H}$ на кромку полуплоскости в локальных координатах, связанных с этой кромкой, показана на рис. 2.

Аналогичные выражениям (9) сингулярные дифракционные коэффициенты f ⁰ и g⁰ для ТН- и ТЕ-волны соответственно можно получить вдали от границы “свет–тень”, решая задачу дифракции на полуплоскости в приближении физической оптики [5]:

Общее соотношение между строгим решением двумерной задачи (1) и физоптическим соответствует формуле из [1], устанавливающей, что двумерное решение в приближении физической оптики v⁰(r, ψ) для рассеянного поля, непрерывного на двулистной римановой поверхности, имеет вид, с точностью до множителя sin(ψ/2) совпадающий со строгим решением v(r, ψ) (1):

Выражение (11), справедливое во всей области углов, в том числе и вблизи границы “свет–тень”, отражает соотношение между сингулярными дифракционными коэффициентами (9) строгого двумерного решения и сингулярными физоптическими дифракционными коэффициентами (10) в случае дифракции на полуплоскости.

Что касается трехмерного случая, то для него строгого решения не существует, поэтому непосредственно проверить соотношение, аналогичное (11), невозможно. Однако можно предположить, что для отдельных кромок соотношение (11) сохранится и в трехмерном случае. Именно это предположение мы будем использовать при построении эвристического решения.

4. ПОСТАНОВКА ЗАДАЧИ ДИФРАКЦИИ

Пусть в безграничном пространстве существует электромагнитное поле ${{\vec {E}}^{{(i)}}},$ ${{\vec {H}}^{{(i)}}},$ удовлетворяющее волновому уравнению Гельмгольца. Внесем в это поле рассеиватель. Возмущение, вносимое рассеивателем в первичное электромагнитное поле, можно выразить при помощи поверхностных токов на рассеивателе. В случае дифракции электромагнитной волны на теле конечных размеров решение для комплексных амплитуд векторов электрического и магнитного полей рассеянного поля можно записать через векторные потенциалы [9]:

Здесь ${{\vec {A}}^{e}}$ и ${{\vec {A}}^{m}}$ – электрический и магнитный векторные потенциалы; ${{\vec {j}}^{e}}$ и ${{\vec {j}}^{m}}$ – и электрический и магнитный поверхностные токи; S – поверхность рассеивателя; $r = \left| {\vec {R} - \vec {\rho }} \right|$ – расстояние от точки рассеивающей поверхности с радиус-вектором $\vec {\rho } = \left( {\xi ,\eta ,\zeta } \right)$ до точки наблюдения с радиус-вектором 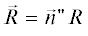= 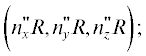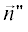– единичный вектор направления на приемник; R – расстояние от центра координат до приемника; k = 2π/λ – волновое число; с – скорость света; i – мнимая единица. Зависимость от времени выбрана в виде exp(–iωt).

Для поля на произвольной поверхности, охватывающей рассеиватель, электрический и магнитный поверхностные токи ${{\vec {j}}^{e}}$ и ${{\vec {j}}^{m}}$ выражаются через фактические значения ${{\vec {E}}^{0}}$ и ${{\vec {H}}^{0}}$ полей на поверхности рассеивателя [9]:

здесь нормаль $\vec {n}$ к поверхности S направлена в сторону области, занятой полем.

Если пренебречь возмущением поля на краях рассеивателя и подставить в (13) вместо ${{\vec {E}}^{0}}$ и ${{\vec {H}}^{0}}$ поля ${{\vec {E}}^{{(i)}}},$ ${{\vec {H}}^{{(i)}}},$ падающие на поверхность, то получим поверхностные токи идеально проводящего рассеивателя в приближении физической оптики.

5. УСЛОВИЕ ДАЛЬНЕЙ ЗОНЫ

Для тела конечных размеров в случае выполнения условия дальней зоны

где r – расстояние от точки на рассеивателе до точки наблюдения, D – характерный размер объекта (например, максимальный поперечный размер), λ – длина волны, имеет место равенство

Здесь R – расстояние от центра координат до точки наблюдения, 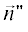– направляющий вектор рассеянной волны, $\vec {\rho }$ – радиус-вектор точки на рассеивателе.

Физический смысл условия дальней зоны (14) заключается в том, что все точки рассеивателя видны из расположенной в дальней зоне точки наблюдения под близкими углами. Это означает, что при удалении от рассеивателя его угловые размеры стремятся к нулю, и он визуально стягивается в точку.

Очевидно, что в случае удаления точки наблюдения от полубесконечного рассеивателя условие дальней зоны (14) не будет выполняться ни на каком расстоянии от рассеивателя. Тем не менее, формулы, полученные с использованием условия дальней зоны, нужны, поскольку на их основе строят эвристические решения. Поэтому мы будем формально применять соотношение (15) даже к полубесконечным рассеивателям, называя такой подход “навязанным” условием дальней зоны.

При выполнении соотношения (15) многие дифракционные формулы упрощаются, вектора электрического и магнитного полей $\vec {E},$ $\vec {H}$ в сферических координатах (r, φ, ϑ) связаны с электрическим и магнитным векторными потенциалами ${{\vec {A}}^{e}},$ ${{\vec {A}}^{m}}$ соотношениями

а интегралы (12) для векторного потенциала А в точке наблюдения могут быть сведены к ряду скалярных соотношений типа

На поверхности идеально проводящего рассеивателя в соответствии с методом зеркальных токов [9] вместо (13) имеет место:

Таким образом, в приближении физической оптики, с учетом (18), при возбуждении плоского рассеивателя плоской электромагнитной волной векторные потенциалы ${{\vec {A}}^{e}},$ ${{\vec {A}}^{m}}$ зависят от полей $\vec {E}_{R}^{0},$ $\vec {H}_{R}^{0}$ в начале координат на поверхности рассеивателя:

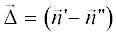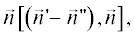где введен вспомогательный вектор – $\vec {n}{\kern 1pt} '$ – направляющий вектор падающей волны, $\vec {n}$ – нормаль к поверхности рассеивателя S.

6. ДИФРАКЦИЯ НА ПОЛУПЛОСКОСТИ С “НАВЯЗАННЫМ” УСЛОВИЕМ ДАЛЬНЕЙ ЗОНЫ

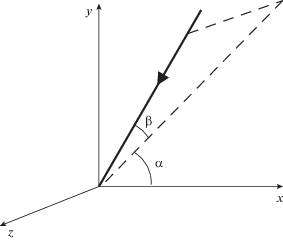
Пусть на идеально проводящую полуплоскость, кромка которой расположена вдоль оси z, падает плоская волна [2]:

Выделим вектора Т-поляризаций: вектора $\vec {t},$ перпендикулярные кромке и направляющим векторам падающего и рассеянного поля $\vec {n}{\kern 1pt} '$ или 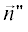и вектора $\vec {p},$ перпендикулярные как векторам $\vec {t},$ так и направляющим векторам $\vec {n}{\kern 1pt} '$ или 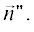Для этих векторов в случае падающего (индекс i) и рассеянного (индекс s) поля имеет смысл ввести новые обозначения: ${{\vec {t}}_{i}},$ ${{\vec {p}}_{i}},$ ${{\vec {t}}_{s}}$ и ${{\vec {p}}_{s}}.$ В координатах [2] эти вектора равны:

Индекс “1” означает, что углы α₁, β₁ и θ₁ связаны уже не с глобальными координатами, как α, β и θ в [2], а с локальными координатами кромки. Геометрия задачи из [2] приведена на рис. 3.

В случае двух поляризаций получаем соответственно две плоские волны

Полученные выражения представляют собой форму записи формул из работы [2]. Там же получены выражения для рассеянного поля. Однако, эти выражения мы не перепишем, а существенно упростим, применив “навязанное” условие дальней зоны (15).

Решение для рассеянного поля из работы [2] зависит от функции G(a). Функция G(a) определяется следующим образом

При a → ∞ справедлива асимптотика

Кроме того, имеет место асимптотика для производной

Заметим, что по модулю величина производной (25) меньше, чем $G\left( a \right) \cong - {{\left( {2ia} \right)}^{{ - 1}}}$ при больших значениях аргумента a.

Подстановка асимптотик (24) и (25) вместо строгих формул (23) с физической точки зрения соответствует “навязыванию” условия дальней зоны и применению соотношения (15) в задаче дифракции на полубесконечном рассеивателе.

Если подставить (24) и (25) в формулы из [2], выражения для рассеянного поля принимают простую форму, очень похожую на выражения для падающего поля:

Строгие f, g и физоптические f ⁰, g⁰ двумерные векторные коэффициенты для полуплоскости определяются выражениями (9), (10) [5] (соответствие углов между [5] и [2]: φ₀ ↔ α₁, φ ↔ θ₁) [7, 10].

Для наклонного падения (упрощая решение [2]) получим в дальней зоне:

Здесь U_THβ и U_TEβ – решения для наклонного падения, U_TH0 и U_TE0 – решения для нормального падения (при β₁ = 0) [2]:

где ${{u}_{1}} = - \sqrt {2kr} \cos \tfrac{{{{{\theta }}_{1}} - {{{\alpha }}_{1}}}}{2},$ ${{{v}}_{1}} = - \sqrt {2kr} \cos \tfrac{{{{{\theta }}_{1}} + {{{\alpha }}_{1}}}}{2}.$

Сравнивая между собой формулы (22) и (26), обратим внимание на симметрию и ясность, с которой они описывают явление дифракции. Все компоненты рассеянного поля для случая наклонного падения на кромку (26) можно получить, просто заменив в выражениях (22) для падающего поля угол падения α₁ на угол рассеяния θ₁, а функцию U₁ на функцию U_THβ или U_TEβ в зависимости от того, какая именно составляющая падающего поля является Т-поляризованной.

Из формул (21), (26) следует, что в строгом двумерном решении Т-поляризации падающей волны (22) сохраняются для всех углов наклонного падения. Для физоптики это не так, происходит взаимное “подмешивание” поляризаций. В этом заключается принципиальное отличие между строгим решением и физоптическим.

Для трехмерного случая строгие выражения будут отличаться от физоптики лишь поляризационными компонентами, которые мы возьмем из (26) на “условной кромке” и на которые заменим векторную составляющую физоптики. Угол положения условной кромки γ/2 [7, 10] войдет во все формулы для векторной составляющей решения.

Для случая наклонного падения поляризации строгого и физоптического решения складываются по-разному. Т-поляризация строгого решения остается неизменной для всех углов наклонного падения и точек наблюдения расположенных на дифракционном конусе. В то же время, Т-поляризация физоптического решения “подмешивается” в другую поляризацию. Поэтому для получения эвристического решения мы на полоске интегрирования заменяем обе поляризации сразу, а не по отдельности (т.е. заменяем всю векторную составляющую решения, которая характеризуется дифракционными коэффициентами).

7. ЛИНЕЙНЫЙ ИНТЕГРАЛ I В ПРИБЛИЖЕНИИ ФИЗИЧЕСКОЙ ОПТИКИ

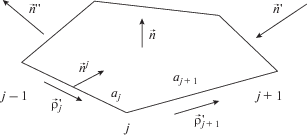
Рассмотрим в приближении физической оптики плоский идеально проводящий многоугольник конечных размеров, на который падает плоская электромагнитная волна (рис. 4).

На рис. 4 использованы следующие обозначения: ${{\vec {n}}^{j}}$ – вектор единичной внутренней нормали к контуру C, окружающему рассеиватель, $\vec {\rho }{\kern 1pt} '$ – единичный вектор, касательный к контуру, N – количество сторон и вершин многоугольника, вектора $\vec {n}{\kern 1pt} ',$ 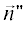и $\vec {n}$ были определены ранее.

Решение задачи дифракции в приближении физической оптики при выполнении условия дальней зоны (14), (15) будем искать при помощи формул (16) и (19), из которых следует, что рассеянное поле определяется видом поверхностного интеграла I.

Применяя теорему Стокса, можно свести поверхностный интеграл I к интегралу по кромке:

где $\Phi = k\left( {\vec {\Delta },\vec {\rho }} \right)$ – функция фазы, ${{\vec {n}}^{i}}$ – единичная внутренняя нормаль к контуру C, окружающему рассеиватель, $\vec {\rho }{\kern 1pt} '$ – единичный вектор, касательный к контуру, t – координата, отсчитываемая вдоль контура. Если контур представляет собой многоугольник с N сторонами, тогда:

где I_j – вклад j-ой стороны, ${{\Phi }_{j}} = k\left( {\vec {\Delta },{{{\vec {\rho }}}_{j}}} \right)$ – фаза сигнала j-ой вершины с направляющим вектором ${{\vec {\rho }}_{j}},$ ${{a}_{j}}$ – длина j-ой стороны многоугольника (расположенной между j – 1-ой и j-ой вершинами).

Изменив порядок суммирования, можно записать сумму вкладов отдельных сторон (30) в виде суммы вкладов от отдельных вершин [7]:

здесь I  ^j – рассеяние в приближении физической оптики от j-ой вершины (а именно – плоского углового сектора с прилегающими полубесконечными лучами, проиндексированными j и j + 1).

Если точка наблюдения расположена на дифракционном конусе j-ой стороны, когда вектора $\vec {n}{\kern 1pt} '$ и 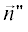составляют одинаковый угол с кромкой, вследствие чего выполняется условие $\left( {\vec {\Delta },\vec {\rho }{\kern 1pt} '} \right) = 0,$ то:

где (φ₀ + π) и φ – углы между проекциями направляющих векторов $\vec {n}{\kern 1pt} '$ и 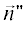на плоскость, перпендикулярную касательной к стороне $\vec {\rho }{\kern 1pt} ',$ и внутренней нормалью ${{\vec {n}}^{j}}$ к контуру C, β – угол между вектором $\vec {\rho }{\kern 1pt} '$ и $\vec {n}{\kern 1pt} '$ или 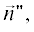причем каждый из этих векторов направлен вдоль образующей дифракционного конуса.

Отметим некоторые важные свойства интеграла I. Линейные интегралы I_j и I ^j, имеющие размерность площади, составляют основу решения задачи дифракции при выполнении условия дальней зоны. Применение этих интегралов в приближении физической оптики дает строгое решение соответствующей задачи. При помощи интегралов I_j и I ^j можно также строить решения в приближении метода эквивалентных контурных токов [7].

8. ПЕРЕХОД ОТ ТРЕХМЕРНОЙ КРОМКИ К ДВУМЕРНОЙ

Рассмотрим формулы (19) и (32) для случая нормального падения и рассеяния электромагнитной волны на отдельной (j-ой) стороне рассеивателя (идущей от вершины j – 1 к вершине j). В случае нормального падения оба вектора $\vec {n}{\kern 1pt} '$ и 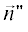перпендикулярны кромке и расположены в плоскости, нормальной к стороне рассеивателя, а фаза ${{\Phi }_{j}}$ для всех точках j-ой стороны (в том числе – и в j-ой вершине) одинакова. Тогда для случая идеально проводящего рассеивателя получим из (19), (32) [10]:

здесь ${{E}_{{\varphi }}}$ и ${{E}_{\vartheta }}$ – пространственные компоненты поля, k – волновое число, ${{a}_{j}}$ – длина j-ой стороны рассеивателя, i – мнимая единица, R₀ – расстояние от центра рассеивателя до точки наблюдения.

Выражение (33) соответствует случаю трехмерной дифракции на стороне ограниченной длины a_j. Для перехода к двумерному случаю следует провести интегрирование по всей стороне от −∞ до ∞. При этом используем локальные цилиндрические координаты (r_j, φ_j, z_j), связанные с j-ой кромкой. Координата z_j направлена вдоль кромки, координата r_j – перпендикулярно кромке. С учетом выражения для функции Ганкеля и его асимптотики:

Здесь r_j – это расстояние от кромки до точки наблюдения в плоскости, перпендикулярной j-ой кромке. Переменная r_j – аналог r из двумерного пространства, рассматриваемого в [5]. В координатах, использованных в [5], для ТН- и ТЕ-поляризаций (когда Н- или Е-вектор перпендикулярен кромке) векторные произведения из (19) будут соответственно равны sinφ₀ и –sinφ. В результате из (19), (33) и (34) получаем предельный переход для j-ой кромки, устремив ее длину к ∞:

Здесь f ⁰ и g⁰ – дифракционные коэффициенты в приближении физической оптики, введенные в [5]. Полученные выражения (35) в точности совпадают с результатом из [5]. Этот важный результат означает, что сингулярные физоптические дифракционные коэффициенты из двумерной задачи остаются точно такими же и в трехмерном случае. Другой важный результат состоит в том, что физоптические выражения (35) имеют точно такую же форму, как строгие выражения (8).

Формулу, аналогичную “трехмерному” выражению (33) и “двумерному” (35), можно получить еще одним способом. Для этого в приближении физической оптики решают двумерную задачу дифракции на идеально проводящей полуплоскости, формально применив соотношение (15) (т.е. “навязав” условие дальней зоны). Нетрудно показать, что при этом:

где ${{E}_{z}}$ и ${{E}_{{\varphi }}}$ соответствуют случаям падения ТН- или ТЕ-поля, а ${{f}^{0}}$ и ${{g}^{0}}$ также определяются формулами (10).

В дальнейшем мы будем использовать установленные факты и полученные формулы при построении эвристических решений трехмерных задач.