Радиотехника и электроника, 2020, T. 65, № 11, стр. 1109-1115
Применение весовых функций Кравченко для повышения помехоустойчивости приема OFDM-сигналов при наличии сосредоточенных по спектру помех
А. С. Зудилин a, В. Ф. Кравченко b, Л. Е. Назаров a, *, В. И. Пустовойт c
a Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация
b Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая 11, стр. 7, Российская Федерация
c Научно-технологический центр уникального приборостроения РАН
117342 Москва, ул. Бутлерова, 15, Российская Федерация
* E-mail: levnaz2018@mail.ru
Поступила в редакцию 27.01.2020
После доработки 27.01.2020
Принята к публикации 17.05.2020
Аннотация
Приведены описания алгоритмов формирования и приема сигнальных конструкций на основе OFDM-сигналов, устойчивых к влиянию сосредоточенных по спектру помех. Показано, что алгоритм приема этих сигнальных конструкций при наличии сосредоточенных по спектру помех основан на использовании весовых функций. Приведены результаты исследования весовых функций Кравченко на основе атомарных функций для повышения помехоустойчивости рассматриваемых сигнальных конструкций при наличии сосредоточенных по спектру помех и даны результаты моделирования разработанного алгоритма приема.
ВВЕДЕНИЕ
В теории цифровой обработки сигналов широко применяются весовые функции – с их использованием решается ряд проблем, связанных с разрешением сигналов, со снижением эффективности межканальных помех, с повышением помехоустойчивости передачи информации по каналам с сосредоточенными по спектру помехами [1].
Поиск конструктивных решений для последней из перечисленных проблем составляет самостоятельное научное направление в статистической теории связи, в рамках которой создаются процедуры обработки сигналов при их приеме [2, 3]. Методы снижения искажающего влияния класса рассматриваемых помех основаны на увеличении базы сигналов и на компенсации помех с использованием весовых функций [2]. В работах [4–6] приведены описания сигнальных конструкций на основе OFDM-сигналов (orthogonal frequency division multiplexing), разработанные алгоритмы их приема реализуют данное направление. Снижение эффективности действия рассматриваемых помех зависит от используемых весовых функций [5].
Актуальными являются проблемы определения критериев оптимальности весовых функций и их практический выбор, определяющих максимальную помехоустойчивость передачи информации с использованием исследуемых сигнальных конструкций, а также анализ помехоустойчивости при их приеме при наличии рассматриваемых помех.
1. ПОСТАНОВКА ЗАДАЧИ
OFDM-сигналы $\dot {s}(t)$ представляют сумму $N$ парциальных гармонических сигналов на интервале определения $T$ и задаются соотношением [3, 7]
(1)
$\dot {s}(t) = \frac{1}{{\sqrt N }}\sum\limits_{m = 0}^{N - 1} {{{{\dot {\alpha }}}_{m}}exp} (j2\pi {{f}_{m}}t).$Здесь ${{f}_{m}} = {m \mathord{\left/ {\vphantom {m T}} \right. \kern-0em} T}$ – частоты, определяющие ортогональность в усиленном смысле парциальных сигналов; символы ${{\dot {\alpha }}_{m}}$ в блоке (${{\dot {\alpha }}_{0}},{{\dot {\alpha }}_{1}},...,{{\dot {\alpha }}_{{N - 1}}}$) задаются информационными последовательностями длительностью $L = N{{\log }_{2}}J$ с учетом сигнальных “созвездий” объемом $J$ используемых сигналов. Для “созвездия” с двухфазовой манипуляцией (ФМ2-сигналы) $J = 2$ и $L = N.$
Теории OFDM-сигналов посвящен ряд работ [7–9]. Перспективность их использования в приложениях определяется спектральной эффективностью, а также возможностью организации надежной передачи информации по каналам с многолучевостью, обусловливающей наличие мультипликативных помех и нестационарность каналов передачи [2, 3]. При формировании и приеме OFDM-сигналов используется аппарат быстрых спектральных преобразований в базисе Фурье (БПФ) [1].
Сосредоточенные по спектру помехи (ССП) определяются соотношением
(2)
$\dot {N}(t) = \sum\limits_{k = 1}^Q {{{{\dot {p}}}_{k}}(t)exp} (j2\pi {{f}_{k}}(t) + {{\varphi }_{k}}(t)).$Здесь $Q$ – количество помех; ${{\dot {p}}_{k}}(t),{{f}_{k}}(t),{{\varphi }_{k}}(t)$ – амплитуда, частота и фаза помех, полагаемых случайными величинами и постоянными ${{\dot {p}}_{k}}(t) = {{\dot {p}}_{{k0}}},$ ${{f}_{k}}(t) = {{f}_{{k0}}},$ ${{\varphi }_{k}}(t) = {{\varphi }_{{k0}}}$ на длительности $T$ OFDM-сигналов.
Сосредоточенные по спектру помехи (2) подобны по структуре парциальным сигналам в (1), что обусловливает их эффективность по снижению помехоустойчивости OFDM-сигналов (1) по сравнению с базовой моделью помехи в виде аддитивного белого гауссовского шума (АБГШ) [3, 8, 9]. Количественной мерой помехоустойчивости является вероятность ошибки на один информационный бит ${{P}_{{\text{б}}}}$ при приеме сигналов [2].
Помехи ${{\dot {N}}_{m}},$ соответствующие ССП, на выходе согласованного фильтра для $m$-го парциального сигнала определяются соотношением [6]
(3)
${{\dot {N}}_{m}} = \sum\limits_{k = 1}^Q {{{{\dot {p}}}_{{k0}}}\frac{{1 - \exp (j(2\pi (m - {{f}_{{k0}}}) + {{\varphi }_{{k0}}}))}}{{1 - \exp ({{j(2\pi (m - {{f}_{{k0}}}) + {{\varphi }_{{k0}}})} \mathord{\left/ {\vphantom {{j(2\pi (m - {{f}_{{k0}}}) + {{\varphi }_{{k0}}})} N}} \right. \kern-0em} N})}}} .$Вероятность ошибки ${{P}_{{\text{б}}}}(m)$ для $m$-го парциального сигнала при наличии рассматриваемых помех определяется отношением сигнал/помеха [2]
где ${{E}_{б}}$ – энергия на один информационный бит; ${{N}_{{m0}}}$ – эффективная спектральная плотность ССП (2) в полосе $m$-го парциального сигнала; $\overline {{{{\left| {{{{\dot {N}}}_{m}}} \right|}}^{2}}} $ – средняя мощность помех (3).
Известные методы снижения эффективности ССП основаны на использовании методов их компенсации и на увеличении базы $B$ сигналов [2, 3, 9, 10]. При использовании сигналов с базой $B$ вероятность ${{P}_{{\text{б}}}}$ зависит от отношения мощности сигналов ${{P}_{{\text{с}}}}$ к мощности ССП ${{P}_{{\text{п}}}}$ и зависит от отношения $\sqrt {{{B{{P}_{{\text{с}}}}} \mathord{\left/ {\vphantom {{B{{P}_{{\text{с}}}}} {{{P}_{{\text{п}}}}}}} \right. \kern-0em} {{{P}_{{\text{п}}}}}}} $ – происходит снижение эффективности ССП в $B$ раз [10].
При условии Pп/Pc > B существенно снижается помехоустойчивость передачи информации. В этом случае повышение надежности передачи возможно обеспечить, используя сигнальные конструкции на основе OFDM-сигналов с увеличением базы $B$ в сочетании с компенсацией ССП [6, 10]. Разработанные алгоритмы приема этих сигнальных конструкций основаны на использовании весовой обработки входных реализаций [4]. Снижение действия рассматриваемых помех зависит от используемых весовых функций. В работах [4–11] показано, что функции Хэмминга, Кайзера, Дольфа–Чебышева, Кайзера–Кравченко являются эффективными для весовой обработки рассматриваемых сигнальных конструкций.
Цель данной работы – детально исследовать весовые функции Кравченко на основе атомарных функций [11, 12] для повышения помехоустойчивости рассматриваемых сигнальных конструкций при наличии ССП. Приведены результаты моделирования разработанных алгоритмов приема.
2. ОПИСАНИЕ СИГНАЛЬНЫХ КОНСТРУКЦИЙ НА ОСНОВЕ OFDM-СИГНАЛОВ
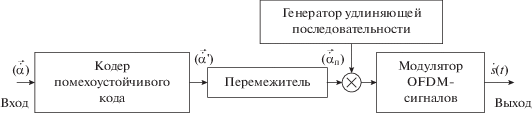
На рис. 1 представлена схема алгоритма формирования сигнальных конструкций на основе OFDM-сигналов [4, 6]. Информационные символы $(\vec {\dot {\alpha }})$ объемом $K$ битов поступают на вход кодера помехоустойчивого кода. Выходная последовательность двоичных кодовых символов $(\vec {\dot {\alpha }}{\kern 1pt} ')$ с объемом ${K \mathord{\left/ {\vphantom {K R}} \right. \kern-0em} R}$ (R – кодовая скорость кода [2]) поступает на вход перемежителя, каждый символ ${{\vec {\dot {\alpha }}}_{{{\text{п,}}i}}}$ с его выхода отображается в последовательность (${{\dot {\alpha }}_{{{\text{п,}}i}}}{{\dot {p}}_{0}}(i),...,{{\dot {\alpha }}_{{{\text{п,}}i}}}{{\dot {p}}_{{l - 1}}}(i)$) длительностью $l$ действием генератора удлиняющей последовательности. Здесь ${{\dot {p}}_{j}}(i),$ $j = 0,1,...,l - 1$ – символы удлиняющей последовательности с компонентами $ \pm 1.$ Последовательность символов с выхода умножителя длительностью ${{Kl} \mathord{\left/ {\vphantom {{Kl} R}} \right. \kern-0em} R}$ поступает на вход модулятора OFDM-сигналов размерностью $N,$ формирующего последовательность $L = {{Kl} \mathord{\left/ {\vphantom {{Kl} {RN}}} \right. \kern-0em} {RN}}$ OFDM-сигналов (1). Для фиксированной частотной полосы удлиняющая последовательность увеличивает базу сигналов по отношению к базе исходных OFDM-сигналов в $l$ раз [9].
Отсчеты входной реализации $\vec {\dot {z}}$ при приеме задаются соотношением
Здесь ${{\dot {s}}_{i}},{{\dot {n}}_{i}},{{\dot {N}}_{i}}$ – комплексные отсчеты, соответствующие сигнальной составляющей, АБГШ и ССП.
Обработка реализации $\vec {\dot {z}}$ при приеме включает следующие этапы [4–6, 11]:
умножение отсчетов $\vec {\dot {z}}$ на весовую функцию с коэффициентами $w(k),$ $k = 0,1,2,...,N - 1;$
вычисление спектральных составляющих ${{\dot {S}}_{j}}(k),$ $j = 1,2,...,l$ с использованием БПФ с размерностью $N$ для взвешенной реализации;
компенсацию помех ССП путем нелинейного преобразования спектральных составляющих, в частности, их ограничение с амплитудой, превышающей порог $P;$
демодуляцию OFDM-сигналов; деперемежение отсчетов с выхода демодулятора и декодирование с их использованием.
На вход модуля компенсации ССП поступают нормированные спектральные отсчеты
где осуществляется их ограничение
(5)
$\begin{gathered} \operatorname{Re} (\dot {S}_{j}^{'}(k)) = \\ = \left\{ {\begin{array}{*{20}{c}} {\operatorname{Re} ({{{\dot {S}}}_{j}}(k)),{\text{ }}если{\text{ }}\left| {({{{\dot {S}}}_{j}}(k))} \right| < P,{\text{ }}} \\ {sign(\operatorname{Re} ({{{\dot {S}}}_{j}}(k)))P,\,\,\,\,если\,\,\,\,\left| {({{{\dot {S}}}_{j}}(k))} \right| \geqslant P.} \end{array}} \right. \\ \end{gathered} $Здесь $sign(x)$ – знак аргумента $x.$ Операция (5) осуществляется над мнимой частью $\operatorname{Im} ({{\dot {S}}_{i}}(k))$ при формировании $\operatorname{Im} (\dot {S}_{j}^{'}(k)).$
Частным случаем нелинейного преобразования (5) отсчетов $\operatorname{Re} ({{\dot {S}}_{i}}(k))$ и $\operatorname{Im} ({{\dot {S}}_{i}}(k))$ является жесткое ограничение, учитывающее лишь их знак.
Демодуляция OFDM-сигналов заключается в вычислении решений $\vec {\dot {y}}$ с отсчетами
Использование весовых функций обусловливает уменьшение значений боковых лепестков рассматриваемых помех относительно основного лепестка в частотной области [1] по отношению к прямоугольной весовой функции, что снижает искажающее влияние ССП при приеме парциальных сигналов. Вместе с тем при весовой обработке уменьшаются значения сигнал/помеха на выходе демодулятора по отношению к согласованной фильтрации с использованием прямоугольной функции, а также нарушается ортогональность парциальных сигналов, что обусловливает возникновение помех межканальной интерференции (МКИ) [1, 11].
Существуют оптимальные значения порогов ${{P}_{{опт}}},$ определяющие минимальные значения вероятности ошибки ${{P}_{{\text{б}}}}$ для алгоритма приема сигнальных конструкций на основе OFDM-сигналов при наличии ССП. Действительно, вероятность ошибки ${{P}_{{\text{б}}}}$ при реализации правила нелинейной обработки (5) определяется совместным действием двух взаимных факторов.
Во-первых, нелинейная операция ограничения приводит к известному эффекту энергетических потерь – снижению отношения сигнал/помеха при уменьшении значений порога $P$ и, соответственно, к увеличению вероятности ошибки ${{P}_{{\text{б}}}}$ по отношению к линейной обработке [2]. Результаты исследований этого эффекта приведены в [12, 13] – для предельного случая жесткого ограничения энергетические потери достигают максимального значения и для АБГШ составляют 2 дБ.
Во-вторых, при увеличении значений порога $P$ с целью уменьшения влияния ограничения на вероятностные характеристики приема увеличивается эффективность искажающего действия ССП. В этом случае рассматриваемые помехи в частотной области с использованием весовых функций подобны импульсным помехам во временной области. Результаты по разработке алгоритмов оптимальных либо близких к оптимальным алгоритмам приема при наличии помех импульсного типа приведены в [14, 15]. Эти алгоритмы приема основаны на безынерционной нелинейной обработке отсчетов входных реализаций, практически эквивалентной ограничению, которое реализуется путем включения регулировки усиления на основе взвешивания отсчетов с учетом плотности их распределения (в общем случае негауссовой).
Таким образом, должен существовать оптимальный порог ограничения ${{P}_{{опт}}},$ определяющий минимизацию совместного влияния ограничения и ССП и, соответственно, минимальную вероятность ${{P}_{{\text{б}}}}.$
Оптимальность весовых функций при решении рассматриваемой задачи основывается на следующих критериях [11]:
– обеспечение минимальных значений боковых лепестков функций в частотной области;
– достижение минимума энергии спектра частотной характеристики функций за пределами задаваемой полосы;
– минимизация энергетических потерь по отношению к согласованной фильтрации;
– обеспечение максимальной ортогональности для парциальных сигналов (1) с весовой обработкой.
Известен ограниченный ряд весовых функций со свойствами, близкими к сформулированным свойствам оптимальности, например, функция Кайзера с коэффициентами [1]
Здесь $0 \leqslant k < N;$ ${{I}_{0}}(x)$ – модифицированная функция Бесселя первого рода нулевого порядка. Основные характеристики функции (ширина главного лепестка, значения амплитуд боковых лепестков в частотной области) задаются через параметр $\beta ,$ оптимальным является значение $\beta = 6$ [4].
Альтернативу этим весовым функциям относительно эффективности для решения рассматриваемой задачи составляет класс функций Кравченко на основе атомарных функций [16].
3. ВЕСОВЫЕ ОКНА КРАВЧЕНКО НА ОСНОВЕ АТОМАРНЫХ ФУНКЦИЙ
Атомарные функции $c{{h}_{{a,n}}}(t)$ с параметрами $a,n$ определяются как финитные решения дифференциального уравнения [16–18]
(6)
${{y}^{{(n)}}}(t) = {{a}^{{n + 1}}}{{2}^{{ - n}}}\sum\limits_{k = 0}^n {C_{n}^{k}y(at + n - 2k)} .$Решение $y(t) = c{{h}_{{a,n}}}(t)$ имеет носитель [${{ - n} \mathord{\left/ {\vphantom {{ - n} {(a - 1)}}} \right. \kern-0em} {(a - 1)}};$ ${n \mathord{\left/ {\vphantom {n {(a - 1)}}} \right. \kern-0em} {(a - 1)}}$] и представляется в виде
Здесь $sinc(x)$ = ${{sin(x)} \mathord{\left/ {\vphantom {{sin(x)} x}} \right. \kern-0em} x}.$
Коэффициенты w(k) функций Кравченко задаются соотношением
В табл. 1 приведены характеристики для ряда функций Кравченко и функции Кайзера с параметром $\beta = 6.$
Таблица 1.
Характеристики весовых функций Кравченко
| $a$ | $n$ | $K$, дБ | $W$, дБ | ${{W}_{{{\text{МКИ}}}}}$, дБ | $\Delta E$, дБ |
|---|---|---|---|---|---|
| 3.0 | 1 | –38.90 | –42.1 | 5.0 | –3.50 |
| 2 | –80.4 | –76.9 | 3.1 | –8.45 | |
| 3 | –51.3 | –50.6 | 1.9 | –10.20 | |
| 7.0 | 1 | –16.9 | –0.8 | –9.8 | –0.85 |
| 2 | –27.0 | –29.5 | 5.1 | –6.95 | |
| 3 | –43.3 | –41.1 | 3.1 | –8.35 | |
| 15.0 | 1 | –5.8 | –0.2 | –6.2 | –0.60 |
| 2 | –28.0 | –34.5 | 5.7 | –6.20 | |
| 3 | –37.50 | –38.2 | 8.3 | –9.50 | |
| Функция Кайзера, $\beta = 6$ | –58.70 | –47.9 | 6.3 | –6.50 | |
Примечание: $K$ – максимальное значение бокового лепестка относительно значения главного лепестка; $W$ – энергия функции вне полосы $\Delta F$ (по уровню –3 дБ), нормированная на полную энергию весовой функции; ${{W}_{{{\text{МКИ}}}}}$ – оценка сигнал/помеха за счет МКИ; $\Delta E$ – энергетические потери при использовании весовой функции по отношению к согласованной фильтрации.
При оценивании характеристики ${{W}_{{{\text{МКИ}}}}} = $ $ = {{{{P}_{c}}} \mathord{\left/ {\vphantom {{{{P}_{c}}} {{{P}_{{МКИ}}}}}} \right. \kern-0em} {{{P}_{{МКИ}}}}}$ мощность парциального сигнала ${{P}_{c}}$ вычислялась на основе корреляции сигнала и его копии с взвешенными отсчетами. Оценивание мощности ${{P}_{{МКИ}}}$ производилось на основе корреляции парциального сигнала и OFDM-сигналов без данного парциального сигнала с учетом весовой функции.
Анализ табл. 1 показывает, что существует ряд весовых функций Кравченко со свойствами, практически удовлетворяющими сформулированным критериям оптимальности и сравнимых по этим свойствам с функцией Кайзера с оптимальным параметром $\beta = 6.$ В этот ряд входят функции с параметрами $n = 1$ и $n = 2.$ Ниже приведены результаты их исследований.
4. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ ВЕСОВЫХ ФУНКЦИЙ КРАВЧЕНКО
Исследование вероятностных характеристик при приеме выполнено для сигнальных конструкций с использованием помехоустойчивого сверточного кода с кодовой скоростью $R$ = 1/2, задаваемого порождающими многочленами ${{g}_{1}}$ и ${{g}_{2}}$ в восьмеричном представлении ${{g}_{1}} = 133,$ ${{g}_{2}} = 171$ [2]. Этот код включен в состав помехоустойчивых кодов, рекомендованных для спутниковых систем связи [19]. Кодер сверточного кода представляется решетчатой диаграммой [2]. Оптимальный прием сигналов, соответствующих сверточным кодам, выполняется на основе алгоритма Витерби – осуществляется динамический перебор возможных путей по кодовой решетке с выбором наиболее правдоподобного пути [2].
Возможность существенного снижения эффективности сосредоточенных по спектру помех при использовании рассматриваемых сигнальных конструкций показана путем моделирования алгоритма приема при наличии АБГШ и до пяти помеховых сигналов с вариацией их количества и произвольного размещения в полосе OFDM-сигналов, размерность БПФ $N = 1024,$ сигнальное “созвездие” ФМ2. Отношение мощности OFDM-сигналов ${{P}_{{\text{с}}}}$ к общей мощности ССП ${{P}_{{\text{п}}}}$ при моделировании равно $\chi = {{{{P}_{{\text{с}}}}} \mathord{\left/ {\vphantom {{{{P}_{{\text{с}}}}} {{{P}_{{\text{п}}}}}}} \right. \kern-0em} {{{P}_{{\text{п}}}}}} = - 20$ дБ. Результаты экспериментальных исследований показывают, что эта модель ССП является адекватной для ряда спутниковых информационных систем, например, для канала P-диапазона: наблюдается в среднем до пяти помех рассматриваемого типа, отношение мощности информационных сигналов к мощности помех может достигать –20…–25 дБ [6].
При моделировании производилась интервальная оценка вероятности ${{P}_{{\text{б}}}}$ путем вычисления частости $p = {x \mathord{\left/ {\vphantom {x u}} \right. \kern-0em} u}{\text{,}}$ где $x$ – число ошибочных битов при приеме из переданных информационных битов объемом $u.$ Требуемый объем $u$ определяется вероятностью ${{P}_{{\text{б}}}},$ доверительной вероятностью ${{P}_{{{\text{дов}}}}} = 0.95$ и размером доверительного интервала $[0.5{{P}_{{\text{б}}}},1.5{{P}_{{\text{б}}}}].$
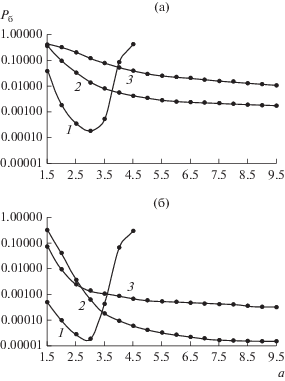
На рис. 2а, 2б приведены зависимости вероятности ${{P}_{{\text{б}}}}$ для ${{P}_{{опт}}}$ от параметра $a$ для изложенного выше алгоритма приема сигнальных конструкций на основе OFDM-сигналов (для значений $l = 2$ и $l = 4$ соответственно) с использованием весовых функций Кравченко с параметром $n = 1,$ 2 и 3 при наличии АБГШ (${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 5.5$ дБ) и ССП. Видно, что минимальное значение ${{P}_{{\text{б}}}}$ достигается для параметра $n = 1$ и значения $a = 3.$ Для параметров $n = 2$ и $n = 3$ наблюдается выравнивание вероятностных характеристик при увеличении значений $a{\text{:}}$ для $l = 2$ минимальные значения ${{P}_{{\text{б}}}}$ для $n = 3$ и $n = 2$ по отношению к минимальным значениям ${{P}_{{\text{б}}}}$ для $n = 1$ превышают в 100 и в 10 раз соответственно.
Рис. 2.
Зависимости вероятностей ошибки ${{P}_{{\text{б}}}}$ от параметра $a$ при приеме сигнальной конструкции на основе OFDM-сигналов с использованием весовых функций Кравченко при $l = 2$ (а) и 4 (б), параметр окна: $n = 1$ (1), 2 (2) и 3 (3).
Оптимальные пороги ${{P}_{{опт}}}$ определялись путем изменения значений порога $P$ и анализа вероятности ${{P}_{{\text{б}}}}.$ На рис. 3а, 3б приведены вероятностные кривые, соответствующие рассматриваемым сигнальным конструкциям для $l = 2$ и $l = 4$ соответственно, даны зависимости вероятности ошибки ${{P}_{{\text{б}}}}$ от порога ограничения $P$ при компенсации помех с использованием функций Кравченко с параметрами $n = 1$ и 2 и функции Кайзера. Видно, что в соответствии со сделанным выше утверждением существуют оптимальные значения порогов ограничения ${{P}_{{{\text{опт}}}}},$ определяющие минимальные вероятности ошибки ${{P}_{{\text{б}}}}.$ В табл. 2 приведены полученные значения порогов ${{P}_{{{\text{опт}}}}}.$
Рис. 3.
Зависимости вероятностей ошибки ${{P}_{{\text{б}}}}$ от порога $P$ при приеме сигнальной конструкции на основе OFDM-сигналов с использованием весовых функций при $l = 2$ (а) и 4 (б): кривая 1 – функция Кравченко ($n = 1,$ $a = 3$); кривая 2 – функция Кравченко ($n = 2,$ $a = 9.5$); кривая 3 – функция Кайзера ($\beta = 6$).
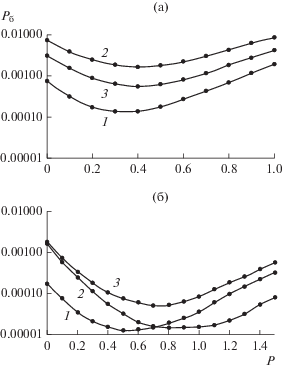
Таблица 2.
Оптимальные значения порогов ограничения ${{P}_{{{\text{опт}}}}}$ для весовых функций Кравченко и Кайзера при приеме сигнальных конструкций на основе OFDM-сигналов
| $l$ | Функция Кравченко | Функция Кайзера ($\beta = 6$) | |
|---|---|---|---|
| $a = 9.5,\,\,n = 2$ | $a = 3.0,\,\,n = 1$ | ||
| $2$ | 0.40 | 0.35 | 0.40 |
| $4$ | 0.90 | 0.50 | 0.80 |
На рис. 4 приведены результирующие вероятностные кривые для сигнальных конструкций при наличии рассматриваемого комплекса помех, варьируемым параметром является сигнал/помеха ${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}$ для АБГШ.
Рис. 4.
Вероятностные кривые для сигнальных конструкций на основе OFDM-сигналов и помехоустойчивого сверточного кода с кодовой скоростью 1/2 при наличии АБГШ (кривая 1) и ССП: функция Кайзера ($\beta = 6$) при $l = 2$ (2) и 4 (6); функция Кравченко ($n = 2,$ $a = 9.5$) при $l = 2$ (3) и 4 (5); функция Кравченко ($n = 1,$ $a = 3.0$) при $l = 2$(4) и 4 (7).
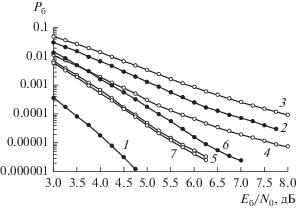
Для АБГШ задаваемая вероятность ошибки ${{P}_{б}} = 1{{0}^{{ - 4}}}$ обеспечивается при ${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 3.5$ дБ. Представлены также кривые для функции Кайзера ($\beta = 6$), функции Кравченко с параметрами $n = 2,$ $a = 9.5$ и $n = 1,$ $a = 3.0$ для $l = 2.$ Видно, что наиболее эффективной является функция Кравченко с параметрами $n = 1,$ $a = 3.0$ – задаваемая вероятность ошибки достигается при ${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 5.75$ дБ и энергетические потери кривых 2–4 по отношению к кривой 1 не превышают 2.25 дБ. Для функции Кайзера задаваемая вероятность ошибки достигается при ${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 6.75$ дБ и энергетические потери по отношению к кривой 1 достигают 3.25 дБ. Функция Кравченко с параметрами $n = 2,$ $a = 9.5$ характеризуется меньшей эффективностью – задаваемая вероятность ошибки обеспечивается при ${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 8.0$ дБ и энергетические потери по отношению к кривой 1 достигают 4.5 дБ.
При увеличении значения $l = 4$ подавление СCП увеличивается. В этом случае вероятностные кривые для функций Кравченко с параметрами $n = 1,$ $a = 3.0$ и $n = 2,$ $a = 9.5$ практически совпадают – задаваемая вероятность ошибки обеспечивается при ${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 4.75$ дБ и энергетические потери по отношению к кривой 1 достигают 1.25 дБ. Функция Кайзера характеризуется меньшей эффективностью – задаваемая вероятность ошибки при его применении обеспечивается при ${{{{E}_{б}}} \mathord{\left/ {\vphantom {{{{E}_{б}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} = 5.25$ дБ и энергетические потери по отношению к кривой 1 достигают 2.25 дБ.
ЗАКЛЮЧЕНИЕ
Таким образом, приведены описания сигнальных конструкций на основе OFDM-сигналов и помехоустойчивых кодов, устойчивых к влиянию сосредоточенных по спектру помех. Разработанные алгоритмы приема основаны на увеличении базы этих сигналов по отношению к базе исходных OFDM-сигналов и на компенсации помех в частотной области. Алгоритмы приема включают БПФ с весовой функцией, пороговое ограничение спектральных составляющих и вычисление решений на их основе, используемых при приеме помехоустойчивых кодов. Даны критерии оптимальности весовых функций и показано, что ряд функций Кравченко на основе атомарных функций практически удовлетворяют сформулированным критериям оптимальности.
Путем моделирования разработанного алгоритма приема с использованием весовых функций Кравченко с вариацией их параметров $n,$ $a,$ а также для весовой функции Кайзера произведен анализ помехоустойчивости для сигнальных конструкций ($l = 2,4$), формируемых с использованием сверточного кода с кодовой скоростью 1/2. Моделирование произведено при наличии в канале АБГШ и до пяти ССП с отношением $\chi = - 20$ дБ, эта модель адекватно описывает ряд спутниковых каналов передачи. Для исследуемого ряда весовых функций определены оптимальные значения порогов ограничения, определяющие минимальные вероятности ошибки ${{Р}_{б}}.$
Результаты моделирования показывают, что для рассматриваемой модели помех весовая обработка с использованием функций Кравченко с оптимальными параметрами $n = 1,$ $a = 3.0$ является наиболее эффективной по отношению к рассмотренным весовым функциям, включая функцию Кайзера.
Для вероятности ${{P}_{б}} = 1{{0}^{{ - 4}}}$ и параметра $l = 2$ энергетические потери при использовании весовой функции Кайзера по отношению к функции Кравченко с оптимальными параметрами достигают 1 дБ, при использовании функции Кравченко с параметрами $n = 2$ и $a = 9.5,$ рассмотренной в [11], потери достигают 2.25 дБ. Для $l = 4$ вероятностные кривые, соответствующие весовым функциям Кравченко с параметрами $n = 1,$ $a = 3.0$ и $n = 2,$ $a = 9.5$, практически совпадают, по отношению к этим кривым использование функции Кайзера обусловливает энергетические потери до 0.5 дБ. При уменьшении ${{P}_{б}}$ значения энергетических потерь увеличиваются.
Список литературы
Оппенгейм А., Шафер Р. Цифровая обработка сигналов / Пер. с англ. М.: Техносфера, 2006.
Зюко А.Г., Фалько А.И., Панфилов И.П. и др. Помехоустойчивость и эффективность систем передачи информации. М.: Радио и связь, 1985.
Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи. Базовые методы и характеристики. М.: Эко-Трендз, 2005.
Назаров Л.Е., Зудилин А.С. // Журн. радиоэлектроники. 2018. № 3. http://jre.cplire.ru/jre/mar18/4/text.pdf.
Назаров Л.Е., Зудилин А.С. // Физ. основы приборостроения. 2018. Т. 7. № 3. С. 26.
Haзapoв Л.E. // PЭ. 2019. T. 64. № 8. C. 787.
Бакулин М.Г., Крейнделин В.Б., Шлома А.М., Шумов А.П. Технология OFDM. М.: Горячая линия-Телеком, 2016.
Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные сети передачи. М.: Техносфера, 2005.
Liu H., Li G. OFDM-Based Broadband Wireless Networks. N.J.: John Wiley & Sons Ltd, 2005.
Schulze H., Luders C. Theory and Application of OFDM and CDMA. Wideband Wireless Communications. Chichester, West Sussex: John Wiley & Sons Ltd., 2005.
Кравченко В.Ф., Назаров Л.Е., Пустовойт В.И. // РЭ. 2019. Т. 64. № 10. С. 976.
Шинаков Ю.С. // Радиотехника. 2016. № 2. С. 66.
Назаров Л.Е., Зудилин А.С. // РЭ. 2015. Т. 60. № 5. С. 522.
Aнтoнoв O.E. // PЭ. 1967. T. 12. № 4. C. 579.
Акимов П.С., Бакут П.А., Богданович В.А. Теория обнаружения сигналов. М.: Радио и связь, 1984.
Кравченко В.Ф., Кравченко О.В. Конструктивные методы алгебры логики, атомарных функций, вейвлетов, фракталов в задачах физики и техники. М.: Техносфера, 2018.
Кравченко В.Ф., Коновалов Я.Ю., Пустовойт В.И. // РЭ. 2015. Т. 60. № 9. С. 931.
Кравченко В.Ф., Чуриков Д.В. Цифровая обработка сигналов атомарными функциями и вейвлетами. М.: Техносфера, 2018.
TM synchronization and channel coding – summary of concept and rationale. Information report CCSDS 130.1-G-1. Green Book. Washinhton, 2006.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника