Радиотехника и электроника, 2020, T. 65, № 12, стр. 1170-1175
К расчету периодических структур на основе идеально проводящих квадратов
В. И. Пономаренко a, *, И. М. Лагунов a
a Крымский федеральный университет им. В.И. Вернадского
295007 Симферополь, просп. Акад. Вернадского, 4, Российская Федерация
* E-mail: vponom@gmail.com
Поступила в редакцию 14.01.2020
После доработки 22.03.2020
Принята к публикации 31.03.2020
Аннотация
Показана применимость к расчету структур с плоскими идеальными решетками метода решения задачи дифракции на резистивных решетках, основанного на решении задачи возбуждения канала Флоке токовыми элементами. Получена формула квазистатического приближения для эффективной диэлектрической проницаемости плоской однослойной решетки на основе идеально проводящих квадратов. Проведены сравнительные расчеты коэффициента отражения дифракционным и квазистатическим методами для однослойных и двухслойных решеток с диэлектрическими слоями.
ВВЕДЕНИЕ
Дифракционные решетки на основе идеально проводящих элементов используются в качестве частотно-селективных поверхностей в антенной и измерительной технике, в оптических и квазиоптических волномерах и интерферометрах и в других областях техники [1, 2]. Проектирование устройств с решетками основывается на решении задач дифракции на периодических структурах такими методами, как метод задачи Римана–Гильберта, метод Галеркина, метод интегральных уравнений [1–5]. В плане расширения возможности оптимального выбора метода анализа структур с решетками актуальной является разработка новых подходов. Одной из целей данной работы является распространение на идеальные решетки метода анализа резистивных решеток, основанного на решении задачи возбуждения канала Флоке элементарными токами [6–8].
Длительность расчетного времени при использовании дифракционных методов анализа решеток обусловлена необходимостью решения систем с большим числом уравнений и неизвестных. Это обстоятельство затрудняет решение задач оптимизации свойств решеток, поскольку решение обратной задачи основывается на многократном решении прямой задачи дифракции с варьированием параметров решетки [9]. В связи с этим остаются актуальными более простые приближенные подходы к расчету решеточных структур [10–12]. Их применение в ряде случаев снимает необходимость исследования структур дифракционными методами, а также позволяет выбрать начальные приближения при решении задач оптимизации. Второй целью данной работы является обоснование приближенного метода анализа в длинноволновой области плоских решеток с квадратными элементами, основанного на сопоставлении решетке предельно тонкого диэлектрического однородного слоя.
1. ЭФФЕКТИВНАЯ ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ РЕШЕТКИ
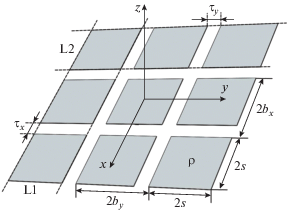
На рис. 1 изображена плоская решетка из предельно тонких резистивных квадратов со стороной $2s$ и поверхностным сопротивлением ${\rho }{\text{.}}$ Полупериоды решетки по осям $х,$ $y$ равны ${{b}_{x}}$ и ${{b}_{y}}.$ Зазоры ${{{\tau }}_{x}},$ ${{{\tau }}_{y}}$ между соседними квадратами в “лентах” ${\text{L}}1$ и ${\text{L}}2$ равны соответственно $2({{b}_{x}} - s)$ и $2({{b}_{y}} - s).$ Окружающее решетку пространство имеет относительную диэлектрическую проницаемость ${\tilde {\varepsilon }}{\text{.}}$ Однородное внешнее электрическое поле, в которое помещена решетка, направлено вдоль оси $y$ и зависит от времени по закону $\exp \left( { - i{\omega }t} \right),$ где ${\omega }$ – циклическая частота, ${{i}^{2}} = - 1.$
При ${{b}_{x}} = s$ решетка, изображенная на рис. 1, переходит в однородную вдоль оси $х$ решетку из лент ${\text{L}}1$ без зазоров между квадратами. Такой ленточной решетке соответствует эффективное поверхностное сопротивление (импеданс) ${{{\tilde {\rho }}}_{{{\text{эф}}}}},$ вычисляемое по формуле [12]
(1)
${{\tilde {\rho }}_{{{\text{эф}}}}} = \frac{{i\pi }}{{\omega {{b}_{y}}{{\varepsilon }_{0}}\left( {{{\varepsilon }_{1}} + {{\varepsilon }_{2}}} \right)\ln \left( {{2 \mathord{\left/ {\vphantom {2 K}} \right. \kern-0em} K}} \right)}},\,\,\,\,K = \sin \frac{{\pi s}}{{2{{b}_{y}}}},$Пусть ${{b}_{x}} \ne s,$ т.е. “лента” ${\text{L}}1$ составлена из квадратов, разделенных зазорами шириной τx = $ = 2\left( {{{b}_{x}} - s} \right).$ Рассматривая решетку как состоящую из “лент” ${\text{L}}2$ с эффективным поверхностным сопротивлением (1), разделенных зазорами шириной ${{{\tau }}_{x}},$ применим аналогично [6, 16] формулу теории цепей:
где ${{\rho }_{{{\text{эф}}}}}$ – эффективное поверхностное сопротивление решетки из прямоугольных ячеек с размерами $2{{b}_{x}},$ $2{{b}_{y}},$ содержащих идеально проводящие квадраты со стороной $2s.$Пусть ячейки квадратные, ${{b}_{x}} = {{b}_{y}} = b.$ Рассматриваемой плоской решетке можно сопоставить предельно тонкий, по сравнению с длиной волны и геометрическими размерами, слой толщиной ${\tau }$ с эффективной диэлектрической проницаемостью ${{\varepsilon }_{{{\text{эф}}}}},$ используя для этого соотношение [17]:
(3)
${{\varepsilon }_{{{\text{эф}}}}} = {i \mathord{\left/ {\vphantom {i {\left( {\omega \tau {{\varepsilon }_{0}}{{\rho }_{{{\text{эф}}}}}} \right)}}} \right. \kern-0em} {\left( {\omega \tau {{\varepsilon }_{0}}{{\rho }_{{{\text{эф}}}}}} \right)}}.$Подставляя (1) и (2) в (3) и полагая ${{b}_{x}} = {{b}_{y}} = b,$ получим для структуры с квадратными ячейками:
(4)
${{\varepsilon }_{{{\text{эф}}}}} = \frac{{s\left( {{{\varepsilon }_{1}} + {{\varepsilon }_{2}}} \right)}}{{\tau \pi }}\ln \frac{2}{K}.$Как следует из (4), при вещественном $\tilde {\varepsilon },$ не зависящем от частоты, сопоставляемый решетке диэлектрический слой является, как и следовало ожидать, недиспергирующим.
Отметим, что приближенный расчет коэффициента отражения (КО) многослойных структур, содержащих решетки, можно проводить методом импедансов с применением формулы (2). Однако при использовании матричного метода более удобна трактовка решеток как предельно тонких слоев с диэлектрической проницаемостью (4).
2. ДИФРАКЦИОННО-КВАЗИСТАТИЧЕСКИЙ И ДИФРАКЦИОННЫЙ РАСЧЕТ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ
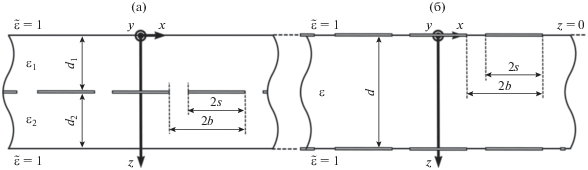
Расчет коэффициента отражения по амплитуде (КО) нормально падающей электромагнитной волны проводился для структур из лент и структур с квадратными ячейками с одной решеткой (рис. 2а) и двумя одинаковыми решетками (рис. 2б), содержащих диэлектрические слои с проницаемостями ${{\varepsilon }_{1}},$ ${{\varepsilon }_{2}},$ $\varepsilon $ и толщинами ${{d}_{1}},$ ${{d}_{2}},$ $d.$ Над структурами и под ними находятся полупространства с диэлектрической проницаемостью $\tilde {\varepsilon } = 1.$ Ленточные структуры бесконечны по оси $y$ и имеют период $P = 2b$ по оси $x.$ Структуры на основе квадратных ячеек имеют период $P = 2b$ как по оси $x,$ так и по оси $y.$ Размер элементов равен $2s.$ В случае ленточных решеток электрический вектор падающей волны нормален оси $y,$ параллельной лентам. Что касается структур с квадратными ячейками, то они поляризационно независимы.
Решение задачи дифракции проводилось методом, примененным в [6–8] к структурам с резистивными проводами, диполями и квадратами, при этом в отличие от [6] поверхностное сопротивление квадратов полагалось равным нулю. Метод заключается в решении задачи возбуждения канала Флоке токами малых элементов, на которые разделяются большие элементы, каковыми в данной работе служат ленты и квадраты. Число разбиений на малые элементы и число учитываемых гармоник канала Флоке выбиралось так, чтобы точность вычисления КО по амплитуде составляла 0.01. Метод можно назвать методом токовых элементов (МТЭ).
Приближенный метод расчета КО, который можно охарактеризовать как дифракционно-квазистатический (ДКМ), основан на замене решеток сплошными слоями-пленками с диэлектрической проницаемостью (4) с последующим вычислением КО от многослойной структуры матричным методом [18]. Как показали расчеты, результат не зависит от толщины ${\tau }$, если выбрать ее на два порядка меньше наименьшего геометрического размера структуры и длины волны.
3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ
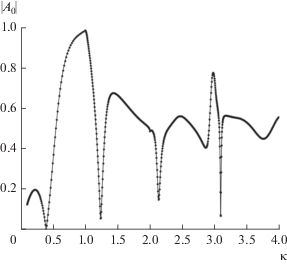
Поскольку метод МТЭ ранее применялся лишь к решеткам с резистивными элементами, была проведена проверка его применимости в случае решеток с идеально проводящими элементами. Для двухслойной ленточной решетки (см. рис. 2) была рассчитана по МТЭ зависимость модуля амплитуды $\left| {{{A}_{0}}} \right|$ основной моды отраженной волны от отношения $\kappa = {P \mathord{\left/ {\vphantom {P {\lambda }}} \right. \kern-0em} {\lambda }},$ где λ – длина волны. Сравнение этой зависимости, изображенной на рис. 3, с аналогичной зависимостью, полученной методом задачи Римана–Гильберта и приведенной в [1, рис. 18 ], показывает их совпадение с такой точностью, о которой можно судить из сравнения графиков.
Рис. 3.
Зависимость амплитуды основной моды отраженной волны от обратной относительной длины волны для двухслойной ленточной решетки при $\varepsilon = 1,$ $d = {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2},$ $s = P{\text{/}}4.$
На рис. 4–8 приведены зависимости КО от отношения длины волны к периоду структуры для ленточных решеток и решеток на основе квадратных элементов, с диэлектрическими слоями и без них, полученные как в приближении ДКМ с использованием формулы (4) (кривые 1, 3), так и из решения задачи дифракции методом МТЭ (кривые 2, 4). Из рисунков видно, что простой, по сравнению с дифракционным подходом, метод ДКМ позволяет приближенно вычислять КО при длинах волн, в два и более раз превосходящих период ленточной решетки и в четыре и более раз превосходящих период решетки на основе квадратных элементов. Абсолютная погрешность вычисления КО при ${\lambda } \to 10P$ приближается к нулю для ленточных структур и составляет приблизительно 0.05 для структур с квадратными элементами. Вблизи резонансных минимумов погрешность вычисления КО возрастает, однако положение резонансных частот определяется с относительной точностью около 5%.
Рис. 4.
Зависимости коэффициента отражения от относительной длины волны для однослойных ленточных решеток, $s = 0.4P,$ при ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 1$ (кривые 1, 2) и при ${{\varepsilon }_{1}} = 2,$ ${{\varepsilon }_{2}} = 1,$ ${{d}_{1}} = {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}$ (кривые 3, 4), полученные методом ДКМ (кривые 1, 3) и методом МТЭ (кривые 2, 4).
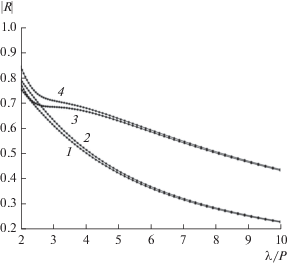
Рис. 5.
Зависимости коэффициента отражения от относительной длины волны однослойной ленточной решетки при $s = 0.4P,$ ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 2,$ ${{d}_{1}} = {{d}_{2}} = P{\text{/}}2$ (кривые 1, 2) и двухслойной ленточной решетки при $s = 0.4P,$ $\varepsilon = 2,$ $d = {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}$ (кривые 3, 4), полученные методом ДКМ (кривые 1, 3) и методом МТЭ (кривые 2, 4).
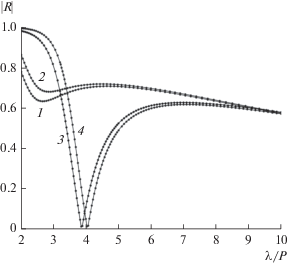
Рис. 6.
Зависимости коэффициента отражения от относительной длины волны однослойных решеток с квадратными ячейками, $s = 0.45P,$ при ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 1$ (кривые 1, 2) и при ${{\varepsilon }_{1}} = 2,$ ${{\varepsilon }_{2}} = 1,$ ${{d}_{1}} = {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}$ (кривые 3, 4), полученные методом ДКМ (кривые 1, 3) и методом МТЭ (кривые 2, 4).
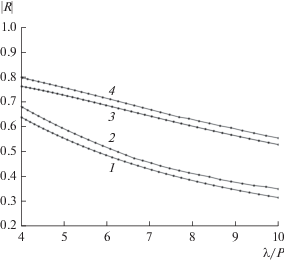
Рис. 7.
Зависимости коэффициента отражения от относительной длины волны однослойной решетки с квадратными ячейками при $s = 0.45P,$ ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 2,$ ${{d}_{1}} = {{d}_{2}} = {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}$ (кривые 1, 2) и двухслойной решетки с квадратными ячейками при $s = 0.45P,$ $\varepsilon = 2,$ $d = {P \mathord{\left/ {\vphantom {P 2}} \right. \kern-0em} 2}$ (кривые 3, 4), полученные методом ДКМ (кривые 1, 3) и методом МТЭ (кривые 2, 4).
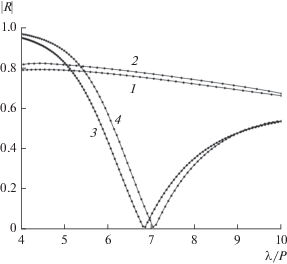
При длинах волн, превосходящих период решеток, канал Флоке является одномодовым волноводом. Поскольку идеальные решетки не поглощают энергию электромагнитного поля, в одномодовом канале Флоке коэффициент прохождения по амплитуде выражается через КО из условия равенства суммы квадратов этих коэффициентов единице. Таким образом, приведенные на рис. 5–8 значения КО по амплитуде могут быть пересчитаны в значения коэффициента прохождения.
4. СРАВНЕНИЕ С ИЗВЕСТНЫМИ РЕЗУЛЬТАТАМИ
В [11] получены в квазистатическом приближении индуктивные поправки ${{L}_{x}}$ и ${{L}_{y}}$ к емкостному импедансу (1):
Точность формулы (5) проверена путем сравнения с дифракционным расчетом при малых значениях отношения ширины зазоров между квадратами к периоду, ${{(b - s)} \mathord{\left/ {\vphantom {{(b - s)} b}} \right. \kern-0em} b} \leqslant 0.05.$ Показано, что учет поправок ${{L}_{x}},$ ${{L}_{y}}$ позволяет повысить точность квазистатического приближения, а также что применение вместо (5) формулы
позволяет улучшить точность. Уменьшение вдвое индуктивной части импеданса, некорректно трактуемое как усреднение, в [11] не обосновано. Поэтому число “2” в знаменателе формулы (6) следует рассматривать как подгоночный параметр, применимость которого показана лишь при весьма малых зазорах между квадратами и лишь в случае, когда решетка лежит между полупространствами с диэлектрическими проницаемостями ${{\varepsilon }_{1}} = 1$ и ${{\varepsilon }_{2}} = 2.$ В связи с этим расчеты с применением формулы (4) сравниваются ниже с результатами применения формулы (5), не содержащей подгоночного параметра.
Сравнительные расчеты КО по амплитуде проводились для двух решеток, период которых, как и в [11], $2b = 3$ мм и которые расположены на границе полупространств с проницаемостями ${{\varepsilon }_{1}} = 1$ и ${{\varepsilon }_{2}} = 2.$ Результаты расчетов КО на разных частотах приведены в табл. 1. Из таблицы видно, что точность расчета КО с применением формулы (4) и формулы (5) в среднем близка.
Таблица 1.
Значения КО по амплитуде на разных частотах для решеток с квадратными ячейками с периодом 3 мм
| Частота, ГГц |
Для стороны квадрата | |||||||
|---|---|---|---|---|---|---|---|---|
| $2s = 2.85$ мм | $2s = 2.7$ мм | |||||||
| Д | Б | А | П | Д | Б | А | П | |
| 1 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 |
| 10 | 0.62 | 0.56 | 0.54 | 0.59 | 0.45 | 0.45 | 0.41 | 0.46 |
| 20 | 0.81 | 0.82 | 0.78 | 0.81 | 0.69 | 0.72 | 0.65 | 0.70 |
| 30 | 0.90 | 0.93 | 0.88 | 0.90 | 0.83 | 0.87 | 0.79 | 0.83 |
| 40 | 0.95 | 0.97 | 0.93 | 0.94 | 0.91 | 0.95 | 0.86 | 0.89 |
| 50 | 0.97 | 0.99 | 0.95 | 0.96 | 0.94 | 0.98 | 0.90 | 0.92 |
Примечание. Введены следующие сокращения: Д – значения, полученные из решения задачи дифракции; Б – значения, вычисленные с применением формулы (5), в которую подставлялись полученные в [11] выражения для компонент импеданса ${{L}_{x}},$ ${{L}_{y}};$ A – значения, вычисленные с применением формулы (4); П – результаты расчетов при $p = 0.87.$
Для перехода от ленточной решетки к решетке из квадратов можно вместо умножения импеданса (1) на отношение ${b \mathord{\left/ {\vphantom {b s}} \right. \kern-0em} s}$ умножить его на величину $p({b \mathord{\left/ {\vphantom {b s}} \right. \kern-0em} s}),$ где $p$ – подгоночный параметр, близкий к единице. Величину $p({b \mathord{\left/ {\vphantom {b s}} \right. \kern-0em} s})$ при $p \ne 1$ можно назвать эффективным отношением периода к размеру квадратов. Результаты расчетов при $p = 0.87$ также приведены в табл. 1. Видно, что введение подгоночного параметра существенно повысило точность вычислений. Однако, по нашему мнению, введение подгоночного параметра целесообразно лишь в случае, если этот параметр достаточно универсален, чего нельзя сказать как о параметре $p,$ так и о примененном в [11] уменьшении вдвое индуктивной компоненты импеданса. В связи с этим представленные в разд. 3 расчеты проводились без использования подгоночного параметра. Отметим, что для параметра $p,$ по-видимому, возможно построить на основе достаточно большого числа дифракционных расчетов аппроксимационную формулу, аналогичную полученным для некоторых решеток в [5]. Это позволило бы применять подгоночный параметр при расчете решеток с разными размерами квадратов и зазоров между ними, а также с разными значениями диэлектрической проницаемости сред, окружающих решетки.
ЗАКЛЮЧЕНИЕ
На основе сравнения с методом задачи Римана–Гильберта показана применимость к расчету идеальных решеток метода токовых элементов, ранее применявшегося для анализа резистивных решеток.
Плоской решетке с прямоугольными ячейками, содержащей квадратные идеально проводящие элементы, сопоставлен предельно тонкий однородный слой и получено в квазистатическом приближении выражение для его эффективной диэлектрической проницаемости. Проведено сравнение результатов расчетов с известными, относящимися к малым зазорам между квадратными проводниками, и показано, что поправка к емкостному импедансу ленточной решетки в виде множителя, соответствующего теории цепей, обеспечивает практически такую же точность расчета отражения от решетки из квадратов, что и введение индуктивных поправок к импедансу.
На основе сравнения расчетов КО дифракционным методом с расчетами дифракционно-квазистатическим методом показана степень точности последнего для структур с ленточными и квадратными элементами, содержащих слои диэлектрика.
Список литературы
Шестопалов В.П., Литвиенко Л.Н., Масалов С.А., Сологуб В.Г. Дифракция волн на решетках. Харьков: Изд-во Харьков. ун-та, 1973.
Казьмин И.А. Дифракция электромагнитных волн на планарных мультирезонансных частотно-селективных поверхностях с элементами канонической формы. Автореферат дис. … канд. физ.-мат. наук. Ростов-на-Дону, 2008. 20 с.
Dickie R., Cahill R., Gamble H.S. et al. // Proc IEE Microwaves Antennas and Propagation. 2004. V. 151. № 1. P. 31.
Lerer A.M., Zelenchuk D.E., Makhno V.V. et al. // Proc. 1st Int. Congr. on Advanced Electromagnetic Matenals in Microwaves and Optics “Metamaterials–2007”. Rome, 2007. P. 750.
Бaнкoв C.E. // PЭ. 2018. T. 63. № 4. C. 301.
Пономаренко В.И., Лагунов И.М. // РЭ. 2019. Т. 64. № 5. С. 440.
Пономаренко В.И., Лагунов И.М. Композиционные материалы: разработка и применение. Новосибирск: Изд. АНС “СибАК”, 2017. С. 112.
Пономаренко В.И., Лагунов И.М. // РЭ. 2017. Т. 62. № 7. С. 657.
Sadiku Matthew N.O. Numerical Techniques in Electromagnetics. L.: CRC Press LLC, 2001.
Нефедов Е.И., Сивов А.Н. Электродинамика периодических структур. М.: Наука, 1977.
Беляев Б.А., Тюрнев В.В., Волков Н.В. // РЭ. 2019. Т. 64. № 7. С. 666.
Al-Joumayly M.A., Behdad N. // IEEE Trans. 2010. V. AP-58. № 12. P. 4030.
Пономаренко В.И. // Изв. вузов. Электромеханика. 1982. № 5. С. 518.
Пономаренко В.И., Мировицкий Д.И., Будагян И.Ф. // Радиотехника. 1984. Т. 39. № 11. С. 68.
Пономаренко В.И., Журавлев С.И. // РЭ. 1992. Т. 37. № 5. С. 812.
Казанцев Ю.Н., Бабаян В.А., Казанцева Н.Е. и др. // РЭ. 2013. Т. 58. № 3. С. 264.
Слуцкая В.В. Тонкие пленки в технике СВЧ. М.: Госэнергоиздат, 1962.
Борн М., Вольф Э. Основы оптики. М.: Мир, 1970.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника