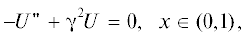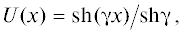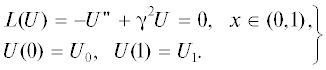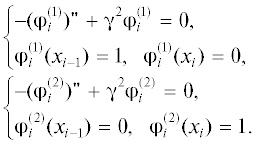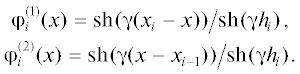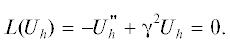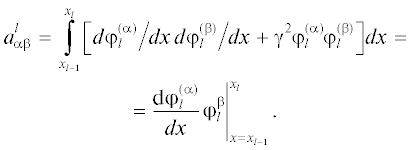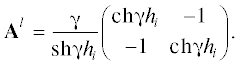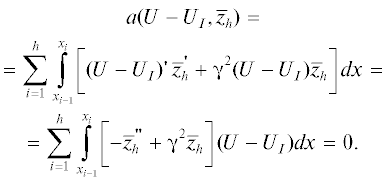Радиотехника и электроника, 2020, T. 65, № 12, стр. 1198-1205

Метод конечных распределенных элементов для анализа фрактальных элементов на основе многослойных резистивно-емкостных сред

А. Х. Гильмутдинов^a, b, *, Р. З. Даутов^c, П. А. Ушаков^d

^a Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ (КНИТУ-КАИ)
420111 Казань, ул. К. Маркса, 10, Российская Федерация

^b Научно-производственное объединение “Радиоэлектроника” им. В.И. Шимко
420029 Казань, ул. Журналистов, 50, Российская Федерация

^c Казанский (Приволжский) федеральный университет
420008 Казань, ул. Кремлевская, 18, Российская Федерация

^d Ижевский государственный технический университет им. М.Т. Калашникова
426069 Ижевск, ул. Студенческая, 7, Российская Федерация

^* E-mail: agilmutdinov@rambler.ru

Поступила в редакцию 15.01.2020
После доработки 15.01.2020
Принята к публикации 31.03.2020

DOI: 10.31857/S0033849420120062

Полный текст (PDF)

Аннотация

Показано, что анализ фрактальных элементов, реализованных на основе неоднородной многослойной резистивно-емкостной среды, с помощью классического метода конечных элементов (МКЭ) дает неудовлетворительные результаты для нормированных частот ωRC > 10. Предложена гибридная вычислительная схема МКЭ на основе L-сплайнов в качестве конечных элементов (КЭ), которые на каждом КЭ являются решением дифференциального уравнения однородной RC-линии. Предложено одномерные и двумерные КЭ различной формы (трех-, четырех-, и т.д. угольные) заменить соответствующей физической схемой замещения, где сторонами многоугольного КЭ являются отрезки однородной RC-линии, названного нами одномерным однородным RC-элементом с распределенными параметрами (ОО RC-ЭРП). Таким образом, задача определения характеристик и параметров исследуемого фрактального элемента заменяется задачей определения импеданса полученной электрической схемы замещения на основе ОО RC-ЭРП. Такой метод анализа был назван нами методом конечных распределенных элементов.

ВВЕДЕНИЕ

Известно, что на основе многослойной резистивно-емкостной среды можно создавать пассивные электронные элементы, импеданс которых ${{\dot {Z}}_{F}}$ зависит от частоты в дробной степени:

${{\dot {Z}}_{F}} = \frac{1}{{{{{(j\omega )}}^{\alpha }}F}},$

где 0 ≤ |α| ≤ 1, ω − круговая частота, F − некоторая вещественная постоянная. Такой импеданс получил название фрактальный импеданс, а элементы, характеризующиеся фрактальным импедансом, – фрактальными элементами (ФЭ) [1–3].

В работах [1, 2] показано, что изменять дробно-степенную зависимость импеданса от частоты можно за счет использования статических и/или динамических неоднородностей в резистивных или диэлектрических слоях: заданием законов изменения толщины и геометрических размеров конфигурации слоев; изменением количества, местоположения контактов и их формы; вводя вырезы различной формы в слои, а также заданием определенных электрофизических свойств материалов слоев и законов их изменения.

Очевидно, что для создания ФЭ на данной основе необходимо в первую очередь разработать методы анализа многослойных, в общем случае неоднородных, резистивно-емкостных элементов с распределенными параметрами (RC-ЭРП), что и является целью данной работы.

1. МЕТОДЫ АНАЛИЗА ОДНОМЕРНЫХ НЕОДНОРОДНЫХ РЕЗИСТИВНО-ЕМКОСТНЫХ ЭЛЕМЕНТОВ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

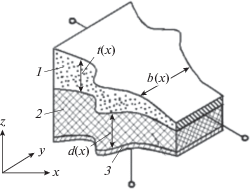
Рассмотрим достаточно простой случай элемента, который образован последовательным формированием пленок (в частном случае, слоев): проводящего (слой с нулевым сопротивлением – слой 0), диэлектрического (слой С) и резистивного (слой R). Пусть ширина формируемых слоев b будет одинакова и зависит от координаты по длине слоев х по произвольному закону b(x). Толщины диэлектрического и резистивного слоев также зависят от х по законам соответственно d(x) и t(x). Поскольку распределение потенциала в резистивном слое будет зависеть только от одной координаты, то такой элемент в дальнейшем будем называть “одномерный неоднородный резистивно-емкостный элемент с распределенными параметрами со структурой слоев вида R-C-0” (ОН R-C-0 ЭРП). Общий вид конструкции ОН R-С-0 ЭРП представлен на рис. 1.

Рис. 1.

Конструкция ОН R-С-0 ЭРП: 1 – резистивный слой, 2 – диэлектрик, 3 – идеальный проводник.

В работе [1] показано, что уравнение для распределения потенциала U в его резистивном слое будет иметь вид

(1)

$\begin{gathered} \frac{{{{\partial }^{2}}U(x,p)}}{{\partial {{x}^{2}}}} - \frac{1}{{{{r}_{п}}(x)}}\frac{{d{{r}_{п}}(x)}}{{dx}}\frac{{\partial U(x,p)}}{{\partial x}} = \\ = p{{r}_{п}}(x){{c}_{п}}(x)U(x,p), \\ \end{gathered} $

где с_п(х) и r_п(х) – соответственно погонная емкость и погонное сопротивление ОН R-С-0 ЭРП; р – комплексная частота.

В таком общем виде уравнение (1) из-за сложности зависимости погонных параметров RС-ЭРП от координаты х не имеет решения в замкнутой форме. Очевидно, что с той или иной степенью приближения задачу можно решить численными методами. В настоящее время для решения подобного рода задач широко используют метод конечных элементов (МКЭ).

1.1. Конечно-элементная постановка задачи (классическая схема)

Рассмотрим ОН R-C-0-ЭРП в случае постоянной зависимости его погонных параметров от координаты х. При этом

(2)

${{r}_{{\text{п}}}}(x){{c}_{{\text{п}}}}(x) = {\text{const}}{\text{.}}$

Уравнение (1) в этом случае запишем в виде

(3)

где γ² = jωRC. Учитывая, что конечной целью анализа является определение первичных у-параметров элемента как четырехполюсника, для примера рассмотрим следующие краевые условия для уравнения (3):

(4)

$U(0) = 0,\,\,\,\,U(1) = 1.$

Решением задачи (3), (4) является функция

а интересующие нас у-параметры равны y₂₁ = $ = - U{\kern 1pt} '(0),\,\,\,\,{{y}_{{22}}} = U{\kern 1pt} '(1).$

Приближенное решение задачи (3), (4) классическим методом конечных элементов отыскивается в виде

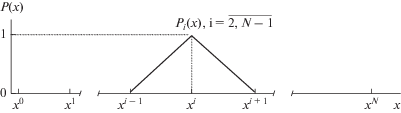
$\tilde {U}(x) = \sum\limits_{i = 2}^{N - 1} {{{{\dot {U}}}_{i}}{{P}_{i}}(x) + {{P}_{N}}(x)} ,$

где P_i(x) – базисные функции, графическое представление которых показано на рис. 2 в предположении, что сетка по оси х равномерная, т.е. xⁱ = $ = (i - 1)h,$ $h = {1 \mathord{\left/ {\vphantom {1 {(N - 1)}}} \right. \kern-0em} {(N - 1)}}$, где h – длина конечного элемента (КЭ).

Рис. 2.

Графическое представление базисных функций.

Узловые потенциалы ${{U}_{i}}$ находятся из решения системы уравнений

$a\left( {\tilde {U},{{P}_{i}}} \right) \equiv \int\limits_0^1 {\left( {\tilde {U}{\kern 1pt} 'P_{i}^{'} + {{\gamma }^{2}}\tilde {U}{{P}_{i}}} \right)} dx = 0,\,\,\,\,i = \overline {2,N - 1} ,$

которая равносильна следующей системе алгебраических уравнений:

(5)

$\left\{ \begin{gathered} - {{U}_{{i - 1}}} + 2{{U}_{i}} - {{U}_{{i + 1}}} + \frac{{{{h}^{2}}{{{\gamma }}^{2}}}}{6}({{U}_{{i - 1}}} + 4{{U}_{i}} + {{U}_{{i + 1}}}) = 0, \hfill \\ i = \overline {2,N - 1} \hfill \\ {{U}_{1}} = 0,\,\,\,\,{{U}_{N}} = 1. \hfill \\ \end{gathered} \right.$

Найдя решение системы (5) получаем искомые значения у-параметров ${{\tilde {y}}_{{2i}}}$:

${{\tilde {y}}_{{21}}} = a(\tilde {U},{{P}_{1}}) = \frac{{{{U}_{1}} - {{U}_{2}}}}{h} + \frac{{{{{\gamma }}^{2}}h}}{6}({{U}_{2}} + 2{{U}_{1}}),$

${{\tilde {y}}_{{22}}} = a(\tilde {U},{{P}_{N}}) = \frac{{{{U}_{N}} - {{U}_{{N - 1}}}}}{h} + \frac{{{{{\gamma }}^{2}}h}}{6}(2{{U}_{N}} + {{U}_{{N - 1}}}),$

представленные в табл. 1.

Таблица 1.

у-Параметры ОО R-С-0 ЭРП, полученные методом конечных элементов в диапазоне частот ω_н = ωRC от 1 до 100 для различных шагов сетки

ω_н	h	${{{{y}_{{21}}}} \mathord{\left/ {\vphantom {{{{y}_{{21}}}} {{{{\tilde {y}}}_{{21}}}}}} \right. \kern-0em} {{{{\tilde {y}}}_{{21}}}}}$		${{{{y}_{{22}}}} \mathord{\left/ {\vphantom {{{{y}_{{22}}}} {{{{\tilde {y}}}_{{22}}}}}} \right. \kern-0em} {{{{\tilde {y}}}_{{22}}}}}$
ω_н	h	Re	Im	Re	Im
1	0	–0.980763	0.164638	1.022013	0.331238
	1/15	–0.980832	0.164654	1.021874	0.331256
	1/30	–0.980778	0.164641	1.021983	0.331242
10	0	–0.088180	0.668284	2.174056	2.272742
	1/15	–0.086953	0.671765	2.168975	2.278306
	1/30	–0.087910	0.669042	2.172950	2.273952
50	0	0.045499	–0.083721	4.999372	4.999866
	1/15	0.044399	–0.090324	4.946428	5.053342
	1/30	0.045252	–0.085121	4.987794	5.011464
100	0	–0.016986	0.000042	7.071058	7.071078
	1/15	–0.019762	0.002432	6.922388	7.222934
	1/30	–0.017551	0.000530	7.038418	7.103868

Примечание. Для каждого ω_н в первой cтроке (h = 0) приведены точные значения, соответствующие y_2i, во второй − значения ${{\tilde {y}}_{{2i}}}$ при h = 1/15, в третьей – при h = 1/30.

Как видно из таблицы, МКЭ очень чувствителен к значению ω_н. При больших значениях ω_н (ω_н>10) результаты вычислений явно неудовлетворительны. Особенно большую погрешность имеет Im(y₂₁).

Итак, рассмотрение модельной задачи (3), (4) показывает, что метод конечных элементов, основанный на линейных функциях на конечном элементе, дает хороший результат лишь при ω_н ≤ 1 и не может обеспечивать требуемой точности при больших значениях ω_н. Объяснить это можно тем, что при ω_н$ \gg $ 1 решение искомой задачи имеет сложный вид: φ колеблется примерно как $\sin \sqrt {\omega } {{x}_{1}}$ и имеет пограничный слой при x₁= 1 шириной порядка ${1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\omega }}_{{\text{н}}}}} }}} \right. \kern-0em} {\sqrt {{{{\omega }}_{{\text{н}}}}} }}$.

Функции U(x) плохо приближаются линейными функциями при небольшом числе КЭ. Для повышения точности решения рассматриваемой задачи необходимо уменьшать размеры КЭ в пограничном слое шириной ${1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\omega }}_{{\text{н}}}}} }}} \right. \kern-0em} {\sqrt {{{{\omega }}_{{\text{н}}}}} }}$, поэтому размеры КЭ вблизи границ контактных площадок должны быть $h \ll {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\omega }}_{{\text{н}}}}} }}} \right. \kern-0em} {\sqrt {{{{\omega }}_{{\text{н}}}}} }}$.

1.2. Гибридная схема

Поскольку классическая схема МКЭ, основанная на линейных функциях, мало пригодна для анализа RC-ЭРП даже с простейшей структурой слоев вида R-С-0 на частотах ω_н>10, то построим схему, которая лишена этого недостатка.

При построении расчетной схемы методом конечных элементов в качестве базисных функций будем использовать не полиномиальные сплайны, а так называемые L-сплайны. В связи с этим рассмотрим следующую задачу: найти такую конечно-элементную функцию U_h, которая является решением задачи

(6)

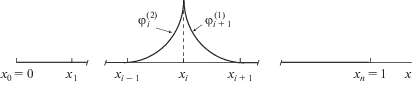
Для определения U_h разобьем нормированную длину ОН R-С-0 ЭРП, т.е. отрезок (0, 1), на конечные элементы так, как показано на рис. 3. Отрезки [x_i _{– 1}, x_i] являются конечными элементами, где $i = \overline {1,n} .$ Их длины обозначим через h_i. Нa каждом КЭ [x_i _{– 1}, x_i] введем две функции, $\varphi _{i}^{{(1)}},\varphi _{i}^{{(2)}}$, как решения следующих задач::

(7)

Рис. 3.

Функция φ_i(x) для конечного элемента.

Нетрудно видеть, что решения системы уравнений (7) соответственно имеют вид

(8а)

Определим функции $\left\{ {{{\varphi }_{i}}(x)} \right\}_{{i = 1}}^{{n - 1}}$ в соответствии с рис. 3:

(8б)

${{{\varphi }}_{i}}(x) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\varphi }_{i}^{{(2)}}(x),}&{x \in \left[ {{{x}_{{i - 1}}},{{x}_{i}}} \right],} \end{array}} \\ {\begin{array}{*{20}{c}} {{\varphi }_{i}^{{(1)}}(x),}&{x \in \left[ {{{x}_{i}},{{x}_{{i + 1}}}} \right],} \end{array}} \\ {\begin{array}{*{20}{c}} {0,}&{{\text{иначе}}{\text{.}}} \end{array}} \end{array}} \right.$

Для начального $\left[ {{{x}_{0}},{{x}_{1}}} \right]$ и последнего $\left[ {{{x}_{{n - 1}}},{{x}_{n}}} \right]$ КЭ потребуем:

$\begin{gathered} {{{\varphi }}_{0}}(x) = \left\{ \begin{gathered} {\varphi }_{1}^{{(1)}}(x),\,\,\,\,x \in \left[ {{{x}_{0}},{{x}_{1}}} \right], \hfill \\ 0,\,\,\,\,x \notin \left[ {{{x}_{0}},{{x}_{1}}} \right], \hfill \\ \end{gathered} \right. \hfill \\ {{{\varphi }}_{n}}(x) = \left\{ \begin{gathered} {\varphi }_{n}^{{(2)}}(x),\,\,\,\,x \in \left[ {{{x}_{{n - 1}}},{{x}_{n}}} \right], \hfill \\ 0,\,\,\,\,x \notin \left[ {{{x}_{{n - 1}}},{{x}_{n}}} \right]. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $

Функцию U_h(x) определим следующим образом:

(9)

${{U}_{h}}(x) = \sum\limits_{i = 0}^n {{{c}_{i}}{{{\varphi }}_{i}}(x)} ,$

где c_i − комплексные числа, $i = \overline {1,n - 1} $, c₀ = U₀, c_n = = U₁. Функция U_h(x) вида (9) называется $L$-сплайном. Очевидно, U_h(x) − непрерывная на (0, 1) функция, c_i = U_h(x_i). Кроме того, на каждом конечном элементе U_h(x) удовлетворяет уравнению

(10)

Для определения коэффициентов c_i воспользуемся методом Галеркина [5]. Обозначим через ${{H}_{0}}$ множество $L$-сплайнов ${{\vartheta }_{h}}$, удовлетворяющих условию

${{\vartheta }_{h}}(0) = {{\vartheta }_{h}}(1) = 0.$

Сплайн ${{U}_{h}}$ определим из тождества:

(11)

$a({{U}_{h}},{{\vartheta }_{h}}) = 0\,\,\,\,{\text{для любых}}~\,\,\,\,{{\vartheta }_{h}} \in {{H}_{0}}.$

Как видим, отличие от стандартного метода конечных элементов заключается лишь в том, что вместо кусочно-линейных сплайнов и соответствующих базисных функций используются L-сплайны и базисные функции, построенные выше.

Для определения коэффициентов сплайна U_h(x) стандартно, как это принято в МКЭ, получается система алгебраических уравнений Ac = F. Матрица A собирается из локальных матриц проводимости конечных элементов ${{{\mathbf{A}}}^{l}} = \left\{ {a_{{\alpha \beta }}^{l}} \right\}_{{\alpha ,\beta = 1}}^{2}$, с элементами

(12)

Подставляя сюда выражение (8а), можно записать окончательно матрицу проводимости для l-го конечного элемента в следующем виде:

(13)

Обозначим H_i = γh_i, a_i = (H_i/shH_i)/h_i и проведем сборку матриц проводимости конечных элементов. Получим систему алгебраических уравнений МКЭ в следующем виде:

$\left\{ \begin{gathered} - {{a}_{i}}{{c}_{{i - 1}}} + \left( {{{a}_{i}}{\text{ch}}{{H}_{i}} + {{a}_{{i + 1}}}{\text{ch}}{{H}_{i}}} \right){{c}_{i}} - {{a}_{{i + 1}}}{{c}_{{i + 1}}} = 0, \hfill \\ i = \overline {1,n - 1} , \hfill \\ {{c}_{0}} = {{U}_{0}},\,\,\,\,{{c}_{n}} = {{U}_{1}}. \hfill \\ \end{gathered} \right.$

или

(14)

$\left\{ \begin{gathered} {{a}_{i}}({{c}_{i}} - {{c}_{{i - 1}}}) - {{a}_{{i + 1}}}({{c}_{{i + 1}}} - {{c}_{i}}) + \hfill \\ + \,\,\left[ {{{a}_{i}}({\text{ch}}{{H}_{i}} - 1) + {{a}_{{i + 1}}}({\text{ch}}{{H}_{{i + 1}}} - 1)} \right]{{c}_{i}} = 0, \hfill \\ i = \overline {1,n - 1,} \hfill \\ {{c}_{0}} = {{U}_{0}},\,\,\,\,{{c}_{n}} = {{U}_{1}}. \hfill \\ \end{gathered} \right.$

Поскольку

$\begin{gathered} {{a}_{i}}({\text{ch}}{{H}_{i}} - 1) = 2{{a}_{i}}{\text{s}}{{{\text{h}}}^{2}}\frac{{{{H}_{i}}}}{2} = \frac{{{\gamma s}{{{\text{h}}}^{2}}\frac{{{{H}_{i}}}}{2}}}{{{\text{sh}}\frac{{{{H}_{i}}}}{2}{\text{ch}}\frac{{{{H}_{i}}}}{2}}} = \\ = {\gamma th}\frac{{{{H}_{i}}}}{2} = {{{\gamma }}^{2}}\left( {{\text{th}}\frac{{{{H}_{i}}}}{2}} \right)\frac{{{{h}_{i}}}}{{{{H}_{i}}}}, \\ \end{gathered} $

то, определяя

${{\hbar }_{i}} = \left( {{\text{th}}\frac{{{{H}_{i}}}}{2}} \right)\frac{{{{h}_{i}}}}{{{{H}_{i}}}} + \left( {{\text{th}}\frac{{{{H}_{{i + 1}}}}}{2}} \right)\frac{{{{h}_{{i + 1}}}}}{{{{H}_{{i + 1}}}}},$

представим систему (14) в следующем виде:

(15)

$\left\{ \begin{gathered} - {{\left( {D_{x}^{2}c} \right)}_{i}} + {{{\gamma }}^{2}}{{c}_{i}} = 0,\,\,\,\,i = \overline {1,n - 1} , \hfill \\ {{c}_{0}} = {{U}_{0}},\,\,\,\,{{c}_{n}} = {{U}_{1}}, \hfill \\ \end{gathered} \right.$

где

(16)

${{\left( {D_{x}^{2}c} \right)}_{i}} = \frac{1}{{{{\hbar }_{i}}}}\left[ {\frac{{{{H}_{{i + 1}}}}}{{{\text{sh}}{{H}_{{i + 1}}}}}\frac{{({{c}_{{i + 1}}} - {{c}_{i}})}}{{{{h}_{{i + 1}}}}} - \frac{{{{H}_{i}}}}{{{\text{sh}}{{H}_{i}}}}\frac{{({{c}_{i}} - {{c}_{{i - 1}}})}}{{{{h}_{i}}}}} \right].$

Сравнивая (15) с дифференциальным уравнением (6) видим, что $D_{x}^{2}$ может рассматриваться как сеточная аппроксимация второй производной, где оператор $D_{x}^{2}$ определен выражением (16).

Оператор $D_{x}^{2}$ имеет простой и ясный вид в случае равномерной сетки, т.е. когда ${{h}_{i}} = h,$ где $i = \overline {1,n} $. В этом случае имеем

${{\left( {D_{x}^{2}c} \right)}_{i}} = - \delta \frac{{{{c}_{{i - 1}}} - 2{{c}_{i}} + {{c}_{{i + 1}}}}}{{{{h}^{2}}}},$

где $\delta = {{\left( {{H \mathord{\left/ {\vphantom {H {{\text{sh}}H}}} \right. \kern-0em} {{\text{sh}}H}}} \right)}^{2}},$ $H = {{{\gamma }h} \mathord{\left/ {\vphantom {{{\gamma }h} 2}} \right. \kern-0em} 2}$, а система уравнений (14) записывается в виде

(17)

$\left\{ \begin{gathered} - \delta \frac{{{{c}_{{i - 1}}} - 2{{c}_{i}} + {{c}_{{i + 1}}}}}{{{{h}^{2}}}} + {{{\gamma }}^{2}}{{c}_{i}} = 0,\,\,\,\,i = \overline {1,n - 1,} \hfill \\ {{c}_{0}} = {{U}_{0}},\,\,\,\,{{c}_{n}} = {{U}_{1}}. \hfill \\ \end{gathered} \right.$

Найдя решение системы (17), вычисляем первичные параметры по формулам ${{\tilde {y}}_{{21}}} = - U_{h}^{'}(0),$ ${{\tilde {y}}_{{22}}} = - U_{h}^{'}(1)$. Расчеты показывают, что для этой схемы, названной нами “гибридной”, с ростом ω_н точность вычисляемых у-параметров ОН R-С-0 ЭРП не ухудшается, как в случае использования линейных функций. Более того, рассчитанные у-параметры совпадают с у-параметрами, вычисленными по аналитическим выражениям. Поэтому гибридная схема стала основой для разработки метода конечных распределенных элементов (МКРЭ).

Отмеченный выше факт легко понять, если рассмотреть лишь один конечный элемент. В этом случае ясно, что сплайн U_h является решением задачи (6). Докажем, что это верно и при произвольном числе конечных элементов. Для этого достаточно убедиться в том, что схема (16) является точной для задачи (6) в том смысле, что после решения системы алгебраических уравнений мы получаем вектор c = (U₀, c1, …, c_n _{– 1}, U₁) такой, что c_i = U(x_i), где U − аналитическое решение задачи (6).

Докажем это. Обозначим через z_k функцию погрешности:

${{z}_{h}} = \sum\limits_{i = 0}^n {\left[ {{{c}_{i}} - U({{x}_{i}})} \right]{{{\varphi }}_{i}}(x)} \equiv {{U}_{h}} - {{U}_{I}},$

где

${{U}_{h}} = {{U}_{h}}(x) = \sum\limits_{i = 0}^n {{{c}_{i}}{{{\varphi }}_{i}}(x)} ,\,\,\,\,{{U}_{I}} = \sum\limits_{i = 0}^n {U({{x}_{i}}){{{\varphi }}_{i}}(x).} $

Через ${{\bar {z}}_{h}}$ обозначим сопряженную к ${{z}_{h}}$ функцию. На каждом элементе в соответствии с (10) имеем 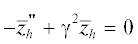. Поэтому

(18)

Учитывая, что по определению $a({{U}_{h}},{{\bar {z}}_{h}}) = 0,$ $a(U,{{\bar {z}}_{h}}),$ получим

(19)

$\begin{gathered} a({{z}_{h}},{{{\bar {z}}}_{h}}) = a({{U}_{h}} - {{U}_{I}},{{{\bar {z}}}_{h}}) = a({{U}_{h}},{{{\bar {z}}}_{h}}) - a({{U}_{I}},{{{\bar {z}}}_{h}}) = \\ = a(U,{{{\bar {z}}}_{h}}) - a({{U}_{I}},{{{\bar {z}}}_{h}}) = a(U - {{U}_{I}},{{{\bar {z}}}_{h}}) = 0. \\ \end{gathered} $

Поскольку из равенства

$a({{z}_{h}},{{\bar {z}}_{h}}) = \int\limits_0^1 {\left( {{{{\left| {z_{h}^{'}} \right|}}^{2}} + {{{\gamma }}^{2}}{{{\left| {{{z}_{h}}} \right|}}^{2}}} \right)dx = 0} $

следует, что z_h ≡ 0, то c_i = U(x_i), т.е. утверждение доказано.

1.3. Метод конечных распределенных элементов

Анализируя выражение для матрицы проводимости для l-го конечного элемента (13), можно заметить, что оно полностью совпадает с соответствующим выражением для отрезка однородной RC-линии со структурой слоев вида R-C-0 [1], который мы назвали одномерным однородным R-C-0-ЭРП.

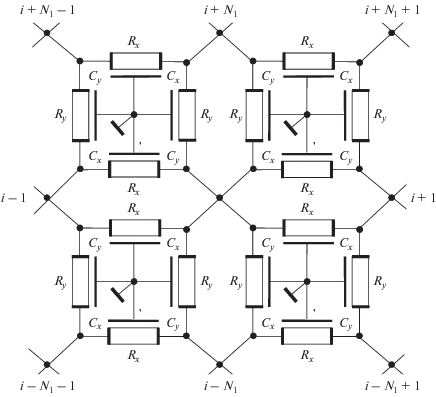
Таким образом, конечный элемент “гибридной” схемы МКЭ может быть представлен в виде ее электрического аналога – ОО R-C-0-ЭРП, который назовем ОО конечным распределенным элементом (ОО КРЭ) со структурой слоев вида R-C-0. Тогда модель ОН R-C-0-ЭРП (см. рис. 1) на основе метода конечных распределенных элементов (МКРЭ) может быть представлена схемой замещения в виде каскадного соединения ОО КРЭ (рис. 4).

Рис. 4.

Иллюстрация метода конечных распределенных элементов: а – ОН R-C-0 ЭРП, разбитый на КЭ; б – схема замещения ОН R-C-0-ЭРП на основе МКРЭ; 1 – резистивный слой, 2 – диэлектрик, 3 – идеальный проводник.

В данном случае при анализе конструкции ОН RC-ЭРП, представленной на рис. 4, схема замещения i-го КРЭ – ОО R_i-C_i-0 ЭРП (рис. 4б) имеет следующую Y-матрицу:

(20)

${{[{{Y}_{i}}]}_{{R - C{\text{ - 0}}}}} = \frac{{{{\theta }_{i}}}}{{{{R}_{i}}sh{{\theta }_{i}}}}\left( {\begin{array}{*{20}{c}} {ch{{\theta }_{i}}}&{ - 1} \\ { - 1}&{ch{{\theta }_{i}}} \end{array}} \right),$

где ${{\theta }_{i}} = \sqrt {j{\omega }{{R}_{i}}{{C}_{i}}} $ − постоянная распространения i-го КРЭ, R_i, C_i – соответственно полное сопротивление и полная емкость i-го КРЭ.

В более общем случае в качестве КРЭ могут быть использованы и ОН RC-ЭРП с соответствующей структурой слоев, для которых имеются точные аналитические решения. Как видно, МКРЭ позволяет перевести задачу анализа конструкций RC-ЭРП (см. рис. 1) из области численных методов в область теории цепей (см. рис. 4б), которая отличается большей наглядностью.

В случае более сложной структуры слоев резистивно-емкостной среды для анализа конкретной конструкции RC-ЭРП необходимо разбить эту конструкцию на n КЭ, представить каждый КЭ соответствующим ему КРЭ, определить аналитически или численно параметры соответствующих многополюсников и применить МКРЭ.

Использование для решения этого класса задач классических методов решения уравнений в частных производных в известной нам литературе не встречалось.

2. АНАЛИЗ ДВУМЕРНЫХ ОДНОРОДНЫХ RC-ЭРП МЕТОДОМ КОНЕЧНЫХ РАСПРЕДЕЛЕННЫХ ЭЛЕМЕНТОВ

Рассмотрим приближенное решение двумерной задачи на основе гибридной схемы применительно к трехслойному двумерному однородному (ДО) R-C-0 ЭРП, в котором потенциал в резистивном слое является функцией двух координат на плоскости. Уравнение распределения потенциала в его резистивном слое в установившемся режиме имеет вид [1]

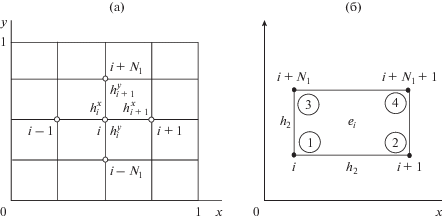
$\begin{array}{*{20}{c}} { - \frac{{{{\partial }^{2}}{\dot {\varphi }}}}{{\partial {{x}^{2}}}} - {{T}^{2}}\frac{{{{\partial }^{2}}{\dot {\varphi }}}}{{\partial {{y}^{2}}}} + {{{\gamma }}^{2}}{\dot {\varphi }} = 0,}&{(x,y) \in \Omega } \end{array},$

где Т = l/b – коэффициент формы ДО R-C-0 ЭРП (l – длина, b – ширина элемента).

Пусть в области нормированных координат $\Omega = \overline {(0,1)} \times \overline {(0,1)} $ введена ортогональная сетка (рис. 5а). Узлы сетки пронумерованы в сквозном порядке слева-направо-снизу-вверх (глобальная нумерация), число узлов по оси x − N₁, по оси y – N₂. Пусть далее, ${{\dot {U}}_{i}} = \dot {U}({{x}_{i}})$ − значение функции $U$ в точке сетки x_i.

Рис. 5.

Нумерация узлов сетки: а – глобальная; б − локальная.

Сеточную задачу с учетом соотношений (15) и (16) запишем в виде

$\begin{array}{*{20}{c}} { - {{{\left( {D_{x}^{2}{\varphi }} \right)}}_{i}} - {{{\left( {D_{y}^{2}{\varphi }} \right)}}_{i}} + {{{\gamma }}^{2}}{{{\varphi }}_{i}} = 0,}&{{{x}_{i}} \in {{{\omega }}_{h}},} \end{array}$

${{\left( {D_{x}^{2}{\varphi }} \right)}_{i}} = \frac{1}{{\hbar _{i}^{x}}}\left[ {\frac{{H_{{i + 1}}^{x}}}{{{\text{sh}}H_{{i + 1}}^{x}}}\frac{{{{{\varphi }}_{{i + 1}}} - {{{\varphi }}_{i}}}}{{h_{{i + 1}}^{x}}} - \frac{{H_{i}^{x}}}{{{\text{sh}}H_{i}^{x}}}\frac{{{{{\varphi }}_{i}} - {{{\varphi }}_{{i - 1}}}}}{{h_{i}^{x}}}} \right],$

${{\left( {D_{y}^{2}{\varphi }} \right)}_{i}} = \frac{1}{{\hbar _{i}^{y}}}\left[ {\frac{{H_{{i + 1}}^{y}}}{{{\text{sh}}H_{{i + 1}}^{y}}}\frac{{{{{\varphi }}_{{i + {{N}_{1}}}}} - {{{\varphi }}_{i}}}}{{h_{{i + 1}}^{y}}} - \frac{{H_{i}^{y}}}{{{\text{sh}}H_{i}^{y}}}\frac{{{{{\varphi }}_{i}} - {{{\varphi }}_{{i - {{N}_{1}}}}}}}{{h_{i}^{y}}}} \right],$

где $D_{x}^{2}$ и $D_{y}^{2}$ − одномерные операторы, аппроксимирующие соответственно

$\begin{gathered} \begin{array}{*{20}{c}} {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}},}&{\frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \end{array},\,\,\,\,\begin{array}{*{20}{c}} {H_{i}^{x} = {\gamma }h_{i}^{x},}&{H_{i}^{y} = {{{\gamma }h_{i}^{y}} \mathord{\left/ {\vphantom {{{\gamma }h_{i}^{y}} T}} \right. \kern-0em} T},} \end{array} \\ \hbar _{i}^{x} = \frac{{h_{i}^{x}}}{{H_{i}^{x}}}{\text{th}}\frac{{H_{i}^{x}}}{2} + \frac{{h_{{i + 1}}^{x}}}{{H_{{i + 1}}^{x}}}{\text{th}}\frac{{H_{{i + 1}}^{x}}}{2}, \\ \hbar _{i}^{y} = \frac{{h_{i}^{y}}}{{H_{i}^{y}}}{\text{th}}\frac{{H_{i}^{y}}}{2} + \frac{{h_{{i + 1}}^{y}}}{{H_{{i + 1}}^{y}}}{\text{th}}\frac{{H_{{i + 1}}^{y}}}{2}. \\ \end{gathered} $

При равномерной по каждому направлению сетки с шагами h₁ = 1/(N₁ – 1), h₂ = 1/(N₂ – 1) сеточная задача значительно упрощается и принимает вид

(21)

$\begin{gathered} - {{\delta }_{x}}\frac{{{{{\varphi }}_{{i - 1}}} - 2{{{\varphi }}_{i}} + {{{\varphi }}_{{i + 1}}}}}{{h_{1}^{2}}} - \\ - \,\,{{\delta }_{y}}\frac{{{{{\varphi }}_{{i + {{N}_{1}}}}} - 2{{{\varphi }}_{i}} + {{{\varphi }}_{{i - {{N}_{1}}}}}}}{{h_{2}^{2}}} + {{{\gamma }}^{2}}{{{\varphi }}_{i}} = 0, \\ {{\delta }_{x}} = {{\left( {{{{{H}^{x}}} \mathord{\left/ {\vphantom {{{{H}^{x}}} {{\text{sh}}{{H}^{x}}}}} \right. \kern-0em} {{\text{sh}}{{H}^{x}}}}} \right)}^{2}},\,\,\,\,{{\delta }_{y}} = {{\left( {{{{{H}^{y}}} \mathord{\left/ {\vphantom {{{{H}^{y}}} {{\text{sh}}{{H}^{y}}}}} \right. \kern-0em} {{\text{sh}}{{H}^{y}}}}} \right)}^{2}}, \\ {{H}^{x}} = {{{\gamma }{{h}_{1}}} \mathord{\left/ {\vphantom {{{\gamma }{{h}_{1}}} 2}} \right. \kern-0em} 2},\,\,\,\,{{H}^{y}} = {{{\gamma }{{h}_{2}}} \mathord{\left/ {\vphantom {{{\gamma }{{h}_{2}}} {2T}}} \right. \kern-0em} {2T}}. \\ \end{gathered} $

Матрица проводимости i-го конечного элемента (рис. 5б) в случае равномерной сетки имеет вид

${{A}^{{(i)}}} = \left[ {\begin{array}{*{20}{c}} c&{ - {{S}_{1}}}&{ - {{S}_{2}}}&0 \\ { - {{S}_{1}}}&c&0&{ - {{S}_{2}}} \\ { - {{S}_{2}}}&0&c&{ - {{S}_{1}}} \\ 0&{ - {{S}_{2}}}&{ - {{S}_{1}}}&c \end{array}} \right],$

где с учетом (21) получаем

${{S}_{1}} = \frac{1}{2}\frac{{{{h}_{2}}}}{{{{h}_{1}}}}{{\delta }_{x}},\,\,\,\,{{S}_{2}} = \frac{1}{2}\frac{{{{h}_{1}}}}{{{{h}_{2}}}}{{\delta }_{y}},\,\,\,\,c = \frac{{{{h}_{1}}{{h}_{2}}{{{\gamma }}^{2}}}}{4} + {{S}_{1}} + {{S}_{2}}.$

Проведя сборку глобальной матрицы проводимости, учитывая матрицы проводимостей каждого конечного элемента и краевые условия, получим окончательную систему алгебраических уравнений, решение которой и даст приближенный ответ исходной задачи.

Физическая интерпретация сеточной задачи изображена на рис. 6, на котором представлен фрагмент схемы замещения участка ДО RC-ЭРП со структурой слоев вида R-C-0.

Рис. 6.

Фрагмент схемы замещения участка ДО RC-ЭРП со структурой слоев вида R-C-0.

y-Параметры ДО R-C-0 ЭРП с заданной топологией при использовании МКРЭ легко вычислить в математических пакетах Mathcad, Matlab или в программах схемотехнического моделирования.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе предложен метод анализа элементов, выполненных на основе многослойной, в общем случае неоднородной, резистивно-емкостной среды, основанный на методе конечных элементов. Однако в отличие от классического МКЭ, основанном на линейных или билинейных функциях на конечном элементе, здесь используется гибридная схема, в которой функция, аппроксимирующая распределение потенциала на конечном элементе, является точным решением уравнения однородной или неоднородной RC-линии. На основе гибридной схемы предложен метод конечных распределенных элементов, суть которого заключается в том, что каждый конечный элемент замещается ОО или ОН RC-ЭРП с соответствующей структурой слоев (ОО КРЭ для одномерной задачи) или набором ОО КРЭ по граням КЭ (ДО КРЭ для двумерной задачи). При этом для вычисления у-параметров функционального элемента на основе резистивно-емкостной среды нет необходимости находить распределение потенциалов в резистивных слоях этой среды. Достаточно определить первичные у-параметры полученного многополюсника – схемы замещения, составленной из КРЭ.

Список литературы

Гильмутдинов А.Х. Резистивно-емкостные элементы с распределенными параметрами: анализ, синтез и применение. Казань: Изд-во Казан. гос. техн. ун-та, 2005.
Гильмутдинов А.Х., Ушаков П.А. Фрактальные элементы: Учебное пособие / Под ред. А.Х. Гильмутдинова / Казань: Изд-во Казан. гос. техн. ун-та, 2013.
Гильмутдинов А.Х., Ушаков П.А. // РЭ. 2017. Т. 62. № 5. С. 413.
Сильвестер П., Феррари Р. Метод конечных элементов для радиоинженеров и инженеров-электриков. М.: Мир, 1986.
Флетчер К. Численные методы на основе метода Галёркина. М.: Мир, 1988.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал