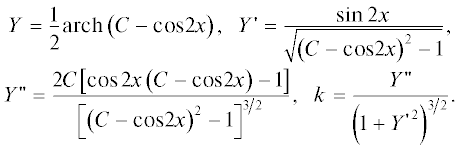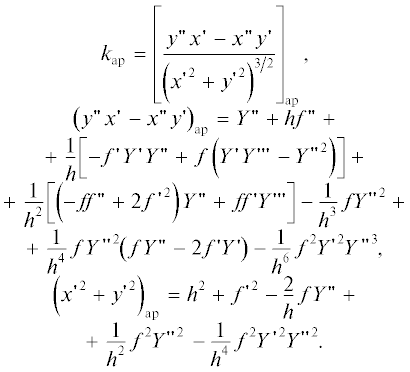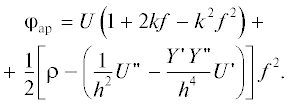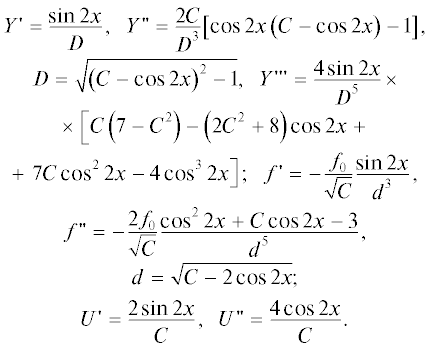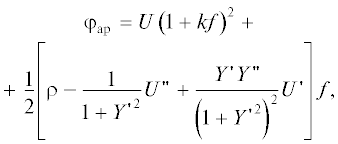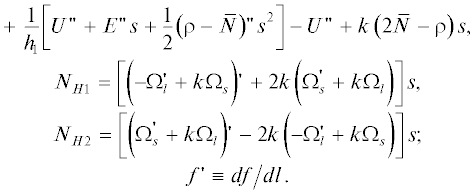Радиотехника и электроника, 2020, T. 65, № 12, стр. 1209-1233
Тестирование параксиальной модели ленточных электронных пучков
Т. М. Сапронова a, В. А. Сыровой a, *
a ВЭИ – филиал ФГУП РФЯЦ-ВНИИТФ
111250 Москва, ул. Красноказарменная, 12, Российская Федерация
* E-mail: red@cplire.ru
Поступила в редакцию 17.05.2019
После доработки 17.05.2019
Принята к публикации 17.05.2020
Аннотация
Проведено исследование параксиальной модели плотного электронного потока с привлечением аналитических решений, описывающих криволинейные ленточные пучки в однородном магнитном поле и при его отсутствии. Отмечена важность использования понятия невязки как критерия точности приближенного решения, величина которой соотнесена с ошибкой, известной в случае рассмотренных эталонных течений.
ВВЕДЕНИЕ
Параксиальная теория интенсивных электронных пучков сводится к построению решения в виде асимптотического ряда по малому геометрическому параметру $\varepsilon $, характеризующему узость занятой зарядами области. Она приводит к модели, описываемой обыкновенными дифференциальными уравнениями для квазиаксиально-симметричных потоков с пространственной осью, трубчатых осесимметричных пучков и криволинейных ленточных течений. С основными результатами и библиографией по этой теме можно ознакомиться в монографиях [1, 2].
В отличие от популярных в настоящее время коммерческих пакетов траекторного анализа параксиальный подход в совокупности с теорией антипараксиальных разложений позволяют сформулировать имеющие теоретическое обоснование алгоритмы реализации теплового зазора и торцевых областей ленточных пучков с близким к прямоугольному сечением, а при наличии сносовой скорости (планарный гиротрон) – и в случае сечения в виде параллелограмма [3–5].
В соответствии с обычными представлениями о точности приближенного решения в виде асимптотического ряда для толщины пучка порядка $\varepsilon $ при расчете траекторий можно ожидать ошибки порядка ${{\varepsilon }^{2}}$, притом что само понятие малого параметра по отношению к характерному масштабу длины задачи нуждается в обосновании. Во всякой приближенной теории естественным является желание выйти за рамки основных предположений: для параксиального подхода распространить рассмотрение на более широкие пучки с неоднородным распределением плотности по сечению при сохранении допустимого уровня ошибки. Общие соображения не позволяют оценить результат подобного рода испытания модели “на прочность”. Соответствующая информация может быть получена при тестировании на известных точных решениях уравнений пучка. Особенно удобны для этой цели решения в элементарных функциях.
В последнее время интерес специалистов по сильноточной электронике, в которой необходимо учитывать самосогласованное электромагнитное поле, привлекают устройства с планарной геометрией (см., например, библиографию в [3–7]) и ленточными электронными пучками с прямоугольным или эллиптическим сечением.
Цель работы – тестирование параксиальной модели ленточных пучков с использованием известных точных решений в элементарных функциях. Подобное исследование проводится, по-видимому, впервые. В работе [8] возможности модели тонких трубчатых пучков рассматривались по отношению к геометризованной теории двумерных потоков.
1. УРАВНЕНИЯ ЛЕНТОЧНОГО ПУЧКА
Нерелятивистский ленточный пучок с подобными трубками тока описывается обыкновенным уравнением второго порядка относительно толщины $f\left( l \right)$ при условии задания на оси потока с кривизной $k\left( l \right)$ распределений потенциала $U\left( l \right)$ и компонент напряженности магнитного поля ${{\Omega }_{l}}\left( l \right)$, ${{\Omega }_{s}}\left( l \right)$, ${{\Omega }_{x}}\left( l \right)$. Это уравнение дополняется рядом соотношений для параметров пучка [2]. Уравнения сформулированы в системе l, s (длина дуги оси, расстояние по нормали к ней) в нормировках, исключающих все физические постоянные используемой системы единиц [2]:
(1)
$\begin{gathered} \frac{{{{d}^{2}}f}}{{d{{t}^{2}}}} = {{V}_{l}}\frac{d}{{dl}}\left( {{{V}_{l}}\frac{{df}}{{dl}}} \right) = - \bar {P}B\left( l \right) + \left[ {\rho - N\left( l \right)} \right]f, \\ \frac{d}{{dt}} = {{V}_{l}}\frac{d}{{dl}};\,\,\,\,B\left( l \right) = - 2k{{V}_{x}} - {{\Omega }_{l}} - \frac{{{{V}_{x}}}}{{{{V}_{l}}}}{{\Omega }_{x}}, \\ 2U = V_{l}^{2} + V_{x}^{2},\,\,\,\,\bar {P} = {{f}_{0}}{{\Omega }_{{l0}}}, \\ N\left( l \right) = \frac{{{{d}^{2}}U}}{{d{{l}^{2}}}} + 2{{k}^{2}}V_{l}^{2} + \Omega _{l}^{2} + \Omega _{x}^{2} + 2k{{V}_{l}}{{\Omega }_{x}} - {{V}_{x}}\frac{{d{{\Omega }_{s}}}}{{dl}}; \\ {\varphi } = U + {{E}_{s}}s + \frac{1}{2}\left( {\rho - \bar {N}} \right){{s}^{2}}, \\ {{E}_{s}} = kV_{l}^{2} - {{V}_{x}}{{\Omega }_{l}} + {{V}_{l}}{\kern 1pt} {{\Omega }_{x}},\,\,\,\,\bar {N} = \frac{{{{d}^{2}}U}}{{d{{l}^{2}}}} - k{{E}_{s}}, \\ {{v}_{l}} = {{V}_{l}} + \left( {k{{V}_{l}} + {{\Omega }_{x}}} \right)s,\,\,\,\,{{v}_{s}} = \frac{{ds}}{{dt}} = \xi {{v}_{l}}\frac{{df}}{{dl}} = \frac{{{{v}_{l}}}}{f}\frac{{df}}{{dl}}s, \\ {{v}_{x}} = {{V}_{x}} - {{\Omega }_{l}}s,\,\,\,\,{{V}_{x}} = \int {{{\Omega }_{s}}dl} ,\,\,\,\,s = \xi f\left( l \right), \\ {{H}_{l}} = {{\Omega }_{l}} + \left( {\frac{{d{{\Omega }_{s}}}}{{dl}} + k{{\Omega }_{l}}} \right)s, \\ {{H}_{s}} = {{\Omega }_{s}} + \left( { - \frac{{d{{\Omega }_{l}}}}{{dl}} + k{{\Omega }_{s}}} \right)s. \\ \end{gathered} $Здесь ${\varphi }$, $\rho $ – потенциал электрического поля и плотность пространственного заряда; ${{v}_{l}}$, ${{v}_{s}}$, ${{v}_{x}}$ – компоненты скорости; циклическая координата х дополняет пару l, s до правой тройки; $\xi $ – параметр, маркирующий трубки тока, $\xi = 1$ на границе пучка.
При выполнении условий термоэмиссии на стартовой поверхности плотность пространственного заряда выражается из уравнения сохранения тока
где J – плотность тока эмиссии; индекс нуль относится к стартовой поверхности (эмитирующей поверхности или поверхности инжекции).
Для электростатических потоков соотношения (1) упрощаются:
(3)
$\begin{gathered} \frac{{{{d}^{2}}f}}{{d{{t}^{2}}}} = 2U\frac{{{{d}^{2}}f}}{{d{{l}^{2}}}} + \frac{{dU}}{{dl}}\frac{{df}}{{dl}} = \left[ {\rho - \left( {\frac{{{{d}^{2}}U}}{{d{{l}^{2}}}} + 4{{k}^{2}}U} \right)} \right]f, \\ {\varphi } = U + 2kUs + \frac{1}{2}\left[ {\rho - \left( {\frac{{{{d}^{2}}U}}{{d{{l}^{2}}}} - 2{{k}^{2}}U} \right)} \right]{{s}^{2}}, \\ 2U = V_{l}^{2},\,\,\,{{E}_{s}} \equiv E = 2kU. \\ \end{gathered} $2. ТЕЧЕНИЕ С ТРАЕКТОРИЯМИ-ОКРУЖНОСТЯМИ
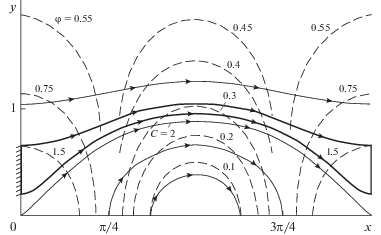
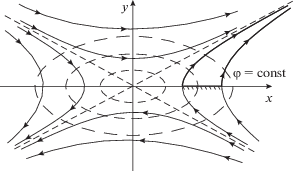
Решение [9] описывает эмиссию в ρ-режиме с полуплоскости $\psi = 0$ и траекториями $R = {\text{const}}$ (R, $\psi $ – полярные координаты) при отсутствии магнитного поля (рис. 1):
(4)
$\begin{gathered} 2{\varphi } = \frac{{2U\left( \psi \right)}}{{{{R}^{2}}}},\,\,\,\,2U = V_{l}^{2} = {{\left( {2{{J}_{0}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{\sin }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\frac{{3\psi }}{2}, \\ J = \frac{{{{J}_{0}}}}{{{{R}^{5}}}},\,\,\,\,\rho = \frac{J}{{{{V}_{l}}}} = \frac{1}{{{{R}^{4}}}}\frac{{{{J}_{0}}}}{{\sqrt {2U} }}. \\ \end{gathered} $Рис. 1.
Течение с траекториями-окружностями (параксиальная область выделена более толстыми линиями).
Выберем в качестве оси окружность ${{R}_{0}} = 1$, потенциал на которой определен функцией $U\left( \psi \right)$ в соответствии с (4), а плотность ρ на основании (2) описывается формулой
Тогда уравнение для f из (3) примет вид
(6)
$\begin{gathered} \frac{{{{d}^{2}}f}}{{d{{\psi }^{2}}}} + {\text{ctg}}\frac{{3\psi }}{2}\frac{{df}}{{d\psi }} = \frac{1}{2}\left( {f - {{f}_{0}}} \right){{\sin }^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\frac{{3\psi }}{2}, \\ l = {{R}_{0}}\psi = \psi . \\ \end{gathered} $Оно имеет точное решение, удовлетворяющее параксиальной постановке задачи об узком ленточном пучке:
Таким образом, приближенное решение для траектории совпадает с точным решением (4):
Представление об ошибке приближенного решения (${{{\varphi }}_{{{\text{ap}}}}}$) получим, сопоставляя параметры потока с соответствующими точными выражениями (${{{\varphi }}_{{{\text{ex}}}}}$). Результаты приведены в табл. 1 при использовании следующих обозначений:
(9)
$\begin{gathered} \bar {\varphi } = \frac{\varphi }{U},\,\,\,\,\bar {E} = \frac{E}{U},\,\,\,\,{{{\bar {\rho }}}_{{{\text{ex}}}}} = \frac{{\rho \left( R \right)}}{{\rho \left( 1 \right)}}; \\ {{\delta }_{\varphi }} = \left| {{{{{\varphi }_{{{\text{ap}}}}}} \mathord{\left/ {\vphantom {{{{\varphi }_{{{\text{ap}}}}}} {{{\varphi }_{{{\text{ex}}}}} - 1}}} \right. \kern-0em} {{{\varphi }_{{{\text{ex}}}}} - 1}}} \right|,\,\,\,\,{{\delta }_{E}} = \left| {{{{{E}_{{{\text{ap}}}}}} \mathord{\left/ {\vphantom {{{{E}_{{{\text{ap}}}}}} {{{E}_{{{\text{ex}}}}} - 1}}} \right. \kern-0em} {{{E}_{{{\text{ex}}}}} - 1}}} \right|; \\ {{{\bar {\varphi }}}_{{{\text{ex}}}}} = \frac{1}{{{{R}^{2}}}},\,\,\,\,{{{\bar {\varphi }}}_{{{\text{ap}}}}} = 1 + 2s + 3{{s}^{2}}, \\ {{{\bar {E}}}_{{{\text{ex}}}}} = \frac{2}{{{{R}^{3}}}},\,\,\,\,{{{\bar {E}}}_{{{\text{ap}}}}} = 2 + 6s,\,\,\,\,{{{\bar {\rho }}}_{{{\text{ex}}}}} = \frac{1}{{{{R}^{4}}}}. \\ \end{gathered} $Таблица 1.
Сопоставление результатов параксиальной модели с точным решением (4) – траектории-окружности
| $f$ | R | ${{{\bar {\varphi }}}_{{{\text{ap}}}}}$ | ${{{\bar {\varphi }}}_{{{\text{ex}}}}}$ | ${{\delta }_{\varphi }}$, % | ${{\bar {E}}_{{{\text{ap}}}}}$ | ${{\bar {E}}_{{{\text{ex}}}}}$ | ${{\delta }_{E}}$, % | ${{\bar {\rho }}_{{{\text{ex}}}}}$ | ${{N}_{\rho }}$ |
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.95 | 1.1075 | 1.1080 | 0.045 | 2.3 | 2.3327 | 1.40 | 1.228 | –1.05 |
| –0.05 | 1.05 | 0.9075 | 0.9070 | 0.052 | 1.7 | 1.7277 | 1.60 | 0.823 | 0.96 |
| 0.1 | 0.9 | 1.2300 | 1.2346 | 0.37 | 2.6 | 2.7435 | 5.23 | 1.524 | –2.2 |
| –0.1 | 1.1 | 0.8300 | 0.8264 | 0.48 | 1.4 | 1.5026 | 6.85 | 0.683 | 1.84 |
Следует иметь в виду, что для правой системы l, s нормаль s направлена в сторону уменьшения радиуса, так что имеем $R < 1$ при $f > 0$ и $R > {\text{1}}$ при $f < {\text{0}}$.
Из табл. 1 следует, что информация, необходимая для расчета формирующих электродов при точной постановке задачи (потенциал и нормальное поле на границе) для пучка с толщиной 0.1 ($\left| f \right| = 0.05$) при перепаде плотности в 40% известна с ошибкой порядка 1.5%; при толщине 0.2 ($\left| f \right| = 0.1$) соответствующие цифры составляют 80% и ~7%.
Величина ${{N}_{\rho }}$ имеет смысл невязки для уравнения Пуассона и обсуждается далее в разд. 5.
3. ПЛОСКОЕ ПЕРИОДИЧЕСКОЕ ЭЛЕКТРОСТАТИЧЕСКОЕ ТЕЧЕНИЕ
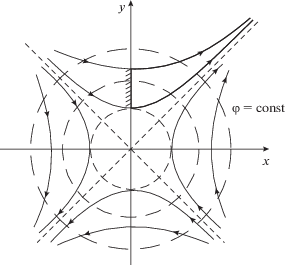
Эталонное решение. Решение получено в работе [10], картина течения изображена на рис. 2. Компоненты скорости u, v в декартовых координатах x, y, потенциал ${\varphi }$ и плотность пространственного заряда описываются формулами
(10)
$\begin{gathered} u = \frac{{{\text{sh}}2y}}{{{\text{ch}}2y + \cos 2x}},\,\,\,\,v = \frac{{{\text{sin}}2x}}{{{\text{ch}}2y + \cos 2x}}, \\ 2{\varphi } = \frac{{{\text{ch}}2y - \cos 2x}}{{{\text{ch}}2y + \cos 2x}},\,\,\,\,\rho = \frac{8}{{{{{\left( {{\text{ch}}2y + \cos 2x} \right)}}^{2}}}}. \\ \end{gathered} $Уравнения траекторий
определяют области финитного (С < 2) и инфинитного (С > 2) движений, разделенные траекторией-сепаратрисой С = 2.
Так как длину дуги l оси (11) параксиального пучка не удается выразить в элементарных функциях, а тем более перейти к этой переменной в параметрах потока (10) при $\eta = C$, то параксиальное уравнение (3) необходимо переписать с координатой х в качестве аргумента:
Кривизна линии $\eta = {\text{const}}$ точного решения описывается выражением
(13)
$k = \frac{2}{{\sqrt C }}\frac{{\cos 2x(C - \cos 2x) - 1}}{{{{{(C - 2\cos 2x)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}.$В качестве поверхности инжекции выберем плоскость $х = 0$. Видно, что при $х = 0$ и $С \to {\text{2}}$ значение кривизны стремится к бесконечности.
Параксиальное уравнение. Выпишем выражения для потенциала U, нормального поля ${{E}_{s}}$ и плотности заряда на траектории для решения (10):
(14)
$\begin{gathered} U = \frac{{C - 2\cos 2x}}{{2C}},\,\,\,\,E = \frac{2}{{C\sqrt C }}\frac{{\cos 2x\left( {C - \cos 2x} \right) - 1}}{{\sqrt {C - 2\cos 2x} }}, \\ \rho = \frac{8}{{{{C}^{2}}}}. \\ \end{gathered} $С учетом соотношений (12)–(14) уравнение (3) принимает вид
(15)
$\begin{gathered} \frac{{{{{\left( {C - \cos 2x} \right)}}^{2}} - 1}}{{{{C}^{3}}}}\frac{{{{d}^{2}}f}}{{d{{x}^{2}}}} + \\ + \,\,\frac{{\sin 4x}}{{{{C}^{3}}}}\,\,\frac{{2\cos 2x - 3C}}{{C - 2\cos 2x}}\,\,\frac{{df}}{{dx}} - \\ - \,\,\left\{ {\frac{8}{{{{C}^{2}}}} - \frac{4}{{{{C}^{3}}}}\frac{1}{{{{{\left( {C - 2\cos 2x} \right)}}^{2}}}}} \right. \times \\ \times \,\,\left[ {3 - C\left( {6 - {{C}^{2}}} \right)\cos 2x} \right. + 2\left( {3 - {{C}^{2}}} \right){{\cos }^{2}}2x - \\ \left. {\begin{array}{*{20}{c}} {} \\ {} \end{array}\left. { - \,\,2C{{{\cos }}^{3}}2x - {{{\cos }}^{4}}2x} \right]} \right\}f = 0; \\ \frac{d}{{dl}} = \frac{1}{{\sqrt {1 + {{Y}^{{'2}}}} }}\frac{d}{{dx}}. \\ \end{gathered} $Необходимо найти решение уравнения (15) со следующими начальными условиями при х = 0:
(16)
$f = f\left( 0 \right) = {\text{const}},\,\,\,\,{{df} \mathord{\left/ {\vphantom {{df} {dx}}} \right. \kern-0em} {dx}} = 0,$соответствующими условиям инжекции из точного решения.
Достаточно сложный вид уравнения (15) предполагает использование численных методов, однако мы построим решение в элементарных функциях.
Точное решение уравнения (15). В монографии [1] при возможности использования ортогональной системы $\xi $, $\eta $ отмечено формальное совпадение точного соотношения на трубке тока для коэффициента Ляме по поперечной координате $\eta $ геометризованной теории и приближенного уравнения для толщины пучка f параксиальной модели трубчатых пучков. Этот факт означает, что для любого двумерного точного решения исходных уравнений пучка, если с ним удается связать ортогональную систему с трубками тока $\eta = {\text{const}}$, можно указать точное решение параксиального уравнения $f = {{h}_{2}}$.
При заданном семействе координатных линий $\eta = {\text{const}}$ ортогональное семейство $\xi = {\text{const}}$ удовлетворяет соотношению
(17)
$\nabla \eta \cdot \nabla \xi = \eta {{,}_{x}}\xi {{,}_{x}} + \,\,\eta {{,}_{y}}\xi {{,}_{y}} = 0.$Здесь и далее частные производные будем обозначать соответствующим индексом после запятой: $\xi {{,}_{x}} \equiv {{\partial \xi } \mathord{\left/ {\vphantom {{\partial \xi } {\partial x}}} \right. \kern-0em} {\partial x}}$.
Дифференцируя выражение $\xi = {\text{const}}$ и используя свойство (17), для решения (11) приходим к дифференциальному уравнению, определяющему эту функцию, а затем к ее окончательному виду:
(18)
$\begin{gathered} \xi {{,}_{x}}dx + \xi {{,}_{y}}dy = 0,\,\,\,\,\frac{{dy}}{{dx}} = - \frac{{\xi {{,}_{x}}}}{{\xi {{,}_{y}}}} = \frac{{\eta {{,}_{y}}}}{{\eta {{,}_{x}}}} = - \frac{{{\text{sh}}2y}}{{\sin 2x}}, \\ \xi = {\text{tg}}{\kern 1pt} x{\kern 1pt} {\kern 1pt} {\text{th}}{\kern 1pt} y. \\ \end{gathered} $Для подсчета коэффициентов Ляме в системе $\xi $, $\eta $ необходимы пока неизвестные производные $x{{,}_{\xi }}$, $x{{,}_{\eta }}$, $y{{,}_{\xi }}$, $y{{,}_{\eta }}$:
(19)
$\begin{gathered} d{{x}^{2}} + d{{y}^{2}} = {{\left( {x{{,}_{\xi }}d\xi + x{{,}_{\eta }}d\eta } \right)}^{2}} + \\ + \,\,{{\left( {y{{,}_{\xi }}d\xi + y{{,}_{\eta }}d\eta } \right)}^{2}} = \\ = \left( {x,_{\xi }^{2} + y,_{\xi }^{2}} \right)d{{\xi }^{2}} + \left( {x,_{\eta }^{2} + y,_{\eta }^{2}} \right)d{{\eta }^{2}} = h_{1}^{2}d{{\xi }^{2}} + h_{2}^{2}d{{\eta }^{2}}. \\ \end{gathered} $Они вычисляются с помощью следующего приема. Рассмотрим функции $\xi = \xi \left( {x,y} \right)$, $\eta = \eta \left( {x,y} \right)$ и продифференцируем обе части этих равенств по $\xi $:
(20)
$\xi {{,}_{x}}x{{,}_{\xi }}\,\, + \xi {{,}_{y}}y{{,}_{\xi }} = 1,\,\,\,\,\eta {{,}_{x}}x{{,}_{\xi }}\,\, + \eta {{,}_{y}}y{{,}_{\xi }} = 0.$Выполнив аналогичные действия с дифференцированием по $\eta $, получим две системы линейных уравнений для требуемых производных, решение которых определяет их значения:
(21)
$\begin{gathered} x{{,}_{\xi }} = \frac{{\eta {{,}_{y}}}}{\Delta },\,\,\,\,x{{,}_{\eta }} = - \frac{{\xi {{,}_{y}}}}{\Delta },\,\,\,\,y{{,}_{\xi }} = - \frac{{\eta {{,}_{x}}}}{\Delta },\,\,\,y{{,}_{\eta }} = \frac{{\xi {{,}_{x}}}}{\Delta }; \\ \Delta = \xi {{,}_{x}}\eta {{,}_{y}} - \,\,\xi {{,}_{y}}\eta {{,}_{x}} = \frac{{{\text{c}}{{{\text{h}}}^{2}}2y - {{{\cos }}^{2}}2x}}{{{{{\cos }}^{2}}x{\kern 1pt} {\kern 1pt} {\text{c}}{{{\text{h}}}^{2}}y}}. \\ \end{gathered} $Таким образом, метрика в системе $\xi $, $\eta $ описывается следующими выражениями [11]:
(22)
$h_{{\,1}}^{2} = \frac{{4{{{\cos }}^{4}}x\,{\text{c}}{{{\text{h}}}^{4}}y}}{{{\text{c}}{{{\text{h}}}^{2}}2y - {{{\cos }}^{2}}2x}},\,\,\,\,h_{{\,2}}^{2} = \frac{1}{{{\text{4}}\left( {{\text{c}}{{{\text{h}}}^{2}}2y - {{{\cos }}^{2}}2x} \right)}}.$Частное решение уравнения (15) имеет вид
Константа в выражении для f по сравнению с ${{h}_{2}}$ из (15) изменена в силу того, что уравнение (15) допускает преобразование растяжения: $\bar {f} = af$, $a = {\text{const}}$. Решение (23) при $x = 0$ удовлетворяет начальным условиям (16), в силу чего в численном интегрировании уравнения (15) нет необходимости.
Приближенное решение. Приближенная траектория описывается параметрическими уравнениями с переменной х в качестве параметра
(24)
$\begin{gathered} {{y}_{{{\text{ap}}}}} = Y + f\cos \vartheta ,\,\,\,\,{{x}_{{{\text{ap}}}}} = x - f\sin \vartheta , \\ {\text{tg}}\vartheta = Y{\kern 1pt} ', \\ h = \sqrt {1 + {{Y}^{{'2}}}} = \sqrt {\frac{{C\left( {C - 2\cos 2x} \right)}}{{{{{\left( {C - \cos 2x} \right)}}^{2}} - 1}}} \\ \end{gathered} $и кривизной ${{k}_{{{\text{ap}}}}}$, определяемой формулой
Потенциал ${{{\varphi }}_{{{\text{ap}}}}}$ на границе пучка в соответствии с (3) имеет вид
Кривизна траекторий достигает максимального значения при $x = 0$, определяя характерный масштаб длины $L*\sim {1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0em} k}$ и допустимую величину начальной толщины узкого пучка, в то время как потенциал принимает наибольшее значение при $x = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Приближенные и точные значения нормального поля имеет смысл сравнивать в точках $x = 0$ и $x = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, где направления нормалей для точной и приближенной траекторий совпадают. Меньшую ошибку при вычислении нормального поля на границе пучка дает условие баланса сил на этой кривой, а не результат дифференцирования формулы (26).
Производные от функций Y(x), f(x), U(x) определены формулами
В первом из упомянутых выше контрольных сечений (x = 0) имеем
(28)
$\begin{gathered} {{k}_{{{\text{ex}}}}} = \frac{2}{{\sqrt {{{C}_{*}}\left( {{{C}_{*}} - 2} \right)} }},\,\,\,\,{{C}_{*}} = {\text{ch}}2{{y}_{*}} + 1, \\ {{y}_{*}} = Y + f\left( 0 \right),\,\,\,{{k}_{{{\text{ap}}}}} = \frac{2}{{\sqrt {C\left( {C - 2} \right)} }}{{\left[ {\frac{{C\left( {C - 2} \right)}}{{C\left( {C - 2} \right) - {{f}_{0}}}}} \right]}^{3}} \times \\ \times \,\,\left[ {1 - \frac{{C + 2}}{{C\left( {C - 2} \right)}}{{f}_{0}} + \frac{{C + 1}}{{{{C}^{2}}{{{\left( {C - 2} \right)}}^{2}}}}f_{0}^{2}} \right]; \\ {{{\varphi }}_{{{\text{ex}}}}} = \frac{{{{C}_{*}} - 2}}{{2{{C}_{*}}}},\,\,\,\,{{{\varphi }}_{{{\text{ap}}}}} = \frac{{C - 2}}{{2C}}\left[ {1 + \frac{2}{{C\left( {C - 2} \right)}}{{f}_{0}}} \right] - \\ - \,\,\frac{{C - 1}}{{2{{C}^{3}}\left( {C - 2} \right)}}f_{0}^{2};\,\,\,{{E}_{{{\text{ex}}}}} = {{\left( {2k{\varphi }} \right)}_{{{\text{ex}}}}} = \frac{{2\sqrt {{{C}_{*}} - 2} }}{{{{C}_{*}}\sqrt {{{C}_{*}}} }}, \\ {{E}_{{{\text{ap}}}}} = {{\left( {2k{\varphi }} \right)}_{{{\text{ap}}}}};\,\,\,{{f}_{0}} = 2\sqrt {C\left( {C - 2} \right)} f\left( 0 \right). \\ \end{gathered} $Параметр С соответствует оси пучка, ${{С}_{*}}$ – точной траектории с теми же условиями старта, что и параксиальная кривая.
Во втором контрольном сечении $x = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ получаем
(29)
$\begin{gathered} {{k}_{{{\text{ex}}}}} = - \frac{2}{{\sqrt {{{C}_{*}}\left( {{{C}_{*}} + 2} \right)} }},\,\,\,\,{{k}_{{{\text{ap}}}}} = - \frac{2}{{\sqrt {C\left( {C + 2} \right)} }} \times \\ \times \,\,{{\left[ {\frac{{C\left( {C + 2} \right)}}{{C\left( {C + 2} \right) + {{f}_{0}}}}} \right]}^{3}}{\kern 1pt} \left[ {1 + \frac{{C - 2}}{{C\left( {C + 2} \right)}}{{f}_{0}} + \frac{{C - 1}}{{{{C}^{2}}{{{\left( {C + 2} \right)}}^{2}}}}{\kern 1pt} f_{0}^{2}} \right]; \\ {{{\varphi }}_{{{\text{ex}}}}} = \frac{{{{C}_{*}} + 2}}{{2{{C}_{*}}}}, \\ {{{\varphi }}_{{{\text{ap}}}}} = \frac{{C + 2}}{{2C}}\left[ {1 - \frac{2}{{C\left( {C + 2} \right)}}{{f}_{0}}} \right] + \\ + \,\,\,\,\frac{{C + 1}}{{2{{C}^{3}}\left( {C + 2} \right)}}f_{0}^{2};\,\,\,\,\,{{E}_{{{\text{ex}}}}} = {{\left( {2k\varphi } \right)}_{{{\text{ex}}}}} = \\ = - \frac{{2\sqrt {{{C}_{*}} + 2} }}{{{{C}_{*}}\sqrt {{{C}_{*}}} }},\,\,\,\,{{E}_{{{\text{ap}}}}} = {{\left( {2k{\varphi }} \right)}_{{{\text{ap}}}}}. \\ \end{gathered} $Положение максимального различия точной и параксиальной траекторий $Y\left( {x;{{C}_{*}}} \right) - {{y}_{{{\text{ap}}}}}$ определяет условие
(30)
$\begin{gathered} С{{\left( {2X - C} \right)}^{2}}\left[ {\sqrt {{{X}^{2}} - 1} {\kern 1pt} \,{\text{arch}}{\kern 1pt} X - \sqrt {{{Z}^{2}} - 1} \,{\kern 1pt} {\text{arch}}{\kern 1pt} Z} \right] - \\ - \,\,{{f}_{0}}\left[ {\sqrt {{{Z}^{2}} - 1} {\kern 1pt} \,{\text{arch}}{\kern 1pt} Z\left( {2 - CX} \right)} \right. - \\ \left. { - \,\,\,\,\left( {2X - C} \right)\left( {{{X}^{2}} - 1} \right)} \right] = 0, \\ X = C - \cos 2x,\,\,\,\,Z = {{C}_{*}} - \cos 2x. \\ \end{gathered} $Сопоставление приближенного и эталонного решений. Результаты сравнения параксиального и эталонного решений приведены в табл. 2–5. В табл. 2 в сечении х = 0 для базовой траектории С = 2.1 с кривизной k(С) = 4.364358, определяющей характерный линейный размер $L*\sim 0.23$, сопоставлены значения кривизны k, потенциала $\varphi $ и нормального поля Е для начальной ширины пучка $f\left( 0 \right) = 0.01$ и $f\left( 0 \right) = 0.02$. Поперечный градиент плотности $\rho $ невелик, поэтому относительное изменение этого параметра составляет 0.89% в первом случае и 1.8% во втором. Максимальное отличие по координате y точной траектории от приближенной для варианта $C = 2.1$, $C{\text{*}} = 2.119215$, $f\left( 0 \right) = 0.02$ после решения уравнения (30) не превышает 2% при $x\sim {\pi \mathord{\left/ {\vphantom {\pi {18}}} \right. \kern-0em} {18}}.$
Таблица 2.
Сравнение параксиальной модели и точного решения (10) – периодическое течение – при x = 0 (С = 2.1, Y = 0.221784, k = 4.364358, $L* = 0.23$)
| Вариант | $f\left( 0 \right) = 0.01,$${{f}_{0}} = 0.009165$, ${{C}_{*}} = 2.109386$ | $f\left( 0 \right) = 0.02,$${{f}_{0}} = 0.018330$, ${{C}_{*}} = 2.119215$ | ||||
|---|---|---|---|---|---|---|
| k | φ | E | k | φ | E | |
| Приближенное значение | 4.126191 | 0.0258379 | 0.213224 | 3.821422 | 0.0277665 | 0.212215 |
| Точное значение | 4.163620 | 0.0259284 | 0.215912 | 3.979028 | 0.0281270 | 0.223838 |
| Относительная ошибка, % | 0.9 | 0.35 | 1.24 | 3.96 | 1.28 | 5.19 |
Таблица 3.
Сравнение параксиальной модели и точного решения (10) – периодическое течение – при $x = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (С = 2.1, Y = 0.221784, k = 4.364358, $L* = 0.23$, $f\left( 0 \right) = 0.02$)
| Вариант | k | φ | E |
|---|---|---|---|
| Приближенное значение | –0.677411 | 0.972048 | –1.316952 |
| Точное значение | –0.676917 | 0.971873 | –1.315755 |
| Относительная ошибка, % | 0.073 | 0.018 | 0.09 |
Таблица 4.
Сравнение параксиальной модели и точного решения (10) – периодическое течение – при x = 0 (С = 2.18, Y = 0.295673, k = 3.192754, $L* = 0.31$)
| Вариант | $f\left( 0 \right) = 0.02,$${{f}_{0}} = 0.0250567$, ${{C}_{*}} = 2.206007$ | $f\left( 0 \right) = 0.03,$${{f}_{0}} = 0.0375851$, ${{C}_{*}} = 2.219732$ | ||||
|---|---|---|---|---|---|---|
| k | φ | E | k | φ | E | |
| Приближенное значение | 2.903392 | 0.0463582 | 0.269192 | 2.715574 | 0.0487461 | 0.264747 |
| Точное значение | 2.966781 | 0.0466923 | 0.277052 | 2.863737 | 0.0494952 | 0.283482 |
| Относительная ошибка, % | 2.1 | 0.7 | 2.8 | 5.2 | 1.5 | 6.6 |
Таблица 5.
Сравнение параксиальной модели и точного решения (10) – периодическое течение – при x = 0 (С = = 2.54, Y = 0.498687, k = 1.707718, $L* = 0.59$)
| Вариант | $f\left( 0 \right) = 0.03,$${{f}_{0}} = 0.0702692$, $C* = 2.613084$ | $f\left( 0 \right) = 0.05,$${{f}_{0}} = 0.117115$, $C* = 2.665017$ | ||||
|---|---|---|---|---|---|---|
| k | φ | E | k | φ | E | |
| Приближенное значение | 1.553063 | 0.116761 | 0.362674 | 1.424394 | 0.123259 | 0.351139 |
| Точное значение | 1.580132 | 0.117310 | 0.370731 | 1.502324 | 0.124768 | 0.374884 |
| Относительная ошибка, % | 1.7 | 0.53 | 2.2 | 5.2 | 1.2 | 6.3 |
В табл. 3 приведена информация, соответствующая сечению $x = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ при С = 2.1, $C* = 2.119215$, $f\left( 0 \right) = 0.02$. Сравнение данных табл. 2 и 3 показывает, что ошибка приближенного решения определяется сечением х = 0. Таблицы 4 и 5 относятся к случаям, когда в качестве оси пучка выбраны точные траектории с меньшей по сравнению с табл. 2 кривизной, стартующие из точек Y = 0.295673 (С = 2.18, k = 3.192754, $L{\text{*}}\sim 0.31$) и Y = 0.498687 (С = 2.54, k = = 1.707718, ${{L}_{*}}\sim 0.59$). Начальная толщина пучка в первом случае составляет $f\left( 0 \right) = 0.02$, 0.03, во втором $f\left( 0 \right) = 0.03$, 0.05.
Во всех вариантах при $\varepsilon \sim 0.05L{\text{*}}$ максимальная ошибка параксиальной модели имеет порядок 1%; при $\varepsilon \sim 0.1L{\text{*}}$ она возрастает до 5…7%.
4. ЭЛЕКТРОСТАТИЧЕСКИЙ ПОТОК С ГИПЕРБОЛИЧЕСКИМИ ТРАЕКТОРИЯМИ
Эталонное решение. Решение с равнобочными гиперболами в качестве траекторий построено в работе [12] – первой работе по интенсивным криволинейным пучкам (рис. 3):
(31)
$u = by{\text{,}}\,\,\,v = bx,\,\,\,2{\varphi } = {{b}^{2}}\left( {{{x}^{2}} + {{y}^{2}}} \right),\,\,\,\,\rho = 2{{b}^{2}}.$Константа b не влияет на оценки и может быть принята равной единице.
Траектории потока определены формулами
(32)
$\eta = \frac{1}{2}\left( {{{y}^{2}} - {{x}^{2}}} \right) = C,\,\,\,\,Y = \sqrt {{{x}^{2}} + 2C} .$Выбрав линию $\eta = C$ в качестве оси узкого пучка, для потенциала на ней имеем
Решение параксиального уравнения. Переходя к переменной x в уравнении (3), получим соотношение, которому должна удовлетворять функция f при выполнении начальных условий (16):
(34)
$\left( {{{x}^{2}} + 2C} \right)\frac{{{{d}^{2}}f}}{{d{{x}^{2}}}} + x\frac{{df}}{{dx}} - \frac{{{{x}^{4}} + 2C{{x}^{2}} + 2{{C}^{2}}}}{{{{{\left( {{{x}^{2}} + C} \right)}}^{2}}}}f = 0.$С траекториями (32) связана ортогональная система $\xi $, $\eta $ с конформной метрикой
(35)
$\xi = xy,\,\,\,\eta = \frac{1}{2}\left( {{{y}^{2}} - {{x}^{2}}} \right),\,\,\,\,{{h}_{{\,1}}} = {{h}_{{\,2}}} = \frac{1}{{\sqrt {{{x}^{2}} + {{y}^{2}}} }}.$В соответствии со сказанным в разд. 2 частное решение уравнения (27) с начальными условиями (16) имеет вид
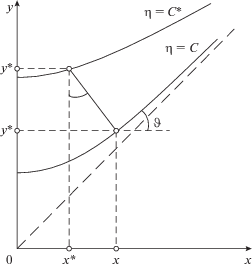
Расстояние f по нормам между двумя точными траекториями $\eta = C$, $\eta = C{\text{*}}$ найдем из квадратного уравнения (рис. 4)
(37)
$\begin{gathered} \frac{1}{2}\left( {{{y}^{2}} - {{x}^{2}}} \right) = C,\,\,\,\,\frac{1}{2}\left( {y_{*}^{2} - x_{*}^{2}} \right) = {{C}_{*}}, \\ {{x}_{*}} = x - f\sin \vartheta ,\,\,\,\,{{y}_{*}} = Y + f\cos \vartheta , \\ {\text{tg}}\vartheta = \frac{{dY}}{{dx}} = \frac{x}{{\sqrt {{{x}^{2}} + 2C} }},\,\,\,\,\sin \vartheta = \frac{x}{{\sqrt {2\left( {{{x}^{2}} + C} \right)} }}, \\ \cos \vartheta = \frac{{\sqrt {{{x}^{2}} + 2C} }}{{\sqrt {2\left( {{{x}^{2}} + C} \right)} }};\,\,\,\,{{f}_{{{\text{ex}}}}} = \frac{{\sqrt 2 }}{C}{{\left( {{{x}^{2}} + C} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left\{ {{{{\left[ {1 - C\left( {C - {{C}_{*}}} \right)\frac{1}{{{{{\left( {{{x}^{2}} + C} \right)}}^{2}}}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 1} \right\}, \\ f\left( 0 \right) = \sqrt {2{{C}_{*}}} - \sqrt {2C} ,\,\,\,\,{{f}_{0}} = \sqrt C f\left( 0 \right). \\ \end{gathered} $Существование асимптоты для траекторий приводит к ряду особенностей эталонного и приближенного решений. Обе функции ${{f}_{{{\text{ex}}}}}$, ${{f}_{{{\text{ap}}}}}$ из (36), (37) монотонно стремятся к нулю по одному закону:
(38)
$\begin{gathered} {{f}_{{{\text{ex}}}}}\left( \infty \right) = \frac{{C{\text{*}} - C}}{{\sqrt 2 }}\frac{1}{x} = \frac{{f\left( 0 \right)\left[ {2\sqrt {2C} + f\left( 0 \right)} \right]}}{{2\sqrt 2 }}\frac{1}{x}, \\ {{f}_{{{\text{ap}}}}}\left( \infty \right) = \frac{{{{f}_{0}}}}{x} = \sqrt C f\left( 0 \right)\frac{1}{x}. \\ \end{gathered} $В результате относительная ошибка δ = 1 – $ - \,\,{{{{f}_{{{\text{ap}}}}}} \mathord{\left/ {\vphantom {{{{f}_{{{\text{ap}}}}}} {{{f}_{{{\text{ex}}}}}}}} \right. \kern-0em} {{{f}_{{{\text{ex}}}}}}}$, равная нулю в точке старта, при $x \to \infty $ возрастает и стремится к константе:
При С = 1 и ${{f}_{0}} = 0.05$, 0.2 значения ${{\delta }_{\infty }}$ составляют 1.74 и 6.6%. В этой ситуации имеет смысл обратиться к величине $\left| {{{f}_{{{\text{ex}}}}} - {{f}_{{{\text{ap}}}}}} \right|$, которая равна нулю при x = 0, $\infty $ и достигает максимума внутри этого интервала. При С = 1 и ${{f}_{0}} = 0.1$ он имеет место при $x\sim 1.2$ причем $\left| {{{f}_{{{\text{ex}}}}} - {{f}_{{{\text{ap}}}}}} \right|$ = 0.0658791 – ‒ 0.00640711 = 0.00186.
Сравнение приближенного и точного решений. Параметрические уравнения параксиальной траектории $x* = x{\text{*}}\left( x \right)$, $y* = y{\text{*}}\left( y \right)$ из (37) и уравнение траектории точного решения (32) позволяют вычислить кривизны внешней границы пучка, причем максимального значения эти функции достигают при х = 0:
(40)
$\begin{gathered} {{k}_{{{\text{ex}}}}} = \frac{1}{{\sqrt {2{{C}_{*}}} }} = \frac{1}{{\sqrt {2C} + f\left( 0 \right)}}, \\ {{k}_{{{\text{ap}}}}} = \frac{1}{{\sqrt {2C} }}{{{{\left[ {1 - \frac{{3f\left( 0 \right)}}{{\sqrt {2C} }}} \right]} \mathord{\left/ {\vphantom {{\left[ {1 - \frac{{3f\left( 0 \right)}}{{\sqrt {2C} }}} \right]} {\left[ {1 - \frac{{f\left( 0 \right)}}{{\sqrt {2C} }}} \right]}}} \right. \kern-0em} {\left[ {1 - \frac{{f\left( 0 \right)}}{{\sqrt {2C} }}} \right]}}}^{3}}. \\ \end{gathered} $Результаты расчетов для нескольких значений $f\left( 0 \right)$ приведены в табл. 6 . Из стартовой точки исходят две траектории: точная $\eta = {{C}_{*}}$ и приближенная. Их кривизны, подобно функциям ${{f}_{{{\text{ex}}}}}$, ${{f}_{{{\text{ap}}}}}$, убывают по одному закону, а отношение стремится к константе при $x \to \infty $:
(41)
$\begin{gathered} {{k}_{{{\text{ex}}}}}\left( \infty \right) = \frac{{{{C}_{*}}}}{{\sqrt 2 }}\frac{1}{{{{x}^{3}}}},\,\,\,\,{{k}_{{{\text{ap}}}}}\left( \infty \right) = \frac{{C + \bar {C}}}{{\sqrt 2 }}\frac{1}{{{{x}^{3}}}}, \\ \bar {C} = \sqrt {\frac{C}{2}} f\left( 0 \right),\,\,\,\,\frac{{{{k}_{{{\text{ap}}}}}}}{{{{k}_{{{\text{ex}}}}}}}\left( \infty \right) = \frac{{\sqrt {2C} }}{{\sqrt {2C} + f\left( 0 \right)}}. \\ \end{gathered} $При С = 1, $f\left( 0 \right) = 0.1$ отношение кривизн составляет 0.93396, что соответствует относительной ошибке $\delta = 6.6\% $. В контрольной точке х = 1.2, которая была использована при оценке траекторий, при абсолютной разности ${{k}_{{{\text{ex}}}}} - {{k}_{{{\text{ap}}}}}$ = 0.194886 – ‒ 0.186037 = 0.00885, относительная ошибка равна 4.5%.
Таблица 6.
Сравнение параксиальной модели и точного решения (31) – ось-гипербола, $\vec {H} = 0$
| Параметры | С, k, ${{L}_{*}}$ | ||
|---|---|---|---|
| 0.5, 1, 1 | 1, 0.707, 1.414 | 5, 0.316, 3.16 | |
| $f\left( 0 \right) = 0.025$ | |||
| ${{C}_{*}}$ | 0.525313 | 1.071961 | 5.079369 |
| ${{k}_{{{\text{ex}}}}}$ | 0.975561 | 0.694824 | 0.313747 |
| ${{k}_{{{\text{ap}}}}}$ | 0.997994 | 0.706412 | 0.316167 |
| $\delta ,\% $ | 2.3 | 1.7 | 0.77 |
| ${{N}_{{m1}}}$ | 0.0152 | 0.0107 | 0.0048 |
| ${{N}_{{m2}}}$ | $2.8 \times {{10}^{{ - 4}}}$ | $1.4 \times {{10}^{{ - 4}}}$ | $2.8 \times {{10}^{{ - 5}}}$ |
| ${{N}_{J}}$ | 0.0221 | 0.0155 | 0.0069 |
| N | 0.0270 | 0.0188 | 0.0084 |
| $f\left( 0 \right) = 0.05$ | |||
| ${{C}_{*}}$ | 0.551250 | 1.071960 | 5.159364 |
| ${{k}_{{{\text{ex}}}}}$ | 0.952380 | 0.682960 | 0.311306 |
| ${{k}_{{{\text{ap}}}}}$ | 0.991398 | 0.704188 | 0.315980 |
| $\delta ,\% $ | 4.1 | 3.1 | 1.5 |
| ${{N}_{{m1}}}$ | 0.0307 | 0.0216 | 0.0096 |
| ${{N}_{{m2}}}$ | $1.1 \times {{10}^{{ - 3}}}$ | $5.6 \times {{10}^{{ - 4}}}$ | $1.13 \times {{10}^{{ - 4}}}$ |
| ${{N}_{J}}$ | 0.0453 | 0.0316 | 0.0139 |
| N | 0.0547 | 0.038 | 0.017 |
| $f\left( 0 \right) = 0.1$ | |||
| ${{C}_{*}}$ | 0.605000 | 1.146420 | 5.321228 |
| ${{k}_{{{\text{ex}}}}}$ | 0.909090 | 0.660409 | 0.306534 |
| ${{k}_{{{\text{ap}}}}}$ | 0.960220 | 0.694202 | 0.315194 |
| $\delta ,\% $ | 5.6 | 5.1 | 2.8 |
| ${{N}_{{m1}}}$ | 0.0620 | 0.0436 | 0.0190 |
| ${{N}_{{m2}}}$ | 0.02 | 0.01 | 0.004 |
| ${{N}_{J}}$ | 0.0952 | 0.0654 | 0.0282 |
| N | 0.115 | 0.079 | 0.034 |
Для решения (31) точное выражение для потенциала на параксиальной траектории
(42)
${{{\varphi }}_{{{\text{ex}}}}} = \frac{1}{2}\left( {x_{*}^{2} + y_{*}^{2}} \right) = U + \frac{{2C}}{{\sqrt {2\left( {{{x}^{2}} + C} \right)} }}f + \frac{1}{2}{{f}^{2}}$совпадает с результатом параксиальной теории
в чем можно убедиться подстановкой соответствующих функций в формулы (42), (43). Таким образом, ошибка при вычислении нормального электрического поля определяется неточностью при расчете кривизны приближенной траектории.
5. ГИПЕРБОЛИЧЕСКИЙ ПОТОК В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
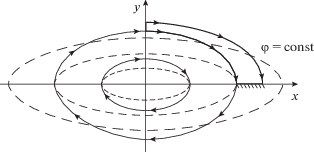
Эталонное решение. В однородном магнитном поле11 ${{H}_{z}}$ возможно течение с гиперболическими траекториями [10], кривизна которых в вершине может значительно превышать кривизну равнобочной гиперболы и меняться с существенно большей скоростью (рис. 5):
(44)
$\begin{gathered} u = \left( {\Omega + \omega } \right)y,\,\,\,\,v = \left( {\Omega - \omega } \right)x, \\ \omega = \frac{1}{2}{{H}_{z}},\,\,\,\,\Omega > \omega ; \\ 2\varphi = {{\left( {\Omega - \omega } \right)}^{2}}{{x}^{2}} + {{\left( {\Omega + \omega } \right)}^{2}}{{y}^{2}},\,\,\,\,\rho = 2\left( {{{\Omega }^{2}} + {{\omega }^{2}}} \right). \\ \end{gathered} $Течение (44) является моноэнергетическим и потенциальным. Траектории определены выражением
(45)
$\left( {\Omega + \omega } \right){{y}^{2}} - \left( {\Omega - \omega } \right){{x}^{2}} = {\text{const}}.$Ортогональная система, связанная с кривыми (45), имеет вид
(46)
$\begin{gathered} {\xi } = y{{x}^{{\bar {\Omega }}}},\,\,\,\,\eta = {{x}^{2}} - \bar {\Omega }{{y}^{2}},\,\,\,\,\bar {\Omega } = \frac{{\Omega + \omega }}{{\Omega - \omega }}; \\ {{h}_{1}} = \frac{{{{x}^{{1 - \bar {\Omega }}}}}}{{\sqrt {{{x}^{2}} + {{{\bar {\Omega }}}^{2}}{{y}^{2}}} }},\,\,\,\,{{h}_{2}} = \frac{1}{{2\sqrt {{{x}^{2}} + {{{\bar {\Omega }}}^{2}}{{y}^{2}}} }}. \\ \end{gathered} $В качестве оси параксиального пучка выберем линию
с кривизной, которая в отличие от случая равнобочной гиперболы будет отрицательной (l, s – правая система, знак k определяется в соответствии с направлением нормали s)
(48)
$k{\text{ = }} - \frac{{\bar {\Omega }C}}{{{{{\left[ {\bar {\Omega }\left( {\bar {\Omega } + 1} \right){{y}^{2}} + C} \right]}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}.$Удобно ввести новую нормировку параметров потока на оси
(49)
$\begin{gathered} \bar {U} = \frac{{2U}}{{{{{\left( {\Omega - \omega } \right)}}^{2}}}} = \bar {\Omega }\left( {\bar {\Omega } + 1} \right){{y}^{2}} + C,\,\,\,\,2\bar {U} = \bar {V}_{l}^{2}, \\ \bar {\rho } = \frac{{2\rho }}{{{{{\left( {\Omega - \omega } \right)}}^{2}}}},\,\,\,\bar {\Omega }_{x}^{2} = \frac{{2\Omega _{x}^{2}}}{{{{{\left( {\Omega - \omega } \right)}}^{2}}}}. \\ \end{gathered} $Решение параксиального уравнения. Параксиальное уравнение (1) в переменных (49) принимает вид
(50)
$\begin{gathered} {\text{2}}\bar {U}\frac{{{{d}^{2}}f}}{{d{{l}^{2}}}} + \frac{{d\bar {U}}}{{dl}}\frac{{df}}{{dl}} = \\ = \left[ {\bar {\rho } - \left( {\frac{{{{d}^{2}}\bar {U}}}{{d{{l}^{2}}}} + 4{{k}^{2}}\bar {U} + \bar {\Omega }_{x}^{2} + 2k{{{\bar {V}}}_{l}}{{{\bar {\Omega }}}_{x}}} \right)} \right]f. \\ \end{gathered} $После перехода от продольной переменной l к y имеем
(51)
$\begin{gathered} \frac{d}{{dl}} = \frac{1}{h}\frac{d}{{dy}},\,\,\,\,{{h}^{2}} = 1 + {{X}^{{'2}}} = \frac{{\bar {\Omega }\left( {\bar {\Omega } + 1} \right){{y}^{2}} + C}}{{\bar {\Omega }{{y}^{2}} + C}}; \\ \left( {\bar {\Omega }{{y}^{2}} + C} \right)\frac{{{{d}^{2}}f}}{{d{{y}^{2}}}} + \bar {\Omega }y\frac{{df}}{{dy}} - \\ - \,\,\frac{{\bar {\Omega }\left( {\bar {\Omega } + 1} \right)\left[ {{{{\bar {\Omega }}}^{2}}\left( {\bar {\Omega } + 1} \right){{y}^{4}} + 2C{{{\bar {\Omega }}}^{2}}{{y}^{2}} - {{C}^{2}}} \right]}}{{{{{\left[ {\bar {\Omega }\left( {\bar {\Omega } + 1} \right){{y}^{2}} + C} \right]}}^{2}}}}f = 0. \\ \end{gathered} $Необходимо найти решение этого уравнения при начальных данных
Коэффициент Ляме h2 из (46), записанный на оси (47) с произвольным множителем ${{f}_{0}}$, определяет аналитическое решение этой задачи
(53)
$\begin{gathered} {{f}_{{{\text{ap}}}}} = \frac{{{{f}_{0}}}}{{\sqrt {\bar {\Omega }\left( {\bar {\Omega } + 1} \right){{y}^{2}} + C} }}, \\ f\left( 0 \right) = \sqrt C - \sqrt {{{C}_{*}}} = \frac{{{{f}_{0}}}}{{\sqrt C }}. \\ \end{gathered} $Расстояние ${{f}_{{{\text{ex}}}}}$ между двумя траекториями $\eta = C$ и $\eta = C{\text{*}}$ точного решения задает формула
(54)
$\begin{gathered} {{f}_{{{\text{ex}}}}} = \frac{{{{{\left[ {\bar {\Omega }\left( {\bar {\Omega } + 1} \right){{y}^{2}} + C} \right]}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{\bar {\Omega }\left( {1 - {{{\bar {\Omega }}}^{2}}} \right){{y}^{2}} + C}} \times \\ \times \,\,\left\{ {1 - {{{\left[ {1 - \left( {C - {{C}_{*}}} \right)\frac{{\bar {\Omega }\left( {1 - {{{\bar {\Omega }}}^{2}}} \right){{y}^{2}} + C}}{{{{{\left[ {\bar {\Omega }\left( {\bar {\Omega } + 1} \right){{y}^{2}} + C} \right]}}^{2}}}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\}. \\ \end{gathered} $Асимптотика функций (53), (54) при $y \to \infty $ описывается выражениями
(55)
$\begin{gathered} {{f}_{{{\text{ex}}}}}\left( \infty \right) = \frac{{f\left( 0 \right)\left[ {2\sqrt C - f\left( 0 \right)} \right]}}{{2\sqrt {\bar {\Omega }\left( {\bar {\Omega } + 1} \right)} }}\frac{1}{y}, \\ {{f}_{{{\text{ap}}}}}\left( \infty \right) = \frac{{\sqrt C f\left( 0 \right)}}{{\sqrt {\bar {\Omega }\left( {\bar {\Omega } + 1} \right)} }}\frac{1}{y}. \\ \end{gathered} $Как и для равнобочной гиперболы, относительная ошибка δ стремится к константе
(56)
$\delta \left( \infty \right) = \left| {1 - \frac{{{{f}_{{{\text{ap}}}}}}}{{{{f}_{{{\text{ex}}}}}}}\left( \infty \right)} \right| = \frac{{f\left( 0 \right)}}{{2\sqrt C - f\left( 0 \right)}}.$Для сопоставления с данными, приведенными в разд. 3, в формулах этого раздела необходимо выполнить замены
которые обеспечивают равноудаленность оси пучка в точке старта от начала координат и правильное расположение границы пучка относительно оси.
Сравнение приближенного и точного решений. Подобно случаю равнобочной гиперболы оценим кривизну приближенной траектории по сравнению с точной кривой с теми же условиями старта при y = 0:
(58)
$\begin{gathered} {{k}_{{{\text{ex}}}}} = - \frac{{\bar {\Omega }}}{{\sqrt {{{C}_{*}}} }} = - \frac{{\bar {\Omega }}}{{\sqrt C - f\left( 0 \right)}}, \\ {{k}_{{{\text{ap}}}}} = - \frac{{\bar {\Omega }\sqrt C \left[ {\sqrt C + \left( {2\bar {\Omega } + 1} \right)f\left( 0 \right)} \right]}}{{{{{\left[ {\sqrt C + \bar {\Omega }f\left( 0 \right)} \right]}}^{3}}}}. \\ \end{gathered} $В табл. 7 для нескольких значений $\bar {\Omega } = {{k_{{{\text{ex}}}}^{H}} \mathord{\left/ {\vphantom {{k_{{{\text{ex}}}}^{H}} {k_{{{\text{ex}}}}^{0}}}} \right. \kern-0em} {k_{{{\text{ex}}}}^{0}}}$ приведены соответствующие величины вторых производных кривизны (первые производные в вершинах гипербол – нули) при наличии магнитного поля и его отсутствии ($\bar {\Omega } = 1$), отношение кривизн по параксиальной теории и точному решению при одинаковых условиях старта (дополнительные индексы Н, 0 маркируют случаи $H \ne {\text{0}}$, Н = 0 соответственно) и относительная ошибка δ в процентах
(59)
$\begin{gathered} \frac{{{{{\left( {k_{{{\text{ex}}}}^{H}} \right)}}^{{''}}}}}{{{{{\left( {k_{{{\text{ex}}}}^{0}} \right)}}^{{''}}}}}\left( 0 \right) = \frac{{{{{\bar {\Omega }}}^{2}}\left( {\bar {\Omega } + 1} \right)}}{2}, \\ K = \frac{{k_{{{\text{ap}}}}^{H}\left( 0 \right)}}{{k_{{{\text{ex}}}}^{H}\left( 0 \right)}} = \sqrt C \left[ {\sqrt C - f\left( 0 \right)} \right]\frac{{\sqrt C + \left( {2\bar {\Omega } + 1} \right)f\left( 0 \right)}}{{{{{\left[ {\sqrt C + \bar {\Omega }f\left( 0 \right)} \right]}}^{3}}}}. \\ \end{gathered} $Таблица 7.
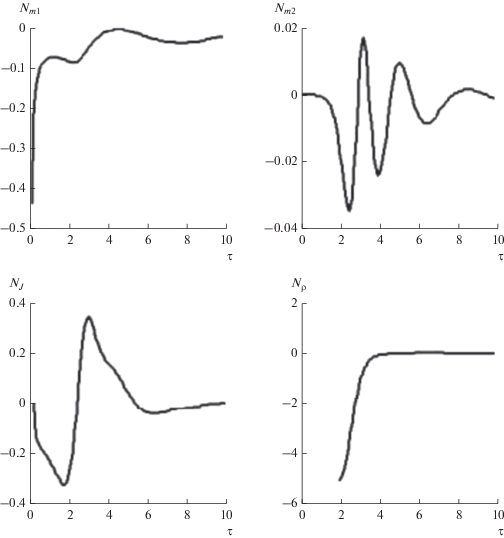
Сравнение параксиальной модели и точного решения (44) – ось-гипербола, $\vec {H} \ne 0$ (С = 1 при ${{H}_{z}} = 0$, C = 2 при ${{H}_{z}} \ne 0$, $f\left( 0 \right) = - 0.1$)
| Параметр | $\bar {\Omega }$ | ${{\bar {\Omega }}_{*}} = 2.786$ | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
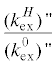 |
1 | 6 | 18 | 40 | 75 | 14.69 |
| $K$ | 1.051 | 1.093 | 1.0555 | 1.0553 | 0.880 | 1.107 |
| $\delta ,\% $ | 5.1 | 9.3 | 5.55 | 5.53 | 12.0 | 10.7 |
Отношение кривизн К имеет максимум при $\bar {\Omega } = {{\bar {\Omega }}_{*}}$
(60)
$\begin{gathered} {{{\bar {\Omega }}}_{*}} = - \frac{{\sqrt C }}{{4f\left( 0 \right)}} - \frac{3}{4}, \\ {{K}_{*}} = \frac{{32\sqrt C }}{{27\left[ {\sqrt C - f\left( 0 \right)} \right]}},\,\,\,\,f\left( 0 \right) < 0. \\ \end{gathered} $Из табл. 7 следует, что в интервале ${\text{1}} \leqslant \bar {\Omega } \leqslant 5$ ошибка в определении кривизны не превышает 12%, хотя кривизна оси меняется в пять
раз, а ответственная за распрямление траектории производная 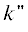 увеличивается в 75 раз. Малый параметр $\varepsilon $, определенный по отношению к ${{L}_{*}}$ из табл. 6
, в электростатическом случае составляет 0.07, а при $\bar {\Omega } = 5$ возрастает до 0.35. Делать какие-либо общие выводы из этого факта не представляется
возможным: в частном случае параксиальное приближение далеко выходит за границы ожидаемой
от него точности за счет пересечения кривых для точной и приближенной зависимостей.
увеличивается в 75 раз. Малый параметр $\varepsilon $, определенный по отношению к ${{L}_{*}}$ из табл. 6
, в электростатическом случае составляет 0.07, а при $\bar {\Omega } = 5$ возрастает до 0.35. Делать какие-либо общие выводы из этого факта не представляется
возможным: в частном случае параксиальное приближение далеко выходит за границы ожидаемой
от него точности за счет пересечения кривых для точной и приближенной зависимостей.
Как и в случае с равнобочной гиперболой, параксиальное выражение для потенциала на рассчитанной границе пучка совпадает с его точным значением:
В табл. 8 приведено сравнение точного и параксиального значений кривизны в вершине гиперболы. Видно, что для принятых констант увеличение кривизны оси $k{\text{ = }} - \bar {\Omega }$ в 2.5 раза при фиксированной величине $f\left( 0 \right)$ примерно во столько же раз увеличивает ошибку; для фиксированной кривизны пятикратное изменение $f\left( 0 \right)$ приводит к той же вариации величины δ.
Таблица 8.
Сравнение параксиальной модели и точного решения (44) – ось-гипербола, $\vec {H} \ne 0$ (С = 1, $\Omega = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, $\bar {\Omega } = {{\left( {1 + {{H}_{z}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {{H}_{z}}} \right)} {\left( {1 - {{H}_{z}}} \right)}}} \right. \kern-0em} {\left( {1 - {{H}_{z}}} \right)}}$)
| Параметры | $\bar {\Omega }$, ${{H}_{z}}$, $L{\text{*}}$ | |||
|---|---|---|---|---|
| 2, ${1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$, 0.50 | 3, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, 0.33 | 4, ${3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0em} 5}$, 0.25 | 5, ${2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$, 0.20 | |
| $f\left( 0 \right) = 0.01$ | ||||
| ${{k}_{{{\text{ex}}}}}$ | 2.020 | 3.030 | 4.040 | 5.0505 |
| ${{k}_{{{\text{ap}}}}}$ | 1.979 | 2.938 | 3.876 | 4.794 |
| $\delta ,\% $ | 2.0 | 3.0 | 4.1 | 5.1 |
| ${{N}_{{m1}}}$ | 0.0121 | 0.0494 | 0.1222 | 0.2417 |
| ${{N}_{{m2}}}$ | 0.0012 | 0.0036 | 0.0080 | 0.0180 |
| ${{N}_{J}}$ | 0.012 | 0.025 | 0.0496 | 0.0820 |
| ${{N}_{\rho }}$ | 0.001173 | 0.007313 | 0.02480 | 0.06279 |
| N | 0.0171 | 0.05596 | 0.1344 | 0.26345 |
| $f\left( 0 \right) = 0.02$ | ||||
| ${{k}_{{{\text{ex}}}}}$ | 2.041 | 3.061 | 4.082 | 5.102 |
| ${{k}_{{{\text{ap}}}}}$ | 1.956 | 2.871 | 3.747 | 4.583 |
| $\delta ,\% $ | 4.2 | 6.2 | 8.2 | 10.0 |
| ${{N}_{{m1}}}$ | 0.0243 | 0.0990 | 0.2455 | 0.4867 |
| ${{N}_{{m2}}}$ | 0.0048 | 0.0144 | 0.0320 | 0.0720 |
| ${{N}_{J}}$ | 0.0244 | 0.0502 | 0.1001 | 0.1660 |
| ${{N}_{\rho }}$ | 0.004784 | 0.03010 | 0.1030 | 0.2631 |
| N | 0.03510 | 0.1159 | 0.2672 | 0.5821 |
| $f\left( 0 \right) = 0.05$ | ||||
| ${{k}_{{{\text{ex}}}}}$ | 2.105 | 3.158 | 4.211 | 5.263 |
| ${{k}_{{{\text{ap}}}}}$ | 1.878 | 2.663 | 3.356 | 3.968 |
| $\delta ,\% $ | 11 | 16 | 20 | 25 |
| ${{N}_{{m1}}}$ | 0.061 | 0.2499 | 0.6229 | 1.2412 |
| ${{N}_{{m2}}}$ | 0.030 | 0.0900 | 0.2000 | 0.4500 |
| ${{N}_{J}}$ | 0.0653 | 0.1275 | 0.2569 | 0.4311 |
| ${{N}_{\rho }}$ | 0.0316 | 0.2041 | 0.7155 | 1.8688 |
| N | 0.099 | 0.3586 | 1.0030 | 2.3284 |
Сравнение моделей для гиперболической оси с магнитным полем и при его отсутствии приведено в табл. 9. Для варианта первого столбца табл. 6 с k = 1, С = 0.5 та же кривизна в начальной точке при $\bar {\Omega } = 2$, ${{\Omega }_{x}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ достигается при С = 4. Видно, что при $f\left( 0 \right) = - 0.025$, $ - 0.05$ ошибки в этих двух случаях примерно равны, но при $f\left( 0 \right) = - 0.1$ и ${{\Omega }_{x}} \ne 0$ ошибка резко (пятикратно) возрастает.
Таблица 9.
Сравнение случаев гиперболической оси с одинаковой кривизной в вершине при ${{H}_{z}} = 0$ и ${{H}_{z}} \ne 0$ (${{H}_{z}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$, $\bar {\Omega } = 2$, С = 4)
| Параметр | $f\left( 0 \right)$ | ||
|---|---|---|---|
| –0.025 | –0.05 | –0.1 | |
| ${{H}_{z}} \ne 0$ | |||
| ${{k}_{{{\text{ex}}}}}$ | 0.988 | 0.976 | 0.952 |
| ${{k}_{{{\text{ap}}}}}$ | 1.011 | 1.021 | 1.200 |
| $\delta ,\% $ | 2.4 | 4.6 | 26.1 |
| ${{H}_{z}} = 0$ | |||
| ${{k}_{{{\text{ex}}}}}$ | 0.976 | 0.952 | 0.909 |
| ${{k}_{{{\text{ap}}}}}$ | 0.998 | 0.991 | 0.960 |
| $\delta ,\% $ | 2.3 | 4.1 | 5.6 |
6. ЭЛЛИПТИЧЕСКИЙ ПОТОК В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
Эталонное решение. Приведенное в работе [10] решение при отличном от (44) соотношении констант $\Omega $, $\omega $ ($\Omega < \omega $) описывает течение с финитными эллиптическими орбитами частиц (рис. 6), координата х для которых определена на интервале (0, $\sqrt {{C \mathord{\left/ {\vphantom {C {\bar {\Omega }}}} \right. \kern-0em} {\bar {\Omega }}}} $):
(62)
$\begin{gathered} \left( {\omega - \Omega } \right){{x}^{2}} + \left( {\omega + \Omega } \right){{y}^{2}} = {\text{const}}, \\ Y = \sqrt {C - \bar {\Omega }{{x}^{2}}} ,\,\,\,\,\bar {\Omega } = \frac{{\omega - \Omega }}{{\omega + \Omega }}. \\ \end{gathered} $Выражения для параметров потока (44) остаются справедливыми. Ортогональная система координат $\xi ,\eta $ и коэффициенты Ляме ${{h}_{1}}$, ${{h}_{2}}$ определены формулами
(63)
$\begin{gathered} \xi = {{{{y}^{{\bar {\Omega }}}}} \mathord{\left/ {\vphantom {{{{y}^{{\bar {\Omega }}}}} x}} \right. \kern-0em} x},\,\,\,\,\eta = \bar {\Omega }{{x}^{2}} + {{y}^{2}}, \\ h_{1}^{2} = \frac{{{{x}^{2}}{{y}^{{2 - 2\bar {\Omega }}}}}}{{{{y}^{2}} + {{{\bar {\Omega }}}^{2}}{{x}^{2}}}},\,\,\,\,h_{2}^{2} = \frac{1}{{4\left( {{{y}^{2}} + {{{\bar {\Omega }}}^{2}}{{x}^{2}}} \right)}}. \\ \end{gathered} $Кривизна оси $\eta = C$ имеет вид
(64)
$k = - \frac{{\bar {\Omega }C}}{{{{{\left[ {\bar {\Omega }\left( {\bar {\Omega } - 1} \right){{x}^{2}} + C} \right]}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}.$Расстояние между двумя траекториями точного решения описывается выражением
(65)
$\begin{gathered} {{f}_{{{\text{ex}}}}} = \frac{{{{{\left[ {\bar {\Omega }\left( {\bar {\Omega } - 1} \right){{x}^{2}} + C} \right]}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{\bar {\Omega }\left( {{{{\bar {\Omega }}}^{2}} - 1} \right){{x}^{2}} + C}} \times \\ \times \,\,\left\{ {{{{\left[ {1 + \left( {{{C}_{{\text{*}}}} - C} \right)\frac{{\bar {\Omega }\left( {{{{\bar {\Omega }}}^{2}} - 1} \right){{x}^{2}} + C}}{{{{{\left[ {\bar {\Omega }\left( {\bar {\Omega } - 1} \right){{x}^{2}} + C} \right]}}^{2}}}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 1} \right\}. \\ \end{gathered} $Новая нормировка параметров потока при $\eta = C$, аналогичная (49), выполняется с использованием константы $\Omega + \omega $:
(66)
$\bar {U} = \frac{{2U}}{{{{{\left( {\Omega + \omega } \right)}}^{2}}}} = \bar {\Omega }\left( {\bar {\Omega } - 1} \right){{x}^{2}} + C.$Решение параксиального уравнения. Аналитическое решение параксиального уравнения, получающегося из уравнения (51) формальной заменой $y \to x$, $\bar {\Omega } \to - \bar {\Omega }$, определено формулой
(67)
$\begin{gathered} {{f}_{{{\text{ap}}}}} = \frac{{{{f}_{0}}}}{{\sqrt {\bar {\Omega }\left( {\bar {\Omega } - 1} \right){{x}^{2}} + C} }}, \\ f\left( 0 \right) = \sqrt {{{C}_{{\text{*}}}}} - \sqrt C = \frac{{{{f}_{0}}}}{{\sqrt C }}; \\ \end{gathered} $инжекция осуществляется с плоскости х = 0 при выполнении условий (52).
Сравнение приближенного и точного решений. Приближенное и точное значения функции f совпадают не только при х = 0, но и при y = 0 ($x = \sqrt {{C \mathord{\left/ {\vphantom {C {\bar {\Omega }}}} \right. \kern-0em} {\bar {\Omega }}}} $):
(68)
$\begin{gathered} {{f}_{{{\text{ap}}}}}\left( 0 \right) = {{f}_{{{\text{ex}}}}}\left( 0 \right) = \sqrt {C{\text{*}}} - \sqrt C , \\ {{f}_{{{\text{ap}}}}}\left( {\sqrt {{C \mathord{\left/ {\vphantom {C {\bar {\Omega }}}} \right. \kern-0em} {\bar {\Omega }}}} } \right) = {{f}_{{{\text{ex}}}}}\left( {\sqrt {{C \mathord{\left/ {\vphantom {C {\bar {\Omega }}}} \right. \kern-0em} {\bar {\Omega }}}} } \right) = \frac{{\sqrt {C{\text{*}}} - \sqrt C }}{{\sqrt {\bar {\Omega }} }}. \\ \end{gathered} $Максимальная ошибка решения имеет место в вершине эллипса с большей кривизной. Значения кривизн точной и приближенной траекторий в этой точке описываются формулами
(69)
$\begin{gathered} {{k}_{{{\text{ex}}}}}\left( {\sqrt {{C \mathord{\left/ {\vphantom {C {\bar {\Omega }}}} \right. \kern-0em} {\bar {\Omega }}}} } \right) = - \frac{1}{{\sqrt {{{C}_{*}}\bar {\Omega }} }} = - \frac{1}{{\sqrt {\bar {\Omega }} \left[ {\sqrt C + f\left( 0 \right)} \right]}}, \\ {{k}_{{{\text{ap}}}}}\left( {\sqrt {{C \mathord{\left/ {\vphantom {C {\bar {\Omega }}}} \right. \kern-0em} {\bar {\Omega }}}} } \right) = - \frac{{\sqrt {\bar {\Omega }} \left[ {\bar {\Omega }\sqrt C + \left( {2 - \bar {\Omega }} \right)f\left( 0 \right)} \right]}}{{{{{\left[ {\bar {\Omega }\sqrt C + f\left( 0 \right)} \right]}}^{2}}}}. \\ \end{gathered} $Точность вычислений существенно зависит от этой величины (табл. 10), поскольку при больших значениях отношения полуосей ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$ обход контура сопровождается резким убыванием кривизны. Для ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = - k = 2$ при $\varepsilon = {{L{\text{*}}} \mathord{\left/ {\vphantom {{L{\text{*}}} {10}}} \right. \kern-0em} {10}}$ ошибка составляет 1.6%; для ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 4$ и том же $\varepsilon $ – 7.2%; для ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 10$ и $\varepsilon = {{L{\text{*}}} \mathord{\left/ {\vphantom {{L{\text{*}}} {20}}} \right. \kern-0em} {20}}$ – уже 12.2% при уменьшении ошибки до 0.8% для $\varepsilon = {{L{\text{*}}} \mathord{\left/ {\vphantom {{L{\text{*}}} {100}}} \right. \kern-0em} {100}}$.
Таблица 10.
Сравнение параксиальной модели и точного решения (62), ось-эллипс
| $f\left( 0 \right)$ | ${{k}_{{{\text{ex}}}}}$ | ${{k}_{{{\text{ap}}}}}$ | $\delta $, % |
|---|---|---|---|
| C = 1, $\bar {\Omega } = 0.25$, ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 2$, $k = 2$, $L* = 0.5$ | |||
| 0.03 | 1.942 | 1.929 | 0.7 |
| 0.05 | 1.905 | 1.875 | 1.6 |
| 0.1 | 1.818 | 1.735 | 4.8 |
| 0.2 | 1.670 | 1.481 | 12.8 |
| C = 1, $\bar {\Omega } = 0.0625$, ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 4$, $k = 4$, $L* = 0.25$ | |||
| 0.01 | 3.96 | 3.894 | 1.7 |
| 0.015 | 3.94 | 3.811 | 3.3 |
| 0.025 | 3.90 | 3.622 | 7.2 |
| 0.05 | 3.81 | 3.148 | 17.4 |
| C = 1, $\bar {\Omega } = 0.01$, ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 10$, $k = 10$, $L* = 0.1$ | |||
| 0.001 | 9.99 | 9.91 | 0.8 |
| 0.005 | 9.95 | 8.87 | 12.2 |
| 0.01 | 9.9 | 7.475 | 24.4 |
| 0.02 | 9.804 | 5.53 | 43.6 |
Несмотря на существенное различие значений ${{k}_{{{\text{ex}}}}}$, ${{k}_{{{\text{ap}}}}}$ при ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 10$ в табл. 10, приближенная траектория вычисляется гораздо более точно, чем можно было ожидать. При уменьшении $f\left( 0 \right)$ уменьшаются и значения ${{f}_{{{\text{ex}}}}}$, ${{f}_{{{\text{ap}}}}}$, поэтому величина относительной ошибки перестает быть информативной. Абсолютная разность $\left| {{{f}_{{{\text{ex}}}}} - {{f}_{{{\text{ap}}}}}} \right|$ должна соотноситься с меньшей полуосью эллипса $b = 1$ и, как видно из табл. 11 ($f\left( 0 \right) = 0.1$), составляет 6.6% от этой величины при пятикратном отличии точного и приближенного значений кривизны. При этом параксиальная траектория в вершине эллипса на оси х отстоит от базовой кривой на расстояние, равное b.
Таблица 11.
Сравнение параксиальной модели и точного решения (62) при х = 9.5, ось – эллипс (С = 1, $\bar {\Omega } = 0.01$, ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 10$, k = 10, $L* = 0.1$)
| Параметр | f(0) | |||||
|---|---|---|---|---|---|---|
| 0.002 | 0.005 | 0.01 | 0.02 | 0.05 | 0.1 | |
| ${{k}_{{{\text{ex}}}}}$ | 9.98 | 9.95 | 9.9 | 9.8 | 9.52 | 9.09 |
| ${{k}_{{{\text{ap}}}}}$ | 9.72 | 8.87 | 7.475 | 5.53 | 2.99 | 1.73 |
| ${{f}_{{{\text{ex}}}}}$ | 0.0061 | 0.0160 | 0.0296 | 0.0573 | 0.132 | 0.241 |
| ${{f}_{{{\text{ap}}}}}$ | 0.0064 | 0.0150 | 0.032 | 0.0613 | 0.160 | 0.306 |
| ${{\delta }_{k}},\% $ | 2.7 | 12.2 | 132 | 177 | 333 | 526 |
| $\Delta f$ | 0.00032 | 0.001 | 0.0024 | 0.004 | 0.0276 | 0.0659 |
Факт точного вычисления траекторий имеет важное значение по той причине, что кроме классической формы решения внешней задачи, использующей информацию о потенциале и поле на границе потока, существует новый вид решения, в котором под двойным интегралом при $\rho = \rho \left( l \right)$ стоит квадрат коэффициента Ляме $h\left( {u,v} \right)$ системы u, v, связанной с границей пучка v = 0:
(70)
$\varphi = {{\varphi }_{i}} - \rho \left( l \right)\operatorname{Re} \int\limits_0^v {d\eta } \int\limits_0^{v - \eta } {{{h}^{2}}\left( {u + i\xi ,\eta } \right)d\xi } ,$где ${{\varphi }_{i}} = \varphi \left( {l,s} \right)$ – потенциал в потоке из (1).
Существование асимптот у траекторий в случае оси-гиперболы и выход величины δ на константу при движении вдоль пучка не позволяли судить о влиянии постоянной плотности на точность параксиального описания. Из анализа течения с эллиптической осью и сравнения с результатами разд. 4, 5 видно, что условие $\rho = {\text{const}}$ не приводит к заметному уменьшению ошибки, как этого можно было бы ожидать от параксиальной теории, описывающей пучки с постоянной в поперечном сечении плотностью.
7. ПЛОСКИЙ МАГНЕТРОН
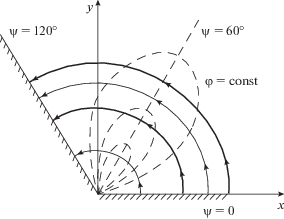
Эталонное решение. Одномерное решение для плоского магнетрона, все параметры течения в котором зависят от координаты ${{x}_{m}}$ в декартовой системе ${{x}_{m}}$, ${{y}_{m}}$, может быть построено в параметрической форме [13]. Помимо системы ${{x}_{m}}$, ${{y}_{m}}$, связанной с катодом ${{x}_{m}} = 0$, удобно использовать координаты y, z с осью z, направленной вдоль однородного магнитного поля Ω, составляющего угол ${\alpha }$ с катодом (рис. 7):
(71)
$\begin{gathered} {{x}_{m}} = y\cos \alpha + z\sin \alpha , \\ {{y}_{m}} = - y\sin \alpha + z\cos \alpha {\kern 1pt} . \\ \end{gathered} $Рис. 7.
Системы координат для плоского магнетрона (здесь и далее сплошная линия соответствует точному решению, штриховая линия – приближенному).
Конфигурация трубки тока в плоскости ${{x}_{m}}$, ${{y}_{m}}$ и зависимость сноса по х от параметра τ описываются формулами
(72)
$\begin{gathered} {{x}_{m}} = \frac{{J{{{\cos }}^{2}}\alpha }}{{{{\Omega }^{3}}}} \times \\ \times \,\,\left[ {\frac{1}{6}\left( {{\text{t}}{{{\text{g}}}^{2}}\alpha {\kern 1pt} } \right){\kern 1pt} {{\tau }^{3}} + \tau - \sin \tau + \gamma \left( {\frac{1}{2}\left( {{\text{t}}{{{\text{g}}}^{2}}\alpha } \right){{\tau }^{2}} - \cos \tau + 1} \right)} \right], \\ {{y}_{m}} = \frac{{J{{{\cos }}^{2}}\alpha }}{{{{\Omega }^{3}}}} \times \\ \times \,\,{\text{tg}}\alpha \left[ {\frac{1}{6}{{\tau }^{3}} + \sin \tau - \tau + \gamma \left( {\frac{1}{2}{{\tau }^{2}} + \cos \tau - 1} \right)} \right], \\ x = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\left[ {\frac{1}{2}{{\tau }^{2}} + \cos \tau - 1 + \gamma \left( {\tau - \sin {\kern 1pt} \tau } \right)} \right]; \\ \gamma = \frac{{E\Omega }}{J},\,\,\,\,\tau = \Omega t,\,\,\,\frac{d}{{dt}} = \Omega \frac{d}{{d\tau }}. \\ \end{gathered} $Здесь t – время; J, E – плотность тока эмиссии и электрическое поле на катоде; при $\gamma \ne 0$ и $\gamma = 0$ имеет место эмиссия в Т- и ρ-режиме соответственно; дифференцирование по параметру τ далее будем отмечать точкой.
Заметим, что две правые системы ${{x}_{m}}$, ${{y}_{m}}$, х и l, s, x имеют противоположно направленные оси по циклической координате х. По этой причине сносовая скорость $w = {{dx} \mathord{\left/ {\vphantom {{dx} {dt}}} \right. \kern-0em} {dt}}$ точного решения отличается по знаку от той же величины в параксиальной модели:
В координатах x, y, z для траектории, компонент скорости и потенциала имеем
(74)
$\begin{gathered} y = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\left[ {\tau - \sin \,\tau + \gamma \left( {1 - \cos \tau } \right)} \right], \\ z = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\frac{1}{2}{\text{tg}}{\kern 1pt} \alpha \left( {\frac{1}{3}{{\tau }^{3}} + \gamma {{\tau }^{2}}} \right), \\ \frac{{dy}}{{dt}} = \Omega \dot {y} = \frac{{J\cos \alpha }}{{{{\Omega }^{2}}}}\left( {1 - \cos \,\tau + \gamma \sin \tau } \right), \\ \frac{{dz}}{{dt}} = \Omega \dot {z} = \frac{{J\cos \alpha }}{{{{\Omega }^{2}}}}\frac{1}{2}{\text{tg}}\alpha \left( {{{\tau }^{2}} + 2\gamma \tau } \right), \\ \frac{{dx}}{{dt}} = \Omega \dot {x} = \Omega y,\,\,\,\,{{V}_{l}} = \Omega \sqrt {{{{\dot {y}}}^{2}} + {{{\dot {z}}}^{2}}} , \\ \rho {{V}_{l}}f = J{{f}_{0}},\,\,\,\,\varphi = \frac{{{{J}^{2}}{{{\cos }}^{2}}\alpha }}{{{{\Omega }^{4}}}} \times \\ \times \,\,\left[ {\frac{1}{8}\left( {{\text{t}}{{{\text{g}}}^{2}}\alpha } \right){{\tau }^{4}} + \frac{1}{2}{{\tau }^{2}} - \cos \tau + 1 - \tau \sin \tau + } \right. \\ + \,\,{{\gamma }^{2}}\left( {\frac{{\text{1}}}{{\text{2}}}\left( {{\text{t}}{{{\text{g}}}^{2}}\alpha } \right){{\tau }^{2}} - \cos \tau + 1} \right) + \\ \left. { + \,\,\gamma \left( {\frac{1}{2}\left( {{\text{t}}{{{\text{g}}}^{2}}\alpha } \right){{\tau }^{3}} + \tau - \tau \cos \tau } \right)} \right]. \\ \end{gathered} $Параксиальное уравнение. Для параметрической формы решения (72), (74) левая часть параксиального уравнения (1) равна ${{\Omega }^{2}}\ddot {f}$, а в правой части необходимо перейти от дифференцирования по координате l к переменной τ при помощи соотношения
(75)
$\frac{d}{{dl}} = \frac{1}{{{{V}_{l}}}}\frac{d}{{dt}} = \frac{\Omega }{{{{V}_{l}}}}\frac{d}{{d{\tau }}}.$Исключим постоянные множители при функциях от τ в формулах (74), обозначая результат перенормировки чертой
(76)
$\begin{gathered} y = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\bar {y},\,\,\,\,z = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\bar {z},\,\,\,\dot {y} = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\dot {\bar {y}}, \\ \dot {z} = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\dot {\bar {z}},\,\,\,\,{{x}_{m}} = \frac{{J{{{\cos }}^{2}}\alpha }}{{{{\Omega }^{3}}}}{{{\bar {x}}}_{m}}, \\ {{y}_{m}} = \frac{{J{{{\cos }}^{2}}\alpha }}{{{{\Omega }^{3}}}}{{{\bar {y}}}_{m}},\,\,\,\,{{V}_{l}} = \frac{{J\cos \alpha }}{{{{\Omega }^{2}}}}{{{\bar {V}}}_{l}}, \\ {{V}_{x}} = \frac{{J\cos \alpha }}{{{{\Omega }^{2}}}}{{{\bar {V}}}_{x}},\,\,\,\,\varphi \equiv U = \frac{{{{J}^{2}}{{{\cos }}^{2}}\alpha }}{{{{\Omega }^{4}}}}\bar {U}, \\ E = \frac{{J\cos \alpha }}{\Omega }\bar {E},\,\,\,\,N = {{\Omega }^{2}}\bar {N},\,\,\,\,\rho = {{\Omega }^{2}}\bar {\rho }, \\ {{\Omega }_{l}} = \Omega {{{\bar {\Omega }}}_{l}},\,\,\,\,{{\Omega }_{s}} = \Omega {{{\bar {\Omega }}}_{s}}, \\ h = \frac{{J\cos \alpha }}{{{{\Omega }^{3}}}}\bar {h},\,\,\,k = \frac{{{{\Omega }^{3}}}}{{J\cos \alpha }}\bar {k}. \\ \end{gathered} $Для величин, входящих в правую часть уравнения (1), имеем
(77)
$\begin{gathered} 2\bar {U} = {{{\bar {h}}}^{2}} + {{{\bar {y}}}^{2}},\,\,\,\,\bar {h} = \sqrt {{{{\dot {\bar {y}}}}^{2}} + {{{\dot {\bar {z}}}}^{2}}} ,\,\,\,\,{{{\bar {V}}}_{l}} = \bar {h},\,\,\,\,{{{\bar {V}}}_{x}} = - \bar {y}, \\ {{{\bar {\Omega }}}_{l}} = \frac{{\dot {\bar {z}}}}{{\bar {h}}},\,\,\,\,{{{\bar {\Omega }}}_{s}} = - \frac{{\dot {\bar {y}}}}{{\bar {h}}},\,\,\,\,{{\Omega }_{{l0}}} = \Omega \sin \alpha , \\ \bar {k} = \frac{1}{{{{{\bar {h}}}^{3}}}}\left( {\ddot {\bar {y}}{\kern 1pt} \dot {\bar {z}} - \ddot {\bar {z}}{\kern 1pt} \dot {\bar {y}}} \right),\,\,\,\,\bar {E} = \bar {k}{{{\bar {h}}}^{2}} + \bar {y}{{{\bar {\Omega }}}_{l}}, \\ \bar {\rho } = \frac{{{{f}_{0}}}}{{f{\kern 1pt} \bar {h}\cos {\alpha }}},\,\,\,\,{\text{tg}}\vartheta = \frac{{\dot {y}}}{{\dot {z}}}, \\ - {{V}_{x}}\frac{{d{{\Omega }_{s}}}}{{dl}} = {{\Omega }^{2}}\frac{1}{{\bar {h}}}\bar {k}{\kern 1pt} \dot {\bar {z}}{{{\bar {V}}}_{x}},\,\,\,\frac{{{{d}^{2}}U}}{{d{{l}^{2}}}} = {{\Omega }^{2}}\frac{1}{{\bar {h}}}{{\left( {\frac{1}{{\bar {h}}}\dot {\bar {U}}} \right)}^{\centerdot }}. \\ \end{gathered} $После введения новой искомой функции
уравнение для $\bar {f}$ приобретает универсальный вид и содержит два параметра: γ, α . Опуская символ нормировки (черту), имеем
(79)
$\begin{gathered} \ddot {f} = \frac{1}{{h\cos \alpha }} - \\ - \,\,\left[ {\frac{1}{h}{{{\left( {\frac{1}{h}\dot {U}} \right)}}^{\centerdot }} + 2{{k}^{2}}{{h}^{2}} + \frac{1}{{{{h}^{2}}}}{{{\dot {z}}}^{2}} - \frac{1}{h}ky\dot {z}} \right]f + \\ + \,\,\sin \alpha \left( {\frac{1}{h}\dot {z} - 2ky} \right). \\ \end{gathered} $Асимптотическое поведение функции ${f \mathord{\left/ {\vphantom {f {{{f}_{0}}}}} \right. \kern-0em} {{{f}_{0}}}}$ при ${\tau } \to \infty $ определено соотношениями
(80)
$\begin{gathered} \dot {z} = h\sim \frac{1}{2}\left( {{\text{tg}}\alpha } \right){{\tau }^{{\text{2}}}},\,\,\,\,k\sim \frac{1}{{{{{\tau }}^{{\text{4}}}}}},\,\,\,\,k{{V}_{l}}\sim \frac{1}{{{{\tau }^{{\text{2}}}}}}, \\ \frac{1}{h}{{\left( {\frac{1}{h}\dot {U}} \right)}^{\centerdot }}\sim \frac{1}{{{{\tau }^{2}}}},\,\,\,\,\frac{{\dot {z}}}{h} = 1. \\ \end{gathered} $В результате уравнение (78) принимает вид
Функция $\bar {f}$ описывает установившиеся колебания возле величины $\sin \,\alpha $ с периодом по τ = $ = \Omega t = 2\pi $ и амплитудой А, определяемой предысторией решения.
В соответствии с теорией антипараксиальных разложений [1] кривизна траектории вблизи катода в Т-режиме описывается соотношением
(82)
$k = - \frac{1}{6}\frac{{{{\Omega }^{2}}\sin \,2\alpha }}{E}\left( {1 - \frac{7}{{16}}\frac{J}{{E\sqrt {2E} }}{{X}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right),$где Х – расстояние по нормали к стартовой поверхности. Учитывая асимптотику (82), можно предположить, что максимальное по модулю значение этот параметр имеет в точке старта. Расчеты это предположение подтверждают.
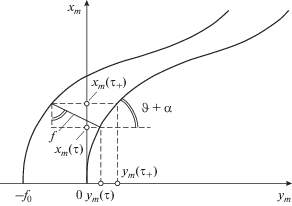
Сравнение точной и параксиальной траекторий. Точная траектория с начальными условиями параксиальной задачи получается при трансляции осевой кривой пучка вдоль оси ${{y}_{m}}$ (рис. 8). Параксиальная траектория определена параметрическими уравнениями
(83)
$\begin{gathered} x_{m}^{{{\text{ap}}}} = x_{m}^{{{\text{ex}}}} + f\cos \left( {\vartheta + {\alpha }} \right), \\ y_{m}^{{{\text{ap}}}} = y_{m}^{{{\text{ex}}}} - f\sin \left( {\vartheta + {\alpha }} \right). \\ \end{gathered} $Ниже при решении трансцендентного уравнения с отысканием параметра ${{{\tau }}_{*}}$ удобно перейти от ${{x}_{m}}$, ${{y}_{m}}$ к ${{\bar {x}}_{m}}$, ${{\bar {y}}_{m}}$; в результате перенормировки функция f в (83) имеет следующий смысл:
Точное расстояние f между двумя траекториями решения (72) следует из соотношений (см. рис. 8)
(85)
$\begin{gathered} {{x}_{m}}\left( \tau \right) + f\left( \tau \right)\cos \left[ {\vartheta \left( \tau \right) + \alpha } \right] = {{x}_{m}}\left( {\tau {\kern 1pt} *} \right), \\ {{y}_{m}}\left( \tau \right) - f\left( \tau \right)\sin \left[ {\vartheta \left( \tau \right) + \alpha } \right] = {{y}_{m}}\left( {\tau {\kern 1pt} *} \right) - {{f}_{0}}. \\ \end{gathered} $Параметр ${\tau *}$ при заданном ${\tau }$ удовлетворяет уравнению
(86)
$\begin{gathered} \frac{{{{x}_{m}}\left( {\tau {\kern 1pt} *} \right)}}{{\cos \left[ {\vartheta \left( \tau \right) + \alpha } \right]}} + \frac{{{{y}_{m}}\left( {\tau {\kern 1pt} *} \right)}}{{\sin \left[ {\vartheta \left( \tau \right) + \alpha } \right]}} = \\ = \frac{{{{x}_{m}}\left( \tau \right)}}{{\cos \left[ {\vartheta \left( \tau \right) + \alpha } \right]}} + \frac{{{{y}_{m}}\left( \tau \right) + {{f}_{0}}}}{{\sin \left[ {\vartheta \left( \tau \right) + \alpha } \right]}}. \\ \end{gathered} $Зная значение $\tau {\kern 1pt} *$, величину f можно определить из любого уравнения (85).
Кривизна линии (83) описывается выражением
(87)
${{k}_{{{\text{ap}}}}} = \frac{{\ddot {x}_{m}^{{{\text{ap}}}}\dot {y}_{m}^{{{\text{ap}}}} - \ddot {y}_{m}^{{{\text{ap}}}}\dot {x}_{m}^{{{\text{ap}}}}}}{{{{{\left[ {{{{\left( {\dot {x}_{m}^{{{\text{ap}}}}} \right)}}^{2}} + {{{\left( {\dot {y}_{m}^{{{\text{ap}}}}} \right)}}^{2}}} \right]}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}.$Для производных в формуле (87) имеем
(88)
$\begin{gathered} {{\left( {\cos \vartheta } \right)}^{\centerdot }} = - \dot {y}k,\,\,\,\,{{\left( {\sin \vartheta } \right)}^{\centerdot }} = \dot {z}k; \\ \dot {x}_{m}^{{{\text{ap}}}} = {{{\dot {x}}}_{m}}\left( {1 - fk} \right) + \dot {f}\cos \left( {\vartheta + \alpha } \right), \\ \dot {y}_{m}^{{{\text{ap}}}} = {{{\dot {y}}}_{m}}\left( {1 - fk} \right) - \dot {f}\sin \left( {\vartheta + \alpha } \right); \\ h_{{{\text{ap}}}}^{2} = {{\left( {\dot {x}_{m}^{{{\text{ap}}}}} \right)}^{2}} + {{\left( {\dot {y}_{m}^{{{\text{ap}}}}} \right)}^{2}} = {{h}^{2}}{{\left( {1 - fk} \right)}^{2}} + \\ + \,\,{{{\dot {f}}}^{2}} + 2\dot {f}\left( {1 - fk} \right)\left( {\dot {y}\cos \vartheta - \dot {z}\sin \vartheta } \right); \\ \ddot {x}_{m}^{{{\text{ap}}}}\dot {y}_{m}^{{{\text{ap}}}} - \ddot {y}_{m}^{{{\text{ap}}}}\dot {x}_{m}^{{{\text{ap}}}} = k{{h}^{3}}{{\left( {1 - fk} \right)}^{2}} + \\ + \,\,\ddot {f}\left( {1 - fk} \right)\left( {\dot {y}\sin \vartheta + \dot {z}\cos \vartheta } \right) + \\ + \,\,\dot {f}\left( {1 - fk} \right)\left[ { - \ddot {y}\sin \left( {\vartheta + 2\alpha } \right) + \ddot {z}\cos \left( {\vartheta + 2\alpha } \right)} \right] + \\ + \,\,\dot {f}\left( {f\dot {k} + 2\dot {f}k} \right)\left[ {\dot {y}\sin \left( {\vartheta + 2\alpha } \right) - \dot {z}\cos \left( {\vartheta + 2\alpha } \right)} \right] - \\ - \,\,2\dot {f}\ddot {f}\sin \,\left( {\vartheta + \alpha } \right)\cos \left( {\vartheta + \alpha } \right). \\ \end{gathered} $Согласно теории антипараксиальных разложений при эмиссии в Т-режиме с плоскости при $E,{\kern 1pt} \,\Omega = {\text{const}}$ траекторная функция при малых ${\tau }$ имеет вид [1]
(89)
$\bar {f} = 1 + 0 \cdot {\tau } + 0 \cdot {{{\tau }}^{2}} + 0 \cdot {{{\tau }}^{3}} + {{f}_{4}}{{{\tau }}^{4}} + ...$Этот же результат следует из локального рассмотрения параксиального уравнения (79). Принимая во внимание соотношения (88), (89), для кривизны приближенной траектории в точке старта получаем
(90)
${{k}_{{{\text{ap}}}}}\left( 0 \right) = \frac{k}{{1 - {{f}_{0}}k}},\,\,\,\,K = \frac{{{{k}_{{{\text{ap}}}}}}}{k} = \frac{1}{{1 - {{f}_{0}}k}}.$Для параметров пучка, близких к параметрам планарного гиротрона [14] ($\Omega = 2.9$, J = 0.116, $\alpha = 30^\circ $, $\gamma = 15$), которые в дальнейшем используются во всех численных примерах, формулы (90) принимают вид
В табл. 12 приведены значения отношения кривизн $K$, а также соответствующие величины малого геометрического параметра $\varepsilon = {{{{f}_{0}}} \mathord{\left/ {\vphantom {{{{f}_{0}}} {L{\text{*}}}}} \right. \kern-0em} {L{\text{*}}}}$ при нескольких значениях ${{f}_{0}}$.
Таблица 12.
Сравнение параксиальной модели и точного решения (72) – плоский магнетрон
| Параметр | ${{f}_{0}}$ | |||
|---|---|---|---|---|
| 0.01 | 0.02 | 0.05 | 0.1 | |
| K | 0.980 | 0.961 | 0.908 | 0.832 |
| $\delta ,\% $ | 2.0 | 3.9 | 9.2 | 16.8 |
| $\varepsilon $ | 0.0202 | 0.0404 | 0.101 | 0.202 |
| ${{N}_{{m1}}}$ | 8.812 × 10–4 | 3.504 × 10–3 | 0.022 | 0.085 |
| ${{N}_{{m2}}}$ | 3.201 × 10–4 | 1.232 × 10–3 | 7.583 × 10–3 | 0.035 |
| ${{N}_{J}}$ | 0.042 | 0.081 | 0.184 | 0.347 |
| ${{N}_{\rho }}\,\,(\tau = 2)$ | 0.293 | 0.636 | 2.000 | 5.444 |
| ${{N}_{\rho }}\,\,(\tau = 1)$ | 0.454 | 1.286 | 6.088 | 22.044 |
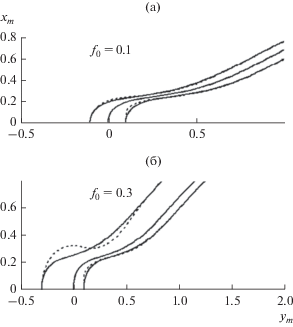
Сравнение функций ${{f}_{{{\text{ex}}}}}\left( \tau \right)$ из (85) и решения ${{f}_{{{\text{ap}}}}}\left( \tau \right)$ дифференциального уравнения (79) при ${{f}_{0}}$ = 0.1, 0.3 иллюстрирует рис. 9а, 9б соответственно. В табл. 13 представлены значения этих функций. Максимальная ошибка в 34% и 83% имеет место при $\tau = 3$ на расстоянии ${{x}_{m}}$ = 0.18 от катода, в то время как после ${{x}_{m}}$ = 0.54 ($\tau = 7$) различие между точным и приближенным решениями не превышает 2 и 7% соответственно; упомянутые расстояния ${{x}_{m}}$ составляют примерно $0.4L{\text{*}}$ и $1.25L{\text{*}}$.
Рис. 9.
Сравнение точного (сплошная линия) и приближенного (пунктирная линия) значений функции f для магнетрона.
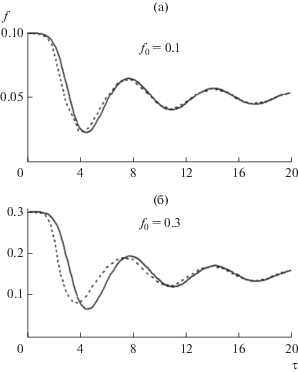
Таблица 13.
Сопоставление функций ${{f}_{{{\text{ex}}}}}\left( {\tau } \right)$ и ${{f}_{{{\text{ap}}}}}\left( {\tau } \right)$ для решения (72) – плоский магнетрон
| τ | ${{\tau }_{*}}$ | ${{f}_{{{\text{ex}}}}}$ | ${{f}_{{{\text{ap}}}}}$ | δ, % |
|---|---|---|---|---|
| ${{f}_{0}} = 0.1$ | ||||
| 0 | 0 | 0.1 | 0.1 | 0 |
| 1 | 1.1482 | 0.0996 | 0.0997 | 0.1 |
| 1.5 | 1.7746 | 0.0975 | 0.0983 | 0.8 |
| 2 | 2.4711 | 0.0894 | 0.0935 | 4.6 |
| 2.5 | 3.1926 | 0.0696 | 0.0816 | 17.2 |
| 3 | 3.7938 | 0.0462 | 0.0618 | 33.7 |
| 4 | 4.6963 | 0.0242 | 0.0278 | 14.9 |
| 4.3 | 4.9545 | 0.0236 | 0.0240 | 1.7 |
| 4.7 | 5.3045 | 0.0261 | 0.0233 | 10.7 |
| 5 | 5.5701 | 0.0301 | 0.0257 | 14.6 |
| 6 | 6.4486 | 0.0489 | 0.0442 | 9.6 |
| 7 | 7.3306 | 0.0627 | 0.0612 | 2.4 |
| 8 | 8.2725 | 0.0642 | 0.0647 | 0.8 |
| 9 | 9.2590 | 0.0552 | 0.0568 | 2.9 |
| ${{f}_{0}} = 0.3$ | ||||
| 0 | 0 | 0.3 | 0.3 | 0 |
| 1 | 1.4104 | 0.2982 | 0.2991 | 0.3 |
| 1.3 | 1.9110 | 0.2936 | 0.2973 | 1.3 |
| 1.5 | 2.2875 | 0.2867 | 0.2948 | 2.8 |
| 1.7 | 2.7077 | 0.2737 | 0.2908 | 6.25 |
| 2 | 3.4049 | 0.2364 | 0.2804 | 18.6 |
| 3 | 5.0207 | 0.1011 | 0.1855 | 83.5 |
| 3.5 | 5.4510 | 0.0835 | 0.1240 | 48.5 |
| 4 | 5.8348 | 0.0856 | 0.0835 | 2.45 |
| 4.3 | 6.0627 | 0.0936 | 0.0719 | 23.2 |
| 4.5 | 6.2145 | 0.1011 | 0.0692 | 31.55 |
| 5 | 6.5854 | 0.1245 | 0.0771 | 38.1 |
| 6 | 7.2561 | 0.1693 | 0.1325 | 21.7 |
| 7 | 7.9410 | 0.1925 | 0.1835 | 5.3 |
На рис. 10 представлены точная и приближенная конфигурации электронного потока.
Точное и приближенное значения потенциала на параксиальной траектории. Задав на оси пучка точку, соответствующую параметру $\tau $, величину $\tau {\kern 1pt} *$ найдем из уравнения (см. рис. 8, где вместо точной траектории взята приближенная)
Точное значение потенциала в точке сравнения определяет функция $\bar {U}\left( {\tau {\kern 1pt} *} \right)$. Параксиальное выражение для потенциала при $\tau = \tau {\kern 1pt} *$ описывается формулой
(93)
$\begin{gathered} {{{\bar {U}}}_{{{\text{ap}}}}} = \bar {U}\left( \tau \right) + \frac{{{{\Omega }^{3}}{{f}_{0}}}}{{J\cos \alpha }}\bar {E}{\kern 1pt} \bar {f} + \frac{1}{2}{{\left( {\frac{{{{\Omega }^{3}}{{f}_{0}}}}{{J\cos \alpha }}} \right)}^{2}} \times \\ \times \,\,\left[ {\frac{1}{{\bar {h}{\kern 1pt} \bar {f}\cos \alpha }} - \frac{1}{{\bar {h}}}{{{\left( {\frac{1}{{\bar {h}}}\dot {\bar {U}}} \right)}}^{\centerdot }} + \bar {k}{\kern 1pt} \bar {E}} \right]{{{\bar {f}}}^{2}}. \\ \end{gathered} $В табл. 14 приведены результаты сравнения, показывающие, что максимальное отличие приближенного потенциала на параксиальной траектории от точной величины при ${{f}_{0}}$ = 0.1, 0.3 составляет 4 и 9.2% соответственно.
Таблица 14.
Сопоставление на приближенной траектории точного ${{\varphi }_{{{\text{ex}}}}}$ и параксиального ${{\varphi }_{{{\text{ap}}}}}$ значений потенциала для плоского магнетрона (72)
| τ | ${{f}_{0}} = 0.1$ | ${{f}_{0}} = 0.3$ | ||||||
|---|---|---|---|---|---|---|---|---|
| ${{\tau }_{*}}$ | ${{\varphi }_{{{\text{ex}}}}}$ | ${{\varphi }_{{{\text{ap}}}}}$ | δ, % | ${{\tau }_{*}}$ | ${{\varphi }_{{{\text{ex}}}}}$ | ${{\varphi }_{{{\text{ap}}}}}$ | δ, % | |
| 0.2 | 0.226 | 7.497 | 7.718 | 2.96 | 0.269 | 10.359 | 11.027 | 6.44 |
| 0.3 | 0.338 | 16.944 | 17.448 | 2.97 | 0.405 | 23.456 | 24.967 | 6.44 |
| 1 | 1.148 | 190.34 | 196.53 | 3.25 | 1.412 | 270.90 | 289.64 | 6.92 |
| 2 | 2.494 | 719.76 | 749.02 | 4.07 | 3.783 | 1105.5 | 1200.5 | 8.59 |
| 3 | 4.142 | 1243 | 1291 | 3.86 | 6.075 | 1860.7 | 2031.8 | 9.20 |
| 4 | 4.793 | 1424 | 1451 | 1.90 | 5.808 | 1777.9 | 1859.9 | 4.61 |
8. ВЫЧИСЛЕНИЕ НЕВЯЗОК
Невязки параксиальной модели. При проведении практических расчетов с параксиальной моделью суждения о величине ошибки можно получить, подставляя в точные уравнения пучка в системе l, s, x [2]
(94)
$\begin{gathered} {\text{2}}\varphi = v_{l}^{2} + v_{s}^{2} + v_{x}^{2},\,\,\,\,{{h}_{1}} = 1 - ks, \\ {{v}_{s}}\left[ {\frac{{\partial {{v}_{s}}}}{{dl}} - \frac{\partial }{{\partial s}}\left( {{{h}_{1}}{{v}_{l}}} \right) + {{h}_{1}}{{H}_{x}}} \right] + {{v}_{x}}\left( {\frac{{\partial {{{v}}_{x}}}}{{\partial l}} - {{h}_{1}}{{H}_{s}}} \right) = 0, \\ \frac{{{{v}_{l}}}}{{{{h}_{1}}}}\left( {\frac{{\partial {{v}_{x}}}}{{\partial l}} - {{h}_{1}}{{H}_{s}}} \right) + {{v}_{s}}\left( {\frac{{\partial {{v}_{x}}}}{{\partial s}} + {{H}_{l}}} \right) = 0, \\ \frac{\partial }{{\partial l}}\left( {\rho {{v}_{l}}} \right) + \frac{\partial }{{\partial s}}\left( {{{h}_{1}}\rho {{v}_{s}}} \right) = 0, \\ \frac{\partial }{{\partial l}}\left( {\frac{1}{{{{h}_{1}}}}\frac{{\partial \varphi }}{{\partial l}}} \right) + \frac{\partial }{{\partial s}}\left( {{{h}_{1}}\frac{{\partial \varphi }}{{\partial s}}} \right) = {{h}_{1}}\rho , \\ \frac{{\partial {{H}_{s}}}}{{\partial l}} - \frac{\partial }{{\partial s}}\left( {{{h}_{1}}{{H}_{l}}} \right) = 0,\,\,\,\frac{{\partial {{H}_{l}}}}{{\partial l}} + \frac{\partial }{{\partial s}}\left( {{{h}_{1}}{{H}_{s}}} \right) = 0, \\ {{H}_{x}} = {\text{const}} \\ \end{gathered} $выражения для параметров потока из (1) и сообразуясь с соотношением невязки N и относительной ошибки δ для рассмотренных выше точных решений.
В качестве критерия точности N можно использовать корень квадратный из суммы квадратов невязок по уравнениям (94), локальный максимум $\left| N \right|$ для уравнения с наибольшим значением этой величины, так или иначе определенное среднее значение $\left| N \right|$ по области, в которой строится решение. Как правило, все эти величины имеют один порядок. Для невязок, соответствующих интегралу энергии, двум уравнениям движения $\vec {v} \times {\text{rot}}\vec {P} = 0$ ($\vec {P}$ – обобщенный импульс), уравнению сохранения тока, уравнению Пуассона, уравнениям для ${\text{rot}}{\kern 1pt} \vec {H}$ и ${\text{div}}{\kern 1pt} \vec {H}$ в (94), примем обозначения ${{N}_{{m1}}}$, ${{N}_{{m2}}}$, ${{N}_{{m3}}}$, ${{N}_{J}}$, ${{N}_{{\rho }}}$, ${{N}_{{H1}}}$, ${{N}_{{H2}}}$. В результате имеем
(95)
$\begin{gathered} {{N}_{J}} = \frac{1}{f}\left( {\rho {{V}_{l}}f} \right){\kern 1pt} '\,\, + \left[ {\rho \left( {k{{V}_{l}} + {{\Omega }_{x}}} \right)} \right]{\kern 1pt} 's + \\ + \,\,\left[ {2{{\Omega }_{x}} - 3k\left( {k{{V}_{l}} + {{\Omega }_{x}}} \right)s} \right]\rho \frac{{f{\kern 1pt} '}}{f}s, \\ {{N}_{{\rho }}} = \frac{1}{{h_{1}^{2}}}k{\kern 1pt} '\left[ {U{\kern 1pt} '\,\, + E{\kern 1pt} 's + \frac{1}{2}\left( {\rho - \bar {N}} \right){\kern 1pt} '{{s}^{2}}} \right]s + \\ \end{gathered} $Решение (4) с траекториями-окружностями. Отличие решения (9) от точного решения (4) характеризуется единственной отличной от нуля невязкой ${{N}_{{\rho }}}$
(96)
$\begin{gathered} {{N}_{{\rho }}} = \frac{1}{{{{h}_{1}}}}{{\sin }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\frac{{3\psi }}{2} \times \\ \times \,\,\left[ {\left( {4{\kern 1pt} {\text{ct}}{{{\text{g}}}^{2}}\frac{{3\psi }}{2} - 20} \right)s + \left( {{\text{2ct}}{{{\text{g}}}^{2}}\frac{{3\psi }}{2} + 2} \right){{s}^{2}}} \right]. \\ \end{gathered} $В последнем столбце табл. 1 приведены значения ${{N}_{{\rho }}}$ на линии симметрии решения $\psi = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$. Параксиальный подход не дает возможности восстановить структуру особенности на катоде при существенно неоднородном токоотборе, заменяя точную зависимость для плотности тока J из (4) константой. По этой причине невязка ${{N}_{{\rho }}}$ при $\psi \to 0$ обращается в бесконечность, но затем быстро убывает (при ${{3\psi } \mathord{\left/ {\vphantom {{3\psi } 2}} \right. \kern-0em} 2} = 10^\circ $, $s = 0.1$, ${{N}_{{\rho }}} = 1.12$), проходит через нуль и приближается к приведенному в таблице значению. Видно, что ${{N}_{{\rho }}}\sim 1$ соответствует ошибке в 1.5%, ${{N}_{{\rho }}}\sim 2$ – ошибке в 5.5%. Подобного же соответствия можно ожидать при эмиссии со слабо искривленной поверхности с неоднородным токоотбором.
Решение (44) с осью пучка в виде гиперболы. Для параксиальных течений с гиперболической осью формулы (95) принимают вид
(97)
$\begin{gathered} {{N}_{J}} = - 2\bar {\Omega }\left( {\bar {\Omega } + 1} \right)\sqrt {\bar {\Omega }{{y}^{2}} + C} F{{D}^{5}}y\left( {1 + \frac{3}{2}C\bar {\Omega }{{D}^{3}}s} \right)s, \\ {{N}_{{\rho }}} = \left( {\bar {\Omega } - 1} \right)C{{D}^{{10}}}\left[ {\frac{3}{2}{{{\bar {\Omega }}}^{3}}{{{\left( {\bar {\Omega } + 1} \right)}}^{2}}} \right. \times \\ \times \,\,\left( {2{{{\bar {\Omega }}}^{3}} + 2{{{\bar {\Omega }}}^{2}} - 1} \right){{y}^{6}} + C{{{\bar {\Omega }}}^{2}}\left( {\bar {\Omega } + 1} \right) \times \\ \times \,\,\left( {4{{{\bar {\Omega }}}^{4}} + 9{{{\bar {\Omega }}}^{3}} + 5{{{\bar {\Omega }}}^{2}} - 2\bar {\Omega } - \frac{5}{2}} \right){{y}^{4}} + \\ + \,\,{{C}^{2}}\bar {\Omega }\left( {3{{{\bar {\Omega }}}^{4}} + {{{\bar {\Omega }}}^{3}} + 3{{{\bar {\Omega }}}^{2}} - \frac{1}{2}\bar {\Omega } - \frac{1}{2}} \right){{y}^{2}} + \\ + \,\,\left. {{{C}^{3}}\left( { - {{{\bar {\Omega }}}^{3}} - \bar {\Omega } + \frac{1}{2}} \right)} \right]{{s}^{2}} + {{C}^{2}}\bar {\Omega }\left( {\bar {\Omega } - 1} \right){{D}^{{13}}} \times \\ \times \,\,\left\{ { - \frac{3}{2}{{{\bar {\Omega }}}^{4}}{{{\left( {\bar {\Omega } + 1} \right)}}^{3}}{{y}^{8}} + {{{\bar {\Omega }}}^{3}}} \right.{{\left( {\bar {\Omega } + 1} \right)}^{2}}\left[ {\frac{3}{2} + } \right. \\ \end{gathered} $При $y \to \infty $ все невязки в (97) обращаются в нуль, а при $y = 0$, где кривизна оси максимальна, имеем
(98)
$\begin{gathered} {{N}_{{m1}}} = 0,\,\,\,\,{{N}_{{m2}}} = \frac{{{{{\bar {\Omega }}}^{2}}\left( {\bar {\Omega } + 1} \right)}}{C}{{s}^{2}},\,\,\,{{N}_{J}} = 0, \\ {{N}_{{\rho }}} = - \frac{{\bar {\Omega } - 1}}{C}\left[ {{{{\bar {\Omega }}}^{2}}\left( {\bar {\Omega } + 1} \right) - \frac{1}{2}} \right]\left( {1 + \frac{{\bar {\Omega }}}{{\sqrt C }}s} \right){{s}^{2}}. \\ \end{gathered} $Из формул (98) видно, что при нулевой невязке по интегралу энергии ${{N}_{{m1}}}$ невязки по второму уравнению движения ${{N}_{{m2}}}$ и уравнению Пуассона ${{N}_{{\rho }}}$, примерно сравнивающиеся при $\bar {\Omega } = 2$, различаются в четыре раза при $\bar {\Omega } = 5$. Как и следовало ожидать, небольшая невязка по интегралу энергии, часто анализируемая в программах траекторного анализа, является необходимым, но далеко не достаточным условием близости приближенного решения к точному. Для модельной задачи о пучке с гиперболической осью ошибка может быть сколь угодно велика при увеличении начальной кривизны оси и толщины пучка при ${{N}_{{m1}}} = 0$.
При отсутствии магнитного поля формулы (97) принимают вид
(99)
$\begin{gathered} {{N}_{{m1}}} = \frac{{C\left( {{{x}^{2}} + 2C} \right)}}{{\sqrt 2 {{{\left( {{{x}^{2}} + C} \right)}}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}}}}\left[ {2 + \frac{C}{{\sqrt 2 {{{\left( {{{x}^{2}} + C} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}s} \right]s, \\ {{N}_{{m2}}} = - \frac{{C\left( {3{{x}^{4}} + 6C{{x}^{2}} - 2{{C}^{2}}} \right)}}{{2{{{\left( {{{x}^{2}} + C} \right)}}^{4}}}}{{s}^{2}},\,\,\,{{N}_{{\rho }}} \equiv 0, \\ {{N}_{J}} = \frac{{C\sqrt 2 x\sqrt {{{x}^{2}} + 2C} }}{{{{{\left( {{{x}^{2}} + C} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\left[ {1 + \frac{{3C}}{{2\sqrt 2 }}\frac{1}{{{{{\left( {{{x}^{2}} + C} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}s} \right]s. \\ \end{gathered} $В вершине гиперболы отлична от нуля только невязка ${{N}_{{m2}}}$:
причем функции ${{N}_{{m1}}}$, ${{N}_{{m2}}}$ и ${{N}_{J}}$ на интервале (0, $\infty $) достигают максимума. Для ${{N}_{{m2}}}$ это значение $N_{{m2}}^{*}$
(101)
${{\left( {x_{*}^{2} + C} \right)}^{2}} = \frac{{10}}{3}{{C}^{2}},\,\,\,\,N_{{m2}}^{*} = \frac{9}{{40C}}{{s}^{2}},$составляет 0.225 от $\left| {N_{{m2}}^{{}}\left( 0 \right)} \right|$ из (100). Квадратичными членами в выражениях для ${{N}_{{m1}}}$, ${{N}_{J}}$ можно пренебречь при вычислении максимальных величин. В результате получаем
(102)
$\begin{gathered} {{\left( {x_{*}^{2} + C} \right)}^{2}} = \frac{7}{3}{{C}^{2}},\,\,\,\,N_{{m1}}^{*} = \frac{4}{{7\sqrt {2C} }}{{\left( {\frac{3}{7}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}} \times \\ \times \,\,\left[ {2 + \frac{1}{{\sqrt {2C} }}{{{\left( {\frac{3}{7}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}s} \right]s;\,\,\,\, \\ {{\left( {x_{*}^{2} + C} \right)}^{2}} = \frac{5}{3}{{C}^{2}},\,\,N_{J}^{*} = \frac{6}{{5\sqrt {5C} }}\left[ {1 + \frac{1}{{2\sqrt {2C} }}{{{\left( {\frac{3}{5}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}s} \right]s. \\ \end{gathered} $В этом случае невязку имеет смысл оценивать по формуле
(103)
$N = {{\left[ {N_{{m1}}^{{*2}} + N_{{m2}}^{2}\left( 0 \right) + N_{J}^{{*2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$Приведенные в табл. 6 значения N показывают, что, выраженная в процентах, эта величина практически совпадает с δ. Исключение составляют варианты С = 0.5, 1, $f\left( 0 \right) = 0.1$, где соответствующие значения превышает ошибку в 2 и 1.5 раза.
Функция $N$ практически линейна по s. Типичный закон изменения различных невязок приведен на рис. 11. Упомянутое соотношение величин δ и $N$ может быть принято для электростатических потоков в области, удаленной от катода, при характерных значениях кривизны базовой траектории порядка единицы.
Рис. 11.
Невязки для электростатического потока с осью-гиперболой (С = 0.5, $f\left( 0 \right) = 0.025$).
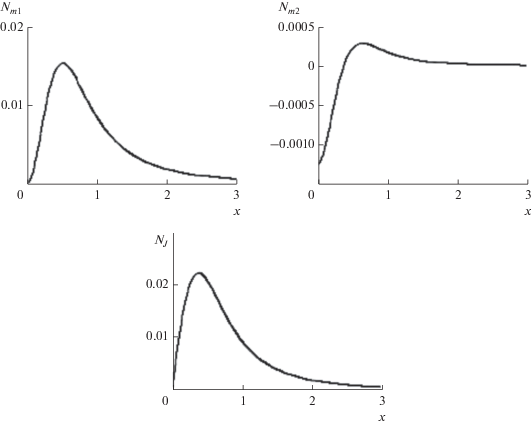
В табл. 8 приведены значения невязок для случая $\vec {H} \ne 0$, а на рис. 12 представлено типичное поведение этих функций при $\bar {\Omega } = 5$, $f\left( 0 \right) = 0.05$. Из табл. 8 видно, что при $\bar {\Omega } = 2$ выраженное в процентах значение N близко к ${\delta }$, при кривизне оси в диапазоне 3…4 имеем ${\delta }\,\,{\sim }{N \mathord{\left/ {\vphantom {N {{\text{(}}\bar {\Omega } - 1)}}} \right. \kern-0em} {{\text{(}}\bar {\Omega } - 1)}}$, при $\bar {\Omega } = 5$ соотношение принимает форму ${\delta }\,\,{\sim }{N \mathord{\left/ {\vphantom {N {\bar {\Omega }}}} \right. \kern-0em} {\bar {\Omega }}}$. Увеличение кривизны оси соответствует возрастанию магнитного поля ${{H}_{z}}$.
Рис. 12.
Невязки для гиперболического потока в магнитном поле ($\bar {\Omega } = 5,$ $f(0) = 0.05$).
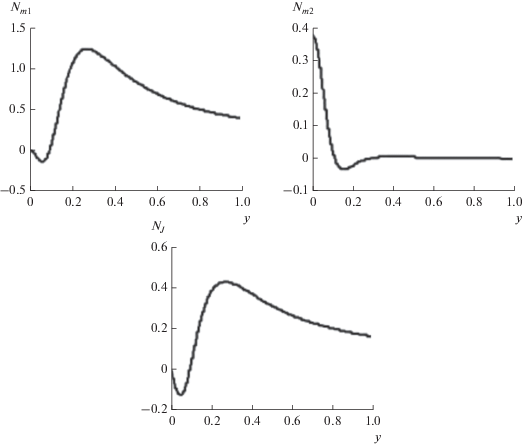
Решение (72) для плоского магнетрона. Выражения (95) для невязок в этом случае принимают вид
(104)
$\begin{gathered} {{N}_{{m3}}} = \bar {\Omega }{{\Omega }^{2}}T\bar {h}\left[ {\frac{{\bar {k}}}{{{{h}_{1}}}}\left( { - \frac{1}{{\bar {h}}}{{{\dot {\bar {\Omega }}}}_{l}} + \bar {k}{{{\bar {\Omega }}}_{s}}} \right)} \right. + \\ \left. { + \,\,\frac{1}{{\bar {h}}}\frac{{\dot {f}}}{f}\left( {\frac{1}{{\bar {h}}}{{{\dot {\bar {\Omega }}}}_{s}} + \bar {k}{{{\bar {\Omega }}}_{l}}} \right)} \right]{{s}^{2}}, \\ {{N}_{J}} = \frac{{\bar {\Omega }{\kern 1pt} {\kern 1pt} {{\Omega }^{3}}}}{{\bar {h}\cos {\alpha }}}\left[ {{{{\left( {\frac{{\bar {k}}}{f}} \right)}}^{\centerdot }} - 3\bar {\Omega }{{{\bar {k}}}^{2}}\frac{{\dot {f}}}{{{{f}^{2}}}}s} \right]s, \\ {{N}_{{\rho }}} = {{\left( {\frac{{\bar {\Omega }\Omega }}{{{{h}_{1}}\bar {h}}}} \right)}^{2}}\dot {\bar {k}}\left[ {\frac{1}{{\bar {\Omega }}}\dot {\bar {U}} + \dot {\bar {E}}s + \frac{1}{2}\bar {\Omega }{{{\left( {{\bar {\rho }} - \bar {N}} \right)}}^{\centerdot }}{{s}^{2}}} \right]s + \\ + \,\,\frac{{\bar {\Omega }{{\Omega }^{2}}}}{{{{h}_{1}}}}\left\{ {\left[ {\frac{1}{{\bar {h}}}{{{\left( {\frac{{\dot {\bar {E}}}}{{\bar {h}}}} \right)}}^{\centerdot }} + \frac{{\bar {k}}}{{\bar {h}}}{{{\left( {\frac{{\dot {\bar {U}}}}{{\bar {h}}}} \right)}}^{\centerdot }} + \bar {k}\left( {2\bar {N} - {\bar {\rho }}} \right)} \right]s + } \right. \\ \left. { + \,\,\bar {\Omega }\left[ {\frac{1}{{2\bar {h}}}{{{\left( {\frac{1}{{\bar {h}}}{{{\left( {{\bar {\rho }} - \bar {N}} \right)}}^{\centerdot }}} \right)}}^{\centerdot }} - {{{\bar {k}}}^{2}}\left( {2\bar {N} - {\rho }} \right)} \right]{{s}^{2}}} \right\}, \\ \end{gathered} $Как и при эмиссии в ${\rho }$-режиме с полуплоскости, сингулярная стартовая поверхность магнетрона приводит к бесконечной невязке ${{N}_{{\rho }}}$ при ${{x}_{m}} = 0$. Две последние строки в табл. 12 дают представление о затухании этого эффекта при $\tau = 1$ (${{x}_{m}} = 0.0343$) и $\tau = 2$ (${{x}_{m}} = 0.1175$). Невязки ${{N}_{{m3}}}$, ${{N}_{{H1}}}$, ${{N}_{{H2}}}$ практически равны нулю. Главную роль играет функция ${{N}_{{\rho }}}$, превышающая невязку по интегралу энергии ${{N}_{{m1}}}$ в 60…330 раз. Значения ${\delta }$ из табл. 12, 13 имеют один порядок (~20 и ~30% соответственно). Закон изменения невязок по длине пучка иллюстрирует рис. 13.
ЗАКЛЮЧЕНИЕ
Тестирование параксиальной модели ленточных пучков проведено на эталонных точных решениях, описывающих электростатические потоки в отсутствие эмитирующих поверхностей (неограниченное в продольном направлении периодическое течение, пучок с гиперболической осью и увеличивающейся компрессией), а также при рассмотрении потока с полуплоскости с траекториями-окружностями, эмиссией в ${\rho }$-режиме и существенно неоднородным токоотбором [9]. В присутствии однородного магнитного поля исследованы потоки с гиперболической осью, финитной эллиптической базовой траекторией, решение для плоского магнетрона в Т-режиме в магнитном поле, составляющем острый угол с катодом.
Относительная ошибка параксиальной модели оценивалась по возмущенному значению кривизны оси в точке максимума, из сравнения потенциала на приближенной траектории и толщины пучка. Для достижения ошибки порядка 2% оказалось недостаточным выбрать эту толщину, на порядок меньшей характерного линейного размера $L* = {1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0em} k}$, определяемого кривизной оси, но потребовалось уменьшить ее в 15…50 раз. Параксиальная модель, предполагающая постоянство плотности в поперечном сечении, обнаружила нечувствительность к этому параметру: эталонные решения с постоянной плотностью не имели преимуществ перед решениями с поперечным градиентом.
Ошибка по кривизне параксиальной траектории оказалась довольно жестким критерием: геометрически приближенная граница пучка могла быть достаточно близка к точной при существенном (пятикратном в случае эллиптической оси) отличии кривизн.
Параксиальная модель для течения [9] и осью $R = 1$ при толщине пучка 0.1 дает ошибку порядка 1.5% при перепаде плотности в 40%. Подобных результатов естественно ожидать для слабо искривленного катода с неоднородным токоотбором в ρ-режиме.
При практических расчетах представление о точности приближенного решения можно получить, вычисляя невязку при подстановке этого решения в точные уравнения пучка и сопоставляя результат с соотношением относительной ошибки и невязки в рассмотренных выше эталонных задачах. Так, для решения [9] невязка ${{N}_{{\rho }}}\sim \,1$ соответствует $\delta \sim 1.5\% $, ${{N}_{{\rho }}}\sim \,2$ – ошибке $\delta \sim 5.5\% $.
Рассмотренные примеры показали, что невязка по интегралу энергии ${{N}_{{m1}}}$, часто используемая в численных моделях, является необходимым, но далеко не достаточным критерием близости приближенного решения к точному. Так, для плоского магнетрона невязка по уравнению Пуассона ${{N}_{{\rho }}}$ превышала ${{N}_{{m1}}}$ в 60…330 раз, невязка по уравнению сохранения тока ${{N}_{J}}$ – в 4…48 раз.
Наметившаяся в последние годы тенденция проведения электронно-оптических расчетов пучков с высокой компрессией и близким к прямоугольному сечением исключительно при помощи коммерческих программ траекторного анализа порождает ряд неадекватных результатов, обсуждавшихся в работе [6]. При реализации электронных приборов подобный подход приводит к необходимости экспериментальной доводки, в то время как совместное использование приближенных и численных моделей, основанное на знании теории интенсивных пучков, могло бы способствовать устранению этого недостатка.
Список литературы
Сыровой В.А. Теория интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Сыровой В.А. Введение в теорию интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Cыpoвoй B.A. // PЭ. 2017. T. 62. № 6. C. 584.
Сапронова Т.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 11. С. 1106.
Сапронова Т.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 11. С. 1116.
Акимов П.И., Никитин А.П., Сыровой В.А. // Электрон. техника. Сер. 1. СВЧ-техника. 2018. № 1. С. 32.
Акимов П.И., Гаврилин А.А., Никитин А.П. и др. // РЭ. 2018. Т. 63. № 11. С. 1303.
Сапронова Т.М., Сыровой В.А. // РЭ. 2010. Т. 55. № 6. С. 726.
Meltzer B. // J. Electr. Contr. 1956. V. 2. № 2. P. 118.
Kirstein P.T. // J. Electr. Contr. 1958. V. 4. № 5. P. 425.
Cыpoвoй B.A. // PЭ. 2012. T. 57. № 3. C. 365.
Meltzer B. // Proc. Phys. Soc. 1949. V. 62B. № 355. P. 431.
Цимринг Ш.Е. // Изв. вузов. Радиофизика. 1977. Т. 20. № 10. С. 1550.
Manuilov V.N., Zaslavsky V.Yu., Ginzburg N.S. et al. // Phys. Plasmas. 2014. V. 21. № 2. P. 023106.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника