Радиотехника и электроника, 2020, T. 65, № 12, стр. 1190-1197

ВВЕДЕНИЕ

В настоящее время наблюдается повышенный интерес к применению композитных материалов на высоких и сверхвысоких частотах. Исследование материальных параметров композитов может дать информацию о структуре, необходимую для многих практических применений, в частности в химии [1], в медицине (оценка пористости костей [2]), сейсмологии, геофизике [3–5], а также в радиофизике (антенны, материалы для электромагнитной совместимости, поглотители СВЧ [6, 7] и др.). При этом часто возникает потребность в определении электромагнитных характеристик компонентов композитных материалов по характеристикам самих композитов. Причиной этому является то, что прямые измерения магнитной проницаемости металлов на высоких частотах невозможны из-за негативного влияния скин-эффекта. Определение проницаемости компонента-металла по характеристикам композитов с этим металлом в дисперсном состоянии является, по сути, единственным методом, позволяющим оценить магнитные свойства металлов и сплавов на высоких и сверхвысоких частотах.

1. ПОСТАНОВКА ЗАДАЧИ

Для того чтобы корректно описать электромагнитные характеристики композитов необходимо правильно выбрать формулу смешения. Среди всех существующих формул смешения, одними из наиболее известных являются обобщенная модель Максвелла–Гарнетта [8, 9] и симметричная модель Брюггемана [9]. Недостаток обобщенной симметричной модели Брюггемана в том, что в случае элипсоидальных включений, оба компонента могут иметь один форм-фактор N только в случае сфер [10–12], в результате порог протекания определяется исключительно форм-фактором включений (p_c = N).

К недостаткам моделей, учитывающих форму включений и изменение структуры композита вблизи порога протекания, можно отнести пренебрежение взаимодействием компонентов, поскольку порог протекания p_c в данном случае определяется исключительно формой включений.

В целях упрощения сравнения и анализа все формулы ниже переписаны с точки зрения восприимчивости χ, нормированной на материальный параметр (например, диэлектрическую проницаемость, магнитную проницаемость, коэффициент диффузии и т.д.) второго компонента, обычно называющегося связующим. Такой подход позволяет легко адаптировать рассматриваемые формулы к расчету “обобщенной проводимости” (т.е. любой проводимости, обусловленной диффузионным механизмом переноса) гетерогенных систем, например, диэлектрической проницаемости ε, магнитной проницаемости µ, электропроводности σ и т.д. [8]. В частности, для диэлектрической проницаемости нормированная восприимчивость записывается в виде

для магнитной проницаемости как

где индексы 1, 2, 3 относятся к включениям, связующему и смеси соответственно.

Широко известна формула Винера, описывающая анизотропный композит, в котором включения расположены параллельно внешнему полю:

где χ₁₂ и χ₃₂ – восприимчивости компонента 1 с объемным содержанием p₁ и смеси (обозначенной как компонент 3) соответственно. Восприимчивости нормированы на диэлектрическую проницаемость ε₂ компонента 2 с объемным содержанием p₂ = 1 – p₁.

Более общий вид формулы Винера описывает зависимость диэлектрической проницаемости ε₃ анизотропного бинарного композита от концентрации p_i и диэлектрической проницаемости ε_i i-компонента.

В сравнении с оригинальной формулой [13] выражение (2) переписано в терминах восприимчивости, нормированной на диэлектрическую проницаемость ε₂ компонента 2. Правая часть (2) является обобщением для эллипсоидальных включений с коэффициентом деполяризации N.

Параметр U зависит от диэлектрической проницаемости ε_local в окрестности включений; индексы 1, 2, 3 обозначают компонент 1, компонент 2 и сам композит (компонент 3) соответственно. Легко видеть, что при U = 0 формула (2) становится (1). При $U = \infty $ выражение (2) превращается в формулу (3), которая, так же как и (1), описывает анизотропный композит, но для случая ориентации компонентов перпендикулярно внешнему полю:

Существуют также формулы смешения с двумя эмпирическими параметрами, определяемыми из эксперимента. Первым параметром является форм-фактор включений N, второй параметр – порог протекания p_c, зависящий в общем случае от ряда факторов помимо формы включений. Простейшей моделью такого типа является формула Оделевского [14–16]:

Недостатками формулы являются ограниченный диапазон наполнений p < p_c, предположение о регулярности структуры с одинаковым взаимодействием всех включений и низкоконтрастная асимптотика, которая расходится со строгой формулой Ландау–Лифшица–Лойенги [17, 18]. Предполагается [8], что за порогом протекания (p > p_c) смесь описывается известной версией формулы Винера.

Подход, предложенный Оделевским, заключается в соединении матричных и симметричных моделей с переключением между различными структурами на пороге протекания p_c. Вблизи порога протекания точность этой модели низкая, поскольку, по всей видимости, перестройка структуры при изменении концентрации происходит постепенно.

Более близкая к реальности, по сравнению с формулами Оделевского и Брюггемана, модель Сихволы [19] содержит в качестве эмпирических параметров форм-фактор включений N, а также второй параметр a, который Сихвола определяет как некий формальный параметр структуры ($0 < a < \infty $). Ранее показано [15], что параметр a связан с критической концентрацией как a = = N($p_{c}^{{ - 1}}$ – 1). Для упрощения анализа и сравнения оригинальная формула Сихволы записана для анизотропного композита с регулярно ориентированными включениями:

Выражение (5) может быть приведено к прямой формуле Максвелла–Гарнетта и к симметричной формуле Брюггемана с помощью выбора подходящего значения порога протекания p_c = 1 или p_c = N соответственно [20]. В отличие от диапазона 0 < p < p_c, присущего формуле Оделевского, формула Сихволы (5) описывает диапазон наполнения 0 < p < 1 и позволяет учитывать неоднородное взаимодействие между включениями.

Целью данной работы является разработка модели смешения (формулы связывающей свойства смеси со свойствами компонентов и их объемной концентрацией p), подходящей для восстановления магнитной СВЧ-проницаемости металлических включений из измеренных материальных параметров бинарных двухкомпонентных гетерогенных систем (композитов), наполненных металлическими порошками.

2. ОБЪЕДИНЕННАЯ ФОРМУЛА СМЕШЕНИЯ

При разработке модели смешения была использована теория локальной эффективной среды Винера. В отличие от модели Оделевского, предлагаемая модель учитывает постепенный переход между прямой и обратной матричными структурами. Предполагается, что симметричная структура формируется в переходной области концентраций Δp_c; восприимчивость эффективной среды в этом диапазоне должна иметь некоторое среднее значение между восприимчивостью матриц граничных (при ${{p}_{1}} \to 0$ и ${{p}_{1}} \to 1$ ) структур. В предлагаемой модели, в отличие от моделей эффективной среды [10, 19], локальная восприимчивость χ_local2 в широком диапазоне концентраций отличается от восприимчивости смеси ${{\chi }_{{{\text{local2}}}}} \ne {{\chi }_{{32}}}$, но χ_local2 должна увеличиваться с увеличением концентрации. При $p \ll {{p}_{c}}$ локальная среда является компонентом матрицы χ_local2= 0, при $p \approx {{p}_{c}}$ локальная среда должна быть близка к смеси ${{\chi }_{{{\text{local2}}}}} \approx {{\chi }_{{32}}}$, но при $p \gg {{p}_{c}}$ локальная среда формируется с учетом коэффициента наполнения, и ее восприимчивость пропорциональна концентрации частиц первого компонента смеси: ${{\chi }_{{{\text{local2}}}}} \approx p \times {{\chi }_{{12}}}$. Диапазон концентраций Δp_c зависит от множества факторов, отсутствующих в идеализированных строгих моделях.

Таким образом, необходимо выбрать функцию усреднения восприимчивости от концентрации p, которая постепенно изменяет локальную восприимчивость от χ_local2= 0 при $p \to 0$ до χ_local2= χ₁₂ при $p \to 1$ с переходным диапазоном Δp_c и точкой инверсии p_c в качестве свободных параметров, получаемых из измеряемых данных.

В качестве такой функции для расчета локальной восприимчивости принято обобщенное среднее (другие функции усреднения не учитывают явление перколяции) между прямой ${{\chi }_{{{\text{local2}}}}} = \left( {1 - p} \right){{\chi }_{{22}}} = 0$ и обратной ${{\chi }_{{{\text{local2}}}}} = p{{\chi }_{{12}}}$ матричными смесями:

Весовой фактор w зависит от расстояния от точки инверсии структуры $\left| {{{p}_{c}} - p} \right|$ и описывает гладкость инверсии матричной структуры. При w = 0 переход происходит ступенчато и резко; при w = 1 матричная структура не формируется вовсе, так как переходная зона Δp_c занимает весь (0 < p < 1) диапазон наполнения.

Наполнение p обычно является средним значением по объему исследуемого образца смеси. Структура смеси в масштабе расстояний между соседними включениями определяется локальным наполнением, которое колеблется вокруг среднего значения. Среднее значение амплитуды этих флуктуаций может быть описано коэффициентом флуктуации δ, который определяется технологией смешивания ($0 < \delta < \,\,\infty $). Чем ближе смесь к чистому компоненту ($p \to 0$ или $p \to 1$), тем меньшее влияние коэффициент флуктуации оказывает на структуру смеси.

Ниже предполагается, что среднеквадратичное отклонение от инверсного наполнения p_c определяется гауссовым распределением φ, где коэффициент флуктуации δ является стандартным отклонением:

Таким образом, переходный диапазон Δp_c – это статистическая величина, зависящая от точки инверсии структуры p_c и коэффициента флуктуаций δ. Переходный диапазон определяется как диапазон наполнения, при котором локальное наполнение отклоняется от точки инверсии структуры с вероятностью 95%:

Весовой множитель w в (6) является распределением отклонений от точки инверсии p_c:

где t – переменная интегрирования.

Следует обратить внимание на то, что (8a) получено для гауссового распределения отклонений концентрации от точки инверсии p_c, но также могут быть применены и другие функции распределения. Более того, распределение w(p) может быть заменено на более простую функцию, удовлетворяющую ограничениям: w(0) = 0, w(1) = 1 и w(p_c) = 0.5, например:

Учитывая множитель, нормализующий коэффициент деполяризации и порог протекания $\left( {\frac{N}{{{{p}_{c}}}}\frac{{1 - {{p}_{c}}}}{{1 - N}}} \right)$ (множитель такой же, как и в формуле Сихволы), можно переписать (6) в виде

Заменяя локальную восприимчивость в формуле Винера значением, полученным из (9), получаем формулу смешения, которая учитывает инверсию матричной структуры:

где χ₃₂ и χ₁₂ – восприимчивости смеси и включений соответственно; p – объемное содержание включений. Форма включений описывается фактором деполяризации N, как и в других формулах, p_c – точка инверсии структуры, t – переменная интегрирования. Весовой фактор w(p) описывает плавность преобразования структуры за счет флуктуаций наполнения и определяет ширину переходного диапазона Δp_c.

Мы обозначили точку инверсии p_c, так же как порог протекания, поскольку эти величины близки друг к другу по физическому смыслу. Трансформация структуры описывается двумя параметрами, второй параметр δ относится к ширине переходного диапазона Δp_c = 2δ(1 – p_c)p_c. Порог протекания совпадает с точкой инверсии структуры только при Δp_c → 0; чем шире область переходных концентраций Δp_c, тем выше концентрация в точке инверсии структуры в сравнении с порогом протекания. Различие обусловлено тем, что порог протекания – это наполнение, при котором формируется первый бесконечный кластер включений, а точка инверсии – наполнение, при котором происходит инверсия матричной структуры.

3. КОНЦЕНТРАЦИОННАЯ И ЧАСТОТНАЯ ЗАВИСИМОСТИ КОМПЛЕКСНОЙ ВОСПРИИМЧИВОСТИ ДЛЯ МАТРИЧНОЙ ИНВЕРСНОЙ МОДЕЛИ И МОДЕЛИ СИХВОЛЫ

Выполнено численное сравнение формул (5) и (10). Контраст свойств компонентов выбран достаточно большим (χ₁₂ = 0 + i100) для выявления влияния формы включений на восприимчивость смеси. Рассчитанные зависимости восприимчивости смеси от концентрации по формуле Сихволы и по предложенной формуле показаны на рис. 1.

Рис. 1.

Зависимости действительной (а) и мнимой (б) частей восприимчивости от концентрации для композита с χ₁₂ = = 0 + i100, p_c = 0.33, N = 0.24, рассчитанные по модели Сихволы (5) (кривая 3) и по формуле (10) для δ = 0.05 (2), 0.5 (4), 4 (1).

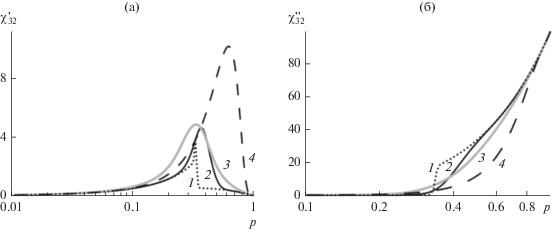
Форм-фактор включений N = 0.24 и порог протекания p_c = 0.33 (точка инверсии структуры в предложенной модели) близки к значениям, полученным для композитов, наполненных сферическими частицами [12, 21]. Флуктуационный множитель δ = 0.5 взят таким, чтобы получить достаточно широкую переходную зону Δp_c с концентрационной зависимостью восприимчивости смеси, близкой к таковой в модели Сихволы.

Рассчитанные зависимости действительной $\chi _{{32}}^{'}$ и мнимой $\chi _{{32}}^{{''}}$ восприимчивости композита от наполнения p показаны на рис. 1.

Отличие (10) от (5) в том, что на кривой $\chi _{{32}}^{{''}}$(p) видны три области (рис. 1б): область внутри прямой матрицы $\chi _{{32}}^{{''}}$ ниже, чем таковая в формуле Сихволы; внутри зоны обратной матрицы $\chi _{{32}}^{{''}}$ достигает значений по формуле Сихволы, в то время как внутри переходной зоны наклон $\chi _{{32}}^{{''}}$(p) выше, чем таковой в уравнении (5). Значения $\chi _{{32}}^{{''}}$ приблизительно равны вблизи p_c для обеих моделей.

Годографы коэффициента наполнения для одного и того же композита с χ₁₂ = 0 + i100 показаны на рис. 2 и 3. Точками на рис. 2 обозначено значение p_c, соответствующее порогу протекания по модели Сихволы (серый круг) и точке инверсии структуры (черный круг) для предложенной модели. На рис. 2 показаны результаты расчета для выражения (10) (черные линии) и для выражения (6) (серая линия). В случае модели Сихволы, ширина и высота пика $\chi _{{32}}^{'}$ связана только с контрастом свойств компонентов; в случае (10) форма пика определяется значением δ, которое является эмпирическим параметром. Чем выше восприимчивость χ₁₂, тем ниже должно быть значение δ для лучшего согласия с (6) и тем ближе критическая концентрация (p_c в 6) в модели Сихволы нужна для инверсии структуры в предлагаемой модели (p_c в (10)). На рис. 3 представлена зависимость весового фактора w от наполнения (8а), (8б) для δ = = 0.05, 0.5 и 4.

Рис. 2.

Годограф фактора наполнения, рассчитанный по модели Сихволы (5) (кривая 3) и по формуле (10) с χ₁₂ = 0 + i100, p_c = 0.33, N = 0.24 и δ = 0.05 (2), 0.5 (4) и 4 (1); черная точка – инверсия структуры; серая – порог перколяции в модели Сихволы.

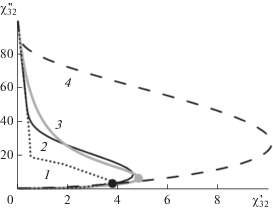
Рис. 3.

Зависимости весового фактора w от концентрации, рассчитанные по формулам (8а) для δ = 0.05 (1), 0.5 (2) и 4 (3) и (8б) для δ = 4 (4).

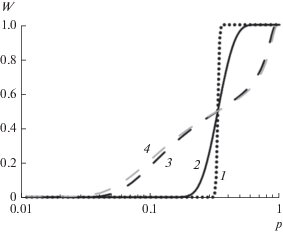
Отличия между весовым фактором Гаусса (8а) и упрощенной аппроксимацией (8б) становятся видны при δ > 4, когда переходный диапазон Δp_c покрывает наполнение 0 < p < 1 и матричная структура не формируется вовсе. Таким образом, расчет весового фактора w(p) по формуле (8б) гораздо проще, чем по формуле (8а), и не приводит к потере точности.

Частотная зависимость восприимчивости от частоты по формуле Сихволы (серые кривые) и по предложенной модели (черные кривые) показана на рис. 4. Штриховая серая линия соответствует равным значениям порога протекания и инверсного наполнения.

Рис. 4.

Зависимости действительной (а) и мнимой (б) частей восприимчивости смеси от частоты для композита с 20%‑ным объемным содержанием проводящих включений (параметры σ₁ = 55.62 Ом^–1 м^–1, p_c = 0.33, N = 0.24, δ = 0.5), рассчитанные для модели Сихволы с p_c = 0.33 (кривые 3) и p_c = 0.7 (кривые 2) и по формуле (10) (кривые 1).

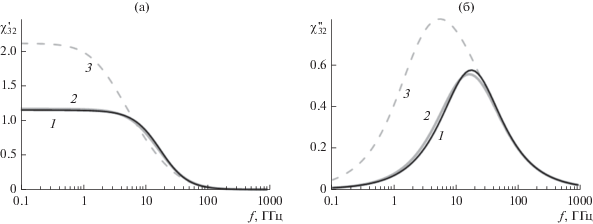
Легко видеть, что параметры p_c и δ кривых частотной дисперсии восприимчивости χ₃₂(f) для одного произвольного наполнения p могут быть сделаны одинаковыми для обеих моделей (сплошные серые и черные кривые).

4. СРАВНЕНИЕ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

Вычисления по формуле Сихволы и по предложенной формуле (10) сравнивались с материальными параметрами, измеренными для модельного композита на основе парафина (ε₂ = 2.3), с карбонильным никелем; методика изготовления и измерения образцов описана в [20]. Измерения статической диэлектрической проницаемости и частотной зависимости комплексной магнитной проницаемости были выполнены для набора образцов, наполненных сферическими частицами (∅12 мкм) вплоть до концентрации p ≈ 0.35 [21]; измерения статической диэлектрической проницаемости на бо́льших концентрациях затруднительны. На основании измеренных данных возможно вычислить эффективный форм-фактор включений (N = 0.2) и порог протекания (p_с = = 0.43).

Здесь мы аппроксимируем измеренную зависимость комплексной диэлектрической проницаемости от частоты ε₃(f) для композита, наполненного карбонильным никелем, как можно ближе к порогу протекания. Концентрация (p = 0.375) ограничена хрупкостью и пористостью шайбы холодной прессовки. Значения N = 0.2 и p_с = 0.43 взяты из работы [17], параметр δ получен из измеренной зависимости диэлектрической восприимчивости от частоты.

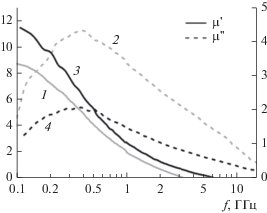
Частотная зависимость магнитной проницаемости µ₁(f) для никелевых включений (рис. 5) получена с помощью (8а) и (10) из измеренной зависимости магнитной восприимчивости от частоты при p = 0.375, N = 0.2, p_с = 0.43 и δ = 1. Кривыми 1 и 2 представлена магнитная проницаемость, полученная из измерений композитов, описанных выше; зависимости материальных параметров от концентрации аппроксимировались с помощью (8а) и (10). Частотные зависимости магнитной проницаемости частиц, рассчитанные по предложенной формуле, близки к кривым, полученным из формулы (5), хотя низкочастотная магнитная проницаемость из формулы (10) оказывается примерно на 20% выше приведенных данных. Измерения диэлектрической проницаемости показывают, что формула (10) при высоком наполнении ближе к измеренным данным, чем модель Сихволы, поэтому магнитная СВЧ-проницаемость никелевых сфер, представленная на рис. 5 (кривые 3 и 4), точнее по сравнению с данными, приведенными ранее [21].

Рис. 5.

Действительная (1, 3) и мнимая (2, 4) части магнитной проницаемости сфер Ni, полученные из измеренных магнитных проницаемостей композитов (1 и 2) при p = 0.05…0.34 [11]; измеренная магнитная СВЧ-проницаемость никелевых сфер (кривые 3 и 4).

Измеренная диэлектрическая проницаемость образца с p = 0.375 из Ni [21] показана на рис. 6 как годограф восприимчивости χ₃₂; частотный диапазон 0.15…15 ГГц. Кривая 1 соответствует модели Сихволы с N = 0.2, p_с = 0.43 и проводимостью включений σ₁ = 10⁶ Ом^–1 м^–1; кривая 2 соответствует формуле (10) с весовым множителем (8а) при N = 0.2, p_с = 0.43, δ = 1. Кривая 3 соответствует модели Сихволы при p_с = 0.38. Кривой 4 показана измеренная частотная зависимость для композита из карбонильного никеля в парафиновой матрице.

Рис. 6.

Годограф восприимчивости (${{{{\chi }_{{32}}} = {{\varepsilon }_{3}}} \mathord{\left/ {\vphantom {{{{\chi }_{{32}}} = {{\varepsilon }_{3}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}} - 1$) композита с объемным содержанием металлических включений p = 0.375 с форм-фактором N = 0.2 и p_c = = 0.43 и проводимостью включений σ₁ = 10⁶ Ом^–1 м^–1. Кривая 1 рассчитана по модели Сихволы (5), кривая 2 – по формуле (10) с весовым множителем (8а) при δ = 1, кривая 3 – по формуле (5) при p_c = 0.38, кривой 4 показана измеренная частотная зависимость для композита из карбонильного никеля в парафиновой матрице.

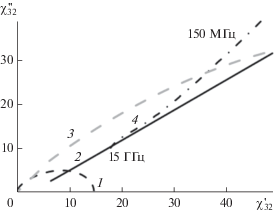
Измеренная диэлектрическая проницаемость образца с p = 0.375 из Ni [21] показана на рис. 6 (пунктир) как годограф восприимчивости χ₃₂; частотный диапазон 0.15…20 ГГц. Сплошная серая кривая соответствует модели Сихволы с N = = 0.2, p_с = 0.43 и проводимостью включений σ₁ = = 10⁶ Ом^–1 м^–1; сплошная черная кривая соответствует формулам (8а) и (10) при N = 0.2, p_с = = 0.43, δ = 1.

Измеренная диэлектрическая восприимчивость больше соответствует формуле (10), чем (5), но расхождение с измеренными данными здесь сильно зависит от точности эмпирических параметров. Выбор формулы для диапазона концентраций p < p_с проблематичен (см. рис. 4). Причина в том, что выбор между гораздо более различными формулами смешения для низконаполненных ($p \ll {{p}_{c}}$) композитов практически невозможен: чем ближе модели смешения, тем выше концентрация, на которой проявляются различия. Достоверный выбор между (5) и (10) возможен лишь при исследовании материальных параметров композитов, наполненных вблизи и выше точки инверсии. Изготовление таких образцов затруднительно.

ЗАКЛЮЧЕНИЕ

Разработана модель смешения, в которой прямая матричная структура преобразуется в обратную при увеличении объемной доли. Структура симметричного типа рассматривается как переход между прямой и обратной матричными структурами. В отличие от подхода Оделевского, трансформация структуры происходит постепенно в пределах переходного наполнения Δp_c. Порог протекания p_c совпадает с точкой инверсии структуры только при Δp_c → 0. Предложенная модель имеет три эмпирических параметра: форм-фактор N, точка инверсии структуры p_c и параметр локальных флуктуаций наполнения δ, зависящий от технологии изготовления образца и определяющий ширину переходной зоны Δp_c(δ). Учет преобразования структуры смеси в пределах зоны Δp_c(δ) увеличивает максимальное наполнение, где формула является точной по сравнению с двухпараметрическими моделями Оделевского и Сихволы.

Предложенная формула проверена сравнением частотных зависимостей комплексной диэлектрической и магнитной проницаемостей для образца, наполненного карбонильным никелем до концентрации (p = 0.375), близкой к порогу протекания. Значения форм-фактора и критического наполнения определяются из измеренной зависимости диэлектрической проницаемости от наполнения [21]. Измеренный годограф диэлектрической восприимчивости оказывается ближе к предложенной формуле, чем к модели Сихволы, (см. рис. 2 и 3), что подтверждает корректность предложенной формулы смешения. При низких наполнениях (p $ \ll $ p_c) предложенная формула и формула Сихволы трудно различимы (см. рис. 1–4).

Предлагаемая формула (10) получена для гауссова распределения локальных наполнений вблизи точки инверсии матричной структуры p_c (8а). Другие распределения или более простые функции w(p), аппроксимирующие постепенную инверсию матричной структуры (например, выражение (8б)) могут также быть использованы в формуле (10) вместо (8а). Проблемы с точными измерениями как диэлектрической проницаемости, так и объемных долей компонентов смесей с высоким наполнением металлическими порошками делают пока практически нецелесообразным уточнение функции распределения w(p) или увеличение числа эмпирических параметров.

Учет преобразования структуры смеси от прямой матричной к симметричной и далее к инверсной матричной делает предложенную модель более общей и точной до более высокого наполнения p по сравнению с известными моделями смешения. Поэтому применение модели для расчета проницаемости включений µ₁ из измеренных материальных параметров композита может повысить точность на низких частотах, где проницаемость µ₁ приближается к статической и, следовательно, может достигать высоких величин.