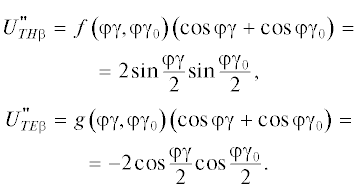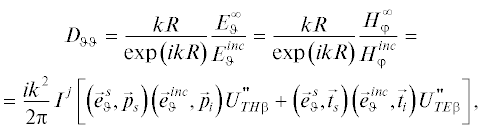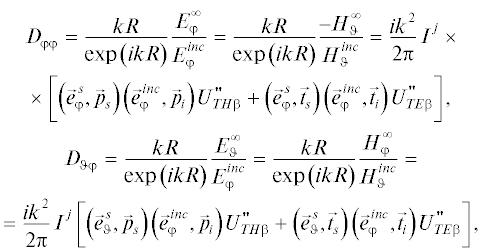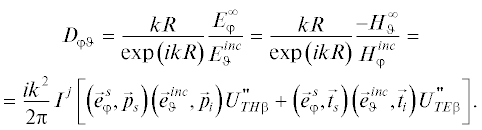Радиотехника и электроника, 2020, T. 65, № 12, стр. 1147-1159

ВВЕДЕНИЕ

В первой части [1] статьи были изложены основы метода базовых компонентов (МБК), при помощи которого можно строить эвристические аналитические решения двумерных и трехмерных задач теории дифракции. Во второй части статьи при помощи МБК получено эвристическое аналитическое решение задачи дифракции на трехмерном плоском многоугольнике.

В работе [2] было построено эвристическое аналитическое решение задачи дифракции плоской электромагнитной волны на плоском угловом секторе. Оно было получено на основе строгого решения задачи дифракции на кромке из [3], преобразованного при помощи “навязанного” условия дальней зоны и с применением подхода “условная кромка” [1]. В качестве основы при построении решения был применен линейный интеграл по контуру рассеивателя [1]. Кроме того, было применено решение на “условной кромке” [2]. В результате получились компактные эвристические аналитические выражения.

Приведем для удобства полный список применяемых сокращений.

МБК – метод базовых компонентов;

ГТД – геометрическая теория дифракции;

ФТД – физическая теория дифракции; (=приближенные и эвристические подходы)

МКВ – метод краевых волн;

ЧР – численное решение;

ФО – физическая оптика, физоптический;

МЭКТ – метод эквивалентных контурных токов;

ММЭКТ – модифицированный МЭКТ.

1. ПРИМЕНЕНИЕ РЕШЕНИЯ НА УСЛОВНОЙ КРОМКЕ

В эвристических методах двумерные решения используются для решения трехмерных задач. При этом берут кромку конечного размера. Если на ней есть точка стационарной фазы, то эвристическое решение задачи дифракции на кромке можно найти, проведя интегрирование вдоль кромки. Если выполняется условие дальней зоны, то фаза сигнала на кромке будет постоянна.

Однако может быть ситуация, когда точка стационарной фазы на кромке отсутствует. В этом случае точка наблюдения находится вне дифракционного конуса, а эвристическое решение для дифракционного коэффициента можно построить в соответствии с методом дифференциальных дифракционных коэффициентов, осуществив интегрирование по элементарной полоске, расположенной перпендикулярно кромке [4].

Можно действовать и по-другому, проведя на поверхности рассеивателя линию (“условную кромку”), которая является образующей дифракционного конуса для заданных положений источника и точки наблюдения. Такой подход позволяет напрямую (т.е. без интегрирования по элементарной полоске, расположенной перпендикулярно кромке) использовать двумерные дифракционные коэффициенты на “условной кромке”, что гарантирует выполнение принципа взаимности и дает возможность строить эффективные эвристические аналитические формулы. Решение на условной кромке можно считать объединением концепций ГТД и МКВ.

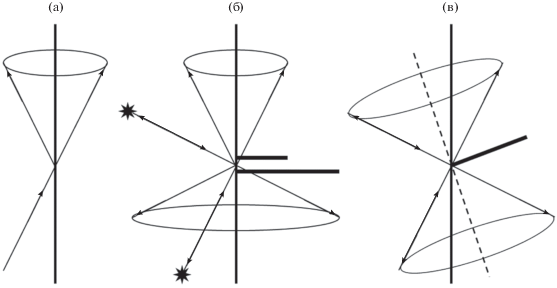
На рис. 1 приведены схемы, объясняющие применение подхода “условная кромка”. На рис. 1а показано направление волны, падающей на бесконечную кромку, и дифракционный конус рассеянных лучей. Все рассеяние происходит только в направлении дифракционных конусов, в других направлениях рассеяния не происходит. Кстати, именно этот эффект определяет форму трехмерных радиолокационных объектов, выполненных по технологии “Стелс”. Кромки объекта расположены параллельно друг другу, максимальное рассеяние происходит в двух основных направлениях, в других направлениях рассеяние минимально.

Рис. 1.

Применение решения на условной кромке.

На рис. 1б представлен фрагмент кромки трехмерного рассеивателя. Точка наблюдения расположена вне дифракционного конуса. В этом случае, если поменять местами источник и точку наблюдения, то поменяется и конфигурация дифракционного конуса, которая определяется проекциями направляющего вектора падающей волны на кромку и на направление, перпендикулярное кромке. При этом для соответствующих решений может нарушаться принцип взаимности в электродинамике.

На рис. 1в изображена “условная кромка”. Это прямая в пространстве, расположенная на поверхности плоского рассеивателя под углом к реальной кромке таким образом, что направления на источник и точку наблюдения составляют один и тот же угол с условной кромкой. Таким образом, по отношению к условной кромке точка наблюдения лежит на дифракционном конусе. Поэтому для построения решения можно использовать дифракционные коэффициенты на условной кромке, подставляя в соответствующие выражения углы, связанные уже не с реальной, а с условной кромкой.

2. ДИФРАКЦИОННЫЕ КОЭФФИЦИЕНТЫ ЭВРИСТИЧЕСКОГО РЕШЕНИЯ

Рассмотрим сингулярные дифракционные коэффициенты решения задачи дифракции электромагнитной волны на идеально проводящей полуплоскости [5]:

строгие (f, g)

и в приближении физической оптики (f ⁰, g⁰)

Сингулярные дифракционные коэффициенты (1) входят в состав интегрального представления двумерной задачи дифракции на идеально проводящей полуплоскости [1, 4]. В трехмерных задачах дифракции при выполнении условия дальней зоны для построения эвристического решения можно ограничиться сингулярными дифракционными коэффициентами [4, 6, 7].

Поскольку эти дифракционные коэффициенты входят в состав эвристического решения задачи дифракции в приближении метода эквивалентных контурных токов, мы будем также называть их МЭКТ. Сингулярные дифракционные коэффициенты (2) входят в состав решения той же задачи в приближении физической оптики, поэтому мы будем называть их ФО или МЭКТ-ФО. Сингулярные дифракционные коэффициенты (1) и (2) входят в состав базовых компонентов [1, 8]. Дифракционные коэффициенты (1) описывают решение задачи дифракции с учетом возмущения на кромке, а дифракционные коэффициенты (2) – без учета такого возмущения. Отметим полезное соотношение:

С целью построения эвристического решения трехмерной задачи дифракции на плоском многоугольнике разобьем дифракционные коэффициенты f(φ, φ₀) и g(φ, φ₀) из (1) на две части: геометрическую и поляризационную. Геометрическая часть представляет собой знаменатель дифракционного коэффициента и определяет характер его сингулярности в направлении дифракционного конуса. Поляризационная часть дифракционного коэффициента представляет собой его числитель и характеризует форму профиля кромки, вид поляризации или граничные условия [1, 4, 8]. Геометрическая часть содержится в соответствующем линейном интеграле I, а поляризационную часть берем из дифракционного коэффициента, взятого на условной кромке, при этом в (1) вместо углов (φ, φ₀), связанных с реальной кромкой, подставляем (φγ, φγ₀), связанных с условной кромкой [4]. Если точка наблюдения лежит на дифракционном конусе, то φγ = φ, φγ₀ = φ₀.

Таким образом, вместо поляризационной составляющей физоптики на условной кромке берем числители дифракционных коэффициентов (1) двумерного решения 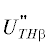и 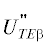с учетом коэффициентов разложения поляризаций падающего и рассеянного поля по TE- и TH-поляризациям, перпендикулярным кромке. В локальных координатах φγ и φγ₀ (аналогичных локальным координатам φ и φ₀ из [5]), представляющим собой углы между проекциями направляющих векторов −$\vec {n}{\kern 1pt} '$ и 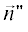на плоскость, перпендикулярную условной кромке, и внутренней нормалью к условной кромке, числители дифракционных коэффициентов принимают вид:

(4)

Выражения (4) описывают поляризационные составляющие на условной кромке (т.е. числители дифракционных коэффициентов), зависящие от координат (φγ, φγ₀). Геометрические составляющие, зависящие от (φ, φ₀), содержатся в интегралах I.

Решения на условной кромке имеет смысл применять в тех задачах, где этот подход экономит объем вычислений. В данной работе рассмотрена геометрия, в которой подход “условная кромка” совпадает с подходом “дифференциальные дифракционные коэффициенты”, когда интегрирование поля проводят по элементарной полоске, расположенной перпендикулярно кромке. Кроме того, рассеяние происходит вдоль дифракционных конусов, поэтому углы (φγ, φγ₀) и (φ, φ₀) совпадают.

3. ФОРМУЛЫ ДЛЯ КОЭФФИЦИЕНТОВ D

Рассмотрим представление поля в виде коэффициентов передачи по поляризациям D, которые определяются выражениями [2, 4, 9]:

Здесь E – компоненты векторов падающего и рассеянного полей. Нижние индексы соответствуют обозначениям ортов соответствующих углов, верхние обозначают падающее (inc) поле и рассеянное (∞) в точке наблюдения на большом расстоянии R от рассеивателя.

Обозначим вектора координат φ и ϑ падающего (inc) и рассеянного (s) поля [9] как $\vec {e}_{\varphi }^{{inc}}$, $\vec {e}_{\vartheta }^{{inc}}$, $\vec {e}_{\varphi }^{s}$ и $\vec {e}_{\vartheta }^{s}$ в глобальных сферических координатах (r, ϑ, φ), а вектора Т-поляризаций (по отношению к условной кромке) падающей (i) и рассеянной (s) волн в локальных координатах, связанных с условной кромкой как ${{\vec {t}}_{i}}$, ${{\vec {p}}_{i}}$, ${{\vec {t}}_{s}}$ и ${{\vec {p}}_{s}}$. Тогда при выполнении условия дальней зоны можно получить эвристические выражения для коэффициентов D в случае дифракции на плоском угловом секторе [2, 4]:

(6)

Формулы (6) дают решение в приближении метода эквивалентных контурных токов. Для перехода от коэффициентов D к полям применяют формулы (5).

В выражениях (6) значения скалярного интеграла I ^j определены в координатах, связанных с реальными кромками, образующими вершину. Для расчета дифракции на многоугольнике можно применять те же формулы, заменив в (6) интегралы по плоскому угловому сектору I ^j на интегралы по кромкам I_j [1, 4]. Таким образом, эвристические формулы (6) обладают высокой степенью универсальности, а интегралы I ^j и I_j могут быть включены в набор базовых компонентов [8] наряду с общей формулой для интеграла I [1, 4].

Кроме интегралов I, в формулах (6) использованы и другие составляющие из решений простейших задач, допускающих математически строгую постановку, которые могут быть включены в набор базовых компонентов [1, 4, 8].

4. ВИДЫ ГЕОМЕТРИЙ ЗАДАЧИ ДИФРАКЦИИ НА ПЛОСКОМ МНОГОУГОЛЬНИКЕ

Рассмотрим задачу дифракции электромагнитной волны на плоском идеально проводящем многоугольнике. На рис. 2 показана геометрия задачи дифракции на плоском идеально проводящем многоугольнике для двух поляризаций падающей электромагнитной волны. Угол ϑ1 отсчитывается от отрицательного направления оси Oz. Единичные орты падающей (inc) и рассеянной (s) волн $\vec {e}_{\varphi }^{{inc}}$, $\vec {e}_{\vartheta }^{{inc}}$, $\vec {e}_{\varphi }^{s}$ и $\vec {e}_{\vartheta }^{s}$ задаем в глобальных сферических координатах (r, ϑ, φ) [9] (см. также [2, 4]). Вектора Т- поляризаций (по отношению к условной кромке) падающей (i) и рассеянной (s) волн ${{\vec {t}}_{i}}$, ${{\vec {p}}_{i}}$, ${{\vec {t}}_{s}}$ и ${{\vec {p}}_{s}}$ [1] определяем в локальных координатах, связанных с условной кромкой [3] (см. также [2, 4]). 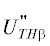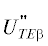Значения дифракционных коэффициентов и определяем по формулам (4) в локальных координатах через углы φγ и φγ₀, связанные с условной кромкой, с учетом соответствия углов φγ₀ ↔ α₁, φγ ↔ θ₁ [3] (см. также [2, 4]).

Рис. 2.

Геометрия задачи дифракции на плоском многоугольнике.

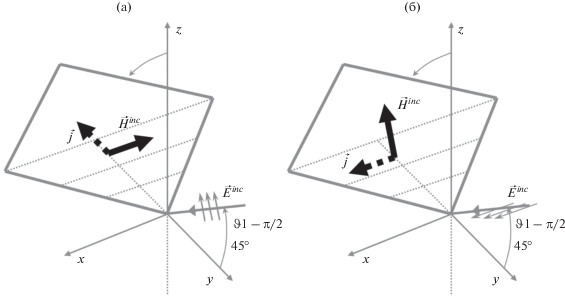
На рис. 3 показаны схемы падения и рассеяния волны в задаче дифракции на плоском угловом секторе и плоском многоугольнике. На рис. 3а представлены схемы падения и рассеяния волны в задаче дифракции на плоском угловом секторе. Проекция направляющего вектора падающей волны $\vec {n}{\kern 1pt} '$ на плоскость XOY совпадает с отрицательным направлением оси Oy. Проекция направляющего вектора рассеянной волны 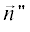на плоскость XOY совпадает с положительным вектором оси Ox. Если в решение МЭКТ на условной кромке подставить дифракционные коэффициенты ФО, то получим приближение МЭКТ-ФО. Эвристические решения этой задачи для различных приближений приведены в работах [2, 4, 10].

Рис. 3.

Схемы задач дифракции на плоском угловом секторе и плоском многоугольнике.

На рис. 3б приведены схемы падения и рассеяния волны в задаче дифракции на плоском многоугольнике, одна из вершин которого ориентирована так же, как плоский угловой сектор (рис. 3a). Данная геометрия соответствует рис. 2. Результаты счета опубликованы в [11] и [12].

На рис. 3 изображены схемы падения и рассеяния волны в задаче дифракции на плоском многоугольнике. Падение и рассеяние происходит в одной и той же плоскости YOZ (рис. 2). Результаты частично опубликованы в работе [12].

В данной статье мы более детально проанализируем свойства решения задачи дифракции на идеально проводящем прямоугольнике, геометрия которой соответствует рис. 3в.

5. ОСОБЕННОСТИ ДИФРАКЦИОННЫХ КОЭФФИЦИЕНТОВ ПРИ РАССЕЯНИИ “ПРЯМО ВПЕРЕД” И ПРИ ДИФРАКЦИИ НА ПОЛОСЕ

Случай рассеяния “прямо вперед” (нормальное падение на кромку и рассеяние в плоскости падения) – удачная геометрия трехмерной задачи дифракции для отработки эталонных решений с целью их дальнейшего применения при построении эвристических формул. В такой геометрии влияние вершин минимально. Влияние переотражений в этой геометрии максимально, но данное влияние можно выделить, решая дополнительную двумерную эталонную задачу – дифракцию на полосе.

Рассмотрим сингулярные дифракционные коэффициенты (1) и их поляризационные составляющие (числители) при рассеянии в плоскости падения (рис. 3в). Как уже было сказано ранее, в данной геометрии рассеяние происходит вдоль дифракционных конусов, направление условной кромки совпадает с направлением реальных кромок, и в (4) выполняется φγ = φ, φγ₀ = φ₀.

Знаменатели дифракционных коэффициентов (1) и (2) равны, причем они характеризуют свойства интеграла по “теневому контуру” в терминологии [13], или “линейного интеграла по кромке плоского рассеивателя” в терминах [1, 4]. Линейный интеграл правильно описывает направления максимумов рассеянного излучения, но не учитывает влияние поляризации.

Сравним свойства поляризационных частей дифракционных коэффициентов (числителей) дифракционных коэффициентов (1) и (2). Физоптические дифракционные коэффициенты (2) не учитывают возмущения вблизи края плоского рассеивателя, но с целью лучшего понимания физических особенностей решения мы не будем исключать их из рассмотрения. Отмеченные нижним индексом “p” поляризационные части дифракционных коэффициентов (1) характеризуются выражениями

а дифракционные коэффициенты (2) – выражениями

Поведение дифракционных коэффициентов (1) и (2), а также их поляризационных частей (7) и (8) отличается при различных воздействиях на эти функции, таких как:

а) замена φ₀ ⇔ φ (проверка выполнения принципа взаимности);

б) одновременная подстановка вместо α угла (π–α), где α = φ или α = φ₀ (дифракционные коэффициенты на разных кромках полоски).

Принцип взаимности является ключевым свойством задач электродинамики [14]. Одним из следствий этого принципа является то, что при взаимной смене положений точек источника и точки наблюдения значение рассеянного сигнала остается прежним.

В эвристических формулах МБК выполнение принципа взаимности обеспечивается применением подхода “условная кромка” (см. разд. 1).

Как следует из формул (7) и (8), для МЭКТ принцип взаимности выполняется (при перестановке φ₀ ⇔ φ ничего не меняется). Для МЭКТ-ФО в случае перестановки φ₀ ⇔ φ принцип взаимности не выполняется, и происходит изменение (смена знака дифракционных коэффициентов), соответствующее смене поляризации.

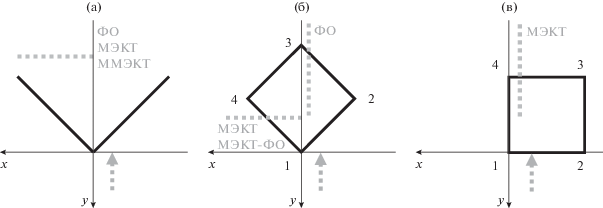
Второе свойство относится к двумерной задаче дифракции на полосе (рис. 4). Замена угла α на (π – α) соответствует отсчету угла в локальных координатах, связанных с внутренней нормалью к кромке. На рис. 4 кромка идет вдоль оси х, а внутренняя нормаль к кромке направлена в положительном или в отрицательном направлении оси y. Это приводит к подстановке соответственно углов α или (π – α) в формулы дифракционных коэффициентов (1) и (2) или в формулы поляризационных частей дифракционных коэффициентов (7) и (8).

Рис. 4.

Двумерная задача дифракции на полосе.

При замене углов α на (π – α) в аргументе (φ, φ₀) получим (π – φ, π – φ₀), при этом поляризационные составляющие дифракционных коэффициентов (7) и (8) изменятся следующим образом.

В зеркальном направлении точки наблюдения выполняется φ = π – φ₀. Подставив этот угол в аргумент (φ, φ₀), получим (π – φ₀, φ₀). Подставив угол φ = π – φ₀ в аргумент (π – φ, π – φ₀), получим (φ₀, π – φ₀). При этом функции (7), (8) и (9) принимают значения:

Анализ формул (7), (8) и (9) показывает, что свойства взаимности и подстановки аргументов на разных концах полоски выполняются по-разному как для дифракционных коэффициентов МЭКТ и МЭКТ-ФО, так и для их поляризационных частей. Совпадение решений МЭКТ и МЭКТ-ФО происходит только на одинаковых поляризациях в направлении зеркального отражения (10).

Несмотря на то, что приближение МЭКТ-ФО не учитывает возмущение на границах рассеивателя, нельзя считать, что приближение МЭКТ будет во всех случаях более корректным, чем МЭКТ-ФО. В данной статье мы рассматриваем идеальные граничные условия. В случае неидеальных граничных условий можно построить эвристическое решение, одновременно применяя приближения МЭКТ и МЭКТ-ФО и находя оптимальный баланс между ними [8, 15].

Рассмотрим влияние подстановки (π – α) в преобразование МЭКТ-ФО для задачи дифракции на полосе. Пусть ширина полоски стремится к нулю. В направлении зеркального отражения каждый из дифракционных коэффициентов является сингулярным. Однако при интегрировании по замкнутому контуру в трехмерном случае получаем значение, пропорциональное площади рассеивателя [4, 6, 7], а в двумерном – соответственно, значение, пропорциональное ширине полосы. Поляризационные части обеих поляризаций на концах полоски равны, поэтому при уменьшении длины полоски умножение этой величины на линейный интеграл устремляет рассеянный сигнал к нулю.

В зеркальном направлении выполняется φ = π – – φ₀, при этом поляризационные части дифракционных коэффициентов в приближениях МЭКТ и МЭКТ-ФО для соответствующих поляризаций равны (10). Таким образом, в зеркальном направлении компенсация сингулярностей полных дифракционных коэффициентов (1) и (2) дает для МЭКТ то же значение, что и для МЭКТ-ФО. При отклонении от зеркального направления дифракция на полосе в приближениях МЭКТ и МЭКТ-ФО происходит по-разному.

Для преобразования МЭКТ выражения на краях полоски (9) отличаются, поэтому вклад каждой из кромок линейного интеграла нужно учитывать по отдельности, умножая этот вклад на соответствующую поляризационную составляющую (9). Следует отметить, что при уменьшении ширины полоски применять приближение МЭКТ без учета переотражений между кромками некорректно.

Введем обозначения для дифракционных коэффициентов на разных сторонах трехмерного рассеивателя в соответствии со схемой рис. 3в. На этой схеме кромки расположены параллельно, как и в случае двумерной задачи дифракции на полосе (рис. 4). Дифракционные коэффициенты на стороне 4, расположенной между 3-й и 4‑й вершинами, обозначим fg4THβ и fg4TEβ. Дифракционные коэффициенты на стороне 2, расположенной между 1-й и 2-й вершинами, обозначим fg2THβ и fg2TEβ. Индексы THβ и TEβ соответствуют поляризациям в соответствии с (4) (см. также [2, 4]). В соответствии с этими обозначениями:

6. ОСОБЕННОСТИ РЕШЕНИЯ ПРИ РАССЕЯНИИ В ПЛОСКОСТИ ПАДЕНИЯ

Рассмотрим результаты расчетов диаграмм рассеяния на плоском идеально проводящем многоугольнике при выполнении условия дальней зоны. Геометрия задачи соответствует рис. 3в. Рассеиватель представляет собой плоский квадрат. Размер стороны квадрата изменяется в пределах от ka=2 до ka=60. Положение реальных кромок и условной кромки совпадают. Источник и точка наблюдения расположены на бесконечном расстоянии до кромки, а плоскость наблюдаемой диаграммы совпадает с плоскостью падения. На рассеиватель падает плоская волна единичной амплитуды. Рассматриваем два типа поляризации: с вектором падающего поля Е, расположенным в плоскости падения (и наблюдения) или перпендикулярно этой плоскости. В точке наблюдения находим модуль рассеянного поля.

Аналитические эвристические формулы соответствуют выражениям (6) с заменой интегралов по плоскому угловому сектору I ^j на интегралы по кромкам I_j, которые описывают рассеянный сигнал на дифракционном конусе, соответствующем геометрии нормального падения на кромку. Дополнительные подробности можно найти в источниках [1, 4, 12].

Решения, рассчитанные по эвристическим формулам, сравниваем с численным решением, полученным с помощью метода моментов. Результаты численного расчета были предоставлены В.И. Калиничевым.

Сравнение численного решения и эвристических формул лучше всего проводить в одной и той же программной среде. В противном случае между объектами сравнения могут возникать не обусловленные физикой дополнительные погрешности, связанные с особенностями вычислителей и затрудняющие физическую интерпретацию результатов. В связи с невозможностью внедрения эвристических формул в ту же программную среду, в которой было получено численное решение, сравнение численного решения и эвристических формул проводим по внешнему виду графиков диаграмм рассеяния и отношения амплитуд поляризаций. Будем также называть его “отношение ТЕ/ТН”.

Численные расчеты дифракции на плоском идеально проводящем плоском многоугольнике были приведены в работах [11, 12]. В данной работе мы обсудим часть этих результатов, а также новые расчеты.

На рис. 5–7 приведены результаты расчета дифракции на идеально проводящем прямоугольнике для схемы рис. 3в. Сплошными черными линиями показаны амплитуды ТЕ-поляризации, черными пунктирными линиями – амплитуда ТН- поляризации, сплошными серыми линиями – отношение поляризаций ТЕ/ТН, умноженное на константу coeff. Эта константа введена для того, чтобы кривая отношения поляризаций не накладывалась на другие кривые на рисунках. Прямая, совпадающая на графиках с константой coeff, соответствует значению отношения поляризаций |ТЕ/ТН| = 1.

Рис. 5.

Сравнение при ka = 40 и coeff = 200 эвристических решений МЭКТ (а), МЭКТ-ФО (б) и численного решения (в) для задачи дифракции на идеально проводящем плоском многоугольнике. На рис. 5г показано эвристическое решение МЭКТ + cfg с имитацией осцилляций при cfg = 0.08.

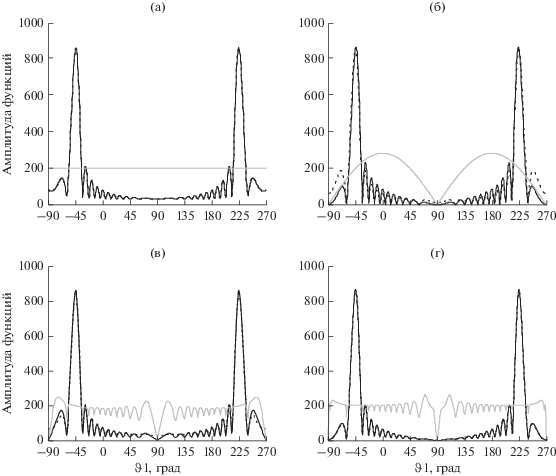
Рис. 6.

Диаграммы рассеяния при ka = 2 и coeff = 2 для эвристических решений МЭКТ (а), МЭКТ-ФО (б) и численного решения (в).

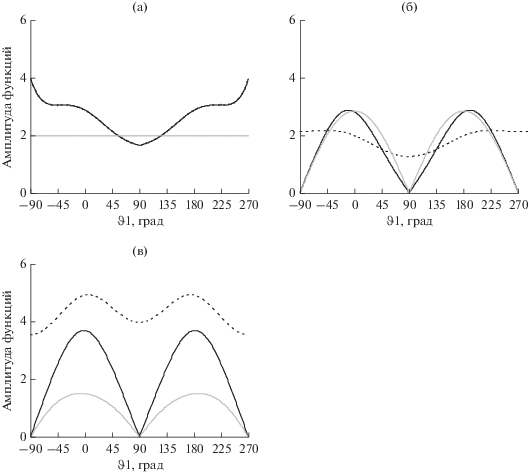
Рис. 7.

Имитации осцилляций. Слева – результаты численного решения при ka = 14 и coeff = 50 (а), ka = 20 и coeff = 50 (в), ka = 60 и coeff = 500 (в). Справа – результаты эвристического решения МЭКТ + cfg (12) при cfg: 0.25 (б), 0.15 (г), 0.05 (е).

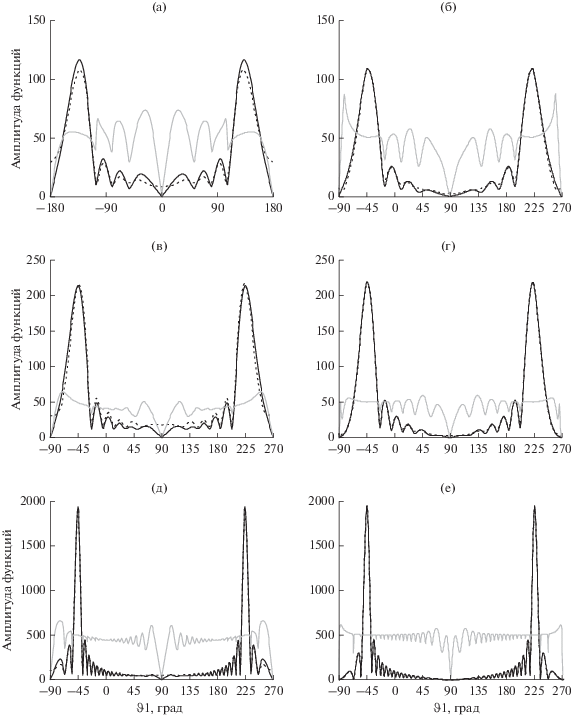
На рис. 5 приведены результаты для ka = 40 и coeff = 200. На рис. 5а показано приближение МЭКТ, на рис. 5б – приближение МЭКТ-ФО, на рис. 5в – численное решение. На рис. 5г показано решение с имитацией осцилляций (см. ниже) в приближении МЭКТ + cfg при cfg = 0.08.

Анализ графиков показывает, что общая структура решения (огибающая диаграммы рассеяния, количество лепестков и т.п.) похожа для всех типов приближений. Эта структура определяется линейным интегралом по контуру рассеивателя. Напротив, графики отношения поляризаций ТЕ/ТН имеют существенные отличия, которые определяются поляризационными составляющими.

Численное решение на рис. 5в имеет осцилляции на фоне константы coeff, но если сгладить осцилляции, то можно прийти к выводу, что диаграмма рассеяния близка к эвристическому решению МЭКТ. То же самое справедливо и для других, не слишком малых значений ka (ориентировочно ka ≥ ≥ 12) [12].

На рис. 6 приведены результаты расчета дифракции на идеально проводящем прямоугольнике с ka = 2 и coeff =2. На рис. 6а показано приближение МЭКТ, на рис. 6б – приближение МЭКТ-ФО, на рис. 6в – численное решение. Из этих графиков следует, что при малых значениях ka численному решению больше соответствует приближение МЭКТ-ФО. Очевидно, это связано с влиянием вершинных волн и переотражений.

Сделаем несколько замечаний относительно построения эвристического решения.

1. Мы применяем подход МБК, в котором решение для рассеянного поля представляет собой поляризационную составляющую, умноженную на линейный интеграл, связанный с отдельной кромкой. Этот подход согласуется с МКВ (хотя есть отличия в методике) и с МЭКТ.

2. Линейный интеграл [1, 4] по кромке плоского рассеивателя правильно описывает структуру рассеянного поля (направления максимумов и количество лепестков), но ничего не говорит о поляризации.

3. Поляризационная составляющая ФО (8) зависит от направления вектора поляризации падающей волны и от направления нормали к плоскости рассеивателя, но не зависит от положения кромки. Эта составляющая правильно описывает амплитуду поля на различных поляризациях в направлениях зеркального отражения.

4. Поляризационная составляющая МЭКТ (7) связана с взаимным расположением кромки и вектора поляризации падающей волны. Эта составляющая правильно описывает амплитуду поля на различных поляризациях в направлениях дифракционных конусов.

5. Поляризационная составляющая МЭКТ-ФО строится на аналитических выражениях, при помощи которых строят приближение МЭКТ [1]. Для получения приближения МЭКТ-ФО в выражениях МЭКТ заменяем поляризационные составляющие строгого решения (7) на физоптические (8). В случае нормального падения на кромку приближения ФО и МЭКТ-ФО совпадают.

6. Эвристические решения МЭКТ и МЭКТ-ФО отличаются как друг от друга, так и от численного решения. Несмотря на то, что приближение МЭКТ лучше описывает граничные условия на полуплоскости, МЭКТ-ФО в некоторых случаях геометрий трехмерных задач, а также при малых размерах рассеивателя (ka < 12) дает лучшее совпадение с численным решением [11]. Это можно объяснить влиянием заложенной методической погрешности, а именно – тем, что в эвристических формулах (6) не заложен учет влияния “вершинных волн” (дополнительного возмущения поля вблизи концов кромок) и переотражений между кромками [2, 4, 10]. В рассматриваемой задаче дифракции на многоугольнике указанное влияние проявляется в осцилляциях численного решения [11, 12]. В данной работе имитация осцилляций проводится при помощи физоптических дифракционных коэффициентов. Поэтому не исключено, что присутствие именно этих компонентов в эвристических формулах позволит уточнить решение МЭКТ. Окончательные выводы можно будет сделать только при проведении исследований с численными решениями эталонных задач дифракции на плоском угловом секторе и на полосе.

7. ИМИТАЦИИ ОСЦИЛЛЯЦИЙ

В работе [11] была сделана попытка учесть влияние на рассеянное поле возмущения вблизи вершин многоугольника при помощи того же множителя, который позволил учесть это влияние в задаче дифракции на плоском угловом секторе [2, 4, 10]. Эта попытка оказалась неудачной. Более корректным подходом является применение надежных решений эталонных задач, к которым относятся дифракция на полосе и дифракция на плоском угловом секторе.

В отсутствии таких надежных решений была проведена имитация осцилляций отношения амплитуд поляризаций при помощи добавления к дифракционным коэффициентам небольших возмущений, построенных на основе уже имеющегося набора базовых компонентов.

Дифракционные коэффициенты, имитирующие осцилляции, можно подобрать, выбирая их из набора базовых компонентов и последовательно сравнивая получающееся эвристическое решение с численным. Мы предполагаем, что осцилляции возникают в результате влияния неучтенных факторов. Поэтому одну из поляризаций будем “возмущать” при помощи малой добавки. В качестве поляризационных составляющих дифракционных коэффициентов, вносящих основной вклад, возьмем $g_{p}^{0}$ и g_p. В качестве малой добавки возьмем g_p или f_p. В качестве коэффициента, характеризующего порядок малости добавки, введем постоянную cfg. Обозначим соответствующее приближение МЭКТ+cfg. В итоге получим по аналогии с (11):

Заметим, что при cfg = 0 отношение поляризаций ТЕ/ТН представляет собой постоянную величину.

Начальная комбинация дифракционных коэффициентов для имитации осцилляций в приближении МЭКТ + cfg (g, g⁰), хотя и похожа, но отличается отличается от начальных комбинаций в приближении МЭКТ (f, g) и МЭКТ-ФО (f⁰, g⁰). Целью имитации осцилляций было не получить эвристическое решение в конечном виде, а лишь продемонстрировать перспективы применения МБК для уточнения приближений ФО, ГТД и МКВ.

На рис. 7 приведены результаты имитации осцилляций по формулам (12) на идеально проводящем прямоугольнике. На рис. 7а, 7в, 7д показаны результаты численного расчета с различными значениями ka и coeff, на рис. 7б, 7г, 7е – результаты расчета по эвристическим формулам (12) в приближении МЭКТ + cfg при различных значения коэффициента cfg.

Расчеты показывают, что феноменологическая формула (12) воссоздает многие характерные особенности отношения ТЕ/ТН в численном решении. К этим особенностям относятся количество и расположение нулей диаграммы рассеяния, количество лепестков и амплитуда осцилляций. Единственное значительное отличие – это поведение отношения ТЕ/ТН вблизи нулей.

Амплитуда осцилляций зависит от значения коэффициента cfg, который мы подобрали феноменологически, причем общая тенденция его поведения понятна: cfg ~ π/ka. Из этого можно сделать вывод, что область, занимаемая вблизи кромок полем, влияющим на изменение дифракционных коэффициентов, не зависит от размеров рассеивателя.

Имитация осцилляций была проведена при помощи выражений, входящих в набор базовых компонентов. Если из выражений, описывающих осцилляции, вычесть физоптику, получим краевые токи. Если вычесть МЭКТ, получим добавки, описывающие влияние вершин и переотражений. Тем не менее, данный способ получения осцилляций не является корректным.

Как уже было сказано, корректный способ исследования осцилляций – это не имитировать их, а получить при помощи уточненных эвристических формул, основанных на эталонных решениях для полубесконечных структур. Есть все основания полагать, что исследование эталонных решений на полубесконечных рассеивателях также позволит с помощью МБК построить решение с осцилляциями, но это решение будет уже более обоснованным и позволит проводить исследование процесса дифракции на более глубоком уровне.

8. РЕКОМЕНДАЦИИ ПО СОЗДАНИЮ ПАКЕТА РЕШЕНИЙ ДЛЯ ВЕРИФИКАЦИИ

1. Линейный интеграл по кромке рассеивателя работает хорошо, и может являться основой решения. Он отличается от физоптики с точностью до известного множителя (поляризационной составляющей физоптики). Для сверки работы линейного интеграла в эвристических формулах и в верификационном решении нужно в численном пакете предусмотреть возможность получения физоптического решения.

2. С целью отработки эвристических формул для краевых токов нужно иметь возможность получать численные решения для полубесконечных структур, таких как полуплоскость (или полупластина) и плоский угловой сектор. Для отделения друг от друга этих факторов нужно в численном пакете предусмотреть возможность получения решения на полосе.

3. С целью отделения решений в дальней зоне от решений в ближней зоне нужно в численном пакете предусмотреть возможность получения обоих соответствующих типов решений.

ЗАКЛЮЧЕНИЕ

В работе [1] и в данной статье исследованы свойства формул сингулярных дифракционных коэффициентов в трехмерной задаче дифракции электромагнитной волны на идеально проводящем плоском многоугольнике при выполнении условия дальней зоны. Эти формулы очень важны как при рассмотрении тех задач, в которых они играют главную роль, так и в других задачах, где их применяют в составе более сложных формул или в модифицированном виде. На основе сингулярных дифракционных коэффициентов построены эвристические аналитические решения трехмерных задач дифракции.

Все эвристические методы позволяют существенно увеличивать быстродействие по сравнению с численными методами. Метод ФО позволяет получать точные решения вблизи границ тени, методы ГТД и МКВ позволяют получать точные решения на дифракционных конусах, метод МБК позволяет получать точные решения во всех точках пространства.

Главное преимущество МБК состоит в том, что для построения быстродействующих и точных эвристических аналитических формул метод позволяет использовать широкий спектр верификационных решений, полученных разными методами, в том числе – численных, и не требует в обязательном порядке получать новые математически строгие решения аналитических задач.

Конечной целью данной работы, а также других публикаций автора из этого цикла [1, 2, 4, 8, 10–12, 15] является обеспечение возможности построения эвристических формул, с заданной точностью описывающих решения разнообразных задач дифракции. По сравнению с численными решениями эвристические формулы обладают увеличенным быстродействием (на несколько порядков выше, в зависимости от размера рассеивателя [1]) и возможностью проведения физической интерпретации особенностей решения. Оба этих свойства эвристических формул играют ключевую роль при решении практических задач, связанных с применением теории дифракции.