Радиотехника и электроника, 2020, T. 65, № 2, стр. 169-173

Одним из направлений повышения достоверности передачи дискретной информации по радиоканалам, включая каналы спутниковой связи, является применение сигналов с расширенным спектром, формируемых на основе псевдослучайных последовательностей (ПСП) [1–3]. Данное положение относится к системам связи и управления, включая системы спутниковой связи с кодовым разделением сигналов [4, 5], к системам радионавигации и радиолокации [6, 7], а также к системам мобильной связи [8]. В качестве ПСП широко используются МП, последовательности Голда, малого и большого множеств Касами, а также ГМВП [9–11].

Среди ПСП, обладающих двухуровневой периодической автокорреляционной функцией (ПАКФ), можно выделить МП и ГМВП [12, 13]. При этом ГМВП обладают более высокой структурной скрытностью, что определяет приоритетность их использования в системах передачи дискретной информации, к которым предъявляются повышенные требования по конфиденциальности.

Формирование двоичных ГМВП осуществляется над конечными полями с двойным расширением GF[(2^m)ⁿ] = GF(2^s) (s = mn). Период последовательностей является составным числом, т.е. N = 2^mn – 1.

Символы d_i ГМВП с периодом N = 2^mn – 1 определяются выражением [7, 12]

где tr_mn,m(·) – след элемента, принадлежащего полю GF[(2^m)ⁿ], в расширенном поле GF(2^m); tr_m1(⋅) – след элемента поля GF(2^m) в простом поле GF(2); α ∈ GF[(2^m)ⁿ] – примитивный элемент; r – натуральное число, взаимно простое с порядком мультипликативной группы поля GF(2^m), равным 2^m – 1.

Структурная скрытность ПСП характеризуется эквивалентной линейной сложностью (ЭЛС), которая для двоичных ГМВП определяется выражением [7, 13]

где g(r) – количество единиц в двоичном представлении числа r в (1).

Количество различных ГМВП М_ГМВП определяется как произведение числа примитивных полиномов в подпо́ле GF(2^m) на число примитивных полиномов в поле GF[(2^m)ⁿ] [12, 13]

где φ(a) – функция Эйлера, равная числу чисел, взаимно простых с числом а, в ряду от 1 до (а – 1).

При формировании ГМВП в соответствии с (1) необходимо построить конечное поле GF(2^s), содержащее 2^s элементов, и найти функции следа для каждого элемента. Среднее число операций сложения и умножения по mod2 при формировании всех ГМВП с периодом N = 2^s – 1 может быть определено выражением K ≈ M_ГМВПs2^s(s + 2). Например, для формирования всех ГМВП с периодом N = 2⁸ – 1 = 255 необходимо выполнить K ≈ 3 × × 10⁵ операций, а для периода N = 2¹⁴ – 1 = 16 383 требуется уже K ≈ 4 × 10¹⁰ операций.

Для полей GF[(2^m)ⁿ] при n = 2 известен алгоритм формирования ГМВП [14, 15], основанный на матричном представлении базисной МП. При использовании данного алгоритма для формирования каждой ГМВП необходимо строить матрицу МП, в которой осуществляется замена столбцов. Среднее число операций с учетом формирования МП равно K≈ φ(2^s – 1)2^s + φ(2^m – 1)2^{m+ 1}. Например, для формирования всех ГМВП с периодом N = 255 необходимо выполнить K ≈ 4 × × 10⁴ операций, а для периода N = 16383 требуется K ≈ 2 × 10⁸ операций.

Также известен алгоритм формирования ГМВП с помощью совокупности регистров сдвига с линейной обратной связью (РС ЛОС) [16]. При использовании данного алгоритма для каждого периода ГМВП выполняется вычисление проверочного полинома h_ГМВП(x) с помощью алгоритма Берлекэмпа–Месси и разложение полученного полинома на сомножители. Среднее число операций с учетом формирования МП и выполнения алгоритма Берлекэмпа–Месси равно K ≈ s2^s + + φ(2^m – 1)2^{m+ 1} + 2s³. Например, для формирования всех ГМВП с периодом N = 255 необходимо выполнить K ≈ 8 × 10³ операций, а для периода N = 16383 требуется K ≈ 3 × 10⁵ операций.

Цель данной статьи – разработать метод синтеза ГМВП, основанный на аналитическом определении полиномов-сомножителей h_сi(x) проверочного полинома h_ГМВП(x) ГМВП при формировании последовательностей с произвольным составным периодом N = 2^mn – 1.

Метод синтеза включает три составляющих: алгоритм определения полиномов-сомножителей h_сi(x) проверочного полинома ГМВП, методику определения полных перечней проверочных полиномов h_ГМВП(x) и алгоритм определения начальных состояний регистров сдвига, построенных по полиномам h_сi(x) в устройствах формирования ГМВП.

Основу метода синтеза составляет алгоритм определения полиномов-сомножителей h_сi(x), отличительной особенностью которого является то, что общий проверочный полином h_ГМВП(x) ГМВП не вычисляется, а его сомножители h_сi(x) определяются непосредственно по значению параметра r.

Вторая составляющая метода – это методика определения полных перечней проверочных полиномов h_ГМВП(x), разработанная в [16, 17]. Основой методики является положение о том, что корни полиномов h_сi(x) – сомножителей проверочного полинома h_ГМВП(x) – являются определенными фиксированными степенями корней проверочного полинома h_МП(x) базисной МП, с помощью которой формируется ГМВП.

Третьей составляющей метода является предложенный в [16] алгоритм определения начальных состояний регистров сдвига, входящих в устройство формирования ГМВП, который основан на децимации символов базисной МП по индексам, определяемым соотношением показателей степени корней полинома h_МП(x) базисной МП и корней полиномов-сомножителей h_сi(x).

При реализации метода число операций сложения и умножения по mod 2 сокращается, так как не требуется построения расширенного поля, формирования базисной МП и вычисления общего проверочного полинома h_ГМВП(x) ГМВП. Среднее число операций может быть определено как K = (2^{s– 2}+ φ(2^s – 1))/s. Например, для формирования всех проверочных полиномов ГМВП с периодом N = 16383 необходимо выполнить K ≈ ≈ 10³ операций.

Научная новизна предлагаемого метода заключается в разработке алгоритма определения полиномов-сомножителей h_сi(x), которая проводилась на основе анализа результатов, полученных в [15–17].

Для допустимых значений периода N и параметров m и n расширенного поля GF[(2^m)ⁿ] вид формируемой ГМВП, ЭЛС и перечень сомножителей проверочного полинома полностью определяется значением параметра r в выражении (1). При этом показатели степени корней всех полиномов-сомножителей формируемой ГМВП должны иметь одинаковые значения функции g(r).

Алгоритм определения полиномов-сомножителей h_сi(x) основан на том, что для элемента β^r = = (tr_mn,m(αⁱ))^r, принадлежащего подпо́лю GF(2^m), его p-сопряженные элементы с нечетными показателями степени являются, во-первых, непосредственно корнями части сомножителей степени s = mn проверочного полинома ГМВП, а во-вторых, выступают в качестве образующих элементов для различных p-сопряженных классов поля GF[(2^m)ⁿ] при вычислении остальных сомножителей h_сi(x). Данные элементы рассматриваются как корни полиномов-сомножителей нулевого уровня. Отметим, что для каждого значения r общее число элементов с нечетными показателями степени в подпо́ле GF(2^m), равно значению функции g(r). Например, в подпо́ле GF(2⁵) поля GF[(2⁵)²] для значения r = 13 р-сопряженными элементами для элемента β¹³ являются элементы β²⁶, β²¹, β¹¹, β²². Число элементов с нечетными показателями степени равно значению функции g(13₁₀) = g(1101₂) = 3, т.е. это элементы β¹³, β²¹, β¹¹.

Для определения полиномов первого и более высоких уровней вводится вспомогательный параметр k_i, необходимый для вычисления показателей степени корней данных полиномов:

Выражение для параметра k_i получено эмпирическим путем на основе анализа показателей степени корней полиномов-сомножителей для ГМВП с периодами N = 63, 255, 511, 1023.

На i-м уровне показатели степени корней полиномов определяются путем сложения показателей нулевого уровня и параметра k_i. При выполнении данной операции могут быть получены показатели степени корней неприводимых полиномов, не являющихся полиномами-сомножителями проверочного полинома ГМВП. Поэтому полученные показатели необходимо проверить, во-первых, по параметру g(r) и, во-вторых, по совпадению с показателями корней полиномов более низкого уровня. Обе проверки являются достаточно тривиальными. Вычисления для более высоких уровней продолжаются до получения общего числа сомножителей M = l_s/s степени s проверочного полинома ГМВП.

Рассмотрим алгоритм определения полиномов-сомножителей h_сi(x).

Шаг 1. Ввод исходных данных для формирования ГМВП с требуемыми характеристиками над полем GF[(2^m)ⁿ]:

– выбор периода ГМВП N = 2^mn – 1;

– выбор значений m и n для периодов N = 2^mn – 1;

– выбор примитивного полинома базисной МП с корнем α¹;

– задание ЭЛС l_s ГМВП для выбранного периода с соответствующим числом M полиномов-сомножителей;

– выбор параметра r для заданной ЭЛС со значением g(r).

Шаг 2. Определение полиномов-сомножителей h_ci(x) нулевого уровня:

– вычисление p-сопряженных элементов для элемента β^r в подпо́ле GF(2^m);

– выбор элементов с нечетными показателями степени r₀₁, r₀₂, …, r_0d, которые являются корнями искомых полиномов-сомножителей нулевого уровня h_с1(x), h_с2(x), …, h_cd(x); общее число элементов с нечетными показателями степени равно значению функции g(r), то есть d = g(r).

Шаг 3. Если d = М, то переходим в конец алгоритма, т.е. искомый проверочный полином ГМВП определяется выражением

Если d < М, то в соответствии с (4) определяются значения вспомогательного параметра k_i, необходимого для вычисления показателей степени корней возможных полиномов-сомножителей первого, второго и более высоких уровней.

Шаг 4. Определение полиномов i-го уровня для i = 1, 2, 3, …:

– вычисление показателей степени i-го уровня r_i1, r_i2, …, r_id для нечетных показателей степени корней полиномов нулевого уровня r₀₁, r₀₂, …, r_0d:

– проверка полиномов с вычисленными степенями корней:

а) если g(r_il) ≠ d (l = 1, 2, …, d), то полином с данным корнем отбрасывается;

б) если r_il (l = 1, 2, …, d) является показателем степени элемента, являющегося p-сопряженным корнем полинома-сомножителя более низкого уровня, то полином с данным корнем повторно не учитывается;

в) число полиномов i-го уровня, прошедших проверку, обозначается d_i.

Шаг 5. Если d + ∑d_i = М, то переходим в конец алгоритма, иначе – к шагу 4.

Шаг 6. Конец алгоритма.

Пример. В качестве примера определим проверочный полином для ГМВП с периодом N = 1023 и ЭЛС l_s = 80.

Шаг 1. Исходные данные: период N = 1023; поле GF[(2^m)ⁿ] = GF[(2⁵)²], т.е. m = 5, n = 2; полином базисной МП h_МП(x) = x¹⁰ + x³ + 1; параметр r = = 15₁₀ = 1111₂; d = g(r) = g(15) = 4; ЭЛС l_s = 5 × 2⁴ = 80; число сомножителей M = 8.

Шаг 2. Определение полиномов-сомножителей h_ci(x) нулевого уровня:

– p-сопряженные элементы в поле GF(2⁵) для элемента α¹⁵: α³⁰, α²⁹, α²⁷, α²³;

– элементы с нечетными показателями степени r₀₁ = 15, r₀₂ = 23, r₀₃ = 27, r₀₄ = 29 являются корнями искомых сомножителей нулевого уровня h_с1(x) = h₁₅(x), h_с2(x) = h₂₃(x), h_с3(x) = h₂₇(x), h_с4(x) = = h₂₉(x), где нижний числовой индекс здесь и далее соответствует наименьшим показателям степени корней полиномов [18];

Шаг 3. Так как d = 4 < М = 8, то определяется значение вспомогательного параметра k_i для вычисления показателей степени корней полиномов первого, второго и более высоких уровней:

Шаг 4. Определение полиномов первого уровня для i = 1 (k₁ = 62):

– показатели степени r₁₁, r₁₂, r₁₃, r₁₄ корней полиномов первого уровня:

r₁₁ = r₀₁ + k₁ = 15 + 62 = 77, g(77) = 4: полином h₇₇(x) соответствует;

r₁₂ = r₀₂ + k₁ = 23 + 62 = 85; g(85) = 4: полином h₈₅(x) соответствует;

r₁₃ = r₀₃ + k₁ = 27 + 62 = 89; g(89) = 4: полином h₈₉(x) соответствует;

r₁₄ = r₀₄ + k₁ = 29 + 62 = 91; g(91) = 5 > 4: полином h₉₁(x) отбрасывается;

– корни α⁷⁷, α⁸⁵, α⁸⁹ не являются p-сопряженными элементами для корней полиномов нулевого уровня, поэтому полиномы с данными корнями являются искомыми сомножителями первого уровня h_с5(x) = h₇₇(x), h_с6(x) = h₈₅(x), h_с7(x) = h₈₉(x);

– число полиномов первого уровня, прошедших проверку, равно d₁ = 3.

Шаг 5. Так как d + d₁ = 7 < М = 8, то вычисляются полиномы второго уровня.

Шаг 6. Определение полиномов второго уровня для i = 2 (k₂ = 124):

– вычисление показателей степени r₂₁, r₂₂, r₂₃, r₂₄:

r₂₁ = r₀₁ + k₂ = 15 + 124 = 139, g(139) = 4: полином h₁₃₉(x) соответствует;

r₂₂ = r₀₂ + k₂ = 23 + 124 = 147; g(147) = 4: полином h₁₄₇(x) соответствует;

r₂₃ = r₀₃ + k₂ = 27 + 124 = 151; g(151) = 5 > 4: полином h₁₅₁(x) отбрасывается;

r₂₄ = r₀₄ + k₂ = 29 + 124 = 153; g(153) = 4: полином h₁₅₃(x) соответствует;

– корень α¹³⁹ является p-сопряженным элементом для корня α⁸⁹, корень α¹⁵³ является p-сопряженным элементом для корня α¹⁴⁷, поэтому полиномы с данными корнями повторно не учитываются; корень α¹⁴⁷ не является p-сопряженным элементом для корней полиномов более низкого уровня, поэтому единственным полиномом-сомножителем второго уровня является полином h_с8(x) = h₁₄₇(x), d₂ = 1.

Шаг 7. Так как d + d₁ + d₂ = 8 = М, то искомый полином ГМВП имеет вид

Шаг 8. Конец алгоритма.

Проверочный полином h_ГМВП(x) ГМВП вида (7) совпадает с результатами, полученными в [17] при определении данного полинома с помощью алгоритма, основанного на матричном представлении последовательностей, применении алгоритма Берлекэмпа–Месси для вычисления полинома h_ГМВП(x) и разложения его на полиномы-сомножители h_сi(x).

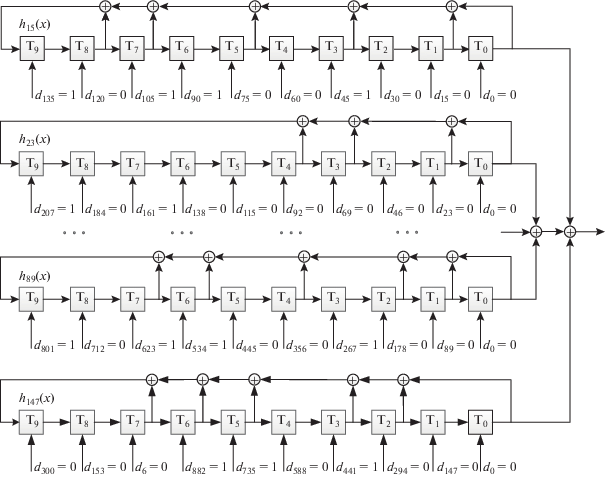
Устройство формирования ГМВП с периодом N = 1023 и проверочным полиномом (7) показано на рисунке. Приведено четыре РС ЛОС из восьми с полиномами [18]

Начальные состояния регистров определены путем децимации символов базисной МП с h_МП(x) = h₁(x) = x¹⁰ + x³ + 1 [18] по индексам 15, 23, …, 89, 147 в соответствии с алгоритмом, разработанным в [16].

Таким образом, в статье разработан метод синтеза ГМВП, основу которого составляет алгоритм определения полиномов-сомножителей h_сi(x) проверочного полинома h_ГМВП(x) ГМВП. Алгоритм позволяет вычислять неприводимые полиномы-сомножители без построения базисной МП и определения проверочного полинома ГМВП с использованием итеративного алгоритма Берлекэмпа–Месси.

ЭЛС ГМВП превышает ЭЛС МП в 2–10 раз в зависимости от значения периода N и выбранного параметра r. С увеличением периода выигрыш возрастает.

Полученные результаты позволяют применять ГМВП в широкополосных радиоканалах систем передачи дискретной информации, к которым предъявляются повышенные требования по конфиденциальности, включая требования по повышению их структурной скрытности.