Радиотехника и электроника, 2020, T. 65, № 2, стр. 128-134
Плазмонные резонансы в квадратной и прямоугольной нанопластинах из благородных металлов
А. П. Анютин *
Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Московской обл., Фрязино, пл. Введенского, 1, Российская Федерация
* E-mail: anioutine@mail.ru
Поступила в редакцию 21.05.2018
После доработки 21.05.2019
Принята к публикации 05.06.2019
Аннотация
Рассмотрена двумерная задача дифракции плоской электромагнитной волны ТМ-типа на цилиндрической структуре из серебра или золота, контур поперечного сечения которой представляет собой квадрат или прямоугольник. В диапазоне длин волн $300\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}$ строгим численным методом рассчитаны спектры поперечника рассеяния и диаграммы рассеяния. Исследовано влияние потерь среды, геометрических размеров структуры и угла падения плоской волны на поперечник рассеяния и диаграмму рассеяния. Показано, что реальные потери золота делают невозможным существование мультипольных резонансов при размерах пластины, существенно меньше длины волны. В случае серебряной пластины положение дипольного и наличие мультипольного резонансов зависит как от длины и толщины пластины, так и от угла падения плоской волны.
ВВЕДЕНИЕ
Как известно, дифракция электромагнитных волн на наноструктурах из благородных металлов (серебра, золота) в световом диапазоне длин волн сопровождается как образованием поверхностных волн (плазмон-поляритонов), так существованием их резонансов. При этом интерес к исследованию свойств плазмон-поляритонов связан главным образом с высокой локализацией электромагнитного поля вблизи поверхности наноструктур, которая позволяет использовать их в субволновом и ближнепольном зондировании. Так, нанопровода из серебра и золота широко применяются в качестве сенсоров [1]. Отметим, что плазмонные резонансы в цилиндрических наноструктурах (нитях) с круглым сечением реализуются в ультрафиолетовой части спектра. Используя нанотрубки, можно сместить частоты плазмонных резонансов в видимую область светового диапазона [2, 3]. В работе [4] исследованы плазмонные резонансы в кварцевой нанонити, покрытой слоем золота переменной толщины в предположении, что границами оболочки являются круговые цилиндры со смещенными центрами. Различные геометрии оболочек из серебра и кварца, контуры поперечного сечения которых образованы круговыми или круговыми и эллиптическими цилиндрами рассматривались в работах [5–7].
Цель данной работы состоит в исследовании особенностей плазмонных резонансов в 2D-наноструктурах из серебра (золота) в случае, когда контур поперечного сечения структуры представляют собой квадрат (прямоугольник) с разными соотношениями сторон. Из близких по тематике работ отметим [8–11].
1. ФОРМУЛИРОВКА ЗАДАЧИ
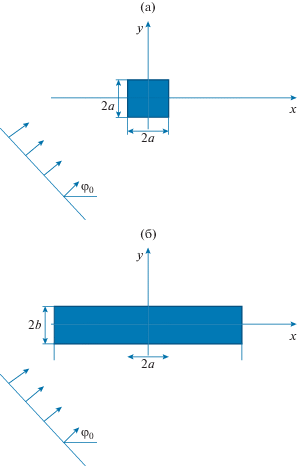
Рассмотрим двумерную задачу дифракции плоской электромагнитной линейно-поляризованной волны на двумерной цилиндрической диэлектрической структуре (пластине), поперечное сечение которой представляет собой квадрат (рис. 1а) или прямоугольник (рис. 1б). Плоская волна распространяется в направлении единичного вектора ($\cos {{\varphi }_{0}},\,\,\sin {{\varphi }_{0}},\,0$) и характеризуется следующими компонентами электромагнитного поля:
(1)
$\begin{gathered} H_{z}^{0} = \exp ( - ikx\cos {{\varphi }_{0}} - iky\sin {{\varphi }_{0}}), \\ E_{x}^{0} = - \eta \sin {{\varphi }_{0}}\exp ( - ikx\cos {{\varphi }_{0}} - iky\sin {{\varphi }_{0}}), \\ E_{y}^{0} = \eta \cos {{\varphi }_{0}}\exp ( - ikx\cos {{\varphi }_{0}} - iky\sin {{\varphi }_{0}}). \\ \end{gathered} $Зависимость от времени выбрана в виде $\exp (i\omega t),$ где $\omega = kc$ – круговая частота, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число свободного пространства, $c$ – скорость света в вакууме, $\lambda $ − длина волны, $\eta = 120\pi \,\,Ом$ − волновое сопротивление вакуума.
Для структуры, изображенной на рис. 1б, контур поперечного сечения описывается формулой
(2)
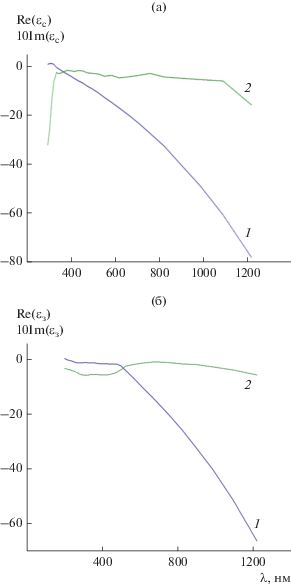
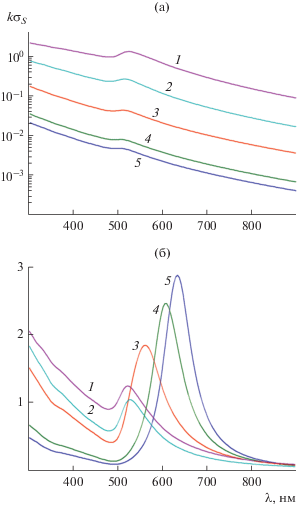
${{({x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a})}^{N}} + {{({y \mathord{\left/ {\vphantom {y b}} \right. \kern-0em} b})}^{N}} = 1,$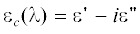 ≡ $\operatorname{Re} ({{\varepsilon }_{c}}) - i\operatorname{Im} ({{\varepsilon }_{c}})$ серебра (или золота ${{\varepsilon }_{з}}(\lambda )$) рассчитывалась на основе интерполяции экспериментальных данных работы [12] кубическими сплайнами. На рис. 2а представлена зависимость действительной и мнимой частей относительной диэлектрической
проницаемости серебра. Аналогичные зависимости для случая золота изображены на рис. 2б.
≡ $\operatorname{Re} ({{\varepsilon }_{c}}) - i\operatorname{Im} ({{\varepsilon }_{c}})$ серебра (или золота ${{\varepsilon }_{з}}(\lambda )$) рассчитывалась на основе интерполяции экспериментальных данных работы [12] кубическими сплайнами. На рис. 2а представлена зависимость действительной и мнимой частей относительной диэлектрической
проницаемости серебра. Аналогичные зависимости для случая золота изображены на рис. 2б.
Рис. 2.
Зависимости действительной (1) и мнимой (2) частей относительной диэлектрической проницаемости серебра (а) и золота (б) от длины волны.
Пространственное распределение диэлектрической проницаемости для структур, изображенных на рис. 1, имеет вид
(3)
$\bar {\varepsilon }(x,y) = \left\{ \begin{gathered} {{\varepsilon }_{{{\text{с,з}}}}},\,\,\,\,{{({x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a})}^{N}} + {{({y \mathord{\left/ {\vphantom {y b}} \right. \kern-0em} b})}^{N}} < 1. \hfill \\ 1,\,\,\,\,{{({x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a})}^{N}} + {{({y \mathord{\left/ {\vphantom {y b}} \right. \kern-0em} b})}^{N}} > 1. \hfill \\ \end{gathered} \right.$Исследование сформулированной задачи дифракции удобнее проводить, используя $z$-компоненту $U(x,y) = {{H}_{z}}(x,y)$ магнитного поля, так как краевая задача для функции $U(x,y)$ является скалярной. Полное поле $U(x,y),$ т.е. суперпозиция падающего и рассеянного полей, в кусочно-постоянной среде (3) удовлетворяет уравнению Гельмгольца
(4)
$\frac{{{{\partial }^{2}}U(x,y)}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}U(x,y)}}{{\partial {{y}^{2}}}} + {{k}^{2}}\bar {\varepsilon }(x,y)U(x,y) = 0.$Компоненты электрического поля могут быть выражены через функцию $U(x,y)$
(5)
$\begin{gathered} {{E}_{x}}(x,y) = \frac{\eta }{{ik\bar {\varepsilon }(x,y)}}\frac{{\partial U(x,y)}}{{\partial y}}, \\ {{E}_{y}}(x,y) = - \frac{\eta }{{ik\bar {\varepsilon }(x,y)}}\frac{{\partial U(x,y)}}{{\partial x}}. \\ \end{gathered} $На границах структуры должны быть непрерывны величины $U$ и $\frac{1}{{\bar {\varepsilon }}}\frac{{\partial U}}{{\partial N}},$ где $\frac{{\partial U}}{{\partial N}}$ – производная по направлению нормали к границе раздела сред.
Как уже отмечалось, полное поле вне пластины состоит из падающего (${{U}^{0}}$) и рассеянного (${{U}^{s}}$) полей. Падающее поле задано функцией
Рассеянное поле в цилиндрической системе координат ($r,\varphi $), где $x = r\cos \varphi $ и $y = r\sin \varphi ,$ в дальней зоне ($kr \to \infty $) должно удовлетворять условию излучения
(7)
${{U}^{s}} = \Phi (\varphi )\sqrt {\frac{2}{{\pi kr}}} \exp \left( { - ikr + i\frac{\pi }{4}} \right),$Полное сечение рассеяния ${{\sigma }_{S}}$ определяется формулой
2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
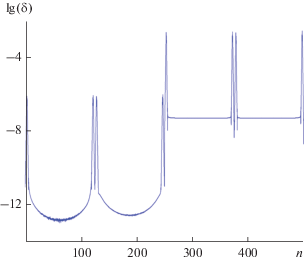
Численное решение сформулированной задачи проводилось модифицированным методом дискретных источников [13, 14]. При этом точность решения задачи контролировалась путем вычисления невязки $\delta $ граничных условий в линейной норме в точках, расположенных в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом [13]). Во всех приведенных ниже расчетах максимальная невязка граничных условий не превышает величину $\delta < {{10}^{{ - 3}}}.$ Пример типичного распределения невязки $\delta (n)$ вдоль контура (2) пластины из серебра ($n$ – номер точки на контуре) представлен на рис. 3 (параметры контура (2) полагали следующими: $N = 18,\,\,a = 50\,\,{\text{нм}},$ $b = 5\,\,{\text{нм}}$).
Рис. 3.
Распределение абсолютных значений невязки граничных условий вдоль контура серебряной пластины при а = 50, b = 5 нм.
Рассмотрим сначала поведение нормированного поперечника рассеяния $k{{\sigma }_{S}}$ в зависимости от длины волны $\lambda $ (во всех представленных ниже результатах $\lambda $ изменяется в пределах $300\,\,{\text{нм}} < \lambda < 600\,\,{\text{нм}}$ для серебра и $300\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}$ для золота) для случая серебряной пластины при различных углах падения ${{\varphi }_{0}}$ плоской волны.
На рис. 4 представлены результаты расчета нормированного поперечника рассеяния $k{{\sigma }_{S}}$ для угла падения ${{\varphi }_{0}} = 0,$ т.е. когда плоская волна падает (“освещает”) на узкую часть пластины и распространяется вдоль ее широкой части. При этом кривая 1 соответствует случаю квадратной пластины, а кривые 2–5 – прямоугольной пластины с $a = 50\,\,{\text{нм}}$ и b = 25, 125, 6.25 и 5 нм. Из рисунка следует, что во всех случаях кривые 1–5 содержат два максимума, соотношение амплитуд которых изменяются при уменьшении толщины пластины. При этом максимумы лежат в диапазоне длин волн $320\,\,{\text{нм}} < \lambda < 360\,\,{\text{нм}}$ и практически мало изменяют свое положение.
Рис. 4.
Зависимость нормированного поперечника рассеяния от длины волны при угле падения ${{\varphi }_{0}} = 0$ плоской волны для серебряной пластины с параметрами: а = 50 нм и b = 50 (1), 25 (2), 12.5(3), 6.25 (4) и 5 нм (5).
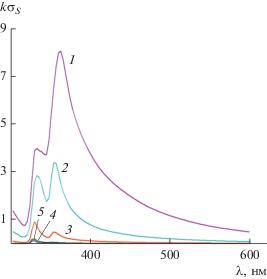
Для понимания происхождения этих максимумов на рис. 5 приведены результаты расчета нормированного поперечника рассеяния $k{{\sigma }_{S}}$ при $a = b = 50\,\,{\text{нм,}}$ ${{\varphi }_{0}} = 0$ и различных значениях мнимой части относительной диэлектрической проницаемости серебра, которые определяют потери среды. Из этого рисунка следует, что при малых значениях потерь среды ($\operatorname{Im} (\varepsilon ) \leqslant \operatorname{Im} ({{\varepsilon }_{c}})$) можно наблюдать как дипольный, так и мультипольные резонансы. Кроме того, видно, что для реальных значений $\operatorname{Im} ({{\varepsilon }_{с}})$ у такой серебряной пластины первый (правый) максимум поперечника рассеяния $k{{\sigma }_{S}}$ соответствует дипольному резонансу, а второй (левый) максимум – результат слияния нескольких мультипольных резонансов.
Рис. 5.
Зависимость нормированного поперечника рассеяния от длины волны при ${{\varphi }_{0}} = 0,$ $a = b = 50\,\,{\text{нм,}}$ ${{\varphi }_{0}} = 0$ и различных потерях серебра: $\operatorname{Im} (\varepsilon ) = 0$ (1), 0.1Im( εc) (2) и 0.001 Im( εc ) (3).
Следует обратить внимание, что применение методики и результаты работы [14] вызывают серьезные сомнения для случая тонких нанопластин из благородных металлов. С одной стороны, это связано с тем, что толщина пластины $2b$ не должна быть меньше $2b \leqslant 10\,\,{\text{нм,}}$ так как при толщине пластины $2b < 10\,\,{\text{нм}}$ необходимо учитывать эффекты, связанные с пространственной дисперсией, а при $2b \leqslant 5\,\,{\text{нм}}$ – привлекать квантовую механику для описания взаимодействия электромагнитной волны с пластиной [1]. С другой стороны, при $2b > 10\,\,{\text{нм}}$ имеет место достаточно сильное изменение поля поперек пластины, что принципиально не учитывается в методике работы [14]. Кроме того, заметим, что ссылка на работу [13] в качестве теста является некорректной, поскольку в ней отсутствуют соответствующие расчеты поперечника рассеяния на основе применения метода поверхностных интегральных уравнений, подтверждающие результат работы [14].
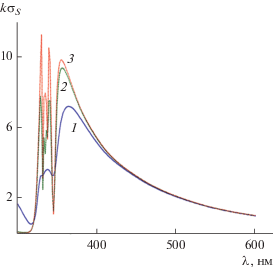
На рис. 6а и 6б представлены результаты расчета нормированного поперечника рассеяния $k{{\sigma }_{S}}$ для углов падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ т.е. когда “освещены” обе грани пластины. Размеры серебряной пластины и нумерация кривых полагались аналогичными предыдущему случаю. Как следует из рисунков, поперечник рассеяния $k{{\sigma }_{S}}$ имеет один максимум (правый и главный), связанный с дипольным резонансом, и второй максимум (левый с существенно меньшим уровнем), который является результатом слияния мультипольных резонансов. Отметим, что положение главного максимума $k{{\sigma }_{S}}$ зависит от толщины пластины – с уменьшением толщины пластины он перемещается в сторону увеличенных значений λ. При этом максимумы поперечника рассеяния $k{{\sigma }_{S}}$ лежат в диапазоне длин волн $320\,\,{\text{нм}} < \lambda < 550\,\,{\text{нм,}}$ что значительно превышает случай падения плоской волны с углом ${{\varphi }_{0}} = 0.$ Кроме того, сравнение результатов, представленных на рис. 6а и 6б, показывает, что положения резонансов поперечника рассеяния $k{{\sigma }_{S}}$ для углов падения ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4},$ ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ при одинаковых толщинах пластин практически совпадают.
Рис. 6.
Зависимость нормированного поперечника рассеяния от длины волны при углах падения ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ (а) и ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (б) плоской волны для серебряной пластины с параметрами: а = 50 нм и b = 50 (1), 25 (2), 12.5(3), 6.25 (4) и 5 нм (5).
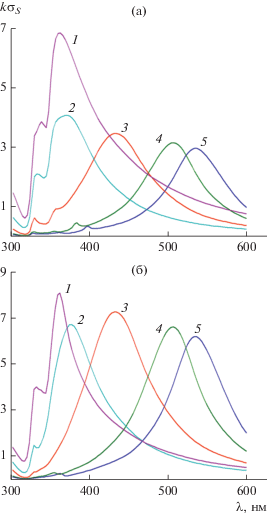
Результаты расчета нормированного поперечника рассеяния $k{{\sigma }_{S}}$ для золотой пластины и углов падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ представлены на рис. 7а и 7б. Размеры золотых пластин такие же, как и серебряных. Как видим, частотная зависимость поперечника рассеяния $k{{\sigma }_{S}}$ имеет только один максимум, определяемый дипольным резонансом. Уменьшение толщины пластины здесь, как и в случае серебряной пластины, приводит к аналогичному изменению положения поперечника рассеяния $k{{\sigma }_{S}}$-смещению в область больших длин волн. Однако диапазон длин волн, в котором располагаются максимумы $k{{\sigma }_{S}}$ – $510\,\,{\text{нм}} < \lambda < 640\,\,{\text{нм,}}$ меньше, чем в случае серебряной пластины.
Рис. 7.
Зависимость нормированного поперечника рассеяния от длины волны при угле падения ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ (а) и ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (б) плоской волны для золотой пластины с параметрами: а = 50 нм и b = 50 (1), 25 (2), 12.5 (3), 6.25 (4) и 5 нм (5).
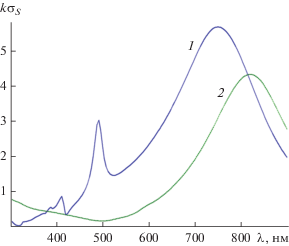
Влияния материала пластины на частотную зависимость поперечника рассеяния $k{{\sigma }_{S}}$ представлено на рис. 8. На нем изображены результаты расчетов поперечника рассеяния $k{{\sigma }_{S}}$ для серебряной и золотой пластин с одинаковыми размерами $a = 100\,\,{\text{нм}},\,\,b = 5\,\,{\text{нм}}$ и угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}.$ Из рисунка следует, что для серебряной пластины имеет место ярко выраженные дипольный и один мультипольный резонансы. При этом у золотой пластины присутствует только дипольный резонанс. Различия в поведении частотной зависимости потерь серебра и золота (см. кривые 2 рис. 2а и рис. 2б) объясняют такое поведение кривых.
Рис. 8.
Зависимость нормированного поперечника рассеяния от длины волны для серебряной (1) и золотой (2) пластин с параметрами $a = 100\,\,{\text{нм}},\,\,b = 5\,\,{\text{нм}}$ и угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}.$
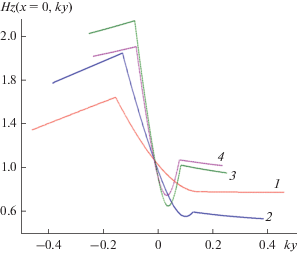
На рис. 9 представлены результаты расчета пространственного распределения поля U = $ = {{H}_{z}}(x = 0,y)$ вдоль оси $y$ для четырех длин волн $\lambda $ = 367.27, 400, 539 и 600 нм. Геометрические размеры серебряной пластины $a = 50\,\,{\text{нм,}}$ $b = 5\,\,{\text{нм;}}$ угол падения плоской волны на пластину ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ Отметим, что при $\lambda \approx 400\,\,{\text{нм}}$ и $\lambda = 539\,\,{\text{нм}}$ имеют место локальные максимумы поперечника рассеяния. Из этого рисунка следует, что даже в случае относительно тонкой пластины (толщина $2a = 10\,\,{\text{нм}}$) в поперечном направлении наблюдается достаточно сильное изменение поля, которое никак не может быть признано приблизительно постоянным. Это также ставит под сомнение использование интегрального уравнения, полученного на основе метода двусторонних граничных условий [14] для описания взаимодействия электромагнитных волн с “тонкими пластинами” из благородных металлов.
Рис. 9.
Пространственное распределение поля $U = {{H}_{z}}(x = 0,y)$ вдоль оси $y$ для серебряной пластины с параметрами $a = 50\,\,{\text{нм}},$ $b = 5\,\,{\text{нм}},$ угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и фиксированной длине волны $\lambda $ = 367.27 (1), 400 (2), 539 (3), 600 нм (4).
Наконец, обсудим результаты расчета диаграмм рассеяния. На рис. 10 представлены результаты расчетов, иллюстрирующие влияние потерь серебра на диаграмму рассеяния серебряной пластины с параметрами $a = 50\,\,{\text{нм,}}$ угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ на двух длинах волн – 396 и 539 нм. Как видим, потери сильнее сказываются на диаграмме рассеяния при мультипольном резонансе ($\lambda \approx 396\,\,{\text{нм}}$), чем при дипольном резонансе ($\lambda \approx 539\,\,{\text{нм}}$).
Рис. 10.
Диаграмма рассеяния серебряной пластины с параметрами $a = 50\,\,{\text{нм,}}$ $b = 5\,\,{\text{нм}}$ и угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ на длине волны $\lambda \approx 396\,\,{\text{нм}}$ (1, 2) и $\lambda \approx 539\,\,{\text{нм}}$(3, 4) в зависимости от потерь серебра: кривые 1 и 3 – 0.001Im(εc), кривые 2 и 4 – Im(εc).
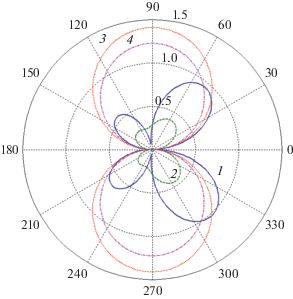
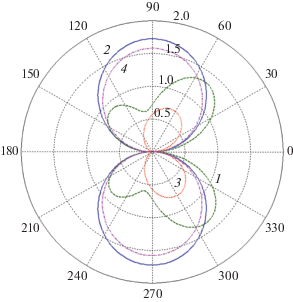
Рисунок 11 иллюстрирует влияние длины воны $\lambda $ на диаграмму рассеяния серебряной пластины с параметрами $a = 100\,\,{\text{нм,}}$ $b = 5\,\,{\text{нм}}$ при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ на длинах волн λ = 490, 750, 450 и 800 нм. Видно, что изменение длины волны λ приводит формированию диаграмм рассеяния с различным числом ее максимумов.
Рис. 11.
Диаграмма рассеяния серебряной пластины с параметрами $a = 100\,\,{\text{нм,}}$ $b = 5\,\,{\text{нм}}$ при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ в зависимости от длины волны: λ = 490 (1), 750 (2), 450 (3) и 800 нм (4).
ЗАКЛЮЧЕНИЕ
Рассмотрена дифракция плоской волны на цилиндрической 2D-структуре, представляющей собой квадратную или прямоугольную серебряную (золотую) пластину. Строгими численными методами рассчитаны спектральные и пространственные характеристики рассеянного поля. Показано, что в малых по сравнению с длиной волн реальных структурах из золота присутствуют только дипольные резонансы плазмонов. Для серебряных пластин дипольный и “совокупный” квадрупольный резонанс наблюдается лишь при достаточно большой ее длине. Продемонстрировано влияние геометрических размеров пластины, угла падения плоской волны и ее длины волны на положения максимума поперечника рассеяния и диаграммы рассеяния.
Список литературы
Климов В.В. Наноплазмоника. М.: Физматлит, 2009.
Velichko E.A., Nosich A.I. // Opt. Lett. 2013. V. 38. № 23. P. 4978.
Анютин А.П., Коршунов И.П., Шатров А.Д. // РЭ. 2015. Т. 60. № 9. С. 896.
Анютин А.П., Коршунов И.П., Шатров А.Д. // РЭ. 2016. Т. 61. № 8. С. 757.
Анютин А.П., Коршунов И.П., Шатров А.Д. // РЭ. 2017. Т. 62. № 1. С.35 .
Анютин А.П., Коршунов И.П., Шатров А.Д. // Изв. вузов. Радиофизика. 2017. Т. 60. № 7. С. 600.
Анютин А.П., Коршунов И.П., Шатров А.Д. // РЭ. 2017. Т. 62. № 12. С. 1197.
Giannini V., Sánchez-Gil J.A. // J. Opt. Soc. Am. A. 2007. V. 24. № 9. P. 2822.
Søndergaard T. // Phys. Status Solidi (b). 2007. V. 244. P. 3448.
Søndergaard T., Bozhevolnyi S.I. // Phys. Status Solidi (b), 2008. V. 245. P. 9.
Shapoval O.V., Sauleau R., Nosich A.I. // IEEE Trans. 2013.V. NT-12. № 3. P. 442.
Johnson P.B., Christy R.W. // Phys. Rev. B. 1972. V. 6. № 12. P. 4370.
Кюркчан А.Г., Минаев С.А., Соловейчик А.Л. // РЭ. 2001. Т. 46. № 6. С. 666.
Anyutin A.P., Stasevich V.I. // J. Quantitative Spectroscopy and Radiation Transfer. 2006. V. 100. № 1–3. P. 16.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника