Радиотехника и электроника, 2020, T. 65, № 3, стр. 250-256
Синтез и анализ антенны вытекающей волны с полупрозрачной стенкой из металлических цилиндров
В. А. Калошин a, *, К. Т. Нгуен b, Е. В. Фролова a, **
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация
b Московский физико-технический институт (национальный исследовательский университет)
141701 Московской обл., Долгопрудный, Институтский пер., 7, Российская Федерация
* E-mail: vak@cplire.ru
** E-mail: frolova.e@mail.ru
Поступила в редакцию 31.05.2019
После доработки 10.06.2019
Принята к публикации 19.07.2019
Аннотация
Рассмотрены задачи синтеза и анализа антенны вытекающей волны в виде нерегулярного полого прямоугольного металлического волновода с узкой стенкой в виде решетки круглых металлических цилиндров. С использованием метода поперечных сечений, приближенного выражения для коэффициента отражения плоской волны от мелко-периодической решетки круглых металлических цилиндров и дисперсионного уравнения волновода с частично прозрачной стенкой решена задача синтеза заданного линейного фронта с заданным амплитудным распределением. В качестве примера найдены законы изменения периода расположения цилиндрических проводников и их расстояний до противоположной узкой стенки волновода с целью реализации линейной антенны вытекающей волны с равномерным распределением амплитуды нулевой пространственной гармоники вдоль волновода. С использованием метода конечных элементов проведено электродинамическое моделирование линейной антенны и антенной решетки из шести линейных антенн вытекающей волны от частоты.
ВВЕДЕНИЕ
Исследование антенн вытекающей волны, излучающих основную (нулевую) пространственную гармонику, продолжается в течение ряда лет, начиная с середины прошлого века [1–4]. Конструктивно такие антенны чаще всего выполняются в виде металлического волновода или решетки волноводов с частично прозрачной стенкой. Частичная прозрачность стенки обеспечивается наличием в ней продольной щели или мелко-периодической решетки щелей или отверстий. Одним из возможных вариантов является использование в качестве частично прозрачной стенки решетки круглых металлических цилиндров (проволочной решетки), которая может быть выполнена, в частности, с применением технологии SIW (substrate integrated waveguide) [2, 3]. Однако использование SIW-технологии предполагает заполнение волновода диэлектриком, что приводит к дополнительным тепловым потерям и уменьшению пропускаемой мощности, а также увеличению скорости изменения углового положения луча с изменением частоты, что при необходимости реализации фиксированного луча является нежелательным.
В работе [4] проведено исследование линейной антенны вытекающей волны в виде полого прямоугольного металлического волновода со стенкой в виде решетки металлических цилиндров. Показано, что антенна в виде двух таких волноводов, расположенных под определенным углом, обеспечивает при изменении частоты фиксированный в пространстве луч с высоким КИП (коэффициентом использования поверхности). Для реализации высокого КИП в работе [4] с использованием численной процедуры синтезировано распределение амплитуды поля вытекающей волны вдоль волновода, близкое к равномерному. Однако исследованная антенна не обеспечивает высокий КИП в широкой полосе частот.
В данной работе развита численно-аналитическая методика синтеза антенны вытекающей волны в виде нерегулярного полого прямоугольного металлического волновода с узкой стенкой в виде решетки круглых металлических цилиндров. Методика основана на замене периодического нерегулярного волновода эквивалентным непрерывным волноводом с соответствующей зависимостью коэффициента вытекания вдоль волновода. Для обеспечения заданного амплитудного распределения вытекающей моды используется известное соотношение [1], связывающее величину постоянной затухания вытекающей моды с амплитудным распределением излученного поля. С использованием дисперсионного уравнения для планарного волновода вытекающей волны с известными коэффициентами отражения плоских волн (волн Бриллюена) от стенок [5] и известных выражений для коэффициента отражения от мелко-периодической решетки круглых металлических цилиндров [6] получено приближенное дисперсионное уравнение для прямоугольного волновода с узкой стенкой в виде такой решетки. Для синтеза линейного фазового фронта вытекающей волны вдоль волновода получена формула, связывающая изменение периода решетки цилиндров с изменением расстояния от осей цилиндров до узкой стенки волновода и обеспечивающая приближенное постоянство фазовой скорости вдоль волновода. Соотношение этих параметров может уточняться путем численной процедуры с использованием методики работы [7]. В качестве примера применения развитой теории синтезируется линейная антенна вытекающей волны с равномерным амплитудным распределением. Цель работы – с использованием электродинамического моделирования на основе метода конечных элементов провести синтез и анализ синтезированной антенны вытекающей волны и решетки таких антенн.
1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА
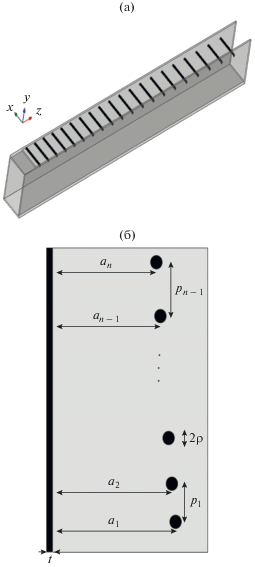
Рассмотрим полый прямоугольный металлический волновод с размерами широкой и узкой стенки a и b, соответственно (рис. 1). Одна из узких стенок волновода образована решеткой круглых металлических цилиндров радиусом $\rho $, расположенных параллельно оси x c переменными периодом р(z) и расстоянием от их осей до другой узкой стенки a(z). Задача синтеза заключается в определении функций р(z) и a(z), обеспечивающих заданный линейный фронт излучения с заданным распределением амплитуды.
В первом приближении метода поперечных сечений [8] задача синтеза нерегулярного волновода сводится к соответствующей задаче для регулярного волновода “сравнения” (с параметрами, совпадающими с параметрами нерегулярного волновода для данного значения z). Используя известное соотношение [1], связывающее величину постоянной затухания вытекающей моды α(z) с амплитудным распределением излученного поля A(z):
где Lλ= L/λ – нормированная на длину волны λ в свободном пространстве длина волновода, а zλ = = z/λ – нормированная координата, сводим исходную задачу синтеза к задаче определения функций р(z) и a(z), которые находятся из дисперсионного уравнения для регулярного волновода сравнения и обеспечивают заданную функцию α(z) и постоянную распространения β, независящую от координаты z.2. СИНТЕЗ НЕРЕГУЛЯРНОГО ВОЛНОВОДА С ПОСТОЯННОЙ ВЕЛИЧИНОЙ β
Дисперсионное уравнение для основной волны планарного волновода с частично прозрачной стенкой имеет вид [5]
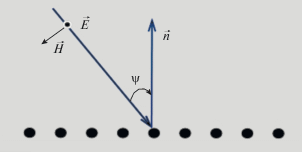
Здесь R1,2 – коэффициенты отражения плоских волн Бриллюена, падающих на стенки волновода. Уравнение (2) остается справедливым и для основной моды прямоугольного волновода. В этом случае волна Бриллюена падает на узкую стенку волновода под углом ψ (рис. 2), ψ = arccos(χ/k), где χ –поперечное волновое число для основной моды, k = 2π/λ – волновое число в свободном пространстве, λ – длина волны.
Коэффициент отражения от решетки для случая Е-поляризации (когда вектор $\vec {E}$ параллелен осям цилиндров) для мелко-периодических решеток (p $ \ll $ λ) можно записать в виде [6]
(3)
${{R}_{1}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} {\left( {1 + i\left( {\frac{{2p}}{\lambda }\left( {{\text{cos}}\psi } \right){\text{ln}}\frac{p}{{2\pi \rho }}} \right)} \right)}}} \right. \kern-0em} {\left( {1 + i\left( {\frac{{2p}}{\lambda }\left( {{\text{cos}}\psi } \right){\text{ln}}\frac{p}{{2\pi \rho }}} \right)} \right)}},$где ρ – радиус цилиндра, p – период решетки.
Поставляя выражение (3) в уравнение (1), получим уравнение относительно cos ψ:
где d = (2p/λ)ln(p/2πρ). Коэффициент отражения от металлической стенки R2 = –1.Разлагая левую часть уравнения (4) в ряд Тейлора, получим приближенное решение уравнения (4)
(5)
$\cos \psi = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {(d}}} \right. \kern-0em} {(d}} + 2ka) + i \times 2{{\pi }^{2}}{{{{d}^{2}}} \mathord{\left/ {\vphantom {{{{d}^{2}}} {(d}}} \right. \kern-0em} {(d}} + 2ka{{)}^{3}}.$Выражение для продольного волнового числа записывается в виде
Формулы (5), (6) определяют величину постоянной распространения β = Re(γ) и затухания ά = = Im(γ).
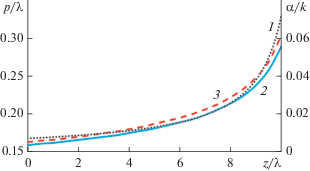
Зависимости нормированной на волновое число постоянной распространения от нормированного на длину волны периода рλ, полученные по формулам (5), (6) и численным методом [7] показаны на рис. 3а семействами кривых 1, 2, 3, 4 для а/λ = 0.5, 0.525, 0.55, 0.6 соответственно.
Рис. 3.
Зависимости постоянной распространения (а) и постоянной затухания (б) от периода для a/λ = 0.5 (1), 0.525 (2), 0.55 (3), 0.6 (4), cплошные кривые – расчет по формулам, штриховые кривые – расчет с использованием методики [7].
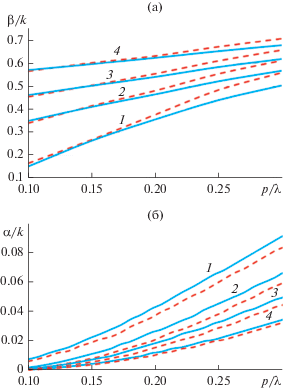
На рис. 3а видно, что величина постоянной распространения довольно существенно меняется с увеличением периода решетки, формулы (5), (6) достаточно точно описывают это изменение при малых р/λ (р/λ < 0/2), при этом точность формул растет с увеличением величины а/λ.
Зависимости для нормированной постоянной затухания, рассчитанные с использованием формул (5), (6) и методики [7], в аналогичных обозначениях представлены на рис. 3б. На рисунке видно, что точность формул (5), (6) при вычислении постоянной затухания, как и в предыдущем случае (см. рис. 3а), возрастает с уменьшением величины р/λ и с увеличением величины а/λ.
Применяя параболическую интерполяцию зависимости величины β/k от величины р/λ для дискретного набора величин а/λ, в результате решения ряда квадратных уравнений β/k = β0 можно найти дискретный набор расстояний a от цилиндров до узкой стенки волновода в зависимости от периода p при использовании двух разных методов расчета (численным и на основе полученных выражений), обеспечивающих заданную постоянную величину β0. Используя параболическую интерполяцию между дискретными значениями, получаем приближенные формулы, описывающие непрерывные зависимости аλ(рλ). В частности, при β0/κ = 0.5
(7)
${{а}_{\lambda }}\left( {{{р}_{\lambda }}} \right) = - 0.5176{{\left( {{{р}_{\lambda }}} \right)}^{2}} - 0.1064\left( {{{р}_{\lambda }}} \right) + 0.5769,$(8)
${{а}_{\lambda }}\left( {{{р}_{\lambda }}} \right) = - 1.3208{{\left( {{{р}_{\lambda }}} \right)}^{2}} + 0.10098\left( {{{р}_{\lambda }}} \right) + 0.5632,$где аλ = а/λ, рλ = p/λ.
Были найдены зависимости нормированной величины аλ от нормированного периода рλ, рассчитанные по формуле (7) и (8) (рис. 4). Соответствующие зависимости нормированных постоянных распространения β/κ и затухания α/κ были получены численным методом и показаны соответственно на рисунках 5а, 5б в аналогичных обозначениях.
Рис. 4.
Зависимость размера волновода в Н-плоскости от периода: кривая 1 – расчет по формуле (7), 2 – расчет по формуле (8).
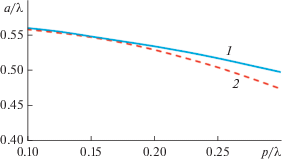
Рис. 5.
Зависимости постоянной распространения (а) и постоянной затухания (б) от периода при одновременном изменении параметров аλ и рλ, рассчитанные по формуле (7) (кривая 1) и по формуле (8) (кривая 2).
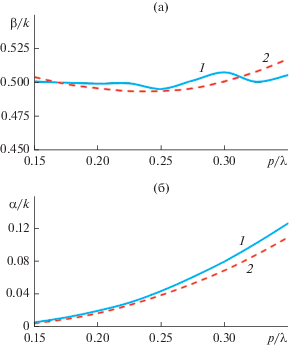
Зависимости, представленные на рис. 5а, 5б кривыми 1, 2 можно аппроксимировать параболическими функциями:
3. СИНТЕЗ И АНАЛИЗ ЛИНЕЙНОЙ АНТЕННЫ ВЫТЕКАЮЩЕЙ ВОЛНЫ
В качестве примера применения описанной выше методики рассмотрим задачу синтеза антенны с равномерным амплитудным распределением $\left| {A\left( z \right)} \right|$ = 1, которое обеспечивает максимальную величину КИП. Подставляя в формулу (1) значения Lλ = 10, P(0) = 1 и P(L) = 0.1 и приравнивая полученную функцию α(z) функциям α(р), которые определены формулами (9), (10), находим соответствующие зависимости нормированного периода р/λ от нормированной координаты zλ:
(11)
$\begin{gathered} {{p}_{\lambda }} = \\ = \frac{{0.4959 + \sqrt {0.2459 - 8.7732(0.0312 - \alpha ({{z}_{\lambda }}))} }}{{4.3866}}, \\ \end{gathered} $(12)
$\begin{gathered} {{p}_{\lambda }} = \\ = \frac{{0.3843 + \sqrt {0.14768 - 7.2388(0.0217 - \alpha ({{z}_{\lambda }}))} }}{{3.6194}}. \\ \end{gathered} $Зависимость постоянной затухания была рассчитана по формуле (1), зависимости периода от координаты z – по формулам (11), (12). Полученные результаты представлены на рис. 6 кривыми 1–3 соответственно.
Нормированное распределение амплитуды электрического поля внутри волновода было полученно в результате электродинамического моделирования с использованием метода конечных элементов для зависимости рλ(zλ), рассчитанной по формуле (11) и по формуле (12), при синтезе антенны на частоте 9 ГГц. Полученные зависимости представлены на рис. 7а кривыми 1, 2 соответственно.
Рис. 7.
Нормированное распределение амплитуды электрического поля внутри волновода (а) и вдоль антенны на растоянии λ/4 от решетки (б) при синтезе по формуле (11) (кривая 1) и по формуле (12) (кривая 2).
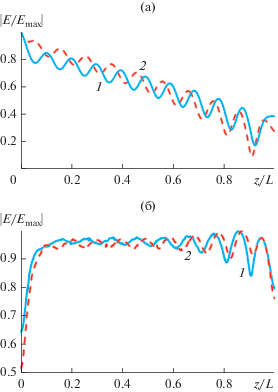
Также в результате электродинамического моделирования были найдены соответствующие нормированные распределения амплитуды электрического поля вдоль антенны на растоянии λ/4 от решетки, которые изображены рис. 7б. На рисунке видно, что кривые имеют относительно небольшие колебания вокруг постоянной величины и незначительно спадают на концах антенны. При этом амплитуда колебаний кривых для антенны, синтезированной по формуле (11), несколько больше, чем у антенны, синтезированной по формуле (12).
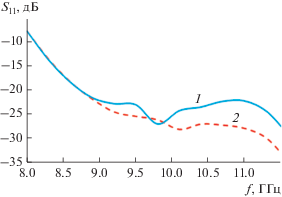
Далее для антенн, синтезированных по формулам (13), (14), были получены зависимости от частоты коэффициента отражения S11. Результаты представлены на рис. 8 (кривые 1, 2).
Рис. 8.
Зависимость коэффициента отражения от частоты при синтезе антенны по формуле (11) (кривая 1) и по формуле (12) (кривая 2).
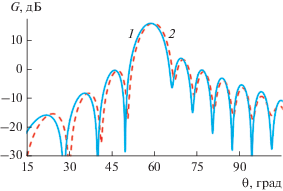
Для антенн, синтезированных на частоте 9 ГГц по формулам (11), (12), были рассчитаны диаграммы направленности в Н-плоскости. Результаты представлены на рис. 9 (кривые 1, 2). Как видно на рисунке, разницы между диаграммами антенн, синтезированных численным и численно-аналитическим методом, практически нет.
Рис. 9.
Диаграмма направленности антенны в Н‑плоскости при синтезе антенны по формуле (11) (кривая 1) и по формуле (12) (кривая 2).
4. АНАЛИЗ ФАЗИРОВАННОЙ РЕШЕТКИ ШЕСТИ ЛИНЕЙНЫХ АНТЕНН ВЫТЕКАЮЩЕЙ ВОЛНЫ
Синтезированная выше антенна вытекающей волны сканирует с частотой в Н-плоскости. Для сканирования в Е-плоскости можно использовать фазированную антенную решетку линейных антенн вытекающей волны [1]. Электродинамическое моделирование решетки шести линейных антенн вытекающей волны, модель которой изображена на рис. 10, проведено с использованием метода конечных элементов. Результаты моделирования представлены на рис. 11–14.
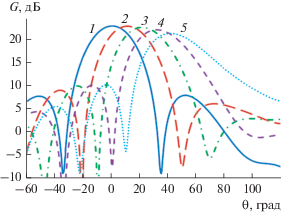
Рис. 11.
Диаграммы направленности антенной решетки в Н-плоскости на частотах: 8.5 (1), 9 (2), 9.5 (3), 10 (4), 11 ГГц (5).
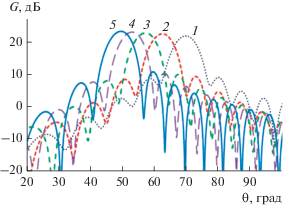
Рис. 13.
Частотные зависимости коэффициента усиления (1) и КИП синтезированной антенны (2) в сравнении с коэффициентом усиления и КИП с апертурой с равномерным амплитудным и линейным фазовым распределениями (кривые 3,4).
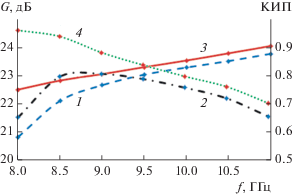
Рис. 14.
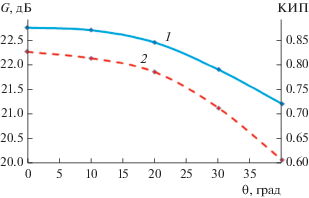
Зависимость коэффициента усиления (кривая 1) и КИП (кривая 2) от угла отклонения луча при фазовом сканировании на частоте 9 ГГц.
На рис. 11 показаны диаграммы направленности антенной решетки в Н-плоскости на частотах 8.5, 9, 9.5, 10, 11 ГГц при синфазном возбуждении волноводов решетки. На рис. 12 представлены диаграммы направленности антенной решетки в E-плоскости при фазовом сканировании на частоте 9 ГГц.
На рис. 13 показаны зависимости коэффициента усиления антенной решетки и КИП антенны от частоты (кривые 1 и 2 соответственно). Для сравнения на рисунке приведены зависимости коэффициента усиления и КИП аналогичной плоской апертуры с равномерным амплитудным и линейным фазовым распределением, соответствующим углу частотного сканирования (кривые 3 и 4).
Как видно на рисунке в полосе частот 9…11 ГГц величины усиления и КИП близки к предельно возможным (разница с характеристиками идеальной апертуры менее 0.5 дБ). При этом в полосе частот 8…11 ГГц величина КИП более 0.65.
На рис. 14 в аналогичных обозначениях показаны зависимости коэффициента усиления и КИП при фазовом сканировании на частоте 9 ГГц. Как видно из рисунка, обе зависимости близки к косинусоидальным, что соответствует теории фазированных решеток антенн вытекающей волны [1].
ЗАКЛЮЧЕНИЕ
На основании полученных результатов можно сделать следующие выводы.
1. Развитая численно-аналитическая методика позволяет на заданной частоте синтезировать распределение амплитуды вытекающей волны вдоль антенны, близкое к равномерному, а фазовое распределение – близкое к линейному.
2. В полосе частот более 20% усиление и КИП решетки шести синтезированных линейных антенн вытекающей волны близки к предельно возможным значениям.
3. В полосе частот более 30% КИП решетки шести синтезированных линейных антенн вытекающей волны выше 0.65.
Список литературы
Уолтер К. Антенны бегущей волны / Пер. с англ. под ред. А.Ф. Чаплина. М.: Энергия, 1970.
Deslandes D., Wu Ke. Asia-Pacific Microwave Conf. Proc. Suzhou, China. 4–7 Dec. 2005. V. 1. P. 4.
Martinez-Ros A.J., Gómez-Tornero J.L., Goussetis G. // IEEE Trans. 2012. V. AP-60. № 3. P. 1625.
Калошин В.А., Нгуен К.Т. // Журн. радиоэлектроники. 2019. № 1. http://jre.cplire.ru/jre/jan19/14/text.pdf.
Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1973.
Айзенберг Г.З., Ямпольский В.Г., Терешин О.Н. Антенны УКВ. М.: Связь, 1977. Ч. 2.
Калиничев В.И., Бабаскин А.А. // Журн. радиоэлектроники. 2015. № 7. http://jre.cplire.ru/jre/jul15/ 2/text.pdf.
Каценеленбаум Б.З. Теория нерегулярных волноводов с медленно меняющимися параметрами. М.: Изд-во АН СССР, 1961.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника