Радиотехника и электроника, 2020, T. 65, № 4, стр. 363-371

ВВЕДЕНИЕ

Задачи рассеяния на полубесконечных структурах – клиньях, полуплоскостях и полупластинах – относятся к числу классических задач электродинамики. Несмотря на то что первая из них была решена около 100 лет назад [1], интерес к анализу подобных объектов не ослабевает до настоящего времени. Такие структуры являются ключевыми в том смысле, что их исследование позволяет объяснить процессы рассеяния электромагнитных волн в значительно более широком классе объектов, чем сами по себе идеализированные полубесконечные структуры. Интерес к ним обусловлен также рядом практически важных приложений, связанных с расчетом характеристик рассеяния сложных объектов. Оказывается, что основной вклад в рассеянное поле вносят острые кромки, входящие в структуру такого объекта. В ряде работ для них предложен специальный термин – центры рассеяния [2]. Для корректного их описания весьма полезными оказываются компактные и простые аналитические решения граничных задач для ключевых структур. Такие задачи можно по аналогии назвать ключевыми задачами [3].

Импедансные полуплоскости также относятся к числу традиционных ключевых задач электродинамики. Обычно под импедансной плоскостью/полуплоскостью понимают поверхность, на которой выполняются граничные условия Леонтовича [4]. Такая структура является непрозрачной. Она полностью отражает электромагнитные волны. Задачи дифракции на таких полуплоскостях решались начиная с 50-х годов ХХ в. Здесь уместно отметить работы Т. Сениора [5, 6].

Наряду с непрозрачными импедансными полуплоскостями известны полупрозрачные структуры, которые описываются двухсторонними импедансными граничными условиями (см., например, [7]). Они связывают поля на двух поверхностях бесконечно тонкой пленки при помощи одного параметра, который можно рассматривать в качестве поверхностного импеданса пленки. Такие структуры исследовались значительно менее интенсивно, чем их непрозрачные аналоги. Можно отметить решение задачи о дифракции на тонком слое диэлектрика [8], а также работу [9], в которой рассматривается полупрозрачная пленка, расположенная на поверхности диэлектрической пластины.

Следует сказать, что двухсторонние импедансные граничные условия [7] являются лишь частным случаем граничных условий, описывающих полупрозрачные структуры. Например, можно отметить граничные условия [10] на поверхности металлического слоя с конечной проводимостью. Назовем их обобщенными двухсторонними импедансными граничными условиями. Они, так же как и условия [7], связывают поля на двух поверхностях слоя, однако указанная связь описывается не одним, а двумя параметрами. Достоинством таких граничных условий является возможность с их помощью описать переход от слоя, толщина которого много меньше глубины скин-слоя, к слою с толщиной много большей указанной глубины. Интересно, что в первом предельном случае обобщенные граничные условия переходят в двухсторонние граничные условия, а в другом случае – в условия Леонтовича.

Обобщенные двухсторонние граничные условия приводятся в книге [11]. С их помощью удается описать тонкий слой сверхпроводящего материала. Особенно ценно, что они дают возможность корректного описания динамики поведения сверхпроводящей структуры при переходе температуры через критическое значение.

Отметим, что обобщенные двухсторонние импедансные граничные условия могут использоваться не только для построения моделей проводящих и сверхпроводящих слоев, но и для описания более широкого класса объектов, содержащих такие структуры как слои магнито-диэлектриков, периодические структуры и т.д. Интерес к полупрозрачным импедасным структурам заметно вырос в последние годы, что связано с активным применением частотно-селективных экранов и подобных им структур [12], которые могут при определенных условиях описываться с помощью двухсторонних граничных условий.

Следует сказать, что граничные условия с двумя параметрами хорошо описывают только слои, обладающие определенной симметрией. Они должны иметь одинаковые свойства на обеих поверхностях. При отсутствии такой симметрии и при наличии невзаимных сред граничные условия наиболее общего вида включают четыре параметра. В данной работе мы ограничимся анализом симметричных структур.

Цель данной работы – исследование симметричной полупрозрачной полуплоскости с обобщенными двухсторонними импедансными граничными условиями на ее поверхностях. Основой исследования является работа [10], в которой решена задача о рассеянии плоской волны на такой полуплоскости. Решение получено строгим методом Винера–Хопфа [13] в виде интеграла Фурье. В нашей работе представлена численная реализация аналитического решения [10]. Далее на основе анализа строгого решения в работе предложены приближенные эвристические соотношения, которые с приемлемой для многих ситуаций точностью описывают поведение рассеянного полуплоскостью поля в дальней зоне.

1. ФОРМУЛИРОВКА ГРАНИЧНОЙ ЗАДАЧИ ПО МЕТОДУ СИММЕТРИИ

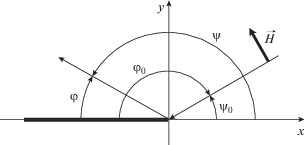
Исследуемая структура показана на рис. 1. Задача двумерная, поле не зависит от координаты z. В двумерной структуре поле разделяется на электрические и магнитные волны, для которых граничная задача решается по отдельности. Оба решения аналогичны. Поэтому рассмотрим только случай электрических или Е-волн. Такие волны имеют компоненты поля ${{E}_{z}},{{H}_{x}},{{H}_{y}}.$

Рис. 1.

Исследуемая структура.

На симметричной полуплоскости при $x < 0,$ $y = 0$ выполняются обобщенные импедансные двухсторонние граничные условия:

где ${{Z}_{{1,2}}}$ – импедансы полуплоскости, знак плюс соответствует полям на верхней поверхности, а минус – на нижней. Импеданс ${{Z}_{1}}$ описывает собственные свойства поверхности, а импеданс ${{Z}_{2}}$ – связь полей на разных сторонах полуплоскости.

Приведем граничные условия (1) для частного случая тонкого слоя металла с толщиной $d$, сравнимой с толщиной скин-слоя $\delta $. Отметим, что они справедливы также для сверхпроводящих слоев [11]. Граничные условия имеют структуру, совпадающую с соотношениями (1). Параметры ${{Z}_{{1,2}}}$ в них описываются следующим образом:

где $k,{{W}_{0}}$ – волновое число и волновое сопротивление свободного пространства. Отметим, что соотношения (2) получены для зависимости от времени $\exp (i\omega t),$ $\omega $ – круговая частота.

Поле падающей волны зададим следующим образом:

где ${{\psi }_{0}}$ – угол падения плоской волны.

При решении граничной задачи учтем симметрию структуры относительно плоскости $y = 0$. Воспользуемся методом симметрии [14], последовательно решая две задачи – для четного и нечетного возбуждения. Отметим, что при четном возбуждении для $Е_{z}^{{\text{ч}}}$ выполняются следующие соотношения:

аналогично при нечетном возбуждении для поля $Е_{z}^{{\text{ч}}}$ получаем – соотношения

Верхние индексы ч,н показывают соответствие данной величины четному или нечетному возбуждению. Нетрудно увидеть, что исходные поля связаны с четными и нечетными полями следующим образом:

Соотношения (4), (5) позволяют связать поля на поверхностях полуплоскости при $y = \pm 0$:

где верхний знак берется для четного случая, а нижний для нечетного. Соотношения (7) позволяют получить из (1) два граничных условия для четного и нечетного возбуждения соответственно:

Оба условия (8) получены для поля на верхней поверхности. Поэтому индекс “плюс” в них опущен. Отметим, что граничные условия (8) выполняются при $x < 0,$ $y = 0.$ Из соотношений (4), (5) следует, что при четном возбуждении при $x > 0,$ $y = 0,$ равно нулю тангенциальное магнитное поле, а при нечетном возбуждении тангенциальное электрическое:

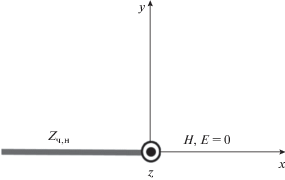
Таким образом, при четном возбуждении мы имеем при $x > 0,$ $y = 0$ магнитную стенку, а при нечетном возбуждении – электрическую. Можно сделать вывод, что решение исходной граничной задачи с использованием метода симметрии свелось к анализу двух парциальных структур. В них поле существует только в верхнем полупространстве. При $x < 0,$ $y = 0$ выполняются граничные условия Леонтовича (8), а при $x > 0,$ $y = 0$ граничные условия (9). Возбуждаются парциальные структуры полями $E_{{z0}}^{{{\text{ч,н}}}}.$

2. ЧИСЛЕННОЕ РЕШЕНИЕ ГРАНИЧНОЙ ЗАДАЧИ ПО МЕТОДУ ВИНЕРА–ХОПФА

Вывод интегральных уравнений для полубесконечных структур и переход к функциональным уравнениям многократно описаны в литературе, а также в цитированной работе [10], поэтому подробно останавливаться на нем не имеет смысла. Перейдем к численной реализации решения, основным этапом которого является факторизация двух функций ${{G}^{{{\text{ч,н}}}}}(\kappa ){\kern 1pt} :$

где k – волновое число, W₀ – сопротивление свободного пространства, индексы ± означают, что данная функция регулярна соответственно в верхней или нижней полуплоскости комплексного аргумента.

Отметим, что факторизация функции $\gamma $ осуществляется элементарно [13]. Поэтому мы можем свести факторизацию функций $G(\kappa )$ к факторизации функции $K\left( \kappa \right)$ при помощи, используя следующие соотношения:

(здесь индексы ч, н опущены). Еще раз отметим, что факторизация сомножителей $L\left( \kappa \right),\gamma ,{{\gamma }_{e}}$ элементарно находится аналитически. Для требуемого представления функции $K\left( \kappa \right)$ воспользуемся теоремой о факторизации [13]:

Формула (12) записана с учетом четности функции $K\left( \kappa \right).$

Численно взять интеграл из (12) невозможно, так как он имеет особенности на контуре интегрирования. Для исключения этих особенностей, а также для улучшения сходимости интеграла на бесконечности мы использовали эквивалентные преобразования:

Постоянные ${{\alpha }_{{0,1,2}}},\xi $ выбираются произвольным образом из соображений удобства численных расчетов. Слагаемое, пропорциональное $\ln K\left( \kappa \right)$, устраняет особенности подынтегральной функции в точках $\alpha = \pm \kappa $, второе слагаемое под интегралом улучшает скорость сходимости несобственного интеграла на бесконечности, что позволяет нам заменить бесконечный предел конечным ${{\alpha }_{m}}$. Таким образом, соотношение (13) пригодно для численных расчетов.

Рассеянное полуплоскостью поле представляется интегралом Фурье:

Последний этап решения состоит в определении рассеянного поля в дальней зоне. Для этого целесообразно использовать цилиндрические координаты, изображенные на рис. 1. Декартовы координаты x, y связаны с ними известным образом:

Для применения к соотношениям (14) метода перевала введем замену переменной:

С учетом (15), (16) преобразуем выражения для полей (14):

При $kr \to \infty $ подынтегральные функции имеют точку стационарной фазы при $\alpha = \psi ,$ что позволяет приближенно взять интегралы в (17):

Соотношения (18) дают решение граничных задач для парциальных структур (рис. 2). Решение для исходной задачи находится из выражений (6).

Рис. 2.

Парциальные структуры.

3. ЭВРИСТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ДИФРАКЦИИ НА ИМПЕДАНСНОЙ ПОЛУПЛОСКОСТИ

Математически строгое решение отражает комплексное воздействие на решение всех параметров постановки задачи. Численные решения не имеют аналитических выражений. Форма аналитического решения зачастую бывает громоздкой, при этом влияние отдельных факторов неразличимо.

В отличие от математически строгих подходов, эвристические формулы основаны на физических принципах [15–18]. Эвристическая формула представляет собой гипотезу о поведении решения на основе нашего понимания физики процесса и известных аналитических решений простейших задач. Наличие математически строгого решения не делает бесполезным применение аналитических эвристических формул, потому что они помогают лучше разобраться в физике решения. Эвристические формулы позволяют выразить зависимость от физических характеристик в наиболее компактной и понятной форме. В отличие от математически строгих формул, эвристические формулы нуждаются в верификации при помощи решения, точность которого известна.

Функциональная зависимость от условий задачи компактно входит в эвристические формулы в явном виде. С физической точки зрения граничные условия удобно описывать коэффициентами отражения и прохождения R и T, наглядно выражающими взаимодействие плоской волны с безграничной плоской поверхностью. К задаче физической интерпретации результатов относится выявление факторов влияния условий задачи на те или иные характеристики решения.

При взаимодействии волны с безграничной поверхностью с граничными условиями (1), (8) коэффициенты отражения и прохождения R и T определяются так:

Здесь ${{W}_{0}} = 120\pi ,$ ${{q}_{0}} = k\sin \left( {{{\psi }_{0}}} \right),$ $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число, ${{Z}_{{\text{ч}}}} = i{{X}_{{\text{ч}}}},$ ${{Z}_{{\text{н}}}} = i{{X}_{{\text{н}}}}$ (Х_ч и Х_н – действительные параметры, характеризующие величину реактивных импедансов Z_ч и Z_н). Отметим, что для R и T выполняется соотношение |R|² + |T|² =1.

Если в (19) выполняется условие

то при любых значениях Х_ч имеем:

Этот случай соответствует сверхпроводящему слою, толщина которого существенно превышает толщину скин-слоя. При этих условиях сверхпроводящий слой становится непрозрачным, а на его поверхностях выполняются условия Леонтовича. Построим эвристическое решение задачи дифракции на полуплоскости (1) при выполнении условия (20).

Для удобства представления результатов введем вспомогательную переменную β:

В то время как 0 < X_ч < ∞, вспомогательная переменная меняется в пределах 0 < β < 1.

Из строгого решения задачи дифракции на идеально проводящей полуплоскости [17–19] можно получить дифракционные коэффициенты:

для ТМ- и ТЕ-полей соответственно

Обозначения ТМ и ТЕ характеризуют перпендикулярность кромке векторов магнитного и электрического полей соответственно.

В работах [17, 18, 20] в рамках концепции метода базовых компонентов (МБК) была рассмотрена эвристическая формула обобщенного дифракционного коэффициента (ОДК), основанного на дифракционных коэффициентах (23) и на коэффициентах отражения и прохождения для безграничной поверхности R и T

Первое слагаемое в правой части (24) можно условно сопоставить с рассеянием падающего поля на кромке, второе слагаемое – с рассеянием отраженного поля [17]. Для поверхности с идеальными граничными условиями имеет место Т = 0 и R = −1 (ТМ) или R = 1 (TE), причем эти значения не зависят от угла падающей волны. Нетрудно видеть, что подстановка этих значений в (24) приведет к выражениям (23).

При подстановке в (24) других значений R и T получим эвристическую формулу для дифракционного коэффициента полуплоскости с неидеальными граничными условиями. В отличие от дифракционных коэффициентов (23), формула (24) не является строгой, поэтому нуждается в верификации для каждого вида граничных условий. В рамках МБК, помимо верификации, проводят еще и настройку, т.е. коррекцию эвристической формулы с целью повышения ее точности до необходимых значений.

Следует отметить, что эвристические формулы, аналогичные (24), применялись в работах [21–23] и др. Однако в отличие от МБК в этих работах отсутствовала процедура настройки, что не позволяло проводить дальнейшее увеличение точности решения.

В данной работе проведена верификация и настройка эвристической формулы (24) с коэффициентом отражения (21) для ряда углов падения и ряда значений параметра X_ч. Исследуя численные результаты, сравнивая их с результатами счета по эвристической формуле (24) и проводя коррекцию этой формулы, можно осуществить настройку эвристической формулы и провести физическую интерпретацию численного решения.

Геометрия задачи рассеяния на полуплоскости поляризованного ТМ-поля показана на рис. 1. Полуплоскость расположена в области отрицательных значений координаты х. Для удобства сравнения результатов данной работы с другими источниками введены две пары углов. Углы направления на источник и точки наблюдения φ₀ и φ отсчитываются в отрицательном направлении от внутренней нормали к кромке. Углы направления на источник и точки наблюдения ψ₀ и ψ отсчитываются в положительном направлении от внешней нормали к кромке. Связь между углами характеризуется выражениями φ₀ = π − ψ₀ и φ = π − ψ.

Формальное применение формулы ОДК (24) не принесло желаемых результатов. Выяснилось, что формула ОДК плохо воспроизводит ноль амплитуды диаграммы рассеяния (ДР) из-за наличия у R мнимой части. При построении эвристических выражений для дифракционного коэффициента на основе выражения (24) следует принять во внимание, что Т = 0 и |R| = 1, поэтому для выражения зависимости дифракционного коэффициента от свойств поверхности остается только функция arg(R) (21). График зависимости этой функции от вспомогательной переменной β показан на рис. 3 для случаев: ψ₀ = 90, 120 и 160 град. На первом этапе построения эвристических формул дополнительный множитель введен только ко второму слагаемому.

Рис. 3.

График функции arg(R) при ψ₀ = 90° (сплошная кривая), 120° (штриховая) и 160°(пунктирная).

В процессе настройки эвристических формул на основе численного решения задачи дифракции (1) была получена следующая эвристическая формула для дифракционного коэффициента:

Здесь С – функция входных параметров, не зависящая от φ и характеризующая поправку к множителю [1 − 2arg(R)/π + C], стоящему в (25), для заданного набора параметров (X_ч, ψ₀). В большинстве случаев можно ограничиться эвристическим выражением без этой поправки (положив С = 0). Однако на участке изменения параметра X_ч от 0 до ∞ значение множителя [1 − 2arg(R)/π + C] проходит через нулевую точку, и в окрестности этой точки добавка небольшой величины С может существенно уточнить значения диаграммы рассеяния.

Эвристическая формула (25) в будущем может быть уточнена за счет ее усложнения, однако физическую интерпретацию решения можно провести уже на данном этапе работы. Физическая интерпретация при помощи МБК не только позволяет дать аналитическое описание таких общих характеристик численного решения, как его поведение в окрестности сингулярностей, но и выявить тонкую структуру решения, а именно – его изменения в зависимости от параметров граничных условий.

По мере изменения реактивного импеданса Х_ч поведение множителя из эвристической формулы (25) характеризуется следующим образом:

В точке, где множитель равен нулю, он меняет знак. В целом характер диаграммы рассеяния непрозрачной полуплоскости с реактивным импедансом постепенно меняется от f(φ, φ₀) при X_ч → 0 к g(φ, φ₀) при X_ч →∞ (см. также выражения (23)).

На рис. 4 представлены результаты сравнения диаграмм рассеянного поля численного решения (1) и эвристического решения (25) для различных значений X_ч и ψ₀ и при выполнении условия (20), а также отношение амплитуд численного и эвристического решений. Чем ближе это отношение к 1, тем лучше совпадают численное и эвристическое решения. Выбросы в графиках отношения амплитуд характеризуют неточность положения нуля эвристического решения относительно нуля численного решения и не свидетельствуют о сильном расхождении между ними.

Рис. 4.

Диаграммы рассеяния амплитуды численного решения (1) (сплошная кривая), амплитуды эвристического решения (25), нормированного для удобства сравнения (кривая с точками) и отношение амплитуд численного и эвристического решений (пунктир) при различных параметрах: а) Х_ч = 20, ψ₀ = 120, С = 0; б) Х_ч = 800, ψ₀ = 90, С = 0; в) Х_ч = = 2000, ψ₀ = 120, С = 0; г) Х_ч = 400, ψ₀ = 160, С = 0.0457; д) Х_ч = 1000, ψ₀ = 160, С = 0.011; е) Х_ч = 1400, ψ₀ = 160, С = −0.037.

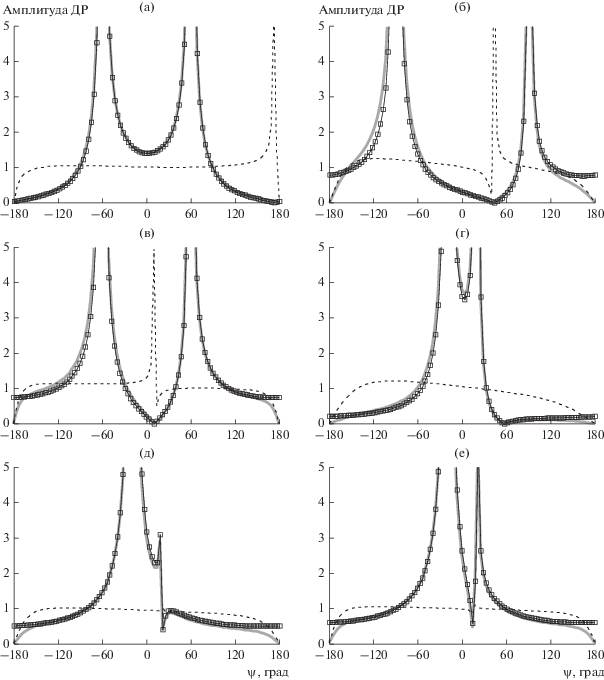
Рассмотрим диаграммы рассеяния для случая С = 0 (см. рис. 4а–4в). При Х_ч = 20 численное решение практически совпадает с дифракционным коэффициентом f(φ, φ₀) (3), при Х_ч = 2000 численное решение практически совпадает с дифракционным коэффициентом g(φ, φ₀) (3), случай Х_ч = 800 представляет собой промежуточный вариант решения.

Диаграммы рассеяния для случая С ≠ 0 показаны на рис. 4г–4е. Коррекцию множителя [1 – – 2arg(R)/π + C] пришлось проводить в связи с тем, что чувствительность решения к значению параметра С возрастала. Это происходило из-за того, что значения множителя для соответствующих комбинаций входных параметров (X_ч, ψ₀) были близки к нулю. Несмотря на стремление множителя к нулю, совпадение численного и эвристического решений в окрестности этих точек можно считать хорошим.

Таким образом, мы получили достаточно простую эвристическую аналитическую формулу, пригодную для описания тонких особенностей решения и позволившую провести его физическую интерпретацию.

Полученное в данной работе эвристическое решение для дифракционного коэффициента импедансной полуплоскости (25) значительно отличается от полученных ранее эвристических формул для полупрозрачной полуплоскости с реактивным импедансом [18, 20]. В данных работах показано, что по мере того как реактивный импеданс изменяется от 0 к ∞, характер диаграммы рассеяния полупрозрачной полуплоскости постепенно меняется от f(φ, φ₀) к f  ⁰(φ, φ₀), где f  ⁰(φ, φ₀) – дифракционный коэффициент решения соответствующей задачи в приближении физической оптики [17–20].

Таким образом, в задаче дифракции на полупрозрачной полуплоскости [20] амплитуда диаграммы рассеяния зависит только от амплитуды коэффициента отражения R, а в задаче дифракции на непрозрачной полуплоскости (25) – только от фазы R. И, что очень важно, оба эти эвристических решения получили существенные отличия от первоначальной формулы (24) после процедуры настройки.

Цель применения МБК состоит не в том, чтобы получить как можно больше аналитических решений для новых типов граничных условий. Для большинства задач реально получить только численные решения, что связано с быстрым развитием компьютерной техники и вычислительных методов, в то время как развитие аналитических методов происходит гораздо медленнее. Поэтому получать новые строгие аналитические решения становится все сложнее, а новые численные решения – все проще.

Задача МБК состоит в том, чтобы разработать универсальную (т.е. для разных типов задач и не зависящую от способа верификации) методику получения простых и физически ясных эвристических аналитических формул на основе численных, строгих аналитических решений или экспериментальных результатов. Такие формулы могут оказаться критически важными в практических задачах при необходимости увеличения быстродействия компьютерного вычислителя, при необходимости увеличения максимального размера рассеивателя, который можно исследовать, для проведения физической интерпретации численного решения или при необходимости решения обратных задач [17].