Радиотехника и электроника, 2020, T. 65, № 4, стр. 390-416

1. ПОСТАНОВКА ЗАДАЧИ

В различных областях физики (радиоастрономии, радиолокации, радиотеплолокации, различных видах микроскопии и других типов измерений) требуется учитывать влияние измерительного тракта технической системы и канала связи (инерционность среды, по которой распространяется сигнал) на регистрируемые сигналы или изображения. При этом имеют место искажения реального распределения сигнала, зависящие от аппаратной функции технической системы, и добавляется шум. Если форма аппаратной функции известна, то задача восстановления полезного сигнала или, по крайней мере, задача повышения качества регистрируемого распределения сигнала сводится к решению интегрального уравнения, которое связывает регистрируемое и исходное распределения искомой величины. При математическом описании данной задачи достаточно широко используется сверточная модель представления измерительного процесса, в которой рассматривается решение интегрального уравнения Фредгольма 1-го рода типа свертки. Как известно, такая задача является некорректной, т.е. неустойчивой к сколь угодно малым погрешностям измерений. Поэтому при ее решении выполняется оценка полезного сигнала на основе имеющейся априорной информации о сигнале, шуме, аппаратной функции и технических требованиях к системе обработки.

Общая форма записи интегрального уравнения типа свертки имеет вид

Оператор свертки $\mathcal{L}$ определяется следующим образом:

С точки зрения практического применения наиболее интересна следующая постановка задачи: выполнить оценку полезного сигнала х(t) первоначально искаженного импульсной характеристикой λ(t) линейной стационарной системы с последующим действием шума n(t)

Шум n(t) предполагается аддитивным и белым гауссовским (АБГШ) с дисперсией σ². АБГШ в качестве модели хорошо подходит для математического описания многих физических процессов.

Для решения (1) существует много разнообразных методов [1–7]. На основе преобразования Фурье (ПФ) наиболее широкое распространение получили методы ПФ с регуляризацией Тихонова, метод фильтрации Винера, которые используют регуляризующий компонент R(ω).

Ослабление усиленного шума ${{\hat {n}(\omega )} \mathord{\left/ {\vphantom {{\hat {n}(\omega )} {\hat {\lambda }(\omega )}}} \right. \kern-0em} {\hat {\lambda }(\omega )}}$ выполняется с помощью фильтра с частотной характеристикой [1–7]

Отметим, что при R → 0 спектр $\hat {K}(\omega )$ переходит в выражение для инверсной или псевдоинверсной фильтрации. Таким образом, задача становится некорректной, а решение неустойчивым.

Для ПФ оценки полезного сигнала x_р, вычисленное с помощью методов регуляризации ПФ, имеет место следующее соотношение:

Здесь ${{\hat {x}}_{P}}$ и ${{{{{\hat {n}}}_{P}}} \mathord{\left/ {\vphantom {{{{{\hat {n}}}_{P}}} {\hat {\lambda }}}} \right. \kern-0em} {\hat {\lambda }}}$ – слагаемые спектра решения ${{\hat {\tilde {x}}}_{P}}$ соответственно ПФ очищенного сигнала x_p и прошедшего шума ${{\mathcal{L}}^{{ - 1}}}{{n}_{P}},$ входящие в состав оценки полезного сигнала ${{\tilde {x}}_{P}}$.

Отличительной особенностью использования ПФ для решения (1) является компактное представление шума ${{\mathcal{L}}^{{ - 1}}}n,$ поскольку ПФ действует как разложение Карунена–Лоэва [10–12] и декоррелирует шум ${{\mathcal{L}}^{{ - 1}}}n.$ Поэтому среди всех линейных преобразований при ПФ основная энергия шума ${{\mathcal{L}}^{{ - 1}}}n$ концентрируется в минимально возможном числе коэффициентов. Наилучших результатов в решении интегрального уравнения типа свертки методами ПФ удается достичь, когда неискаженный сигнал x(t) является равномерно гладким и эффективно аппроксимируется базисом Фурье.

Однако базис Фурье хорошо выделяет частоты, но не дает информации о резких и коротких всплесках, перепадах, точках разрыва, изолированных особенностях и вообще о локальном поведении функции, так как базис exp(jωt) покрывает всю вещественную прямую, а ПФ функции $\hat {x}(\omega )$ зависит от значений x(t) при всех $t \in \mathbb{R}$ [13–23]. В лучшем случае локальная особенность будет иметь очень широкий спектр, а энергия сигнала сосредоточена в значительном числе коэффициентов Фурье. Ошибка оценки полезного сигнала x(t) сконцентрирована в окрестности особых точек. В таком случае для компактного представления сигнала x(t), имеющего указанные особенности, желательно, чтобы элементы базиса были как можно лучше локализованы по времени и частоте. Вейвлет-базисы удовлетворяют такому требованию. Кроме того, накладываются и дополнительные условия, такие как ортогональность базиса, компактность носителей вейвлетов и т.д. В дальнейшем, выполняя пороговую обработку коэффициентов разложения в подходящем базисе вейвлетов согласно [13, 14, 24], можно добиться почти оптимальной оценки полезного сигнала x(t).

Применение вейвлет-преобразования (ВП) предполагает, что выбор вейвлет-базиса делается на основе его свойств. Так как решение интегрального уравнения типа свертки реализуется в спектральной области, то необходимо выбирать вейвлет-базис, который имеет компактный носитель в частотной области, достаточно быстрое убывание и небольшое число коэффициентов вейвлет-фильтров. Оптимальным с этой точки зрения являются вейвлеты Кравченко [25–28], которые имеют лучшие характеристики по сравнению с известными системами вейвлетов с финитным спектром (вейвлеты Мейера, Котельникова–Шеннона). Кроме того, можно применить вейвлеты финитные во временной области (например, вейвлеты Добеши), имеющие хорошую крутизну фронтов в частотной области. Возникающая при этом систематическая погрешность должна оцениваться для каждого конкретного случая.

Таким образом, Фурье и вейвлет-базисы обладают рядом преимуществ в представлении и обработке сигналов. Эти преимущества можно использовать для создания комбинированного подхода к решению интегрального уравнения типа свертки (1), который должен состоять из отдельных блоков [29]: быстрое ПФ (БПФ), деконволюции, обратное быстрое ПФ (ОБПФ), дискретное ВП (ДВП), пороговая обработка коэффициентов, обратное дискретное ВП (ОДВП). Это неизбежно приводит к дополнительным аппаратным и временным затратам. Для обеспечения максимальной эффективности при минимальных затратах вычислительных ресурсов необходимо объединить в одном вейвлетном преобразовании решения нескольких задач обработки. Это делается в рамках ДВП с помощью модификации выбранной ортогональной системы вейвлетов Кравченко [25–28]. При этом модифицированные вейвлеты Кравченко должны отвечать всем требованиям теории кратномасштабного анализа (КМА), чтобы можно было построить блоки фильтров быстрых вейвлетных преобразований. Такая модификация порождает нестационарный КМА на основе семейства биортогональных вейвлет-базисов Кравченко.

2. ВЕЙВЛЕТ-АППРОКСИМАЦИЯ РЕШЕНИЯ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ТИПА СВЕРТКИ

Пусть масштабирующие функции и вейвлеты $\{ {{\varphi }_{{{{j}_{0}},k}}}(t),{{\psi }_{{j,k}}}(t):j \geqslant {{j}_{0}},k \in \mathbb{Z}\} $ формируют ортогональное кратномасштабное разложение L²($\mathbb{R}$)($ - \infty $,$\infty $). Рассмотрим кратномасштабную аппроксимацию кусочно-непрерывной функции f(x) $ \in $ ${{L}^{2}}(\mathbb{R}),$ которая имеет ограниченную вариацию

В случае недифференцируемости функции полная вариация f(x) может быть вычислена путем рассмотрения производных в смысле обобщенных функций [13, 30–32]. При масштабе J ортогональная проекция f(t) на ${{{\mathbf{V}}}_{J}} \subset {{L}^{2}}(\mathbb{R})$ имеет вид

где ${{P}_{{{{j}_{0}}}}},$ ${{Q}_{j}}$ – операторы ортогонального проектирования на подпространства ${{{\mathbf{V}}}_{{{{j}_{0}}}}}$ и W_j, параметр j = = j₀, …, J – 1, а j₀– самый грубый масштаб; ${{\varphi }_{{j,k}}}(t) = {{2}^{{j/2}}}\varphi ({{2}^{j}}t - k),$ ${{\psi }_{{j,k}}}(t) = {{2}^{{j/2}}}\psi ({{2}^{j}}t - k)$ – сдвиги/сжатия масштабирующих и вейвлет-функций; ${{a}_{{j,k}}} = \int {f(t)} {{\varphi }_{{j,k}}}(t)dt,$ ${{b}_{{j,k}}} = \int {f(t)} {{\psi }_{{j,k}}}(t)dt$ – коэффициенты разложения по базису масштабирующих и вейвлет-функций.

Так как V_J допускает ортонормированный базис $\{ {{\varphi }_{{J,k}}}(t):k \in \mathbb{Z}\} ,$ то эта проекция может быть переписана в виде конечной суммы масштабирующих функций при масштабе J с равномерным сдвигом k

Вейвлеты могут эффективно аппроксимировать равномерно гладкие сигналы конечным числом базисных функций. Погрешность аппроксимации связана с дифференцируемостью по Соболеву [30, 31]. Она может быть вычислена для разрывных сигналов, имеющих ограниченную вариацию [39, 40]. Пространства функций Соболева ${{H}^{s}}(\mathbb{R}),$ которые s раз дифференцируемы являются пространствами функций $f \in {{L}^{2}}(\mathbb{R})$, преобразование Фурье которых удовлетворяет неравенству

Здесь рассматриваем вейвлет $\psi (t) \in {{С}^{q}},$ имеющий быстрое убывание и q нулевых моментов. Это означает, что для любого 0 ≤ p ≤ q и $m \in \mathbb{Z}$ существует константа C_m такая, что

Вейвлет-преобразование можно рассматривать как многомасштабный дифференциальный оператор порядка q [13, 14]. Это устанавливает связь между дифференцируемостью функции f и убыванием ее вейвлет-преобразования при малых масштабах [13]. Поэтому для эффективной аппроксимации $f \in {{H}^{s}}(\mathbb{R})$ требуется q > s. Согласно [13] гладкость по Соболеву эквивалентна быстрому убыванию вейвлет-коэффициентов |(f,ψ_j,k)| при убывании масштаба j. Если f – кусочно-гладкая функция, то более эффективной является нелинейная вейвлет-аппроксимация, при которой масштаб аппроксимации уточняется в окрестности каждой особенности. Тогда аппроксимация вычисляется по коэффициентам вейвлет-разложения наибольшей амплитуды, что может быть получено с применением пороговой обработки вейвлет-коэффициентов линейной аппроксимации. Для изучения реализации нелинейных вейвлет-аппроксимаций используются пространства Бесова $B_{{\beta ,\gamma }}^{s},$ которые являются естественным обобщением пространств Соболева в случае дробного порядка дифференцирования. При этом во многих случаях получены соответствующие теоремы вложения [13, 33, 34]:

Пространства Бесова содержат функции, которые не дифференцируемы s раз во всех точках. Если даже f разрывна, но число разрывов конечно и f удовлетворяет равномерному условию Липшица α между этими разрывами, то $f \in B_{{\beta ,\gamma }}^{s}$ (при 1/p < α +1/2, p = β = γ).

Для удобства обозначения будем считать, что в (5) не нарушается последовательность масштабов j и сдвигов k, а нелинейная аппроксимация получается, когда часть коэффициентов b_j,k принимает нулевые значения в результате пороговой обработки.

Уравнение (5) в частотной области имеет вид

Здесь ${{\hat {\varphi }}_{{{{j}_{0}}}}}(\omega ) = {{2}^{{ - j/2}}}\hat {\varphi }\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{0}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{0}}}}}}}} \right),$ ${{\hat {\psi }}_{j}}(\omega ) = {{2}^{{ - j/2}}}\hat {\psi }\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{j}}}}} \right. \kern-0em} {{{2}^{j}}}}} \right),$ a ${{a}_{{{{j}_{0}}}}}(\omega )$ и ${{b}_{j}}(\omega )$ – периодические частотные функции с периодом ${{2}^{{{{j}_{0}} + 1}}}\pi $ и 2^j + 1π, получаемые из коэффициентов разложения ${{a}_{{{{j}_{0}},k}}}$ и ${{b}_{{j,k}}}$

Запишем (6) в частотной области

Используя масштабирующие уравнения [13–20]

покажем, что a_J(ω) можно получить из частотных функций a_J – 1(ω) и b_J – 1(ω). В (9) и (10) ${{H}_{0}}(\omega ) = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}\sum\nolimits_k {{{h}_{k}}\exp ( - ik\omega )} $ = ${1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}Н(\omega )$ – частотная функция отклика масштабирующей функции с коэффициентами фильтра $\{ {{h}_{k}}:k \in \mathbb{Z}\} $; ${{G}_{0}}(\omega ) = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}\sum\nolimits_k {{{g}_{k}}\exp ( - ik\omega )} $ = ${1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}G(\omega )$ – частотная функция отклика вейвлета с коэффициентами фильтра $\{ {{g}_{k}}:k \in \mathbb{Z}\} .$

Преобразование Фурье ${{\hat {f}}_{J}}(\omega )$ определяется уравнением (8) при масштабе J и с помощью $\hat {\varphi }(\omega )$, $\hat {\psi }(\omega )$ при масштабе J – 1

Тогда

Таким образом, формула для восстановления a_J(ω) по a_J – 1(ω) и b_J – 1(ω) имеет вид

Похожим образом с помощью масштабирующих уравнений (9), (10) можно получить [13–20] алгоритм разложения в частотной области

Рассмотрим аппроксимацию вейвлетами решения интегрального уравнения типа свертки (1) в частотной области в случае $\lambda \in {{L}^{1}}(\mathbb{R}),$ $\hat {\lambda }(\omega ) \ne 0$ при ограниченной правой части $y(t) \in {{H}^{p}}$

В случае применения вейвлетов Кравченко с финитным спектром справедлива следующая теорема.

Теорема 1. Пусть $y(t) \in {{{\mathbf{V}}}_{J}},$ $\lambda \in {{L}^{1}}(\mathbb{R})$ и $\hat {\lambda }(\omega ) \ne 0$ при ${{\hat {\varphi }}_{J}}(\omega ) \ne 0,$ $\sup {\kern 1pt} {\text{p}}{\kern 1pt} \,{{\hat {\varphi }}_{J}}(\omega )$ = $\left[ { - {{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right].$ Тогда интегральное уравнение типа свертки (1) имеет единственное решение в подпространстве V_J + 1.

Доказательство. Если $y\, \in {{{\mathbf{V}}}_{J}}$ то $y(t) = {{P}_{J}}y(t)$ = $ = {{y}_{J}}(t) = \sum\nolimits_k {a_{{J,k}}^{y}{{\varphi }_{{j,k}}}(t)dt} ,$ где $a_{{J,k}}^{y} = \int {y(t)} {{\varphi }_{{J,k}}}(t)dt,$ $\{ a_{{J,k}}^{y}\} \in {{l}^{2}},k \in \mathbb{Z}{\kern 1pt} {\kern 1pt} .$ Отсюда в частотной области ${{\hat {y}}_{J}}(\omega ) = a_{J}^{y}(\omega ){{\hat {\varphi }}_{J}}\left( \omega \right),$ $k \in \mathbb{Z}\,,$ где $a_{J}^{y}(\omega )$ – периодическая функция с периодом 2^J + 1π.

С помощью частотной функции $\hat {K}(\omega )$ ПФ регуляризованного решения интегрального уравнения типа свертки (1) имеет вид

Так как

то

Функция ${{H}_{0}}\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}}} \right)$ периодическая с периодом 2^J + 2π и не равна нулю на интервалах $\left[ { - {{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k;{{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k} \right],$ $k \in \mathbb{Z}$.

Так как $a_{J}^{y}(\omega )$ имеет период 2^J + 1π, то произведение $a_{J}^{y}(\omega ){{H}_{0}}\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}}} \right)$ – 2^J + 2π-периодическая функция. Если $\hat {K}(\omega )$ будет периодически продолжено с периодом 2^{J+ 2}π, то это не изменит (17)

где ${{\left[ {{{{\left. {\hat {K}(\omega )} \right|}}_{{\omega \in \left[ { - {{2}^{J}}\frac{{4\pi }}{3};{{2}^{J}}\frac{{4\pi }}{3}} \right]}}}} \right]}_{{{{2}^{{J + 2}}}\pi }}}$ – 2^{J+ 2}π-периодическое продолжение функции $\hat {K}(\omega )$, ограниченной интервалом $\left[ { - {{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right].$

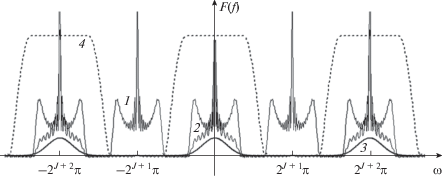
Таким образом, произведение первых трех членов в выражении (18) является 2^J + 2π-периодической функцией (рис. 1).

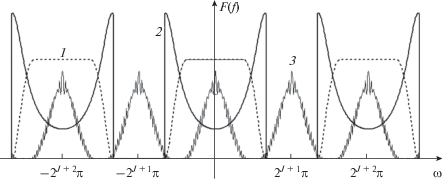
Введем обозначение

$a_{{J + 1}}^{{{{{\tilde {x}}}_{P}}}}(\omega ) = {{\left[ {{{{\left. {\hat {K}(\omega )} \right|}}_{{\omega \in \left[ { - {{2}^{J}}\frac{{4\pi }}{3};{{2}^{J}}\frac{{4\pi }}{3}} \right]}}}} \right]}_{{{{2}^{{J + 2}}}\pi }}}a_{J}^{y}(\omega ){{H}_{0}}\left( {\frac{\omega }{{{{2}^{{J + 1}}}}}} \right)$ – 2^J + 2π-периодическая частотная функция.

Получим, что

Следовательно, ${{\tilde {x}}_{P}} \in {{{\mathbf{V}}}_{{J + 1}}}.$ Вместе с тем, если частотная характеристика $\hat {\lambda }(\omega )$ непрерывна и не равна нулю на $\left[ { - {{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{J}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right],$ то и частотная функция $\hat {K}(\omega )$ обладает такими же свойствами. Тогда (1) имеет единственное решение, что и требовалось доказать.

Если $y(t) \notin {{{\mathbf{V}}}_{J}}$, то осуществляем проекцию y(t) на пространство масштабирующих функций самого точного масштаба ${{V}_{J}}$. В результате уравнение свертки преобразуется к виду

Это уравнение имеет единственное решение ${{\tilde {x}}_{{J + 1}}}(t) \in {{{\mathbf{V}}}_{{J + 1}}}$ такое, что $\left( {\lambda {\text{*}}{{{\tilde {x}}}_{{J + 1}}}} \right)(t) = {{y}_{J}}(t).$ Таким образом, $\tilde {x}_{{J + 1}}^{{}}(t)$ является вейвлет-аппроксимацией точного решения $\bar {x}$ и можно получить оценку.

Теорема 2. Пусть ядро интегрального уравнения типа свертки $\lambda \in {{L}^{1}}(\mathbb{R})$ имеет ненулевое преобразование Фурье, $\hat {\lambda }(\omega ) \ne 0$ на ${\text{supp(}}\hat {\varphi }{\text{)}}$, где φ(t) – масштабирующая функция из вейвлет-систем Кравченко. Если α, β – действительные числа такие, что 1 ≤ α ≤ β, $\hat {\lambda }(\omega ) \geqslant C{{\left( {1 + {{\omega }^{2}}} \right)}^{{ - \alpha /2}}},$ $y \in {{H}^{\beta }}$, то имеет место следующая оценка:

Доказательство. Используя унитарность преобразования Фурье, запишем

Так как регуляризующий компонент R(ω) всегда положительный и $\hat {\lambda }(\omega ) \ne 0,$ то стабилизирующий множитель принимает значение $0 < \frac{{{{{\left| {\hat {\lambda }(\omega )} \right|}}^{2}}}}{{{{{\left| {\hat {\lambda }(\omega )} \right|}}^{2}} + R(\omega )}} \leqslant 1.$

Тогда

Теорема доказана.

Согласно теореме 1, если функция правой части $y(t) \in {{{\mathbf{V}}}_{J}},$ то

Так как наблюдается не сигнал x(t), а его линейное преобразование $\mathcal{L}x(t)$, то коэффициенты разложения в (22) вычислить сразу нельзя. Поэтому будем использовать последовательность функций {${{\xi }_{{J,k}}}(t)$: k $ \in \mathbb{Z}$} таких, что

Так как преобразование $\mathcal{L}$ однородно, то функция ${{\xi }_{{J,k}}}(t)$ также представляет собой сдвиги и растяжения/сжатия некоторой функции $\xi (t)$. При этом семейство функций $\{ {{\xi }_{{J,k}}}(t):k \in \mathbb{Z}\} $ уже не обладает свойством ортонормированности, но образует устойчивый базис. Следовательно, должны существовать такие константы 0 < A ≤ B < ∞, что

для всех квадратично суммируемых последовательностей $\{ {{с}_{{J,k}}}\} $ (доказательство см. ниже).

Задача построения функций ${{\xi }_{{J,k}}}(t)$ может быть решена с использованием двойственного базиса ${{\tilde {\xi }}_{{J,k}}}(t)$ в ${{L}^{2}}(\mathbb{R})$. Известно [13–15], что базис ${{\tilde {\xi }}_{{J,k}}}(t)$, удовлетворяющий соотношениям двойственности $\left( {{{\xi }_{{J,n}}}(t),{{{\tilde {\xi }}}_{{J,k}}}(t)} \right) = {{\delta }_{{n,k}}},$ существует и более того, допускает построение биортогональной системы вейвлетов [13–15], с помощью которой можно выполнить оценку полезного сигнала х(t) первоначально искаженного импульсной характеристикой λ(t) с последующим действием шума n(t).

3. ПОСТРОЕНИЕ БИОРТОГОНАЛЬНЫХ ЧАСТОТНО-МОДИФИЦИРОВАННЫХ ВЕЙВЛЕТОВ

Пусть неизвестная функция $x\,(t)$ в (1) принадлежит пространству масштабирующих функций ${{{\mathbf{V}}}_{{J + 1}}} = \overline { \cup \{ {{\varphi }_{{J + 1,k}}}:k \in \mathbb{Z}\} } ,$ где $\varphi (t)$ – ортонормированная масштабирующая функция с финитным спектром. В качестве $\varphi (t)$ в соответствии с описанными ранее преимуществами примем масштабирующую функцию из семейства вейвлет-базисов Кравченко {$\widetilde {up}(\omega )$} [25–28]. Представим оценку полезного сигнала ${{\tilde {x}}_{P}}(t)$ по наблюдаемому сигналу $y(t)$ в виде разложения по $\{ {{\varphi }_{{J + 1,k}}}:k \in \mathbb{Z}\} $

Если (4) записать в виде $\hat {K}{{(\omega )}^{{ - 1}}}{{\hat {\tilde {x}}}_{P}}(\omega ) = \hat {y}(\omega ),$ то получим

Обозначим

тогда уравнение (24) примет следующий вид:

Таким образом, решение интегрального уравнения типа свертки (1) относительно неизвестной функции $x\,(t)$ соответствует решению (26) относительно неизвестной последовательности коэффициентов разложения $\{ a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}:k \in \mathbb{Z}\} $, которые находятся как скалярное произведение известной функции y(t) и функций $\{ {{\tilde {\xi }}_{{J,k}}}(t):k \in \mathbb{Z}\} $, являющихся двойственным базисом по отношению к $\{ {{\xi }_{{J,k}}}(t):k \in \mathbb{Z}\} .$

С учетом того, что в практике обработки сигналов существуют разные способы задания стабилизирующего множителя $\hat {K}(\omega )$, а иногда требуется и дополнительная коррекция этой частотной характеристики сигнала, введем функцию $\hat {D}(\omega )$ модифицирующую $\hat {\varphi }_{{j,k}}^{{}}(\omega )$, которая допускает представление (25) в виде ${{\hat {\xi }}_{{j,k}}}(\omega ) = \hat {D}(\omega )\hat {\varphi }_{{j,k}}^{{}}(\omega )$.

Для решения (1) с использованием ДВП необходима новая биортогональная вейвлет-система, которая включает модифицированные в частотной области масштабирующие функции и вейвлеты, образующие две пары функций $\xi (t)$, $\gamma (t)$ и $\tilde {\xi }(t)$, $\tilde {\gamma }(t)$ такие, что ${{\xi }_{{j,k}}}(t)$, ${{\gamma }_{{j,k}}}(t)$ порождают пространство масштабирующих функций ${{{\mathbf{U}}}_{j}}$ и пространство вейвлетов ${{{\mathbf{S}}}_{j}}$, а функции ${{\tilde {\xi }}_{{j,k}}}(t)$, ${{\tilde {\gamma }}_{{j,k}}}(t)$ образуют двойственные базисы. Как это следует из [13–21, 35], подпространства ${{{\mathbf{S}}}_{j}},\,\,{{\widetilde {\mathbf{S}}}_{j}}$ получаются как ортогональное дополнение к вложенной системе подпространств ${{{\mathbf{U}}}_{j}},\,\,{{\widetilde {\mathbf{U}}}_{j}}$

Подпространства ${{{\mathbf{S}}}_{j}},\,\,{{\widetilde {\mathbf{S}}}_{j}}$ взаимно ортогональны и образуют ортогональное разложение ${{L}^{2}}(\mathbb{R}).$ Рассмотрим функции ${{\xi }_{{j,k}}}(t) = {{\xi }_{j}}(t - {{2}^{{ - j}}}k),$ ${{\gamma }_{{j,k}}}(t) = $ $ = {{\gamma }_{j}}(t - {{2}^{{ - j}}}k),$ $j,k \in \mathbb{Z}$ такие, что

где $\hat {\varphi }(\omega )$, $\hat {\psi }(\omega )$ – спектры функций из ортонормированной вейвлет-системы (ранее приняты вейвлеты Кравченко {$\widetilde {up}(\omega )$}). Преобразования (27), (28) осуществляют линейное отображение подпространств КМА V_j и W_j в новые подпространства U_j и S_j. Новые функции ξ_j,k, γ_j,k являются образами масштабирующей функции φ_j,k и вейвлета ψ_j,k в подпространствах U_j и S_j. Согласно требованиям КМА [13–21, 35] эти функции должны образовывать базис Рисса.

Лемма 1. Если j < j_max, то системы функций $\{ {{\xi }_{{j,k}}}(t):k \in \mathbb{Z}\} ,$ $\{ {{\gamma }_{{j,k}}}(t):k \in \mathbb{Z}\} $ являются базисом Рисса подпространств U_j и S_j.

Доказательство. Линейная оболочка $\{ {{\xi }_{{j,k}}}(t):j,k \in \mathbb{Z}\} $ плотна в L²($\mathbb{R}$). Для доказательства того, что ${{\xi }_{{j,k}}}(t)$ образует базис Рисcа, покажем, что существуют положительные константы A и B (0 < A ≤ B < ∞) в U₀ такие, что

для всех бесконечных суммируемых с квадратом последовательностей {${{c}_{k}}$}.

Согласно определению нормы и равенству Парсеваля имеем

Пусть при некотором $\left| \omega \right| \geqslant \Omega ,$ $\hat {\varphi }(\omega ) \approx 0.$ Тогда

При значениях масштаба j ≥ j_max (j_max > 0) может возникнуть ситуация, когда B = $ = {{\sup }_{{\omega \in \left[ { - {{2}^{{{{j}_{{\max }}}}}}\Omega ,\,{{2}^{{{{j}_{{\max }}}}}}\Omega } \right]}}}\left| {\hat {D}(\omega )} \right|_{{}}^{2}$ становится бесконечно большим и условие устойчивости (29) нарушается. В другом случае, когда j ≤ j_min (j_min < 0) может оказаться, что

и система функций ${{\xi }_{{j,k}}}(t)$ вырождается в ортонормированный базис. При $j \ne 0$ лемма доказывается аналогично. Повторяя приведенные выше действия для случая ${{\gamma }_{{j,k}}}(t)$ можно доказать, что ${{\gamma }_{{j,k}}}(t)$ образует базис Риcса.

Следующая лемма показывает, что подпространства {U_j} образуют вложенную последовательность и удовлетворяют таким пунктам определения КМА

Лемма 2. Последовательность вложенных подпространств {U_j} удовлетворяет всем требованиям КМА и ${{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}.$

Доказательство. Преобразование (27) переводит любую функцию $f(t) \in {{{\mathbf{V}}}_{j}}$ в соответствующий единственный элемент $u(t) \in {{{\mathbf{U}}}_{j}}.$ Так как {V_j} образуют вложенную систему подпространств, то $f(t) \in {{{\mathbf{V}}}_{{j + 1}}},$ следовательно, справедливо, что $u(t) \in {{{\mathbf{U}}}_{{j + 1}}}$ и существует цепочка

Таким образом, {U_j} образуют последовательность вложенных подпространств.

Требование $\bigcap\nolimits_{j \in Z} {{{{\mathbf{U}}}_{j}}} = \{ 0\} $ из определения КМА проверяется от обратного.

Утверждение КМА $\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{V}}}_{j}}} } = {{L}^{2}}$ будет доказано, если ${{{\mathbf{V}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}$ и ${{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}.$

Пусть некоторая функция $f(t) \in {{{\mathbf{V}}}_{j}},$ тогда $f(t) \in {{{\mathbf{U}}}_{{j + 1}}}$ если

где $a_{{j + 1}}^{f}(\omega )$ – должна быть 2^j + 2π-периодической функцией. Поскольку $f(t) \in {{{\mathbf{V}}}_{j}},$ то

где $b_{j}^{f}(\omega )$ – 2^j + 1π-периодическая функция, а масштабирующая функция φ принадлежит вейвлет-системе Кравченко. С учетом масштабирующего уравнения в частотной области имеем

где произведение первых двух членов является 2^j + 2π-периодической функцией, поскольку функция ${{H}_{0}}\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{J + 1}}}}}} \right. \kern-0em} {{{2}^{{J + 1}}}}}} \right)$ периодическая с периодом 2^j + 2π, а также не равна нулю на интервалах $\left[ { - {{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k;} \right.$ $\left. {{{2}^{J}}\left( {{{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3}} \right) + {{2}^{{J + 2}}}\pi k} \right],$ $k \in \mathbb{Z}$.

Из (18) и (27) получаем

Равенства (34) и (35) эквивалентны, когда $a_{{j + 1}}^{f}(\omega )$ – 2^j+2π-периодическая функция, а $\hat {D}(\omega )$ периодически продолжена с периодом 2^j+2π (рис. 2). Следовательно, ${{{\mathbf{V}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}.$

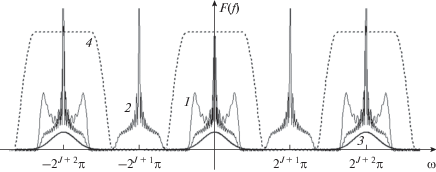
Справедливость вложенности подпространств ${{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}$ можно показать, если предположить, что некоторая функция $f(t) \in {{{\mathbf{U}}}_{j}}.$ Тогда $f(t) \in {{{\mathbf{V}}}_{{j + 1}}},$ если

где $b_{{j + 1}}^{f}(\omega )$ есть 2^j + 2π-периодическая функция, а функция φ также из вейвлет-системы Кравченко. Поскольку $f(t) \in {{{\mathbf{U}}}_{j}},$ то $\hat {f}(\omega ) = a_{j}^{f}(\omega )\hat {\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{j}}}}} \right. \kern-0em} {{{2}^{j}}}}),$ где $a_{j}^{f}(\omega )$ – 2^j + 1π-периодическая функция. После преобразования это равенство принимает вид

где произведение первых трех членов является 2^j + 2π-периодической функцией $b_{{j + 1}}^{f}(\omega )$ (рис. 3). Следовательно, ${{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}$ и выполняется требование КМА $\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{U}}}_{j}}} } = {{L}^{2}},$ так как $\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{V}}}_{j}}} } = {{L}^{2}}.$

Обобщив условия ${{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}}$ и ${{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}},$ получим доказательство утверждения ${{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}}.$ Выполнение условия, чтобы сдвиги частотно-модифицированной масштабирующей функции $\{ {{\xi }_{j}}(t - {{2}^{{ - j}}}k):k \in \mathbb{Z}\} $ образовывали базис Рисcа, следует из леммы 1.

Покажем справедливость соотношения масштабируемости. Пусть некоторая функция $f(t) \in {{{\mathbf{U}}}_{j}}.$ Тогда

где $a_{j}^{f}(\omega )$ – 2^j + 1π-периодическая функция.

Если $f(2t) \in {{{\mathbf{U}}}_{{j + 1}}},$ то

где $a_{{j + 1}}^{f}(\omega )$ должна быть 2^j + 2π-периодической функцией.

Действительно, производя замену переменной w = ω/2 в (38), получим $a_{{j + 1}}^{f}(\omega ) = a_{j}^{f}\left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-0em} 2}} \right).$ Следовательно, $a_{{j + 1}}^{f}(\omega )$ является 2^j+2π-периодической функцией. При этом справедливо соотношение масштабируемости $f(t) \in {{{\mathbf{U}}}_{j}} \Leftrightarrow f(2t) \in {{{\mathbf{U}}}_{{j + 1}}}.$ От соотношения масштабируемости классического КМА это отличается тем, что пространства {U_j} образуют нестационарные по отношению к масштабу функции ${{\xi }_{j}}$, что следует из (27). При каждом значении масштаба j функция ${{\xi }_{j}}(t)$ уже не является результатом растяжения/сжатия одной функции, как в случае классического КМА. В зависимости от масштаба j изменяется носитель функции ${{\hat {\varphi }}_{j}}(\omega ),$ а также охватываемый ${{\hat {\varphi }}_{j}}(\omega )$ частотный поддиапазон функции $\hat {D}(\omega )$. Поэтому функции ${{\xi }_{j}}$ существуют только в диапазоне масштабов, которые ограничены частотным диапазоном функции $\hat {D}(\omega )$. На практике другие значения масштабов не используются, так как спектр наблюдаемого сигнала всегда находится в пределах спектрального диапазона функции $\hat {D}(\omega )$. Сформулируем требования к подпространству модифицированных вейвлет-функций.

Лемма 3. Если j < j_max, то подпространства S_j, являются ортогональным дополнением к вложенной системе подпространств U_j

Доказательство. Преобразование (27) переводит любую функцию $f(t) \in {{{\mathbf{V}}}_{{j + 1}}}$ в соответствующий единственный элемент $u(t) \in {{{\mathbf{U}}}_{{j + 1}}}$. Так как {V_j} образуют КМА, то для каждого j существует ортогональное дополнение W_j к пространству V_j в пространстве V_j + 1:

Следовательно,

Исходя из того, что $\{ {{{\mathbf{U}}}_{j}}\} $ удовлетворяют всем требованиям КМА и $u(t) \in {{{\mathbf{U}}}_{{j + 1}}}$ является проекцией $f(t)$ из ${{{\mathbf{V}}}_{{j + 1}}} = {{{\mathbf{V}}}_{j}} \oplus {{{\mathbf{W}}}_{j}},$ имеет место представление ${{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}},$ ${{{\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}},$ ${{{\mathbf{S}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}.$ Базисом для подпространства S_j являются сдвиги и масштабирование одной функции $\gamma $.

Таким образом, с учетом нестационарности по отношению к масштабу запишем

Рассуждая аналогичным образом, можно показать, что ${{{\mathbf{U}}}_{j}} = {{{\mathbf{U}}}_{{j - 1}}} \oplus {{{\mathbf{S}}}_{{j - 1}}}.$ Следовательно, ${{{\mathbf{U}}}_{{j + 1}}}$ = $ = {{{\mathbf{U}}}_{{j - 1}}} \oplus {{{\mathbf{S}}}_{{j - 1}}} \oplus {{{\mathbf{S}}}_{j}}.$ Продолжая эту процедуру, получим ортогональное разложение пространства ${{{\mathbf{U}}}_{{j + 1}}}:{{{\mathbf{U}}}_{{j + 1}}}$ = ${{\overline { \oplus _{{k = - \infty }}^{j}{\mathbf{S}}} }_{k}}.$ Свойство КМА $\overline {\bigcup\nolimits_{j \in Z} {{{{\mathbf{U}}}_{j}}} } = {{L}^{2}}$ формально позволяет представить ${{L}^{2}} = {{\overline { \oplus _{{k = - \infty }}^{{ + \infty }}{\mathbf{S}}} }_{k}}.$ Так же как и для модифицированных масштабирующих функций $\xi (t)$, для вейвлет-функций $\gamma (t)$ существует ограничение по масштабу j < j_max, больше которого условие устойчивости нарушается. На рис. 4 показано взаимное расположение образов Фурье функций $\hat {\varphi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}}),$ $\hat {\psi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}}),$ $\hat {D}(\omega ).$

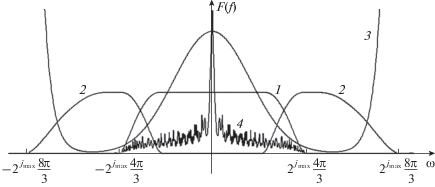
Получается, что если даже произведение $\hat {D}(\omega )\hat {\varphi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}})$ ограничено, то $\hat {D}(\omega )\hat {\psi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{{{j}_{{\max }}}}}}}}} \right. \kern-0em} {{{2}^{{{{j}_{{\max }}}}}}}})$ может выйти за динамический диапазон измерения.

C помощью теоремы о двойственном базисе [13–15] и с учетом доказанных выше лемм найдем остальные модифицированные функции ${{\tilde {\xi }}_{{j,k}}}(t),$ ${{\tilde {\gamma }}_{{j,k}}}(t),$ которые образуют двойственные базисы к ${{\xi }_{{j,k}}}(t),$ ${{\gamma }_{{j,k}}}(t)$, порождают пространство масштабирующих функций ${\mathbf{\tilde {U}}}{}_{j}$ и пространство вейвлетов ${{{\mathbf{\tilde {S}}}}_{j}}$ такие, что ${{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}},$ ${\mathbf{\tilde {U}}}{\kern 1pt} {}_{j} \bot {{{\mathbf{S}}}_{j}},$ ${{{\mathbf{S}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{l}}$ при $j \ne l,$ ${{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{{\mathbf{\tilde {S}}}}_{j}},$ ${{{\mathbf{\tilde {U}}}}_{j}} \cap {{{\mathbf{\tilde {S}}}}_{j}} = \{ 0\} ,$ ${{{\mathbf{\tilde {U}}}}_{j}} \subset {{{\mathbf{\tilde {U}}}}_{{j + 1}}}$, ${{{\mathbf{\tilde {S}}}}_{j}} \subset {{{\mathbf{\tilde {U}}}}_{{j + 1}}}$.

Непосредственное применение теоремы о двойственном базисе из [13–15] определяет преобразование Фурье базисной функции, двойственной к ${{\xi }_{j}}(t)$, в том смысле, что $\left( {{{\xi }_{{j,n}}}(t),{{{\tilde {\xi }}}_{{j,k}}}(t)} \right) = {{\delta }_{{n,k}}},$ следующим образом:

Знаменатель в (42) ограничен почти всюду с границами Рисcа [13–15] A и B, 0 < A ≤ B < ∞, которые получены в доказательстве леммы 1

Поскольку $\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} $ ограничена снизу положительной константой, очевидно, что ${1 \mathord{\left/ {\vphantom {1 {\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} }}} \right. \kern-0em} {\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} }}$ также 2π-периодическая функция, принадлежащая ${{L}^{1}}(0,2\pi ).$

Таким же образом [13–15] определим преобразование Фурье двойственного к вейвлет-функции ${{\gamma }_{j}}(t)$ базиса ${{\tilde {\gamma }}_{j}}(t),$ для которого справедливо равенство $\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right) = {{\delta }_{{j,l}}}{{\delta }_{{n,k}}}$

Так как соотношение двойственности $\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right) = {{\delta }_{{j,l}}}{{\delta }_{{n,k}}}$ коммутативно, то ${{\tilde {\gamma }}_{j}}(t)$ – двойственное вейвлета ${{\gamma }_{j}}(t),$ само является вейвлетом с двойственным ${{\gamma }_{j}}(t).$

Полученные пары модифицированных функций удовлетворяют соотношениям биортогональности $\left( {{{\xi }_{{j,n}}}(t),{{{\tilde {\xi }}}_{{j,k}}}(t)} \right) = {{\delta }_{{n,k}}},$ $\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right)$ = ${{\delta }_{{j,l}}}{{\delta }_{{n,k}}},$ но нарушаются обязательные условия существования биортогональной вейвлет-системы $\left( {{{\xi }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{j,k}}}(t)} \right) = 0,$ $\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\xi }}}_{{j,k}}}(t)} \right) = 0.$ Поэтому необходимо перейти к новой стратегии формирования модифицированных двойственных базисов.

Для этого введем 2π-периодическую функцию $E_{j}^{\xi }(\omega ) \in {{L}_{1}}(0,2\pi ){\kern 1pt} :$

Из (44) следует, что $\sum\nolimits_{p \in Z} {{{{\left| {{{{\hat {\xi }}}_{j}}(\omega + 2\pi p)} \right|}}^{2}}} $ = $E_{j}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{j}}}}} \right. \kern-0em} {{{2}^{j}}}})$ и $E_{j}^{\xi }\left( \omega \right)$ также ограничена почти всюду константами A и B, 0 < A ≤ B < ∞, $A \leqslant E_{j}^{\xi }\left( \omega \right) \leqslant B.$ Тогда ${1 \mathord{\left/ {\vphantom {1 {E_{j}^{\xi }\left( \omega \right)}}} \right. \kern-0em} {E_{j}^{\xi }\left( \omega \right)}}$ является ограниченной 2π-периодической функцией в ${{L}^{1}}(0,2\pi ),$ ${1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-0em} B} \leqslant {1 \mathord{\left/ {\vphantom {1 {E_{j}^{\xi }\left( \omega \right)}}} \right. \kern-0em} {E_{j}^{\xi }\left( \omega \right)}} \leqslant {1 \mathord{\left/ {\vphantom {1 A}} \right. \kern-0em} A}.$ Обращаясь к масштабирующим уравнениям в частотной области сформулируем теорему.

Теорема 3. Пусть масштабирующая функция ${{\xi }_{{j,k}}}(t) \in {{{\mathbf{U}}}_{j}},$ определяемая (27), порождает КМА в пространстве ${{L}^{2}}(\mathbb{R})$, а вейвлет ${{\gamma }_{{j,k}}}(t) \in {{{\mathbf{S}}}_{j}}$ при разложении ${{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}$ задан (28). Тогда существуют двойственные базисы ${{\tilde {\xi }}_{{j,k}}}(t),$ ${{\tilde {\gamma }}_{{j,k}}}(t),$ заданные формулами

где

такие, что

a) системы функций {${{\tilde {\xi }}_{{j,k}}}(t){\kern 1pt} :$ $k \in \mathbb{Z}$}, {${{\tilde {\gamma }}_{{j,k}}}(t)$: $k \in \mathbb{Z}$} являются базисами Риcса подпространств ${{\widetilde {\mathbf{U}}}_{j}}$ и ${{\widetilde {\mathbf{S}}}_{j}}$;

б) вложенная система базисных подпространств {${{\widetilde {\mathbf{U}}}_{j}}$} с ортогональными дополнениями ${{\widetilde {\mathbf{S}}}_{j}}$ образует, возможно, новый КМА и ${{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{\tilde {U}}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}},$ ${{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{{\mathbf{\tilde {S}}}}_{j}};$

в) справедливо соотношение масштабируемости $f(t) \in {{{\mathbf{\tilde {U}}}}_{j}} \Leftrightarrow f(2t) \in {{{\mathbf{\tilde {U}}}}_{{j + 1}}};$

г) обладают свойствами

Таким образом, ${{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}},$ ${\mathbf{\tilde {U}}}{}_{j} \bot {{{\mathbf{S}}}_{j}}$ и ${{{\mathbf{S}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{l}}$ при $j \ne l.$ Cледовательно, две пары функций $\xi $(t), $\gamma $(t) и $\tilde {\xi }(t)$,$\tilde {\gamma }(t)$ формируют биортогональную вейвлет-систему.

Доказательство. Сначала покажем, что ${{\tilde {\xi }}_{{j,k}}}(t),$ ${{\tilde {\gamma }}_{{j,k}}}(t)$ двойственные базисы. Из непосредственного применения равенства Парсеваля и периодичности функций ${{H}_{0}}\left( \omega \right),$ ${1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }\left( \omega \right)}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }\left( \omega \right)}}$ при p = k – n получим

Отсюда

Исходя из того, что ${{H}_{0}}(\omega )$ = $ = \frac{1}{{\sqrt 2 }}\sum\nolimits_{n \in Z} {{{h}_{n}}\exp ( - in\omega )} ,$ получим

Также доказывается биортогональность по сдвигу для модифицированных вейвлетов ${{\gamma }_{{j,n}}}(t)$ и ${{\tilde {\gamma }}_{{l,k}}}(t).$ При j = l и p = k – n

Ортогональность относительно масштаба при $j \ne l$ будет доказана ниже.

Доказательство того, что ${{\tilde {\xi }}_{{j,k}}}(t)$ образует базис Рисcа проведем аналогично лемме 1. Пусть существуют положительные константы $\tilde {A}$ и $\tilde {B}$ ($0 < \tilde {A} \leqslant \tilde {B} < \infty $) в ${{\widetilde {\mathbf{U}}}_{0}}$ такие, что

для всех $\left\| {{\text{\{ }}{{c}_{{j,k}}}{\text{\} }}} \right\|_{{{{l}_{2}}}}^{2} = \sum\nolimits_k {{{{\left| {{{c}_{{j,k}}}} \right|}}^{2}}} < 0.$ Следовательно,

Пусть при некотором $\left| \omega \right| \geqslant \Omega ,$ $\hat {\varphi }(\omega ) \approx 0$. Тогда

Подобным образом,

При $j \ne 0$ доказательство проводится аналогично. Для ${{\tilde {\xi }}_{{j,k}}}(t)$ также будет существовать ограничение на значения масштаба j ≥ j_max (j_max > 0), при котором условие устойчивости (47) нарушается. Похожим образом проводится доказательство того, что ${{\tilde {\gamma }}_{{j,k}}}(t)$ образует базис Рисcа.

Справедливость того, что последовательность вложенных подпространств {${{\widetilde {\mathbf{U}}}_{j}}$} образует новый КМА и ${{{\mathbf{V}}}_{{j - 1}}} \subset {{{\mathbf{\tilde {U}}}}_{j}} \subset {{{\mathbf{V}}}_{{j + 1}}},$ а также то, что подпространства ${{{\mathbf{\tilde {S}}}}_{j}}$ являются ортогональным дополнением к базисной системе {${{\widetilde {\mathbf{U}}}_{j}}$} и ${{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{\widetilde {\mathbf{U}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}}$ доказывается, так же как в лемме 2 и лемме 3.

Покажем справедливость соотношения масштабируемости в соответствии с ранее проведенным доказательством в лемме 2. Пусть некоторая функция $f(t) \in {{{\mathbf{\tilde {U}}}}_{j}},$ следовательно

где $a_{j}^{f}(\omega )$ – 2^j+1π-периодическая функция.

Тогда $f(2t) \in {{{\mathbf{\tilde {U}}}}_{{j + 1}}},$ если

где $a_{{j + 1}}^{f}(\omega )$ должна быть 2^j + 2π-периодической функцией.

Производя замену переменной w = ω/2 в (48) получим $a_{{j + 1}}^{f}(\omega ) = a_{j}^{f}\left( {{\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-0em} 2}} \right).$ Следовательно, $a_{{j + 1}}^{f}(\omega )$ это 2^j + 2π-периодическая функция и справедливо соотношение масштабируемости $f(t) \in {{{\mathbf{\tilde {U}}}}_{j}} \Leftrightarrow f(2t) \in {{{\mathbf{\tilde {U}}}}_{{j + 1}}}.$

Отметим, что пространства $\{ {{\widetilde {\mathbf{U}}}_{j}}\} $ также образуют нестационарные по отношению к масштабу функции ${{\tilde {\xi }}_{j}}$.

Чтобы показать, что удовлетворяется свойство ортогональности подпространств ${{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}}$ и ${\mathbf{\tilde {U}}}{\kern 1pt} {}_{j} \bot {{{\mathbf{S}}}_{j}},$ определим соответствующее скалярное произведение порождающих функций

Поступая аналогично для доказательства ортогональности ${\mathbf{\tilde {U}}}{\kern 1pt} {}_{j} \bot {{{\mathbf{S}}}_{j}},$ имеем

Покажем биортогональность относительно масштаба для модифицированных вейвлетов $\left( {{{\gamma }_{{j,n}}}(t),{{{\tilde {\gamma }}}_{{l,k}}}(t)} \right)$ = ${{\delta }_{{n,k}}}{{\delta }_{{j,l}}}.$ Ранее был рассмотрен случай при j = l. Если $j \ne l$, то для l < j имеем ${{\tilde {\gamma }}_{{l,k}}} \in {{{\mathbf{\tilde {S}}}}_{l}},$ $k \in \mathbb{Z}$ и ${{{\mathbf{\tilde {S}}}}_{l}} \subset {{{\mathbf{\tilde {U}}}}_{{l + 1}}}$ $ \subset ... \subset $ ${{{\mathbf{\tilde {U}}}}_{{j - 1}}} \subset {{{\mathbf{\tilde {U}}}}_{j}}.$ Исходя из утверждения ${\mathbf{\tilde {U}}}{\kern 1pt} {}_{j}\, \bot {{{\mathbf{S}}}_{j}}$, получим $({{\gamma }_{{j,n}}}(t),{{\tilde {\gamma }}_{{l,k}}}(t)) = 0,$ $n,k \in \mathbb{Z}.$ Для l > j могут быть сделаны такие же заключения с использованием второго утверждения ${{{\mathbf{U}}}_{j}} \bot {{{\mathbf{\tilde {S}}}}_{j}}.$

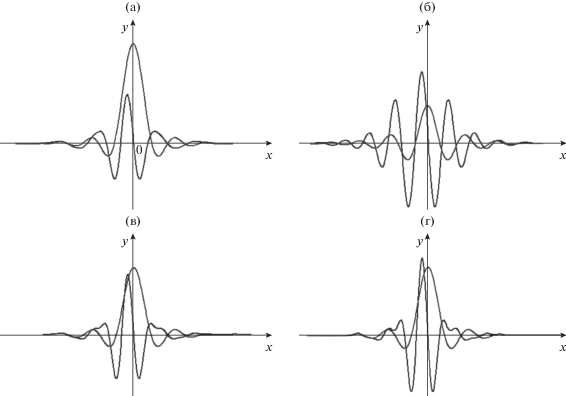
Это завершает доказательство теоремы. Таким образом, из теоремы следует, что две пары функций $\xi $, $\gamma $ и $\tilde {\xi }$, $\tilde {\gamma }$ формируют биортогональную вейвлет-систему (рис. 5).

При этом обеспечивается выполнение следующих необходимых условий на вейвлеты и масштабирующую функции [13–21]:

Таким образом, новые модифицированные базисные функции полученной вейвлет-системы:

– образуют биортогональную систему базисных функций, формирующих нестационарный кратномасштабный анализ сигналов в ${{L}^{2}}(\mathbb{R})$;

– являются нестационарными по отношению к масштабу j, так как в зависимости от j изменяется носитель спектра функций ${{\varphi }_{j}}(t),$ ${{\psi }_{j}}(t)$ и, соответственно, интервал охватываемого ими частотного поддиапазона функции $\hat {D}(\omega )$;

– вырождаются при $\hat {D}(\omega )$ = const в соответствующие исходные функции ${{\varphi }_{j}}(t)$ и ${{\psi }_{j}}(t)$.

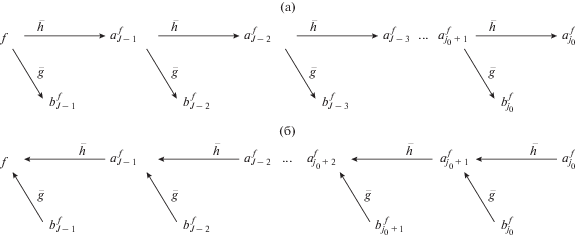
4. МАСШТАБИРУЮЩИЕ УРАВНЕНИЯ БИОРТОГОНАЛЬНЫХ ЧАСТОТНО-МОДИФИЦИРОВАННЫХ ВЕЙВЛЕТОВ

Так как базисные подпространства ${\mathbf{U}}{}_{j}$ и ${\mathbf{\tilde {U}}}{}_{j}$ формируют КМА, то функции ${{\xi }_{j}} \in {\mathbf{U}}{}_{j},$ ${{\gamma }_{j}} \in {{{\mathbf{S}}}_{j}},$ ${{\tilde {\xi }}_{j}} \in {\mathbf{\tilde {U}}}{}_{j},$ ${{\tilde {\gamma }}_{j}} \in {{{\mathbf{\tilde {S}}}}_{j}}$ аналогично классическим масштабирующим уравнениям [13–21, 35] могут быть выражены в виде линейной комбинации своих масштабирующих функций ${{\xi }_{{j + 1}}} \in {\mathbf{U}}{}_{{j + 1}}$ или ${{\tilde {\xi }}_{{j + 1}}} \in {\mathbf{\tilde {U}}}{}_{{j + 1}}.$

Для функции ${{\xi }_{{j,k}}}(t)$ имеем соотношение

Скалярное произведение под знаком суммы будет равно

Следовательно,

или в области частот

Аналогичным образом определим скалярное произведение для масштабирующего соотношения

Таким образом,

Построим масштабирующие соотношения, которым должны удовлетворять модифицированные вейвлет-функции ${{\gamma }_{{j,n}}}$ и ${{\tilde {\gamma }}_{{j,n}}}$. Для ${{\gamma }_{{j,n}}}$ имеем

В результате вычисления коэффициентов фильтра получим

Теперь (56) перепишем в виде

После преобразования Фурье это соотношение примет вид

Аналогичным образом для ${{\tilde {\gamma }}_{{j,n}}}$ получим

В частотной области это соотношение принимает вид

Свойства частотных функций построенной биортогональной вейвлет-системы хорошо известны [13–21, 35], так как они же являются соответствующими частотными функциями исходных вейвлет-базисов Н(ω) для $\hat {\varphi }(\omega )$ и G(ω) для $\hat {\psi }(\omega )$. Условие на биортогональные частотные функции

полностью подтверждается условием для ортонормированного случая [13–21, 35]

Согласно утверждениям леммы 2 и теоремы 3 о вложенности подпространств

можно получить другие масштабирующие соотношения. Так как ${\mathbf{U}}{}_{j} \subset {{{\mathbf{V}}}_{{j + 1}}},$ ${{\xi }_{j}} \in {\mathbf{U}}{}_{j},$ ${{\varphi }_{{j + 1}}} \in {\mathbf{V}}{}_{{j + 1}},$ то существует такая 2^{j+ 2}π-периодическая функция ${{\Theta }_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}),$ что

Для определения ${{\Theta }_{{j + 1}}}$ воспользуемся уравнением

Здесь произведение первых двух членов должно образовывать 2^j + 2π-периодическую функцию. Для этого введем 2^j + 2π-периодическое продолжение функции $\hat {D}(\omega )$ с промежутком $\left[ { - {{2}^{j}}(4{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3});{{2}^{j}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right]$ на $\mathbb{R}$ (в случае использования вейвлетов Кравченко).

Тогда

Здесь ${{D}_{{j + 1}}}{\kern 1pt} *{\kern 1pt} (\omega )$ – 2π-периодическая функция, определяемая равенством

где ${{\chi }_{{\omega \in \left[ { - {{2}^{j}}\frac{{4\pi }}{3};{{2}^{j}}\frac{{4\pi }}{3}} \right]}}}(\omega )$ – характеристическая функция интервала $\left[ { - {{2}^{j}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3});{{2}^{j}}({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})} \right],$ при котором имеет место равенство $\hat {D}(\omega ) = {{D}_{{j + 1}}}*({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}).$

Следовательно,

В результате обратного преобразования Фурье выражения (64) с учетом произвольного значения сдвига n имеем

Исходя из (66) формула для вычисления ${{\theta }_{{j + 1,k}}}$ будет следующая:

Поступая аналогичным образом, получим выражение для преобразования Фурье модифицированного вейвлета ${{\gamma }_{{j,n}}}(t)$

где ${{{\rm N}}_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})$ является 2^j + 2π-периодической функцией.

Отсюда следует, что

Тогда масштабирующее соотношение с коэффициентами фильтра можно представить в виде

Сдвиги биортогональной к ${{\xi }_{j}} \in {\mathbf{U}}{}_{j}$ масштабирующей функции ${{\tilde {\xi }}_{j}}$ порождают подпространство ${\mathbf{\tilde {U}}}{}_{j}$, а согласно теореме 3 выполняется условие вложенности подпространств ${\mathbf{\tilde {U}}}{\kern 1pt} {}_{j}\, \subset {{{\mathbf{V}}}_{{j + 1}}}.$ Следовательно, существует такая 2^j + 2π-периодическая функция $\tilde {\Theta }(\omega ),$ что

После соответствующих преобразований имеем

Тогда справедливо равенство

В (74) представим ${{\tilde {\Theta }}_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})$ в виде разложения в ряд Фурье

где

В результате преобразования Фурье получим масштабирующее соотношение

Аналогично для вейвлет-функции ${{\tilde {\gamma }}_{{j,n}}}$ соответствующие выражения в частотной области будут иметь вид

где 2^j + 2π-периодическая функция ${{\tilde {{\rm N}}}_{{j + 1}}}({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}),$ которая определяется следующим образом:

После обратного преобразования Фурье масштабирующее соотношение (80) во временной области представим в виде

где

Рассмотрим некоторые свойства коэффициентов фильтров $\{ {{\theta }_{{j,k}}}:k \in \mathbb{Z}\} ,$ $\{ {{\tilde {\theta }}_{{j,k}}}:k \in \mathbb{Z}\} ,$ $\{ {{\eta }_{{j,k}}}:k \in \mathbb{Z}\} ,$ $\{ {{\tilde {\eta }}_{{j,k}}}:k \in \mathbb{Z}\} .$ Коэффициенты $\{ {{\theta }_{{j,k}}}:k \in \mathbb{Z}\} $ и $\{ {{\tilde {\theta }}_{{j,k}}}:k \in \mathbb{Z}\} $ биортогональны по отношению к двойному сдвигу

Это следует из равенства $\left( {{{\xi }_{{j - 1,0}}}(t),{{{\tilde {\xi }}}_{{j - 1,p}}}(t)} \right) = {{\delta }_{{p,0}}}.$

Коэффициенты масштабирующих $\{ {{\theta }_{{j,k}}}:k \in \mathbb{Z}\} $ и вейвлетных $\{ {{\tilde {\eta }}_{{j,k}}}:k \in \mathbb{Z}\} $ фильтров обладают свойствами

Кроме того, выполняются следующие условия на сумму коэффициентов

Соответствующие частотные функции должны удовлетворять соотношению, аналогичному (61)

Рассмотрим скалярное произведение при p = k – n

Используем равенство Парсеваля и полученные выше масштабирующие соотношения

Полученное равенство имеет место только в том случае, когда

Это равенство справедливо для произвольного значения масштаба j < j_max.

Еще один новый комплекс масштабирующих уравнений удается получить на основе построенной биортогональной системы функций, если выполнить преобразование формулы для двойственных базисов (45) с помощью соотношения (52)

Здесь $H({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})$ и ${1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}})}}$ – 2^j+2π-периодические функции и их произведение, также является 2^j + 2π-периодической функцией. Откуда следует справедливость масштабирующего уравнения в частотной области для ${{\tilde {\xi }}_{j}} \in \widetilde {\mathbf{U}}{}_{j}$ и ${{\xi }_{{j + 1}}} \in {\mathbf{U}}{}_{{j + 1}}$

где

Если переписать соотношение для двойственного базиса (45) в виде ${{\hat {\xi }}_{j}}(\omega ) = E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}){{\hat {\tilde {\xi }}}_{j}}(\omega )$, то таким же образом с учетом (55) получается масштабирующее уравнение в частотной области, которое выражает функцию ${{\xi }_{j}} \in {\mathbf{U}}{}_{j}$ через масштабированную версию своего дуального базиса ${{\tilde {\xi }}_{{j + 1}}} \in \widetilde {\mathbf{U}}{}_{{j + 1}}$

где 2^j + 2π-периодическая функция имеет вид

Переписав соотношение (46) в виде ${{\hat {\gamma }}_{j}}(\omega )$ = $ = E_{{j + 1}}^{\xi }({\omega \mathord{\left/ {\vphantom {\omega {{{2}^{{j + 1}}}}}} \right. \kern-0em} {{{2}^{{j + 1}}}}}){{\hat {\tilde {\gamma }}}_{j}}(\omega )$, аналогичным образом построим новые масштабирующие уравнения для вейвлет-функций ${{\tilde {\gamma }}_{j}} \in {{{\mathbf{\tilde {S}}}}_{j}}$ и ${{\gamma }_{j}} \in {{{\mathbf{S}}}_{j}}$

где

и

где

Обращаясь к полученным масштабирующим уравнениям в частотной области можно сформулировать теорему.

Теорема 4. Если j < j_max, то справедлива вложенность подпространств

а подпространства ${{{\mathbf{S}}}_{j}}$и ${{{\mathbf{\tilde {S}}}}_{j}}$ являются также ортогональным дополнением к вложенной системе подпространств ${{{\mathbf{U}}}_{j}}$ и ${{\widetilde {\mathbf{U}}}_{j}}$ до ${{\widetilde {\mathbf{U}}}_{{j + 1}}}$ и ${{{\mathbf{U}}}_{{j + 1}}}$ соответственно

Доказательство. Для того чтобы показать вложенность масштабирующих подпространств, достаточно убедиться, что ${{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}$ и ${{{\mathbf{U}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}.$ Для доказательства ${{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}$ предположим, что некоторая функция $f(t) \in {{\widetilde {\mathbf{U}}}_{j}}.$ Тогда $f(t) \in {{{\mathbf{U}}}_{{j + 1}}},$ если $\hat {f}(\omega ) = \tilde {a}_{{j + 1}}^{f}(\omega ){{\xi }_{{j + 1}}}\left( \omega \right),$ а $\tilde {a}_{{j + 1}}^{f}(\omega )$ должна быть 2^j + 2π-периодической функцией. Поскольку $f(t) \in {{\widetilde {\mathbf{U}}}_{j}},$ то $\hat {f}(\omega ) = a_{j}^{f}(\omega ){{\hat {\tilde {\xi }}}_{j}}\left( \omega \right).$ Преобразование этого равенства дает

где произведение двух первых членов является 2^j + 2π-периодической функцией $\tilde {a}_{{j + 1}}^{f}(\omega )$. Следовательно, ${{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}.$ Аналогичным образом доказывается, что ${{{\mathbf{U}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}$. Обобщив эти условия, получим доказательство утверждений ${{{\mathbf{U}}}_{{j - 1}}} \subset {{\widetilde {\mathbf{U}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}$ и ${{\widetilde {\mathbf{U}}}_{{j - 1}}} \subset {{{\mathbf{U}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}.$

Для доказательства второй части теоремы ${{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}$ необходимо показать, что семейство функций $\{ {{\xi }_{{j,n}}}(t),{{\gamma }_{{j,k}}}(t):n,k \in \mathbb{Z}\} $ образует базис всего подпространства ${{\widetilde {\mathbf{U}}}_{{j + 1}}}$. Согласно теореме 3 справедливо условие ${{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{\widetilde {\mathbf{U}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}},$ тогда если $f(t) \in {{\widetilde {\mathbf{U}}}_{{j + 1}}}$, то $\hat {f}(\omega ) = a_{{j + 1}}^{f}(\omega ){{\tilde {\xi }}_{{j + 1}}}\left( \omega \right)$, где $a_{{j + 1}}^{f}(\omega )$ есть 2^{j+ 2}π-периодическая функция.

Итак,

где $a_{j}^{f}(\omega )$ и $b_{j}^{f}(\omega )$ – 2^j + 1π-периодические функции. Преобразуем дуальные базисы масштабирующей функции и вейвлета в правой части этого выражения

Тогда

а произведение первых двух членов в правой части представляет собой по-прежнему 2^j+2π-периодическую функцию, что доказывает ${{\widetilde {\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}$ и ${{{\mathbf{S}}}_{j}} \subset {{\widetilde {\mathbf{U}}}_{{j + 1}}}.$

Аналогичным образом, если $f(t) \in {{{\mathbf{U}}}_{{j + 1}}}$ и $\hat {f}(\omega ) = \tilde {a}_{{j + 1}}^{f}(\omega ){{\xi }_{{j + 1}}}\left( \omega \right),$ то согласно условию леммы 3

где $\tilde {a}_{{j + 1}}^{f}(\omega )$ – 2^j + 2π-периодическая функция, $\tilde {a}_{j}^{f}(\omega )$ и $\tilde {b}_{j}^{f}(\omega )$ – 2^j + 1π-периодические функции.

Следовательно,

Тогда ${{{\mathbf{U}}}_{{j + 1}}} = {{\widetilde {\mathbf{U}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}}$, ${{{\mathbf{\tilde {S}}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}$, что и требовалось доказать.

Коэффициенты масштабирующих и вейвлет-фильтров будем искать исходя из того, что частотные функции модифицированной вейвлет-системы в (91), (93), (95), (97), представляют собой произведение частотной функции исходной ортонормированной вейвлет-системы с коэффициентами фильтров $\{ {{h}_{k}}:k \in \mathbb{Z}\} $, $\{ {{g}_{k}}:k \in \mathbb{Z}\} $, которые известны, и периодической функции $E_{{j + 1}}^{\xi }(\omega )$. Для $E_{{j + 1}}^{\xi }(\omega )$ коэффициенты фильтра определяются следующим образом:

Коэффициенты фильтра для ${1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }(\omega )}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }(\omega )}}$ можно получить так

Тогда масштабирующее уравнение (91) запишется в виде

Введем обозначение коэффициентов фильтра для (100), которые представляют собой свертку известных числовых последовательностей:

Тогда

Во временной области масштабирующее уравнение имеет вид

Аналогично для (93) имеем

где

После выполнения обратного преобразования Фурье масштабирующее уравнение (104) примет вид

Подобным образом для вейвлет-функций имеем

где

Во временной области (107) имеет вид

Аналогичным образом для выражения

получим

где

Во временной области (111) примет вид

Коэффициенты фильтров $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} ,$ $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} ,$ $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} ,$ $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} _{{j,k}}^{\xi }:k \in \mathbb{Z}\} $ обладают следующими свойствами:

В биортогональном случае частотные функции $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{H} _{j}^{\xi }\left( \omega \right)$ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} _{j}^{\xi }\left( \omega \right)$ удовлетворяют равенству

Выполнение этого равенства легко показать с помощью непосредственной подстановки соотношений (92) и (94) в (121).

5. КРАТНОМАСШТАБНАЯ АППРОКСИМАЦИЯ РЕШЕНИЯ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ТИПА СВЕРТКИ С ПРИМЕНЕНИЕМ БИОРТОГОНАЛЬНЫХ ЧАСТОТНО-МОДИФИЦИРОВАННЫХ ВЕЙВЛЕТОВ КРАВЧЕНКО

Как было показано ранее, решение интегрального уравнения типа свертки (1) заключается в получении оценки полезного сигнала ${{\tilde {x}}_{P}}(t)$ по наблюдаемому сигналу $y(t)$ на основе регуляризованного спектра решения [1–7]

где $\hat {D}(\omega )$ – стабилизирующий множитель, который может быть задан как $\hat {D}(\omega ) = \;{{\hat {K}}^{{ - 1}}}(\omega )$.

Воспользовавшись интегральным уравнением типа свертки в частотной области $\hat {y}(\omega ) = $ $ = \hat {\lambda }(\omega )\hat {x}(\omega ) + \hat {n}(\omega ),$ из (122), получим оценку ${{\hat {\tilde {x}}}_{P}}(\omega ) = \hat {\lambda }(\omega ){{\hat {D}}^{{ - 1}}}(\omega )\hat {x}(\omega )$ + ${{\hat {D}}^{{ - 1}}}(\omega )\hat {n}(\omega ).$ Если $\hat {D}(\omega ) = \hat {\lambda }(\omega ),$ то оценка полезного сигнала имеет вид инверсного фильтра. В случае отсутствия шума решение (122) позволяет точно восстановить сигнал $\hat {x}(\omega )$, искаженный импульсной характеристикой $\hat {\lambda }(\omega )$ линейной стационарной системы. При наличии шума происходит его бесконечное усиление на частотах, при которых $\hat {\lambda }(\omega ) \to 0,$ что и приводит к необходимости использования математических подходов эффективного подавления шума, к которым относится вейвлет-фильтрация [13–21].

Согласно (22) оценка полезного сигнала ${{\tilde {x}}_{P}}(t)$ определяется так

где ${{\varphi }_{{J + 1,k}}}(t) \in {{{\mathbf{V}}}_{{J + 1}}}$ – исходные масштабирующие функции, выбранные из ортонормированных вейвлет-систем Кравченко; $a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}$ = $\left( {x(t),{{\varphi }_{{J + 1,k}}}(t)} \right)$ – коэффициенты разложения x(t) по масштабирующим функциям $\{ {{\varphi }_{{J + 1,k}}}(t):k \in \mathbb{Z}\} .$

Таким образом, решение интегрального уравнения типа свертки (1) относительно функции $x\,(t)$ сводится к нахождению неизвестной последовательности коэффициентов разложения {$a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}$: $k \in \mathbb{Z}$} [29, 36–41]. Представим (22) в частотной области

Умножив (123) слева и справа на $\hat {D}(\omega )$, получим

С учетом (27), (122) можно показать, что коэффициенты {$a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}$: $k \in \mathbb{Z}$} определяются в виде разложения наблюдаемого сигнала $y(t)$ по базисной системе функций ${{\xi }_{{j,k}}}(t),k \in \mathbb{Z},$ в котором $a_{{J + 1,k}}^{y} = a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}.$ Действительно, так как

то

Следовательно, $y(\omega ) \in {{{\mathbf{U}}}_{{j + 1}}}$ и условие теоремы 1 выполняется, так как ${{{\mathbf{V}}}_{j}} \subset {{{\mathbf{U}}}_{{j + 1}}}$ согласно лемме 2.

Итак, оценка полезного сигнала ${{\tilde {x}}_{P}}(t)$ будет определяться следующим разложением по базису ${{\varphi }_{{J + 1,k}}},\,\,k \in \mathbb{Z}\,:$

Подлежащие определению коэффициенты {$a_{{J + 1,k}}^{y}$: $k \in \mathbb{Z}$} находятся исходя из существования биортогональной системы функций ${{\xi }_{{j,k}}}(t),\,\,{{\tilde {\xi }}_{{j,k}}}(t),\,\,k \in \mathbb{Z}$

Здесь оценка приближенного решения интегрального уравнения типа свертки (1) в виде (127) сводится к определению коэффициентов (128). Исходя из того, что предложенная и обоснованная биортогональная система вейвлет-функций ${{\xi }_{{j,k}}}(t),$ ${{\gamma }_{{j,k}}}(t)$ и ${{\tilde {\xi }}_{{j,k}}}(t),$ ${{\tilde {\gamma }}_{{j,k}}}(t)$, $k \in \mathbb{Z}$ порождает две цепочки КМА, любую функцию из ${{{\mathbf{U}}}_{{J + 1}}}$ можно представить в виде ортогонального разложения по базисам подпространств низшего масштаба ${{{\mathbf{U}}}_{j}}$, ${{{\mathbf{S}}}_{j}}$ так, что ${{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}}.$ Тогда для создания вычислительных алгоритмов оценки полезного сигнала будем искать ${{\tilde {x}}_{P}}(t)$ в виде разложения

которое описывает ДВП классического КМА по вейвлетам, обладающим компактным носителем в частотной области, в частности, по вейвлетам Кравченко [25–28].

В частотной области (129) имеет вид

Коэффициенты {$a_{{{{j}_{0}},k}}^{{{{{\tilde {x}}}_{P}}}},\,\,b_{{j,k}}^{{{{{\tilde {x}}}_{P}}}}$: $k \in \mathbb{Z}$} являются результатом ДВП ${{\tilde {x}}_{P}}(t)$ при разложении до некоторого масштаба j₀ так, что ${{\tilde {x}}_{P}}(t)$ представляется как сумма грубой аппроксимации ${{P}_{{{{j}_{0}}}}}{{\tilde {x}}_{{P\,}}}(t) \in {{{\mathbf{V}}}_{{{{j}_{0}}}}}\;$ и множества деталей $\;{{Q}_{j}}{{\tilde {x}}_{P}}(t) \in {{{\mathbf{W}}}_{j}}$

Согласно концепции КМА коэффициенты вейвлет-разложения при более грубом приближении могут быть получены рекурсивно. Действительно, пусть некоторый сигнал f(t) задан отсчетами в моменты времени ${{t}_{m}} = m{{2}^{{ - N}}},$ $m \in \mathbb{Z}{\kern 1pt} .$ Тогда, умножив скалярно масштабирующие уравнения ${{\varphi }_{{j,n}}}(t)$ = $ = \sum\nolimits_k {{{h}_{{k - 2n}}}} {{\varphi }_{{j + 1,k}}}(t),$ ${{\psi }_{{j,n}}}(t)$ = $\sum\nolimits_k {{{g}_{{k - 2n}}}} {{\varphi }_{{j + 1,k}}}(t)$ слева и справа на $f(t)$, для произвольного масштаба j можно получить рекурсивные формулы расчета коэффициентов вейвлет-разложения от более точного масштаба   j + 1 к более грубому масштабу j [13–21]

Графически алгоритм вейвлет-разложения сигнала f(t) можно представить в виде схемы (рис. 6а). Данный алгоритм реализуется с помощью многокаскадного последовательного соединения блоков фильтров, обеспечивающих быстрые вычисления ДВП.

Начальные значения коэффициентов $a_{{j,k}}^{f}$ определяются формулами $a_{{j,k}}^{f} = (f(t),{{\varphi }_{{j,k}}}(t)),$ $b_{{j,k}}^{f} = $ $ = (f(t),{{\psi }_{{j,k}}}(t))$ при таком значении масштаба j, при котором в пределах спектрального диапазона сигнала $\hat {f}(\omega )$ функция ${{\hat {\varphi }}_{j}}(\omega )$ остается практически постоянной, т.е. чтобы аппроксимация вейвлетами достаточно точно отражала сигнал f(t). Такой расчет является трудоемким и может не обеспечить необходимую точность вычисления. Так как сигнал f(t) практически задан своими значениями, то при большом масштабе j коэффициенты $\{ {{a}_{{j,k}}}:k \in \mathbb{Z}\} $ можно положить равными отсчетам функции

Отсюда следует, что при выборе вейвлет-системы Кравченко $a_{{j,k}}^{f} \approx {{\left. {f(t)} \right|}_{{t = k{{2}^{{ - j}}}}}} = {{f}_{k}}.$

Следовательно, быстрое вычисление ДВП позволяет представить оценку приближенного решения (1) в дискретном виде как последовательность коэффициентов $\{ a_{{{{j}_{0}},k}}^{{{{{\tilde {x}}}_{P}}}},b_{{j,k}}^{{{{{\tilde {x}}}_{P}}}}:$ ${{j}_{0}} \leqslant j \leqslant J,k \in \mathbb{Z}\} ,$ по которым раскладывается ${{\tilde {x}}_{P}}(t)$ в (129).

Как показано в (122), оценка полезного сигнала ${{\tilde {x}}_{P}}(t)$, определяемая обработкой наблюдаемого сигнала y(t) фильтром с частотным откликом ${{\hat {D}}^{{ - 1}}}(\omega )$, соответствует вейвлет-разложению наблюдаемого сигнала y(t) по базису ${{\xi }_{{j,k}}}(t)$, $k \in \mathbb{Z}$ на самом точном масштабе J. Аналогичным образом получим разложение ${{\hat {\tilde {x}}}_{P}}(t)$ в виде ДВП, умножая слева и справа выражение (130) на $\hat {D}(\omega )$

С учетом (27), (28) имеем

Следовательно, коэффициенты {$a_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}$, $b_{{J + 1,k}}^{{{{{\tilde {x}}}_{P}}}}$: $k \in \mathbb{Z}$} получаются при разложении наблюдаемого сигнала $y(t)$ по базисной системе функций ${{\xi }_{{j,k}}}(t),{{\gamma }_{{j,k}}}(t),$ $k \in \mathbb{Z},$ ${{j}_{0}} \leqslant j \leqslant J$, в котором $a_{{{{j}_{0}},k}}^{y} = a_{{{{j}_{0}},k}}^{{{{{\tilde {x}}}_{P}}}}$, $b_{{j,k}}^{y} = b_{{j,k}}^{{{{{\tilde {x}}}_{D}}}}$. Таким образом, оценка приближенного решения (1) будет определяться следующим разложением по базисам ${{\varphi }_{{{{j}_{0}},k}}}(t),{{\psi }_{{j,k}}}(t),$ $k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J$:

где $\{ a_{{{{j}_{0}},k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J\} $ – коэффициенты разложения наблюдаемого сигнала $y(t)$ по частотно-модифицированным биортогональным вейвлетам ${{\xi }_{{j,k}}}(t),{{\gamma }_{{j,k}}}(t),$ $k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J.$

Предложенная и обоснованная биортогональная система функций ${{\xi }_{{j,k}}}(t)$, ${{\gamma }_{{j,k}}}(t)$ и ${{\tilde {\xi }}_{{j,k}}}(t)$, ${{\tilde {\gamma }}_{{j,k}}}(t)$, $k \in \mathbb{Z}$ порождает КМА, поэтому для эффективного решения задачи (1) по оценке полезного сигнала ${{\tilde {x}}_{P}}(t)$, искаженного импульсной характеристикой $\lambda (t)$, необходимо разработать алгоритм быстрого вычисления вейвлет-коэффициентов {$a_{{{{j}_{0}},k}}^{y}$, $b_{{j,k}}^{y}$: $k \in \mathbb{Z},{{j}_{0}} \leqslant j \leqslant J$} исходя из полученных ранее масштабирующих уравнений (51), (54), (57), (59), (67), (72), (79), (82), (103), (106), (109), (113), а также масштабирующих и вейвлет-фильтров $\{ h\} $, $\{ g\} $, $\{ {{\theta }_{j}}\} $, $\{ {{\eta }_{j}}\} $, $\{ {{\tilde {\theta }}_{j}}\} $, $\{ {{\tilde {\eta }}_{j}}\} $, $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} _{j}^{\xi }\} $, $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} _{j}^{\xi }\} $, $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} _{j}^{\xi }\} $, $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} _{j}^{\xi }\} $, затем провести эффективное подавление шума и компенсировать его бесконечное усиление с использованием математических подходов обработки вейвлет-коэффициентов [13–21, 42, 43].

Разработанные частотно-модифицированные биортогональные вейвлеты позволяют получить рекурсивные алгоритмы для вычисления коэффициентов ДВП с учетом локализации и компенсации частотно-временных особенностей наблюдаемого сигнала y(t), частотной функции отклика $\hat {\lambda }(\omega )$ или фильтра с частотным откликом $\hat {D}(\omega )$ за счет существования масштабирующих уравнений (51), (54), (57), (59), (67), (72), (79), (82), (103), (106), (109), (113). Масштабирующие уравнения (103), (106), (109), (113) позволяют осуществлять переходы при вейвлет-разложении наблюдаемого сигнала y(t) от базиса ${{\xi }_{{j + 1,k}}}(t)$ к базисам ${{\tilde {\xi }}_{{j,k}}}(t)$, ${{\tilde {\gamma }}_{{j,k}}}(t)$ или от базиса ${{\tilde {\xi }}_{{j + 1,k}}}(t)$ к базисам ${{\xi }_{{j,k}}}(t)$, ${{\gamma }_{{j,k}}}(t)$ (следующий уровень разложения выполняется по биортогональному базису) в рамках единого ДВП в необходимых частотных диапазонах, где свойства вейвлет-базисов ${{\xi }_{{j,k}}}(t)$, ${{\gamma }_{{j,k}}}(t)$ или ${{\tilde {\xi }}_{{j,k}}}(t)$, ${{\tilde {\gamma }}_{{j,k}}}(t)$ позволяют лучшим образом аппроксимировать сигнал y(t). Из этого следует, что в едином алгоритме ДВП становится возможным оптимизировать процесс получения коэффициентов вейвлет-разложения для дальнейшей их обработки с целью эффективного восстановления сигнала х(t), подавления шума и компенсации его бесконечного усиления. Для масштабирующих функций подпространства ${\mathbf{U}}{}_{j}$ и соответствующих вейвлет-функций подпространства ${{{\mathbf{S}}}_{j}}$ справедливы масштабирующие соотношения (51), (57), (67), (72), (106), (113), а для подпространств ${\mathbf{\tilde {U}}}{}_{j}$и ${{{\mathbf{\tilde {S}}}}_{j}}$ – масштабирующие соотношения (54), (59), (79), (82), (103), (109).

Коэффициенты разложения $\{ a_{{j,k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z}\} $ в (137) при произвольном значении масштаба j определяются по формулам

Рекурсивные алгоритмы для вычисления этих коэффициентов получим, подставляя в (138), (139) вместо ${{\tilde {\xi }}_{{j,k}}}(t)$ и ${{\tilde {\gamma }}_{{j,k}}}(t)$ масштабирующие соотношения (54), (59), (79), (82), (103), (109). Воспользовавшись (54), (59), получим

Из масштабирующих уравнений (51), (57), (67), (72), (79), (82), (103), (106), (109), (113) также следует, что возможны другие рекурсивные алгоритмы вычисления как коэффициентов разложения $\{ a_{{{{j}_{0}},k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z}\} $ наблюдаемого сигнала y(t) по базисным функциям ${{\xi }_{{j,k}}}(t),$ ${{\gamma }_{{j,k}}}(t)$, так и коэффициентов разложения y(t) по биортогональным к этим базисам функциям ${{\tilde {\xi }}_{{j,k}}}(t),$ ${{\tilde {\gamma }}_{{j,k}}}(t).$

Введем обозначения для коэффициентов разложения наблюдаемого сигнала y(t) по базисным функциям ${{\tilde {\xi }}_{{j,k}}}(t)$, ${{\tilde {\gamma }}_{{j,k}}}(t)$ при произвольном масштабе j

а для коэффициентов разложения наблюдаемого сигнала y(t) по исходным вейвлет-базисам ${{\varphi }_{{j,k}}}(t)$, ${{\psi }_{{j,k}}}(t)$

Из (79), (82) следуют

Используя (103), (109), имеем

Рекурсивный алгоритм для вычисления коэффициентов разложения $\{ \tilde {a}_{{{{j}_{0}},k}}^{y},\tilde {b}_{{j,k}}^{y}:k \in \mathbb{Z}\} $ наблюдаемого сигнала y(t) по базисным функциям ${{\tilde {\xi }}_{{j,k}}}(t)$ ${{\tilde {\gamma }}_{{j,k}}}(t)$ представляется аналогично рассмотренным выше случаям следующим образом:

Как и в случае классического КМА, полученные рекурсивные алгоритмы для вычисления коэффициентов $\{ a_{{{{j}_{0}},k}}^{y},b_{{j,k}}^{y}:k \in \mathbb{Z}\} $ или $\{ \tilde {a}_{{{{j}_{0}},k}}^{y},\tilde {b}_{{j,k}}^{y}:k \in \mathbb{Z}\} $ требуют, чтобы были известны соответствующие начальные значения коэффициентов разложения $a_{{J,k}}^{y}$ или $\tilde {a}_{{J,k}}^{y}$ при самом точном масштабе J. Для вычисления начальных коэффициентов $\{ a_{{J,k}}^{y}:k \in \mathbb{Z}\} $ по известным отсчетам наблюдаемого сигнала y(t) подставим в (138) масштабирующее соотношение (79)

Откуда при выборе вейвлет-системы Кравченко получаем

Подобным образом согласно (82), (139) запишем

Отсюда при выборе вейвлет-системы Кравченко имеем

Аналогично вычисляются начальные коэффициенты $\{ \tilde {a}_{{J,k}}^{y}:k \in \mathbb{Z}\} $ по известным отсчетам наблюдаемого сигнала y(t) с использованием (67) и (142), (72) и (143)

Таким образом, воспользовавшись формулами (140), (141), (146)–(159), можно получить различные варианты рекурсивного алгоритма разложения наблюдаемого сигнала y(t) по его отсчетам от более точного разрешения J к грубому разрешению j₀. Для вычисления каждых последующих коэффициентов из предыдущих с большим масштабом, характеризующим более широкополосный процесс, лучше использовать базисные функции и их масштабирующие и вейвлет-фильтры в (140), (141), (146)–(159), которые учитывают и компенсируют частотно-временные особенности наблюдаемого сигнала y(t) и частотных функций $\hat {\lambda }(\omega ),\hat {D}(\omega )$ в соответствующем диапазоне. Схема одного из возможных алгоритмов вейвлет-разложения наблюдаемого сигнала y(t) показана на рис. 7а.

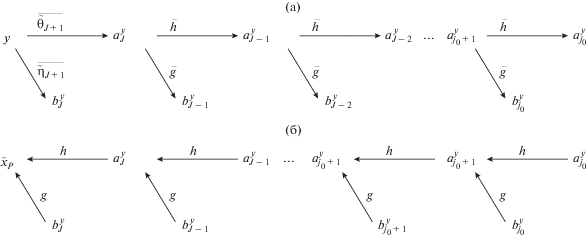
В отличие от классической схемы вейвлет-разложения [13–21] отсчеты наблюдаемого сигнала y(t) в первом каскаде обрабатываются низкочастотным и высокочастотным фильтрами $\{ {{\tilde {\theta }}_{{J + 1}}}\} $, $\{ {{\tilde {\eta }}_{{J + 1}}}\} $. Фильтры на последующих этапах обработки не изменяются.

Далее получим рекурсивный алгоритм восстановления аппроксимирующих коэффициентов, характеризующих низкочастотную составляющую сигнала с большим масштабом, из коэффициентов вейвлет-разложения меньшего масштаба (один уровень обратного дискретного вейвлет преобразования). Тогда, учитывая, что ${{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}}$, масштабирующую функцию ${{\tilde {\xi }}_{{j,k}}}(t)$, $k \in \mathbb{Z}$ можно представить в виде суммы

Умножая (160) скалярно слева и справа на y(t), получим

что соответствует следующему представлению коэффициентов разложения $a_{{j + 1,k}}^{y}$:

Таким образом, по формуле (161) получен рекурсивный алгоритм восстановления оценки ${{\tilde {x}}_{P}}(t)$ по коэффициентам вейвлет-разложения от грубого к точному разрешению с использованием фильтров исходных вейвлет-базисов $\{ {{h}_{k}}\} $ и $\{ {{g}_{k}}\} $. Схема восстановления отсчетов оценки ${{\tilde {x}}_{P}}(t)$ не отличается от схемы классического КМА (см. рис. 7б).

Благодаря предложенному и обоснованному конструктивному подходу получения частотно-модифицированных вейвлет-базисов схема разложения наблюдаемого сигнала y(t) и восстановления коэффициентов вейвлет-разложения оценки ${{\tilde {x}}_{P}}(t)$ не единственная. В схеме разложения наблюдаемого сигнала y(t) могут использоваться другие рекурсивные формулы (148)–(159). По полученным в результате коэффициентам вейвлет-разложения должна быть восстановлена оценка ${{\tilde {x}}_{P}}(t)$.

Для подпространств ${{{\mathbf{U}}}_{{j + 1}}}$ и ${{{\mathbf{\tilde {U}}}}_{{j + 1}}}$ масштабирующих функций ${{\xi }_{{j + 1,k}}}(t)$ и ${{\tilde {\xi }}_{{j + 1,k}}}(t)$, $k \in \mathbb{Z}$ справедливы ортогональные разложения ${{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus {{{\mathbf{S}}}_{j}},$ ${{{\mathbf{U}}}_{{j + 1}}} = {{{\mathbf{\tilde {U}}}}_{j}} \oplus {{\widetilde {\mathbf{S}}}_{j}},$ ${{{\mathbf{\tilde {U}}}}_{{j + 1}}} = {{{\mathbf{U}}}_{j}} \oplus \;{{{\mathbf{S}}}_{j}}$. Тогда масштабирующие функции ${{\xi }_{{j + 1,k}}}(t)$, ${{\tilde {\xi }}_{{j,k}}}(t)$, $k \in \mathbb{Z}$ можно представить в виде сумм

из которых следуют формулы для коэффициентов разложения $a_{{j + 1,k}}^{y}$ и $\tilde {a}_{{j + 1,k}}^{y}$:

Следовательно, с использованием рекурсивных соотношений (161) и (165) можно восстанавливать коэффициенты разложения большего масштаба по коэффициентам разложения того же базиса меньшего масштаба, а с помощью соотношений (166) и (167) восстанавливаются коэффициенты разложения большего масштаба по коэффициентам разложения биортогонального базиса меньшего масштаба. Кроме того, возможны смешенные рекурсивные соотношения, где коэффициенты разложения большего масштаба получаются из коэффициентов разложения по масштабирующим функциям той же или биортогональной вейвлет-системы и вейвлет-функциям биортогональной или той же вейвлет-системы при меньшем масштабе. Действительно, если воспользоваться (160), а затем (45), (46) и (92), (96), то во временной области получим

Аналогичным образом, из (163) с учетом (45), (46) и (94), (98) во временной области имеем

Тогда смешанные рекурсивные формулы восстановления аппроксимирующих коэффициентов разложения $a_{{j + 1,k}}^{y},$ $\tilde {a}_{{j + 1,k}}^{y}$ имеют следующий вид:

Таким образом, получены рекурсивные формулы для одного уровня ДВП и ОДВП, позволяющие строить гибкие вычислительные схемы кратномасштабной аппроксимации решения интегрального уравнении типа свертки (1) с учетом частотно-временных особенностей наблюдаемого сигнала y(t), частотной функции отклика $\hat {\lambda }(\omega )$ или фильтра с частотным откликом $\hat {D}(\omega )$. Обобщенная схема, реализующая кратномасштабный алгоритм восстановления оценки полезного сигнала ${{\tilde {x}}_{P}}(t)$, показана на рис. 8.

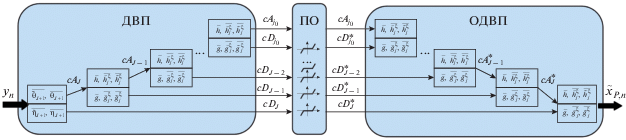
Полезный сигнал х(t), первоначально искаженный импульсной характеристикой λ(t) с последующим действием шума n(t) в виде временных отсчетов y_n = y(t_n), подвергается вейвлет-разложению с использованием низкочастотного фильтра $\{ \overline {{{{\tilde {\theta }}}_{{J + 1,k}}}} \} $ (или $\{ \overline {{{\theta }_{{J + 1,k}}}} \} $) и высокочастотного фильтра $\{ \overline {{{{\tilde {\eta }}}_{{J + 1,k}}}} \} $ (или $\{ \overline {{{\eta }_{{J + 1,k}}}} \} $). В результате получают аппроксимирующие коэффициенты вейвлет-разложения $c{{A}_{J}} = \{ a_{J}^{y}\} $ (или $c{{A}_{J}} = \{ \tilde {a}_{J}^{y}\} $) и детализирующие коэффициенты вейвлет-разложения $c{{D}_{J}} = \{ b_{J}^{y}\} $ (или $c{{D}_{J}} = \{ \tilde {b}_{J}^{y}\} $) масштаба J. Далее каждые аппроксимирующие коэффициенты вейвлет-разложения $c{{A}_{j}} = \{ a_{j}^{y}\} $ (или $c{{A}_{j}} = \{ \tilde {a}_{j}^{y}\} $) при ${{j}_{0}} - 1 \leqslant j \leqslant J$ должны быть обработаны низкочастотным фильтром $\{ \overline {{{h}_{k}}} \} $ (или $\{ \overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} {{{_{{}}^{\xi }}}_{{j,k}}}} \} $, или $\{ \,\overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} {{{_{{}}^{\xi }}}_{{j,k}}}} \} $) и высокочастотным фильтром $\{ \overline {{{g}_{k}}} \} $ (или $\{ \overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} {{{_{{}}^{\xi }}}_{{j,k}}}} \} $, или $\{ \,\overline {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} {{{_{{}}^{\xi }}}_{{j,k}}}} \} $). Итак, образуется дискретная последовательность коэффициентов вейвлет-разложения $\{ c{{A}_{{{{j}_{0}}}}},c{{D}_{j}}:$ ${{j}_{0}} \leqslant j \leqslant J\} .$ Детализирующие коэффициенты $\{ c{{D}_{j}}:\,{{j}_{0}} \leqslant j \leqslant J\} $ впоследствии подвергаются пороговой обработке. После этого выполняется ОДВП с использованием низкочастотного фильтра $\left\{ {{{h}_{k}}} \right\}$ (или $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} $, или $\{ \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} $) и высокочастотного фильтра $\left\{ {{{g}_{k}}} \right\}$ (или $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} {{_{{}}^{\xi }}_{{j,k}}}\} $, или $\{ \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} {{_{{}}^{\xi }}_{{j,k}}}\} $). При этом схема вейвлет-восстановления должна обеспечивать решение интегрального уравнения (1).

Получение оценки полезного сигнала ${{\tilde {x}}_{P}}$ с помощью кратномасштабного алгоритма с использованием новых биортогональных частотно-модифицированных вейвлетов проводится в несколько этапов.

1. Выбор частотной модифицирующей функции $\hat {D}(\omega )$. На этом этапе для выбора частотной модифицирующей функции $\hat {D}(\omega )$ учитывается априорная информация о полезном и наблюдаемом сигнале $x(t)$, $y(t)$, импульсной характеристике λ(t), параметрах шума n(t).

На практике для подавления бесконечного усиления шума используют фильтр, регуляризирующий усиление на высоких частотах (3), который может быть использован при построении функции $\hat {D}(\omega )$ в виде $\hat {D}(\omega ) = \hat {K}{{(\omega )}^{{ - 1}}}.$ Подавление бесконечного усиления шума также может быть достигнуто применением оконной функции w(ω), в том числе масштабирующей функции ${{\hat {\varphi }}_{J}}(\omega )$, которая при самом точном разрешении J должна удовлетворять следующим требованиям:

– бесконечный рост высокочастотной части спектра $\hat {\lambda }{{(\omega )}^{{ - 1}}}$ должен быть скомпенсирован убыванием высокочастотной части масштабирующей функции;

– спектр масштабирующей функции ${{\hat {\varphi }}_{J}}(\omega )$ в пределах спектральной полосы $\hat {y}(\omega )$ должен быть максимально плоским;

– масштабирующая функция ${{\hat {\varphi }}_{J}}(\omega )$ должна быть достаточно гладкая для устранения эффекта Гиббса (как можно большее число раз непрерывно дифференцируемой).

Указанными свойствами обладают масштабирующие функции из вейвлет-систем Кравченко [25–28].

Дополнительно частотная характеристика системы может быть подвергнута коррекции. Для этого функцию $\hat {D}(\omega )$ необходимо умножить на подходящий полином от ω.

2. Выбор ортонормированного вейвлет-базиса $\varphi (t)$, $\psi (t)$ с оптимальными свойствами. Для достижения большей точности и получения вычислительных преимуществ вейвлет-базис должен обладать финитным спектром, малым числом коэффициентов фильтров $\{ h_{k}^{{}}\} ,\,\,\,\{ g_{k}^{{}}\} $, непрерывной дифференцируемостью как можно большее число раз. Такими свойствами обладают масштабирующие функции из вейвлет-систем Кравченко [25–28].

Исходя из частотно-временных свойств выбранного вейвлет-базиса определяются значения масштабов $J \geqslant j \geqslant {{j}_{0}},$ при которых должно быть выполнено ДВП.

3. Получение биортогональной частотно-модифицированной вейвлет-системы ${{\xi }_{{j,k}}}(t),$ ${{\gamma }_{{j,k}}}(t)$, ${{\tilde {\xi }}_{{j,k}}}(t)$, ${{\tilde {\gamma }}_{{j,k}}}(t)$. Первоначально из выбранного ортонормированного вейвлет-базиса ${{\varphi }_{{j,k}}}(t)$, ${{\psi }_{{j,k}}}(t)$ и модифицирующей функции $\hat {D}(\omega )$ должны быть получены функции ${{\xi }_{{j,k}}}(t)$, ${{\gamma }_{{j,k}}}(t)$ по формулам (27), (28). Далее вводится функция $E_{j}^{\xi }(\omega )$ по формуле (44), с использованием которой строятся биортогональные вейвлет-базисы ${{\tilde {\xi }}_{{j,k}}}(t)$, ${{\tilde {\gamma }}_{{j,k}}}(t)$ согласно (45), (46). Дополнительно, модифицирующая функция $\hat {D}(\omega )$ может быть подвергнута частотной коррекции.

4. Расчет дискретных фильтров новой биортогональной частотно-модифицированной вейвлет-системы. Для проведения прямого ДВП наблюдаемого сигнала y(t) и получения оценки полезного сигнала ${{\tilde {x}}_{P}}(t)$ с помощью ОДВП известные дискретные фильтры $\{ h_{k}^{{}}\} ,\,\,\,\{ g_{k}^{{}}\} $ ортонормированного вейвлет-базиса $\varphi (t)$, $\psi (t)$ дополняются расчетом следующих фильтров:

– по формулам (68), (73), (78), (83) вычисляются коэффициенты фильтров $\{ {{\tilde {\theta }}_{{J + 1,k}}}\} $, $\{ {{\tilde {\eta }}_{{J + 1,k}}}\} $ и $\{ {{\theta }_{{J + 1,k}}}\} $, $\{ {{\eta }_{{J + 1,k}}}\} $, которые определяют первый уровень ДВП;

– по формулам (101), (105), (108), (112) вычисляются коэффициенты фильтров $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} $, $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} _{{j,k}}^{\xi }\} $ и $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} {{_{{}}^{\xi }}_{{j,k}}}\} $, $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} _{{j,k}}^{\xi }\} $, которые наряду с $\{ h_{k}^{{}}\} ,\,\,\,\{ g_{k}^{{}}\} $ могут применяться в расчете последующих уровней ДВП и в ОДВП. Следует, отметить, что коэффициенты этих фильтров не требуют расчета обратного преобразования Фурье для каждого разрешения. Они вычисляются дискретной сверткой известных коэффициентов фильтров $\{ {{h}_{k}}\} ,\{ {{g}_{k}}\} $ с предварительно рассчитанной последовательностью коэффициентов 2^{j+ 2}π-периодической функции $E_{{j + 1}}^{\xi }(\omega )$ и обратной к ней функции ${1 \mathord{\left/ {\vphantom {1 {E_{{j + 1}}^{\xi }(\omega )}}} \right. \kern-0em} {E_{{j + 1}}^{\xi }(\omega )}}$ соответственно $\{ {{\varsigma }_{{j + 1,\;n}}}\} $, $\{ {{\tilde {\varsigma }}_{{j + 1,\;n}}}\} $. При этом коэффициенты $\{ {{\tilde {\varsigma }}_{{j + 1,\;n}}}\} $ могут быть вычислены из коэффициентов $\{ {{\varsigma }_{{j + 1,\;n}}}\} $. Таким образом, наибольших вычислительных затрат требует однократное вычисление коэффициентов фильтров $\{ {{\tilde {\theta }}_{{J + 1,k}}}\} $, $\{ {{\tilde {\eta }}_{{J + 1,k}}}\} $и $\{ {{\theta }_{{J + 1,k}}}\} $, $\{ {{\eta }_{{J + 1,k}}}\} $.

5. Получение начальных коэффициентов разложения наблюдаемого сигнала y(t). На первом этапе разложения наблюдаемого сигнала y(t) вычисляются коэффициенты $\{ a_{{J,n}}^{y},b_{{J,n}}^{y}:n \in \mathbb{Z}\} $ или $\{ \tilde {a}_{{J,n}}^{y},\tilde {b}_{{J,n}}^{y}:n \in \mathbb{Z}\} $ с помощью дискретных фильтров $\{ {{\tilde {\theta }}_{{J + 1,k}}}:k \in \mathbb{Z}\} $, $\{ {{\tilde {\eta }}_{{J + 1,k}}}:k \in \mathbb{Z}\} $ или $\{ {{\theta }_{{J + 1,k}}}:k \in \mathbb{Z}\} $, $\{ {{\eta }_{{J + 1,k}}}:k \in \mathbb{Z}\} $ по формулам (156)–(159). Указанные фильтры получены в частотной области по формулам (66), (71), (76), (81) и учитывают особенности модифицирующей функции $\hat {D}(\omega )$, которая может значительно возрастать в области высоких частот. При этом из (66), (71), (76), (81) следует, что частотные фильтры ${{\tilde {\Theta }}_{j}}(\omega ),{{\tilde {{\rm N}}}_{j}}(\omega )$ могут обеспечивать рост частотных составляющих обрабатываемого сигнала при $\hat {\lambda }(\omega ) \to 0$ (в полосе частот наблюдаемого сигнала $\hat {y}(\omega )$), если эти особенности недостаточно скомпенсированы соответствующим выбором $\hat {D}(\omega )$. В частности, может значительно увеличиваться высокочастотная составляющая сигнала, содержащая основной шум. Фильтры ${{\Theta }_{j}}(\omega ),{{{\rm N}}_{j}}(\omega )$, напротив, не усиливают такие частотные компоненты обрабатываемого сигнала, и могут служить альтернативным подходом для расчета коэффициентов разложения наблюдаемого сигнала y(t) на первом этапе ДВП. Последующие этапы ДВП проводятся фильтрами с меньшей полосой пропускания, где в высокочастотной части рост модифицирующей функции $\hat {D}(\omega )$, как правило, существенно меньше. Поэтому последующие этапы ДВП чаще всего менее критичны к выбору фильтров разложения.

6. ДВП наблюдаемого сигнала y(t). В ходе ДВП подбирается оптимальная схема вейвлет-разложения наблюдаемого сигнала y(t) по формулам (140), (141), (148)–(151), (154), (155) при выбранных значениях масштабов ${{j}_{0}}\,\, \geqslant j \geqslant J$ с учетом частотно-временных особенностей наблюдаемого сигнала y(t), частотной функции отклика $\hat {\lambda }(\omega )$ или фильтра с частотным откликом $\hat {D}(\omega )$. Также применяется избыточное ДВП (вейвлет-коэффициенты не отбрасываются в результате децимации), при котором может достигаться лучшее подавление шума.

7. Пороговая обработка вейвлет-коэффициентов. Процесс очистки наблюдаемого сигнала от шума с помощью вейвлетов может быть выполнен пороговой обработкой вейвлет-коэффициентов [13–21, 42, 43]. Достоинство нелинейных методов пороговой обработки вейвлет-коэффициентов состоит в быстроте алгоритмов построения оценок; возможности лучшей адаптации к функциям, имеющим на разных участках различную степень регулярности. Помимо задачи удаления шума, пороговая обработка позволяет решить задачу сжатия сигнала. При пороговой обработке проводится ограничение уровня детализирующих коэффициентов с использованием пороговой функции ${{p}_{T}}(х)$. Вместо аргумента х в функцию ${{p}_{T}}(х)$ подставляются детализирующие коэффициенты для каждого уровня разложения j ($c{{D}_{j}}$, ${{j}_{0}} \leqslant j \leqslant J$).

Обычно используется функция жесткой или мягкой пороговой обработки с порогом Т. Функция жесткой пороговой обработки описывается следующим выражением:

Очевидно, что функция жесткой пороговой обработки имеет разрыв. Это может привести к нежелательным особенностям обработки достаточно гладкой функции сигнала. Мягкая пороговая обработка задается непрерывной пороговой функцией

Вид функций жесткой и мягкой пороговой обработки показан на рис. 9.

Следовательно, при таком подходе наиболее эффективное удаление шума будет достигаться, когда энергия сигнала в результате ДВП сосредоточена в минимальном числе коэффициентов выше порогового уровня, а энергия шума распределена в максимальном числе коэффициентов ниже порогового уровня. Это происходит, когда выбранный вейвлет-базис хорошо коррелирован с сигналом. Для каждого масштаба j выбирается порог T_j, который в соответствии с [42, 43] определяется так

Этот порог получил название “универсальный”, так как он не зависит от наблюдаемых данных (зависит только от дисперсии шума). При выборе порога T_U обеспечивается близость среднеквадратического риска к минимальному [42–45], а из сигнала удаляется почти весь шум. Дисперсия шума ${{\sigma }^{2}}$ может быть вычислена с помощью калибровочной процедуры устройства регистрации сигнала. Однако, зачастую дисперсия ${{\sigma }^{2}}\;$ неизвестна и вместо ее точного значения необходимо использовать некоторую оценку $\sigma _{{\text{O}}}^{2}$. Оценка дисперсии может быть получена по наблюдаемым данным y_n = y(t_n) путем вычисления медианы M_b вейвлет-коэффициентов $c{{D}_{j}}$ на самом точном масштабе J, так как в силу (157) (или (159)) эти коэффициенты фактически содержат только шум ${{\sigma }_{{\text{O}}}} = {{{{M}_{b}}} \mathord{\left/ {\vphantom {{{{M}_{b}}} {0.6745}}} \right. \kern-0em} {0.6745}}.$ Кроме того, в качестве дисперсии $\sigma _{{\text{O}}}^{2}$ может быть использована выборочная дисперсия. Выборочная дисперсия является самой популярной оценкой величины $\sigma _{{\text{O}}}^{2}$, а в случае отсутствия выбросов, она наиболее предпочтительна. Тогда, если сигнал y_n длиной N имеет N/2 вейвлет-коэффициентов $c{{D}_{j}}$ наименьшего масштаба j = J−1, то $\sigma _{{\text{O}}}^{2}$ оценивается следующим образом:

8. Восстановление оценки полезного сигнала ${{\tilde {x}}_{P}}(t)$ с использованием ОДВП. В ходе ОДВП проводится восстановление дискретных значений оценки сигнала ${{\tilde {x}}_{{P\,,n}}} = {{\tilde {x}}_{P}}({{t}_{n}})$ по коэффициентам вейвлет-разложения наблюдаемого сигнала y_n = y(t_n), которые прошли пороговую обработку. Так как при заданных аппроксимирующих и детализирующих коэффициентах на каждом масштабе j (${{j}_{0}} \leqslant j \leqslant J$) возможно восстанавливать аппроксимирующие коэффициенты $\{ a_{{j + 1}}^{y}\} $ или $\{ \tilde {a}_{{j + 1}}^{y}\} $ в зависимости от фильтров в формулах (161), (165)–(167), (172)–(175), то следующий этап ОДВП может быть проведен с учетом частотно-временных особенностей наблюдаемого сигнала y(t), частотной функции отклика $\hat {\lambda }(\omega )$ или фильтра с частотным откликом $\hat {D}(\omega )$. При этом на последнем этапе восстановления должны применяться формулы, обеспечивающие восстановление ${{\tilde {x}}_{{P\,,n}}}$.

9. Визуализация и интерпретация результатов. Оценка погрешности решения задачи. Полученный результат визуализируется и подвергается дальнейшей обработке (статистической, сравнительной, эмпирической и т.д.) с целью более полного изучения предмета исследования и оценки погрешности решения задачи.

ВЫВОДЫ

Обосновано применение вейвлетных подходов при восстановлении полезного сигнала в случае представления измерительного процесса сверточной моделью. Для реализации алгоритма решения задачи (1) предлагается использовать ортогональные вейвлеты Кравченко с финитным спектром [25–28]. Показано, что можно выполнить модификацию вейвлетов с компактным носителем в частотной области таким образом, чтобы стало возможным проводить оценку полезного сигнала ${{\tilde {x}}_{P}}(t)$ по наблюдаемому сигналу $y(t)$ в рамках быстрых вычислительных алгоритмов на основе ДВП. Предложен и обоснован способ получения новых биортогональных частотно-модифицированных вейвлетов, формирующих две цепочки КМА на основе модифицирующей функции с частотным откликом $\hat {D}(\omega )$. Функция $\hat {D}(\omega )$ позволяет осуществлять построение вейвлетов с учетом стабилизации решения интегрального уравнения типа свертки (1) и эффективного подавления шума. Получены несколько видов масштабирующих уравнений и формулы вычисления вейвлет-коэффициентов для этих уравнений. Предлагаемые биортогональные частотно-модифицированные вейвлеты нестационарны по отношению к масштабу, т.е. они не являются результатом сдвига и масштабирования одной масштабирующей и вейвлетной функций. Однако они формируют эффективный кратномасштабный алгоритм аппроксимации решения интегрального уравнения типа свертки (1). Полученные вейвлетные системы позволяют при ДВП и ОДВП оптимизировать процесс получения и восстановления вейвлет-коэффициентов с точки зрения компенсации частотно-временных особенностей наблюдаемого сигнала y(t), частотной функции отклика $\hat {\lambda }(\omega )$ или фильтра с частотным откликом $\hat {D}(\omega )$. Предложены несколько вариантов ДВП и ОДВП на основе новых биортогональных частотно-модифицированных вейвлетов, которые можно использовать в различных физических приложениях.