Радиотехника и электроника, 2020, T. 65, № 4, стр. 317-329
Новый тип резонатора-накопителя для компрессора электромагнитных импульсов
П. Н. Мележик a, Ю. К. Сиренко a, *
a Институт радиофизики и электроники им. А.Я. Усикова Национальной академии наук Украины
61085 Харьков, ул. Академика Проскуры, 12, Украина
* E-mail: yks2002sky@gmail.com
Поступила в редакцию 12.06.2019
После доработки 20.06.2019
Принята к публикации 25.06.2019
Аннотация
Изучена возможность использования резонатора-накопителя нового типа – открытого резонатора, рабочее колебание в котором формируется встречными поверхностными волнами открытого диэлектрического волновода, в активном компрессоре электромагнитных импульсов. Детально рассмотрена простейшая модель такого устройства, однако результаты, полученные при ее строгом электродинамическом анализе, позволяют сделать вывод о том, что данное устройство перспективно для использования при решении ряда актуальных задач физики и техники миллиметровых и субмиллиметровых волн.
ВВЕДЕНИЕ
В работе [1] впервые были представлены и реализованы основные принципы модельного синтеза активных прямоточных компрессоров электромагнитных импульсов на отрезках регулярных круглых и коаксиальных волноводов. Дальнейшее развитие эти исследования получили в работах [2–6], в которых впервые строго рассчитаны динамические характеристики накопителей на отрезках прямоугольных и круглых волноводов; синтезированы замки́, позволяющие эффективно, быстро и в нужное время сбрасывать накопленную энергию в отводящие волноводы и в свободное пространство; предложены новые схемы формирования и излучения мощных, коротких, направленных радиоимпульсов; рассмотрены ключевые вопросы, связанные с возможностью использования для накопления энергии открытых резонансных систем. Основной итог проведенных исследований заключается в демонстрации важности достоверного электродинамического моделирования, обоснованного численного анализа и оптимизации процессов, реализуемых в активных компрессорах. Было показано, что для создания устройств с заданными характеристиками, необходимо широкомасштабное моделирование, что позволяют значительно упростить и сделать гораздо менее затратным поиск оптимальных конструкций.
Метод точных поглощающих условий (Method of Exact Absorbing Conditions, EAC-метод) [2, 6–15] – его модели использовались в [1–6] – по-видимому, лучше других популярных методов вычислительной электродинамики, базирующихся на дискретизации начально-краевых задач [16, 17], пространство счета которых ограничивается приближенными или эвристическими поглощающими условиями [18–24], приспособлен для решения задач анализа и синтеза активных компрессоров и их функциональных узлов. Он достаточно быстрый и не искажает физику моделируемых процессов. Его вычислительные схемы устойчивы и практически без потерь в точности пробегают миллионы и десятки миллионов временных слоев, необходимость просмотра которых диктуется спецификой рассматриваемых задач [16]. EAC-метод мы используем и в данной работе. Ее основное содержание связано с моделированием и анализом компрессора с накопителем нового типа – открытым резонатором, рабочее колебание в котором формируется встречными поверхностными волнами открытого диэлектрического волновода. Такой компрессор можно было бы ориентировать на работу в миллиметровом диапазоне длин волн. Его тепловые потери значительно меньше, а дифракционные потери сравнимы с теми, которые характерны для компрессоров с резонатором-накопителем в виде отрезка регулярного металлического волновода. Важно также и то, что при стандартном способе подачи энергии в такой накопитель из питающего волновода через запредельную диафрагму в нем не возбуждаются колебания с поперечным индексом бóльшим единицы – фактический спектр открытого резонатора даже с больши́м поперечным размером оказывается хорошо разреженным.
Мы используем систему СИ для всех физических параметров, за исключением “времени” $t$ (измеряется в метрах) – его величина определяется произведением истинного времени и скорости распространения света в вакууме. В статье размерности опущены, т.е. все результаты приведены для линейных размеров объектов и длин волн, заданных в метрах. Очевидно, что эти результаты при использовании стандартных методов масштабирования могут быть распространены и на любые другие геометрически подобные структуры.
1. КРАТКОЕ ОПИСАНИЕ РАССМАТРИВАЕМЫХ ОБЪЕКТОВ И ИХ ЭЛЕКТРОДИНАМИЧЕСКОЙ МОДЕЛИ
Анализ рассматриваемого модельного двумерного объекта – компактного в плоскости $y0z$ и бесконечного, однородного в направлении $x$ открытого резонатора с виртуальным питающим плоско-параллельным волноводом ${{\Omega }_{1}}$ (рис. 1) – проводится на основе численного решения начально-краевой задачи [3, 4, 6]:
(1)
$\left\{ \begin{gathered} \left[ { - \varepsilon \left( g \right)\partial _{t}^{2} - {{\eta }_{0}}P + \partial _{y}^{2} + \partial _{z}^{2}} \right]U\left( {g,t} \right) = 0; \hfill \\ t > 0,\,\,\,\,g \in {{\Omega }_{{{\text{внут}}}}} \hfill \\ {{\left. {U\left( {g,t} \right)} \right|}_{{t = 0}}} = 0,\;\;\;\;\;{{\left. {{{\partial }_{t}}U\left( {g,t} \right)} \right|}_{{t = 0}}} = 0; \hfill \\ g = \left\{ {y,z} \right\} \in {{\Omega }_{{{\text{внут}}}}} \hfill \\ {{{\vec {E}}}_{{{\text{tg}}}}}\left( {q,t} \right)\,\,\,\,{\text{и}}\,\,\,\,{{{\vec {H}}}_{{{\text{tg}}}}}\left( {q,t} \right) \hfill \\ {\text{непрерывны при пересечении}}\,\,\,{{\Sigma }^{{\varepsilon ,\sigma }}}, \hfill \\ {{\left. {{{{\vec {E}}}_{{{\text{tg}}}}}\left( {q,t} \right)} \right|}_{{q = \left\{ {x,y,z} \right\} \in \Sigma }}} = 0\,\,\,\,{\text{и}}\,\,\,\,{{\left. {D\left[ {U\left( {g,t} \right)} \right]} \right|}_{{g \in \Gamma }}} = 0, \hfill \\ {{\left. {{{D}_{1}}\left[ {U\left( {g,t} \right) - U_{p}^{i}\left( {g,t} \right)} \right]} \right|}_{{g \in {{\Gamma }_{1}}}}} = 0,\,\,\,\,t \geqslant 0. \hfill \\ \end{gathered} \right.$Рис. 1.
Геометрия задачи: структура симметрична относительно плоскости $\tilde {y} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$; толщина диафрагмы, отделяющей резонансный объем от питающего волновода, равна 0.02; толщина зеркал и металлических стенок волновода – 0.1. На условных границах I…IV рассчитывается энергия, излучаемая в свободное пространство (в область ${{\Omega }_{{{\text{внеш}}}}}$).
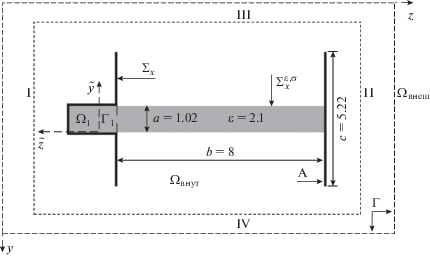
Здесь в случае E-поляризации поля (∂x ≡ 0, ${{E}_{y}} = {{E}_{z}} = {{H}_{x}} \equiv 0$) неизвестная действительная функция $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$ и $P\left[ U \right]$ ≡ $ \equiv {{\partial }_{t}}\left[ {\sigma \left( {g,t} \right)U\left( {g,t} \right)} \right]$, а в случае $H$-поляризации (${{\partial }_{x}} \equiv 0$, ${{H}_{y}} = {{H}_{z}} = {{E}_{x}} \equiv 0$) – $U\left( {g,t} \right) = {{H}_{x}}\left( {g,t} \right)$ и $P\left[ U \right] \equiv \sigma \left( {g,t} \right){{\partial }_{t}}U\left( {g,t} \right);$ $\vec {E}\left( {g,t} \right)$ = $\left\{ {{{E}_{x}},{{E}_{y}},{{E}_{z}}} \right\}$ и $\vec {H}\left( {g,t} \right)$ = $\left\{ {{{H}_{x}},{{H}_{y}},{{H}_{z}}} \right\}$ – векторы напряженности электрического и магнитного поля соответственно; $\varepsilon \left( g \right)$ и $\sigma \left( {g,t} \right)$ (кусочно-постоянные функции пространственных координат) – относительная диэлектрическая проницаемость и удельная проводимость немагнитной и недисперсной среды распространения волн; ${{\eta }_{0}} = {{\left( {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – импеданс свободного пространства; ${{\varepsilon }_{0}}$ и ${{\mu }_{0}}$ – электрическая и магнитная постоянные вакуума; $\Sigma = {{\Sigma }_{x}} \times \left[ {\left| x \right| \leqslant \infty } \right]$ и ${{\Sigma }^{{\varepsilon ,\sigma }}} = \Sigma _{x}^{{\varepsilon ,\sigma }} \times \left[ {\left| x \right| \leqslant \infty } \right]$ – поверхности идеальных проводников и поверхности разрыва функций $\varepsilon \left( g \right)$ и $\sigma \left( {g,t} \right)$; ${{\Omega }_{{{\text{внут}}}}}$ – область анализа задачи (1), ограниченная контурами ${{\Sigma }_{x}}$ и виртуальными границами ${{\Gamma }_{1}}$, $\Gamma $ (см. рис. 1).
Резонатор возбуждается через виртуальную границу ${{\Gamma }_{1}}$ в поперечном сечении питающего волновода ${{\Omega }_{1}}$ импульсной $T{{E}_{{0p}}}$- или $T{{M}_{{0p}}}$-волной
Здесь $\tilde {g} = \left\{ {\tilde {y},\tilde {z}} \right\}$ – локальная система координат, связанная с виртуальным волноводом ${{\Omega }_{1}}$ (см. рис. 1); ${{v}_{p}}\left( {\tilde {z},t} \right)$ – пространственно-временные амплитуды волны $U_{p}^{i}\left( {\tilde {g},t} \right)$; ${{\mu }_{p}}\left( {\tilde {y}} \right) = \sqrt {{2 \mathord{\left/ {\vphantom {2 a}} \right. \kern-0em} a}} \sin \left( {{{\lambda }_{p}}\tilde {y}} \right)$ ($p = 1,2,3,...$) в случае $E$-поляризации и ${{\mu }_{p}}\left( {\tilde {y}} \right)$ = $ = \sqrt {{{\left( {2 - \delta _{0}^{p}} \right)} \mathord{\left/ {\vphantom {{\left( {2 - \delta _{0}^{p}} \right)} a}} \right. \kern-0em} a}} \cos \left( {{{\lambda }_{p}}\tilde {y}} \right)$ ($p = 0,1,2,...$) в случае $H$-поляризации; ${{\lambda }_{p}} = {{p\pi } \mathord{\left/ {\vphantom {{p\pi } a}} \right. \kern-0em} a}$; $\delta _{0}^{p}$ – символ Кронекера.
Точные поглощающие условия ${{\left. {D\left[ {U\left( {g,t} \right)} \right]} \right|}_{{g \in \Gamma }}} = 0$ и ${{\left. {{{D}_{1}}\left[ {U\left( {g,t} \right) - U_{p}^{i}\left( {g,t} \right)} \right]} \right|}_{{g \in {{\Gamma }_{1}}}}} = 0$ на виртуальных границах ${{\Gamma }_{1}}$ и $\Gamma $ являются ключевыми элементами корректно поставленной начально-краевой задачи (1). С их помощью классическая принципиально открытая задача, описывающая пространственно-временные трансформации электромагнитных волн в объектах, подобных рассматриваемым, превращается в эквивалентную закрытую задачу [6, 12], т.е. в задачу, которую можно решить численно стандартными сеточными методами [16, 17]. Соответствующие результаты $f\left( t \right)$ легко конвертируются в необходимые для анализа амплитудно-частотные характеристики $\tilde {f}\left( k \right)$ с использованием преобразования
Здесь $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число ($\lambda $ – длина волны в свободном пространстве), $0 < T < \infty $ – верхний предел интервала времени наблюдения. Подробное изложение теории EAC-метода, приемов эффективного счета при его реализации, а также аналитическую форму точных поглощающих условий, представленных здесь интегро-дифференциальными операторами $D\left[ {...} \right]$ и ${{D}_{1}}\left[ {...} \right]$, можно найти в работах [2, 6–15].
2. РЕЗОНАТОР-НАКОПИТЕЛЬ – ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
Пусть ширина $d$ окна диафрагмы равна 0.3. Возбудим резонатор импульсной $T{{E}_{{01}}}$-волной ($E$-поляризация поля) со следующими характеристиками:
(2)
$\begin{gathered} U_{1}^{i}\left( {\tilde {g},t} \right):{{v}_{1}}\left( {0,t} \right) = 4\sin \left[ {\Delta k\left( {t - \tilde {T}} \right)} \right] \times \\ \times \,\,{{\left( {t - \tilde {T}} \right)}^{{ - 1}}}\cos \left[ {\tilde {k}\left( {t - \tilde {T}} \right)} \right]\chi \left( {\bar {T} - t} \right) = {{F}_{1}}\left( t \right); \\ \tilde {k} = 4.0,\,\,\,\,\Delta k = 1.6,\,\,\,\,\tilde {T} = 75,\,\,\,\,\bar {T} = 150. \\ \end{gathered} $Здесь и дальше $\chi \left( {...} \right)$ – ступенчатая функция Хевисайда, $\tilde {k}$ – центральная частота сигнала, $\tilde {T}$ и $\bar {T}$ – его время запаздывания и длительность. Параметр $\Delta k$ определяет полосу частот $\tilde {k} - \Delta k \leqslant k \leqslant \tilde {k} + \Delta k$ ($2.4 \leqslant k \leqslant 5.6$) [2, 8], которую занимает волна (2). Для значений $k$ из этой полосы из всех $T{{E}_{{0n}}}$-волн, отраженных в питающий волновод ${{\Omega }_{1}}$, одна только $T{{E}_{{01}}}$-волна $U_{1}^{s}\left( {\tilde {g},t} \right)$ = $ = {{u}_{1}}\left( {\tilde {z},t} \right){{\mu }_{1}}\left( {\tilde {y}} \right)$ распространяется здесь без затухания. Ее критическая частота $k_{1}^{ + } \approx 2.1254$. Критическая частота $k_{2}^{ + } \approx 4.2508$ $T{{E}_{{02}}}$-волны также попадает в просматриваемый диапазон частот $2.4 \leqslant k \leqslant 5.6$ ($1.12 < \lambda < 2.62$), но эта волна не возбуждается вследствие симметрии структуры и первичной волны $U_{1}^{i}\left( {\tilde {g},t} \right)$. По этой же причине поля всех возбуждаемых в резонаторе колебаний симметричны относительно плоскости $\tilde {y} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$. Диафрагма, связывающая резонансный объем и питающий волновод, остается запредельной до значения $k \approx 7.2263$.
Рассчитаем функцию $U\left( {g,t} \right)$, $0 < t \leqslant T = 2000$ в точке $g = {{g}_{1}}$, лежащей в плоскости симметрии структуры на равных расстояниях от ее зеркал. Затем согласно [2, 8, 25–28] определим по резонансам на кривых $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tilde {U}} \left( {{{g}_{1}},k} \right) \leftrightarrow U\left( {{{g}_{1}},t} \right)$ $\chi \left( {t - \bar {T}} \right)\chi \left( {T - t} \right)$ (рис. 2) действительные части комплексных собственных частот $\bar {k} = \operatorname{Re} \bar {k} + i\operatorname{Im} \bar {k}$ ($2.4 \leqslant \operatorname{Re} \bar {k} \leqslant 5.6$, $\operatorname{Im} \bar {k} < 0$) резонатора, которым отвечают ${{H}_{{0,1,m}}}$ свободные колебания поля с нечетным значением индекса $m$ (с нечетным числом вариаций поля вдоль оси $z$). Колебания ${{H}_{{0,n,m}}}$ с нечетным значением $n$, большим единицы, не возбуждаются в случае как нечетных, так и четных $m$. В этом заключается одно из основных отличий рассматриваемого резонатора от других подобных ему достаточно добротных резонаторов – конфокального и полуконфокального [2, 5, 28].
Рис. 2.
Спектральные амплитуды свободных симметричных колебаний поля в резонаторе, возбужденных широкополосным $T{{E}_{{01}}}$-импульсом (2). Стрелками показано положение величин $\operatorname{Re} \bar {k}$, отвечающих ${{H}_{{0,1,m}}}$ свободным колебаниям поля.
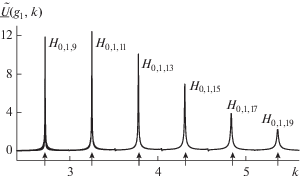
Остановимся подробней на анализе первых трех колебаний, которым на рис. 2 отвечают наибольшие спектральные амплитуды (спектральные амплитуды импульса ${{F}_{1}}\left( t \right)$ распределены на интервале $\tilde {k} - \Delta k$ ≤ $k \leqslant \tilde {k} + \Delta k$ практически равномерно [2, 8]). Действительные части их собственных частот равны соответственно $\operatorname{Re} {{\bar {k}}_{1}} \approx 2.721$ (колебание ${{H}_{{0,1,9}}}$), $\operatorname{Re} {{\bar {k}}_{2}} \approx 3.251$ (${{H}_{{0,1,11}}}$) и $\operatorname{Re} {{\bar {k}}_{3}} \approx 3.778$ (${{H}_{{0,1,13}}}$). Конфигурацию поля и добротность $Q = {{\operatorname{Re} \bar {k}} \mathord{\left/ {\vphantom {{\operatorname{Re} \bar {k}} {2\left| {\operatorname{Im} \bar {k}} \right|}}} \right. \kern-0em} {2\left| {\operatorname{Im} \bar {k}} \right|}}$ этих колебаний определяем, возбуждая резонатор узкополосным гауссовским импульсом:
(3)
$\begin{gathered} U_{1}^{i}\left( {\tilde {g},t} \right):{{v}_{1}}\left( {0,t} \right) = \exp \left[ {{{ - {{{\left( {t - \tilde {T}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {t - \tilde {T}} \right)}}^{2}}} {4{{{\tilde {\alpha }}}^{2}}}}} \right. \kern-0em} {4{{{\tilde {\alpha }}}^{2}}}}} \right] \times \\ \times \,\,\cos \left[ {\tilde {k}\left( {t - \tilde {T}} \right)} \right]\chi \left( {\bar {T} - t} \right) = {{F}_{2}}\left( t \right); \\ \tilde {k} = \operatorname{Re} \bar {k},\,\,\,\,\tilde {\alpha } = 40,\,\,\,\,\tilde {T} = 150,\,\,\,\,\bar {T} = 150, \\ T = 800. \\ \end{gathered} $После выключения источника в поле резонатора доминирует колебание, действительная часть собственной частоты $\bar {k}$ которого задает центральную частоту $\tilde {k}$ сигнала ${{F}_{2}}\left( t \right)$, а поведение модуля огибающей $A\exp \left[ {\operatorname{Im} \bar {k}\left( {t - \bar {T}} \right)} \right]$ функции $U\left( {{{g}_{1}},t} \right)\chi \left( {t - \bar {T}} \right)\chi \left( {T - t} \right),$ $\bar {T} < t \leqslant T$ однозначно определяет величину $\operatorname{Im} \bar {k}$ (рис. 3, см. также работы [2, 8, 25–28]). Результаты, полученные в описанных выше экспериментах, приведены в табл. 1.
Рис. 3.
Возбуждение резонатора импульсной волной (3). Конфигурация полей свободных колебаний (распределение значений ${{E}_{x}}\left( {g,t} \right) = U\left( {g,t} \right)$, $g \in {{\Omega }_{{{\text{внут}}}}}$, $t = 800$) (а) и амплитуды функций ${{E}_{x}}\left( {{{g}_{1}},t} \right) = U\left( {{{g}_{1}},t} \right)$ (б).
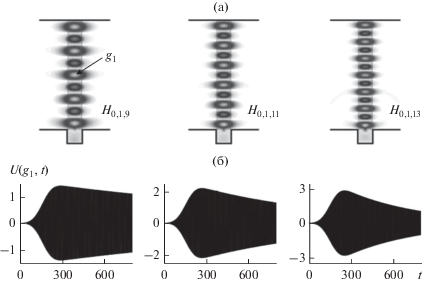
Таблица 1.
Часть спектральных характеристик резонатора с шириной $d$ окна диафрагмы, равной 0.3
| Колебание | Собственная частота | Добротность |
|---|---|---|
| ${{H}_{{0,1,9}}}$ | ${{\bar {k}}_{1}} \approx 2.721 - i0.0004863$ | ${{Q}_{1}} \approx 2798$ |
| ${{H}_{{0,1,11}}}$ | ${{\bar {k}}_{2}} \approx 3.251 - i0.001057$ | ${{Q}_{2}} \approx 1537$ |
| ${{H}_{{0,1,13}}}$ | ${{\bar {k}}_{3}} \approx 3.778 - i0.001933$ | ${{Q}_{3}} \approx 977$ |
Способность резонатора накапливать энергию при использовании в качестве рабочего одного из трех рассмотренных колебаний будем оценивать в рамках следующего вычислительного эксперимента (рис. 4). Возбуждаем структуру длинным квазимонохроматическим импульсом
(4)
$\begin{gathered} U_{1}^{i}\left( {\tilde {g},t} \right):{{v}_{1}}\left( {0,t} \right) = P\left( t \right)\cos \left[ {\tilde {k}\left( {t - \tilde {T}} \right)} \right] = {{F}_{3}}\left( t \right); \\ \tilde {k} = \operatorname{Re} \bar {k},\,\,\,\,\tilde {T} = 0.5,\,\,\,\,P\left( {t;0.01,5,4995,5000} \right), \\ \end{gathered} $Рис. 4.
Возбуждение резонатора длинным квазимонохроматическим импульсом (4). Амплитуды ${{{v}}_{1}}\left( {0,t} \right)$ первичной волны при мелком и крупном временном шаге (а), функции ${{u}_{1}}\left( {0,t} \right)$, ${{E}_{x}}\left( {{{g}_{1}},t} \right) = U\left( {{{g}_{1}},t} \right)$ и ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$, характеризующие процесс накопления энергии на временном интервале $0 < t \leqslant 5000$ и в трех различных свободных колебаниях поля: $\tilde {k} = 2.721$ (б), $\tilde {k} = 3.251$ (в) и $\tilde {k} = 3.778$ (г).
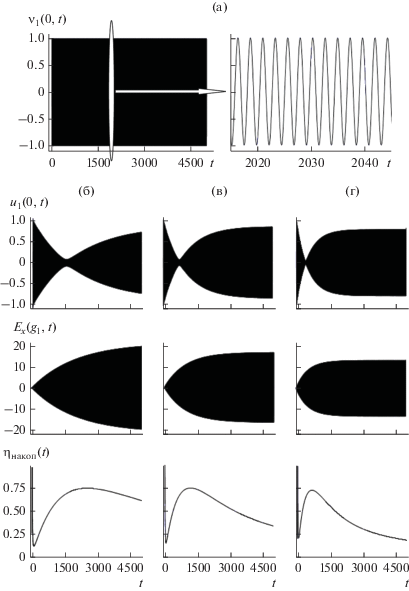
где $P\left( {t;{{T}_{1}},{{T}_{2}},{{T}_{3}},{{T}_{4}}} \right)\;\;$ – трапециевидная огибающая, равная единице при ${{T}_{2}} < t < {{T}_{3}}$ и нулю при $t < {{T}_{1}}$ и $t > {{T}_{4}} = \bar {T}$. Динамика реализуемого физического процесса достаточно полно характеризуется [1–3] следующими факторами:
– поведением пространственно-временных амплитуд ${{u}_{1}}\left( {0,t} \right)$ $T{{E}_{{01}}}$-волны, отраженной в питающий волновод;
– параметрами роста амплитуд функции $U\left( {{{g}_{1}},t} \right) = {{E}_{x}}\left( {{{g}_{1}},t} \right)$ – напряженности поля в пучности поля рабочего колебания;
– изменением функции ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$ = ${{ = \left[ {{{W}^{i}}\left( {t;0} \right) - {{W}^{s}}\left( {t;0} \right) - {{W}^{{{\text{изл}}}}}\left( {t;0} \right)} \right]} \mathord{\left/ {\vphantom {{ = \left[ {{{W}^{i}}\left( {t;0} \right) - {{W}^{s}}\left( {t;0} \right) - {{W}^{{{\text{изл}}}}}\left( {t;0} \right)} \right]} {{{W}^{i}}\left( {t;0} \right)}}} \right. \kern-0em} {{{W}^{i}}\left( {t;0} \right)}}$ – мгновенной эффективности накопления подводимой энергии в поле рабочего колебания;
– достигнутым к моменту времени $t$ уровнем напряженности поля в пучности поля рабочего колебания
Здесь ${{W}^{i}}\left( {{{t}_{2}};{{t}_{1}}} \right)$, ${{W}^{s}}\left( {{{t}_{2}};{{t}_{1}}} \right)$ и ${{W}^{{{\text{изл}}}}}\left( {{{t}_{2}};{{t}_{1}}} \right)$ = $ = W_{{\text{I}}}^{{{\text{изл}}}}\left( {{{t}_{2}};{{t}_{1}}} \right)$ + $W_{{{\text{II}}}}^{{{\text{изл}}}}\left( {{{t}_{2}};{{t}_{1}}} \right)$ + $W_{{{\text{III}}}}^{{{\text{изл}}}}\left( {{{t}_{2}};{{t}_{1}}} \right)$ + $ + \,\,W_{{{\text{IV}}}}^{{{\text{изл}}}}\left( {{{t}_{2}};{{t}_{1}}} \right)$ – энергия, подведенная к накопителю через виртуальную границу ${{\Gamma }_{1}}$, отведенная через эту же границу в питающий волновод ${{\Omega }_{1}}$ и излученная в свободное пространство через условные границы I…IV за промежуток времени ${{t}_{1}} \leqslant t \leqslant {{t}_{2}}$. Все эти величины определяются интегрированием по $t$ в интервале ${{t}_{1}} \leqslant t \leqslant {{t}_{2}}$ значений мгновенных мощностей, “переносимых” через соответствующие границы (см. работы [1–3] и рис. 1).
На рис. 4 приведены данные о трех характеристиках из четырех перечисленных выше: функции ${{u}_{1}}\left( {0,t} \right)$ отражают основные мгновенные потери подводимой энергии, связанные с возбуждением отраженных в питающий волновод $T{{E}_{{01}}}$-волн; функции $U\left( {{{g}_{1}},t} \right) = {{E}_{x}}\left( {{{g}_{1}},t} \right)$ предопределяют мгновенный уровень амплитуды сигнала, на который можно выйти в результате компрессии, скорость нарастания этого уровня и его предельные значения. Вместе функции ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$ и $U\left( {{{g}_{1}},t} \right)$ позволяют судить о том, в какой момент времени следует останавливать процесс накопления и определяют длительность $\bar {T}$ возбуждающего импульса, превысив которую мы существенно понизим эффективность устройства, не добившись значительного роста амплитуды сжатого импульса. Четвертая характеристика, $\alpha \left( t \right)$, – вспомогательная (не приводится здесь), значения соответствующих функций полностью определяются поведением (наблюдаемым и прогнозируемым) огибающих функций $U\left( {{{g}_{1}},t} \right)$.
При фиксированной добротности резонатора-накопителя (при фиксированном размере окна связи и конкретном выборе рабочего колебания) эффективность накопления зависит только от длительности накачки, а характер этой (достаточно сложной) зависимости практически одинаков для резонаторов с большей и меньшей добротностью (см. рис. 4 и работы [2, 3, 6]). Повышение добротности приводит к удлинению временного интервала, необходимого для выхода на то же значение ${{\eta }_{{{\text{накоп}}}}}$ и к росту предельного значения амплитуды формируемого в накопителе сигнала.
Как видно, вариантов, которые необходимо критически оценить при модельном синтезе компрессоров, достаточно много, но без такого исследования создание эффективно работающих устройств невозможно. Первый и важный шаг в этом направлении, как подсказывает сравнение рассмотренных характеристик и характеристик накопителей на отрезках закрытых волноводов [2, 3, 6], должен обеспечить существенное повышение добротности рабочего колебания в резонаторе-накопителе на встречных поверхностных волнах диэлектрического волновода. Нужный результат можно получить, изменяя параметр $d$ – ширину окна диафрагмы или ширину окна связи резонансного объема с питающим волноводом. Положим $d = 0.22$ (диафрагма остается запредельной до значения $k \approx 9.8541$). Электродинамические характеристики структуры приведены в табл. 2 и на рис. 5. Представленные данные позволяют остановиться на варианте резонатора-накопителя с $d = 0.22$ и перейти к анализу физических особенностей в процессах, связанных не только с компрессией энергии длинных монохроматических импульсов, но и с ее излучением в коротких мощных радиоимпульсах. Для этого используем простейшие модели, которые в дальнейшем при решении задач синтеза можно будет сделать более реалистичными, отвечающими конкретным требованиям, вытекающим из предполагаемых условий эксплуатации создаваемых устройств.
Таблица 2.
Часть спектральных характеристик резонатора с шириной $d$ окна диафрагмы, равной 0.22
| Колебание | Собственная частота | Добротность |
|---|---|---|
| ${{H}_{{0,1,9}}}$ | ${{\bar {k}}_{1}} \approx 2.7245 - i0.0001122$ | ${{Q}_{1}} \approx 12132$ |
| ${{H}_{{0,1,11}}}$ | ${{\bar {k}}_{2}} \approx 3.2555 - i0.0002355$ | ${{Q}_{2}} \approx 6910$ |
| ${{H}_{{0,1,13}}}$ | ${{\bar {k}}_{3}} \approx 3.784 - i0.0004186$ | ${{Q}_{3}} \approx 4520$ |
Рис. 5.
Возбуждение резонатора-накопителя с шириной окна связи $d = 0.22$ импульсом (4). Функции ${{u}_{1}}\left( {0,t} \right)$, ${{E}_{x}}\left( {{{g}_{1}},t} \right) = U\left( {{{g}_{1}},t} \right)$ и ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$, характеризующие процесс накопления энергии в трех различных свободных колебаниях поля: $\tilde {k} = 2.7245$ (а), $\tilde {k} = 3.2555$ (б) и $\tilde {k} = 3.7840$ (в).
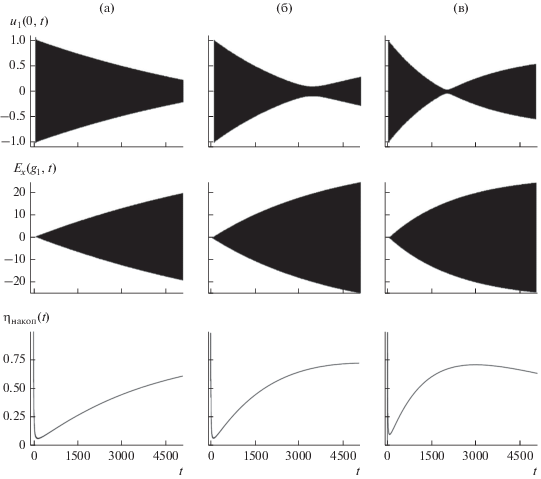
3. ФОРМИРОВАНИЕ И ИЗЛУЧЕНИЕ МОЩНЫХ КОРОТКИХ РАДИОИМПУЛЬСОВ
Предположим, что зеркало ${\text{A}}$ резонатора-накопителя (см. рис. 1) выполнено не из идеального металла, а из материала, относительная диэлектрическая проницаемость которого равна единице, а удельная проводимость $\sigma \left( {g,t} \right)$, равная $57\,000$ при $0 < t \leqslant \bar {T}$ и нулю при $t \geqslant \bar {T} + 1$, линейно убывает в моменты времени $\bar {T} \leqslant t \leqslant \bar {T} + 1$. Собственные частоты резонатора-накопителя и добротность отвечающих им свободных колебаний при такой модификации зеркала изменятся незначительно: новые значения $\operatorname{Re} \bar {k}$ для колебаний ${{H}_{{0,1,9}}}$, ${{H}_{{0,1,11}}}$ и ${{H}_{{0,1,13}}}$ равны соответственно $\operatorname{Re} {{\bar {k}}_{1}} = 2.7213$, $\operatorname{Re} {{\bar {k}}_{2}} = 3.2517$ и $\operatorname{Re} {{\bar {k}}_{3}} = 3.7795$.
Возбудим структуру длинным квазимонохроматическим импульсом $U_{1}^{i}\left( {\tilde {g},t} \right):{{v}_{1}}\left( {0,t} \right)$ = ${{F}_{3}}\left( t \right)$, $\tilde {k} = \operatorname{Re} \bar {k},$ $\tilde {T} = 0.5,$ $P\left( {t;0.01,5,\bar {T} - 5,\bar {T}} \right)$ (см. формулу (4)) и продлим время наблюдения $T$ до $T = \bar {T} + 100$. В момент времени $t = \bar {T} + 1$ зеркало ${\text{A}}$ компрессора полностью “откроется” и накопленная энергия должна выброситься в свободное пространство (в основном, через условную границу ${\text{II}}$) в виде мощного короткого радиоимпульса. Пространственная длительность такого импульса обычно лишь ненамного превышает удвоенную электрическую длину ($2b\sqrt \varepsilon \approx 23.2$) резонатора-накопителя [1–4, 6]. Время $\bar {T}$, исходя из результатов, представленных на рис. 5, выберем равным $\bar {T} = 10\,000.$ Результаты вычислительных экспериментов представлены на рис. 6–8.
Рис. 6.
Компрессор электромагнитных импульсов на колебании ${{H}_{{0,1,9}}}$ ($\tilde {k} = \operatorname{Re} {{\bar {k}}_{1}} = 2.7213$). Функции ${{u}_{1}}\left( {0,t} \right)$, ${{E}_{x}}\left( {{{g}_{1}},t} \right) = U\left( {{{g}_{1}},t} \right)$ и ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$, характеризующие процесс накопления энергии (а). Амплитуды излученного импульса $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$ в точках $g = {{g}_{j}}$, $j = 2,3,4$ (б). Распределение значений $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$, $g \in {{\Omega }_{{{\text{внут}}}}}$ в поле рабочего колебания в момент времени $t = 10000$ (в).
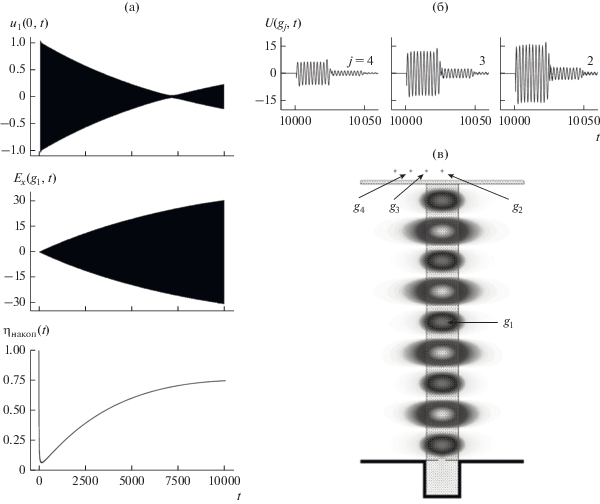
Рис. 7.
Компрессор электромагнитных импульсов на колебании ${{H}_{{0,1,11}}}$ ($\tilde {k} = \operatorname{Re} {{\bar {k}}_{2}} = 3.2517$). Функции ${{u}_{1}}\left( {0,t} \right)$, ${{E}_{x}}\left( {{{g}_{1}},t} \right) = U\left( {{{g}_{1}},t} \right)$ и ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$, характеризующие процесс накопления энергии (а). Амплитуды излученного импульса $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$ в точках $g = {{g}_{j}}$, $j = 2,3,4$ (б). Распределение значений $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$, $g \in {{\Omega }_{{{\text{внут}}}}}$ в поле компрессора с “открытым” зеркалом ${\text{A}}$ в момент времени $t = 10010$ (в).
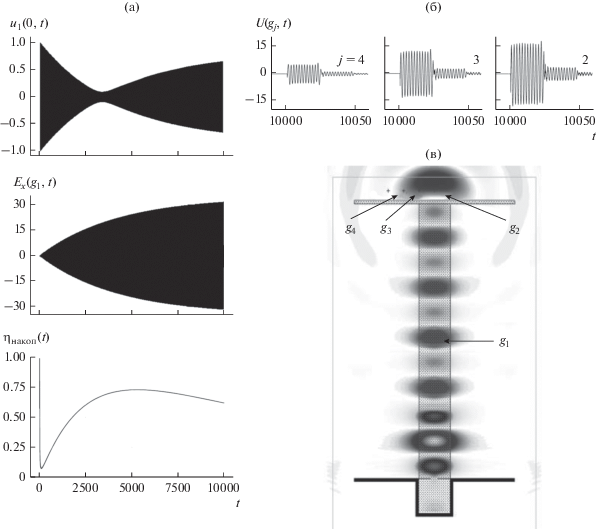
Рис. 8.
Компрессор электромагнитных импульсов на колебании ${{H}_{{0,1,13}}}$ ($\tilde {k} = \operatorname{Re} {{\bar {k}}_{3}} = 3.7795$). Функции ${{u}_{1}}\left( {0,t} \right)$, ${{E}_{x}}\left( {{{g}_{1}},t} \right) = U\left( {{{g}_{1}},t} \right)$ и ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$, характеризующие процесс накопления энергии (а). Амплитуды излученного импульса $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$ в точках $g = {{g}_{j}}$, $j = 2,3,4$ (б). Распределение значений $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$, $g \in {{\Omega }_{{{\text{внут}}}}}$ в поле компрессора с “открытым” зеркалом ${\text{A}}$ в момент времени $t = 10\,020$ (в).
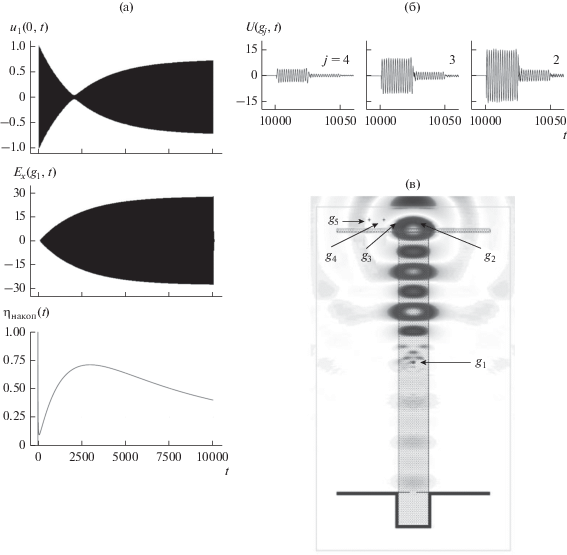
Левый ряд рисунков характеризует процесс накопления энергии, а правый – процесс ее излучения в свободное пространство. Длительность ${{\bar {T}}^{s}} \approx 24$ и амплитуды главной части излученных импульсов практически одинаковы для всех трех рассмотренных случаев (для компрессоров с отличающимися типами рабочих колебаний). За главными частями излученных импульсов следуют резко убывающие по амплитуде послеимпульсы такой же длительности, на которые в сумме приходится меньше 4% энергии, излученной в свободное пространство через границу ${\text{II}}$. Появление этих послеимпульсов связано с отражением от конца диэлектрического волновода вытекающих из накопителя волн в плоскости, в которой в течение всего процесса накопления располагалось металлическое зеркало. Излученный импульс сконцентрирован вблизи плоскости симметрии структуры – в большей степени для более высокой рабочей частоты компрессора.
При практически одинаковой степени компрессии $\beta = {{\bar {T}} \mathord{\left/ {\vphantom {{\bar {T}} {{{{\bar {T}}}^{s}}}}} \right. \kern-0em} {{{{\bar {T}}}^{s}}}} \approx 417$ значительно различаются показатели, характеризующие энергетическую эффективность устройства с накопителем, который использует в качестве рабочих разные свободные колебания поля (см. табл. 3; здесь рабочая частота ${{k}_{{{\text{раб}}}}} = \operatorname{Re} \bar {k}$, эффективность накопления – ${{\eta }_{{{\text{накоп}}}}}\left( {\bar {T}} \right)$, энергетическая эффективность компрессора – $\eta = {{W_{{{\text{II}}}}^{{{\text{изл}}}}\left( {\bar {T} + 3{{{\bar {T}}}^{s}};\bar {T}} \right)} \mathord{\left/ {\vphantom {{W_{{{\text{II}}}}^{{{\text{изл}}}}\left( {\bar {T} + 3{{{\bar {T}}}^{s}};\bar {T}} \right)} {{{W}^{i}}\left( {\bar {T};0} \right)}}} \right. \kern-0em} {{{W}^{i}}\left( {\bar {T};0} \right)}}$, усиление по мощности – $\theta = \beta \eta $). Очевидно (см. рис. 6–8), что при работе на более длинных интервалах времени накопления $0 < t \leqslant \bar {T}$ компрессор с колебаниями ${{H}_{{0,1,11}}}$ и ${{H}_{{0,1,13}}}$ может поднять амплитуды излучаемых импульсов лишь незначительно и только за счет значительного снижения показателей, характеризующих его энергетическую эффективность. У компрессора с рабочим колебанием H0,1,9 перспективы в этом отношении гораздо более благоприятные. Это подтверждают и результаты вычислительного эксперимента, приведенные на рис. 9. Здесь при ${{k}_{{{\text{раб}}}}} = \operatorname{Re} {{\bar {k}}_{1}}$ и повышении времени накопления до $\bar {T} = 15{\kern 1pt} {\kern 1pt} 000$ (степени компрессии до $\beta = {{\bar {T}} \mathord{\left/ {\vphantom {{\bar {T}} {{{{\bar {T}}}^{s}}}}} \right. \kern-0em} {{{{\bar {T}}}^{s}}}} \approx 625$) максимальная напряженность поля в накопителе выросла на 21%, амплитуды главной части излученного импульса – на 22.5%, а усиление по мощности – на 46% (до $\theta \approx 432$). Эффективность накопления понизилась лишь на 2.4% (до ${{\eta }_{{{\text{накоп}}}}}\left( {\bar {T}} \right) \approx 0.726$), а энергетическая эффективность компрессора – на 2.5% (до $\eta \approx 0.692$). В общем, эти характеристики компрессора даже выше тех, которые фиксировались в случае резонаторов-накопителей на отрезках регулярных прямоугольных и круглых волноводов [2, 3, 6].
Таблица 3.
Характеристики компрессора
| Колебание | Рабочая частота | Эффективность накопления | Энергетическая эффективность компрессора | Усиление по мощности |
|---|---|---|---|---|
| ${{H}_{{0,1,9}}}$ | 2.7213 | 0.744 | 0.71 | 296 |
| ${{H}_{{0,1,11}}}$ | 3.2517 | 0.62 | 0.592 | 247 |
| ${{H}_{{0,1,13}}}$ | 3.7795 | 0.4 | 0.38 | 158 |
Рис. 9.
Характеристики компрессора электромагнитных импульсов на колебании ${{H}_{{0,1,9}}}$ (${{k}_{{{\text{раб}}}}} = \tilde {k}$ = $\operatorname{Re} {{\bar {k}}_{1}} = 2.7213$, $\bar {T} = 15\,000$). Функции ${{u}_{1}}\left( {0,t} \right)$, ${{E}_{x}}\left( {{{g}_{1}},t} \right) = U\left( {{{g}_{1}},t} \right)$ и ${{\eta }_{{{\text{накоп}}}}}\left( t \right)$, характеризующие процесс накопления энергии (а). Амплитуды излученного импульса $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$ в точках $g = {{g}_{j}}$, $j = 2{\kern 1pt} - {\kern 1pt} 5$ (б).
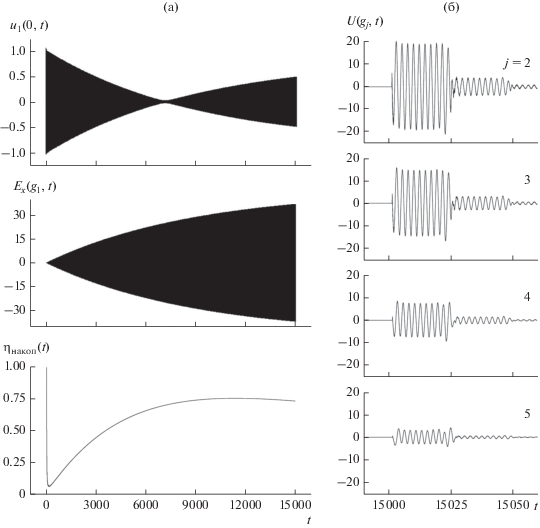
4. ВОЗМОЖНЫЕ СПОСОБЫ ИЗМЕНЕНИЯ ХАРАКТЕРИСТИК ИМПУЛЬСА, “ВЫБРОШЕННОГО” КОМПРЕССОРОМ
От послеимпульсов в излученном из компрессора поле, обусловленных отражением от конца диэлектрического волновода при “открытом” зеркале ${\text{A}}$, можно избавиться, изменив материальные параметры и геометрию (см. рис. 10, фрагмент б) модельной структуры следующим образом. Удельная проводимость $\sigma \left( {g,t} \right)$ открывающегося в моменты времени $\bar {T} \leqslant t \leqslant \bar {T} + 1$ зеркала ${\text{A}}$, как и раньше, изменяется на этом временном интервале от значения 57 000 до нуля. Но его относительная диэлектрическая проницаемость $\varepsilon \left( g \right)$ теперь равна единице только на крыльях, выступающих за диэлектрический волновод. В центральной части зеркала, примыкающей к торцу диэлектрического волновода, $\varepsilon \left( g \right) = 2.1$. За зеркалом ${\text{A}}$ диэлектрический волновод “продолжается” таким же диэлектрическим клином, длина которого равна 4.9. Таким образом, при открытом зеркале A (в режиме сброса накопленной энергии) мы получаем классический штыревой излучатель [2] в виде сужающейся на конце диэлектрической пластины, общая длина которого равна $8 + 0.1 + 4.9 = 13$.
Рис. 10.
Излучение короткого мощного радиоимпульса компрессором с модифицированной геометрией (${{k}_{{{\text{раб}}}}} = \tilde {k}$ = = $\operatorname{Re} {{\bar {k}}_{1}} = 2.7213$, $\bar {T} = 15\,000$). Амплитуды излученного импульса $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$ в точках $g = {{g}_{j}}$, $j = 6{\kern 1pt} - {\kern 1pt} 9$ (а). Распределение значений $U\left( {g,t} \right) = {{E}_{x}}\left( {g,t} \right)$, $g \in {{\Omega }_{{{\text{внут}}}}}$ в поле компрессора с “открытым” зеркалом ${\text{A}}$ в моменты времени $t = 15\,000$ (б), $t = 15\,010$ (в) и $t = 15\,020$ (г).
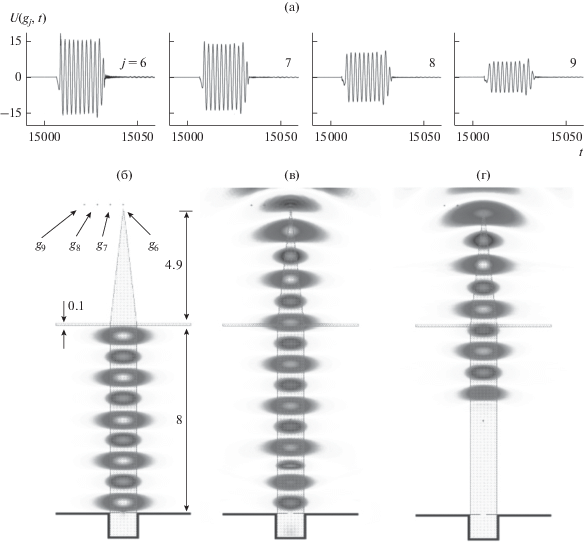
Накачивая модифицированный таким образом компрессор длинным квазимонохроматическим импульсом ($\tilde {k} = {{k}_{{{\text{раб}}}}} = \operatorname{Re} {{\bar {k}}_{1}}$, $\bar {T} = 15000$), приходим к результатам, представленным на рис. 10. После импульсы в излученном компрессором поле исчезли; направленность излучения улучшилась (сравнение характера убывания предельных амплитуд функций $U\left( {g,t} \right)$ в точках $g = {{g}_{j}}$, j = 6…9 на рис. 10 и в точках $g = {{g}_{j}}$, j = 2…5 на рис. 9 позволяет говорить о заметном выравнивании фронта излученной волны); электромагнитное поле из объема накопителя практически полностью излучается за время, равное удвоенной электрической длине резонатора и пространственной длительности ${{\bar {T}}^{s}}$ излученного импульса (см. нижние фрагменты рис. 10: распределение значений ${{E}_{x}}\left( {g,t} \right) = U\left( {g,t} \right)$, $g \in {{\Omega }_{{{\text{внут}}}}}$ в моменты времени $t = 15\,000$, $t = 15\,010$ и $t = 15\,020$).
ЗАКЛЮЧЕНИЕ
Таким образом, показано, что открытые резонаторы, свободные колебания поля в которых формируются встречными поверхностными волнами диэлектрических волноводов, могут быть использованы в качестве накопителей активных компрессоров электромагнитных импульсов миллиметрового и субмиллиметрового диапазонов длин волн. Результаты получены в вычислительных экспериментах с упрощенными, идеализированными моделями, на которых изучены принципиальные для реальных устройств особенности процессов накопления энергии, формирования и направленного излучения мощных коротких радиоимпульсов. Предполагается, что все функционально значимые детали создаваемых устройств будут включаться в расчетные модели на этапе их оптимизации.
Список литературы
Kuzmitchev I., Melezhyk P., Pazynin V. et al. // Радиофизика и электроника. 2008. Т. 13. № 2. С. 166.
Кравченко В., Сиренко Ю., Сиренко К. Преобразование и излучение электромагнитных волн открытыми резонансными структурами. М.: Физматлит, 2011.
Sirenko K., Pazynin V., Sirenko Y., Bagci H. // Progress in Electromagnetics Research. 2011. V. 116. P. 239.
Sirenko K., Pazynin V., Sirenko Y., Bagci H. // Progress in Electromagnetics Research. 2011. V. 116. P. 271.
Burambayeva N., Sautbekov S., Sirenko Y., Vertiy A. // Telecommunications and Radio Engineering. 2015. V. 74. № 1. P. 29.
Electromagnetic Waves in Complex Systems: Selected Theoretical and Applied Problems / Eds. Sirenko Y., Velychko L. N.Y.: Springer, 2016.
Sirenko K., Sirenko Y. // Computational Mathem. Mathem. Phys. 2005. V. 45. № 3. P. 490.
Sirenko Y., Strom S., Yashina N. Modeling and Analysis of Transient Processes in Open Resonant Structures. New Methods and Techniques. N.Y.: Springer, 2007.
Modern Theory of Gratings. Resonant Scattering: Analysis Techniques and Phenomena / Eds. Sirenko Y., Strom S. N.Y.: Springer, 2010.
Sirenko K., Pazynin V., Sirenko Y., Bagci H. // Progress in Electromagnetics Research. 2011. V. 111. P. 331.
Shafalyuk O., Sirenko Y., Smith P. Simulation and Analysis of Transient Processes in Open Axially-Symmetrical Structures: Method of Exact Absorbing Boundary Conditions. Rijeka: InTech, 2011. P. 99.
Shafalyuk O., Smith P., Velychko L. // Progress in Electromagnetics Research B. 2012. V. 41. P. 231.
Sautbekov S., Sirenko Y., Velychko L, Vertiy A. // Intern. J. Antennas and Propagation. 2014. V. 2014. ID 745413.
Orazbekova M., Pazynin V., Sautbekov S. et al. // Физ. основы приборостроения. 2014. Т. 3. № 4. С. 40.
Пазынин В., Сиренко К., Сиренко Ю., Яшина Н. // Физ. основы приборостроения. 2017. Т. 6. № 4. С. 4.
Taflove A., Hagness S. Computational Electrodynamics: the Finite-Difference Time-Domain Method. Boston: Artech House, 2000.
Jin J. The Finite Element Method in Electromagnetics. N.Y.: John Wiley & Sons, 2002.
Engquist B., Majda A. // Mathematics of Computation. 1977. V. 31. № 139. P. 629.
Mur G. // IEEE Trans. 1981. V. EC-23. № 4. P. 377.
Tirkas P., Balanis C., Renaut R. // IEEE Trans. 1992. V. AP-40. № 10. P. 1215.
Mei K., Fang. J. // IEEE Trans. 1992. V. AP-40. № 9. P. 1001.
Berenger J. // J. Comput. Phys. 1994. V. 114. № 1. P. 185.
Berenger J. // J. Comput. Phys. 1996. V. 127. № 2. P. 363.
Sacks Z., Kingsland D., Lee R., Lee J. // IEEE Trans. 1995. V. AP-43. № 12. P. 1460.
Сиренко Ю., Сухаревский И., Сухаревский О., Яшина Н. Фундаментальные и прикладные задачи теории рассеяния электромагнитных волн. Харьков: Крок, 2000.
Sirenko Y., Velychko L., Erden F. // Progress in Electromagnetics Research. 2004. V. 44. P. 57.
Velychko L., Sirenko Y., Velychko O. // Progress in Electromagnetics Research. 2006. V. 61. P. 1.
Velychko L., Sirenko Y. // Progress in Electromagnetics Research, B. 2009. V. 16. P. 85.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


