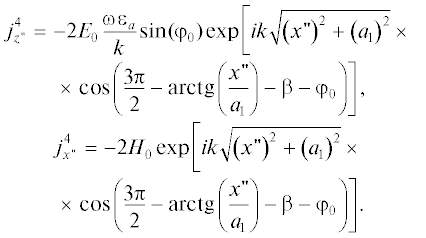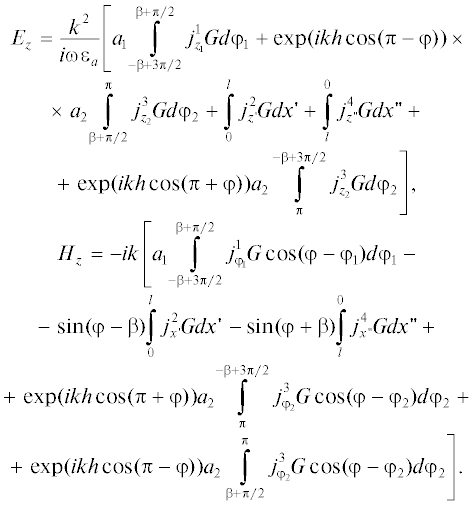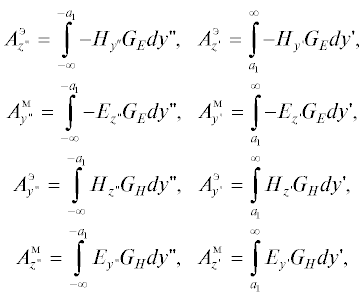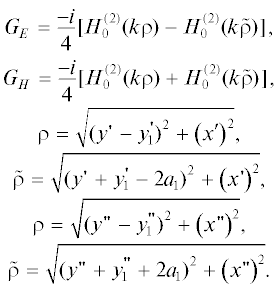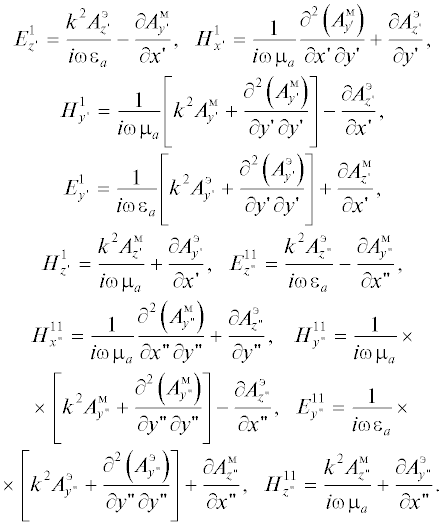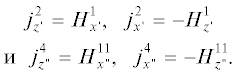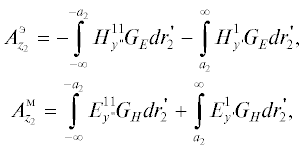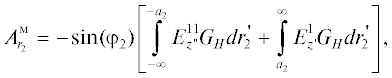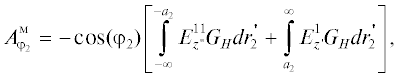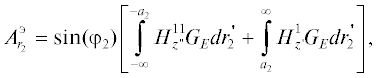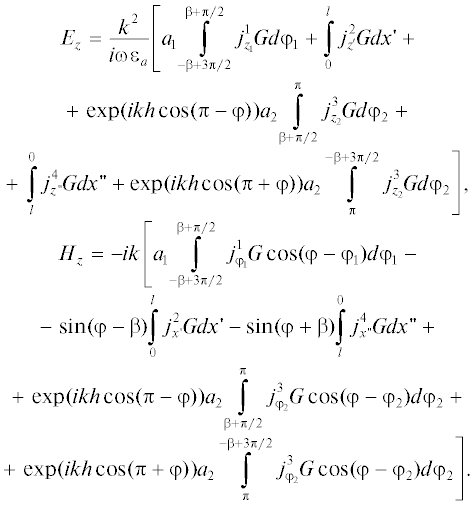Радиотехника и электроника, 2020, T. 65, № 5, стр. 457-463
Рассеяние плоской волны на цилиндре с кусочно-аналитической формой сечения
В. А. Калошин a, *, Д. Т. Луу b, **
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая,7, корп. 11, Российская Федерация
b Московский физико-технический институт (национальный исследовательский университет)
141701 Московской обл., Долгопрудный, Институтский пер., 9, Российская Федерация
* E-mail: vak@cplire.ru
** E-mail: luuductho@phystech.edu
Поступила в редакцию 21.06.2019
После доработки 21.06.2019
Принята к публикации 01.07.2019
Аннотация
Рассмотрена задача рассеяния плоской электромагнитной волны на идеально-проводящем цилиндре, поперечное сечение которого образовано прямыми и дугами окружностей. Для решения задачи использован гибридный метод, сочетающий метод собственных функций, последовательных дифракций и принцип эквивалентности. Проведено сравнение результатов расчета гибридным методом, методом моментов и методом Гюйгенса–Френеля–Кирхгофа.
ВВЕДЕНИЕ
При решении задач рассеяния акустических и электромагнитных волн на телах с кусочно-аналитической формой границы применяются как строгие численные методы: моментов, конечных элементов, Т-матриц, так и асимптотические: метод Гюйгенса–Френеля–Кирхгофа (ГФК), геометрическая теория дифракции, метод параболического уравнения [1–5].
В случае когда все характерные электрические размеры задачи относительно небольшие эффективно применение численных методов. Однако если хотя бы один из характерных электрических размеров задачи велик, то использование численных методов требует больших размеров оперативной памяти компьютера.
В случае когда все характерные электрические размеры задачи, большие по сравнению с длиной волны, для ее решения можно эффективно использовать асимптотические методы, в частности метод ГФК. Если поверхность тела можно разбить на участки, являющиеся координатными поверхностями в одной из ортогональных систем координат, в которых волновое уравнение можно решить методом разделения переменных, то для вычисления интеграла Кирхгофа целесообразно применять метод функций Грина [5]. При этом поля на каждом таком участке, как и в приближении ГФК, полагаются равными падающему полю, а затем эти поля и функция Грина представляются в виде рядов по собственным функциям, что облегчает процесс вычисления интеграла Кирхгофа. Однако, если хотя бы один из характерных электрических размеров задачи мал, такой подход приводит к серьезным погрешностям.
В данной работе для решения задачи рассеяния плоской электромагнитной волны на бесконечном цилиндре, поперечное сечение которого образовано прямыми и дугами окружностей, использован новый гибридный метод решения подобных задач, предложенный в работе [6]. Он основан на сочетании метода собственных функций, последовательных дифракций и принципа эквивалентности (строгой формулировки метода ГФК). Проведено сравнение результатов расчета диаграмм рассеяния гибридным методом, гибридным методом без учета взаимодействия, методом моментов и методом ГФК для различных углов падения и двух типов поляризации падающей плоской волны.
1. ПОСТАНОВКА ЗАДАЧИ
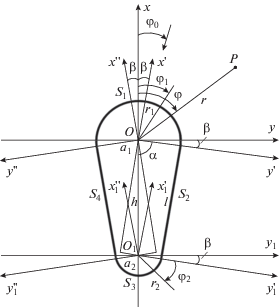
Рассмотрим рассеяние плоской электромагнитной волны, падающей под углом φ0 на идеально-проводящий бесконечный цилиндр, поперечное сечение которого образовано прямыми и дугами окружностей (рис. 1), где a1, a2 – радиусы окружностей, h – расстояние между центрами окружностей, l – длина прямых (l = h sin(–β + π/2), β = π/2 – – arccos[(a1 – a2)/h]).
В силу цилиндрической симметрии пластины задача рассеяния в общем случае сводится к двум двумерным задачам: для Е-поляризации (электрическое поле параллельно образующей цилиндра) и Н-поляризации (электрическое поле ортогонально образующей цилиндра). Будем искать решение этих задач в форме диаграммы рассеяния.
В силу наличия плоскости симметрии y = 0 без ограничения общности будем рассматривать область углов падения 0 ≤ φ0 ≤ π.
2. ГИБРИДНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ РАССЕЯНИЯ БЕЗ УЧЕТА ВЗАИМОДЕЙСТВИЯ
Разобьем границу поперечного сечения цилиндра S на четыре участка: S1 и S3 – дуги окружности, S2 и S4 – отрезки прямых (см. рис. 1).
Решение задачи рассеяния плоской волны на идеально-проводящем цилиндре можно представить в виде ряда Рэлея [1]. Компоненты полного поля для случая Е-поляризации в цилиндрических координатах (r1, φ1) с центром в точке O имеют вид
(1)
$\begin{gathered} {{E}_{{{{z}_{1}}}}} = {{E}_{0}}\sum\limits_{m = 0}^\infty {{{\varepsilon }_{m}}{{i}^{m}}\cos (m({{\varphi }_{1}} - {{\varphi }_{0}}))} \text{[}{{J}_{m}}(k{{r}_{1}}) - \\ - \,\,{{J}_{m}}(k{{a}_{1}})H_{m}^{{(2)}}{{(k{{r}_{1}})} \mathord{\left/ {\vphantom {{(k{{r}_{1}})} {H_{m}^{{(2)}}}}} \right. \kern-0em} {H_{m}^{{(2)}}}}(k{{a}_{1}})], \\ {{H}_{{{{r}_{1}}}}} = \frac{{i\omega {{\varepsilon }_{a}}}}{{{{k}^{2}}{{r}_{1}}}}\frac{{\partial {{E}_{{{{z}_{1}}}}}}}{{\partial {{\varphi }_{1}}}},\,\,\,\,{{H}_{{{{\varphi }_{1}}}}} = \frac{{ - i\omega {{\varepsilon }_{a}}}}{{{{k}^{2}}}}\frac{{\partial {{E}_{{{{z}_{1}}}}}}}{{\partial {{r}_{1}}}}, \\ \end{gathered} $Компоненты полного поля для случая H-поляризации имеют вид
(2)
$\begin{gathered} {{H}_{{{{z}_{1}}}}} = {{H}_{0}}\sum\limits_{m = 0}^\infty {{{\varepsilon }_{m}}{{i}^{m}}\cos (m({{\varphi }_{1}} - {{\varphi }_{0}}))} \text{[}{{J}_{m}}(k{{r}_{1}}) - \\ - \,\,J_{m}^{'}(k{{a}_{1}})H_{m}^{{(2)}}{{(k{{r}_{1}})} \mathord{\left/ {\vphantom {{(k{{r}_{1}})} {H_{m}^{{(2)'}}}}} \right. \kern-0em} {H_{m}^{{(2)'}}}}(k{{a}_{1}})], \\ {{E}_{{{{r}_{1}}}}} = \frac{{ - i\omega {{\mu }_{a}}}}{{{{k}^{2}}{{r}_{1}}}}\frac{{\partial {{H}_{{{{z}_{1}}}}}}}{{\partial {{\varphi }_{1}}}},\,\,\,\,{{E}_{{{{\varphi }_{1}}}}} = \frac{{i\omega {{\mu }_{a}}}}{{{{k}^{2}}}}\frac{{\partial {{H}_{{{{z}_{1}}}}}}}{{\partial {{r}_{1}}}}, \\ \end{gathered} $Ток на дуге S1 определяется по формуле j = [H, n]. Отсюда при r1 = a1 получаем для случая Е- и Н-поляризации соответственно:
(3)
$j_{{{{z}_{1}}}}^{1} = - {{H}_{{{{\varphi }_{1}}}}},\,\,\,\,j_{{{{\varphi }_{1}}}}^{1} = {{H}_{{{{z}_{1}}}}}.$При падении плоской волны под углом φ0, лежащем в пределах β < φ0 ≤ π – β, как будет показано далее, можно пренебречь взаимодействием токов на разных участках образующей пластины в рамках гибридного метода. В этом случае токи на обеих дугах S1 и S3 полагаются равными токам на полных окружностях при рассеянии плоской волны, ток на освещенной прямой S2 находится по формуле j = 2[Нпад, n], а ток на прямой S4 полагается равным нулю. В результате компоненты тока на прямой S2 в повернутой на угол β системе декартовых координат $x{\kern 1pt} 'y{\kern 1pt} '$ с центром в точке O (см. рис. 1) имеют вид:
(4)
$\begin{gathered} j_{{z{\kern 1pt} '}}^{2} = - 2{{E}_{0}}\frac{{\omega {{\varepsilon }_{a}}}}{k}sin({{\varphi }_{0}})exp\left[ {ik\sqrt {{{{\left( {x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {{{a}_{1}}} \right)}}^{2}}} \times \frac{{^{{}}}}{{_{{}}}}} \right. \\ \times \,\,\left. {\cos \left( {\frac{\pi }{2} + arctg\left( {\frac{{x{\kern 1pt} '}}{{{{a}_{1}}}}} \right) + \beta - {{\varphi }_{0}}} \right)} \right], \\ j_{{x{\kern 1pt} '}}^{2} = - 2{{H}_{0}}\exp \left[ {ik\sqrt {{{{\left( {x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {{{a}_{1}}} \right)}}^{2}}} \times \frac{{^{{}}}}{{_{{}}}}} \right. \\ \times \,\,\left. {\cos \left( {\frac{\pi }{2} + arctg\left( {\frac{{x{\kern 1pt} '}}{{{{a}_{1}}}}} \right) + \beta - {{\varphi }_{0}})} \right)} \right]. \\ \end{gathered} $Компоненты тока на дуге S3 в цилиндрической системе координат (r2, φ2) с центром в точке O1 имеют вид
(5)
$\begin{gathered} j_{{{{z}_{2}}}}^{3} = - exp( - ikh\cos ({{\varphi }_{0}})){{H}_{{{{\varphi }_{2}}}}}, \\ j_{{{{\varphi }_{2}}}}^{3} = exp( - ikh\cos ({{\varphi }_{0}})){{H}_{{{{z}_{2}}}}}, \\ \end{gathered} $Далее находим диаграмму рассеяния по известным формулам [1]:
(6)
$\begin{gathered} E = \frac{1}{{i\omega {{\varepsilon }_{a}}}}\left[ {{{k}^{2}}{{A}^{э}} + grad div {{A}^{э}} } \right] - rot {{A}^{м}} , \\ H = \frac{1}{{i\omega {{\mu }_{a}}}}\left[ {{{k}^{2}}{{A}^{м}} + grad div {{A}^{м}} } \right] + rot {{A}^{э}} , \\ \end{gathered} $При интегрировании по дугам S1 и S3 используем полярные координаты (r1, φ1) и (r2, φ2) соответственно, а при интегрировании по прямой S2 – декартовую систему координат $x{\kern 1pt} 'y{\kern 1pt} '.$
В результате для диаграммы рассеяния в случае Е- и Н-поляризации получаем
(7)
$\begin{gathered} {{E}_{z}} = \frac{{{{k}^{2}}}}{{i\omega {{\varepsilon }_{a}}}}\left[ {{{a}_{1}}\int\limits_{ - \beta + 3\pi /2}^{\beta + \pi /2} {j_{{{{z}_{1}}}}^{1}Gd{{\varphi }_{1}}} } \right. + \exp (ikh\cos (\pi - \varphi )) \times \\ \times \,\,{{a}_{2}}\int\limits_{\beta + \pi /2}^\pi {j_{{{{z}_{2}}}}^{3}Gd{{\varphi }_{2}}} + \int\limits_0^l {j_{{z'}}^{2}Gdx{\kern 1pt} '} + \\ + \,\,\exp (ikh\cos (\pi + \varphi )){{a}_{2}}\left. {\int\limits_\pi ^{ - \beta + 3\pi /2} {j_{{{{z}_{2}}}}^{3}Gd{{\varphi }_{2}}} } \right], \\ {{H}_{z}} = - ik\left[ {{{a}_{1}}\int\limits_{ - \beta + 3\pi /2}^{\beta + \pi /2} {j_{{{{\varphi }_{1}}}}^{1}G\cos (\varphi - {{\varphi }_{1}})d{{\varphi }_{1}}} } \right. + \\ + \,\,\exp (ikh\cos (\pi - \varphi )){{a}_{2}}\int\limits_{\beta + \pi /2}^\pi {j_{{{{\varphi }_{2}}}}^{3}G\cos (\varphi - {{\varphi }_{2}})d{{\varphi }_{2}}} - \\ - \,\,\sin (\varphi - \beta )\int\limits_0^l {j_{{x{\kern 1pt} '}}^{2}Gdx{\kern 1pt} '} + \exp (ikh\cos (\pi + \varphi )) \times \\ \times \,\,{{a}_{2}}\left. {\int\limits_\pi ^{ - \beta + 3\pi /2} {j_{{{{\varphi }_{2}}}}^{3}G\cos (\varphi - {{\varphi }_{2}})d{{\varphi }_{2}}} } \right]. \\ \end{gathered} $При падении плоской волны под малыми углами φ0 ≤ β компоненты тока на поверхности S2, S3, S4 полагаются равными нулю. В результате для диаграммы рассеяния в случае Е- и Н-поляризации получаем
(8)
$\begin{gathered} {{E}_{z}} = \frac{{{{k}^{2}}{{a}_{1}}}}{{i\omega {{\varepsilon }_{a}}}}\int\limits_{ - \beta + 3\pi /2}^{\beta + \pi /2} {j_{{{{z}_{1}}}}^{1}Gd{{\varphi }_{1}}} , \\ {{H}_{z}} = - ik{{a}_{1}}\int\limits_{ - \beta + 3\pi /2}^{\beta + \pi /2} {j_{{{{\varphi }_{1}}}}^{1}G\cos (\varphi - {{\varphi }_{1}})d{{\varphi }_{1}}} . \\ \end{gathered} $При падении плоской волны под углами (π – β < < φ0) компоненты тока на прямой S4 в повернутой на угол β декартовой системе координат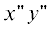 
(рис. 1) имеют вид
При интегрировании по прямой S4 используем систему декартовых координат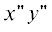 
центром в точке O.
В результате для диаграммы рассеяния в случае Е- и Н-поляризации получаем
3. ГИБРИДНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ РАССЕЯНИЯ С УЧЕТОМ ВЗАИМОДЕЙСТВИЯ
Рассмотрим случай падения плоской волны под углом φ0 < π/2. Будем искать распределение токов на S1, S2, S3, S4 последовательно. Сначала найдем поля на линиях $x{\kern 1pt} '$ = 0, $y{\kern 1pt} '$ > a1 и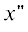 
= 0, 
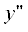< –a1. Для этого воспользуемся решением задачи рассеяния плоской волны на идеально-проводящем
цилиндре по формулам (1) и (2).
Токи на дуге S1 определяется по формуле j = = [H, n]. Отсюда при r1 = a1 получаем для случая Е- и Н-поляризации соответственно:
(11)
$j_{{{{z}_{1}}}}^{1} = - {{H}_{{{{\varphi }_{1}}}}},\,\,\,\,j_{{{{\varphi }_{1}}}}^{1} = {{H}_{{{{z}_{1}}}}}.$Запишем компоненты полного поля, выраженные формулами (1) и (2), в повернутых на угол β прямоугольных системах координат $x{\kern 1pt} 'y{\kern 1pt} '$ и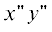 
(см. рис. 1). В результате получаем
Далее определим векторные потенциалы в области между прямыми $x{\kern 1pt} '$ = 0, $y{\kern 1pt} '$ > a1 и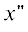 
= –l,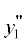 
< < –a1 , а также между прямыми 
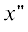= 0,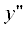 
< –a1 и $x{\kern 1pt} '$ = –l, $y_{1}^{'}$ > a1. В результате получаем
Компоненты полного поля выражаются через векторные потенциалы по формулам
Подставляя в формулу (14) значения $y{\kern 1pt} '$ = a1 при –h sin(–β + π/2) ≤ $x{\kern 1pt} '$ ≤ 0 и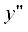 
= –a1 при ‒h sin(–β + π/2) ≤ 
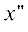≤ 0, находим компоненты магнитного поля и тока на прямых S2 и S4:
Подставляя в формулу (14) значения $x{\kern 1pt} '$ = = ‒hsin(–β + π/2) и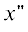 
= –hsin(–β + π/2), находим компоненты полного поля на прямых $x_{1}^{'}$ = 0, $y_{1}^{'}$ > a2 и 
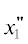= 0,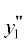 
< –a2.
Далее находим токи на дуге S3. Векторные потенциалы при этом по-прежнему определены в формуле (6), где функции Грина окружности в полярной системе координат (r2, φ2) с центром в точке O1 имеют вид [2]
Для электрической поляризации Ω = 1, а для магнитной $\Omega = {\partial \mathord{\left/ {\vphantom {\partial {\partial {{a}_{2}}}}} \right. \kern-0em} {\partial {{a}_{2}}}},$ r< = $r_{2}^{'},$ r> = r2 при r2> $r_{2}^{'}$ и r< = = r2, r> = $r_{2}^{'}$ при r2< $r_{2}^{'}$. Здесь $r_{2}^{'}$ = $y_{1}^{'}$ и $r_{2}^{'}$ =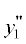 
.
В результате для компонент тока на дуге S3 получаем
(17)
$\begin{gathered} j_{{{{z}_{2}}}}^{3} = \frac{{ - 1}}{{i\omega {{\mu }_{a}}}} \times \\ \times \,\,\left[ {{{k}^{2}}A_{{{{\varphi }_{2}}}}^{м} + \frac{1}{{{{r}_{2}}}}\left[ {\frac{\partial }{{\partial {{\varphi }_{2}}}}\left( {\frac{1}{{{{r}_{2}}}}\frac{{\partial ({{r}_{2}}A_{{{{r}_{2}}}}^{м})}}{{\partial {{r}_{2}}}} + \frac{1}{{{{r}_{2}}}}\frac{{\partial A_{{{{\varphi }_{2}}}}^{м}}}{{\partial {{\varphi }_{2}}}}} \right)} \right]} \right] - \frac{{\partial A_{{{{z}_{2}}}}^{э}}}{{\partial {{r}_{2}}}}, \\ j_{{{{\varphi }_{2}}}}^{3} = \frac{{{{k}^{2}}A_{{{{z}_{2}}}}^{м}}}{{i\omega {{\mu }_{a}}}} + \frac{1}{{{{r}_{2}}}}\left[ {\frac{{\partial ({{r}_{2}}A_{{{{\varphi }_{2}}}}^{э})}}{{\partial {{r}_{2}}}} - \frac{{\partial A_{{{{r}_{2}}}}^{э}}}{{\partial {{\varphi }_{2}}}}} \right], \\ \end{gathered} $
Таким образом, мы нашли токи на S. В результате для диаграммы рассеяния в случае Е- и Н-поляризации получаем
Построение решения при падении плоской волны под углами φ0 > π/2 производится по аналогичной схеме.
4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
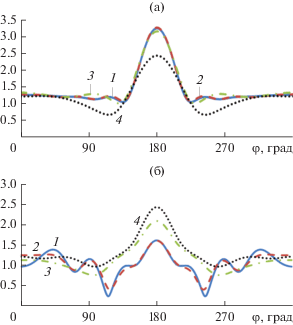
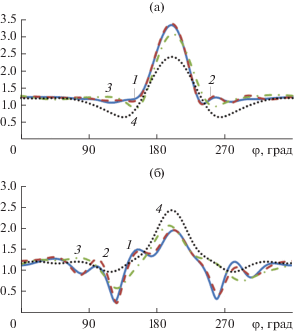
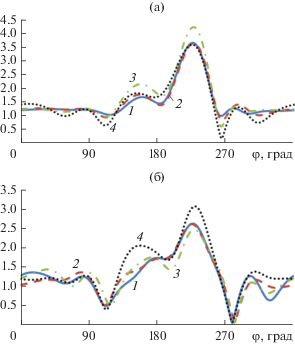
На рис. 2–9 приведены результаты расчета диаграмм рассеяния на цилиндре с параметрами kh = 5, ka1 = 3, ka2 = 1 и 0.1 для Е- и Н-поляризации при четырех значениях угла падения плоской волны: φ0 = 0, 20°, 45°, 180°. На всех рисунках кривая 1 показывает результаты расчета методом моментов, 2 – гибридным методом с учетом взаимодействия, 3 – гибридным методом без учета взаимодействия, 4 – методом Гюйгенса–Френеля–Кирхгофа.
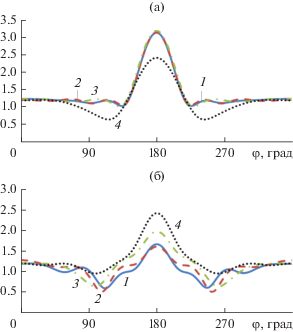
Рис. 5.
Диаграммы рассеяния для Е-поляризации (а) и H-поляризации (б) при φ0= 180°, ka1= 3, ka2 = 1.
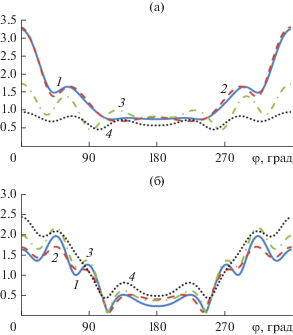
Рис. 7.
Диаграммы рассеяния для Е-поляризации (а) и H-поляризации (б) при φ0= 20°, ka1= 3, ka2 = 0.1.
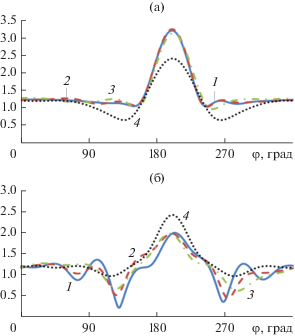
Рис. 8.
Диаграммы рассеяния для Е-поляризации (а) и H-поляризации (б) при φ0= 45°, ka1= 3, ka2 = 0.1.
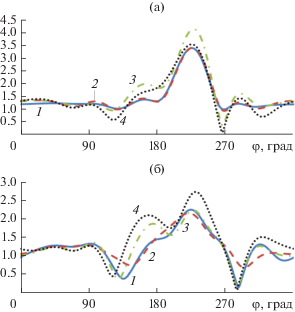
Рис. 9.
Диаграммы рассеяния для Е-поляризации (а) и H-поляризации (б) при φ0= 180°, ka1= 3, ka2 = 0.1.
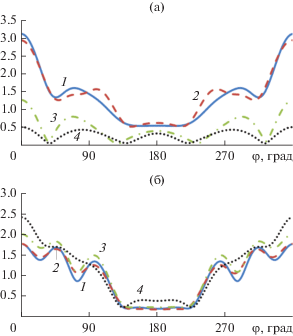
На рис. 2–9 видно, что результаты расчета диаграмм рассеяния методом моментов (кривая 1) и гибридным методом с учетом взаимодействия (кривая 2) хорошо совпадают для всех углов падения и обеих значениях параметра ka2. Результаты расчета гибридным методом без учета взаимодействия (кривая 3) совпадают с ними только при значениях угла φ0, лежащих в пределах β < φ0 ≤ π – β. Результаты точного расчета и методом ГФК (кривая 4) совпали только для одного угла падения φ0= π/4 для Е-поляризации и только в области главного лепестка диаграммы рассеяния.
ЗАКЛЮЧЕНИЕ
Таким образом, в результате сравнения результатов расчета четырьмя методами можно сделать следующие выводы:
1. Предложенный гибридный метод с учетом взаимодействия позволяет решать задачи рассеяния плоской электромагнитной волны на цилиндрических телах с кусочно-аналитической формой образующей и произвольными характерными электрическими размерами при любых углах падения.
2. Гибридный метод без учета взаимодействия позволяет решать задачи рассеяния плоской электромагнитной волны на цилиндрических телах с кусочно-аналитической формой образующей с произвольными характерными электрическими размерами для углов падения, не близких к скользящим.
3. Метод Гюйгенса–Френеля–Кирхгофа даже качественно не описывает диаграмму рассеяния плоской волны на цилиндре при радиусах кривизны границы поперечного сечения цилиндра менее половины длины волны.
Список литературы
Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.; Л.: Энергия, 1967.
Фелсен Л., Маркувиц Н. Излучение и рассеяние волн. М.: Мир, 1978.
Боровиков В.А., Кинбер Б.Е. Геометрическая теория дифракции. М.: Связь, 1978.
Фок В.А. Проблемы дифракции и распространения электромагнитных волн. М.: Сов. радио, 1970.
Kleshchev A.A. // J. Acoust. 2016. V. 6. P. 45.
Kaloshin V.A., Luu D.T. // Intern. Sci. Conf. “Radiation and Scattering of Electromagnetic Waves RSEMW-2019”, Divnomorskoe, Russia. June, 2019. P. 232.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника
Пн.-пт.: 10.00-19.00