Радиотехника и электроника, 2020, T. 65, № 5, стр. 434-441
Численное моделирование прохождения волн очень низкой частоты через магнитоактивную плоскослоистую плазму нижней ионосферы Земли
А. В. Мошков a, *, В. Н. Пожидаев a
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, корп. 7, Российская Федерация
* E-mail: kuzaf@inbox.ru
Поступила в редакцию 13.05.2019
После доработки 13.05.2019
Принята к публикации 18.07.2019
Аннотация
Приведено описание алгоритма вычисления характеристик прохождения низкочастотных электромагнитных волн через магнитоактивную плоскослоистую нижнюю ионосферу. Алгоритм основан на процедуре численного интегрирования волновых уравнений для случая падения плоской волны на ионосферу снизу с учетом ионного состава плазмы. В качестве иллюстрации вычислены основные характеристики прохождения волн в интервале частот 0.05…1 кГц. Показано, что коэффициент прохождения по мощности указанных волн достаточно велик и находится в интервале 0.2…0.4 для большей части используемых частот. Показано, что в дневное время вблизи частоты ~300 Гц коэффициент прохождения в дневное время имеет максимум и превышает ночные значения примерно в два раза.
ВВЕДЕНИЕ
Численному моделированию удаленной регистрации в магнитосфере и на земной поверхности низкочастотных волн от искусственных возмущений в ионосфере уделяется большое внимание (см., например, [1–3]). Это связано с вводом в строй ряда мощных наземных коротковолновых (КВ) передатчиков, излучение которых модулировано на низкой частоте (НЧ). Излучение таких передатчиков (“нагревных стендов”) интенсивно поглощается в нижней ионосфере, приводя к возникновению эффекта нелинейной демодуляции и излучению НЧ-волн в ионосферу и волновод “Земля-ионосфера” [4]. Во всем мире функционирует более десятка нагревных стендов, наиболее мощными и оснащенными научной аппаратурой из которых являются стенды EISCAT (Норвегия) и HAARP (Аляска) [5, 6].
К настоящему времени можно считать, что теория распространения волн очень и сверхнизких частот (ОНЧ и СНЧ) в околоземном пространстве, в частности в волноводе (резонаторе) “Земля–ионосфера”, в основном построена [7–10]. Соответствующие алгоритмы часто физически недостаточно наглядны и требуют значительных усилий для интерпретации результатов. По этой причине задачу можно разбить на связанные части, для каждой из которых строятся относительно простые численные алгоритмы. Это относится, прежде всего, к алгоритмам построения лучевых траекторий в ионосфере, магнитосфере [11–14]. Даже в волноводе “Земля–ионосфера”, где на низких частотах приближение геометрической оптики формально не выполнимо вблизи верхней “стенки”, возможно построение эффективных численных алгоритмов в рамках “метода скачков” [15–17]. При этом коэффициенты отражения от нижней неоднородной анизотропной ионосферы необходимо вычислять независимо.
Вычисление подобных коэффициентов является частью общего решения задачи о прохождении электромагнитных волн через локально плоскослоистую анизотропную плазму нижней ионосферы.
Цель данной работы – представить описание одного из возможных алгоритмов решения такой задачи. В качестве иллюстрации проведены расчеты в случае СНЧ (50…1000 Гц), которым в последнее время уделяется повышенное внимание для диагностики состояния земной коры дистанционными методами и в задачах связи.
1. ОСНОВНЫЕ СООТНОШЕНИЯ
Математически задача о прохождении электромагнитных (ЭМ) волн через локально плоскослоистую анизотропную плазму (ионосферу) была сформулирована относительно давно [18]. Однако при попытках провести численные расчеты величины напряженности ЭМ-поля на трассе и соответствующих коэффициентов отражения и прохождения возникли некоторые трудности принципиального характера, связанные с интегрированием системы однородных дифференциальных уравнений при наличии экспоненциальной численной неустойчивости решения [18, 19]. Приведем здесь краткое описание эффективного алгоритма для решения данной задачи с учетом ионного состава плазмы.
Для расчетов напряженности поля используем уравнения Максвелла совместно с моделью среды в виде неоднородной холодной многокомпонентной магнитоактивной плазмы. Такая среда описывается тензором диэлектрической проницаемости ${\hat {\varepsilon }}$ (магнитная проницаемость ионосферной плазмы равна магнитной проницаемости вакуума μ0). Тензор ${\hat {\varepsilon }}$ в системе координат, в которой ось z направлена вдоль внешнего геомагнитного поля, имеет вид [20]
(1а)
$\hat {\varepsilon } = \left[ {\begin{array}{*{20}{c}} S&{ - iD}&0 \\ {iD}&S&0 \\ 0&0&P \end{array}} \right],$(1б)
$\begin{gathered} R = 1 + \sum {{{{{X}_{k}}} \mathord{\left/ {\vphantom {{{{X}_{k}}} {({{Y}_{k}} - {{U}_{k}})}}} \right. \kern-0em} {({{Y}_{k}} - {{U}_{k}})}}} ; \\ L = 1 - \sum {{{{{X}_{k}}} \mathord{\left/ {\vphantom {{{{X}_{k}}} {({{Y}_{k}} + {{U}_{k}})}}} \right. \kern-0em} {({{Y}_{k}} + {{U}_{k}})}}} ; \\ P = 1 - \sum {{{{{X}_{k}}} \mathord{\left/ {\vphantom {{{{X}_{k}}} {{{U}_{k}}}}} \right. \kern-0em} {{{U}_{k}}}}} ; \\ \end{gathered} $(1в)
$\begin{gathered} S = {{\left( {R + L} \right)} \mathord{\left/ {\vphantom {{\left( {R + L} \right)} 2}} \right. \kern-0em} 2};\,\,\,\,D = {{\left( {R--L} \right)} \mathord{\left/ {\vphantom {{\left( {R--L} \right)} 2}} \right. \kern-0em} 2}; \\ {{U}_{k}} = 1--{{i{{\nu }_{k}}} \mathord{\left/ {\vphantom {{i{{\nu }_{k}}} \omega }} \right. \kern-0em} \omega }, \\ \end{gathered} $νk – эффективная частота соударений частиц сорта k; f – частота волны, ω = 2πf, i – мнимая единица. Суммирование ведется по сорту k заряженных частиц, составляющих плазму, с учетом знака заряда в величинах Yk:
(2)
${{Y}_{k}} \equiv {{{{f}_{{Hk}}}} \mathord{\left/ {\vphantom {{{{f}_{{Hk}}}} f}} \right. \kern-0em} f};\,\,\,\,{{X}_{k}} \equiv {{({{{{f}_{{pk}}}} \mathord{\left/ {\vphantom {{{{f}_{{pk}}}} f}} \right. \kern-0em} f})}^{2}},$где fHk и fpk – гиро- и плазменная частота частицы сорта k: k = 1 (электроны), 2, … (ионы). Для электронов имеем
(3)
${{f}_{{pe}}} = {{({{{{e}^{2}}{{N}_{e}}} \mathord{\left/ {\vphantom {{{{e}^{2}}{{N}_{e}}} {4{{\pi }^{2}}{{\varepsilon }_{0}}{{m}_{e}}}}} \right. \kern-0em} {4{{\pi }^{2}}{{\varepsilon }_{0}}{{m}_{e}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \approx 8.97N_{e}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\,\,{\text{кГц}},$где Ne измеряется в см–3; e, me – заряд и масса электрона; ε0 – диэлектрическая проницаемость вакуума. В максимуме слоя F2 ионосферы имеем днем fpe ≈ 10 МГц, ночью – fpe ≈ 2…5 МГц в зависимости от условий (времени суток, сезона, географического положения и активности Солнца):
(4)
${{f}_{{He}}} = {{e{{B}_{o}}} \mathord{\left/ {\vphantom {{e{{B}_{o}}} {2\pi {{m}_{e}}}}} \right. \kern-0em} {2\pi {{m}_{e}}}}.$В пределах ионосферы пространственная структура вектора геомагнитного поля $\overrightarrow {{{B}_{0}}} $ хорошо описывается моделью точечного магнитного диполя, расположенного вблизи центра Земли с осью, наклоненной под некоторым углом к оси вращения Земли [21]. По аналогии с географическими координатами вводятся понятия геомагнитной широты Φ и долготы Λ. На высоте h и широте Φ значение гирочастоты можно оценить так:
(5)
${{f}_{{He}}} \approx 876.0{{(1 + {h \mathord{\left/ {\vphantom {h {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}})}^{{ - 3}}}{{(1 + 3{{\sin }^{2}}\Phi )}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\,\,{\text{кГц}},$где R0 – средний радиус Земли (~6370 км). Для ионов сорта k в формулах (3), (4) следует использовать соответствующие значения концентрации Nk и массы mk.
Пусть начало правой декартовой прямоугольной системы координат расположено в точке O на поверхности земли, а ось z направлена вертикально вверх. Плоская ЭМ-волна с волновым вектором $\vec {k}$ падает снизу на горизонтальный неоднородный по оси z слой плазмы под углом θ с вертикалью. Верхняя и нижняя границы слоя соответствуют высотам z1 и z2. Направим ось х так, чтобы вектор $\vec {k}$ находился в плоскости XZ. Направление локального геомагнитного поля определяется углом ψ вектора ($ - \overrightarrow {{{B}_{0}}} $) с вертикалью и задаваемым углом азимута A, который отсчитывается от оси х до направления проекции $\overrightarrow {{{B}_{0}}} $ на земную поверхность. Отсчет идет против часовой стрелки, если смотреть на поверхность сверху вниз. Величина угла ψ определяется из соотношения ctgψ = 2 tg Φ [21]. Мы будем использовать для описания направления $\overrightarrow {{{B}_{0}}} $ его направляющие косинусы {l, m, n}, где
Такой выбор системы отсчета позволяет записать любую переменную волновую величину $\vec {V}\left( {x,y,z,t} \right)$ в виде
где k0 = ω/c – волновое число в вакууме; Γ = sin θ. Опуская везде данный экспоненциальный множитель, мы можем превратить систему уравнений в частных производных в систему обыкновенных дифференциальных уравнений первого порядка [18]:
(6)
${{{\text{d}}\vec {e}(z)} \mathord{\left/ {\vphantom {{{\text{d}}\vec {e}(z)} {{\text{d}}z}}} \right. \kern-0em} {{\text{d}}z}} = - i{{k}_{0}}\hat {T}\vec {e}(z),$где $\vec {e}$ – вектор-столбец вида {Ex, –Ey, Z0Hx, Z0Hy}, искусственно образованный из компонент Ex, Ey электрического, и компонент Hx, Hy магнитного поля волны, причем компоненты магнитного поля для уравнивания размерностей умножены на импеданс вакуума Z0 = (µ0/ε0)1/2 = 120π. Компоненты 4 × 4 матрицы $\hat {T}$ выражаются через компоненты 3 × 3 матрицы электрической восприимчивости $\hat {M} = \hat {\varepsilon } - \hat {1}$ ($\hat {1}~$ – единичная матрица):
(7)
$\begin{gathered} {{T}_{{11}}} = {{ - \Gamma {{M}_{{31}}}} \mathord{\left/ {\vphantom {{ - \Gamma {{M}_{{31}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}};\,\,\,\,{{T}_{{12}}} = {{\Gamma {{M}_{{32}}}} \mathord{\left/ {\vphantom {{\Gamma {{M}_{{32}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{14}}} = {{\left( {{{C}^{2}} + {{M}_{{33}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{C}^{2}} + {{M}_{{33}}}} \right)} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{31}}} = --{{M}_{{21}}} + {{{{M}_{{23}}}{{M}_{{31}}}} \mathord{\left/ {\vphantom {{{{M}_{{23}}}{{M}_{{31}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{32}}} = {{C}^{2}} + {{M}_{{22}}} - {{{{M}_{{23}}}{{M}_{{32}}}} \mathord{\left/ {\vphantom {{{{M}_{{23}}}{{M}_{{32}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{34}}} = {{\Gamma {{M}_{{23}}}} \mathord{\left/ {\vphantom {{\Gamma {{M}_{{23}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{44}}} = {{ - \Gamma {{M}_{{13}}}} \mathord{\left/ {\vphantom {{ - \Gamma {{M}_{{13}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{41}}} = 1 + {{M}_{{11}}} - {{{{M}_{{13}}}{{M}_{{31}}}} \mathord{\left/ {\vphantom {{{{M}_{{13}}}{{M}_{{31}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{42}}} = - {{M}_{{12}}} + {{{{M}_{{13}}}{{M}_{{32}}}} \mathord{\left/ {\vphantom {{{{M}_{{13}}}{{M}_{{32}}}} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}}; \\ {{T}_{{13}}} = {{T}_{{21}}} = {{T}_{{22}}} = {{T}_{{24}}} = {{T}_{{33}}} = {{T}_{{43}}} = {\text{ }}0;\,\,\,\,{{T}_{{23}}} = {\text{ }}1, \\ \end{gathered} $где C = cos θ.
В выбранной выше системе координат легко показать, что элементы матрицы $\hat {M}$ имеют вид
(8)
$\begin{gathered} {{M}_{{11}}} = \left( {1 - {{l}^{2}}} \right)S + {{l}^{2}}P - 1; \\ {{M}_{{12}}} = lm\left( {P - S} \right) + inD; \\ {{M}_{{13}}} = ln\left( {P - S} \right) - imD; \\ {{M}_{{21}}} = lm\left( {P - S} \right) - inD; \\ {{M}_{{22}}} = \left( {1 - {{m}^{2}}} \right)S + {{m}^{2}}P - 1; \\ {{M}_{{23}}} = mn\left( {P - S} \right) + ilD; \\ {{M}_{{31}}} = ln\left( {P - S} \right) + imD; \\ {{M}_{{32}}} = mn\left( {P - S} \right) - ilD; \\ {{M}_{{33}}} = \left( {1 - {{n}^{2}}} \right)S + {{n}^{2}}P - 1; \\ \end{gathered} $где параметры S, P, D определены в уравнениях (1) с учетом ионного состава ионосферного слоя и эффективной частоты соударений частиц в слое.
Недостающие в уравнении (6) компоненты Ez и Hz находятся явно из уравнений Максвелла:
(9а)
${{E}_{z}} = - {{\left( {\Gamma {{Z}_{0}}{{H}_{y}} + {{M}_{{31}}}{{E}_{x}} + {{M}_{{32}}}{{E}_{y}}} \right)} \mathord{\left/ {\vphantom {{\left( {\Gamma {{Z}_{0}}{{H}_{y}} + {{M}_{{31}}}{{E}_{x}} + {{M}_{{32}}}{{E}_{y}}} \right)} {\left( {1 + {{M}_{{33}}}} \right)}}} \right. \kern-0em} {\left( {1 + {{M}_{{33}}}} \right)}},$(9б)
${{H}_{z}} = {{\Gamma {{E}_{y}}} \mathord{\left/ {\vphantom {{\Gamma {{E}_{y}}} {{{Z}_{0}}}}} \right. \kern-0em} {{{Z}_{0}}}}.$Для выделения падающих и отраженных волн в волноводе при z < z2 запишем соотношения между компонентами полей в этой области:
(10)
$\begin{gathered} {{H}_{x}} = \mp C{{E}_{y}};\,\,\,\,{{H}_{y}} = {{ \pm {{E}_{x}}} \mathord{\left/ {\vphantom {{ \pm {{E}_{x}}} {(C{{Z}_{0}})}}} \right. \kern-0em} {(C{{Z}_{0}})}}; \\ {{H}_{z}} = {{ \mp \Gamma {{H}_{x}}} \mathord{\left/ {\vphantom {{ \mp \Gamma {{H}_{x}}} C}} \right. \kern-0em} C} = {{\Gamma {{E}_{y}}} \mathord{\left/ {\vphantom {{\Gamma {{E}_{y}}} {{{Z}_{0}}}}} \right. \kern-0em} {{{Z}_{0}}}};\,\,\,\,{{E}_{z}} = \mp C{{E}_{y}}; \\ \end{gathered} $где верхний знак соответствует восходящей волне, а нижний – нисходящей.
Система (6) состоит из четырех обыкновенных линейных дифференциальных уравнений первого порядка. Система однородна, т.е. имеет четыре линейно независимых решения ${{\vec {e}}_{j}}$ (j = 1…4), причем любое другое решение (6) есть линейная комбинация этих решений. Легко показать, что решения ${{\vec {e}}_{j}}$ в однородной среде соответствуют классическим магнитоионным модам, условно называемым обыкновенной и необыкновенной волнами, которые распространяются вверх и вниз [18].
Предположим, что при z > z1 параметры ионосферы мало меняются на длине волны. В этом случае при падении волны на слой снизу на верхней границе слоя возникают только обыкновенная и необыкновенная волны, направленные вверх. Пусть это будут волны j = 1, 2. При z = z1 решение (6) может быть представлено в виде $\vec {e}$ = a1${{\vec {e}}_{1}}$ + a2${{\vec {e}}_{2}}$, где a1,2 – комплексные коэффициенты. В силу линейности и однородности системы (6) подобное представление решения справедливо для любой высоты z < z1, т.е. коэффициенты a1, 2 не зависят от z. Следовательно, необходимо найти только два линейно независимых решения (6), соответствующих восходящим обыкновенной и необыкновенной волнам. Для этого необходимо вычислить начальные значения ${{\vec {e}}_{{1,2}}}$(z1) в однородной среде выше неоднородного слоя. Для существования таких решений требуется выполнение известного условия det($\hat {T}$ – q$\hat {1}$) = 0, где коэффициент q описывает изменение плоской волны вдоль оси z как exp(–ik0qz). Зная значения q1,2 на высоте z1, можем проинтегрировать (6) вниз для соответствующих собственных векторов ${{\vec {e}}_{{1,2}}}$(z) матрицы $\hat {T}$.
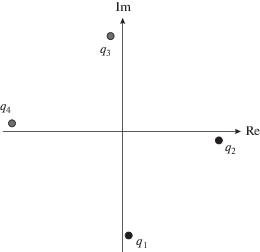
Раскрывая определитель с учетом значений элементов матрицы $\hat {T}$ (7), получим известное комплексное алгебраическое уравнение четвертой степени относительно q (“квадрик Букера”) [18]. На рис. 1 схематически представлено расположение корней квадрика qj (j = 1…4) на комплексной плоскости в случае низких частот, когда различие корней для четырех магнитоионных мод наиболее наглядно. Для восходящих волн Re(q) > 0. Из рисунка видно, что для “обыкновенной” волны |Im(q1)| $ \gg $ Re(q1), и эта волна относительно быстро затухает в неоднородной среде. Для “необыкновенной” волны, наоборот, |Im(q2)| $ \ll $ $ \ll $ Re(q2), затухание волны относительно невелико. По этой причине свистящие атмосферики распространяются на большие расстояния из полушария в полушарие в ионосфере и магнитосфере. Поэтому эту НЧ-моду часто называют “свистовой”.
Определение корней квадрика кажется несложной задачей, поскольку хорошо известно, что алгебраическое уравнение степени 4 с одним неизвестным имеет решение в аналитическом виде. Однако соответствующие формулы содержат вложенные квадратные и кубические корни, а также разности близких по значению величин. Кроме того, мнимые и вещественные части корней могут чрезвычайно сильно различаться по абсолютной величине, а сами корни могут приближаться к осям координат на расстояния, сравнимые с точностью вычислений, что на практике может привести к грубым вычислительным ошибкам. Нами предложен эффективный численный алгоритм вычисления корней квадрика, основанный на упрощенном варианте симплекс-метода, хорошо известного в линейном программировании.
1. На поверхности q в комплексном пространстве строим около начала координат правильный треугольник с характерным размером много меньше показателя преломления волны ${{\vec {e}}_{2}}$ на высоте z1. В качестве характерного размера выбираем, например, величину радиуса описанной окружности.
2. Проверяем значения q в вершинах треугольника и находим наименьшее из них.
3. Переносим центр треугольника в эту вершину и уменьшаем его характерный размер.
При циклическом повторении процедуры 2, 3 треугольник неизбежно “падает” в один из корней, останавливаясь при достижении требуемой точности.
4. Степень полинома понижается на единицу, и процедуры 1–4 повторяются до вычисления всех четырех корней.
Этот простой алгоритм использовался нами в данной задаче продолжительное время и ни разу не выдал ошибочный результат.
Для численного интегрирования (6) используем стабильный метод численного интегрирования с переменным шагом и контролем ошибки интегрирования Рунге–Кутта–Мерсона [22], хотя возможно эффективное применение и других методов [23].
Начальные значения ${{\vec {e}}_{{1,2}}}$(z1) для интегрирования системы уравнений (6) находим как собственные векторы матрицы $\hat {T}$ на высоте z1 при известных собственных значениях qj:
Линейная система уравнений (11) легко решается с точностью до постоянного множителя, например, Ey:
(12)
${{E}_{x}} = - \alpha {{E}_{y}};\,\,\,\,{{Z}_{0}}{{H}_{x}} = - q{{E}_{y}};\,\,\,\,~{{Z}_{0}}{{H}_{y}} = - \beta {{E}_{y}},$где индекс j не приводится,
На низких частотах обыкновенная волна сильно затухает вдоль оси z, следовательно, при интегрировании сверху вниз обыкновенная волна ${{\vec {e}}_{1}}$(z) быстро нарастает в сравнении с необыкновенной волной ${{\vec {e}}_{2}}$(z) (рис. 1). Из-за конечного числа разрядов в мантиссе вещественных чисел на ЭВМ этот эффект сильного нарастания одного из решений может привести к потере их линейной независимости, поэтому ее необходимо периодически восстанавливать в процессе интегрирования уравнений (6), пользуясь тем фактом, что ортогональные векторы всегда линейно независимы [24]. При достижении амплитуды решения ${{\vec {e}}_{1}}$(z) некоторого заданного порога, образуем вектор ${{\vec {e}}_{{20}}}$ = ${{\vec {e}}_{2}}$ + $\xi {{\vec {e}}_{1}}$ и потребуем, чтобы скалярное произведение ($\vec {e}_{1}^{*}$, ${{\vec {e}}_{{20}}}$) было равно 0. Отсюда находим множитель
где звездочка означает комплексное сопряжение. Поскольку вектор ${{\vec {e}}_{{20}}}$ есть линейная комбинация решений (6), то он тоже является решением, линейно независимым с ${{\vec {e}}_{1}}$. Отметим, что в сильно неоднородной среде понятие магнитоионной моды теряет свой изначальный физический смысл. В результате процедуры численного интегрирования, описанной выше, получаем при z = z2 два формально правильных линейно независимых решения (6). Однако в результате применения процедуры ортогонализации эти решения в совокупности не имеют какого-либо физического смысла. С их помощью можно сконструировать все характеристики волнового поля в пустом пространстве при z ≤ z2 [23].
Во-первых, можно разделить волны ниже слоя на восходящие и нисходящие части. Из выражений (7) и (8) легко получить значения q = ±C, причем, верхний знак соответствует волнам вверх ($\vec {U}$), а нижний – вниз ($\vec {D}$), т.е.
Возьмем электрическое поле $\vec {E}$, тогда $\vec {E}$ = $\vec {U}$ + $\vec {D}$ и ${\text{d}}\vec {E}$/dz = –ik0C$\vec {U}$ + ik0C$\vec {D}$. Выражение для производной можно также получить из уравнения (6). Получаем с учетом соотношений (10):
где C = cos θ.
Во-вторых, можно показать, что линейная комбинация ${{\vec {U}}_{{\text{п}}}}$ = ${{\vec {U}}_{2}}$ + $\zeta {{\vec {U}}_{1}}$, где ζ = –($\vec {U}_{1}^{*}$${{\vec {U}}_{2}}$)/($\vec {U}_{1}^{*}$${{\vec {U}}_{1}}$) представляет собой “проникающую” волну, которая порождает наименее затухающую необыкновенную волну выше уровня z1. У линейно независимых решений ${{\vec {e}}_{1}}$ и ${{\vec {e}}_{{\text{п}}}}$ уравнения (6) ниже высоты z2 есть простой физический смысл: они имеют соответственно наименьший и наибольший коэффициенты прохождения по мощности через неоднородный плазменный слой z2 – z1, причем ${{\vec {e}}_{{\text{п}}}}$ = ${{\vec {e}}_{2}}$ + $\zeta {{\vec {e}}_{1}}$.
В-третьих, векторы ${{\vec {e}}_{1}}$ и ${{\vec {e}}_{{\text{п}}}}$ можно использовать как базис для получения характеристик известной плоской волны, падающей на слой снизу (коэффициенты отражения, прохождения, в том числе по мощности). Традиционно рассматриваются падающие плоские волны двух независимых поляризаций. Вертикальная поляризация означает, что вектор $\vec {E}$ напряженности электрического поля волны лежит в плоскости (x, z), в которой лежит и вектор $\vec {k}$. В случае горизонтальной поляризации вектор $\vec {E}$ перпендикулярен этой плоскости, т.е. параллелен оси y. Обозначим эти векторы как ${{\vec {E}}_{\parallel }}$ и ${{\vec {E}}_{ \bot }}$ соответственно. Поскольку волны этих условно выбранных поляризаций должны быть линейными комбинациями базисных решений (${{\vec {e}}_{1}}$, ${{\vec {e}}_{{\text{п}}}}$), то из простейших геометрических соображений легко получить коэффициенты разложений ${{\vec {E}}_{\parallel }}$ и ${{\vec {E}}_{ \bot }}$ для волн вверх (↑) и вниз (↓), которые будут, очевидно, одинаковы для этих направлений: $\vec {E}_{\parallel }^{ \uparrow }$ = A∥${{\vec {U}}_{1}}$ + B∥${{\vec {U}}_{{\text{п}}}}$,
(13а)
$\vec {E}_{\parallel }^{ \downarrow } = {{A}_{\parallel }}{{\vec {D}}_{1}} + {{B}_{\parallel }}{{\vec {D}}_{п}},$(13б)
$\begin{gathered} {{A}_{\parallel }} = {{ - {{E}_{\parallel }}C{{U}_{{{\text{п}}y}}}} \mathord{\left/ {\vphantom {{ - {{E}_{\parallel }}C{{U}_{{{\text{п}}y}}}} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}} - {{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}} \right. \kern-0em} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}} - {{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}; \\ {{B}_{\parallel }} = {{{{E}_{\parallel }}C{{U}_{{1y}}}} \mathord{\left/ {\vphantom {{{{E}_{\parallel }}C{{U}_{{1y}}}} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}}--{{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}} \right. \kern-0em} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}}--{{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}. \\ \end{gathered} $Если задана амплитуда E∥ падающей волны вертикальной поляризации, то структуру поля ниже слоя можно определить из соотношений (13). Аналогично, если задана амплитуда поля E⊥ падающей волны горизонтальной поляризации, то
(14а)
$\vec {E}_{ \bot }^{ \uparrow } = {{A}_{ \bot }}{{\vec {U}}_{1}} + {{B}_{ \bot }}{{\vec {U}}_{п}},\,\,\,\,\vec {E}_{ \bot }^{ \downarrow } = {{A}_{ \bot }}{{\vec {D}}_{1}} + {{B}_{ \bot }}{{\vec {D}}_{{\text{п}}}},$(14б)
$\begin{gathered} {{A}_{ \bot }} = {{ - {{E}_{ \bot }}{{U}_{{{\text{п}}x}}}} \mathord{\left/ {\vphantom {{ - {{E}_{ \bot }}{{U}_{{{\text{п}}x}}}} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}}--{{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}} \right. \kern-0em} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}}--{{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}; \\ {{B}_{ \bot }} = {{ - {{E}_{ \bot }}{{U}_{{1x}}}} \mathord{\left/ {\vphantom {{ - {{E}_{ \bot }}{{U}_{{1x}}}} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}}--{{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}} \right. \kern-0em} {({{U}_{{1y}}}{{U}_{{{\text{п}}x}}}--{{U}_{{1x}}}{{U}_{{{\text{п}}y}}})}}. \\ \end{gathered} $Если на анизотропный слой падает волна, например, горизонтальной поляризации, то отразятся волны и горизонтальной, и вертикальной поляризаций. Поэтому принято представлять коэффициент отражения в виде 2 × 2 матрицы $\hat {R}$ [18]. Приведем определения элементов матрицы:
(15а)
$\begin{gathered} {{R}_{{11}}} = {{H_{y}^{ \downarrow }} \mathord{\left/ {\vphantom {{H_{y}^{ \downarrow }} {H_{y}^{ \uparrow }}}} \right. \kern-0em} {H_{y}^{ \uparrow }}}\,\,{\text{при}}\,\,{{E}_{ \bot }} = 0; \\ {{R}_{{12}}} = {{{{Z}_{0}}H_{y}^{ \downarrow }} \mathord{\left/ {\vphantom {{{{Z}_{0}}H_{y}^{ \downarrow }} {E_{y}^{ \uparrow }}}} \right. \kern-0em} {E_{y}^{ \uparrow }}}\,\,{\text{при}}\,\,{{E}_{\parallel }} = 0; \\ \end{gathered} $(15б)
$\begin{gathered} {{R}_{{21}}} = {{E_{y}^{ \downarrow }} \mathord{\left/ {\vphantom {{E_{y}^{ \downarrow }} {H_{y}^{ \uparrow }}}} \right. \kern-0em} {H_{y}^{ \uparrow }}}\,\,{\text{при}}\,\,{{E}_{ \bot }} = 0; \\ {{R}_{{22}}} = {{E_{y}^{ \downarrow }} \mathord{\left/ {\vphantom {{E_{y}^{ \downarrow }} {E_{y}^{ \uparrow }}}} \right. \kern-0em} {E_{y}^{ \uparrow }}}\,\,{\text{при}}\,\,{{E}_{\parallel }} = 0. \\ \end{gathered} $Из соотношений (10), (13), (14) и (15) получим
(16а)
${{R}_{{11}}} = {{({{U}_{{1y}}}{{D}_{{{\text{п}}x}}} - {{U}_{{{\text{п}}y}}}{{D}_{{1x}}})} \mathord{\left/ {\vphantom {{({{U}_{{1y}}}{{D}_{{{\text{п}}x}}} - {{U}_{{{\text{п}}y}}}{{D}_{{1x}}})} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})}}} \right. \kern-0em} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})}},$(16б)
${{R}_{{12}}} = {{({{D}_{{1x}}}{{U}_{{{\text{п}}x}}} - {{U}_{{1x}}}{{D}_{{{\text{п}}x}}})} \mathord{\left/ {\vphantom {{({{D}_{{1x}}}{{U}_{{{\text{п}}x}}} - {{U}_{{1x}}}{{D}_{{{\text{п}}x}}})} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})C}}} \right. \kern-0em} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})C}},$(16в)
${{R}_{{21}}} = {{C({{U}_{{{\text{п}}y}}}{{D}_{{1y}}} - {{U}_{{1y}}}{{D}_{{{\text{п}}y}}})} \mathord{\left/ {\vphantom {{C({{U}_{{{\text{п}}y}}}{{D}_{{1y}}} - {{U}_{{1y}}}{{D}_{{{\text{п}}y}}})} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})}}} \right. \kern-0em} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})}},$(16г)
${{R}_{{22}}} = {{({{U}_{{1y}}}{{D}_{{{\text{п}}x}}} - {{U}_{{{\text{п}}y}}}{{D}_{{1x}}})} \mathord{\left/ {\vphantom {{({{U}_{{1y}}}{{D}_{{{\text{п}}x}}} - {{U}_{{{\text{п}}y}}}{{D}_{{1x}}})} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})}}} \right. \kern-0em} {({{U}_{{1x}}}{{U}_{{{\text{п}}y}}} - {{U}_{{1y}}}{{U}_{{{\text{п}}x}}})}}.$Определим поляризации ρ базовых решений:
(17)
${{\rho }_{{\text{п}}}} = {{{{E}_{{{\text{п}} \bot }}}} \mathord{\left/ {\vphantom {{{{E}_{{{\text{п}} \bot }}}} {{{E}_{{{\text{п}}\parallel }}}}}} \right. \kern-0em} {{{E}_{{{\text{п}}\parallel }}}}},\,\,\,\,~{{\rho }_{1}} = {{{{E}_{{1 \bot }}}} \mathord{\left/ {\vphantom {{{{E}_{{1 \bot }}}} {}}} \right. \kern-0em} {}}{{E}_{{1\parallel }}},$поскольку ${{\vec {e}}_{1}}$, ${{\vec {e}}_{{\text{п}}}}$ ортогональны, то |ρп||ρ1| = 1 и arg ρ1 = arg ρп + π. Из разложений (13) и (14) получим
(18)
${{\rho }_{{\text{п}}}} = {{C{{U}_{{{\text{п}}y}}}} \mathord{\left/ {\vphantom {{C{{U}_{{{\text{п}}y}}}} {{{U}_{{{\text{п}}x}}}}}} \right. \kern-0em} {{{U}_{{{\text{п}}x}}}}},\,\,\,\,~{{\rho }_{1}} = {{C{{U}_{{1y}}}} \mathord{\left/ {\vphantom {{C{{U}_{{1y}}}} {{{U}_{{1x}}}}}} \right. \kern-0em} {{{U}_{{1x}}}}}.$Коэффициенты прохождения по напряженности электрического поля волны легко получить, учитывая тот факт, что на уровень z1 проходит только одна проникающая волна. Получаем два коэффициента:
(19)
$\begin{gathered} {{t}_{\parallel }} = {{{{E}_{{{\text{п}}x}}}({{z}_{1}})} \mathord{\left/ {\vphantom {{{{E}_{{{\text{п}}x}}}({{z}_{1}})} {{{E}_{\parallel }}}}} \right. \kern-0em} {{{E}_{\parallel }}}}\,\,{\text{при}}\,\,{{E}_{ \bot }} = 0; \\ ~{{t}_{ \bot }} = {{{{E}_{{{\text{п}}x}}}({{z}_{1}})} \mathord{\left/ {\vphantom {{{{E}_{{{\text{п}}x}}}({{z}_{1}})} {{{E}_{ \bot }}}}} \right. \kern-0em} {{{E}_{ \bot }}}}\,\,{\text{при}}\,\,{{E}_{\parallel }} = 0. \\ \end{gathered} $Эти выражения можно переписать в более простом виде:
(20)
${{t}_{ \bot }} = {{C{{E}_{{{\text{п}}x}}}({{z}_{1}})} \mathord{\left/ {\vphantom {{C{{E}_{{{\text{п}}x}}}({{z}_{1}})} {{{U}_{{{\text{п}}x}}}({{\rho }_{p}} - {{\rho }_{1}})}}} \right. \kern-0em} {{{U}_{{{\text{п}}x}}}({{\rho }_{p}} - {{\rho }_{1}})}} = {{ - {{t}_{\parallel }}} \mathord{\left/ {\vphantom {{ - {{t}_{\parallel }}} {{{\rho }_{1}}}}} \right. \kern-0em} {{{\rho }_{1}}}}.$В заключение описательной части приведем выражения для коэффициентов прохождения по мощности. Мощность падающей на слой проникающей волновой моды вдоль оси z составляет
Выше слоя при z = z1 вертикальная часть мощности формируется начальным полем свистовой моды ${{\vec {e}}_{{\text{п}}}}$:
Вертикальный коэффициент прохождения по мощности Dпz определяем так:
(21)
$\begin{gathered} {{D}_{{{\text{п}}z}}} = {{{{P}_{{z1}}}} \mathord{\left/ {\vphantom {{{{P}_{{z1}}}} {{{P}_{{z2}}}}}} \right. \kern-0em} {{{P}_{{z2}}}}} = \\ = {{{{Z}_{0}}\operatorname{Re} \left( {{{E}_{x}}H_{y}^{*} - {{E}_{e}}H_{x}^{*}} \right)} \mathord{\left/ {\vphantom {{{{Z}_{0}}\operatorname{Re} \left( {{{E}_{x}}H_{y}^{*} - {{E}_{e}}H_{x}^{*}} \right)} {C\left( {{{{\left| {{{U}_{{{\text{п}}x}}}} \right|}}^{2}} + {{{\left| {{{U}_{{{\text{п}}y}}}} \right|}}^{2}} + {{{\left| {{{U}_{{{\text{п}}z}}}} \right|}}^{2}}} \right)}}} \right. \kern-0em} {C\left( {{{{\left| {{{U}_{{{\text{п}}x}}}} \right|}}^{2}} + {{{\left| {{{U}_{{{\text{п}}y}}}} \right|}}^{2}} + {{{\left| {{{U}_{{{\text{п}}z}}}} \right|}}^{2}}} \right)}}. \\ \end{gathered} $Определим полный коэффициент прохождения по мощности Dп:
где относительные “боковые” потоки мощности sx, y на высоте z1 вычисляются как отношения соответствующих компонент вектора Умова–Пойнтинга к его z-компоненте:
причем, компоненты напряженности поля волны Ez и Hz определяются из соотношений (9а) и (9б).
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Далее везде будем использовать численные значения параметров плазмы, которые соответствуют приполярной ионосфере на широте 60° в равноденственный период при умеренной солнечной активности [25]. Процент ионных составляющих в слое [z1, z2] приведен в табл. 1.
Таблица 1.
Параметры дневной и ночной ионосферы
| Ионы газа | Атомная масса | Дневная ионосфера | Ночная ионосфера | ||||
|---|---|---|---|---|---|---|---|
| состав, % | fpi, кГц | fHi, кГц | состав, % | fpi, кГц | fHi, кГц | ||
| N+ | 14 | 0.3 | 0.433 | 0.059 | – | – | – |
| O+ | 16 | 50.8 | 5.272 | 0.051 | 37.6 | 6.261 | 0.050 |
| ${\text{N}}_{2}^{ + }$ | 28 | 1.7 | 0.729 | 0.029 | – | – | – |
| NO+ | 30 | 31.5 | 3.032 | 0.027 | 10.0 | 2.358 | 0.027 |
| ${\text{O}}_{2}^{ + }$ | 32 | 15.1 | 2.033 | 0.026 | 37.0 | 4.392 | 0.025 |
Профили Ne(z) и νe(z) аппроксимировались кубическими сплайнами. Такой метод гарантирует отсутствие “паразитных” частичных отражений в сильно неоднородном слое нижней ионосферы. Для дневной ионосферы выбирали слой 50…100 км; для ночной ионосферы – 75…150 км. На верхней границе слоя плазменная частота для электронов днем равна 1268.2 кГц, ночью – 1750.6 кГц, гирочастоты электронов составляют днем 1507.1 кГц, ночью – 1472.7 кГц. Для ионов соответствующие частоты приведены в табл. 1. Частоты нижнего гибридного резонанса fLHR равны соответственно 4.95 и 5.15 кГц.
Расчеты проводились для значений θ = 10°, A = = 180° (направление на магнитный юг) и частот в интервале 50…1000 Гц. Выбор этих величин определялся условиями работы станции HAARP. Однако следует учесть, что длина волны на частоте 50 Гц составляет в атмосфере 6000 км. При длине окружности экватора 40 000 км на ней укладывается шесть целых длин волн. Такой волновой процесс можно лишь условно считать “локальным”, а дальнейшее понижение частоты требует рассмотрения сферической полости “Земля–ионосфера” в виде резонатора, а не волновода. Если учесть, однако, что в нижней ионосфере на высоте z1 показатель преломления волн относительно велик, то получим величину длины волны в среде ~30…40 км. Такую величину вполне можно считать “локальной”.
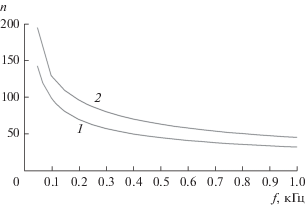
На рис. 2 приведены расчетные зависимости показателя преломления n свистовой моды от частоты при z = z1 для дневной и ночной моделей ионосферы. Величина n для ночи выше дневных значений, поскольку ночная высота z1 значительно больше дневной.
Рис. 2.
Зависимости показателя преломления n свистовой моды от частоты при z = z1 для дневной (кривая 1) и ночной (кривая 2) моделей ионосферы.
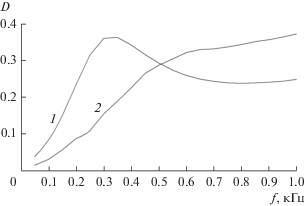
На рис. 3 представлена частотная зависимость полного коэффициента прохождения по мощности D (фактически соответствует величине Dп в тексте) для дневной и ночной моделей ионосферы. Для диапазона сверхдлинных дневные значения D, как правило, заметно меньше ночных из-за столкновительного поглощения волн на высотах 50…70 км в дневное время. Из рис. 3 видно, что подобная закономерность начинает развиваться только на частотах f > 500 Гц. На меньших частотах ионные резонансы в дневное время формируют характерный максимум прохождения на частотах f ~ 30 Гц, что соответствует примерно половине гиро-частоты наилегчайшего иона N+. Отметим, что величина D на частотах 0.2…1 кГц не мала ни днем, ни ночью, и почти достигает значения 0.4. Без учета влияния геомагнитного поля величина D равнялась бы нулю.
Рис. 3.
Зависимость коэффициента прохождения по мощности D от частоты f для дневной (кривая 1) и ночной (кривая 2) моделей ионосферы.
На рис. 4а приведены зависимости от частоты модулей компонентов матрицы $\hat {R}$ коэффициента отражения (см. (15), (16)) для дня (сплошные кривые) и ночи (пунктир). Приведены зависимости от f величин R11 (кривые 1 и 4), R12 (кривые 2 и 5) и R22 для дня (кривая 3). Для выбранного значения азимута из рисунка видно (кривые 1, 3), что значения R11 и R22 очень близки, или практически совпадают (как и значения не диагональных элементов R12 и R21, из которых кривая приведена только для величины R12). По этой причине на рис. 4б изображены только зависимости аргументов R11(f) – кривые 1, 4; и аргументов R12(f) – кривые 2 и 5.
Рис. 4.
Зависимости модулей (а) и аргументов (б) компонентов матрицы $\hat {R}$ коэффициента отражения от частоты f для дня (сплошные кривые) и ночи (пунктир) для величин R11 (1, 4), R12 (2, 5), R22 (3).
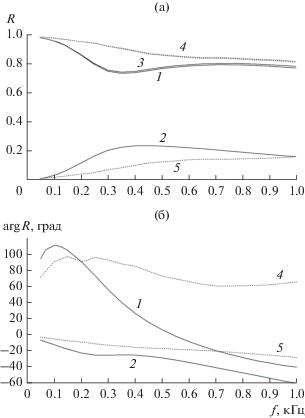
Из рис. 4 видно, что в выбранном интервале частот преобладают диагональные элементы $\hat {R}$, причем в ночное время аргумент элементов матрицы относительно стабилен. В дневное время с ростом частоты при переходе из области ионных колебаний в область электронных волн аргумент диагональных элементов заметно меняется (кривая 1 на рис. 4б). Кривая 3 для аргумента R22 на рис. 4б отсутствует, поскольку практически совпадает с кривой 1. Мы не приводим аналогичные зависимости поляризации отраженной волны в целом, поскольку в используемом интервале частот ионосфера играет роль почти идеального поляризационного фильтра, поэтому поляризация отраженной волны является круговой.
ЗАКЛЮЧЕНИЕ
Приведено описание алгоритма вычисления характеристик прохождения низкочастотных электромагнитных волн через магнитоактивную плоскослоистую нижнюю ионосферу с параметрами, аналогичными параметрам ионосферы над станцией HAARP, Аляска. Алгоритм основан на процедуре численного интегрирования волновых уравнений для случая падения плоской волны на ионосферу снизу с учетом ионного состава плазмы. В качестве иллюстрации работы алгоритма вычислены основные характеристики прохождения волны через нижнюю ионосферу в интервале частот 0.05…1 кГц.
Коэффициент прохождения по мощности указанных НЧ-волн достаточно велик и находится в интервале 0.2…0.4 для большей части используемых частот. В дневное время вблизи частоты ~300 Гц коэффициент прохождения в дневное время имеет максимум и превышает ночные значения примерно в два раза. Во всем исследованном интервале частот поляризация отраженной волны является круговой с хорошей степенью точности.
Список литературы
Moore R.C., Inan U.S., Bell T.F., Kennedy E.J. // J. Geophys. Res. 2007. V. 112. P. A05309. https://doi.org/10.1029/2006JA012063
Мошков А.В., Пожидаев В.Н. // РЭ. 2013. Т. 58. № 9. С. 965. https://doi.org/10.7868/S0033849413090106
Бова Ю.И., Крюковский А.С., Лукин Д.С. // РЭ. 2019. Т. 64. № 1. С. 3. https://doi.org/10.1134/S0033849419010030
Гуревич А.В. // Успехи физ. наук. 2007. Т. 177. № 11. С. 1145.
Белов А.С., Марков Г.А., Фролов В.Л. и др. // Совр. проблемы дист. зондирования Земли из космоса. 2008. Т. 5. № 1. С. 539.
Cohen M.B., Golkowski M., Inan U.S. // Geophys. Res. Lett. 2008. V. 35. P. L02806. https://doi.org/10.1029/2007GL032424
Budden K.G. The wave-guide mode theory of wave propagation. Englewood Cliffs: Prentice-Hall, 1961.
Wait J.R. Electromagnetic waves in stratified media. Oxford: Pergamon press, 1970.
Макаров Г.И., Новиков В.В., Рыбачек С.Т. Распространение радиоволн в волновом канале Земля-ионосфера и в ионосфере. М.: Наука, 1994.
Cummer S.A. // IEEE Trans. 2000. V. AP-48. № 9. P. 1420.
Казанцев А.Н., Лукин Д.С., Спиридонов Ю.Г. // Космич. исслед. 1967. Т. 5. № 4. С. 593.
Лукин Д.С., Савченко П.П. // Геомагнетизм и аэрономия. 1981. Т. 21. № 2. С. 256.
Аксенов В.И., Мошков А.В. // Космич. исслед. 1981. Т. 19. № 6. С. 876.
Мошков А.В., Пожидаев В.Н. // РЭ. 2018. Т. 63. № 2. С. 134. https://doi.org/10.7868/S0033849418020043
Макаров Г.И., Федорова Л.А. // Изв. вузов. Радиофизика. 1982. Т. 25. № 12. С. 1384.
Аксенов В.И., Мошков А.В. // РЭ. 1987. Т. 32. № 5. С. 913.
Мошков А.В., Пожидаев В.Н. // РЭ. 2018. Т. 63. № 5. С. 409. https://doi.org/10.7868/S0033849418050030
Budden K.G. Radio Waves in the Ionosphere. Cambridge: Unive. Press, 1961.
Аксенов В.И., Лишин И.В., Назарова М.В. // Распространение радиоволн. М.: Наука, 1975. С. 228.
Стикс Т. Теория плазменных волн. М.: Атомиздат, 1965.
Дэвис К. Радиоволны в ионосфере. М.: Мир, 1973.
Ланс Дж. Численные методы для быстродействующих вычислительных машин. М.: Изд-во инстр. лит., 1962.
Scarabucci R.R. // Technical Report No. 3412-11 of the Stanford University Radioscience Lab. Stanford: Stanford Univ., 1969. 101 p. https://vlf.stanford.edu/ pubs/interpretation-vlf-signals-observed-ogo-4-satellite.
Курант Р., Гильберт Д. Методы математической физики. М.: Высшая школа, 1966. Т. 1.
Фаткуллин M.H., Зеленова Т.И., Козлов В.К. и др. Эмпирические модели среднеширотной ионосферы. М.: Наука, 1981.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника