Радиотехника и электроника, 2020, T. 65, № 6, стр. 559-567

ВВЕДЕНИЕ

Для флуктуаций фазы и амплитуды трансионосферных сигналов, как известно, характерно наличие участков нерегулярного поведения, в течение которых измеряемая величина особенно сильно отклоняется от своего типичного значения. Подобное поведение называется перемежаемостью. Так как флуктуации сигнала возникают благодаря рассеянию на неоднородностях электронной концентрации при распространении в ионосфере, то естественно считать, что причиной перемежаемости флуктуаций амплитуды и фазы сигнала является перемежаемый характер флуктуаций электронной плотности, являющийся следствием турбулентной структуры ионосферы. Перемежаемость ведет к более частому возникновению флуктуаций большой амплитуды, чем это предсказывает нормальное распределение (Гаусса), т.е. возникают так называемые “распределения с тяжелыми хвостами”, убывающие медленнее, чем распределение Гаусса. Такое негауссовское поведение наблюдается в измерениях, полученных при помощи спутников и ракет [1].

Большинство существующих теорий сцинтилляций трансионосферных сигналов предполагает гауссовский характер флуктуаций электронной плотности в ионосфере. Пространственный спектр ионосферных неоднородностей, как это было неоднократно подтверждено экспериментально [2], наилучшим образом может быть аппроксимирован обратным степенным законом в пространстве волновых чисел. Соответствующая структурная функция флуктуаций электронной плотности в инерционном интервале является степенной функцией расстояния между точками наблюдения. Показатели степени спектра и структурной функции в общем случае являются дробными величинами. Случайные функции такого типа, описывающие пространственное распределение концентрации электронов, с геометрической точки зрения являются стохастическими фракталами, обладают свойством масштабной инвариантности (скейлинга) и характеризуются показателем (экспонентой) Херста $H$. В частности, для изотропной трехмерной колмогоровской турбулентности показатель Херста $H = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$, при этом показатель степени структурной функции второго порядка равен $2H = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$, а соответствующий показатель степени трехмерного спектра флуктуаций равен $ - \left( {2H + 3} \right) = - {{11} \mathord{\left/ {\vphantom {{11} 3}} \right. \kern-0em} 3}$.

Таким образом, корреляционные и спектральные свойства фрактальных гауссовских флуктуаций могут быть охарактеризованы единственным параметром – экспонентой Херста. Однако для полного статистического описания негауссовских стохастических неоднородностей электронной плотности, связанных с явлением перемежаемости, необходимо привлекать моменты не только первого и второго, но также и высших порядков. Современные теории турбулентности позволяют учитывать перемежаемость посредством использования концепции мультифракталов – неоднородных фракталов, включающих в себя весь спектр показателей локальных степенных законов, т.е. мультифрактальный спектр [3].

Задача о распространении волн в негауссовской флуктуирующей среде изучена гораздо менее детально. Распространение радиоволн в межзвездной среде было рассмотрено в работе [4] в предположении, что флуктуации электронной плотности подчиняются устойчивому распределению вероятностей вида полетов Леви. В работе [1] методом множественных фазовых экранов были выполнены численные расчеты трансионосферного распространения радиоволн с использованием двойного экспоненциального распределения (распределения Лапласа) для моделирования флуктуаций электронной плотности. Детальное описание теории фракталов и ее применения в радиофизике и радиолокации содержится в монографиях [5, 6], где также имеется обширная библиография по данному предмету.

В серии работ по экспериментальному исследованию фрактальной структуры ионосферной турбулентности (см., например, [7, 8] и цитированную там литературу) анализируются результаты просвечивания верхней среднеширотной ионосферы и устанавливается, что мультифрактальная структура перемежаемости флуктуаций энергии принимаемого сигнала является следствием перемежаемости флуктуаций электронной концентрации ионосферной плазмы.

Для задач спутниковой навигации представляет интерес исследование как амплитудных, так и фазовых флуктуаций принимаемых трансионосферных сигналов, поскольку именно фазовые характеристики навигационного сигнала используются для точного позиционирования. Для теоретического описания флуктуаций поля с учетом перемежаемости необходимо решать задачу распространения в среде с перемежаемыми флуктуациями показателя преломления, для чего требуется соответствующая модель флуктуаций среды.

В данной работе рассмотрена задача распространения радиоволн в турбулентной ионосфере с учетом явления перемежаемости. Задача решается в приближении тонкого стохастического экрана (фазового экрана), на котором задается негауссовское перемежаемое пространственное распределение флуктуаций фазы, генерируемое с использованием представленной в работе мультифрактальной модели. Варьирование параметров модели позволяет моделировать различные режимы флуктуаций, от полного отсутствия до значительной степени перемежаемости. Задача дифракции падающей плоской волны на построенном экране решается численно, а полученные стохастические распределения амплитуды и фазы поля за экраном подвергаются статистическому анализу с целью исследования зависимости их статистических характеристик от степени перемежаемости фазы на экране.

1. МУЛЬТИФРАКТАЛЬНЫЙ СТОХАСТИЧЕСКИЙ ФАЗОВЫЙ ЭКРАН

Для оценки влияния перемежаемости флуктуаций электронной плотности на рассеиваемое поле в работе используется приближение стохастического фазового экрана. Исторически модель фазового экрана была одной из первых моделей, примененных для решения задачи распространения волн в случайной среде. На настоящий момент теория фазового экрана исчерпывающе разработана для нормального распределения фазы на экране.

Чтобы ввести негауссовскую мультифрактальную модель для случайного статистически однородного распределения фазы на экране, следуя [1], введем обобщенные структурные функции фазы различных порядков:

где $\varphi $ – фаза, $L$ – расстояние между двумя точками, $q$ – порядок структурной функции. Угловые скобки обозначают статистическое усреднение по ансамблю случайных реализаций распределения фазы. Если фаза описывается гауссовским случайным процессом, то для любого заданного расстояния между двумя точками распределение разности фаз между этими точками будет нормальным. Для гауссовских фрактальных процессов (статистически самоподобных случайных процессов со степенным спектром) свойство масштабной инвариантности соответствует следующему скейлингу для структурной функции порядка $q$: где $0 < H < 1$ – экспонента Херста. Здесь показатель степени (скейлинговая экспонента) является линейной функцией порядка $q$, и для гауссовских процессов структурная функция второго порядка полностью определяет структурные функции высших порядков: ${{S}_{q}}\left( L \right) \sim {{S}_{2}}{{\left( L \right)}^{{{q \mathord{\left/ {\vphantom {q 2}} \right. \kern-0em} 2}}}}.$ Для неоднородных фракталов (мультифракталов) структурные функции имеют вид где функция $\zeta \left( q \right)$, называемая скейлинговой экспонентой, зависит от $q$ нелинейно. В некотором интервале изменения переменной $q$ для $\zeta \left( q \right)$ может быть использована аппроксимация отрезком степенного ряда вида

В представлении (4) параметры $h$ и ${{\lambda }^{2}}$ определяют скейлинговые свойства мультифрактального случайного процесса. Отклонение скейлинга $\zeta \left( q \right)$ от линейного закона характеризуется параметром ${{\lambda }^{2}}$: чем больше параметр ${{\lambda }^{2}}$, тем сильнее отклонение случайного процесса от нормального, и тем более перемежаемым становится распределение.

Для генерации стохастического распределения фазы с заданным скейлингом вида (4) в работе используется каскадная модель [10], имитирующая турбулентный процесс, внутренний и внешний масштабы которого определяются параметрами сетки, а передача энергии от больших масштабов к малым моделируется каскадным процессом. Эта модель позволяет генерировать стохастическое двумерное распределение, имеющее скейлинг вида (4) с заданными параметрами $h$ и ${{\lambda }^{2}}$. Полученное при помощи модели распределение после соответствующей нормировки используется в качестве распределения фазы на экране.

Алгоритм генерации основан на представлении искомого пространственного распределения в виде двумерного дискретного разложения по двумерным базисным функциям вейвлет-преобразования:

где $\left\{ {\phi \left( {x,y} \right),} \right.$ $\psi _{{j,m,n}}^{1}\left( {x,y} \right),$ $\psi _{{j,m,n}}^{2}\left( {x,y} \right),$ $\left. {\psi _{{j,m,n}}^{3}\left( {x,y} \right)} \right\}$ – компактный ортонормальный двумерный базис вейвлет-функций. Индексы $\alpha = 1,2,3$ обозначают соответственно горизонтальные, вертикальные и диагональные материнские вейвлеты. Вейвлет-коэффициенты $c_{{j,m,n}}^{\alpha } = \left\langle {\left. {\psi _{{j,m,n}}^{\alpha }} \right|\varphi } \right\rangle $ являются случайными числами и генерируются с использованием мультипликативного каскадного алгоритма [9].

Алгоритм генерации вейвлет-коэффициентов для каждой реализации распределения случайного поля $\varphi (x,y)$ состоит из двух шагов. На первом шаге с использованием каскадного алгоритма (см. ниже) генерируются коэффициенты каскада ${{d}_{{j,m,n}}}$ для последовательно измельчающихся масштабов $1 < j < N$. Вейвлет-коэффициенты $c_{{j,m,n}}^{\alpha }$ связаны с коэффициентами каскада ${{d}_{{j,m,n}}}$ посредством соотношения:

которое на втором шаге используется для определения $c_{{j,m,n}}^{\alpha }$.

При реализации алгоритма сначала задается начальный коэффициент каскада ${{d}_{{0,0,0}}}$, соответствующий $j = 0$. Затем для каждого следующего, более детального уровня разложения $j$, коэффициенты каскада определяются путем произведения коэффициентов предыдущего уровня $(j - 1)$ и случайных множителей $W_{{j - 1,m,n}}^{{({{r}_{1}},{{r}_{2}},{{l}_{1}},{{l}_{2}})}}$:

где $j$ – номер уровня разложения, $1 \leqslant j \leqslant N$; $0 \leqslant m,$ $n \leqslant {{2}^{{N - j}}} - 1$. Множители $\left\{ W \right\}$ – независимые одинаково распределенные случайные величины. Как показано в [8], для того чтобы скейлинг результирующего стохастического распределения имел вид (4), плотность распределения этих случайных величин должна соответствовать логнормальному закону: где ${{\sigma }^{2}},\mu $ – дисперсия и математическое ожидание случайной величины $\ln (W)$.

Далее выполняется вычисление вейвлет-коэффициентов $\{ {{c}_{\alpha }}\} $ для горизонтальных, вертикальных и диагональных материнских вейвлетов. Для обеспечения изотропии результирующего случайного поля $\varphi (x,y)$ необходимо обеспечить одинаковые распределения всех трех коэффициентов:

где $\varphi \in \left[ { - \pi ,\pi } \right],$ $\cos (\theta ) \in \left[ { - 1,1} \right]$ – независимые равномерно распределенные случайные величины. Такое разложение соответствует равномерному распределению направлений векторов с координатами $\left( {c_{{j,m,n}}^{1},c_{{j,m,n}}^{2},c_{{j,m,n}}^{3}} \right)$ длины ${{d}_{{j,m,n}}}$. Отметим, что представленный в данной работе метод задания вейвлет-коэффициентов (9) отличается от предложенного ранее [10]. Только равномерное распределение $\cos (\theta )$ (а не самого значения $\theta $, как в [10]) обеспечивает изотропность получаемого двумерного стохастического поля.

Распределение, сгенерированное при помощи обратного вейвлет-преобразования в соответствии с представлением (5) с коэффициентами (9), имеет скейлинг

что теоретически доказано в [9]. Скейлинг получаемого распределения не зависит от выбора семейства вейвлет-функций [9]. Параметры скейлинга связаны с параметрами логнормального распределения (8) следующим образом:

После соответствующей нормировки сгенерированное таким образом двумерное случайное распределение можно рассматривать как распределение фазы на экране.

При численной реализации описанного алгоритма в среде Matlab используется пакет расширения Wavelet Toolbox. Цель выполненных в работе численных исследований – выявить, как перемежаемость стохастического распределения фазы на экране влияет на статистические характеристики поля за экраном. При этом в численных экспериментах генерируются случайные двумерные реализации распределения фазы на экране для различных значений параметра перемежаемости ${{\lambda }^{2}}$, но обладающие одним и тем же пространственным спектром. Для этого величина параметра $h$ выбирается так, чтобы значение скейлинговой экспоненты структурной функции фазы второго порядка на экране $\zeta (2) = 2(h - {{\lambda }^{2}})$ при всех ${{\lambda }^{2}}$ было постоянной величиной, равной ${5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}$. Выбор значения $\zeta (2) = {5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}$ соответствует “закону 2/3” Колмогорова–Обухова для структурной функции флуктуаций плотности в рассевающем слое. При этом при любом значении параметра λ² флуктуации фазы на экране имеют один и тот же степенной спектр с показателем $p = {{ - 8} \mathord{\left/ {\vphantom {{ - 8} 3}} \right. \kern-0em} 3}$. Значения фазы задаются на прямоугольной сетке $1024 \times 1024$, шаг $\Delta x = 10$ м, частота поля 1 ГГц. Как уже упоминалось, выбор используемого семейства вейвлет-функций не влияет на скейлинг результирующего распределения; все приведенные ниже результаты получены с использованием вейвлетов Добеши порядка 5.

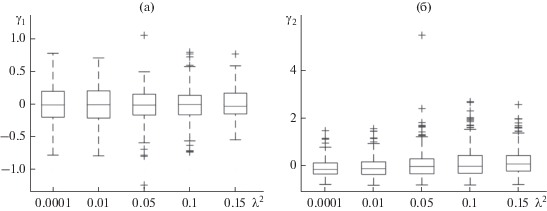
На рис. 1 при помощи так называемых “диаграмм размаха” представлены наблюдаемые статистические разбросы значений коэффициентов асимметрии ${{\gamma }_{1}} = {{{{M}_{3}}} \mathord{\left/ {\vphantom {{{{M}_{3}}} {M_{2}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {M_{2}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}$ и эксцесса ${{\gamma }_{2}} = {{{{M}_{4}}} \mathord{\left/ {\vphantom {{{{M}_{4}}} {M_{2}^{2}}}} \right. \kern-0em} {M_{2}^{2}}} - 3,$ где ${{M}_{n}}$ обозначает центральный момент распределения порядка $n$ разностей фаз между точками, расстояние между которыми равно 10 м, что соответствует одному шагу пространственной сетки. Здесь наблюдается значительный статистический разброс, причем степень разброса растет с ростом значений параметра ${{\lambda }^{2}}.$ Распределения коэффициентов асимметрии выглядят симметричными с медианой в окрестности нуля. Медиана эксцесса распределений положительна и растет с ростом ${{\lambda }^{2}}$, экстремальные значения эксцесса также положительны.

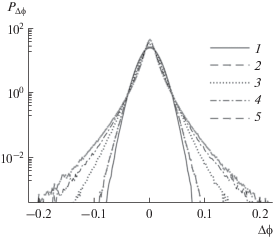
Таким образом, распределения разностей фаз являются симметричными негауссовскими распределениями, более острыми, чем нормальное распределение в области малых значений разностей фаз, и убывающими медленнее, чем нормальное распределение в области больших значений разностей фаз. В явном виде отклонения стохастических реализаций распределений фазы, получаемых с использованием описанного выше алгоритма, продемонстрированы на рис. 2. Для малых значений параметра ${{\lambda }^{2}}$ логарифм плотности вероятностей разностей фаз имеет форму, близкую к параболической, т.е. распределение соответствует нормальному; с ростом параметра ${{\lambda }^{2}}$ вероятность возникновения больших флуктуаций увеличивается, и распределение приобретает так называемые тяжелые хвосты, т.е. становится негауссовским.

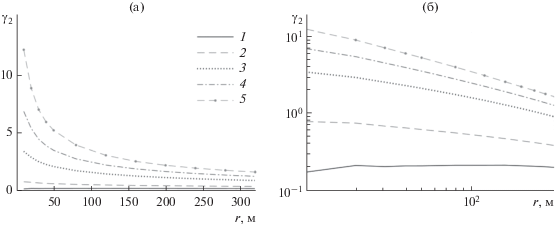
Вид плотностей распределений вероятностей разностей фаз между двумя пространственно разнесенными точками меняется с изменением расстояния между точками. На рис. 3а представлена зависимость коэффициента эксцесса распределения разностей фаз в двух пространственно разнесенных точках на экране от расстояния между точками для различных значений параметра ${{\lambda }^{2}}$. В двойном логарифмическом масштабе (рис. 3б) эти зависимости представляют собой прямые, расположенные тем выше, чем больше величина параметра ${{\lambda }^{2}}$, а их коэффициент наклона отрицателен и растет по абсолютной величине с ростом ${{\lambda }^{2}}$. Таким образом, чем меньше пространственный масштаб флуктуаций фазы, определяемый как величина расстояния между точками, и чем больше параметр перемежаемости ${{\lambda }^{2}}$, тем больше отклонение плотности вероятностей распределения разностей фаз от нормального распределения. Такая зависимость от масштаба характерна для мультифрактальных процессов.

Таким образом, предлагаемая модель путем выбора единственного параметра ${{\lambda }^{2}}$ позволяет моделировать различные степени перемежаемости, от полного ее отсутствия и нормального распределения флуктуаций фазы на экране до сильно перемежаемого режима и негауссовской статистики флуктуаций.

2. ФЛУКТУАЦИИ ПОЛЯ ЗА ЭКРАНОМ

Описанный выше метод позволяет генерировать на экране стохастическое пространственное распределение фазы, обладающее заданными скейлинговыми характеристиками. Будем считать, что на экран падает плоская волна единичной амплитуды, а действие экрана сводится к модуляции первоначально плоского фазового фронта падающей волны посредством добавления к исходной невозмущенной фазе волны величины возмущения фазы на экране $\varphi (\vec {r})$, при этом амплитуда волны не возмущается и остается равной единице. Тогда комплексная амплитуда поля сразу после прохождения фазового экрана равна $\exp (i\varphi (\vec {r}))$, а за экраном определяется интегралом Кирхгофа в приближении Френеля:

где $k$ – волновое число, $z$ – расстояние от экрана до плоскости наблюдения. Функция $\varphi (\vec {r})$ на экране задается в узлах двумерной пространственной сетки $1024 \times 1024$ с шагом 10 м. Двойное интегрирование в (11) выполняется численно с использованием быстрого преобразования Фурье.

При распространении в свободном пространстве за экраном комплексное поле $u(\vec {r},z)$ эволюционирует в соответствии с (11), при этом изменяется как его фаза $\arg (u(\vec {r},z)),$ так и амплитуда $\left| {u(\vec {r},z)} \right|.$ Статистические свойства флуктуаций фазы и амплитуды за экраном с гауссовским распределением фазы хорошо изучены для предельных случаев слабых и насыщенных флуктуаций [11, 12]. В частности, установлено, что в случае слабых флуктуаций фазы на экране флуктуации фазы и логарифма амплитуды (уровня поля) за экраном имеют совместное нормальное распределение, при этом амплитуда оказывается распределенной логнормально. В случае если флуктуации фазы на экране характеризуются степенной структурной функцией ${{S}_{2}}(L) \sim {{L}^{{\zeta \left( 2 \right)}}}$ и, соответственно, убывающим двумерным пространственным спектром степенного вида $ \sim {{k}^{{ - (\zeta \left( 2 \right) + 2)}}}$, то структурная функция и спектр флуктуаций фазы за экраном также являются степенными функциями, в то время как структурная функция и спектр флуктуаций уровня поля имеют подобный степенной характер лишь для масштабов, меньших размера первой зоны Френеля $L < {{L}_{\operatorname{F} }}$ = $\sqrt {{{2\pi z} \mathord{\left/ {\vphantom {{2\pi z} k}} \right. \kern-0em} k}} $ ($k > {{k}_{\operatorname{F} }} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{L}_{F}}}}} \right. \kern-0em} {{{L}_{F}}}}$). Для масштабов, больших ${{L}_{\operatorname{F} }}$ ($k < {{k}_{F}}$), спектр флуктуаций уровня является растущей функцией в соответствии со степенным законом $ \sim {{k}^{{ - 2\zeta \left( 2 \right) + 2}}}$ [10].

В случае негауссовского мультифрактального распределения флуктуаций фазы на экране структурные функции второго порядка фазы и уровня и соответствующие спектры мощности флуктуаций фазы и уровня имеют такой же вид, как и для гауссовского экрана, однако плотности распределения вероятностей их значений отличаются от нормального закона. Поэтому и статистические моменты поля, такие как, например, функции когерентности поля, функция корреляции интенсивности, индекс сцинтилляций, будут отличаться от соответствующих величин, построенных для нормального распределения флуктуаций фазы на экране [13, 14].

Значительный интерес с точки зрения решения обратной задачи определения параметров ионосферной турбулентности представляет выявление и исследование свойств масштабной инвариантности (скейлинга) стохастических реализаций принимаемого поля и связь этих характеристик с соответствующими свойствами флуктуаций электронной плотности ионосферы. Для оценки параметров скейлинговых экспонент стохастических процессов к настоящему времени разработан ряд методов, детальное описание которых выходит за рамки данной статьи. Обзор существующих подходов и методов можно найти, например, в [15, 16] и цитированной там литературе. Одним из наиболее современных и надежных методов является метод, основанный на анализе свойств коэффициентов дискретного вейвлет-разложения исследуемого процесса, который и используется в данной работе. Метод позволяет, в частности, определить коэффициенты ${{C}_{p}}$ в представлении скейлинговой экспоненты $\zeta (q)$ (формулы (3), (4)) исследуемого процесса в виде степенного ряда по степеням параметра $q$ [17]:

Отметим, что (12) совпадает с (4), если принять ${{C}_{1}} = h,$ ${{C}_{2}} = - {{\lambda }^{2}},$ ${{C}_{{p \geqslant 3}}} = 0.$

Таким образом, исследование свойств масштабной инвариантности процесса сводится к оценке коэффициентов ${{C}_{p}}$ в представлении (12).

В соответствии с алгоритмом метода вместо обобщенных структурных функций типа (1) рассматривается статистическая сумма ${{Z}_{q}}(j)$, составленная из моментов порядка $q$ коэффициентов ${{d}_{{j,m,n}}}$ дискретного вейвлет-преобразования для каждого уровня разложения $j$, соответствующего пространственному масштабу ${{L}_{j}} \sim {{2}^{j}}\Delta x$:

Эта статистическая сумма может быть представлена в виде производящей функции моментов распределения логарифмов коэффициентов $\left\{ {{{d}_{j}}} \right\}$, которая затем записывается в виде кумулянтного разложения:

где ${{\kappa }_{p}}(j)$ – кумулянты (или лог-кумулянты) порядка $p$ распределения логарифмов коэффициентов $\left| {{{d}_{j}}} \right|$ на уровне разложения $j$ [16]. Лог-кумулянты оцениваются непосредственно по коэффициентам дискретного вейвлет-разложения исследуемого процесса.

Если в некотором диапазоне значений $j$ зависимость лог-кумулянтов от $j$ может быть аппроксимирована линейной зависимостью вида

то $ln{{Z}_{j}}(q)$ принимает вид где $\ln {{F}_{q}} = \sum\nolimits_{p \geqslant 1} {{{C}_{{p0}}}\frac{{{{q}^{p}}}}{{p!}}} $ не зависит от масштаба.

Детальное описание процедуры оценки параметров ${{C}_{p}}$ можно найти в [17], поэтому здесь приведем основные выводы, полученные в результате проведенного анализа для режима слабых флуктуаций.

1. Анализ стохастического распределения фазы на экране с заданными при генерации параметрами $h$ и ${{\lambda }^{2}}$ во всем диапазоне масштабов ${{L}_{j}}$ приводит к оценкам параметров ${{C}_{1}} \approx h,$ ${{C}_{2}} \approx - {{\lambda }^{2}},$ ${{C}_{3}} \approx 0,$ что подтверждает соответствие генерируемых распределений фазы на экране заданной мультифрактальной модели.

2. Распределение флуктуаций фазы за экраном характеризуется тем же скейлингом, что и на экране, но лишь для масштабов, больших размера зоны Френеля ${{L}_{j}} > {{L}_{F}}$. Для масштабов, меньших зоны Френеля, параметр ${{C}_{2}}$ принимает положительные значения. В этом случае скейлинговая экспонента $\zeta (q)$ более не является выпуклой функцией параметра $q$, что не позволяет на этих масштабах рассматривать флуктуации фазы как мультифрактальный процесс. Степенной характер процесса при этом сохраняется, причем скейлинговая экспонента структурной функции фазы второго порядка $\zeta (2) = 2(h - {{\lambda }^{2}})$ сохраняет заданное значение 5/3.

3. Распределение флуктуаций амплитуды для масштабов, меньших зоны Френеля, характеризуется тем же скейлингом, что и распределение фазы для этих масштабов.

Согласно приведенным выше результатам анализ крупномасштабных (больших зоны Френеля) флуктуаций фазы позволяет в принципе решить обратную задачу определения параметров мультифрактальной модели стохастических флуктуаций фазы на экране по измерениям характеристик сигнала за экраном. Действительно, параметры ${{C}_{1}}$ и ${{C}_{2}}$ представления скейлинговой экспоненты (12), определяемые для крупномасштабных флуктуаций фазы за экраном, являются оценками соответствующих параметров $h$ и ${{\lambda }^{2}}$ мультифрактальной модели распределения фазы на экране. Этот вывод объясняется тем, что для крупномасштабных возмущений реализуется режим геометрической оптики, при котором фаза сигнала практически не искажается при распространении от экрана до земной поверхности. Напротив, скейлинговые свойства мелкомасштабных флуктуаций фазы и амплитуды с масштабами, меньшими зоны Френеля, отличаются от соответствующих характеристик фазы на экране. По всей видимости, для этих масштабов дифракция приводит к нормализации исходно негауссовских процессов, что ведет к разрушению специфического мультифрактального скейлинга.

На рис. 4а, 4б представлены зависимости коэффициентов эксцесса функций распределения флуктуаций разностей фаз и разностей уровней поля за экраном от пространственного разнесения точек (пространственного масштаба флуктуаций). Как видно из рис. 4а, для пространственных масштабов флуктуаций, больших размера зоны Френеля $L > {{L}_{\operatorname{F} }},$ коэффициенты эксцесса распределений разностей фаз за экраном близки к их значениям на экране, а при меньших масштабах, $L \leqslant {{L}_{\operatorname{F} }}$, уменьшаются при уменьшении масштабов флуктуаций, приближаясь к малым значениям, характерным для процессов, близких к нормальному.

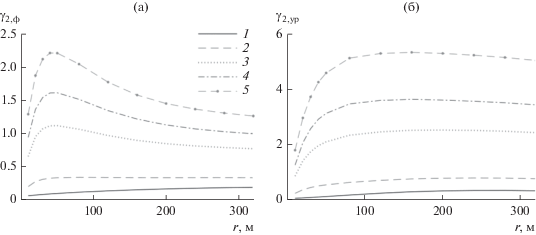
Что касается коэффициентов эксцесса распределения флуктуаций уровня, то для пространственных масштабов флуктуаций, больших размера зоны Френеля, они превышают значения ${{\gamma }_{2}}$ для флуктуаций разностей фаз и убывают с ростом масштаба, а в области масштабов, меньших зоны Френеля, коэффициенты эксцесса флуктуаций уровня также стремятся к нулю, что соответствует нормальному распределению.

Рассмотрим теперь, как наличие перемежаемости влияет на такие статистические характеристики флуктуаций принимаемого поля, как когерентность и индекс сцинтилляций. Функция когерентности комплексного поля $u(\vec {r},z)$ на расстоянии $z$ от стохастического фазового экрана определяется следующими соотношениями:

Отсутствие зависимости функции когерентности от $z$ отражает хорошо известный факт, что функция когерентности плоской волны за экраном не зависит от расстояния от экрана. В случае нормального распределения фазы на экране функция когерентности может быть выражена через структурную функцию фазы второго порядка на экране в явном виде:

Если распределение фазы на экране отлично от нормального, то соотношение (18) не имеет места и усреднение в (17) выполняется численно для различных значений параметра ${{\lambda }^{2}}$.

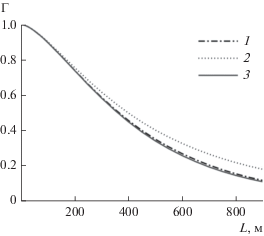
На рис. 5 представлены зависимости $\Gamma (L)$, вычисленные для двух значений ${{\lambda }^{2}}$, 0.0001 и 0.15, при одинаковом спектре мощности флуктуаций фазы. Для сравнения на рис. 5 также представлен результат формального вычисления $\Gamma (L)$ по формуле (18). Как видно из рисунка, с ростом параметра ${{\lambda }^{2}}$ радиус когерентности увеличивается.

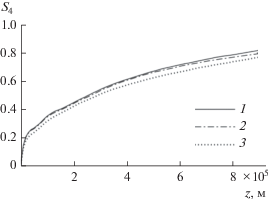
Флуктуации амплитуды за экраном характеризуются индексом мерцаний ${{S}_{4}}$ – среднеквадратичным отклонением нормированных флуктуаций интенсивности:

На рис. 6 представлены зависимости величины индекса мерцаний ${{S}_{4}}$ от расстояния за экраном для нескольких значений параметра ${{\lambda }^{2}}$. Для выбранных параметров расчета индекс мерцаний ${{S}_{4}}$, соответствующий фиксированному ${{\lambda }^{2}}$, монотонно увеличивается при удалении от экрана. При этом индекс мерцаний на фиксированном расстоянии от экрана тем меньше, чем больше значение параметра ${{\lambda }^{2}}$.

ЗАКЛЮЧЕНИЕ

В работе представлены первые результаты моделирования флуктуаций трансионосферных сигналов при распространении в условиях перемежаемой ионосферной турбулентности. Для моделирования флуктуаций поля был использован метод фазового экрана. Перемежаемое распределение фазы на экране задавалось представленной в работе моделью негауссовского мультифрактального фазового экрана, которая позволила моделировать различные режимы перемежаемости, – от полного ее отсутствия до весьма значительной. Результаты исследования функции когерентности поля за экраном выявили увеличение радиуса когерентности с увеличением степени перемежаемости. Расчеты индекса сцинтилляций показали уменьшение индекса на земной поверхности с ростом степени перемежаемости, и более медленную его эволюцию при удалении от экрана. Кроме того, показано, что анализ крупномасштабных (больших зоны Френеля) флуктуаций фазы позволяет решить обратную задачу определения параметров мультифрактальной модели стохастических возмущений фазы на экране по измерениям характеристик сигнала за экраном.

Все расчеты эффектов перемежаемости проведены в работе при одном и том же степенном спектре распределения фазы на экране, специально поддерживаемом постоянным. При этом статистические характеристики флуктуаций результирующего поля были различны при различных значениях перемежаемости. Это значит, что описания флуктуаций на уровне вторых моментов в ряде случаев недостаточно, и необходимо учитывать высшие моменты распределений.