Радиотехника и электроника, 2020, T. 65, № 6, стр. 612-620
Автодинный эффект СВЧ-генераторов с внешней синхронизацией
В. Я. Носков a, *, К. А. Игнатков a, К. Д. Шайдуров a
a Уральский федеральный университет им. первого Президента России Б.Н. Ельцина
620002 Екатеринбург, ул. Мира, 19, Российская Федерация
* E-mail: noskov@oko.ek.ru
Поступила в редакцию 03.04.2019
После доработки 24.04.2019
Принята к публикации 30.04.2019
Аннотация
Представлены результаты исследований особенностей формирования автодинного отклика в генераторах, находящихся под воздействием одновременно собственного отраженного излучения и внешнего синхронизирующего воздействия. Получены основные соотношения для анализа автодинного отклика как при условии квазистатически медленного перемещения объекта локации, так и при быстром его перемещении, когда период сигнала соизмерим с постоянной времени автодинного отклика. Выполнены расчеты параметров и характеристик синхронизированного автодина. Показаны преимущества таких автодинов по сравнению с обычными автодинами без синхронизации. Результаты теоретических исследований подтверждены экспериментальными данными, полученными на примере генератора, выполненного на основе диода Ганна 8-миллиметрового диапазона.
ВВЕДЕНИЕ
Автодинные приемопередатчики (автодины, АД), находят широкое применение в системах ближней радиолокации (СБРЛ), датчиках и измерителях параметров технологических процессов в промышленности и на транспорте, а также в различных научных приложениях, военном деле и медицине [1–4]. Обработка полученных в АД сигналов обеспечивает возможность извлечения информации об электрофизических свойствах объектов локации и их кинематических характеристиках: расстояния, скорости движения, ускорения, параметров вибрации, величины перемещения и пр. Широкому распространению АД способствует прежде всего конструктивная простота и низкая стоимость СВЧ-модулей, а также высокая чувствительность к воздействию собственного отраженного от объекта локации излучения.
Принцип действия данных устройств основан на автодинном эффекте, состоящем в изменении параметров автоколебаний под воздействием отраженного от объекта локации излучения. К настоящему времени автодинный эффект исследован почти во всех типах генераторов, включая оптические квантовые генераторы как с непрерывным излучением, так и с различными видами модуляции [5–7]. Рассмотрены особенности формирования автодинного отклика в условиях слабого и сильного отраженного излучения, а также при различных скоростях движения объектов локации [8‒10]. Кроме того, изучены многочастотные и многоэлементные АД [11–13], а также АД, стабилизированные по частоте, например, посредством дополнительного высокодобротного резонатора [14] или синхронизирующего сигнала от внешнего генератора [15–18].
При этом необходимо отметить, что случай внешней синхронизации АД в известных нам работах рассмотрен без учета ряда специфических факторов, свойственных генераторам СВЧ-диапазона, например, их неизохронности и неизодромности [19]. Кроме того, не исследованы динамические характеристики синхронизированных АД (САД), которые необходимо учитывать в условиях высоких скоростей движения объектов локации [8, 9].
Цель данной работы – исследование поведения амплитуды и фазы колебаний СВЧ-генератора в зависимости от уровня отраженного излучения и частоты автодинного сигнала с учетом внутренних параметров этого генератора и условий его синхронизации.
1. ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ АНАЛИЗА АВТОДИННОГО ЭФФЕКТА
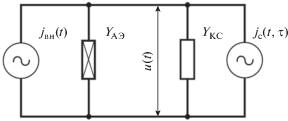
Эквивалентная схема САД, приведенная к плоскости активного элемента (АЭ), представлена на рис. 1. На этой схеме ${{Y}_{{{\text{КС}}}}}$ отображает проводимость колебательной системы (КС). В случае одноконтурной КС выражение для этой проводимости с учетом нагрузки имеет вид
(1)
$\begin{gathered} {{Y}_{{{\text{КС}}}}} \equiv {{Y}_{{{\text{КС}}}}}(\omega ) = {{G}_{{{\text{КС}}}}} + j{{B}_{{{\text{КС}}}}} = \\ = {{G}_{{{\text{КС}}}}}[{\text{1 + }}j{\text{2}}{{Q}_{{\text{н}}}}{{(\omega - {{\omega }_{{\text{с}}}})} \mathord{\left/ {\vphantom {{(\omega - {{\omega }_{{\text{с}}}})} {{{\omega }_{{\text{с}}}}}}} \right. \kern-0em} {{{\omega }_{{\text{с}}}}}}], \\ \end{gathered} $где ${{G}_{{{\text{КС}}}}} = {{G}_{{\text{р}}}} + {{G}_{{\text{н}}}}$ и ${{B}_{{{\text{КС}}}}} = {\text{2}}{{G}_{{{\text{КС}}}}}{{Q}_{{\text{н}}}}{{(\omega - {{\omega }_{{\text{с}}}})} \mathord{\left/ {\vphantom {{(\omega - {{\omega }_{{\text{с}}}})} {{{\omega }_{{\text{с}}}}}}} \right. \kern-0em} {{{\omega }_{{\text{с}}}}}}$ – резистивная и реактивная проводимости КС соответственно; ${{G}_{{\text{р}}}}$, ${{G}_{{\text{н}}}}$ – проводимости собственных потерь резонатора и нагрузки; ${{Q}_{{\text{н}}}}$, ${{\omega }_{{\text{с}}}}$ – нагруженная добротность и собственная частота КС; $\omega $ – текущая частота колебаний генератора. Средняя за период колебаний проводимость АЭ, обладающего вольт-амперной характеристикой N-типа, в общем случае является зависимой от амплитуды A и текущей частоты $\omega $ колебаний
где ${{G}_{{{\text{АЭ}}}}}$, ${{B}_{{{\text{АЭ}}}}}$ – резистивная и реактивная проводимости АЭ соответственно.
Эквивалентные источники мгновенного тока jвн(t) и jс(t, τ) на рис. 1 отображают воздействие на АД внешнего синхронизирующего сигнала и сигнала на нагрузке генератора, вызванного собственным запаздывающим на время τ отраженным СВЧ-излучением. Здесь ${{j}_{{{\text{вн}}}}}(t)$ = ${\text{Re(}}{{J}_{{{\text{вн}}}}}\exp j{{\omega }_{{{\text{вн}}}}}t{\text{)}}$, где ${{J}_{{{\text{вн}}}}}$, ${{\omega }_{{{\text{вн}}}}}$ – амплитуда и частота “внешнего” сигнала. При условии выполнения баланса амплитуд и фаз в схеме под действием тока АЭ возникает генерация незатухающих колебаний $u(t)$. Учитывая обычно достаточно высокое значение нагруженной добротности ${{Q}_{{\text{н}}}}$ КС, полагаем, что колебания на АЭ являются квазигармоническими:
где $A = A{\text{(}}t{\text{)}}$, $\varphi = \varphi {\text{(}}t{\text{)}}$ – медленно меняющиеся за период колебаний амплитуда и фаза. Тогда колебания эквивалентного источника ${{j}_{{\text{с}}}}(t,\tau )$ являются также квазигармоническими:
где ${{J}_{{\text{с}}}}$ – амплитуда и $\delta {\text{(}}t{\text{,}}\tau {\text{)}}$ – набег фазы отраженного СВЧ излучения.
Согласно законам Кирхгофа для цепи, приведенной на рис. 1, имеем
(2)
${\text{Re [}}\dot {A}{\text{(}}{{Y}_{{{\text{АЭ}}}}} + {{Y}_{{{\text{КС}}}}}{\text{)]}} = {\text{ }}{{j}_{{\text{с}}}}{\text{(}}t,\tau {\text{)}} + {{j}_{{{\text{вн}}}}}{\text{(}}t{\text{)}}{\text{.}}$Для получения укороченных уравнений возмущенного генератора в выражении (2) после подстановки в него (1) сначала сделаем замену $\omega $ на выражение ${{\omega }_{{{\text{вн}}}}} + d\varphi {\text{/}}dt$ – $j{\text{(}}{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} A}} \right. \kern-0em} A}{\text{)(}}{{dA} \mathord{\left/ {\vphantom {{dA} {dt}}} \right. \kern-0em} {dt}}{\text{)}}$ [20]. Здесь в силу медленности $\varphi {\kern 1pt} {\text{(}}t{\text{)}}$ и $A{\text{(}}t{\text{)}}$ величины $d\varphi {\text{/}}dt$ и ${\text{(}}{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} A}} \right. \kern-0em} A}{\text{)(}}{{dA} \mathord{\left/ {\vphantom {{dA} {dt}}} \right. \kern-0em} {dt}}{\text{)}}$ являются достаточно малыми по сравнению с частотой ${{\omega }_{{{\text{вн}}}}}$. Далее, после выполнения операции усреднения за период колебаний и ряда элементарных преобразований получим укороченные уравнения для амплитуды $A$ и фазы $\varphi $ в виде
(3)
$\begin{gathered} \frac{{{{Q}_{{\text{н}}}}}}{{{{\omega }_{{\text{с}}}}}}\frac{1}{A}\frac{{dA}}{{dt}} + \frac{{{{G}_{{{\text{АЭ}}}}} + {{G}_{{{\text{КС}}}}}}}{{{\text{2}}{{G}_{{{\text{КС}}}}}}}{\text{ = }} \\ {\text{ = }}\Gamma \eta {\text{cos}}\delta {\text{(}}t{\text{,}}\tau {\text{)}} + {{k}_{{{\text{вн}}}}}\eta \cos \varphi , \\ \end{gathered} $(4)
$\begin{gathered} \frac{{{{Q}_{{\text{н}}}}}}{{{{\omega }_{{\text{с}}}}}}\frac{{d\varphi }}{{dt}} + \frac{{{{B}_{{{\text{АЭ}}}}} + {{B}_{{{\text{КС}}}}}}}{{{\text{2}}{{G}_{{{\text{КС}}}}}}}\,\,{\text{ = }} \\ {\text{ = }} - \Gamma \eta {\text{sin}}\delta {\text{(}}t{\text{,}}\tau {\text{)}} - {{k}_{{{\text{вн}}}}}\eta \sin \varphi , \\ \end{gathered} $где ${\text{Г}}$, ${{k}_{{{\text{вн}}}}} = {{{{J}_{{{\text{вн}}}}}} \mathord{\left/ {\vphantom {{{{J}_{{{\text{вн}}}}}} {{{G}_{{{\text{КС}}}}}A}}} \right. \kern-0em} {{{G}_{{{\text{КС}}}}}A}}$ – коэффициенты, характеризующие относительные уровни на нагрузке генератора, принятого от объекта локации излученного колебания и внешнего синхронизирующего воздействия соответственно; $\eta = {{{{Q}_{{\text{н}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{\text{н}}}}} {{{Q}_{{{\text{вн}}}}}}}} \right. \kern-0em} {{{Q}_{{{\text{вн}}}}}}}$ (${{Q}_{{{\text{вн}}}}}$ – КПД и внешняя добротность КС).
Нетрудно видеть, что система (3), (4) при величине ${{k}_{{{\text{вн}}}}} = 0$, когда внешнее воздействие отсутствует, описывает работу обычного АД без синхронизации [19]. Если при этом принять, что $\Gamma $ и производные равны нулю, то получим известные выражения “баланса проводимостей” для нахождения амплитуды ${{A}_{0}}$ и частоты ${{\omega }_{0}}$ стационарных колебаний автономного генератора [20]:
(5)
$\begin{gathered} {{G}_{{{\text{АЭ}}}}}({{A}_{0}},{{\omega }_{0}}) + {{G}_{{{\text{КС}}}}}({{\omega }_{0}}) = 0, \\ {{B}_{{{\text{АЭ}}}}}({{A}_{0}},{{\omega }_{0}}) + {{B}_{{{\text{КС}}}}}({{\omega }_{0}}) = 0. \\ \end{gathered} $При условии $\Gamma = 0$ система (3), (4) описывает функционирование синхронизированного на частоте ${{\omega }_{{{\text{вн}}}}}$ автогенератора [20]. В этом случае, полагая в уравнениях (3), (4) производные равными нулю, получим основные соотношения для определения амплитуды $A_{{{\text{син}}}}^{0}$ и фазы ${{\varphi }_{0}}$ генерации в стационарном режиме синхронизированных автоколебаний:
(6)
$[{{G}_{{{\text{АЭ}}}}}(A_{{{\text{син}}}}^{0},{{\omega }_{{{\text{вн}}}}}) + {{{{G}_{{{\text{КС}}}}}({{\omega }_{{{\text{вн}}}}})]} \mathord{\left/ {\vphantom {{{{G}_{{{\text{КС}}}}}({{\omega }_{{{\text{вн}}}}})]} {{\text{2}}{{G}_{{{\text{КС}}}}}{\text{ }}}}} \right. \kern-0em} {{\text{2}}{{G}_{{{\text{КС}}}}}{\text{ }}}}{\text{ = }}{{k}_{{{\text{вн}}}}}\eta \cos {{\varphi }_{0}},$(7)
$[{{B}_{{{\text{АЭ}}}}}(A_{{{\text{син}}}}^{0},{{\omega }_{{{\text{вн}}}}}) + {{{{B}_{{{\text{КС}}}}}({{\omega }_{{{\text{вн}}}}})]} \mathord{\left/ {\vphantom {{{{B}_{{{\text{КС}}}}}({{\omega }_{{{\text{вн}}}}})]} {{\text{2}}{{G}_{{{\text{КС}}}}}}}} \right. \kern-0em} {{\text{2}}{{G}_{{{\text{КС}}}}}}}{\text{ = }} - {{k}_{{{\text{вн}}}}}\eta \sin {{\varphi }_{0}}.$Принципиальным отличием уравнений (3), (4) от уравнений обычного АД [19] является то, что их правую часть, связанную с синхронизирующим воздействием, нельзя считать малой. Во многих применениях уровень этого воздействия может значительно превышать уровень отраженного от объекта излучения. Поэтому при таких условиях эти уравнения нельзя линеаризовать вокруг стационарного автономного режима (5), как это обычно выполняется при анализе несинхронизированных АД.
С учетом сделанного замечания полагаем, что относительный уровень отраженного излучения $\Gamma \ll 1$. При этом далее будем считать, что синхронизирующее воздействие также мало ${{k}_{{{\text{вн}}}}} \ll 1$, но оно может вызывать существенные отклонения стационарного режима автономного генератора по сравнению с воздействием отраженного излучения: ${{k}_{{{\text{вн}}}}} \gg \Gamma $. Поэтому для описания автодинного эффекта далее выполним линеаризацию уравнений (3), (4) относительно стационарного режима синхронных колебаний, описываемых выражениями (6), (7).
Отраженное излучение, воздействуя на КС генератора, как отмечалось выше, вызывает в нем изменения амплитуды $\Delta A = A - A_{{{\text{син}}}}^{0}$ и фазы $\tilde {\varphi } = \varphi - {{\varphi }_{0}}$ колебаний САД относительно их стационарных значений $A_{{{\text{син}}}}^{0}$ и ${{\varphi }_{0}}$. При этом полагаем, что вариации амплитуды $\Delta A$ и фазы $\tilde {\varphi }$ в окрестности стационарного режима колебаний по абсолютной величине являются достаточно малыми: $\left| {\Delta A} \right| \ll A_{{{\text{син}}}}^{0},$ $\left| {\tilde {\varphi }} \right| \ll {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Тогда систему (3), (4) с учетом принятых здесь обозначений и равенств (6), (7) запишем для малых относительных изменений амплитуды $a = {{\Delta A} \mathord{\left/ {\vphantom {{\Delta A} {A_{{{\text{син}}}}^{0}}}} \right. \kern-0em} {A_{{{\text{син}}}}^{0}}}$ и расстройки $\chi = ({{\omega }_{{{\text{вн}}}}} - {{{{\omega }_{0}})} \mathord{\left/ {\vphantom {{{{\omega }_{0}})} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ частот ${{\omega }_{{{\text{вн}}}}}$ и ${{\omega }_{0}}$, а также абсолютных изменений фазы $\tilde {\varphi }$ в следующем виде:
(8)
$\begin{gathered} \frac{{da}}{{dt}} + \frac{1}{{{{\tau }_{a}}}}a + \frac{{{\text{tg}}{{\varphi }_{0}}}}{{{{\tau }_{\varphi }}}}\tilde {\varphi } + \rho ({{\omega }_{{{\text{вн}}}}} - {{\omega }_{0}}) = \\ = \Gamma \frac{{{{K}_{a}}}}{{{{\tau }_{a}}}}{\text{cos}}\delta {\text{(}}t{\text{,}}\tau {\text{),}} \\ \end{gathered} $(9)
$\begin{gathered} \frac{{d\tilde {\varphi }}}{{dt}} + \frac{\gamma }{{{{\tau }_{a}}}}a + \frac{1}{{{{\tau }_{\varphi }}}}\tilde {\varphi } + ({{\omega }_{{{\text{вн}}}}} - {{\omega }_{0}}) = \\ = - \Gamma \frac{{{{K}_{a}}}}{{{{\tau }_{a}}}}{\text{sin}}\delta {\text{(}}t{\text{,}}\tau {\text{),}} \\ \end{gathered} $где ${{K}_{{\text{a}}}} = {\eta \mathord{\left/ {\vphantom {\eta \alpha }} \right. \kern-0em} \alpha }$ – коэффициент автодинного усиления; ${{\tau }_{{\text{a}}}}$, ${{\tau }_{\varphi }}$ – постоянные времени изменений (релаксации) амплитуды и фазы соответственно:
(10)
${{\tau }_{{\text{a}}}} = {{{{Q}_{{\text{н}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{\text{н}}}}} {\alpha {{\omega }_{{\text{0}}}}}}} \right. \kern-0em} {\alpha {{\omega }_{{\text{0}}}}}},\,\,\,\,{{\tau }_{\varphi }} = {{{{Q}_{{{\text{вн}}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{{\text{вн}}}}}} {{{k}_{{{\text{вн}}}}}}}} \right. \kern-0em} {{{k}_{{{\text{вн}}}}}}}{{\omega }_{0}}\cos {{\varphi }_{0}};$$\gamma = {\beta \mathord{\left/ {\vphantom {\beta \alpha }} \right. \kern-0em} \alpha },$ $\rho = {\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{Q}_{{\text{н}}}}}}} \right. \kern-0em} {{{Q}_{{\text{н}}}}}}$ – коэффициенты неизохронности и неизодромности САД соответственно; $\alpha = ({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} {{\text{2}}{{G}_{{{\text{КС}}}}}}}} \right. \kern-0em} {{\text{2}}{{G}_{{{\text{КС}}}}}}}){{({{\partial {{G}_{{{\text{АЭ}}}}}} \mathord{\left/ {\vphantom {{\partial {{G}_{{{\text{АЭ}}}}}} {\partial A}}} \right. \kern-0em} {\partial A}})}_{0}}$, $\varepsilon = ({{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} {{\text{2}}{{G}_{{{\text{КС}}}}}}}} \right. \kern-0em} {{\text{2}}{{G}_{{{\text{КС}}}}}}})$ × $ \times \,\,[\partial ({{G}_{{{\text{АЭ}}}}} + {{{{G}_{{{\text{КС}}}}})} \mathord{\left/ {\vphantom {{{{G}_{{{\text{КС}}}}})} {\partial \omega ]}}} \right. \kern-0em} {\partial \omega ]}}$, $\beta = ({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} {{\text{2}}{{G}_{{{\text{КС}}}}}}}} \right. \kern-0em} {{\text{2}}{{G}_{{{\text{КС}}}}}}}){{({{\partial {{B}_{{{\text{АЭ}}}}}} \mathord{\left/ {\vphantom {{\partial {{B}_{{{\text{АЭ}}}}}} {\partial A}}} \right. \kern-0em} {\partial A}})}_{0}}$ – параметры, характеризующие прочность предельного цикла, неизодромность и неизохронность генератора соответственно;
${{\theta }_{0}} = {\text{arctg}}\,\gamma $ – угол смещения фазовых характеристик; ${{\chi }_{{\text{н}}}} = ({{\omega }_{{{\text{вн}}}}} - {{{{\omega }_{0}})} \mathord{\left/ {\vphantom {{{{\omega }_{0}})} {{{\Delta }_{m}}}}} \right. \kern-0em} {{{\Delta }_{m}}}}$ – нормированная расстройка частот ${{\omega }_{{{\text{вн}}}}}$ и ${{\omega }_{0}}$;
– полуширина полосы синхронизации генератора.
Полученная система линеаризованных уравнений (8) и (9) с учетом известного принципа дуальности обладает достаточной общностью для анализа автодинного эффекта в синхронизированных СВЧ генераторах с любым типом АЭ (туннельные диоды, диоды Ганна и лавинно-пролетные диоды, полевые и биполярные транзисторы и др.). Эти уравнения будем использовать при исследовании квазистатических и динамических характеристик АД.
2. КВАЗИСТАТИЧЕСКИЕ ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ СИНХРОНИЗИРОВАННОГО АВТОДИНА
Для получения аналитических решений дифференциальных уравнений, описывающих поведение автоколебательных систем, широко используется так называемый квазистатический метод [21]. Этот метод позволяет сравнительно просто рассчитать характеристики АД, определяющие формирование их выходных сигналов. Для нахождения этих характеристик положим в (8), (9) производные равными нулю и учтем, что в синхронном режиме $\omega = {{\omega }_{{{\text{вн}}}}}$ и набег фазы $\delta {\text{(}}t{\text{,}}\tau {\text{)}} = {{\omega }_{{{\text{вн}}}}}\tau $. Тогда из образовавшейся системы алгебраических уравнений получим выражения для автодинных изменений фазы $\tilde {\varphi }{\text{(}}\tau {\text{)}}$ и амплитуды $a\,{\text{(}}\tau {\text{)}}$ САД:
(12)
$\tilde {\varphi }{\text{(}}\tau {\text{)}} = - ({{{{Q}_{{{\text{вн}}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{{\text{вн}}}}}} {{{k}_{{{\text{вн}}}}}}}} \right. \kern-0em} {{{k}_{{{\text{вн}}}}}}}){{h}_{\varphi }}\chi - ({\Gamma \mathord{\left/ {\vphantom {\Gamma {{{k}_{{{\text{вн}}}}}}}} \right. \kern-0em} {{{k}_{{{\text{вн}}}}}}}){{H}_{\varphi }}{\text{sin(}}{{\omega }_{{{\text{вн}}}}}\tau + \theta ),$(13)
$a{\text{(}}\tau {\text{)}} = - {{K}_{{\text{a}}}}{{Q}_{{{\text{вн}}}}}{{h}_{{\text{a}}}}\chi + \Gamma {{K}_{{\text{a}}}}{{H}_{{\text{a}}}}{\text{cos(}}{{\omega }_{{{\text{вн}}}}}\tau - {{\varphi }_{0}}{\text{),}}$где ${{h}_{\varphi }}$, ${{h}_{{\text{a}}}}$, ${{H}_{\varphi }}$, ${{H}_{{\text{a}}}}$ – коэффициенты передачи, обусловленные внутренними параметрами генератора и условиями его синхронизации:
(14)
${{h}_{\varphi }} = \frac{{1 - \gamma \rho }}{{(1 - \gamma {\text{tg}}{{\varphi }_{0}})\cos {{\varphi }_{0}}}},\,\,\,\,{{h}_{{\text{a}}}} = \frac{{\rho - {\text{tg}}{{\varphi }_{0}}}}{{(1 - \gamma {\text{tg}}{{\varphi }_{0}})}},$(15)
${{H}_{\varphi }} = \frac{{{{{(1 + {{\gamma }^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{(1 - \gamma {\text{tg}}{{\varphi }_{0}})\cos {{\varphi }_{0}}}},\,\,\,\,{{H}_{{\text{a}}}} = \frac{1}{{(1 - \gamma {\text{tg}}{{\varphi }_{0}})\cos {{\varphi }_{0}}}}.$Как видно из (12), (13), первые члены правых частей определяют уровень постоянной составляющей относительно стационарного режима автономного генератора, которая обусловлена действием только внешнего синхронизирующего сигнала. Вторые члены в этих выражениях связаны с воздействием отраженного СВЧ-излучения, они определяют формирование зависимостей мгновенных значений изменений амплитуды и фазы колебаний от времени запаздывания $\tau $ отраженного излучения.
Первую зависимость в теории АД принято называть амплитудной характеристикой [19], вторую назовем фазовой характеристикой САД. В отличие от характеристик обычных (несинхронизированных) АД характеристики САД, как видно из (12), (13), являются гармоническими функциями времени запаздывания $\tau $ отраженного излучения.
На рис. 2 представлены зависимости коэффициентов ${{h}_{\varphi }}({{\chi }_{{\text{н}}}})$, ${{h}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$, ${{H}_{\varphi }}({{\chi }_{{\text{н}}}})$ и ${{H}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$, рассчитанные согласно (14), (15) с учетом (11) при различных значениях коэффициента неизохронности $\gamma $. Из рис. 2а видно, что функция ${{h}_{\varphi }}({{\chi }_{{\text{н}}}})$ обладает центральной симметрией относительно начала координат. При этом вариации коэффициентов $\gamma $ и $\rho $, как показали расчеты, вызывают лишь изменения угла наклона кривых. Функция ${{h}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$ в случае изохронного генератора, когда $\gamma = 0$, обладает осевой симметрией (см. рис. 2б, кривая 1). При этом вариации коэффициентов $\gamma $ и $\rho $ вызывают нарушения этой симметрии при сохранении значительного роста коэффициентов ${{h}_{\varphi }}({{\chi }_{{\text{н}}}})$ и ${{h}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$ на краях полосы синхронизации (см. рис. 2б, кривые 2 и 3).
Рис. 2.
Зависимости ${{h}_{\varphi }}({{\chi }_{{\text{н}}}})$ (а), ${{h}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$ (б), ${{H}_{\varphi }}({{\chi }_{{\text{н}}}})$ (в) и ${{H}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$ (г), рассчитанные при различных значениях коэффициента: $\gamma = 1.5$ (1), 0 (2), –2.5 (3).
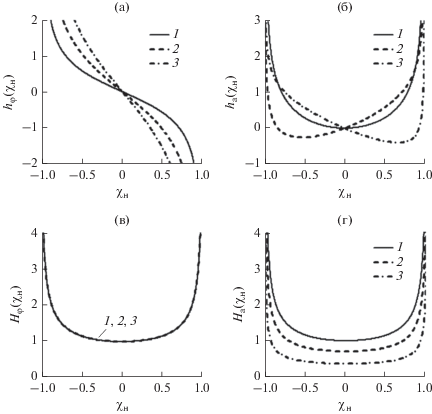
Зависимости ${{H}_{\varphi }}({{\chi }_{{\text{н}}}})$ и ${{H}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$ (см. рис. 2в, 2г) обладают осевой симметрией относительно оси ординат при всех вариациях коэффициента $\gamma $. В центре полосы синхронизации коэффициенты передачи имеют наименьшие значения, а к краям полосы синхронизации наблюдается их быстрый рост. При этом значение коэффициента передачи ${{H}_{{\text{a}}}}({{\chi }_{{\text{н}}}})$ в центре полосы синхронизации изохронного ($\gamma = 0$) САД равно единице (см. рис. 2г, кривая 1), поэтому в этой области расстройки ${{\chi }_{{\text{н}}}}$ значения коэффициентов автодинного усиления САД и обычного АД совпадают.
В случае неизохронного генератора ($\gamma \ne 0$) результирующий коэффициент передачи САД, равный произведению ${{K}_{{\text{а}}}}{{H}_{{\text{а}}}}$, за счет снижения величины Hа (см. рис. 2г, кривые 2 и 3) имеет меньшие значения, чем величина коэффициента автодинного усиления обычного АД Kа. При этом, если внести начальную расстройку между частотами ${{\omega }_{{{\text{вн}}}}}$ и ${{\omega }_{0}}$ ближе к краю полосы синхронизации, то в САД имеется возможность значительного увеличения коэффициента передачи автодинного сигнала по сравнению с обычным АД, что было установлено также в [16, 17].
Необходимо отметить, что сделанные здесь выводы справедливы при соблюдении неравенства: ${{T}_{{\text{a}}}} \gg {{\tau }_{{\text{a}}}},$ где ${{T}_{{\text{а}}}} = {{{\text{2}}\pi } \mathord{\left/ {\vphantom {{{\text{2}}\pi } {{{\Omega }_{{\text{д}}}}}}} \right. \kern-0em} {{{\Omega }_{{\text{д}}}}}}$ – период автодинного сигнала, ${{\Omega }_{{\text{д}}}}$ – его частота, равная доплеровской частоте [21]. Это неравенство выполняется при условии достаточно “медленного” перемещения отражающего объекта, при котором АД успевает “реагировать” на изменения фазы $\delta {\text{(}}t{\text{,}}\tau {\text{)}}$ коэффициента отражения. Для более точного определения предельных возможностей САД далее рассмотрим динамические характеристики АД в случае “быстрого” перемещения объекта локации.
3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ АВТОДИНОВ
Для определения динамических характеристик САД зададим в системе уравнений (8), (9) начальные условия взаимодействия генератора с отраженным от движущегося объекта локации СВЧ излучением, когда $\tau \equiv \tau (t)$. При условии постоянства скорости движения набег фазы $\delta {\text{(}}t{\text{,}}\tau {\text{)}}$ запишем следующим образом:
(16)
$\delta {\text{(}}t{\text{,}}\tau {\text{)}} = {{\omega }_{{{\text{вн}}}}}\tau (t) = {{\Omega }_{{\text{д}}}}t + {{\delta }_{{\text{0}}}},$(17)
$\begin{gathered} \frac{{{{d}^{2}}a}}{{d{{t}^{2}}}} + \frac{{{{\tau }_{{\text{a}}}} + {{\tau }_{\varphi }}}}{{{{\tau }_{{\text{a}}}}{{\tau }_{\varphi }}}}\frac{{da}}{{dt}} + \frac{{1 - \gamma {\text{tg}}{{\varphi }_{0}}}}{{{{\tau }_{{\text{a}}}}{{\tau }_{\varphi }}}}a = \\ = \Gamma \frac{{{{K}_{{\text{a}}}}}}{{{{\tau }_{{\text{a}}}}}}\frac{1}{{{{\tau }_{\varphi }}}}[{\text{cos}}{{\Omega }_{{\text{д}}}}t + ({\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}\Omega {\text{)sin}}{{\Omega }_{{\text{д}}}}t], \\ \end{gathered} $(18)
$\begin{gathered} \frac{{{{d}^{2}}\tilde {\varphi }}}{{d{{t}^{2}}}} + \frac{{{{\tau }_{{\text{a}}}} + {{\tau }_{\varphi }}}}{{{{\tau }_{{\text{a}}}}{{\tau }_{\varphi }}}}\frac{{d\tilde {\varphi }}}{{dt}} + \frac{{1 - \gamma {\text{tg}}{{\varphi }_{0}}}}{{{{\tau }_{{\text{a}}}}{{\tau }_{\varphi }}}}\tilde {\varphi } = \\ = - \Gamma \frac{{{{K}_{{\text{a}}}}}}{{{{\tau }_{{\text{a}}}}}}\frac{1}{{{{\tau }_{{\text{a}}}}}}\left[ {{\text{sin}}{{\Omega }_{{\text{д}}}}t + (\gamma + \Omega )\cos {{\Omega }_{{\text{д}}}}t} \right], \\ \end{gathered} $Правые части уравнений (17), (18) являются тригонометрическими функциями времени. Поэтому общие решения этих уравнений ищем в виде функций
где ${{Z}_{s}}$, ${{Z}_{c}}$, ${{W}_{s}}$, ${{W}_{c}}$ – искомые множители при синусе (индекс “s”) и косинусе (индекс “c”). После ряда элементарных преобразований полученных решений запишем окончательные выражения для установившихся значений динамических изменений фазы $\tilde {\varphi }(t)$ и амплитуды $a\,(t)$ САД:
(19)
$\tilde {\varphi }(t) = - ({\Gamma \mathord{\left/ {\vphantom {\Gamma {{{k}_{{{\text{вн}}}}}}}} \right. \kern-0em} {{{k}_{{{\text{вн}}}}}}}){{H}_{\varphi }}{{\Phi }_{{\text{д}}}}(\Omega )\sin [{{\Omega }_{{\text{д}}}}t + {{\theta }_{{\text{д}}}}(\Omega )],$(20)
$a(t) = \Gamma {{K}_{{\text{a}}}}{{H}_{{\text{a}}}}{{K}_{{\text{д}}}}(\Omega )\cos [{{\Omega }_{{\text{д}}}}t + {{\psi }_{{\text{д}}}}(\Omega )],$где ${{\Phi }_{{\text{д}}}}(\Omega )$, ${{K}_{{\text{д}}}}(\Omega )$ – “динамические” амплитудно-частотные характеристики (АЧХ) САД по изменению фазы и амплитуды колебаний соответственно:
${{\theta }_{{\text{д}}}}(\Omega )$, ${{\psi }_{{\text{д}}}}(\Omega )$ – углы “динамического” смещения изменений фазы и относительных изменений амплитуды колебаний САД соответственно:
(23)
${{\theta }_{{\text{д}}}}(\Omega ) = {\text{arctg[}}{{{{w}_{c}}(\Omega )} \mathord{\left/ {\vphantom {{{{w}_{c}}(\Omega )} {{{w}_{s}}(\Omega )}}} \right. \kern-0em} {{{w}_{s}}(\Omega )}}];$(24)
${{\psi }_{{\text{д}}}}(\Omega ) = {\text{arctg[}}{{{{z}_{s}}(\Omega )} \mathord{\left/ {\vphantom {{{{z}_{s}}(\Omega )} {{{z}_{c}}(\Omega )}}} \right. \kern-0em} {{{z}_{c}}(\Omega )}}],$${{z}_{s}}(\Omega )$, ${{z}_{c}}(\Omega )$, ${{w}_{s}}(\Omega )$, ${{w}_{c}}(\Omega )$ – нормированные относительно значений ${{H}_{{\text{a}}}}$ и ${{H}_{\varphi }}$ квадратурные множители:
(25)
$\begin{gathered} {{z}_{s}}(\Omega ) = \frac{{{{Z}_{s}}}}{{{{H}_{{\text{a}}}}}} = \\ = \frac{{({\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}\Omega )(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}}) + (1 + {{k}_{\Omega }})\Omega }}{{{{H}_{{\text{a}}}}[{{{(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}})}}^{2}} + {{{(1 + {{k}_{\Omega }})}}^{2}}{{\Omega }^{2}}]}}, \\ \end{gathered} $(26)
$\begin{gathered} {{z}_{c}}(\Omega ) = \frac{{{{Z}_{c}}}}{{{{H}_{{\text{a}}}}}} = \\ = \frac{{(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}}) - ({\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}\Omega )(1 + {{k}_{\Omega }})\Omega }}{{{{H}_{{\text{a}}}}[{{{(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}})}}^{2}} + {{{(1 + {{k}_{\Omega }})}}^{2}}{{\Omega }^{2}}]}}, \\ \end{gathered} $(27)
$\begin{gathered} {{w}_{s}}(\Omega ) = \frac{{{{W}_{s}}}}{{{{H}_{\varphi }}}} = \\ = \frac{{(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}}) + (\gamma + \Omega )(1 + {{k}_{\Omega }})\Omega }}{{{{H}_{\varphi }}[{{{(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}})}}^{2}} + {{{(1 + {{k}_{\Omega }})}}^{2}}{{\Omega }^{2}}]\cos {{\varphi }_{0}}}}, \\ \end{gathered} $(28)
$\begin{gathered} {{w}_{c}}(\Omega ) = \frac{{{{W}_{c}}}}{{{{H}_{\varphi }}}} = \\ = \frac{{(\gamma + \Omega )(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}}) - (1 + {{k}_{\Omega }})\Omega }}{{{{H}_{\varphi }}[{{{(1 - \gamma {\text{tg}}{{\varphi }_{0}} - {{k}_{\Omega }}{{\Omega }^{2}})}}^{2}} + {{{(1 + {{k}_{\Omega }})}}^{2}}{{\Omega }^{2}}]\cos {{\varphi }_{0}}}}. \\ \end{gathered} $Анализ выражений (19)–(28) ввиду их сложности выполним численным методом, вводя вариации параметров. При этом будем учитывать, что в САД величины ${{\tau }_{{\text{a}}}}$ и, соответственно, $\Omega = {{\tau }_{{\text{a}}}}{{\Omega }_{{\text{д}}}}$ не зависят от режима синхронизации. Однако постоянная времени ${{\tau }_{\varphi }}$ в зависимости от условий синхронизации может изменяться в широких пределах. Как видно из (10), она имеет наименьшее значение $\tau _{\varphi }^{{{\text{мин}}}} = {{{{Q}_{{{\text{вн}}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{{\text{вн}}}}}} {{{k}_{{{\text{вн}}}}}{{\omega }_{0}}}}} \right. \kern-0em} {{{k}_{{{\text{вн}}}}}{{\omega }_{0}}}}$ в центре полосы синхронизации и резко возрастает на ее краях. Кроме того, величина ${{\tau }_{\varphi }}$ зависит от относительного уровня ${{k}_{{{\text{вн}}}}}$ внешнего синхронизирующего воздействия.
На рис. 3 и 4 представлены результаты вычислений в виде графиков АЧХ коэффициентов передачи автодинных изменений фазы ${{\Phi }_{{\text{д}}}}(\Omega )$ и амплитуды ${{K}_{{\text{д}}}}(\Omega )$ колебаний САД согласно (21) и (22) при различных значениях параметров ${{k}_{\Omega }}$, ${{U}_{{{\text{вн}}}}}$, ${{\chi }_{{\text{н}}}}$ и $\gamma $.
Рис. 3.
Амплитудно-частотные характеристики ${{\Phi }_{{\text{д}}}}(\Omega )$ (а) и ${{K}_{{\text{д}}}}(\Omega )$ (б), рассчитанные для случая $\gamma = 0$, ${{\chi }_{{\text{н}}}} = 0$ и при вариации уровня внешнего воздействия ${{U}_{{{\text{вн}}}}} = 0.1$ (1), 0.05 (2), 0.01 (3).
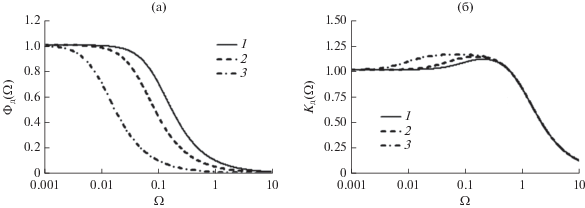
Рис. 4.
Амплитудно-частотные характеристики ${{\Phi }_{{\text{д}}}}(\Omega )$ (а) и ${{K}_{{\text{д}}}}(\Omega )$ (б), рассчитанные для случая ${{U}_{{{\text{вн}}}}} = 0.1$, ${{\chi }_{{\text{н}}}} = 0$ и вариации коэффициента неизохронности: $\gamma = 0$ (1), 1 (2), –1 (3).
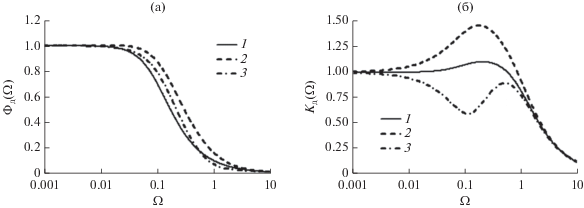
Из рис. 3а и 4а, а также результатов расчета при иных значениях параметров ${{k}_{\Omega }}$, ${{U}_{{{\text{вн}}}}}$, ${{\chi }_{{\text{н}}}}$ и $\gamma $ следует, что АЧХ коэффициентов передачи автодинных изменений фазы ${{\Phi }_{{\text{д}}}}(\Omega )$ САД являются монотонными функциями частоты. При превышении частоты $\Omega $ автодинного сигнала граничного значения $\Omega _{{{\text{гр}}}}^{\varphi }$ величина коэффициента передачи ${{\Phi }_{{\text{д}}}}(\Omega )$ резко спадает. Этот спад АЧХ объясняется инерционностью процесса синхронизации генератора, при котором фаза колебаний синхронизированного генератора не успевает реагировать на быстрые изменения набега фазы $\delta {\text{(}}t{\text{,}}\tau {\text{)}}$. При этом граничная частота коэффициента передачи ${{\Phi }_{{\text{д}}}}(\Omega )$ по уровню ${\text{1/}}{{{\text{2}}}^{{{\text{1}}/{\text{2}}}}}$ определяется постоянной времени ${{\tau }_{\varphi }}$, как у обычного инерционного звена первого порядка:
Из анализа рис. 3б и 4б следует, что АЧХ коэффициента передачи ${{K}_{{\text{д}}}}(\Omega )$ автодинных изменений амплитуды колебаний САД не являются монотонными функциями частоты $\Omega $ автодинного отклика. Вид этих функций в значительной степени определяется условиями синхронизации (значением параметров ${{U}_{{{\text{вн}}}}}$ и ${{\chi }_{{\text{н}}}}$), соотношением ${{k}_{\Omega }}$ постоянных времени ${{\tau }_{{\text{a}}}}$ и ${{\tau }_{\varphi }}$, а также величиной и знаком коэффициента неизохронности $\gamma $.
Причина неравномерности АЧХ коэффициента передачи ${{K}_{{\text{д}}}}(\Omega )$ связана с внутренней “интерференцией” составляющих автодинного отклика по изменению амплитуды колебаний. Первая составляющая связана с преобразованием изменений фазы $\tilde {\varphi }(t)$ СВЧ-генератора в изменения амплитуды его колебаний (см. третий член левой части (8)). Вторая составляющая обусловлена изменениями набега фазы $\delta {\text{(}}t{\text{,}}\tau {\text{)}}$ отраженного СВЧ-излучения (см. правую часть (8)). Динамические смещения фазы ${{\theta }_{{\text{д}}}}(\Omega )$ автодинного отклика в зависимости от частоты Ω, как показали вычисления согласно (23), вызывают изменения фазовых соотношений между этими слагаемыми. Поэтому результирующий отклик по изменению амплитуды $a\,(t)$ колебаний возрастает на тех частотах, на которых составляющие синфазные, и ослабляется на частотах с противофазными слагаемыми.
4. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
В качестве объекта исследований нами использовался гибридно-интегральный генераторный модуль 8-миллиметрового диапазона “Тигель-08М”, изготовленный на основе планарного диода Ганна. Напряжение питания 4 В при токе потребления ~0.2 А, частота генерации модуля 37.5 ГГц, выходная мощность 15 мВт. Для регистрации сигнала по изменению амплитуды колебаний в топологию этого модуля встроен детекторный диод с барьером Шоттки [14, 19].
Экспериментальные исследования модуля выполняли на стенде, описание которого представлено в [14]. Исследуемый автодинный генератор (АГ) связан с доплеровским имитатором сигнала (ДИС) волноводным трактом, в котором находятся также переменный аттенюатор, моделирующий затухание распространяющегося в пространстве излучения, и направленный ответвитель. Одно из плеч ответвителя связано с измерительным генератором, выходной сигнал которого служит для синхронизации АГ. Мощность сигнала синхронизации во всех опытах поддерживалась равной 1 мВт, при этом полуширина полосы синхронизации составляла ${{\Delta }_{m}} = 2\pi \times 50 \times {{10}^{6}}.$
Отрезок волновода сечением $7.2 \times 3.4$ мм2 между АГ и ДИС, моделирующий в стенде запаздывание отраженного излучения, имел длину 12 м ($\tau \approx 100 \times {{10}^{{ - 9}}}$ с). Переменным аттенюатором устанавливалась величина затухания в тракте 20 дБ, автодинная девиация частоты составляла $\Delta {{\omega }_{m}}$$ \approx 2\pi \times 1.3 \times {{10}^{6}}$. При этом обеспечивалась расчетная величина параметра обратной связи ${{C}_{{{\text{о}}{\text{.с}}}}}$ = = $\Delta {{\omega }_{m}}\tau \approx 0.{\text{8}}$ [14]. Обычно при такой величине ${{C}_{{{\text{о}}{\text{.с}}}}}$ сигналы САД имеют заметный уровень ангармонических искажений, что подтверждается представленной на рис. 5а осциллограммой сигнала ${{u}_{{\text{c}}}}(t)$ с выхода диодного детектора.
Рис. 5.
Осциллограммы сигналов ${{u}_{{\text{c}}}}(t)$ САД на диоде Ганна, полученные при отсутствии синхронизации (а) и при ее наличии для случаев, когда ${{\chi }_{{\text{н}}}} = 0$ (б), –0.8 (в) и 0.8 (г).

Остальные осциллограммы получены при воздействии на АГ синхронизирующего сигнала для трех случаев: частота ${{\omega }_{{{\text{вн}}}}}$ соответствует середине полосы синхронизации (рис. 5б), наличие начальной расстройки частоты ${{\omega }_{{{\text{вн}}}}}$ вниз (рис. 5в) и вверх (рис. 5г) на величину 0.8Δm. Скорость движения отражателя ДИС во всех случаях поддерживалась постоянной и составляла 20 м/с.
Из сравнения осциллограмм рис. 5 видно, что сигналы ${{u}_{{\text{c}}}}(t)$ САД являются практически гармоническими. При этом следует отметить, что в середине полосы синхронизации амплитуда автодинного сигнала наименьшая (см. рис. 5б), а при приближении к ее краям – существенно возрастает (см. рис. 5в, 5г). Полученные результаты качественно подтверждают ход кривых на рис. 2г и выводы разд. 2.
Для экспериментального исследования АЧХ САД в широком диапазоне частот использовался косвенный метод их получения, известный как метод “модуляционных характеристик” [22–24]. Косвенный, поскольку прямые измерения этих характеристик с помощью известных нам типов ДИС невозможны из-за их ограниченного быстродействия. Для этого ДИС был заменен диодным модулятором, работающим на отражение (см. [24, рис. 29 ]). Рабочая точка на характеристике диода модулятора была выбрана в середине линейного участка его прямого смещения. На диод через разделительный конденсатор с выхода измерителя комплексных коэффициентов передачи “Обзор-103” подводился модулирующий сигнал уровня 2 дБм. При этом на вход измерителя подавался автодинный сигнал с выхода детекторного диода генераторного модуля “Тигель-08М”. Длина волноводного тракта от АГ до диодного модулятора составляла 0.22 м, затухание аттенюатора в этом тракте устанавливалось около 15 дБ, диапазон анализируемых частот Ω/2π задавался от 0.3 до 300 МГц.
На рис. 6 приведены экспериментальные АЧХ, полученные при отсутствии воздействия на АГ синхронизирующего сигнала (см. кривую 1) и для различных условий синхронизации: частота “внешнего” синхронизирующего сигнала ${{\omega }_{{{\text{вн}}}}}$ соответствует частоте ω0 (кривая 2), наличие начальных расстроек частоты ${{\omega }_{{{\text{вн}}}}}$ вниз (кривая 3) и вверх (кривая 4) относительно частоты ${{\omega }_{0}}$ на величину ${{\chi }_{{\text{н}}}} = 0.8$.
Рис. 6.
Амплитудно-частотные характеристики коэффициентов передачи автодинного отклика по изменению амплитуды колебаний, полученные экспериментально для АД на диоде Ганна при отсутствии синхронизации (кривая 1) и при ее наличии для случаев, когда ${{\chi }_{{\text{н}}}} = 0$ (2), –0.8 (3) и 0.8 (4).
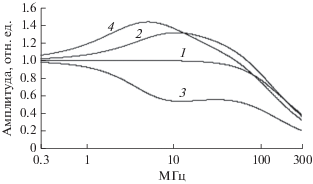
Амплитудно-частотная характеристика генераторного модуля без синхронизации (кривая 1), является равномерной в широком диапазоне частот. Граничная частота этой характеристики по уровню ${{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ составляет ~120 МГц. Величина постоянной времени ${{\tau }_{{\text{а}}}}$ изменений амплитуды равна ${\text{1}}.3 \times {\text{1}}{{0}^{{--{\text{9}}}}}$ с. Это значение ${{\tau }_{{\text{а}}}}$ согласуется с данными, представленными в [22–24]. В случае САД АЧХ модуля, как видно из кривых 2–4 на рис. 6, может иметь существенную неравномерность в области единиц и десятков мегагерц. Эта неравномерность и “асимметрия” АЧХ при наличии расстроек (кривые 3 и 4) относительно АЧХ без них (кривая 2) объясняется различием начальной фазы ${{{\varphi }}_{{\text{0}}}}$ для характеристики ${{\psi }_{{\text{д}}}}(\Omega = 0)$ при смене знака нормированной расстройки ${{\chi }_{{\text{н}}}}$ (11), а также различием дальнейшего хода зависимости ${{\psi }_{{\text{д}}}}(\Omega )$ с увеличением частоты $\Omega $. Изменение фазы ${{{\varphi }}_{{\text{0}}}}$, как видно из (10), изменяет также постоянную времени ${{\tau }_{\varphi }}$, влияющую на значение граничной частоты $\Omega _{{{\text{гр}}}}^{\varphi }$ и, тем самым, на частоту прогиба АЧХ, представленную кривыми 3 и 4 (граничная частота АЧХ кривой 3 получена порядка 1.2…3 МГц). Отметим, что этого диапазона частот с равномерной АЧХ вполне достаточно для регистрации перемещений объектов локации до скоростей 4.8…12 км/с.
Таким образом, полученные результаты экспериментальных исследований подтвердили адекватность разработанной математической модели САД в отношении анализа автодинных параметров и характеристик как при квазистатически малых, так и больших скоростей движения объектов локации.
ЗАКЛЮЧЕНИЕ
Разработана математическая модель автодинного приемопередатчика, стабилизированного по частоте сигналом от дополнительного генератора. Получены основные соотношения для расчета его сигнальных характеристик как при квазистатически медленном перемещении объекта локации, так и при высоких скоростях движения, когда период автодинного сигнала соизмерим с постоянными времени автодинного отклика. Синхронизация автодина от внешнего генератора исключает ангармонические искажения сигналов, характерные для обычных (нестабилизированных) автодинов, что способствует расширению их динамического диапазона. В синхронизированном автодине путем внесения начальной расстройки между частотами внешнего генератора и собственной частотой автодина в пределах полосы синхронизации имеется возможность значительного увеличения коэффициента передачи автодинного сигнала по сравнению с обычными автодинами.
Инерционность процесса фазовой синхронизации генератора вызывает неравномерность формирования амплитудно-частотных характеристик коэффициента передачи синхронизированного автодина по изменению амплитуды колебаний в области высоких частот. Однако эта неравномерность при правильном выборе параметров синхронизации не является препятствием для регистрации сигналов во всем диапазоне существующих на практике скоростей движения объектов локации.
Из результатов исследований следует вывод о перспективности разработки интегральных автодинных модулей с синхронизацией частоты от дополнительного маломощного генератора. Особую актуальность такое техническое решение имеет в диапазоне миллиметровых и более коротких волн.
Список литературы
Усанов Д.А., Скрипаль Ал.В., Скрипаль Ан.В., Постельга А.Э. // ПТЭ. 2004. № 5. С. 130.
Alidoost S.A., Sadeghzade R., Fatemi R. // 11th Intern. Radar Symp. (IRS-2010). Vilnius (Lithuania). 2010. V. 2. P. 406.
Usanov D.A., Postelga A.E. // Biomedical Engineering. 2011. V. 45. № 1. P. 6.
Носков В.Я., Игнатков К.А., Чупахин А.П. // Измерит. техника. 2016. № 7. С. 24.
Гершензон Е.М., Туманов Б.Н., Бузыкин В.Т. и др. // РЭ. 1982. Т. 27. № 1. С. 104.
Воторопин С.Д., Носков В.Я., Смольский С.М. // Изв. вузов. Физика. 2008. Т. 51. № 7. С. 80.
Усанов Д.А., Скрипаль А.В. // Квант. электроника. 2011. Т. 41. № 1. С. 86.
Воторопин С.Д., Носков В.Я. // Изв. вузов. Физика. 2000. Т. 43. № 7. С. 54.
Носков В.Я., Игнатков К.А. // Изв. вузов. Физика. 2013. Т. 56. № 4. С. 56.
Noskov V.Ya., Ignatkov K.A. Chupahin A.P. // 3rd Intern. Workshop on Radio Electronics & Information Technol. Yekaterinburg, 2018. P. 103.
Носков В.Я. // Изв. вузов. Радиофизика. 1992. Т. 35. № 9. С. 778.
Носков В.Я. // ПТЭ. 2015. № 4. С. 65.
Моросанов С.А., Смольский С.М., Филицина Ю.А. // РЭ. 1982. Т. 27. № 4. С. 764.
Носков В.Я., Игнатков К.А. // РЭ. 2016. Т. 61. № 9. С. 905.
Терещенко А.Ф. // Электронная техника. Сер. 1. Электроника СВЧ. 1966. № 2. С. 67.
Артеменков С.Л., Смольский С.М. // Методы и устройства формирования и обработки радиосигналов. Труды МЭИ. М., 1982. Вып. 579. С. 81.
Артеменков С.Л., Смольский С.М. // Современные проблемы стабилизации частоты. Труды МЭИ. М., 1983. Вып. 8. С. 30.
Komarov I.V., Smolskiy S.M. Fundamentals of Short-Range FM Radar. Norwood: Artech House, 2003.
Носков В.Я., Игнатков К.А., Смольский С.М. // Радиотехника. 2012. № 6. С. 24.
Kurokava K. // Proc. IEEE. 1973. V. 61. № 10. P. 1386.
Носков В.Я., Игнатков К.А. // Изв. вузов. Радиоэлектроника. 2014. Т. 57. № 3. С. 44.
Noskov V.Ya., Ignatkov K.A. // Telecommun. Radio Engineering. 2013. V. 72. № 10. P. 919.
Noskov V.Ya., Ignatkov K.A., Smolskiy S.M. // Telecommun. Sci. 2012. V. 3. № 2. P. 44.
Носков В.Я., Игнатков К.А., Смольский С.М. // Успехи совр. радиоэлектроники. 2013. № 6. С. 3.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника