Радиотехника и электроника, 2020, T. 65, № 6, стр. 531-536

ВВЕДЕНИЕ

Как известно, рассеяние электромагнитных волн наноструктурами из благородных металлов (серебра, золота) в световом диапазоне волн ($300\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}$, $\lambda $ – длина волны) сопровождается как образованием поверхностных волн (плазмон-поляритонов), так и наличием у них резонансов. При этом интерес к исследованию свойств плазмон-поляритонов связан главным образом с высокой локализацией электромагнитного поля, которая позволяет их использовать в субволновом и ближнепольном зондировании. Так, нанопровода из серебра и золота широко применяются в качестве сенсоров [1]. Отметим, что плазмонные резонансы в цилиндрических наноструктурах (нитях) из серебра (золота) с круглым поперечным сечением реализуются в ультрафиолетовой части спектра. Используя нанотрубки, можно сместить частоты плазмонных резонансов в видимую область светового диапазона [2, 3]. В [4] исследованы плазмонные резонансы в кварцевой нанонити, покрытой слоем золота переменной толщины в предположении, что границами оболочки являются круговые цилиндры со смещенными центрами. В [5, 6] рассматривались структуры, представляющие собой серебряную оболочку, внутри которой находится цилиндрическая нанонить из стекла (кварца). При этом полагалось, что внешний контур поперечного сечения представляет собой круг или эллипс. Ситуация, когда внешний контур поперечного сечения структуры из серебра является квадратным, а внутренний – круглым, обсуждалась в [7].

Цель данной работы – исследовать особенности плазмонных резонансов в наноструктуре, представляющей собой серебряную пластину с квадратной формой поперечного сечения, в которую симметрично вставлена кварцевая квадратная пластина.

1. ФОРМУЛИРОВКА ЗАДАЧИ

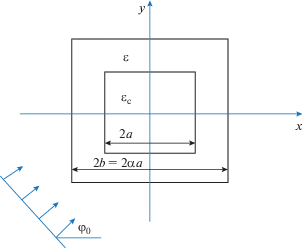
Рассмотрим двумерную задачу дифракции плоской поляризованной электромагнитной ТМ‑волны на двумерной структуре, поперечное сечение которой изображено на рис. 1. Плоская волна распространяется в направлении единичного вектора ($\cos {{\varphi }_{0}},\;\sin {{\varphi }_{0}},\;0$) и характеризуется следующими компонентами электромагнитного поля:

Рис. 1.

Геометрия задачи.

Зависимость от времени выбрана в виде $\exp (i\omega t)$, где $\omega = kc$ – круговая частота, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число свободного пространства, $c$ – скорость света в вакууме, $\eta = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} = 120\pi \,\,Ом$ − волновое сопротивление вакуума, ${{\mu }_{0}},{{\varepsilon }_{0}}$ – магнитная и диэлектрическая проницаемости вакуума.

Для структуры, изображенной на рис. 1, внутренняя и внешняя границы серебряной оболочки описываются соответственно формулами

При значениях $N \gg 1$ (например, при $N = 18$) каждое из уравнений (2), (3), описывает границу оболочки в форме квадрата. Тем самым мы считаем, что слой серебра постоянной толщины d = a – $ - \,b \equiv a(1 - \alpha ),$ $\alpha = {b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$ нанесен на квадратную стеклянную нить. При этом частотная зависимость относительной диэлектрической проницаемости $\varepsilon (\lambda )$ серебра рассчитывалась на основе интерполяции экспериментальных данных работы [8] кубическими сплайнами.

В отличие от серебра стекло в исследуемом диапазоне частот имеет существенно меньшие тепловые потери, а его относительная диэлектрическая проницаемость ${{\varepsilon }_{\operatorname{c} }}$ слабо зависит от длины волны $\lambda $. Поэтому будем полагать, что относительная диэлектрическая проницаемость стекла величина вещественная и равна ${{\varepsilon }_{\operatorname{c} }} = 2.2$.

Пространственное распределение диэлектрической проницаемости $\bar {\varepsilon }(x,y)$ в структуре, изображенной на рис. 1, имеет вид

Исследование сформулированной задачи дифракции удобнее проводить, используя $z$-компоненту $U(x,y) = {{H}_{z}}(x,y)$ магнитного поля, так как краевая задача для функции $U(x,y)$ является скалярной. Полное поле $U(x,y)$, т.е. суперпозиция падающего и рассеянного полей, в кусочно-постоянной среде (4) удовлетворяет уравнению Гельмгольца

Компоненты электрического поля могут быть выражены через функцию $U(x,y)$

На границах оболочки (2), (3) должны быть непрерывны величины $U$ и $\frac{1}{{\bar {\varepsilon }}}\frac{{\partial U}}{{\partial N}}$, где через $\frac{{\partial U}}{{\partial N}}$ обозначена производная по направлению нормали к границам раздела сред.

Как уже отмечалось, полное поле вне оболочки состоит из падающего (${{U}^{0}}$) и рассеянного (${{U}^{s}}$) полей. Падающее поле задано функцией

Рассеянное поле в цилиндрической системе координат ($r,\varphi $), где $x = r\cos \varphi $ и $y = r\sin \varphi $, в дальней зоне ($kr \to \infty $) должно удовлетворять условию излучения

где $\Phi (\varphi )$ − диаграмма рассеяния.

Полное сечение рассеяния ${{\sigma }_{s}}$ определяется формулой

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численное решение сформулированной задачи проводилось модифицированным методом дискретных источников [9–11]. При этом точность решения задачи контролировалась путем вычисления невязки $\Delta $ граничных условий в линейной норме в точках, расположенных в середине интервалов, образованных точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом [9]). Во всех приведенных ниже расчетах максимальная невязка граничных условий не превышала величину $\Delta < {{10}^{{ - 3}}}$.

Рассмотрим сначала поведение нормированного поперечника рассеяния $k{{\sigma }_{s}}$ в зависимости от длины волны $\lambda $. В представленных ниже результатах длина волны $\lambda $ изменялась в пределах $350\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}$. Структура, изображенная на рис. 1, имела следующие параметры: $a = 40\,\,{\text{нм}}$, $\alpha = 0.6,$ $0.7$, $0.8$ (при значениях параметра $\alpha > 0.8$ толщина $d$ слоя серебра становится $d < 8\,\,{\text{нм}}$, что делает невозможным использование уравнений классической электродинамики [1] и результатов работы [8]). При этом угол падения плоской волны ${{\varphi }_{0}}$ принимал следующие значения: ${{\varphi }_{0}} = 0,{\pi \mathord{\left/ {\vphantom {\pi 5}} \right. \kern-0em} 5},{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$

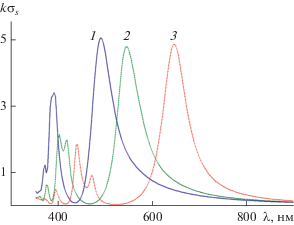
На рис. 2 изображено семейство кривых, описывающих зависимость нормированного полного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = 0$, значениях параметра $\alpha = 0.6$, 0.7, 0.8 и реальных потерь серебра $\operatorname{Im} (\varepsilon )$. Из рисунка видно, что в данном случае каждая кривая содержит один главный максимум и один побочный, который в зависимости от значений $\alpha $ расщепляется на два локальных максимума. Главный максимум кривой $k{{\sigma }_{s}}$ связан с дипольным резонансом плазмонов, а побочный – с квадрупольным резонансом плазмонов. Отсутствие других максимумов у кривых $k{{\sigma }_{s}}$ свидетельствует об отсутствии мультипольных резонансов плазмонов. Ниже будет показано, что их отсутствие связано с влиянием потерь серебра. Из рис. 2 следует, что уменьшение толщины $d$ слоя серебра приводит к смещению дипольного и квадрупольного резонансов в сторону больших значений длин волн, а также различной степени расщепления $k{{\sigma }_{s}}$ в окрестности квадрупольного резонанса плазмонов. Такое поведение кривой $k{{\sigma }_{s}}$ в области квадрупольного резонанса плазмонов свидетельствует о наличии явления вырождения плазмонов в ближнем поле структуры.

Рис. 2.

Зависимость нормированного полного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = 0$, реальных потерях серебра $\operatorname{Im} (\varepsilon )$ и при $\alpha = 0.6$ (1), 0.7 (2), 0.8 (3).

Было исследовано влияние потерь серебра на частотную характеристику амплитуды поля $U(a,y = 0)$ в точке с координатами $x = a,y = 0$ (рис. 3) и поперечника рассеяния $k{{\sigma }_{s}}$ (рис. 4). При этом полагалось, что структура имеет параметры $a = 40\,\,{\text{нм}}$, $\alpha = 0.8,$ угол падения плоской волны ${{\varphi }_{0}} = 0$. Кривые 1–3 этих рисунков соответствуют потерям серебра $0.001 \times \operatorname{Im} (\varepsilon )$, $0.1 \times \operatorname{Im} (\varepsilon )$, $\operatorname{Im} (\varepsilon )$. На рис. 3 изображена частотная зависимость $U(a,y = 0)$. Из рисунка видно, что только в случае малых потерь (кривые 1, 2) наблюдаются как дипольный резонанс, так и расщепленные мультипольные резонансы плазмонов. При реальных потерях серебра мультипольные резонансы практически исчезают и, соответственно, не вносят вклад в поперечник рассеяния.

Рис. 3.

Частотная характеристика амплитуды поля $U(a,y = 0)$ в точке с координатами $x = a,y = 0$ при ${{\varphi }_{0}} = 0$ и параметрах структуры: $a = 40\,\,{\text{нм}}$, $\alpha = 0.8$, а также потерях серебра: $0.001 \times \operatorname{Im} (\varepsilon )$ (кривая 1), $0.1 \times \operatorname{Im} (\varepsilon )$ (кривая 2), $\operatorname{Im} (\varepsilon )$ (кривая 3).

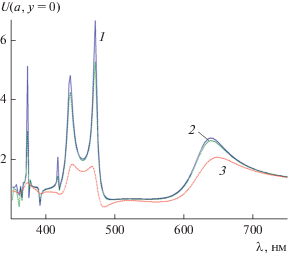
Рис. 4.

Зависимость нормированного полного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при ${{\varphi }_{0}} = 0$ и параметрах структуры: $a = 40\,\,{\text{нм}}$, $\alpha = 0.8$, а также потерях серебра $0.001 \times \operatorname{Im} (\varepsilon )$ (кривая 1), $0.1 \times \operatorname{Im} (\varepsilon )$ (кривая 2), $\operatorname{Im} (\varepsilon )$ (кривая 3).

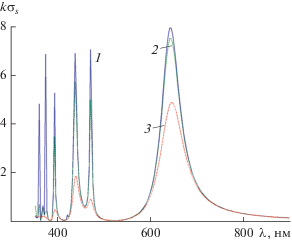
На рис. 4 представлены результаты расчетов частотной зависимости поперечника рассеяния $k{{\sigma }_{s}}$ при различных потерях серебра. Из этого рисунка также видно, что реальные потери серебра (кривая 3) фактически приводят к исчезновению высших мультипольных резонансов. Кроме того, из рис. 2 и 3 следует, что резонансы поля $U(a,y = 0)$ объясняют как наличие резонансов поперечника рассеяния $k{{\sigma }_{s}}$, так и их расположение (максимумы у соответствующих кривых приблизительно (но не точно!) совпадают друг с другом).

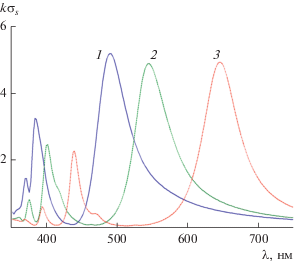
На рис. 5 представлено семейство кривых, описывающих зависимость нормированного полного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$, значениях параметра $\alpha = 0.6$, 0.7, 0.8 и реальных потерях серебра $\operatorname{Im} (\varepsilon )$ для структуры с параметром $a = 40\,\,{\text{нм}}$. Из сравнения результатов, представленных на рис. 5 и 2 следует вывод о том, что основные тенденции в поведении кривых $k{{\sigma }_{s}}$, отмеченные выше для ${{\varphi }_{0}} = 0$, сохраняются и при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$. Различие между этими двумя случаями (${{\varphi }_{0}} = 0$ и ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$) заключается в уменьшении числа побочных колебаний у кривых $k{{\sigma }_{s}}$ в окрестности квадрупольного резонанса. Отметим, что аналогичный характер изменения кривых $k{{\sigma }_{s}}$ имеет место и при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ (эти результаты мы не приводим). Таким образом, из результатов, представленных на рис. 2 и 5 можно сделать вывод о том, что если значение угла падения ${{\varphi }_{0}}$ фиксировано, а значения параметра $\alpha $ меняются, то с увеличением $\alpha $ длина волны дипольного резонанса смещается в сторону больших значений длин волн (при значении $\alpha = 0.6$ дипольный резонанс наблюдается при длине волны $\lambda \approx 490\,\,{\text{нм}}$, а при $\alpha = 0.8$ – при $\lambda \approx 649\,\,{\text{нм}}$).

Рис. 5.

Зависимость нормированного полного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$, $a = 40\,\,{\text{нм}}$, при $\alpha = 0.6$ (1), 0.7 (2), 0.8 (3) и реальных потерях серебра $\operatorname{Im} (\varepsilon )$.

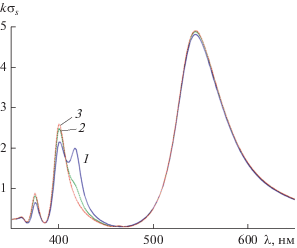
На рис. 6 изображено семейство кривых, описывающих зависимость нормированного полного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при углах падения плоской волны ${{\varphi }_{0}} = 0,{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6},{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и реальных потерях серебра $\operatorname{Im} (\varepsilon )$ для структуры с параметром $a = 40\,\,{\text{нм}}$, $\alpha = 0.7$. Из этого рисунка видно, что при фиксированной толщине стенок структуры ($\alpha = 0.7$, $d = 12\,\,{\text{нм}}$) и различных значениях угла падения ${{\varphi }_{0}}$ не наблюдается изменение расположения дипольного резонанса. В области квадрупольного резонанса меняется характер расщепления кривых $k{{\sigma }_{s}}$.

Рис. 6.

Зависимость нормированного полного сечения рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ при $a = 40\,\,{\text{нм}}$, $\alpha = 0.7$ ($d = 12\,\,{\text{нм}}$), реальных потерях серебра $\operatorname{Im} (\varepsilon )$ и ${{\varphi }_{0}} = 0$ (1), π/6 (2) и π/4 (3).

Было исследовано также влияние геометрических размеров структуры на частотную характеристику поперечника рассеяния $k{{\sigma }_{s}}$ при фиксированной толщине $d = 10\,\,{\text{нм}}$ стенок структуры, фиксированном угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$ и реальных потерях серебра $\operatorname{Im} (\varepsilon )$ (рис. 7). Параметры структур, представленных на рис. 7, следующие: $a = 40\,\,{\text{нм}},$ $b = 30\,\,{\text{нм}}$; $a = 60\,\,{\text{нм}}$, $b = 50\,\,{\text{нм}}$; $a = 80\,\,{\text{нм}}$, $b = 70\,\,{\text{нм}}$. Из результатов рис. 7 следует, что увеличение геометрических размеров структуры в два раза при неизменной толщине слоя серебра ведет к смещению длины волны дипольного резонанса от значения $\lambda \approx 590\,\,{\text{нм}}$ при параметрах структуры $a = 40\,\,{\text{нм}},$ $b = 30\,\,{\text{нм}}$ до значения $\lambda \approx 830\,\,{\text{нм}}$ – при $a = 80\,\,{\text{нм}}$, $b = 70\,\,{\text{нм}}$. При этом также увеличивается разница в расположениях дипольного и квадрупольного резонансов. Кроме того, наблюдается развитие дополнительных колебаний кривых $k{{\sigma }_{s}}$ в области мультипольных резонансов.

Рис. 7.

Частотная характеристика нормированного поперечника рассеяния $k{{\sigma }_{s}}$ при $d = 10\,\,{\text{нм}}$, ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$, реальных потерях серебра $\operatorname{Im} (\varepsilon )$ и различных значениях a и b: кривая 1 – $a = 40\,\,{\text{нм,}}$ $b = 30\,\,{\text{нм}}$; кривая 2 – $a = 60\,\,{\text{нм}}$, $b = 50\,\,{\text{нм}}$; кривая 3 – $a = 80\,\,{\text{нм}}$, $b = 70\,\,{\text{нм}}$.

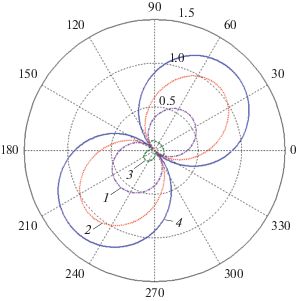
На рис. 8 представлены результаты расчетов диаграммы рассеяния для структуры из реального серебра с параметрами $a = 40\,\,{\text{нм}},$ $\alpha = 0.8$; угле падения плоской волны ${{\varphi }_{0}} = 0$ и различных длинах волн: λ = 394, 440, 470 и 694 нм. Выбранным длинам волн соответствуют максимумы поперечника рассеяния $k{{\sigma }_{s}}$ – рис. 2 кривая 3. Из рис. 8 видно, что при длинах волн λ = 694, 440 и 394 диаграмма рассеяния имеет только два лепестка. При этом максимумы амплитуд лепестков соответствуют направлениям $\varphi = 0$ и $\varphi = \pi $. Отметим, что такая двухлепестковая диаграмма рассеяния характерна для дипольного резонанса ($\lambda = 694\,\,{\text{нм}}$). Однако в нашем случае она имеет место при $\lambda = 440\,\,{\text{нм}}$ и $\lambda = 394\,\,{\text{нм}}$, т.е. в области мультипольных резонансов. Это свидетельствует о наличии вырождения у плазмонов и ближнего поля структуры. Характерная для квадрупольного резонанса четырехлепестковая диаграмма рассеяния наблюдается только при $\lambda = 470\,\,{\text{нм}}$.

Рис. 8.

Модули диаграмм рассеяния для структуры из реального серебра с параметрами $a = 40\,\,{\text{нм,}}$ $\alpha = 0.8$, и различных длинах волн: λ = 394 (1), 440 (2), 470 (3) и 694 нм (4).

На рис. 9 представлены диаграммы рассеяния для структуры из реального серебра с параметрами $a = 40\,\,{\text{нм}},$ $\alpha = 0.8$; угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и длинах волн λ = 394, 440, 530 и 694 нм. Здесь выбранным длинам волн соответствуют максимумы поперечника рассеяния $k{{\sigma }_{s}}$ (см. рис. 2). Как видно из рис. 9, все диаграммы рассеяния в этом случае имеют только два лепестка. Максимумы амплитуд лепестков имеют направления $\varphi = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и $\varphi = \pi + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ Такое поведение диаграммы рассеяния, так же как и в рассмотренном выше случае, свидетельствует о наличии вырождения колебаний ближнего поля структуры.

Рис. 9.

Модули диаграмм рассеяния для структуры из реального серебра с параметрами $a = 40\,\,{\text{нм}},$ $\alpha = 0.8$ и φ₀ = π/4 и различных длинах волн: λ = 394 (1), 440 (2), 530 (3) и 694 нм (4).

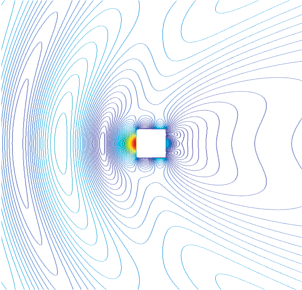
Результаты расчетов пространственного распределения линий равных амплитуд компоненты ${{H}_{z}}$ поля вблизи внешнего контура структуры представлены на рис. 10 (распределение линий равных амплитуд поля внутри структуры не приводится, чтобы не отвлекать внимание от эффекта вырождения внешнего ближнего поля). Структура из реального серебра характеризовалась следующими параметрами: $a = 40\,\,{\text{нм}},$ $\alpha = 0.8$, угол падения плоской волны был равен ${{\varphi }_{0}} = 0$, длина волны $\lambda = 394\,\,{\text{нм}}$. Этот рисунок наглядно иллюстрирует процесс вырождения ближнего поля структуры. Нетрудно заметить, что вблизи задней стенки структуры изменение амплитуды поля носит характер трех полуволн, а на расстоянии порядка $20a$ – только одной полуволны.

Рис. 10.

Пространственное распределение линий равных амплитуд компоненты ${{H}_{z}}$ поля вблизи внешнего контура структуры при $a = 40\,\,{\text{нм,}}$ $\alpha = 0.8$, ${{\varphi }_{0}} = 0$, $\lambda = 394\,\,{\text{нм}}$.

ЗАКЛЮЧЕНИЕ

Рассмотрена двумерная задача дифракции плоской электромагнитной волны ТМ-типа на нано структуре, состоящей из квадратной пластины из серебра с вставленной в нее квадратной стеклянной нанонитью. В световом диапазоне длин волн строгими численными методами рассчитаны ближние и дальние поля, а также спектры поперечника рассеяния. Исследовано влияние потерь серебра, толщины структуры и угла падения плоской поляризованной ТМ-волны на резонансы плазмонов. Показано, что для такой структуры характерно расщепление и вырождение квадрупольных и дипольных резонансов плазмонов.