Радиотехника и электроника, 2020, T. 65, № 6, стр. 587-594
Исследование алгоритмов итеративного приема кодов-произведений на основе низкоплотностных кодов конечных геометрий
Л. Е. Назаров *
Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Московской обл., Фрязино, пл. Введенского, 1, Российская Федерация
* E-mail: levnaz2018@mail.ru
Поступила в редакцию 09.09.2019
После доработки 23.12.2019
Принята к публикации 25.12.2019
Аннотация
Приведены результаты исследований алгоритмов итеративного посимвольного приема кодов-произведений (блоковых турбокодов), формируемых с использованием составляющих низкоплотностных кодов на основе конечных геометрий (Евклидова геометрия, проективная геометрия). Даны результаты моделирования и сравнительного анализа данных алгоритмов итеративного приема для ряда рассматриваемых кодов-произведений при наличии канальной помехи в виде аддитивного белого гауссовского шума.
ВВЕДЕНИЕ
Коды, корректирующие ошибки, используются для повышения помехоустойчивости передачи информации по проводным и беспроводным каналам [1, 2]. Кодовые конструкции под названием коды-произведения (блоковые турбокоды [3]) рассматриваются как одни из наиболее эффективных относительно вероятностных характеристик [3, 4]. Эти коды входят в ряд принятых стандартов, например, для спутниковых систем связи (IESS-15, IESS-315), для широкополосного доступа IEEE 802.16 [5].
Коды-произведения формируются на основе последовательного объединения составляющих блоковых кодов [1–3]. Для сигнальных конструкций, соответствующих этим кодам, разработаны алгоритмы приема, реализующие принцип декодирования для турбокодов (далее – турбодекодирование) [3, 6–8]. Суть данных алгоритмов заключается в итеративном выполнении этапов обработки входных реализаций для составляющих кодов. Это приводит к существенному упрощению процедур приема по сравнению с процедурами оптимального приема. Анализ и моделирование этих алгоритмов приема показал их эффективность по сравнению с известными схемами помехоустойчивого кодирования, включая сверточные коды. При увеличении информационных объемов кодов-произведений и применении алгоритмов итеративного приема достигаются вероятностные характеристики при приеме, близкие к предельным теоретическим характеристикам [2, 4, 8].
Сложность разработанных алгоритмов итеративного приема кодов-произведений определяется сложностью алгоритмов приема составляющих блоковых кодов. Класс составляющих кодов, удовлетворяющих условию низкой сложности алгоритмов приема, ограничен – используются блоковые коды Хэмминга, коды с обобщенной проверкой на четность [3, 4, 8].
Открытой является проблема расширения класса кодов-произведений с вариацией параметров, определяющих перспективность их использования в приложениях. Для решения этой задачи в работах [9, 10] рассмотрен подход формирования ряда производных кодов-произведений на основе порождающего кода-произведения путем укорочения информационных объемов, длин кодовых слов и вариации кодовых скоростей. Для данного ряда производных кодов-произведений разработаны алгоритмы итеративного приема, являющиеся модификациями разработанных алгоритмов итеративного приема, реализующих принцип турбодекодирования.
Другое направление расширения класса кодов-произведений основано на использовании составляющих блоковых низкоплотностных кодов [2, 4], в частности, кодов конечных геометрий (Евклидова и проективная геометрии) [11, 12]. Для этих составляющих кодов известны алгоритмы итеративного приема, основанные на организации ортогональных соотношений относительно кодовых символов. Низкоплотностные коды входят в состав помехоустойчивых кодов CCSDS [13], рекомендованных для спутниковых информационных систем.
Перспективным направлением является использование составляющих блоковых кодов, задаваемых в недвоичных полях [1, 2, 4, 12].
Актуальной задачей является разработка алгоритмов приема для данного класса кодов-произведений, а также исследование и сравнительный анализ их вероятностных характеристик и сложности реализации.
1. ПОСТАНОВКА ЗАДАЧИ
Кодовые слова кода-произведения на основе составляющих кодов ${{C}_{1}}$, ${{C}_{2}}$ с параметрами $({{n}_{1}},{{k}_{1}},{{d}_{1}})$ и $({{n}_{2}},{{k}_{2}},{{d}_{2}})$ эквивалентны двумерной матрице: ее строки – кодовые слова кода ${{C}_{1}}$, столбцы – кодовые слова кода ${{C}_{2}}$ [1]. Здесь $n,k,d$ – длина кодовых символов, информационный объем и минимальный вес Хэмминга кодовых слов кодов. Для кода-произведения $N = {{n}_{1}}{{n}_{2}}$, $K = {{k}_{1}}{{k}_{2}}$, минимальный вес Хэмминга ${{D}_{{мин}}} = {{d}_{1}}{{d}_{2}}$, кодовая скорость $R = {K \mathord{\left/ {\vphantom {K N}} \right. \kern-0em} N}$.
Алгоритмы оптимального приема сигналов, соответствующих коду с параметрами $(n,k,d)$, основаны на реализации ${{2}^{k}}$-корреляторов при наличии аддитивного белого гауссовского шума (АБГШ) [5]. Для $k \gg 1$ исполнение алгоритмов оптимального приема в реальном времени представляет сложную проблему [1].
Для кодов-произведений на основе простых составляющих блоковых кодов ${{C}_{1}}$, ${{C}_{2}}$ (коды Хэмминга, коды с обобщенной проверкой на четность) разработаны алгоритмы итеративного приема [3, 4, 6, 8], реализующие принцип турбодекодирования. Эти алгоритмы по сравнению с алгоритмами оптимального приема имеют существенно меньшую сложность реализации при незначительных энергетических потерях. Итерация включает выполнение двух этапов. На первом этапе на основе отсчетов входной реализации и априорных вероятностей относительно кодовых символов вычисляются апостериорные вероятности приема для символов кода ${{C}_{1}}$ (прием по горизонтали) [3, 6]. Функционалы от вычисленных апостериорных вероятностей принимаются как априорные вероятности для кодовых символов и используются на втором этапе итерации при вычислении апостериорных вероятностей символов кода ${{C}_{2}}$ (прием по вертикали). После выполнения задаваемого числа итераций принимаются решения относительно кодовых символов кода-произведения.
Для кодов-произведений на основе составляющих низкоплотностных кодов можно применить другой ряд алгоритмов итеративного приема, разработанных для низкоплотностных кодов [2, 4]. Обоснование этого утверждения основано на том факте, что эти коды-произведения также входят в класс низкоплотностных кодов [11]. Ниже рассматриваются составляющие низкоплотностные коды конечных геометрий (Евклидова и проективная геометрии) [1, 4].
Суть задачи – разработка и исследование вероятностных характеристик алгоритмов итеративного приема сигнальных конструкций, соответствующих кодам-произведениям на основе составляющих низкоплотностных кодов конечных Евклидовой и проективной геометрий. Приведены результаты моделирования алгоритмов итеративного приема при наличии модели канальной помехи в виде АБГШ для ряда исследуемых кодов-произведений.
2. НИЗКОПЛОТНОСТНЫЕ КОДЫ КОНЕЧНЫХ ГЕОМЕТРИЙ И КОДЫ-ПРОИЗВЕДЕНИЯ НА ИХ ОСНОВЕ
Ниже приведены описания низкоплотных кодов на основе конечной Евклидовой геометрии и конечной проективной геометрии.
Пусть $EG(m,{{2}^{s}})$ – $m$-мерная конечная Евклидова геометрия над полем $GF({{2}^{s}})$, $m,s$ – положительные целые числа [1]. Эта геометрия содержит ${{2}^{{ms}}}$-точек, эквивалентных векторам с $m$-компонентами поля $GF({{2}^{s}})$. Геометрия $EG(m,{{2}^{s}})$ содержит ${{2}^{{(m - 1)s}}}({{2}^{{ms}}} - {{1)} \mathord{\left/ {\vphantom {{1)} {({{2}^{s}}}}} \right. \kern-0em} {({{2}^{s}}}} - 1)$ линий c ${{2}^{s}}$-точками в своем составе и рассматривается как расширение поля $GF({{2}^{{ms}}})$ над $GF({{2}^{s}})$ [1, 15]. Пусть $\alpha $ – примитивный элемент поля $GF({{2}^{{ms}}})$, множество $0,{{\alpha }^{0}},{{\alpha }^{1}},...,{{\alpha }^{{{{2}^{{ms}}} - 2}}}$ эквивалентно ${{2}^{{ms}}}$-точкам геометрии $EG(m,{{2}^{s}})$. Пусть ${{\alpha }^{i}},{{\alpha }^{j}}$ – линейно независимые точки, множество точек $\{ {{\alpha }^{i}} + \beta {{\alpha }^{j}};\beta \in GF({{2}^{s}})\} $ определяет линию, проходящую через 1 и ${{\alpha }^{i}}$. Пусть $H_{{EG}}^{{}}(m,s)$ – матрица с элементами из $GF(2)$, строки которой эквивалентны линиям геометрии $EG(m,{{2}^{s}})$. Эта матрица является проверочной матрицей низкоплотностного кода геометрии $EG(m,{{2}^{s}})$, она содержит $J = ({{2}^{{(m\, - {\kern 1pt} 1)s}}} - {{1)} \mathord{\left/ {\vphantom {{1)} {({{2}^{s}}}}} \right. \kern-0em} {({{2}^{s}}}} - 1)$ строк и $n = {{2}^{{ms}}} - 1$ столбцов. Строки и столбцы матрицы $H_{{EG}}^{{}}(m,s)$ имеют вес Хэмминга ${{J}_{N}} = {{2}^{s}}$ и ${{J}_{D}} = ({{2}^{{ms}}} - {{1)} \mathord{\left/ {\vphantom {{1)} {({{2}^{s}}}}} \right. \kern-0em} {({{2}^{s}}}} - 1) - 1$ соответственно.
Низкоплотностные коды Евклидовой геометрии $EG(m,{{2}^{s}})$ являются циклическими кодами с порождающим многочленом $g_{{EG}}^{{}}(x)$ [1]. Длина кодовых слов равна $n = {{2}^{{ms}}} - 1$, минимальный вес Хэмминга $d \geqslant {{J}_{D}} + 1$, размерность $k$ определяется степенью многочлена $g_{{EG}}^{{}}(x)$. Пусть $\alpha $ – примитивный элемент поля $GF({{2}^{{ms}}})$, элемент ${{\alpha }^{h}}$ является корнем $g_{{EG}}^{{}}(x)$ тогда и только тогда, когда выполняется условие [1]:
(1)
$0 < \mathop {\max }\limits_{0 \leqslant l < s} \left( {{{W}_{{{{2}^{s}}}}}({{h}^{{(l)}}})} \right) \leqslant (m - 1)({{2}^{s}} - 1),$(3)
$\begin{gathered} h = {{\delta }_{0}} + {{\delta }_{1}}{{2}^{s}} + ... + {{\delta }_{{m - 1}}}{{2}^{{(m - 1)s}}}, \\ 0 \leqslant {{\delta }_{i}} < {{2}^{s}},\,\,\,\,0 \leqslant i < m. \\ \end{gathered} $Здесь $0 \leqslant {{\delta }_{i}} < {{2}^{s}},$ $0 \leqslant i < m$ – коэффициенты при разложении (3) показателя степени $h$ элемента $\alpha $; ${{h}^{{(l)}}}$ – остаток $h{{2}^{l}}$ по модулю $({{2}^{{ms}}} - 1)$.
Приведем описание класса низкоплотностных кодов проективной геометрии $PG(m,{{2}^{s}})$ над полем $GF({{2}^{s}})$. Пусть $\alpha $ – примитивный элемент поля $GF({{2}^{{(m + 1)s}}})$, являющийся расширением поля $GF({{2}^{s}})$. Рассмотрим элемент
Порядок элемента $\beta $ равен $({{2}^{s}} - 1)$, множество $\left\{ {0,1,\beta ,...,{{\beta }^{{{{2}^{s}} - 2}}}} \right\}$ представляет поле $GF({{2}^{s}})$. Рассмотрим множество элементов $\{ 1,\alpha ,{{\alpha }^{2}},...,{{\alpha }^{{n - 1}}}\} $ и разбиение поля $GF({{2}^{{(m + 1)s}}})$ на непересекающиеся подмножества $({{\alpha }^{i}}) = \{ {{\alpha }^{i}},\beta {{\alpha }^{i}},...,{{\beta }^{{2s - 2}}}{{\alpha }^{i}}\} $, $0 \leqslant i < n$. Геометрия $PG(m,{{2}^{s}})$ содержит $n$ точек, эквивалентных элементам $({{\alpha }^{i}})$ в виде вектора с $(m + 1)$-компонентами поля $GF({{2}^{s}})$. Множество точек $({{\eta }_{1}}{{\alpha }^{i}} + {{\eta }_{2}}{{\alpha }^{j}})$ определяет линию, проходящую через линейно независимые точки $({{\alpha }^{i}}),({{\alpha }^{j}})$. Здесь ${{\eta }_{1}},{{\eta }_{2}}$ – элементы поля $GF({{2}^{s}})$, не равные нулю одновременно. Геометрия $PG(m,{{2}^{s}})$ содержит
линий из ${{2}^{s}} + 1$ точек. Пусть ${{H}_{{PG}}}(m,s)$ матрица над полем $GF(2)$, строки которой эквивалентны линиям геометрии $PG(m,{{2}^{s}})$. Матрица ${{H}_{{PG}}}(m,s)$ является проверочной матрицей низкоплотностного кода геометрии $PG(m,{{2}^{s}})$, она содержит $J$ строк и $n$ столбцов. Строки и столбцы ${{H}_{{PG}}}(m,s)$ имеют вес Хэмминга ${{J}_{N}} = {{2}^{s}} + 1$ и ${{J}_{D}} = ({{2}^{{ms}}} - {{1)} \mathord{\left/ {\vphantom {{1)} {({{2}^{s}}}}} \right. \kern-0em} {({{2}^{s}}}} - 1)$ соответственно.
Низкоплотностные коды на основе геометрии $PG(m,{{2}^{s}})$ с проверочной матрицей ${{H}_{{PG}}}(m,s)$ являются циклическими и определяются порождающим многочленом ${{g}_{{PG}}}(x)$ [1]. Пусть $\alpha $ – примитивный элемент поля $GF({{2}^{{(m + 1)s}}})$, элемент ${{\alpha }^{h}}$ ($0 < h < {{2}^{{(m + 1)s}}} - 1$, $h$ кратно ${{2}^{s}} - 1$) является корнем ${{g}_{{PG}}}(x)$ тогда и только тогда, когда выполняется условие [1]:
Здесь $0 \leqslant j \leqslant m - 1$, ${{h}^{{(l)}}}$ – остаток деления $h{{2}^{l}}$ на $({{2}^{{(m + 1)s}}} - 1)$; вес ${{W}_{{{{2}^{s}}}}}({{h}^{{(l)}}})$ определяется соотношениями (2), (3).
В табл. 1 приведены параметры $n,k,d,{{J}_{N}},{{J}_{D}}$, а также степени примитивного элемента $\alpha $ для порождающих многочленов $g_{{EG}}^{{}}(x)$ и ${{g}_{{PG}}}(x)$, полученные для ряда кодов $EG(m,{{2}^{s}})$ и $PG(m,{{2}^{s}})$. Коды-произведения на основе низкоплотностных кодов геометрий $EG(m,{{2}^{s}})$, $PG(m,{{2}^{s}})$ с параметрами ${{J}_{N}}$ и ${{J}_{D}}$ входят в класс низкоплотностных кодов с параметрами ${{J}_{N}}$ и $2{{J}_{D}}$ [1]. В табл. 2 приведены параметры $N,K,{{D}_{{мин}}},{{J}_{N}},{{J}_{D}}$ для кодов-произведений на основе рассматриваемых низкоплотностных кодов.
Таблица 1.
Параметры низкоплотностных кодов геометрий EG$(m,{{2}^{s}})$ и PG$(m,{{2}^{s}})$
| $(m,{{2}^{s}})$ | $n$ | $k$ | $d$ | ${{J}_{N}}$ | ${{J}_{D}}$ | Показатели степеней ${{\alpha }^{i}}$ |
|---|---|---|---|---|---|---|
| EG$(2,{{2}^{2}})$ | 15 | 7 | 5 | 4 | 4 | 1, 3 |
| EG$(2,{{2}^{3}})$ | 63 | 37 | 9 | 8 | 8 | 1, 3, 5, 7, 21 |
| PG$(3,{{2}^{2}})$ | 21 | 11 | 6 | 5 | 5 | 1, 3, 9 |
| PG$(3,{{2}^{3}})$ | 73 | 45 | 10 | 9 | 9 | 7, 21, 35 |
Таблица 2.
Параметры кодов-произведений на основе низкоплотностных кодов геометрий EG$(m,{{2}^{s}})$ и PG$(m,{{2}^{s}})$
| Составляющий код | $N$ | $K$ | ${{D}_{{мин}}}$ | ${{J}_{N}}$ | ${{J}_{D}}$ | $R$ |
|---|---|---|---|---|---|---|
| EG$(2,{{2}^{2}})$ | 225 | 49 | 25 | 4 | 8 | 0.22 |
| EG$(2,{{2}^{3}})$ | 3969 | 1369 | 81 | 8 | 16 | 0.34 |
| PG$(3,{{2}^{2}})$ | 441 | 121 | 36 | 5 | 10 | 0.27 |
| PG$(3,{{2}^{3}})$ | 5329 | 2025 | 100 | 9 | 18 | 0.38 |
Далее рассмотрим наиболее эффективные алгоритмы итеративного посимвольного приема низкоплотностных кодов – алгоритм BP (belief propagation) и алгоритм APP (a’posteriori probability) и их модификации [2, 4, 16].
Обозначим $H = ({{h}_{{li}}};0 \leqslant l < n - k;0 \leqslant i < n)$ проверочную матрицу низкоплотностного кода ($n,k$) с кодовыми словами $\vec {B} = ({{b}_{0}},{{b}_{1}},...,{{b}_{{n - 1}}})$. Пусть $\vec {Y} = ({{y}_{0}},{{y}_{1}},...,{{y}_{{n - 1}}})$ – дискретная реализация с отсчетами ${{y}_{i}} = {{s}_{i}} + {{n}_{i}}$ с выхода демодулятора сигналов. Здесь ${{s}_{i}}$ – сигнальные составляющие, соответствующие сигналам с двоичной фазовой манипуляцией (ФМ2), ${{n}_{i}}$ – помеховые составляющие, $i = 0,1,...,n - 1$. Введем обозначение $\vec {x} = ({{x}_{0}},{{x}_{1}},...,{{x}_{{n - 1}}})$ – “жесткие” решения: ${{x}_{i}} = 0$ при условии ${{y}_{i}} \geqslant 0$ и ${{x}_{i}} = 1$ в противном случае.
Низкоплотностные коды конечных геометрий обладают свойством организации ортогональных проверочных соотношений для символов ${{b}_{i}}$ кодовых слов $\vec {B}$ [1, 4]. Пусть $N(m) = (i:{{h}_{{mi}}} = 1)$ – множество номеров кодовых символов объемом ${{J}_{N}}(m)$, образующих $m$-е проверочное соотношение; ${{N(m)} \mathord{\left/ {\vphantom {{N(m)} l}} \right. \kern-0em} l}$ – множество $N(m)$ без $l$-го символа; $D(l) = (m:{{h}_{{ml}}} = 1)$ – множество проверочных ортогональных соотношений для кодового символа ${{b}_{l}}$ объемом ${{J}_{D}}(l)$; $D(l)/m$ – множество ортогональных соотношений $D(l)$ без $m$-й проверки. Для рассматриваемых низкоплотностных кодов выполняются условия ${{J}_{N}}(m) = {{J}_{N}}$, ${{J}_{D}}(l) = {{J}_{D}}$.
3. АЛГОРИТМ ИТЕРАТИВНОГО ПРИЕМА BP
Итерация алгоритма BP включает следующие шаги обработки $\vec {Y}$ [1, 11, 12].
Инициализация. Устанавливаются начальные значения величин ${{z}_{{mi}}} = {{y}_{i}}$, $m \in {{J}_{D}}(i);$ i = 0, 1, ..., $n - 1$.
Шаг 1. Вычисляются “жесткие” решения
(4)
${{\sigma }_{{mi}}} = \left\{ {\begin{array}{*{20}{c}} {1,{{z}_{{mi}}} > 0,} \\ {0,{{z}_{{mi}}} \leqslant 0.} \end{array}} \right.$Для каждой ортогональной проверки $m$ вычисляются величины ${{\sigma }_{m}},{{L}_{{mi}}}$
(6)
${{L}_{{mi}}} = {{( - 1)}^{{{{\sigma }_{m}} \oplus {{\sigma }_{{mi}}} \oplus 1}}}\mathop {min}\limits_{i{\kern 1pt} '\, \in \,N(m)/i} \left( {\left| {{{z}_{{mi{\kern 1pt} '}}}} \right|} \right).$Операция сложения $ \oplus $ в (5), (6) осуществляется в поле $GF(2)$.
Шаг 2. На основе ${{L}_{{mi}}}$ вычисляются величины ${{z}_{{mi}}}$
(7)
${{z}_{{mi}}} = {{y}_{i}} + \sum\limits_{m{\kern 1pt} '\, \in \,D(i)/m} {{{L}_{{m{\kern 1pt} 'i}}}} .$Шаг 3. При невыполнении требуемого числа итераций выполняется шаг 1 следующей итерации, иначе принимается решение относительно кодовых символов ${{b}_{i}}$ с использованием величин ${{z}_{i}}$
Принимается решение ${{b}_{i}} = 0$, если ${{z}_{i}} \geqslant 0$, иначе ${{b}_{i}} = 1$.
Алгоритм ВР осуществляет параллельное использование величин ${{L}_{{ml}}}$ для вычисления ${{z}_{{ml}}}$ при реализации (7), т.е. на шаге 1 вычисляется множество $\{ {{L}_{{ml}}}\} $ и после этого выполняется шаг 2. Модификация этого алгоритма (m-ВP) заключается в последовательном использовании величин ${{L}_{{ml}}}$ при вычислении ${{z}_{{ml}}}$, т.е. шаг 2 выполняется после определения очередного значения ${{L}_{{ml}}}$, $l = 0,1,...,n - 1$}. При этом не требуется память для множества $\{ {{L}_{{ml}}}\} $, что упрощает реализацию алгоритма m-ВP по отношению к ВР.
При реализации итерации алгоритмов ВР и m-ВP объем требуемых вычислительных операций определяется вычислением (4)–(8) и оценивается соотношением ${{B}_{{{\text{ВP}}}}} \cong 4{{J}_{D}}{{J}_{N}}n$. Объем требуемой памяти для алгоритма BP равен ${{\Pi }_{{{\text{ВР}}}}} \cong 3{{J}_{D}}{{J}_{N}}n$, для алгоритма m-ВP равен ${{\Pi }_{{{\text{mВP}}}}} \cong 2{{J}_{D}}{{J}_{N}}n$.
4. АЛГОРИТМ ИТЕРАТИВНОГО ПРИЕМА APP
При применении алгоритма АРР вычисляются ошибки ${{e}_{i}}$ (${{e}_{i}} = 0,1$) для кодовых символов ${{b}_{i}}$, оценка ${{\hat {b}}_{i}}$ задается соотношением [11]
Алгоритм АРР включает следующие шаги обработки $\vec {Y}$ [4, 11].
Инициализация. Полагается ${{L}_{i}} = {{y}_{i}}$. На основе “жестких” решений $\vec {x}$ вычисляются величины $A_{j}^{{(i)}}$ (сложение осуществляется в поле $GF(2)$)
Шаг 1. Вычисляются величины $w_{j}^{{(i)}}$
(11)
$w_{j}^{{(i)}} = \left[ {\prod\limits_{i{\kern 1pt} '{\kern 1pt} \in {\kern 1pt} N(j)/i} {{\text{sign}}({{L}_{{i'}}})} } \right]\mathop {\min }\limits_{i{\kern 1pt} ' \in {\kern 1pt} N(j)/i} (\left| {{{L}_{{i{\kern 1pt} '}}}} \right|).$Здесь $j = 1,2,...,{{J}_{N}}(m)$ – номер ортогональной проверки относительно ${{b}_{i}}$.
Шаг 2. На основе $A_{j}^{{(i)}},w_{j}^{{(i)}}$ вычисляются величины ${{E}_{i}}$
Шаг 3. С использованием ${{E}_{i}}$ вычисляются величины
Шаг 4. Если не выполняется условие на остановку работы алгоритма, то осуществляется следующая итерация, начиная с шага 1. В противном случае вычисляется оценка значения $L(\left. {{{e}_{i}}} \right|\{ A_{j}^{{(i)}}\} ,\vec {Y})$ ошибки ${{e}_{i}}$
(14)
$L(\left. {{{e}_{i}}} \right|\{ A_{j}^{{(i)}}\} ,\vec {Y}) = {{E}_{i}} + 2\left| {{{y}_{i}}} \right|.$При условии $L(\left. {{{e}_{i}}} \right|\{ A_{j}^{{(i)}}\} ,\vec {Y}) \geqslant 0$ полагается ${{e}_{i}} = 0$, в противном случае ${{e}_{i}} = 1$. Оценка кодового символа ${{\hat {b}}_{i}}$ ($i = 0,1,...,n - 1$) вычисляется с использованием соотношения (9).
Алгоритм АРР осуществляет параллельное использование величин ${{E}_{i}}$ для вычисления ${{L}_{i}}$, т.е. на шаге 2 вычисляется множество $\{ {{E}_{i}}\} $ и после этого реализуется шаг 3. Модификация этого алгоритма (m-APP) заключается в реализации последовательного использования величин ${{E}_{i}}$ при вычислении ${{L}_{i}}$, т.е. шаг 3 реализуется после вычисления очередного значения ${{E}_{i}}$, $i = 0,1,...,n - 1$, не требуя вычисления множества $\{ {{E}_{i}}\} $. В этом случае не требуется памяти для хранения множества $\{ {{E}_{i}}\} $, что упрощает сложность реализации алгоритма m-APP по отношению к алгоритму АРР.
При реализации итерации алгоритмов АРР и m-APP объем требуемых вычислительных операций определяется вычислением (10)–(14) и оценивается выражением ${{B}_{{{\text{APP}}}}} \cong 2{{J}_{D}}{{J}_{N}}n$, объем требуемой памяти для алгоритма APP равен ${{\Pi }_{{{\text{АРР}}}}} \cong 2n{{J}_{D}}$, для алгоритма m-APP ${{\Pi }_{{{\text{mАРР}}}}} \cong n{{J}_{D}}$.
Таким образом, сравнивая приведенные выше значения ВВР и ${{B}_{{{\text{APP}}}}}$, делаем вывод, что относительно требуемого объема вычислительных операций алгоритм APP (m-APP) более эффективен (в два раза) алгоритма BP (m-ВP). Относительно требуемого объема памяти алгоритм m-APP является наиболее эффективным, при его реализации требуется в ${{{{\Pi }_{{{\text{mBР}}}}}} \mathord{\left/ {\vphantom {{{{\Pi }_{{{\text{mBР}}}}}} {{{\Pi }_{{{\text{mАРР}}}}}}}} \right. \kern-0em} {{{\Pi }_{{{\text{mАРР}}}}}}} \cong 2{{J}_{N}}$ раз меньше памяти по сравнению с алгоритмом m-ВP.
5. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
На рис. 1–5 приведены результаты моделирования алгоритмов BP, m-BP, APP и m-APP для ряда кодов-произведений на основе низкоплотностных EG- и PG-кодов, параметры которых приведены в табл. 2. Кривые на рисунках соответствуют зависимостям вероятности ошибки на бит ${{P}_{{\text{б}}}}$ от отношения Eб/N0 для сигналов ФМ2 при наличии АБГШ с односторонней спектральной плотностью ${{N}_{0}}$. Здесь Eб – энергия сигналов на 1 бит.
Рис. 1.
Вероятности ${{P}_{{\text{б}}}}$ приема сигналов ФМ2, соответствующих коду-произведению на основе ЕG -кода (15,7): 1 – алгоритм итеративного приема BP (20 итераций); 2 – алгоритм итеративного приема m-BP (20 итераций); 3 – граница случайного кодирования.
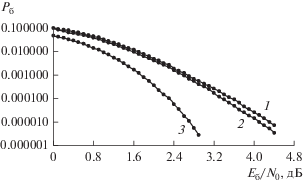
Рис. 2.
Вероятности ${{P}_{{\text{б}}}}$ приема сигналов ФМ2, соответствующих коду-произведению на основе EG-кода (15,7) (а) и PG-кода (21,11) (б): 1 – граница случайного кодирования; 2 – алгоритм m-APP (пять итераций); 3 – алгоритм m-APP (20 итераций); 4 – алгоритм m-BP (пять итераций); 5 – алгоритм m-BP (20 итераций).
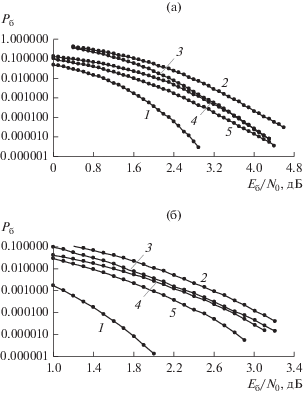
Рис. 3.
Вероятности ${{P}_{{\text{б}}}}$ приема сигналов ФМ2, соответствующих коду-произведению на основе EG-кода (63,37): 1 – граница случайного кодирования; 2 – алгоритм m-APP (пять итераций); 3 – алгоритм m-APP (20 итераций); 4 – алгоритм m-BP (пять итераций); 5 – алгоритм m-BP (20 итераций); 6 – вероятность ${{P}_{{\text{б}}}}$ для сверточного кода с кодовой скоростью 1/3, алгоритм приема Витерби [18].
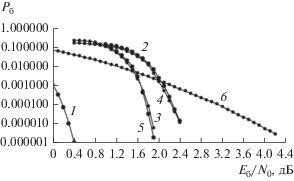
Рис. 4.
Вероятности ${{P}_{{\text{б}}}}$ приема сигналов ФМ2, соответствующих коду-произведению на основе PG-кода (73,45): 1 – граница случайного кодирования; 2 – алгоритм m-APP (пять итераций); 3 – алгоритм m-APP (20 итераций); 4 – алгоритм m-BP (пять итераций); 5 – алгоритм m-BP (20 итераций); 6 – вероятность ошибки для низкоплотностного кода AR4J c кодовой скоростью 1/2 [13].
При моделировании производилась интервальная оценка ${{P}_{{\text{б}}}}$ путем вычисления частности ${x \mathord{\left/ {\vphantom {x u}} \right. \kern-0em} u}$, где $x$ – число ошибочных символов в последовательности переданных символов $u$. Требуемый объем $u$ определялся размером доверительного интервала [$0.5{{P}_{{\text{б}}}},1.5{{P}_{{\text{б}}}}$], вероятностью ${{P}_{{\text{б}}}} = {{10}^{{ - 5}}}$, доверительной вероятностью ${{P}_{{{\text{дов}}}}} = 0.95$ [17].
На рис. 1 приведены значения ${{P}_{{\text{б}}}}$ для кода-произведения на основе EG-кода (15,7) ($N = 225$, $K = 25$, ${{D}_{{мин}}} = 49$, кодовая скорость $R = 0.22$) для алгоритмов приема BP и m-ВP. Видно, что применение алгоритма m-ВP определяет энергетический выигрыш до 0.1 дБ по отношению к алгоритму приема ВР. Энергетический выигрыш достигал значений до 0.1…0.2 дБ при использовании алгоритма m-BP по отношению к алгоритму BP и алгоритма m-APP по отношению к алгоритму APP также и для других кодов-произведений, параметры которых приведены в табл. 2.
На рис. 2а приведены вероятности ошибки ${{P}_{{\text{б}}}}$ при использовании алгоритмов m-BP и m-APP для кода-произведения на основе EG-кода (15,7) при применении пяти итераций (кривая 2 для m-APP, кривая 4 для m-BP) и 20 итераций (кривая 3 для m-APP, кривая 5 для m-BP). Кривая 1 соответствует верхней границе Pб случайного кодирования [1, 9], граница показывает существование кода с приведенными параметрами $(N,K)$, $R = 0.22$ с вероятностными характеристиками, определяемыми соотношениями [18]
(16)
${{E}_{r}}(R) = \mathop {max}\limits_{0 \leqslant \rho \leqslant 1} \mathop {max}\limits_Q ({{E}_{0}}(\rho ,Q) - \rho R),$(17)
${{E}_{0}}(\rho ,Q) = - Ln\left( {{{{\sum\limits_{j = 0}^1 {\left[ {\sum\limits_{k = 0}^1 {Q(k){{{(\Pr (j\left| k \right.))}}^{{{1 \mathord{\left/ {\vphantom {1 {(1}}} \right. \kern-0em} {(1}} + \rho )}}}} } \right]} }}^{{(1 + \rho )}}}} \right).$Здесь $Q(0) = Q(1) = 0.5$, переходные вероятности $\Pr (j\left| {k)} \right.$ определяются вероятностями ошибки для дискретно-непрерывного канала АБГШ.
Видно, что увеличение числа итераций приводит к уменьшению вероятности ${{P}_{{\text{б}}}}$ при фиксированном значении Eб/N0 = 4.1 дБ (табл. 3).
Таблица 3.
Значения ${{P}_{{\text{б}}}}$ для кода-произведения на основе EG-кода (15,7) (Eб/N0 = 4.1 дБ)
| Количество итераций | m-BP | m-APP |
|---|---|---|
| 20 | 10–5 | 3 × 10–5 |
| 5 | 3 × 10–5 | 3 × 10–4 |
Таким образом, для этого кода-произведения алгоритм m-BP является более эффективным по сравнению с алгоритмом m-APP – энергетический выигрыш для пяти итераций и ${{P}_{{\text{б}}}} = {{10}^{{ - 5}}}$ достигает 0.5 дБ. Для 20 итераций эти алгоритмы практически эквивалентны по помехоустойчивости. Выше отмечалось, что алгоритм m-APP в два раза эффективнее алгоритма m-BP по требуемому числу вычислительных операций, также следует отметить, что он для данного кода-произведения в восемь раз эффективнее по требуемой памяти (${{J}_{N}} = 4$). Кривая 5 для алгоритма m-ВP и кривая 3 для m-APP близки к границе ${{P}_{{\text{б}}}}$ случайного кодирования – для ${{P}_{{\text{б}}}} = {{10}^{{ - 5}}}$ различие не превышает 1.4 дБ.
На рис. 2б приведены вероятности ${{P}_{{\text{б}}}}$ для кода-произведения на основе PG-кода (21,11) ($N = 441$, $K = 121$, ${{D}_{{мин}}} = 36$, $R = 0.27$). Кривая 1 соответствует границе ${{P}_{{\text{б}}}}$ случайного кодирования для этого кода-произведения. Кривые 2 и 3 соответствуют применению алгоритма приема m-APP): для пяти итераций значение ${{P}_{{\text{б}}}}$ = 10–5 достигается при Eб/N0 = 3.3 дБ, для 20 итераций при Eб/N0 = 3.2 дБ. Кривые 4 и 5 соответствуют применению алгоритма m-BP: для пяти итераций значение ${{P}_{{\text{б}}}}$ = 10–5 достигается при Eб/N0 = 3.1 дБ, для 20 итераций при Eб/N0 = 2.8 дБ. Таким образом, для ${{P}_{{\text{б}}}} = {{10}^{{ - 5}}}$ различие кривой 5 по отношению к кривой 1 для границы случайного кодирования не превышает 1 дБ. Следует отметить, что для рассматриваемого кода-произведения алгоритм m-APP по сравнению с m-BP в 10 раз эффективнее по требуемой памяти (${{J}_{N}} = 5$).
На рис. 3 приведены вероятности ${{P}_{{\text{б}}}}$ для кода-произведения на основе EG кода (63,37) ($N = 3969$, $K = 1369$, ${{D}_{{мин}}} = 81$, $R = 0.34$). Кривая 1 соответствует границе случайного кодирования для этого кода-произведения. Кривые 2 и 3 соответствуют применению алгоритма приема m-APP: для 5 итераций значение ${{P}_{{\text{б}}}}$ = 10–5 достигается при Eб/N0 = = 2.3 дБ, для 20 итераций при Eб/N0 = 1.9 дБ. Кривые 4 и 5 соответствуют применению алгоритма m-BP, эти кривые практически совпадают с соответствующими кривыми 2 и 3 для m-APP. Для ${{P}_{{\text{б}}}} = {{10}^{{ - 5}}}$ различие наиболее эффективной вероятностной кривой 5 по отношению к кривой 1 границы случайного кодирования не превышает 1.6 дБ. Кривая 6 соответствует известному сверточному коду с эквивалентной кодовой скоростью $R = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$ (длина кодового ограничения $7$, алгоритм приема Витерби) [9]. Для ${{P}_{{\text{б}}}}$= 10–5 и реализации 20 итераций энергетический выигрыш кода-произведения по сравнению с этим сверточным кодом составляет 2.0 дБ. Для рассматриваемого кода-произведения алгоритм m-APP по отношению к алгоритму m-BP в 16 раз эффективнее по требуемой памяти (${{J}_{N}} = 8$).
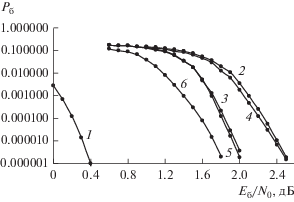
На рис. 4 приведены вероятности ${{P}_{{\text{б}}}}$ для кода-произведения на основе PG кода (73,45) ($N = 5329$, $K = 2025$, ${{D}_{{мин}}} = 100$, $R = 0.38$). Кривая 1 соответствует границе случайного кодирования для этого кода-произведения. Кривые 2 и 3 соответствуют применению алгоритма приема m-APP: для пяти итераций значение ${{P}_{{\text{б}}}}$ = 10–5 достигается при Eб/N0 = 2.4 дБ, для 20 итераций при Eб/N0 = 1.95 дБ (практически совпадает с вероятностными характеристиками кривой 6 для наиболее эффективного низкоплотностного кода AR4J c кодовой скоростью 1/2 (параметры кода (4096.2048)) в составе класса помехоустойчивых кодов, рекомендованных для использования в спутниковых системах связи [13]). Кривые 4 и 5 соответствуют применению алгоритма m-BP, эти кривые практически совпадают с соответствующими кривыми 2 и 3 для m-APP. Вероятностные кривые 3 и 5 близки к теоретической границе 1 – для ${{P}_{{\text{б}}}} = {{10}^{{ - 5}}}$ различие не превышает 1.65 дБ. Для рассматриваемого кода-произведения алгоритм m-APP по сравнению с алгоритмом m-BP в 18 раз эффективнее по требуемой памяти (${{J}_{N}} = 9$).
ЗАКЛЮЧЕНИЕ
Таким образом, представлены результаты исследований вероятностных характеристик и сложности алгоритмов приема для сигналов ФМ2, соответствующих кодам-произведениям, особенностью которых является то, что они формируются на основе составляющих низкоплотностных кодов и также являются низкоплотностными кодами. Вследствие этого можно применить алгоритмы итеративного приема, разработанные для общего класса низкоплотностных кодов, в частности, алгоритмы ВР, APP и их модификации m-ВP и m-APP. Приведены результирующие параметры рассматриваемых кодов-произведений (длительность кодовых слов, информационный объем, минимальный вес Хэмминга, кодовая скорость), формируемых с использованием ряда составляющих низкоплотностных кодов на основе конечной Евклидовой и проективной геометрий.
Для ряда рассматриваемых кодов-произведений проведено моделирование алгоритмов итеративного приема. Показано, что алгоритм m-ВP (m-APP) более эффективен по сравнению с алгоритмом ВР (APP). Наиболее эффективным относительно вероятностных характеристик является алгоритм m-BP, однако относительно требуемых при реализации объема вычислительных операций и объема памяти наиболее эффективен алгоритм m-APP. Показано также, что для кодов-произведений из рассматриваемого ряда с кодовой скоростью $R > 0.3$ алгоритмы итеративного приема m-BP и m-APP практически эквивалентны.
Вероятностные кривые для алгоритма m-BP и m-APP (20 итераций) близки к вероятностным кривым верхней границы случайного кодирования. Энергетический выигрыш для кода-произведения с кодовой скоростью 1/3 по сравнению со сверточным кодом с эквивалентной кодовой скоростью при ${{P}_{{\text{б}}}}$ = 10–5 составляет 2.4 дБ.
Список литературы
Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.: Мир, 1976.
Li J., Lin S., Abdel-Chaffar K. et al. LDPC Code Designs, Constructions and Unification. Cambridge: Univ. Press. United Kingdom, 2017.
Pyndiah R.M. // IEEE Trans.1998. V. Comm-46. № 8. P.1003.
Johnson S.J. Iterative Error Correction: Turbo, Low-Density Parity-Check and Repeat-Accumulate Codes. Cambridge: Univ. Press, 2010.
Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные сети передачи. М.: Техносфера, 2005.
Назаров Л.Е., Головкин И.В. // Цифровая обработка сигналов. 2009. № 2. С. 2.
Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи. Базовые методы и характеристики. М.: Эко-Трендз, 2005.
Назаров Л.Е., Батанов В.В., Кузнецов О.О. // Журн. радиоэлектроники. 2014. № 9. http://jre.cplire.ru/jre/sep14/1/text.pdf.
Zhou L., Wu K., Zhao R. et al. // Procedia Engineering. 2011. V. 15. P. 2538.
Назаров Л.Е., Шишкин П.В. // Радиоэлектроника. Наносистемы. Информ. технологии. 2018. Т. 10. № 2. С. 323.
Назаров Л.Е., Шишкин П.В. // Информ. технологии. 2018. Т. 24. № 6. С. 427.
Назаров Л.Е., Шишкин П.В. // Журн. радиоэлектроники. 2018. № 5. http://jre.cplire.ru/jre/may18/ 1/text.pdf.
Low-Density Parity Check Codes for Use in Near-Earth and Deep Space Application. Experimental Specification. CCSDS 131.1-O-2. 2007, Washington, NASA Headquarters.
Назаров Л.Е., Шишкин П.В. // РЭ. 2019. Т. 64. № 9. С. 910.
Liu Z., Pados D.A. // IEEE Trans. 2005. V. Comm-53. № 3. P. 415.
Sunil K., Jayaraj P., Soman K.P. // IOSR J. Comp. Engineering. 2012. V. 2. № 3. P. 12.
Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике. М.: Гостехтеориздат, 1955.
Витерби А.Д., Омура Дж.К. Принципы цифровой связи и кодирования. М.: Радио и связь, 1982.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


