Радиотехника и электроника, 2020, T. 65, № 7, стр. 684-694

ВВЕДЕНИЕ

Функционирование радиолокационных систем ближнего действия (РЛСБД) в процессе обнаружения объектов на подстилающих поверхностях характеризуется малым временным интервалом принятия решения. Кроме того, необходимо анализировать нестационарный процесс с негауссовым вероятностным распределением. Эффективным методом решения указанной выше задачи является исследование поляризационных свойств отражательных характеристик объекта локации. Теории и практике применения такого подхода посвящены работы [1–5]. В частности, в них изложены фундаментальные положения детерминированной и статистической теории поляризации радиоволн, рассеянных стабильными и флуктуирующими точечными объектами.

Поляризационная структура поля, рассеянного протяженным объектом сложной геометрической формы, является в определенном смысле случайной, поскольку зависит от количества и пространственного расположения центров вторичного интенсивного излучения, распределенных по поверхности объекта локации. Проблемы статистической теории радиолокации протяженных целей наиболее полно рассмотрены в работе [6].

Классическая методология поляризационной селекции объекта на подстилающей поверхности (ПП) предполагает преобразование измеренных сигналов в информативные признаки на основе отображений:

– Паули в терминах ортогональных компонент комплексных амплитуд [3]

где индексы соответствуют горизонтальной HH и вертикальной VV поляризациям соответственно для излучателя и приемника;

– Паули в терминах ортогональных компонент эффективной площади рассеяния (ЭПР) [3, 4]

– контраста в терминах собственных значений ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$ поляризационной матрицы рассеяния (ПМР) цели [5] – Хьюнена в терминах собственных значений ПМР цели [5]

Важно отметить, что указанные выше признаки формируются классическими процедурами статистического оценивания стационарных процессов на достаточно большом временнóм интервале накопления [2, 3]. Кроме того, известные РЛСБД измеряют, как правило, ортогональные компоненты ПМР объекта локации и обладают низким разрешением по дальности. Вместе с тем углубленный анализ убедительно демонстрирует наличие существенных изменений во времени основных статистик принимаемых сигналов, содержащих значимые аномальные значения [5, 6]. Иными словами, эффективное обнаружение объектов на ПП требует генерации информативных признаков на относительно коротком временнóм интервале принятия решения с помощью адаптивных робастных оценок основных статистик полной ПМР объекта локации.

В данной работе рассмотрена методика интеллектуального статистического анализа полной ПМР радиолокационной сцены и формирования пространства информативных признаков для обнаружения антропогенного объекта на ПП. Надежной информационной основой решения этой задачи являются взаимно дополняющие друг друга методы имитационного цифрового моделирования и натурных измерений входных сигналов РЛСБД с высоким разрешением по дальности.

1. ИМИТАЦИОННОЕ ЦИФРОВОЕ МОДЕЛИРОВАНИЕ ПОЛЯРИЗАЦИОННЫХ ХАРАКТЕРИСТИК

Основу методологии имитационного цифрового моделирования радиолокационных сцен в квазиоптическом диапазоне спектра электромагнитных волн составляет представление объекта и ПП в виде совокупности элементарных отражателей [7]. Результирующее поле определено когерентным суммированием полей рассеяния фацетов для текущего момента времени (кадра)

где N – количество фацетов, а ${{a}_{n}}$ – комплексная амплитуда поля элементарного отражателя в апертуре приемной антенны РЛСБД.

Каждый фацет связан с локальными системой координат и базисами плоских падающей и отраженной волн. Спектральная характеристика рассеяния n -го элементарного отражателя определяется его электродинамическими и статистическими свойствами. Электродинамическими параметрами фацетов объекта локации являются относительная диэлектрическая проницаемость покрытия и его толщина, удельная проводимость и относительная магнитная проницаемость. Фацеты ПП, наряду с электродинамическими параметрами, обладают статистическими характеристиками шероховатой поверхности, а именно среднеквадратичными высотами крупномасштабных и мелкомасштабных неровностей, а также соответствующими интервалами корреляции высот неровностей.

Таким образом, методология имитационного цифрового моделирования радиолокационных сцен и входных сигналов РЛСБД включает следующую совокупность математических моделей:

– геометрических образов объекта и ПП, а также их электродинамических и статистических свойств;

– дифракционных полей рассеяния элементарных отражателей;

– спектральных характеристик зондирующего сигнала;

– поляризаций антенной системы;

– траектории относительного сближения.

Цикл работ по созданию аппаратно-программного комплекса синтеза реалистичных радиолокационных сцен и входных сигналов РЛСБЛ прошел многократную апробацию и верификацию по эталонным отражателям и штатным объектам локации в ходе многочисленных работ фундаментального и прикладного характера. Основные возможности методологии имитационного цифрового моделировании сложных радиофизических эффектов (в частности, дифракции на острых кромках, многократного отражения и деполяризации волн, трансформации и обогащения спектра зондирующего сигнала, шероховатости ПП и наличия растительности) отражены в многочисленных статьях и монографиях [8–11].

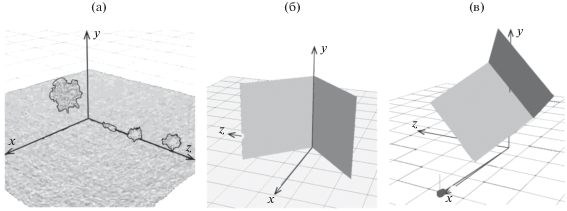
В качестве иллюстрации на рис. 1 представлены результаты синтеза изображений радиолокационных сцен: в частности, сцена с подстилающей поверхностью (рис. 1а) и эталонный двугранный уголковый отражатель в двух положениях: с гранью, перпендикулярной плоскости облучения–наблюдения XOZ и симметрично расположенной относительно направления визирования (рис. 1б), а также с гранью, повернутой на 45° вокруг оси x (рис. 1в).

Типичная радиолокационная сцена, изображенная на рис. 2, представляет собой неровную поверхность с кустарником и отдельно стоящим деревом и собственно объектом локации. Угловой сектор облучения–приема по азимуту составляет 1°, что соответствует ширине диаграммы направленности антенны РЛСБД. Излучаемый сигнал является широкополосным с шириной спектра не менее 20 МГц, что обеспечивает достаточно высокое разрешение радиолокатора по дальности.

При моделировании отраженных сигналов исследовались:

– типовые ракурсы облучения–наблюдения объекта;

– три значения для разрешения радиолокатора по дальности, а именно 1, 4 и 5.5 м. Для уголкового отражателя разрешение по дальности составляло 4 м;

– заранее заданная протяженность радиолокационной сцены M = 40, 10 и 8 стробов дальности, нумерация которых начинается от РЛСБД.

Имитационное цифровое моделирование выполнялось с учетом влияния сложных дифракционных эффектов рассеяния волн таких, как наличие острых кромок и уголковых отражателей на поверхности объекта, скользящих углов его облучения–наблюдения и многократных отражений [10, 11]. В результате получены полные ПМР цели в текущем m-м стробе разрешения по дальности: в терминах комплексных амплитуд сигналов по двум квадратурам –

и в терминах ЭПР – где индексы HH, HV, VH, VV – соответствуют горизонтальной H и вертикальной V поляризациям последовательно для излучения и приема.

Результаты имитационного цифрового моделирования информативных признаков Паули (1) в терминах комплексных амплитуд (5) для ПП (см. рис. 1а) и объекта на ПП (см. рис. 2) представлены на рис. 3а и 3б. Данные соответствуют разрешению РЛСБД по дальности 1 м.

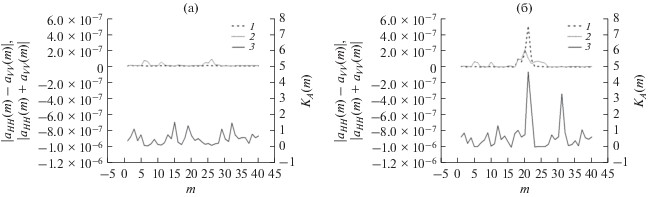
Аналогичные результаты моделирования признаков Паули (1) в терминах комплексных амплитуд (5) для двух положений двугранного уголкового отражателя (см. рис. 1б и 1в) представлены на рис. 4а и 4б. Данные соответствуют разрешению РЛСБД по дальности 4 м.

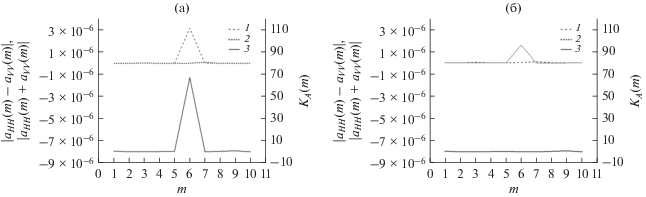
Сравнение полученных результатов моделирования показывает, что объект на ПП более надежно обнаруживает сигнал модуля разности комплексных амплитуд согласованных поляризаций $\left| {{{a}_{{HH}}}\left( m \right) - {{a}_{{VV}}}\left( m \right)} \right|$. Вместе с тем сигнал контраста ${{K}_{A}}\left( m \right)$ наряду с объектом идентифицирует участки ПП в виде кустарника в стробах дальности m (временных интервалах сигнала) 1, 2 и дерева в стробе 8.

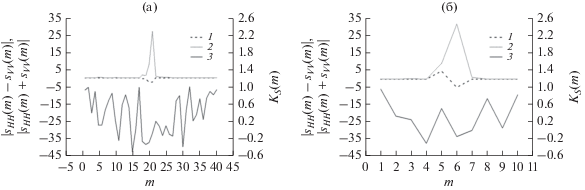
Результаты имитационного цифрового моделирования информативных признаков Паули (2) в терминах ЭПР (6) для объекта на ПП (см. рис. 2) представлены на рис. 5а и 5б. Данные соответствуют разрешению РЛСБД по дальности 1 и 4 м.

Результаты имитационного цифрового моделирования информативных признаков (3) и (4), сформированных по собственным значениям ПМР в терминах ЭПР для ПП (см. рис. 1а) и объекта на ПП (см. рис. 2), представлены на рис. 6а и 6б. Данные соответствуют разрешению РЛСБД по дальности 1 м.

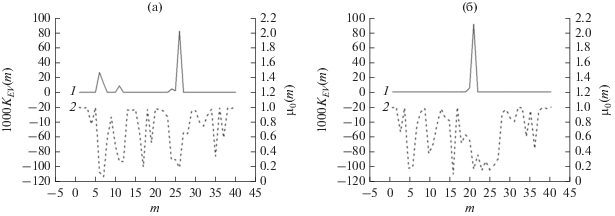
Сравнение полученных результатов моделирования показывает, что более надежный способ селекции объекта на ПП основан на анализе собственных значений ПМР как в терминах комплексных амплитуд (5), так и в терминах ЭПР (6). Вместе с тем контрастные информативные признаки (3) и (4) наряду с обнаружением объекта на ПП также идентифицируют участки ПП. Иными словами, процедура агрегирования собственных значений ПМР как в терминах комплексных амплитуд, так и в терминах ЭПР приводит к снижению информативности контрастов Паули и Хьюнена.

2. НАТУРНЫЕ ИЗМЕРЕНИЯ ПОЛЯРИЗАЦИОННЫХ ХАРАКТЕРИСТИК

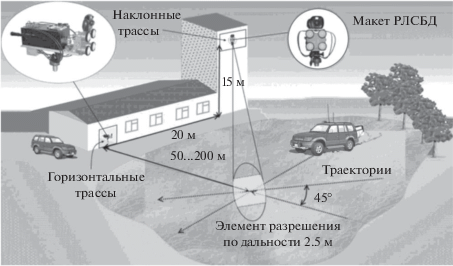
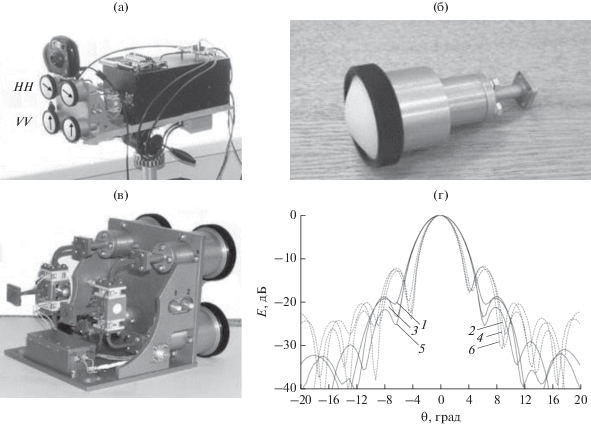
Данные имитационного цифрового моделирования подтверждены результатами натурных измерений полной ПМР объектов локации, измеренных с помощью макетного образца РЛСБД, изготовленного в НИИСМ МГТУ им. Н.Э. Баумана (рис. 7). В макете реализован квазинепрерывный сигнал с несущей частотой 92…95 ГГц, что соответствует длине волны излучения 3 мм. Реализации временных рядов (ВР) для компонентов ПМР (6) в терминах ЭПР записывались с частотой дискретизации 50 МГц. Приемный строб “охватывал” от 18 до 30 элементов разрешения по дальности для различных реализаций отраженных сигналов. Длительность элемента разрешения составила 40 нс, что соответствует дальности 6 м. При этом накопление по времени в пределах строба дальности составило от 100 до 300 отсчетов сигнала для различных объектов. Измерения проводились на горизонтальных и наклонных трассах (рис. 8) в различных метеоусловиях (сухая или влажная погода, дождь, снег).

Объектами локации являлись различные транспортные средства, а также природные образования: травяной или песчаный покров, кустарник, лиственные или хвойные деревья. В качестве антропогенных объектов исследовались каменное здание, бетонная площадка, дорога.

В качестве критериев соответствия данных имитационного цифрового моделирования результатам натурных измерений были использованы спектрограммы ВР полной ПМР в терминах ЭПР объектов локации (рис. 9).

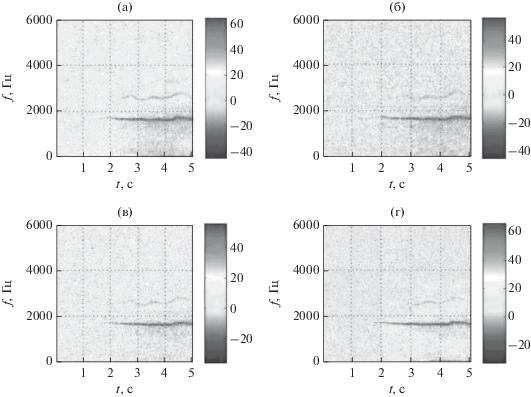
Временные последовательности выборочных спектров (периодограмм Шустера), сформированных в скользящем окне усреднения по времени после низкочастотной фильтрации трендовых компонент, соответствуют текущему азимутальному направлению на объект локации. Относительное среднее квадратичное отклонение отсчетов выборочных спектров, полученных по результатам имитационного цифрового моделирования и натурных измерений, не превышало 11.3%.

3. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПОЛЯРИЗАЦИОННЫХ ХАРАКТЕРИСТИК

Надежной методической основой формирования пространства информативных признаков для обнаружения объекта на ПП является интеллектуальный статистический анализ поляризационных характеристик сигналов, отраженных радиолокационной сценой. Существенная особенность нестационарных негауссовых ВР, порождаемых компонентами ПМР (5) и (6), состоит в наличии аномальных значений, характерных для антропогенных объектов. Такого рода динамика сигналов требует применения процедур адаптивного и робастного оценивания основных статистик ВР, а именно трендов, мер волатильности и матрицы коэффициентов корреляции. Важным параметром этих процедур является временной интервал сглаживания данных 2N + 1, который в нашем исследовании, как отмечалось ранее, соответствует количеству элементов разрешения по дальности.

Для определенности будем рассматривать ПМР в терминах ЭПР. Матрицу (6) разворачивают в вектор-столбец следующего вида:

где

Здесь и далее векторы будем интерпретировать как столбцы, если не оговорено иное. Операция логарифмирования является, как известно, частным случаем преобразования Бокса–Кокса, которое в определенной степени приближает распределения данных к гауссовым. Кластерную структуру ВР ${{s}_{i}}\left( m \right)$, i = 1, 2, 3, 4, полученных в результате имитационного цифрового моделирования ПМР для ПП и объекта на ПП (см. рис. 2), иллюстрируют рис. 10а и 10б. Данные соответствуют разрешению РЛСБД по дальности 1 м.

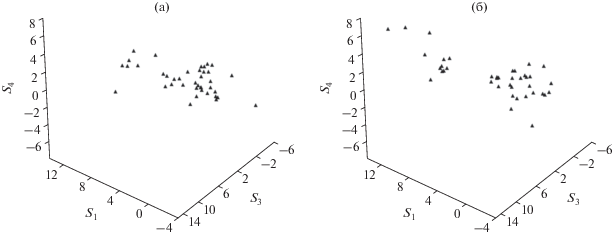
Диаграмма рассеяния ПП (см. рис. 10а) демонстрирует наличие двух кластеров, а именно типичных фацетов ПП, а также кустарника и дерева. Объект на ПП добавляет к указанным выше классам отражений от элементов ПП аномальные значения, которые рационально интерпретировать как непредставительный кластер собственно объекта локации (см. рис. 10б).

Предлагается следующая процедура адаптивного робастного оценивания основных статистик ВР ${{s}_{i}}\left( m \right)$, i = 1, 2, 3, 4. Временной интервал анализа, содержащий M отсчетов данных, разбивают на $K = \left( {{M \mathord{\left/ {\vphantom {M N}} \right. \kern-0em} N}} \right) - 1$ сегментов с 50%-ным перекрытием соседних участков. В пределах k-го текущего сегмента формируют робастные экспоненциально взвешенные оценки (ЭВО) характеристик положения и масштаба, предложенных Л.Д. Мешалкиным [12]. Для выборки векторов ${\mathbf{s}}\left\{ {\left( {k - 1} \right)N + n} \right\},$ n = 1, 2, …, (2N + 1) в k-м сегменте данных получают робастные ЭВО вектора математического ожидания ${\mathbf{e}}\left( {kN + 1} \right)$ и ковариационной матрицы ${\mathbf{B}}\left( {kN + 1} \right)$ в результате решения системы нелинейных уравнений [13, с. 75]

Здесь $\gamma > 0$ – параметр устойчивости статистик к аномальным значениям; $q\left\{ {D\left( n \right)} \right\} = \exp \left\{ { - {{D\left( n \right)} \mathord{\left/ {\vphantom {{D\left( n \right)} 2}} \right. \kern-0em} 2}} \right\}$ – экспоненциальная весовая функция Л.Д. Мешалкина;

– метрика Махаланобиса выборки векторов в k‑м сегменте данных. Для типичных значений параметра $\gamma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ ЭВО обеспечивают автоматическое подавление аномальных значений. Выбросам данных ${\mathbf{s}}\left\{ {\left( {k - 1} \right)N + n} \right\}$ соответствуют большие расстояния $\sqrt {D\left( n \right)} $, поэтому такие отсчеты взвешиваются весами ${{q}^{\gamma }}\left\{ {D\left( n \right)} \right\}$ достаточно малыми, чтобы не вносить значимый вклад в общие суммы системы уравнений (7).

Простейший алгоритм решения системы уравнений (7) состоит в применении метода последовательных приближений. В качестве начальных значений характеристик положения и масштаба удобно выбрать выборочные средние, подверженные влиянию аномалий

Последовательные подстановки указанных выше статистик в правые части уравнений системы (7) и их обновление требуют, как правило, небольшого количества итераций для обеспечения сходимости алгоритма оценивания.

Для отсчетов ВР m = N + 1, N + 2, …, M – N адаптивные оценки трендов и ковариационных матриц формируют с помощью процедуры “сшивания” последовательностей оценок математических ожиданий ${\mathbf{e}}\left( {kN + 1} \right)$ и ковариационных матриц ${\mathbf{B}}\left( {kN + 1} \right)$ в серединных отсчетах сегментов данных k = 1, 2, …, K;

где $w\left( l \right)$ – симметричная функция ядра, неотрицательная на интервале $\left| {\,l{\kern 1pt} } \right| \leqslant 1$ и $w\left( l \right) \to 0$, если $\left| {\,l{\kern 1pt} } \right| > 1$. Популярным на практике является гауссовское ядро вида $w\left( l \right) = 3{{\exp \left( { - {{9{{l}^{2}}} \mathord{\left/ {\vphantom {{9{{l}^{2}}} 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{\exp \left( { - {{9{{l}^{2}}} \mathord{\left/ {\vphantom {{9{{l}^{2}}} 2}} \right. \kern-0em} 2}} \right)} {\sqrt {2\pi } }}} \right. \kern-0em} {\sqrt {2\pi } }}.$

Для начальных m = 1, 2, …, N и конечных m = M – N + 1, M – N + 2, …, M отсчетов ВР в качестве оценок основных статистик принимают начальные ${\mathbf{e}}\left( {N + 1} \right)$, ${\mathbf{B}}\left( {N + 1} \right)$ и конечные оценки ${\mathbf{e}}\left( {M - N} \right)$, ${\mathbf{B}}\left( {M - N} \right)$ соответственно.

Дополнительное преимущество ЭВО состоит в возможности формирования в пространстве векторов ${\mathbf{s}}\left( m \right)$, m = 1, 2, …, M четырехмерных исходных признаков дискриминантной границы в виде гиперэллипсоида, отделяющего кластер сигналов отраженных типичными фацетами ПП от объекта, а также отдельных элементов ПП в виде кустарника и деревьев. Важное преимущество имитационного цифрового моделирования сигналов радиолокационной сцены состоит в наличии априорной информации о принадлежности отражающих фацетов для каждого отсчета ВР одному из трех классов, а именно непосредственно ПП, кустарнику или деревьям и собственно объекту локации. Результаты моделирования показали, что кластер ПП рационально формировать по правилу “двух сигм”:

Дискриминантная граница такого кластера ограничена поверхностью гиперэллипсоида в пространстве исходных признаков [13, с. 82].

Следующим важным этапом поляризационной селекции является формирование пространства информативных признаков для обнаружения объекта на ПП. Классической методологией решения этой проблемы является метод главных компонент. Представленный в данной работе подход, основанный на поиске информативных признаков методом главных компонент, развивает идеи, изложенные в работах Клоуда, Потье, Фримена [14, 15].

4. ПРОСТРАНСТВО ИНФОРМАТИВНЫХ ПРИЗНАКОВ

В соответствии с полученными робастными оценками характеристик положения и масштаба кластера ПП данные центрируют и нормируют

По отсчетам ВР ${{s}_{i}}\left( m \right)$, удовлетворяющих условию (8), формируют выборочную робастную оценку матрицы коэффициентов корреляции подпространства ПП

где ${\mathbf{v}}\left( m \right) = {{\left\{ {{{v}_{1}}\left( m \right),{{v}_{2}}\left( m \right),{{v}_{3}}\left( m \right),{{v}_{4}}\left( m \right)} \right\}}^{T}}$ – вектор-столбец, а $\tilde {M}$ – количество наблюдений в кластере ПП.

Факторизация робастной оценки матрицы коэффициентов корреляции ${\mathbf{\tilde {B}}} = {\mathbf{U}}\Lambda {{{\mathbf{U}}}^{T}}$ по собственным значениям $\Lambda = diag\left( {{{\lambda }_{1}},{{\lambda }_{2}},{{\lambda }_{3}},{{\lambda }_{4}}} \right)$, перечисленным в порядке убывания и соответствующим собственным векторам ${{{\mathbf{u}}}_{i}}$, формирует оптимальный ортонормированный базис ${\mathbf{U}} = \left( {{{{\mathbf{u}}}_{1}}{{{\mathbf{u}}}_{2}}{{{\mathbf{u}}}_{3}}{{{\mathbf{u}}}_{4}}} \right)$ подпространства ПП. Сумма первых двух собственных значений $\left( {{{\lambda }_{1}} + {{\lambda }_{2}}} \right)$ аккумулирует 98.33% от дисперсии $\left( {{{\lambda }_{1}} + {{\lambda }_{2}} + {{\lambda }_{3}} + {{\lambda }_{4}}} \right)$ данных, представленных на рис. 10б. Иными словами, собственные векторы ${{{\mathbf{u}}}_{1}}$ и ${{{\mathbf{u}}}_{2}}$ образуют главный базис. Соответствующие информативные признаки типичных фацетов ПП в терминах факторного анализа имеют вид

5. РАСПОЗНАВАНИЕ ОБЪЕКТА НА ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ

Распознавание объекта на ПП предлагается реализовать в двумерном пространстве главных факторов в два этапа. На первом этапе предварительной кластеризации формируют линейную дискриминантную границу, отделяющую кластер типичных элементов ПП 1 от объединенного кластера, формируемого кустарником, деревьями и собственно объектом 2 (рис. 11а). Дихотомия выполнялась с помощью иерархического алгоритма, а также внутригрупповых К-средних (англ. K-means). В качестве меры расстояния применялась метрика Евклида. Согласно алгоритму К-средних линейная граница, оптимальная по критерию минимума расстояния, представляет собой прямую линию, которая проходит через середину отрезка, соединяющего центры группировки типичных элементов ПП 3 и объединенного класса 4, и перпендикулярна этому отрезку [16, с. 92, 109].

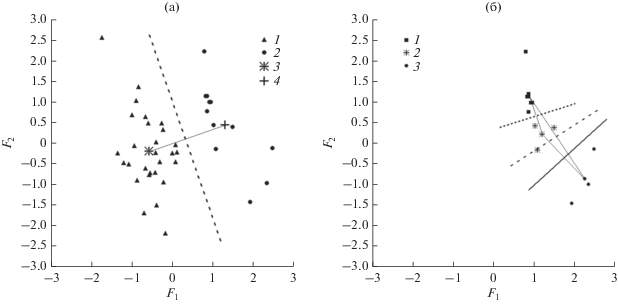
Важно отметить, что результаты предварительной кластеризации в пространстве главных факторов с помощью алгоритма К-средних хорошо согласуются с робастными ЭВО векторов математических ожиданий

для типичных элементов ПП и объединенного кластера соответственно. Здесь ${\mathbf{F}}\left( m \right) = \left\{ {{{F}_{1}}\left( m \right),} \right.$ ${{\left. {{{F}_{2}}\left( m \right)} \right\}}^{T}}$, m = 1, 2, …, M – главные факторы, упорядоченные по принадлежности к кластерам в соответствии с критерием (8), т.е. первые $\tilde {M}$ элементов выборки принадлежат классу типичных элементов ПП.

На втором этапе уточняющей кластеризации с помощью алгоритма К-средних формируют три линейные дискриминантные границы (рис. 11б), разделяющие кустарник 1, деревья 2 и объект 3 в предварительно полученном объединенном кластере, руководствуясь правилом “один против одного”. В соответствии с этим правилом классы попарно разделяют независимо от остальных, т.е. формируют линейные дискриминантные функции:

Здесь ${{{\mathbf{w}}}_{{jk}}} = {{\left( {{{w}_{{0jk}}},{{w}_{{1jk}}},{{w}_{{2jk}}}} \right)}^{T}}$ – вектор параметров границы, разделяющей j-й и k-й классы. Обучающую выборку ${\mathbf{F}}\left( m \right)$, m = $\tilde {M}$ + 1, $\tilde {M}$ + 2, …, M размечают маркерами ${{\delta }_{{jk}}}\left( m \right) = \pm 1$ для каждой пары классов так, чтобы правила классификации имели вид:

для кустарника –

для деревьев –

для объекта локации –

Линейные дискриминантные функции (9) сформированные с помощью алгоритма К-средних иллюстрирует рис. 11б. Границы ${{d}_{{12}}}\left( m \right) = 0$, ${{d}_{{13}}}\left( m \right) = 0$ и ${{d}_{{23}}}\left( m \right) = 0$, разделяющие классы кустарник–деревья, кустарник–объект и деревья–объект, изображены пунктирной, штриховой и сплошной прямыми соответственно.

Результаты синтеза робастных линейных дискриминантных границ с помощью машины опорных векторов (Support Vector Machine, SVM) [17], обеспечивающей максимально широкие разделяющие полосы между классами, представлены на рис. 12. Идентифицированные машиной наиболее сложные для классификации наблюдения (соответствующие опорным векторам) отмечены кружочками.

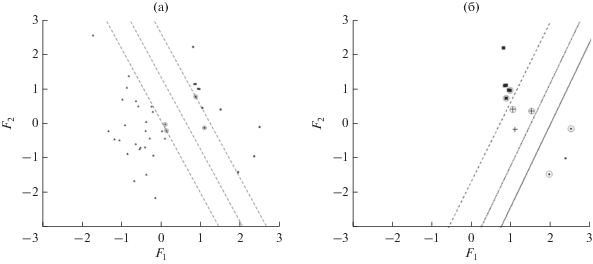
Важно отметить, что в случае линейно неразделимых классов SVM-классификация является более надежной по сравнению с алгоритмом К-средних для обнаружения объекта на ПП, поскольку минимизирует количество ошибочных классификаций, если таковые имеются.

ЗАКЛЮЧЕНИЕ

Таким образом, последовательно изложены этапы интеллектуального анализа полной поляризационной матрицы рассеяния радиолокационной сцены для решения задачи распознавания объекта локации на подстилающей поверхности. По результатам имитационного цифрового моделирования и натурным измерениям нестационарных негауссовых сигналов, порождаемых сценой, предложены адаптивные робастные оценки основных статистик такого рода сигналов и обоснован выбор метода главных компонент для формирования пространства информативных признаков. Верифицированы модели и алгоритмы машинного обучения процедур кластеризации и классификации для распознавания элементов подстилающей поверхности и объекта локации.