Радиотехника и электроника, 2020, T. 65, № 8, стр. 764-768
Повышение точности измерений комплексных диэлектрической и магнитной проницаемостей в сверхвысокочастотном диапазоне волноводным методом
М. П. Пархоменко a, *, Д. С. Каленов a, И. С. Еремин a, Н. А. Федосеев a, В. М. Колесникова a, О. А. Дьяконова a
a Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино Московской обл., пл. Введенского, 1, Российская Федерация
* E-mail: pamikle@yandex.ru
Поступила в редакцию 22.03.2019
После доработки 24.12.2019
Принята к публикации 30.12.2019
Аннотация
Рассмотрен улучшенный волноводный метод определения комплексных диэлектрической и магнитной проницаемостей материалов, не требующий измерения расстояния от плоскостей образца до плоскостей калибровки. Проведенная проверка этого метода и сравнение полученных результатов с классическим волноводным методом на примере образца из высокоомного кремния показали уменьшение ошибки в определении тангенсов углов диэлектрических и магнитных потерь, а также действительной составляющей комплексной магнитной проницаемости.
ВВЕДЕНИЕ
Для определения электромагнитных параметров материалов широко используются резонаторные, волноводные методы и метод свободного пространства [1–9]. Резонаторные методы определяют параметры материалов на отдельных частотах. Основное преимущество волноводного метода заключается в том, что он позволяет определять электромагнитные параметры материалов в широкой полосе частот. Но существует ряд причин, которые ограничивают применение классического волноводного метода, главные из которых – это наличие воздушного зазора между образцом и стенками волновода (особенно между образцом и широкой стенкой волновода) и погрешность, связанная с неточностью определения фазы коэффициентов отражения и прохождения. Последняя обусловлена главным образом ошибкой в определении расстояний от границ образца до границ измерительной секции. Для уменьшения влияния на результаты измерений зазора между образцом и широкой стенкой волновода предложено заполнять его непроводящей пастой, составленной из мелкодисперсного медного порошка, перемешанного с вазелином [7, 9]. Другую погрешность, связанную с неточностью определения расстояний от границ образца до границ измерительной секции, можно уменьшить, используя секции-фланцы, длина которых равнялась бы длине исследуемого образца [9]. Однако существует методическая возможность уменьшения этой погрешности. Эта возможность базируется на том, что современные анализаторы цепей позволяют измерять все четыре S-параметра измерительной секции с образцом за один цикл (два коэффициента отражения и два коэффициента прохождения). Получаемое при этом число уравнений превышает число неизвестных. Это позволяет при определении комплексных диэлектрической и магнитной проницаемостей составить комбинацию уравнений, при решении которых отпадает необходимость определения указанных выше расстояний. Такая комбинация, определяющая улучшенный волноводный метод, рассмотрена в [10].
Цель данной работы – повышение точности измерений диэлектрической и магнитной проницаемостей в СВЧ-диапазоне с помощью волноводного методом.
1. ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИИЯ ЭЛЕКТРОМАГНИТНЫХ ПАРАМЕТРОВ МАТЕРИАЛОВ В КЛАССИЧЕСКОМ И УЛУЧШЕННОМ ВОЛНОВОДНЫХ МЕТОДАХ
В волноводном методе, который строится на базе использования в эксперименте векторного анализатора цепей, измеряются комплексные коэффициенты отражения и прохождения измерительной секции с образцом исследуемого материала (см. рис. 1). В этом случае при отсутствии воздушного зазора аналитическое решение задачи позволяет определить комплексные диэлектрическую и магнитную проницаемости этого материала [5, 6].
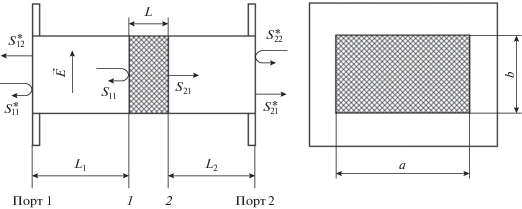
Рис. 1.
Волноводная секция с исследуемым образцом: a × b – поперечные размеры волновода, $\overrightarrow E $ – вектор напряженности электрического поля, L – длина образца; вид спереди (слева) и вид сбоку (справа).
Классический волноводный метод основан на приведенных ниже формулах для комплексных коэффициентов отражения S11 и прохождения S21 на границах 1-го и 2-го образцов (см. рис. 1), т.е. он фактически использует только два S-параметра:
где Γ – коэффициент отражения в волноводе на границе воздух–образец (в случае образца бесконечной длины, т.е. при отсутствии интерференции в образце); P – коэффициент распространения через материал образца в волноводе. Он определяется следующим соотношением: Здесь $\gamma = \alpha + j\beta $ постоянная распространения волны в волноводе, заполненном исследуемым материалом, которая складывается из постоянной затухания α [Нп/м] и фазовой постоянной β [м–1], L – толщина образца.В реальной измерительной секции комплексные коэффициенты отражения $S_{{11}}^{*}$ и прохождения $S_{{21}}^{*}$ измеряются на границах измерительной волноводной секции (см. рис. 1) и связаны с коэффициентами S11 и S21 формулами
Здесь ${{R}_{1}} = \exp ( - {{\gamma }_{0}}{{L}_{1}})$ и ${{R}_{2}} = \exp ( - {{\gamma }_{0}}{{L}_{2}}),$ гдепостоянная распространения в волноводе с воздушным заполнением, λ0 – длина волны в свободном пространстве, λc – критическая длина волны в волноводе. В выражения для R1 и R2 входят величины L1 и L2, которые надо измерять с достаточной точностью.
Соотношения для определения комплексных диэлектрической ε и магнитной μ проницаемостей в классическом волноводном методе находятся в такой последовательности. На первом этапе из системы уравнений (1) и (2) выражаем P и Γ через известные величины S11 и S21 [6]:
(6)
$\Gamma = \frac{{S_{{11}}^{2} - S_{{21}}^{2} + 1}}{{2{{S}_{{11}}}}} \pm \sqrt {\frac{{{{{\left( {S_{{11}}^{2} - S_{{21}}^{2} + 1} \right)}}^{2}}}}{{4S_{{11}}^{2}}} - 1} ,$(7)
$P = \frac{{{{S}_{{21}}}{\text{\;}} + {{S}_{{11}}} - \Gamma }}{{1 - \left( {{{S}_{{21}}}{\text{\;}} + {{S}_{{11}}}} \right)\Gamma }}.$Далее, используя дисперсионное уравнение для волновода с заполнением (ε и μ – параметры материала заполнения) [11] и выражение для коэффициента отражения Γ на границе воздух–исследуемый образец, находим искомые соотношения для определения комплексных диэлектрической ε и магнитной μ проницаемостей исследуемого материала:
(8)
$\mu = - \frac{{1 + \Gamma }}{{1 - \Gamma }}\frac{1}{{{{\gamma }_{0}}L}}\left[ {\ln \left| P \right| + j\left( {\varphi - 2\pi k} \right)} \right],$(9)
$\varepsilon = \frac{{\lambda _{0}^{2}}}{\mu }\left\{ {\frac{1}{{\lambda _{c}^{2}}} - {{{\left( {\frac{1}{{2\pi L}}} \right)}}^{2}}{{{\left[ {\ln \left| P \right| + j\left( {\varphi - 2\pi k} \right)} \right]}}^{2}}} \right\},$Теперь обратимся к улучшенному волноводному методу, который позволяет исключить погрешность, связанную с неточностью определения размеров L1 и L2. В реальной измерительной установке, измеряя комплексные коэффициенты отражения $S_{{11}}^{*}$, $S_{{22}}^{*}$ и прохождения $S_{{21}}^{*}$, $S_{{12}}^{*}$ на границах измерительной волноводной секции, получаем систему из трех уравнений (при двух неизвестных P и Γ) [10]:
(10)
$S_{{11}}^{*} = R_{1}^{2}\left( {\frac{{\Gamma \left( {1 - {{P}^{2}}} \right)}}{{1 - {{\Gamma }^{2}}{{P}^{2}}}}} \right),$(11)
$S_{{22}}^{*} = R_{2}^{2}\left( {\frac{{\Gamma \left( {1 - {{P}^{2}}} \right)}}{{1 - {{\Gamma }^{2}}{{P}^{2}}}}} \right),$(12)
$S_{{21}}^{*} = S_{{12}}^{*} = {{R}_{1}}{{R}_{2}}\left( {\frac{{P\left( {1 - {{\Gamma }^{2}}} \right)}}{{1 - {{\Gamma }^{2}}{{P}^{2}}}}} \right).$Используя эту систему, можно составить комбинацию уравнений, которая не зависит от размеров L1 и L2 [10]:
(13)
$\begin{gathered} S_{{11}}^{*}S_{{22}}^{*} - S_{{21}}^{*}S_{{12}}^{*} = \\ = \exp \left[ { - 2{{\gamma }_{0}}\left( {{{L}_{{{\text{возд}}}}} - L} \right)} \right]\left( {\frac{{{{\Gamma }^{2}} - {{P}^{2}}}}{{1 - {{\Gamma }^{2}}{{P}^{2}}}}} \right), \\ \end{gathered} $(14)
$\frac{{S_{{21}}^{*} + S_{{12}}^{*}}}{2} = \exp \left[ { - {{\gamma }_{0}}\left( {{{L}_{{{\text{возд}}}}} - L} \right)} \right]\frac{{P\left( {1 - {{\Gamma }^{2}}} \right)}}{{1 - {{\Gamma }^{2}}{{P}^{2}}}},$Теперь выражения для P и Γ находим из вновь полученной системы:
гдеЗаметим, что в этом случае P и Γ уже не зависят от L1 и L2. Из (15) выбираются те решения, при которых выполняется условие $\left| P \right| \leqslant 1$.
Для правильного выбора знака в (16) получим коэффициент отражения Γ другим путем. Обозначим его Γ1 и выразим из (10):
(17)
${{\Gamma }_{1}} = \frac{{\alpha \left( {{{P}^{2}} - 1} \right) \pm \sqrt {{{\alpha }^{2}}{{P}^{4}} + 2{{P}^{2}}\left( {2S_{{11}}^{{*2}} - {{\alpha }^{2}}} \right) + {{\alpha }^{2}}} }}{{2S_{{11}}^{*}{{P}^{2}}}},$Знак плюс или минус в выражении (17) выбирают исходя из условия $\left| {{{\Gamma }_{1}}} \right| \leqslant 1$, а знак в выражении (16) – из условия $\Gamma \approx {{\Gamma }_{1}}$.
Далее, по методике, описанной выше, получаем выражения (8) и (9) для определения ε и μ, в которых P и Γ задаются соотношениями (15) и (16). Ниже приведены экспериментальные результаты по определению комплексных диэлектрических и магнитных проницаемостей высокоомного кремния, полученные по обеим методикам, и проведено их сравнение.
2. ИЗМЕРЕНИЕ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ВЫСОКООМНОГО КРЕМНИЯ
Экспериментальная проверка описанных выше волноводных методик проводилась на высокоомном кремнии. Из заготовки кремния с удельным сопротивлением около ρ = 1.1 кОм см изготавливали образец с поперечными размерами 22.72 × 10.09 мм2 и длиной 15.98 мм, который вставляли в волноводную секцию с поперечными размерами волновода a × b = 22.86 × 10.16 мм2. Для волны типа H10 в прямоугольном волноводе критическая длина ${{\lambda }_{c}} = 2a$. Длина волноводной секции была равна 50.07 мм. Воздушный зазор между образцом и широкой стенкой волновода, который не превышал 0.07 мм, заполняли непроводящей пастой, составленной из мелкодисперсного медного порошка, перемешанного с вазелином. Измерения проводили в полосе частот 8.2…12.4 ГГц, а обработку результатов измерений – двумя приведенными выше способами. Полученные зависимости действительной составляющей ε1 и тангенса угла диэлектрических потерь tgδε кремния от частоты представлены на рис. 2а, 2б.
Рис. 2.
Частотные зависимости ε1 (а) и tg δε (б) для образца кремния (поперечные размеры – 22.72 × × 10.09 мм2, длина – 15.98 мм), полученные экспериментально классическим волноводным методом (квадратики) и улучшенным волноводным методом (кружочки); расчет по формуле (18) для образца с ρ = = 1.13 кОм см и ε1 = 11.6 (сплошная кривая на рис. 2б).
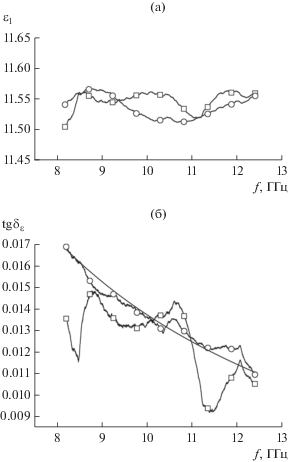
Проведем анализ полученных результатов. Как известно, в рассматриваемом частотном диапазоне действительная составляющая ε1 диэлектрической проницаемости кремния не обнаруживает дисперсии и равняется 11.6. Вычисленные значения ε1 в нашем случае находятся в пределах от 11.5 до 11.56, т.е. погрешность не превышает 1%. Что касается тангенса угла диэлектрических потерь, то их частотные зависимости заметно отличаются (см. рис. 2б). При обработке классическим методом полученная зависимость отображается волнообразной кривой. В улучшенном волноводном методе экспериментальная зависимость тангенса угла диэлектрических потерь от частоты достаточно хорошо описывается уравнением (18). Этому есть объяснение. В высокоомном кремнии решеточные потери существенно ниже потерь на свободных носителях, а тангенс угла потерь на свободных носителях уменьшается с ростом частоты по закону [12]:
(18)
${\text{tg}}{{\delta }_{\varepsilon }} = {1 \mathord{\left/ {\vphantom {1 {\left( {\varepsilon {{\varepsilon }_{0}}\omega \rho } \right)}}} \right. \kern-0em} {\left( {\varepsilon {{\varepsilon }_{0}}\omega \rho } \right)}},$Кремний – немагнитный материал, поэтому при обработке результатов измерений мы полагали μ1 = 1, μ2 = 0. Изложенные выше волноводные методы позволяют определять комплексную магнитную проницаемость материала. Найденные зависимости для μ1 и tg δμ показаны на рис. 3а, 3б. Значения μ1, полученные разными методами, примерно совпадают. Наблюдаемые на графиках выбросы в значении μ1 и tg δμ объясняются приборной погрешностью измерений значений коэффициента отражения в точках его минимумов на частотах, определяемых условием $l = k{{{{\lambda }_{{\text{в}}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{\text{в}}}}} 2}} \right. \kern-0em} 2}$ (k = 1, 2, 3…, λв – длина волны в волноводе на заданной частоте минимума коэффициента отражения). В нашем эксперименте в полосе частот 8.2…12.4 ГГц располагаются два минимума – на частотах 8.5 и 11.2 ГГц – и выбросы при обработке по улучшенному волноводному методу меньше. В окрестностях максимума коэффициента отражения в районе частоты 10 ГГц результаты, полученные обоими способами, примерно одинаковы.
Рис. 3.
Частотные зависимости μ1 (а) и tg δμ (б) для образца кремния (поперечные размеры образца – 22.72 × 10.09 мм2, длина – 15.98 мм), полученные экспериментально классическим волноводным методом (квадратики) и улучшенным волноводным методом (кружочки).
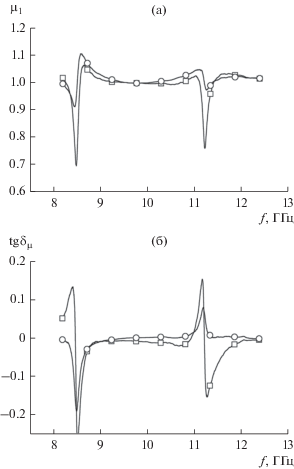
Что касается тангенса угла магнитных потерь, то здесь преимущество улучшенного волноводного метода очевидно: значение tgδμ в окрестностях максимума коэффициента отражения, определенное по улучшенному методу, равняется 1 × 10–3 а в классическом методе оно принимает отрицательную величину с порядком 10–2.
ЗАКЛЮЧЕНИЕ
Представлены два способа определения комплексных диэлектрической и магнитной проницаемостей материалов волноводным методом. Экспериментальная проверка на примере образца из высокоомного кремния показала, что при обработке улучшенным волноводным методом уменьшается ошибка в определении тангенсов углов диэлектрических tg δε и магнитных tg δμ потерь, а также действительной составляющей μ1 комплексной магнитной проницаемости.
Список литературы
Брандт А.А. Исследование диэлектриков на сверхвысоких частотах. М.: Физматгиз, 1963.
Chen L.F., Ong C.K., Neo C.P. et al. Microwave Electronics: Measurement and Materials Characterization. Chichester: John Wiley & Sons, Ltd., 2004.
Пархоменко М.П., Калёнов Д.С., Федосеев Н.А. и др. // РЭ. 2017. Т. 62. № 7. С. 651.
Parkhomenko M.P., Kalenov D.S., Fedoseev N.A. et al. // Phys. Wave Phenomena. 2015. V. 23. № 3. P. 202.
Nicolson A.M., Ross G.F. // IEEE Trans. 1970. V. IM-19. № 4. P. 377.
Weir W.B. // Proc. IEEE. 1974. V. 62. № 1. P. 33.
Пархоменко М.П., Калёнов Д.С., Ерёмин И.С. и др. // Журн. Радиоэлектроники. 2018. № 9. http://jre.cplire.ru/jre/sep18/6/text.pdf.
Пархоменко М.П., Савельев С.В., фон Гратовски С.В. // РЭ. 2017. Т. 62. № 3. С. 276.
Parkhomenko M.P., Kalenov D.S., Eremin I.S. et al. // Phys. Wave Phenomena. 2019. V. 27. № 4. P. 299.
Baker-Jarvis J., Janezic M.D., Grosvenor J.H., Jr., Geyer R.G. Transmission/Reflection and Short-Circuit Line of Methods for Measuring Permittivity and Permeability. NIST Technical Note 1355-R. Boulder: NIST, 1993. 124 p. https://nvlpubs.nist.gov/nistpubs/Legacy/TN/nbstechnicalnote1355r.pdf.
Лебедев И.В. Техника и приборы СВЧ. Т. 1. М.: Высш. шк., 1970.
Гарин Б.М., Копнин А.Н., Пархоменко М.П. и др. // Письма в ЖТФ. 1994. Т. 20. № 21. С. 56.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


