Радиотехника и электроника, 2020, T. 65, № 8, стр. 731-748

ВВЕДЕНИЕ

Одним из современных направлений развития радиосистем различного назначения являются импульсные сигналы, характеристики которых изменяются случайным образом (хаотически) (см., например, [1–5]). Такие сигналы обладают широкими спектрами, позволяют в том числе увеличивать скрытность и помехозащищенность работы систем и обладают рядом других преиму-ществ по сравнению с регулярными сверхширокополосными сигналами. В то же время в опубликованных к настоящему времени результатах исследований полностью отсутствует анализ важного аспекта проблемы, связанного с влиянием среды распространения на характеристики хаотических сигналов. Такая ситуация обусловлена в первую очередь тем, что дисперсионные искажения сигналов всегда рассматриваются на основе интеграла Фурье, а характерные ширины амплитудных и фазовых спектров хаотических сигналов таковы, что препятствуют, по-видимому, получению прямых численных оценок уровня искажений.

В [6] приведено решение задачи о распространении радиоимпульса в резонансно-поглощающей газовой среде, основанное на временном представлении сигнала и не являющееся, таким образом, результатом вычисления интеграла Фурье. Принципиальной особенностью решения является возможность аналитического описания на его основе пространственно-временной эволюции импульса при условии, что в частотном интервале, занимаемым его спектром, показатель преломления среды незначительно отличается от единицы. Для земной атмосферы, в частности, указанное отличие в гига- и терагерцевом диапазонах не превышает ~10^–4 (см., например, [7–9]).

Цель данной работы – представить результаты начального этапа теоретического анализа на основе [6] задачи о дисперсионных искажениях в резонансно-поглощающей среде прямоугольного радиоимпульса с хаотической фазой. Хаотичность фазы моделируется на основе отображения Чебышева первого рода третьего порядка. Аналогичным образом задача может быть рассмотрена с привлечением альтернативных отображений, обсуждаемых в литературе (см., например, [1, 10]). Несущая частота импульса $f{\kern 1pt} '$ совпадает с резонансной частотой водяного пара ${{\nu }_{{{\kern 1pt} \,i\,j}}} = 380.1$ ГГц (длина волны $\lambda = 0.789$ мм). Ближайшая к ней сильная линия молекулы H₂O имеет резонансную частоту $326.4$ ГГц $(\lambda = 0.919$ мм).

1. АНАЛИТИЧЕСКИЕ И РАСЧЕТНЫЕ СООТНОШЕНИЯ

Комплексную напряженность электрического поля, излучаемого прямоугольного импульса примем в виде

Здесь $t$ – время; $\omega {\kern 1pt} ' = 2\pi f{\kern 1pt} ';$ ${{A}_{{{\kern 1pt} 0}}}$ и ${{t}_{{{\kern 1pt} {\text{и}}}}} - $ “высота” и длительность излучаемого импульса; ${{\Phi }_{{\text{х}}}}(t)$ – хаотически изменяющаяся составляющая его текущей фазы (далее – хаотическая фаза) и $\tilde {A}(0;t) = {{A}_{0}}\exp \left( {i{{\Phi }_{{\text{х}}}}(t)} \right)$ – начальная комплексная огибающая импульса.

Полагаем далее, что: а) за время излучения импульса величина ${{\Phi }_{{\text{х}}}}(t)\,$ претерпевает $N$ скачков в моменты времени ${{t}_{{{\kern 1pt} k}}} = {{k{{t}_{{\text{и}}}}} \mathord{\left/ {\vphantom {{k{{t}_{{\text{и}}}}} N}} \right. \kern-0em} N}$ $(k = 1;2;3;...;N),$ оставаясь неизменной в пределах промежутков между скачками, равных ${{{{t}_{{\text{и}}}}} \mathord{\left/ {\vphantom {{{{t}_{{\text{и}}}}} N}} \right. \kern-0em} N}$; б) в пределах промежутка с номером $k$ величина ${{\Phi }_{{\text{х}}}}\,(t)$ определяется как

где ${{\Phi }_{0}}$ – постоянное смещение величины ${{\Phi }_{{\text{х}}}}$ от нуля; $\Delta {\kern 1pt} \Phi \,\; - $ интервал значений скачков (девиация) хаотической фазы и величина ${{X}_{k}}$ определяется через знакопеременное отображение Чебышева первого рода третьего порядка:

Конкретный вид знакопеременной последовательности величин ${{X}_{k}}$ задается выбором начального условия ${{X}_{0}}$, причем $\left| {{{X}_{0}}} \right| < 1$ и $\left| {{{X}_{0}}} \right| \ne 0.5$, как и $\left| {{{X}_{k}}} \right|$.

На рис. 1а и 1б приведены примеры временного хода ступенчатой функции ${{\Phi }_{{\text{x}}}}\,(t)$ для двух значений параметра ${{X}_{0}}$ и прочих равных условиях. Визуально приведенные кривые ${{\Phi }_{{\text{x}}}}\,(t)$ заметно различаются. Однако их средние ${{\bar {\Phi }}_{{\text{x}}}}\,$и среднеквадратические ширины $\Delta ({{\Phi }_{{\text{x}}}}) = {{\left( {\frac{1}{N}\sum\nolimits_{k = 1}^N {{{{\left( {{{\Phi }_{{\text{x}}}} - {{{\bar {\Phi }}}_{{\text{x}}}}} \right)}}^{2}}} } \right)}^{{0.5}}}$ почти не изменяются для указанных в подписи к рис. 1 значений ${{X}_{0}}$. Для рис. 1а (${{X}_{0}} = 0.05$) имеем ${{\bar {\Phi }}_{{\text{x}}}} = 7^\circ $ и $\Delta ({{\Phi }_{{\text{x}}}}) = 68^\circ $ и для рис. 1б $({{X}_{0}} = 0.4)$ – ${{\bar {\Phi }}_{{\text{x}}}} = - 13^\circ $ и $\Delta ({{\Phi }_{{\text{x}}}}) = 70^\circ $.

Рис. 1.

Хаотическая фаза прямоугольного импульса (а, б) и амплитудный спектр его комплексной огибающей (в, г) при ${{A}_{{\,0}}} = 1\,;$${{\Phi }_{0}} = 0{\kern 1pt} {\kern 1pt} ;$ $\Delta \Phi = 180^\circ ;$ $N = 50{\kern 1pt} ;$ ${{t}_{{\text{и}}}} = {{10}^{{ - 9}}}\,\,{\text{c}}$ и ${{X}_{0}} = 0.05\,$ (а, в) и $0.4$ (б, г).

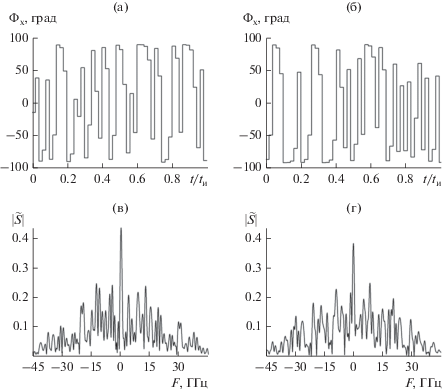
Амплитудные спектры начальных огибающих импульса (1), вычисленные для приведенных кривых ${{\Phi }_{{\text{x}}}}\,(t)$ в интервале от –45 до 45 ГГц, изображены на рис. 1в и 1г. По горизонтали здесь дана разностная частота $F = f - f{\kern 1pt} '.$ Вид спектров практически совпадает, как и их интегральные характеристики, найденные для указанного частотного интервала. В частности, энергии приведенных спектров составляют 0.918 (см. рис. 1в) и 0.911 (см. рис. 1г) от энергии излучаемого импульса, а их среднеквадратические ширины равны 15.1 и 15.9 ГГц соответственно. Обратим также внимание, что при принятых значениях параметров введение хаотической фазы приводит к расширению его спектра почти на два порядка по сравнению со случаем квазимонохроматического импульса равной длительности.

Согласно [6] искажения комплексной огибающей импульсного сигнала (1) в резонансно-поглощающей газовой среде применительно к изложенной выше постановке задачи описываются следующими выражениями:

1) при $0 < t \leqslant {{t}_{{\text{и}}}}$

2) при $t{\kern 1pt} ' > {{t}_{{\text{и}}}}$

Здесь: $z\; - $ длина трассы; $t{\kern 1pt} ' = t - {z \mathord{\left/ {\vphantom {z c}} \right. \kern-0em} c}$; $с\; - $ скорость света; функция Φ_х(t') определена формулой (2); $\tau (z) = {{\gamma }_{{ij}}}z$ и ${{\gamma }_{{ij}}} = \gamma ({{\nu }_{{ij}}})$ – оптическая глубина трассы и коэффициент поглощения среды (по мощности) на резонансной частоте; ${{p}_{{1,2}}} = - \delta \pm i{{\omega }_{1}}$ = $ = - \delta \pm i\sqrt {\omega {\kern 1pt} _{{ij}}^{2} - {{\delta }^{2}}} ;$ ${{\delta }_{{1,2}}} = 0.5\tau \delta \left( {1 \pm {{i\delta } \mathord{\left/ {\vphantom {{i\delta } {{{\omega }_{1}}}}} \right. \kern-0em} {{{\omega }_{1}}}}} \right);$ δ = = 2πdν (dν – полуширина спектральной линии); ${{J}_{{{\kern 1pt} 1}}}(x)\,\; - $ функция Бесселя.

Соотношения (4) и (5) являются следствием обращения по Лапласу полученного в [6] операторного равенства

где $F(\tau ;p) = \int_0^\infty {\tilde {E}(\tau ;t{\kern 1pt} ')\exp ( - pt{\kern 1pt} ')dt{\kern 1pt} '} $ и F(p) = $ = \int_0^\infty {\tilde {E}(0;t{\kern 1pt} ')\exp ( - pt{\kern 1pt} ')dt{\kern 1pt} '} $ – изображения по Лапласу поля импульса в конце и начале трассы (остальные обозначения введены выше).

Решение (4), (5) можно представить в альтернативной форме. С этой целью при получении равенства (6a) вначале следует перейти к безразмерному времени $\bar {t}{\kern 1pt} ' = t{\kern 1pt} '\omega {{{\kern 1pt} }_{{ij}}}$ и безразмерной переменной Лапласа $\bar {p} = {p \mathord{\left/ {\vphantom {p {{{\omega }_{{ij}}}}}} \right. \kern-0em} {{{\omega }_{{ij}}}}}$. Равенство (6a) примет тогда вид

или

Согласно одному из частных случаев теоремы Эфроса [11] при выполнении для ограниченной по модулю функции операторного равенства

справедливо также операторное равенство

Выполнив для равенства (6в) обращение по Лапласу с учетом формул (7) и (8) и возвратившись в полученном соотношении к размерному времени, для комплексной огибающей распространяющегося импульса в итоге получим:

1) при $0 < t \leqslant {{t}_{{\text{и}}}}\,$

2) при $t{\kern 1pt} ' > {{t}_{{\text{и}}}}$

Соотношения (9) и (10) являются аналогами соотношений (4) и (5). Определяемые ими величины $\tilde {A}(\tau ;t{\kern 1pt} ')$ в пределах погрешностей вычислений совпадают с результатами, следующими из (4) и (5). При этом не требуется работа с функцией Бесселя комплексного аргумента. Заметим, что в частном случае ${{X}_{0}} = 0$ они описывают искажения прямоугольного квазимонохроматического импульса. Изложенные ниже результаты получены на основе соотношений (9) и (10) с шагом вычислений по времени $\Delta {\kern 1pt} t{\kern 1pt} ' = 0.001{{t}_{{\text{и}}}}$.

2. ОГИБАЮЩАЯ И КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ РАСПРОСТРАНЯЮЩЕГОСЯ ИМПУЛЬСА С ХАОТИЧЕСКОЙ ФАЗОЙ

Искажения огибающей и корреляционных функций импульса с хаотической фазой рассмотрим применительно к трассе, проходящей на высоте $h = 12$ км, которую условно полагают верхней границей тропосферы. Метеоусловия на трассе: давление 197.8 мб; температура 225 К; влажность 6 × 10^–3 г м^–3 (стандартная модель летней атмосферы [12]). C учетом метеоусловий и приведенных в [13] данных о характеристиках спектральных линий Н₂О находим полуширину линии с резонансной частотой 380.1 ГГц на высоте 12 км: ${\text{d}}\nu = 0.5$ ГГц. При нормальных атмосферных условиях коэффициент поглощения атмосферы на указанной частоте практически полностью определяется линией и равен ≈300 дБ/км [14, 15]. Пересчет этой величины в соответствии с [13] и с учетом метео-условий на трассе дает ${{\gamma }_{{i{\kern 1pt} j}}} \approx 1.44$ дБ или 0.33 км^–1. Следовательно, при длине трассы 3 км ее оптическая глубина на резонансной частоте равна $\tau = 1$.

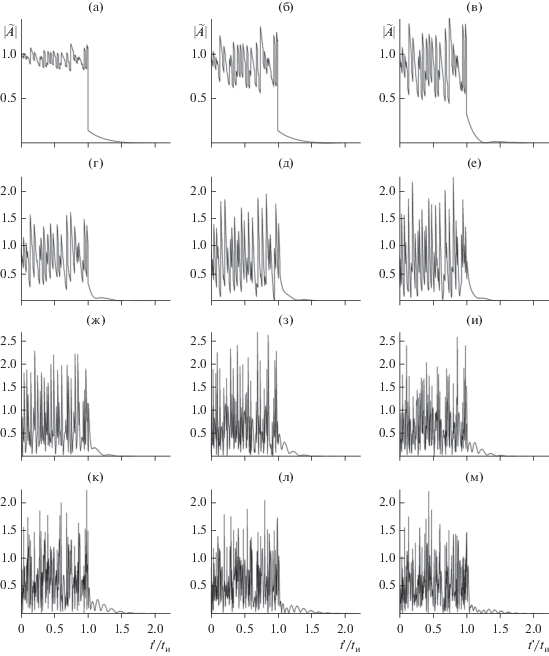
Рисунок 2 дает общее представление о характере эволюции огибающей $\left| {\tilde {A}(\delta ;t{\kern 1pt} ')} \right|$ импульса с хаотической фазой с увеличением оптической глубины трассы. Начальные параметры импульса здесь те же, что и на рис. 1а. Уже при малых величинах $\tau $ изначально прямоугольная огибающая импульса принимает шумоподобный вид (см. рис. 2а, 2б). Другими словами, в пределах интервала $\bar {t}{\kern 1pt} ' \in \left( {0...1} \right)$ величину поля в некоторый момент времени по его значениям в предыдущие моменты указать не представляется возможным даже предположительно. Последующее увеличение $\tau $ сопровождается нарастанием хаотизации поля (рис. 2в–2д). При этом в отдельные моменты времени амплитуда поля в пределах текущей длительности импульса может двукратно превышать начальную величину ${{A}_{0}} = 1$ (рис. 2е–2м). Другой характерной особенностью деформации импульса является формированием у него уже регулярного “хвоста”, протяженность которого и величины поля в котором с увеличением $\tau $ постепенно также возрастают. Физически смену характера изменений поля при $\bar {t}{\kern 1pt} ' = 1$ можно интерпретировать следующим образом. При $\bar {t}{\kern 1pt} ' < 1$ поле, регистрируемое в конце трассы, представляет собой результат сложения поля распространяющегося импульса (первое слагаемое в формуле (9)) и полей, излучаемых молекулами Н₂О, которые оказались возбужденными из-за воздействия на них поля импульса (второе и третье слагаемые в формуле (9)). При $\bar {t}{\kern 1pt} ' > 1$ в конце трассы регистрируется только суммарное поле излучающих молекул (формула (10)).

Рис. 2.

Деформация прямоугольного радиоимпульса с хаотической фазой при распространении в резонансно-поглощающей газовой среде при ${{A}_{0}} = 1;$ $f{\kern 1pt} ' = 380.1$ ГГц; ${{t}_{{\text{и}}}} = {{10}^{{ - 9}}}{\text{c;}}$ ${{X}_{0}} = 0.05;$ ${{\Phi }_{0}} = 0{\kern 1pt} ;$ $\Delta \Phi = 180^\circ {\kern 1pt} ;$ $N = 50{\kern 1pt} ;$ ${\text{d}}\nu = 0.5$ ГГц и $\tau = $ = 1 (а); 3 (б); 5 (в); 10 (г); 20 (д); 30 (е); 50 (ж); 100 (з); 150 (и); 200 (к); 300 (л) и 400 (м).

Дополнительное представление о характере деформации текущей огибающей радиоимпульса с удалением от излучателя дают его интегральные характеристики, определяемые стандартными выражениями [16]. После вычисления поля импульса по формулам (9) и (10) любые его интегральные характеристики находим далее без введения каких-либо упрощений. Если же искажения описывать на основе спектральных представлений, их определение, во-первых, представляет самостоятельную задачу и, во-вторых, обусловлено необходимостью последующих оценок влияния на получаемые результаты вводимых при вычислении интеграла Фурье допущений.

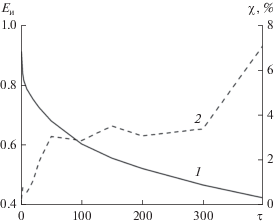
На рис. 3 в интервале значений оптической глубины $\tau $, соответствующих огибающим рис. 2, приведены две интегральные характеристики: текущая энергия импульса

Рис. 3.

Энергия прямоугольного импульса с хаотической фазой (кривая 1) и относительная энергия его “хвоста” (кривая 2) при распространении в резонансно-поглощающей среде (значения параметров те же, что и на рис. 2).

и ее доля, формирующая хвост импульса,

Здесь и далее величина ${{Е}_{{\text{и}}}}\,$ нормирована на начальную энергию импульса, так что ${{\bar {Е}}_{{\text{и}}}} = {{{{Е}_{{\text{и}}}}} \mathord{\left/ {\vphantom {{{{Е}_{{\text{и}}}}} {{{Е}_{{\text{и}}}}}}} \right. \kern-0em} {{{Е}_{{\text{и}}}}}}(0)$. Можно видеть, что на поведении интегральных характеристик импульса нарастающая шумоподобность его текущей огибающей не сказывается. С увеличением $\tau $ оптической глубины трассы энергия импульса монотонно убывает (см. рис. 3, кривая 1), как и должно быть. Поскольку при этом ширина спектра импульса многократно превышает ширину спектральной линии, величина ${{E}_{{\text{и}}}}(\tau )$ при всех рассмотренных $\tau $ остается сопоставимой со своим начальным значением. При этом также при всех $\tau $ энергия хвоста составляет малую долю ($ \leqslant {\kern 1pt} 8\% $) текущей энергии импульса (см. рис. 3, кривая 2). Незначительно отклоняются от своих начальных значений нормированные величины центра тяжести ${{\bar {t}}_{{{\text{цт}}}}} = {{{{t}_{{{\text{цт}}}}}} \mathord{\left/ {\vphantom {{{{t}_{{{\text{цт}}}}}} {{{t}_{{\text{и}}}}}}} \right. \kern-0em} {{{t}_{{\text{и}}}}}}$ и среднеквадратической ширины $\Delta {{\bar {t}}_{{\text{и}}}} = {{\Delta {{t}_{{\text{и}}}}} \mathord{\left/ {\vphantom {{\Delta {{t}_{{\text{и}}}}} {{{t}_{{\text{и}}}}}}} \right. \kern-0em} {{{t}_{{\text{и}}}}}}$ импульса. Так, для огибающих на рис. 2а и 2м имеем ${{\bar {t}}_{{{\text{цт}}}}} = 0.499$ и ${\text{0}}{\text{.567}}$ и $\Delta {{\bar {t}}_{{\text{и}}}}\,$$ = 0.294$ и 0.307 соответственно. Приведенные оценки получены для деформированного импульса в целом. Если же выполнить их без учета полей хвостов (т.е. для временного интервала $\bar {t}' \in \left[ {0...1} \right]\,)$, отклонения величин ${{\bar {t}}_{{{\text{цт}}}}}\,$ и $\Delta {{\bar {t}}_{{\text{и}}}}\,$ от своих начальных значений уменьшаются в разы.

К интегральным характеристикам импульсных радиосигналов относятся и их корреляционные функции (КФ): автокорреляционная (АКФ)

и взаимная корреляционная функция (ВКФ) излученного и деформированного импульсов

В формулах (11) и (12) введено: μ – временной сдвиг; * – знак комплексного сопряжения. Структуры КФ определяют возможности радиосистем по точности измерений дальности и скорости целей [16]. Как и интегральные характеристики, рассмотренные выше, КФ находятся непосредственно по результатам вычислений поля по формулам (9) и (10). На начальном этапе их изучения представляет интерес, по-видимому, установить возможный характер их деформаций, обусловливаемый изменениями $\tau $.

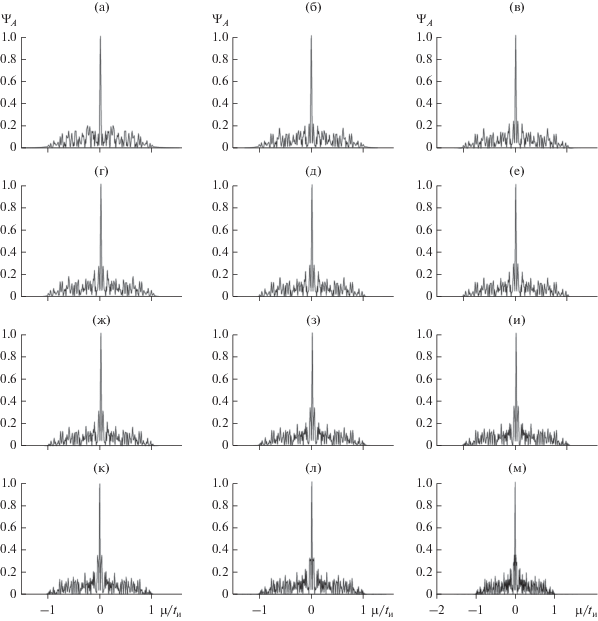
На рис. 4 приведена совокупность АКФ импульса с хаотической фазой, соответствующих огибающим на рис. 2. Хотя вид текущих огибающих с увеличением $\tau $ заметно варьирует, их АКФ различаются лишь незначительными деталями пьедесталов. При этом во всех случаях АКФ имеет узкий и высокий по сравнению с пьедесталом максимум, т.е. близка к идеальной. В отсутствие боковых максимумов единственной характеристикой АКФ является ширина $\Delta {{\mu }_{{0.5}}}(\tau )$ ее центрального пика по уровню 0.5. На рис. 4 ширина АКФ изменяется от $\sim {\kern 1pt} 0.022{{t}_{{\text{и}}}}$ (рис. 4а) до $\sim {\kern 1pt} 0.013{{t}_{{\text{и}}}}$ (рис. 4м), т.е. центральный пик незначительно сужается. Таким образом, с нарастанием хаотизации огибающей при увеличении $\tau $ (см. рис. 2) ее АКФ остается такой же, что и у излученного им-пульса.

Рис. 4.

Автокорреляционная функция прямоугольного радиоимпульса с хаотической фазой в резонансно-поглощающей газовой среде (значения параметров те же, что и на рис. 2).

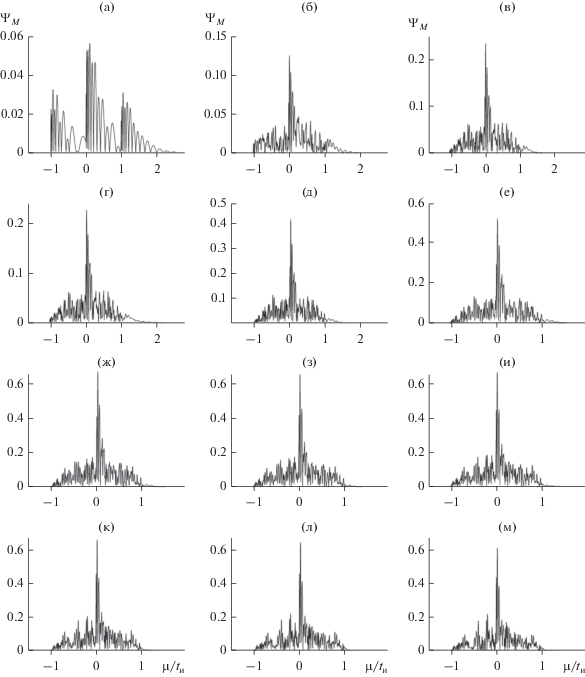
Автокорреляционная функция отрезка слабокоррелированного случайного процесса также близка к идеальной. Поэтому по виду АКФ, изображенных на рис. 4, соответствующие им реализации величины $\left| {\tilde {A}(\tau ;t{\kern 1pt} ')} \right|$ (см. рис. 2) нельзя с определенностью отнести к случаям приема полезного сигнала или шумоподобной помехи. При известном передаваемом сигнале дополнительная информация для принятия адекватного решения обеспечивается параллельным вычислением ВКФ излученного и деформированного импульсов. Совокупность ВКФ, соответствующих кривым $\left| {\tilde {A}} \right|$ на рис. 2 и кривым АКФ на рис. 4, представлена на рис. 5. Как видим, и при значительной деформации распространяющийся импульс сохраняет выраженную корреляционную связь с излученным импульсом. Кривые ВКФ, как и кривые АКФ, имеют единственный максимум и слабо выраженный пьедестал. Их характеристиками являются теперь ширина центрального максимума, определяемая по аналогии с шириной центрального максимума АКФ, и высота центрального пика. На рис. 5 ширина ВКФ возрастает от $\sim \,0.023{{t}_{{\text{и}}}}$ (рис. 5а) до $\sim {\kern 1pt} 0.091{{t}_{{\text{и}}}}$ (рис. 5м), а высота ${{\Psi }_{{M\max }}}(\tau )$ убывает от $\sim {\kern 1pt} 0.99$ до $\sim {\kern 1pt} 0.41$ соответственно. Наличие выраженного пика у кривых ВКФ заведомо обеспечивает идентификацию обработанной реализации $\left| {\tilde {A}(\tau ;t{\kern 1pt} ')} \right|$ как передаваемого сигнала.

Рис. 5.

Взаимная корреляционная функция излученного и деформированного прямоугольных радиоимпульсов с хаотической фазой в резонанснопоглощающей газовой среде (значения параметров те же, что и на рис. 2).

3. О ВЛИЯНИИ ПАРАМЕТРОВ ХАОТИЧЕСКОЙ ФАЗЫ НА ИСКАЖЕНИЯ ОГИБАЮЩЕЙ И КФ ДЕФОРМИРОВАННОГО ИМПУЛЬСА

Деформацию импульса после прохождения трассы заданной длины определяют две группы параметров. К первой из них относятся параметры, непосредственно формирующие временной ход хаотической фазы, т.е. девиация хаотической фазы $\Delta \,\Phi $; число ее скачков $N$ в пределах длительности излучаемого импульса и начальное условие ${{X}_{0}}$. Ко второй – параметры среды (резонансная частота ${{\nu }_{{i{\kern 1pt} j}}}$ и полуширина спектральной линии ${\text{d}}\nu $) и импульса (несущая $f{\kern 1pt} '$ и длительность t_и). Результаты, приведенные на рис. 2–5, и основанные на них выводы получены при неизменном временном ходе величины ${{\Phi }_{{\text{x}}}}$, изображенном на рис. 1а, и параметрах среды и импульса, указанных в подписи к рис. 2. Вместе с тем величины параметров задачи, в принципе, могут значительно отличаться от их значений, принятых для рис. 1 и 2. Здесь рассмотрим влияние на искажения импульса параметров первой группы и с этой целью по отдельности сопоставим их вариации с соответствующими им вариациями огибающей и КФ импульса с хаотической фазой, сопровождающими его распространение в резонансно-поглощающей среде.

3.1. Девиация хаотической фазы

На рис. 6–9 представлены изменения тех же характеристик импульса с хаотической фазой, что и рис. 2–5, но уже в зависимости от девиации $\Delta \,\Phi $. Оптическая глубина трассы здесь постоянна и равна 200, что равносильно длине трассы 600 км, девиация $\Delta \Phi $ изменяется с шагом 30°от 0° до 150° (рис. 6а–6е; 8a–8e; 9a –9e) и от 210° до 360° (рис. 6ж–6м; 8ж–8 м; 9ж–9м), а остальные параметры те же, что и на рис. 2. Отсутствующие на рис. 6, 8 и 9 кривые для $\Delta \Phi = 180^\circ $ уже были приведены на рис. 2к, 4к и 5к соответственно.

Рис. 6.

К вопросу о влиянии девиации хаотической фазы на искажения огибающей прямоугольных радиоимпульсов в резонанснопоглощающей газовой среде при ${{A}_{0}} = 1;$ $f{\kern 1pt} ' = 380.1$ ГГц; ${{t}_{{\text{и}}}} = {{10}^{{ - 9}}}\,\,{\text{c;}}$ ${{X}_{0}} = 0.05;$ ${{\Phi }_{0}} = 0{\kern 1pt} ;$ $N = 50{\kern 1pt} {\kern 1pt} ;$ $\tau = 200;$ ${\text{d}}\nu = 0.5$ ГГц и различных $\Delta \Phi = 0^\circ \,\,({\text{a);}}$ ${\text{30}}^\circ \,({\text{б);}}$ ${\text{60}}^\circ \,({\text{в}});$ $90^\circ \,({\text{г}});$ $120^\circ \,({\text{д}});$ $150^\circ \,({\text{e}});$ $210^\circ \,({\text{ж}});$ $240^\circ \,({\text{з}});$ $270^\circ \,({\text{и);}}$ ${\text{300}}^\circ \,({\text{к}});$ $330^\circ \,({\text{л)}}$ и ${\text{360}}^\circ \,({\text{м}})).$

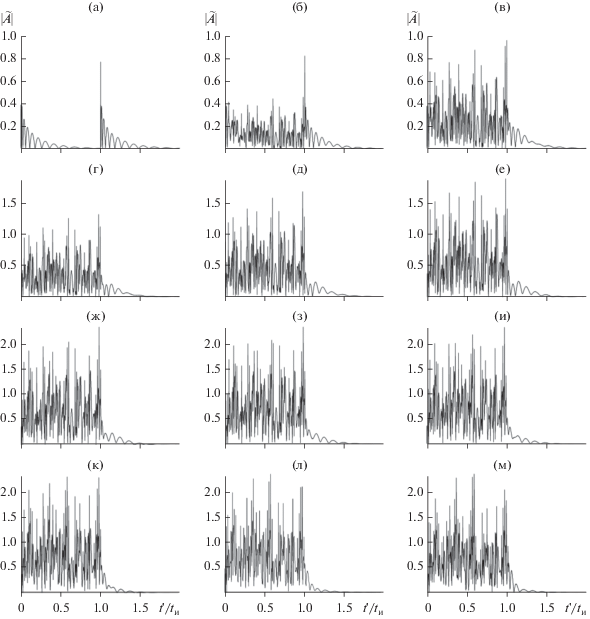
Рис. 7.

К вопросу о влиянии девиации хаотической фазы на энергию прямоугольного импульса (кривая 1) и относительную энергию его “хвоста” (кривая 2) при распространении в резонансно-поглощающей среде (значения параметров те же, что и на рис. 6).

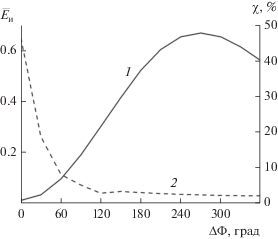
Рис. 8.

К вопросу о влиянии девиации хаотической фазы на искажения АКФ прямоугольного импульса (значения параметров те же, что и на рис. 6).

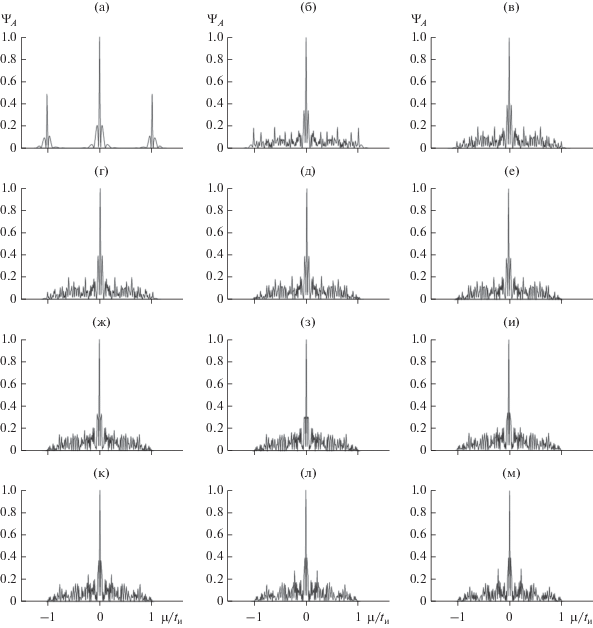
Рис. 9.

К вопросу о влиянии девиации хаотической фазы на искажения ВКФ прямоугольного импульса (значения параметров те же, что и на рис. 6).

Вид огибающей на рис. 6а характерен для случая квазимонохроматического прямоугольного импульса ($\Delta \Phi = 0^\circ $) при значительной оптической глубине трассы (см. [6]). Она представляет собой совокупность двух подымпульсов, первый из которых и есть, собственно, частично поглощенный средой импульс, а второй – проявление высвечивания энергии, приобретенной молекулами среды при прохождении импульса. Текущая энергия импульса на рис. 6а составляет только ~1.3% его начальной энергии, а χ ~ 44.8%, так что почти половина текущей энергии приходится на хвост. С увеличением параметра $\Delta \Phi $ спектр импульса уширяется. Соответственно, величины поля в импульсе постепенно возрастают, а огибающая все больше хаотизируется (см. рис. 6б–6е). Визуальный анализ кривых на рис. 6 позволяет также заключить, что по достижении девиацией фазы величины ~200° ее последующее увеличение практически не приводит к сколько-нибудь выраженным изменениям вида огибающей, в частности, высот отдельных “выбросов” поля (см. рис. 6ж–6м). При этом поле в пределах текущей длительности импульса по-прежнему можно определить, как шумоподобное (или как случайный процесс), а поле в хвосте остается регулярным. Зависимости интегральных характеристик ${{\bar {E}}_{{\text{и}}}}\,$ и $\chi $ от $\Delta \Phi $ приведены на рис. 7. Увеличение девиации фазы сопровождается, как и должно быть, выраженным ростом текущей энергии в конце трассы (см. рис. 7, кривая 1). При этом все меньшая доля текущей энергии приходится на хвост импульса (см. рис. 7, кривая 2). Визуально поведение обеих кривых на рис. 7 указывает также на постепенную стабилизацию описываемых ими величин при увеличении $\Delta \Phi $, что согласуется с отмеченным выше возможным “насыщением” уровня хаотизации огибающей.

Корреляционная функция для огибающих на рис. 6 приведены на рис. 8 (АКФ) и рис. 9 (ВКФ). Как и в случае рис. 6, их следует рассматривать совместно с АКФ и ВКФ, найдеными для $\Delta \Phi = 180^\circ $ и приведенными на рис. 4к и 5к. При $\Delta \Phi = 0^\circ $ АКФ имеет характерную трехпиковую структуру (рис. 8а), боковые пики которой являются следствием сформировавшегося протяженного хвоста (см. рис. 6а). Далее увеличение девиации фазы приводит к выделению центрального пика АКФ из формирующегося пьедестала (рис. 8б–8е) и последующей стабилизации вида АКФ (рис. 8ж–8м). C погрешностью, не превышающей 2%, ширины АКФ на рис. 8ж–8м равны ${{10}^{{ - 2}}}{{t}_{{\text{и}}}}$. При $\Delta \Phi > 0$ кривые ВКФ также имеют выраженный центральный максимум (см. рис. 9), высота которого вначале увеличивается (рис. 9б–9е), а затем незначительно варьирует вблизи уровня ~0.6 (см. рис. 9ж–9м). Полагаем, что в совокупности результаты, представленные на рис. 6–9, обосновывают возможность проявления “эффекта насыщения” уровня искажений импульса с хаотической фазой в резонансно-поглощающей среде, когда дальнейшее увеличение параметра $\Delta \Phi $ при прочих равных условиях уже не приводит к выраженным дополнительным вариациям его текущих характеристик.

3.2. Число скачков хаотической фазы

Отдельные огибающие на рис. 10 различаются только соответствующими им значениями параметра $N \leqslant 100$ (указаны в подписи к рисункам), остальные параметры совпадают с принятыми ранее для рис. 2к, для которого $N = 50$. Уменьшение числа скачков при прочих равных условиях приводит к сужению спектра излучаемого импульса и возрастанию его поглощения средой. Так, при $N = 16$ (рис. 10з) среднеквадратическая ширина спектра равна $\sim {\kern 1pt} 8.1\,\,{\text{ГГц}}$, что в $\sim 1.9$ раза меньше аналогичной величины для импульса, искажения которого показаны на рис. 2к. Соответственно, уменьшение $N$ заметно сказывается не только на частоте выбросов поля в пределах временного интервала $t{\kern 1pt} ' \in \left[ {0...{{t}_{{\text{и}}}}} \right]$, но и на их высотах (ср. рис. 10а и 10з). Одновременно хвост импульса становится все более выраженным (рис. 10д–10з). Чтобы количественно охарактеризовать указанные тенденции, обратимся интегральным характеристикам ${{\bar {Е}}_{{\text{и}}}}\,$ и $\chi $, значения которых для огибающих на рис. 2к и рис. 10 приведены в табл. 1. Можно видеть, что изменение числа скачков в рассмотренном интервале $N \in \left[ {100...16} \right]$ сопровождается в обоих случаях монотонным изменением величин ${{\bar {Е}}_{{\text{и}}}}\,$ и $\chi $ в ~3 и ~18 раз соответственно. Таблица 1 содержит также нормированные величины центра тяжести ${{\bar {t}}_{{{\text{цт}}}}} = {{{{t}_{{{\text{цт}}}}}} \mathord{\left/ {\vphantom {{{{t}_{{{\text{цт}}}}}} {{{t}_{{\text{и}}}}}}} \right. \kern-0em} {{{t}_{{\text{и}}}}}}$ и среднеквадратической ширины $\Delta {{\bar {t}}_{{\text{и}}}} = {{\Delta {{t}_{{\text{и}}}}} \mathord{\left/ {\vphantom {{\Delta {{t}_{{\text{и}}}}} {{{t}_{{\text{и}}}}}}} \right. \kern-0em} {{{t}_{{\text{и}}}}}}$, коэффициента асимметрии ${{\gamma }_{1}}$ и эксцесса ${{\gamma }_{2}}$ для кривых $\left| {\tilde {A}} \right|$, изображенных на рис. 10. Обратим внимание, что на поведении перечисленных характеристик вариации параметра N заметно не сказываются, так что во всех случаях их значения мало отличаются от соответствующих значений для прямоугольного импульса (${{\bar {t}}_{{{\text{цт}}}}}(0) = 0.5;$ $\Delta {{\bar {t}}_{{\text{и}}}}(0) = 0.289;$ ${{\gamma }_{1}}(0) = 0;$ ${{\gamma }_{2}}(0) = - 1.2$).

Рис. 10.

К вопросу о влиянии числа скачков фазы в излучаемом прямоугольном импульсе с хаотической фазой на искажения его огибающей при ${{A}_{0}} = 1;$ $f{\kern 1pt} ' = 380.1$ ГГц; ${{t}_{{\text{и}}}} = {{10}^{{ - 9}}}\,{\text{c;}}$ ${{X}_{0}} = 0.05;$ ${{\Phi }_{0}} = 0{\kern 1pt} {\kern 1pt} ;$ $\Delta \Phi = 180^\circ $; $\tau = 200;$ ${\text{d}}\nu = 0.5$ ГГц и $N = 100\,({\text{a}});$ $80\,({\text{б}});$ $64{\kern 1pt} {\kern 1pt} ({\text{в}});$ $40\,\,({\text{г}});$ $32\,\,({\text{д}});$ $25\,\,({\text{e}});$ $20\,\,({\text{ж)}}$ и ${\text{16}}\,\,{\text{(з))}}{\text{.}}$

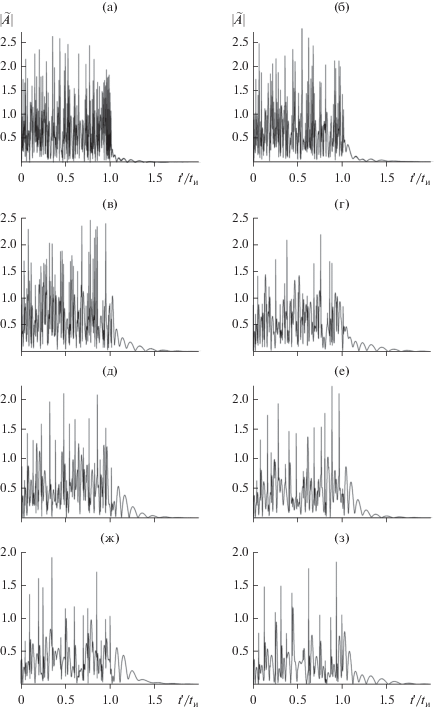
Таблица 1.  

Влияние числа скачков фазы N на интегральные характеристики прямоугольного импульса с хаотической фазой в резонансно-поглощающей газовой среде

$N$	Интегральная характеристика
	${{E}_{{\text{и}}}}\,$	${{\bar {t}}_{{{\text{цт}}}}}\,$	$\Delta {{\bar {t}}_{{\text{и}}}}\,$	${{\gamma }_{1}}$	${{\gamma }_{2}}$	$\chi ,$ %
100	0.602	0.505	0.295	0.103	–1.081	0.89
80	0.607	0.497	0.287	0.158	–0.940	2.07
64	0.597	0.520	0.292	0.126	–0.921	4.72
50	0.523	0.540	0.296	0.077	–0.945	3.08
40	0.451	0.539	0.291	0.098	–0.793	3.80
32	0.415	0.568	0.298	–0.010	–0.879	3.62
25	0.330	0.613	0.319	–0.114	–1.154	11.4
20	0.235	0.588	0.323	0.156	–0.974	10.9
16	0.189	0.598	0.329	0.176	–0.942	16.3

Примечание: ${{A}_{{\,0}}} = 1\,;$$f{\kern 1pt} ' = 380.1$ ГГц; ${{t}_{{\text{и}}}} = {{10}^{{ - 9}}}\,{\text{c;}}$ ${{X}_{0}} = 0.05;$ ${{\Phi }_{0}} = 0{\kern 1pt} ;$ $\Delta \Phi = 180^\circ {\kern 1pt} ;$ ${{\nu }_{{ij}}} = 380.1\,\,{\text{ГГц;}}$ ${\text{d}}\nu = 0.5\,\,{\text{ГГц}};$ $\tau = 200.$

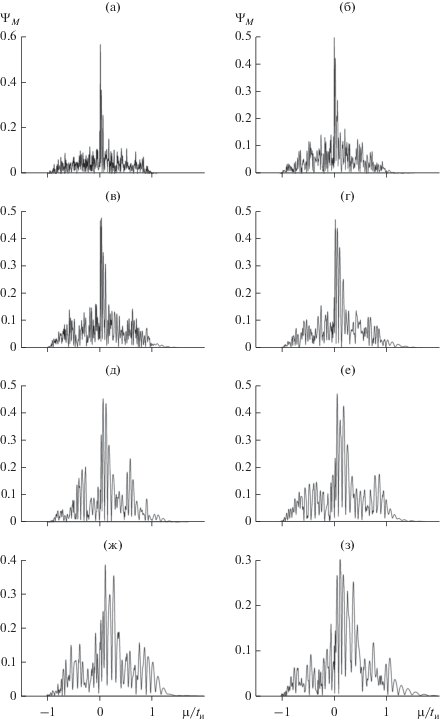
Совокупности корреляционных функций, отвечающих огибающим на рис. 10, приведены на рис. 11 и рис. 12. Их элементами являются также и кривые АКФ и ВКФ, найденные при $N = 50$ и изображенные на рис. 4к и 5к. Видно, что отмеченные ранее для рис. 4 и 8 характерные особенности кривых АКФ сохраняются на рис. 11 до N ≈ 40 (рис. 11а–11г). Дальнейшее уменьшение параметра $N$ приводит к возникновению боковых максимумов АКФ (рис. 11д–11з) с варьирующими характеристиками. Ширина центрального максимума АКФ $\Delta {{\mu }_{{0.5}}}(\tau ) = 0.008{{t}_{{\text{и}}}}$ (рис. 11а) и 0.018t_и (рис. 11з). На рис. 12 при всех N кривые ВКФ имеют несколько выраженных максимумов в окрестности нулевого временного сдвига. Это свидетельствует о заведомо не помеховой природе принятой реализации $\left| {\tilde {A}(\tau ;t{\kern 1pt} ')} \right|$.

Рис. 11.

К вопросу о влиянии числа скачков фазы в излучаемом прямоугольном импульсе на искажения его АКФ (значения параметров те же, что и на рис. 10).

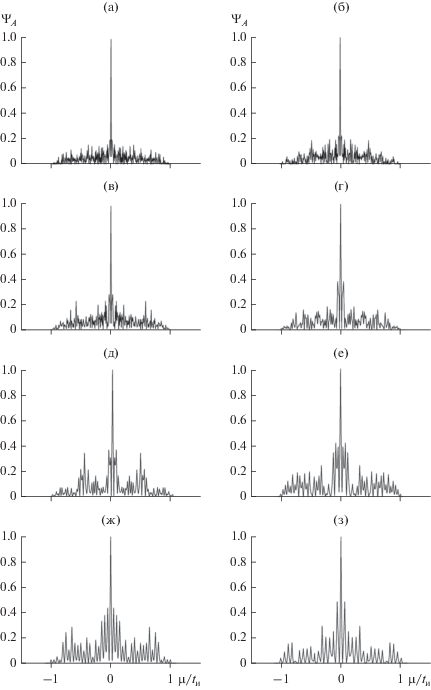
Рис. 12.

К вопросу о влиянии числа скачков фазы в излучаемом прямоугольном импульсе на искажения его ВКФ (значения параметров те же, что и на рис. 10).

3.3. Параметр ${{X}_{0}}\;$

При прочих равных условиях изменения величины ${{X}_{0}}$ не приводят к заметным изменениям спектра импульса (пример см. на рис. 1в, 1г) и, как можно предположить, не будут сопровождаться заметными дополнительными изменениями текущей огибающей импульса и его интегральных характеристик. Приведенные ниже данные это подтверждают. Так, огибающие на рис. 13 отвечают различающимся значениям X₀ ∈ [0.1…0.4]. К их совокупности относится и огибающая на рис. 2к, для которой ${{X}_{0}} = 0.05$. Можно видеть, что различия между отдельными огибающими и, в частности, характерными высотами их локальных максимумов весьма незначительны. Количественно на их близость друг к другу указывают и интегральные характеристики кривых, которые приведены в табл. 2 (обратим внимание, что здесь первая строка совпадает с четвертой строкой табл. 1). Например, относительные отклонения величин ${{\bar {t}}_{{{\text{цт}}}}}\,$ и $\Delta {{\bar {t}}_{{\text{и}}}}\,$ в табл. 2 от их средних значений 0.535 и 0.296 не превышают ~5.8 и 6.8% соответственно. Также незначительно изменяются величины ${{\bar {E}}_{{\text{и}}}}\,$ и $\chi $. Кроме того, величины характеристик ${{\bar {t}}_{{{\text{цт}}}}}\,$; $\Delta {{\bar {t}}_{{\text{и}}}}\,$; ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$ при всех ${{X}_{0}}$ весьма мало отличаются от своих значений для прямоугольного импульса (см. выше).

Рис. 13.

К вопросу о влиянии параметра ${{X}_{0}}$ на искажения огибающей прямоугольного импульса с хаотической фазой при ${{A}_{0}} = 1;$ $f{\kern 1pt} ' = 380.1$ ГГц; ${{t}_{{\text{и}}}} = {{10}^{{ - 9}}}\,{\text{c;}}$ ${{\Phi }_{0}} = 0{\kern 1pt} {\kern 1pt} ;$ $\Delta \Phi = 180^\circ $; $N = 50$; $\tau = 200;$ ${\text{d}}\nu = 0.5$ ГГц и ${{X}_{0}} = 0.1\,\,\,({\text{а}});$ $0.2\,\,\,({\text{б}});$ $0.3\,\,({\text{в}})$ и ${\text{0}}{\text{.4}}\,{\text{(г)}}{\text{.}}$

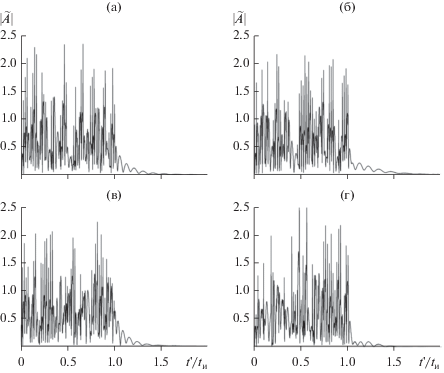
Таблица 2.

Влияние параметра ${{X}_{0}}$ на интегральные характеристики прямоугольного импульса с хаотической фазой в резонансно-поглощающей газовой среде

${{X}_{0}}$	Интегральная характеристика
	${{\bar {E}}_{{\text{и}}}}\,$	${{\bar {t}}_{{{\text{цт}}}}}\,$	$\Delta {{\bar {t}}_{{\text{и}}}}\,$	${{\gamma }_{1}}$	${{\gamma }_{2}}$	$\chi ,\% $
0.05	0.523	0.540	0.296	0.077	–0.945	3.08
0.1	0.497	0.504	0.304	0.116	–1.157	2.72
0.2	0.494	0.524	0.305	0.001	–1.057	3.13
0.3	0.519	0.544	0.298	–0.102	–1.113	2.90
0.4	0.534	0.564	0.276	–0.132	–0.938	2.18

Примечание: ${{A}_{0}} = 1;$ $f{\kern 1pt} ' = 380.1$ ГГц; ${{t}_{{\text{и}}}} = {{10}^{{ - 9}}}\,{\text{c;}}$ $N = 50;$ ${{\Phi }_{0}} = 0{\kern 1pt} {\kern 1pt} ;$ $\Delta \Phi = 180^\circ {\kern 1pt} ;$ ${{\nu }_{{ij}}} = 380.1\,\,{\text{ГГц;}}$ ${\text{d}}\nu = 0.5\,\,{\text{ГГц}};$ $\tau = 200.$

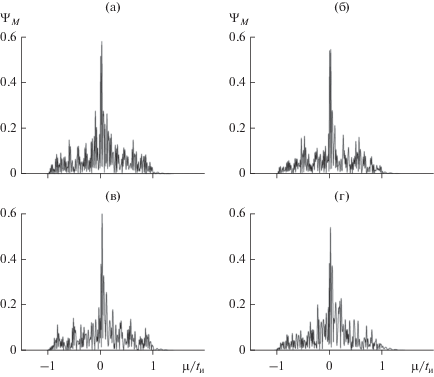
Корреляционные функции для огибающих на рис. 13 приведены на рис. 14 и 15 (см. также рис. 4к и 5к). Визуально в каждой из совокупностей кривые весьма близки. Это замечание относится прежде всего к центральным пикам кривых. Так, на рис. 13 наибольшее относительное отклонение ширины центральных максимумов Δμ_0.5(X₀) от среднего значения ~0.012t_и не превышает 3%; аналогичная оценка для рис. 14 составляет ~2%. Таким образом, варьирование параметра ${{X}_{0}}$, по-видимому, не приводит к дополнительным особенностям искажений импульса (1).

Рис. 14.

К вопросу о влиянии параметра ${{X}_{0}}$ на искажения АКФ прямоугольного импульса с хаотической фазой (значения параметров те же, что и на рис. 13).

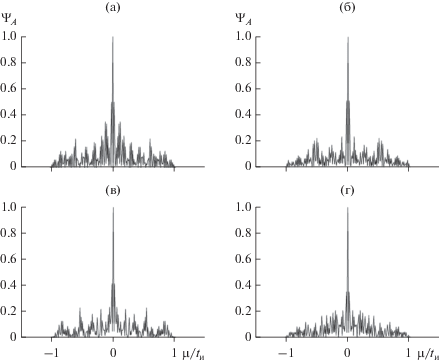
Рис. 15.

К вопросу о влиянии параметра ${{X}_{0}}$ на искажения ВКФ прямоугольного импульса с хаотической фазой (значения параметров те же, что и на рис. 13).

ЗАКЛЮЧЕНИЕ

Приведены результаты начального анализа характера и особенностей дисперсионных искажений распространения прямоугольного радиоимпульса с хаотической фазой в резонансно-поглощающей газовой среде. Хаотичность фазы моделируется на основе отображения Чебышева первого рода третьего порядка. При удалении импульса от излучателя сопровождается постепенной трансформацией, его огибающей к виду шумоподобного сигнала (случайного процесса) и формированием “хвоста”, поле которого регулярно изменяется во времени. При вариациях параметров задачи, формирующих временной ход хаотической фазы, шумоподобность огибающей на текущие величины интегральных характеристик импульса практически не влияет, что означает их малую информативность.

В рассмотренных интервалах значений параметров, описывающих степень хаотичности мгновенной фазы излучаемого импульса, влияние среды не приводит к последующим принципиальным изменениям вида его авто- и взаимной корреляционных функций в процессе распространения. Во всех рассмотренных ситуациях текущие КФ деформирующегося импульса имеют вид узкого пика на фоне широкого пьедестала, характерная высота которого значительно меньше единицы. При этом ширины АКФ и ВКФ по уровню 0.5 удовлетворяют неравенству $\Delta {{\mu }_{{0.5}}} \ll {{t}_{{\text{и}}}}.$ Таким образом, введение хаотической фазы обеспечивает сохранение их характерного вида в условиях последующей значительной деформации, огибающей из-за частотной дисперсии.

Представленные данные указывают на принципиальную необходимость учета влияния среды распространения при выполнении оценок преимуществ применения в радиосистемах хаотических сигналов, в том числе, импульсов с хаотической фазой. Представляет также интерес изучение влияния несущей частоты и длительности хаотического импульса на его характеристики и поиск оптимальных отображений, которые обеспечат наибольшее уширение спектра излучаемого импульса при относительно малом числе скачков фазы.