Радиотехника и электроника, 2020, T. 65, № 9, стр. 881-893

Оконные функции с квазипрямоугольным спектром

З. Д. Лернер^*

Редакция журнала “Радиотехника и электроника”
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

Поступила в редакцию 19.08.2019
После доработки 19.02.2020
Принята к публикации 23.03.2020

DOI: 10.31857/S0033849420080070

Аннотация

Дискретное преобразование Фурье (ДПФ) осуществляется на ограниченном интервале времени, что равноценно умножению анализируемого сигнала на прямоугольное окно, спектр которого имеет наибольшие (среди прочих окон) боковые лепестки. В результате возникает эффект, называемый растеканием спектра сигнала. Умножение сигнала на сглаживающее окно уменьшает размывание спектральных компонент. Известно несколько десятков разновидностей оконных функций, поскольку ДПФ используется в разнообразных задачах. Особое место среди окон занимает уникальное окно с “плоской вершиной”, используемое в широкополосных приложениях. Предлагается новое регулируемое окно с квазипрямоугольным спектром, а также способ, позволяющий уменьшить уровень боковых лепестков спектра.

ВВЕДЕНИЕ

Для синтеза окон будем рассматривать, как это принято [1], четные действительные функции $g\left( t \right)$. Их спектры $G\left( \omega \right)$ также являются четными действительными функциями частоты.

Согласно ГОСТ 24375-80 коэффициент прямоугольности ${{K}_{{\text{п}}}} = $ ${{{{{\left( {\Delta f} \right)}}_{1}}} \mathord{\left/ {\vphantom {{{{{\left( {\Delta f} \right)}}_{1}}} {{{{\left( {\Delta f} \right)}}_{2}}}}} \right. \kern-0em} {{{{\left( {\Delta f} \right)}}_{2}}}}$ амплитудно-частотной характеристики (АЧХ) – это отношение ширины полосы пропускания фильтра по уровню ${{a}_{1}}$ = ${1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ к ширине полосы пропускания по уровню ${{a}_{2}}$ = 0.1. У физически нереализуемого идеального фильтра с прямоугольной АЧХ ${{K}_{{\text{п}}}} = 1$. Распространим понятие коэффициента прямоугольности на спектры оконных функций. Рассмотрим в качестве примера гауссов импульс

(1)

${{g}_{{\text{г}}}}\left( t \right) = \frac{1}{{\sqrt \pi }}\exp ( - {{t}^{2}})~,\,\,\,\, - \infty < t < \infty ,$

спектр которого равен

(2)

$\begin{gathered} {{G}_{{\text{г}}}}\left( \omega \right) = {{G}_{{\text{г}}}}\left( {j\omega } \right) = \\ = \int\limits_{ - \infty }^\infty {{{g}_{{\text{г}}}}\left( t \right)} {\text{exp}}\left( { - j\omega t} \right)~dt = {\text{exp}}\left( {{{ - {{\omega }^{2}}} \mathord{\left/ {\vphantom {{ - {{\omega }^{2}}} 4}} \right. \kern-0em} 4}} \right). \\ \end{gathered} $

Решая алгебраические уравнения

${{G}_{{\text{г}}}}~({{\omega }_{1}}) = {{a}_{1}} = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}\,\,\,\,{\text{и}}\,\,\,\,{{G}_{{\text{г}}}}({{\omega }_{2}}) = {{a}_{2}} = 0.1,$

получим

${{K}_{{\text{п}}}} = \frac{{{{\omega }_{1}}}}{{{{\omega }_{2}}}} = 0.3880.$

Как видим, коэффициент прямоугольности далек от единицы (как и форма спектра импульса – от прямоугольной).

У окна с плоской вершиной ([1], 2.4.3) спектр равен

(3)

$\begin{gathered} F(f)~ = {\text{sin}}c(\pi f) + \\ + \,\,0.5\sum\limits_{k = 1}^4 {{{d}_{k}}} \left[ {\sin c\left( {{\pi }\left( {f~ + ~k} \right)} \right) + \sin c\left( {{\pi }\left( {f~ - ~k} \right)} \right)} \right], \\ \end{gathered} $

где

(4)

$\begin{gathered} ~f = \frac{\omega }{{2\pi }};\,\,\,\,~{{d}_{1}} = 1.932;\,\,\,\,{{d}_{2}} = 1.29; \\ {{d}_{3}} = 0.388;\,\,\,\,{{d}_{4}} = 0.03. \\ \end{gathered} $

Форма спектра окна ближе к прямоугольной, однако коэффициент прямоугольности равен всего лишь ${{K}_{{\text{п}}}} = $ 0.56.

Синтезируем регулируемое окно с более высокими значениями ${{K}_{{\text{п}}}}.$

Все вычисления в данной работе производились с помощью систем Matlab 6.5 и Wolfram Alpha.

1. ПРЕДПОСЫЛКИ ДЛЯ СИНТЕЗА ОКНА ГАУССА–ТЕЙЛОРА

Новое окно, назовем его окном Гаусса–Тейлора (GT) $N$-го порядка, зададим спектром

(5)

$\begin{gathered} G\left( \omega \right) = \sum\limits_{k = 0}^N {\frac{{{{{\left( {\frac{{{{\omega }^{2}}}}{4}} \right)}}^{k}}}}{{k!}}} {\text{exp}}\left( {{{ - {{\omega }^{2}}} \mathord{\left/ {\vphantom {{ - {{\omega }^{2}}} 4}} \right. \kern-0em} 4}} \right) = \\ = {\text{taylor}}\left[ {{\text{exp}}\left( {{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} 4}} \right. \kern-0em} 4}} \right),~2N + 1} \right]{\text{exp}}\left( {{{ - {{\omega }^{2}}} \mathord{\left/ {\vphantom {{ - {{\omega }^{2}}} 4}} \right. \kern-0em} 4}} \right). \\ \end{gathered} $

Здесь ${\text{taylor}}\left[ {{\text{exp}}\left( {{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} 4}} \right. \kern-0em} 4}} \right),~2N + 1} \right]$ – многочлен степени $2N$, полученный усечением ряда Тейлора (Маклорена) для экспоненты ${\text{exp}}\left( {{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} 4}} \right. \kern-0em} 4}} \right)$. Это значит, что, ${\text{taylor}}\left( { \ldots ,~2N + 1} \right)$ представляет собой оператор, воздействуя которым на функцию, получаем первые члены ряда Тейлора (если он существует) до степени $2N$ включительно.

На рис. 1 представлены графики спектра (5) при различных N = 0, 3, 6, 12, 18, 24 и 30 для положительных частот. Следует заметить, что в случае N = 0 окно Гаусса–Тейлора вырождается в известное окно Гаусса.

Рис. 1.

Графики спектра (5) при N = 0 (1), 3 (2), 6 (3), 12 (4), 18 (5), 24 (6) и 30 (7) для положительных частот.

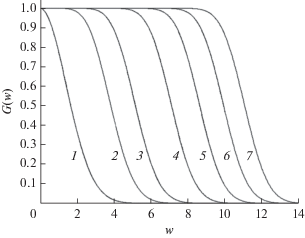
С ростом параметра N увеличиваются ширина спектра и коэффициент прямоугольности:

(6)

$\begin{gathered} N = 3,\,\,\,\,~{{K}_{{\text{п}}}} = \frac{{{{\omega }_{1}}}}{{{{\omega }_{2}}}} = 0.6394; \\ ~N = 6,\,\,\,\,~{{K}_{{\text{п}}}} = \frac{{{{\omega }_{1}}}}{{{{\omega }_{2}}}} = 0.7137; \\ ~N = 12,\,\,\,\,~{{K}_{{\text{п}}}} = \frac{{{{\omega }_{1}}}}{{{{\omega }_{2}}}} = 0.7804. \\ \end{gathered} $

Как видим, коэффициенты прямоугольности спектра (5) в этих случаях заметно выше, чем у известных окон.

Спектру (5) соответствует оригинал

(7)

$\begin{gathered} g\left( t \right) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {G\left( {j\omega t} \right)} {\text{exp}}\left( {j\omega t} \right)~d\omega = \\ = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\sum\limits_{k = 0}^N {\frac{{{{{\left( {\frac{{{{\omega }^{2}}}}{4}} \right)}}^{k}}}}{{k!}}} } {\text{exp}}\left( {{{ - {{\omega }^{2}}} \mathord{\left/ {\vphantom {{ - {{\omega }^{2}}} 4}} \right. \kern-0em} 4} + j\omega t} \right)d\omega = \\ = \frac{{{\text{exp}}\left( { - \frac{{{{t}^{2}}}}{2}} \right)}}{{\sqrt \pi }}\sum\limits_{k = 0}^N {\frac{{{{{( - 1)}}^{k}}{{D}_{{2k}}}\left( {t\sqrt 2 } \right)}}{{{{2}^{k}}k!}}} ~ = \\ = \frac{{{\text{exp}}\left( { - {{t}^{2}}} \right)}}{{\sqrt \pi }}\sum\limits_{k = 0}^N {\frac{{{{{( - 1)}}^{k}}{{H}_{{2k}}}\left( t \right)}}{{{{2}^{{2k}}}k!}}} = \\ ~ = {{\left( { - 1} \right)}^{N}}~\frac{{{{2}^{{ - 2N - 1}}}~{\text{exp}}\left( { - {{t}^{2}}} \right)}}{{\sqrt {\pi ~} N!}}~\frac{{{{H}_{{2N + 1}}}\left( t \right)}}{t}. \\ \end{gathered} $

(8)

$~g\left( t \right)~\,\, = \frac{1}{{\sqrt {\pi ~} }}\exp ( - {{t}^{2}})L_{N}^{{\left( {\frac{1}{2}} \right)}}({{t}^{2}}),\,\,\,\, - \infty < t < \infty .$

Интеграл вычислен по таблицам [2, формула 3.462(3)]. В выражениях (7), (8) ${{D}_{n}}\left( z \right)$ – функция параболического цилиндра, ${{H}_{n}}\left( z \right) - $ полином Эрмита [2, ф-ла (9.253)], $L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( z \right)$ – обобщенный полином Лагерра. Об идентичности правых частей равенств (7) и (8) см. в монографии [3, с. 693].

2. ОКНО ГАУССА–ТЕЙЛОРА

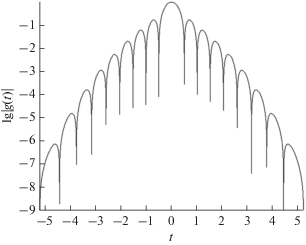
Исследуем свойства четной действительной функции (8). Благодаря экспоненциальному сомножителю функция довольно быстро затухает при $~\left| {~t~} \right| \to \infty $. Благодаря сомножителю $L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {{{t}^{2}}} \right)~$ функция имеет N симметричных пар действительных корней (см. далее Приложение 1). Логично предположить, что функция (8) имеет главный лепесток и по $N - 1~~$ затухающих боковых лепестков слева и справа от него, при этом главный лепесток располагается между парой наименьших по абсолютной величине корней. Эксперименты подтверждают это предположение. Например, на рис. 2, где представлен график логарифма модуля нормированной функции (8) при $N = 9$, мы видим восемь пар боковых лепестков. Последняя пара имеет уровень порядка ${{10}^{{ - 6}}}$.

Рис. 2.

График логарифма модуля нормированной функции (8) $\lg \left| {{{g\left( t \right)} \mathord{\left/ {\vphantom {{g\left( t \right)} {g\left( 0 \right)}}} \right. \kern-0em} {g\left( 0 \right)}}} \right|~$ при $N = 9.$

Чтобы на основе выражения (8) синтезировать оконную функцию, необходимо прежде всего выбрать конечную область определения функции

(9)

$ - r \leqslant t \leqslant r.$

С одной стороны, чем больше $r$, тем меньше уровень боковых лепестков спектра. В предельном случае ($r \to \infty $) боковые лепестки спектра вообще отсутствуют, так как спектр (5) монотонно уменьшается при $\omega \to \infty .$ В этом можно убедиться, перейдя на графике рис. 1 к логарифмической шкале по оси ординат.

С другой стороны, чем больше $r$, тем меньше относительная длина главного лепестка оригинала $g\left( t \right)~~$и тем больше относительная суммарная длина малых по абсолютной величине боковых лепестков, и тем больше теряется информации об анализируемом сигнале при умножении сигнала на оконную функцию.

Кроме того, при выборе интервала (9) учтем, что боковые лепестки спектра тем больше, чем больше разрывы оконной функции и ее производных в точках $t = - r$ и $t = r.$ Поэтому имеет смысл выбрать в качестве границ интервала (9) одну из симметричных пар корней полинома.

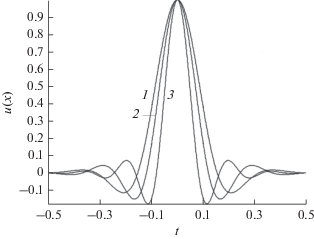
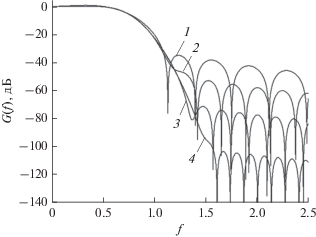
Для подтверждения всех перечисленных выше соображений, рассмотрим четыре графика спектра функции (8) при $N = 5$ (рис. 3), построенные для случаев $r = {{r}_{{2~}}}$, $r = {{r}_{{3~}}}$, $r = {{r}_{{4~~~~}}}$ и $r = {{r}_{{5~}}},$ где ${{r}_{1}} < {{r}_{2}} < {{r}_{{3~}}} < {{r}_{4}} < {{r}_{5}}$ $ - $ положительные корни полинома $L_{5}^{{\left( {\frac{1}{2}} \right)}}\left( {{{t}^{2}}} \right)$. С увеличением длины окна $2r$ уровень боковых лепестков спектра уменьшается.

Рис. 3.

Графики спектра функции (8) при $N = 5$, построенные для случаев r = r₂ (кривая 1), r = r₃ (кривая 2), r = r₄ (кривая 3), r = r₅ (кривая 4).

Оконную функцию Гаусса–Тейлора$~~u\left( x \right)$ получим из оригинала (8), введя относительное время

(10)

$~x = {t \mathord{\left/ {\vphantom {t {\left( {2r} \right)}}} \right. \kern-0em} {\left( {2r} \right)}}$

и выполнив нормировку [1]:

(11)

$\begin{gathered} u\left( x \right) = {\text{exp}}\left( { - 4{{r}^{2}}{{x}^{2}}} \right)~L_{N}^{{\left( {\frac{1}{2}} \right)}}{{\left( {4{{r}^{2}}{{x}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {4{{r}^{2}}{{x}^{2}}} \right)} {L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( 0 \right)}}} \right. \kern-0em} {L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( 0 \right)}},~ \\ \left| x \right| \leqslant 0.5;\,\,\,\,u(x) = 0,\,\,\,\,\left| x \right| > 0.5. \\ \end{gathered} $

На рис. 4 представлены графики оконной функции Гаусса–Тейлора $u\left( x \right)$ для случаев N = 3, $r = 2.6519;$ N = 6, $r = 2.51974~$ и N = 12, $r = 2.70532.$

Рис. 4.

Оконные функции GT при N = 3 (1), 6 (2) и 12 (3).

Следует отметить, что при переходе от времени $t~$ к относительному времени $x$ происходит изменение масштаба. Чтобы оконные функции (или их спектры) для разных значений N можно было сравнивать друг с другом, необходимо, чтобы масштабы времени (или частоты) у них были одинаковы (или хотя бы близки, как для графиков на рис. 4).

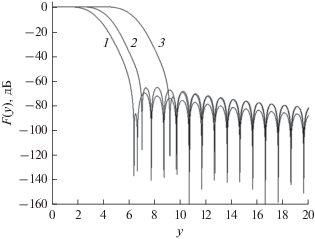
Нормированные спектры F(y) [1] окна Гаусса–Тейлора, заданного выражением (11), определим с помощью быстрого преобразования Фурье (БПФ):

(12)

$F\left( y \right) = ~fft\left( u \right).$

Графики спектров окна GT для случаев N = 3, $r = 2.6519;$ N = 6, $r = $$2.51974~$ и N = 12, $r = 2.70532$ представлены на рис. 5. При одинаковых (или близких) значениях параметра $r$ увеличение параметра $N$ приводит к сужению графиков оконных функций и к расширению графиков нормированных спектров.

Рис. 5.

Спектры оконных функций GT при N = 3 (1), 6 (2) и 12 (3).

3. МОДИФИЦИРОВАННОЕ ОКНО ГАУССА–ТЕЙЛОРА

Как видно из графиков рис. 5, уровень боковых лепестков спектра окна GT велик по сравнению с таковыми для известного окна с “плоской вершиной” (“Flat top window”, FT) [1].

Синтезируем модифицированное окно Гаусса–Тейлора (GTM) с меньшим уровнем боковых лепестков спектра. Для этого необходимо устранить (или хотя бы уменьшить) разрывы оконной функции и ее производных на границах интервала $ - 0.5 \leqslant x \leqslant 0.5$.

Начнем с того, что определим корни окна (11). Нетрудно видеть, что они совпадают с корнями полинома $L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{x}^{2}}} \right)$, а те, в свою очередь, как следует из равенства (10), равны корням полинома $L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {{{t}^{2}}} \right),~$ поделенным на $2r$: ${{ \pm {{r}_{1}}} \mathord{\left/ {\vphantom {{ \pm {{r}_{1}}} {2r}}} \right. \kern-0em} {2r}},~$ $~{{ \pm {{r}_{2}}} \mathord{\left/ {\vphantom {{ \pm {{r}_{2}}} {2r}}} \right. \kern-0em} {2r}},~$ … Например, полиному $L_{6}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{x}^{2}}} \right)$ (см. Приложение 1) при $r = 2.51974$ соответствуют корни: ±0.120239, ±0.242171, ±0.367826, ±0.5, ±0.644424, ±0.814081. Из шести положительных корней полинома $L_{6}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{x}^{2}}} \right)$ нас интересуют два: корень ${{R}_{2}} = 0.5$ и предшествующий ему корень, например, ${{R}_{1}} = 0.367826.$

Заменим относительное время $x$ нелинейным (замедляющимся относительно времени $x$) временем

(13)

$~v = x~{\text{exp}}\left( { - a{{x}^{2}} - b{{x}^{4}}} \right),$

производная которого равна

(14)

$~v{\kern 1pt} {\text{'}} = \frac{{dv}}{{dx}} = \left( {1 - 2a{{x}^{2}} - 4b{{x}^{4}}} \right){\text{exp}}\left( { - a{{x}^{2}} - b{{x}^{4}}} \right).$

Здесь a и b – константы, которые удовлетворяют уравнениям

(15)

$v\left( {{{R}_{2}}} \right) = v\left( {0.5} \right) = 0.5\exp \left( { - {a \mathord{\left/ {\vphantom {a 4}} \right. \kern-0em} 4} - {{~b} \mathord{\left/ {\vphantom {{~b} {16}}} \right. \kern-0em} {16}}~} \right)\,~ = \,~{{R}_{1}},$

(16)

$\begin{gathered} ~v{\kern 1pt} '\left( {{{R}_{2}}} \right) = \left( {1 - {{2a} \mathord{\left/ {\vphantom {{2a} 4}} \right. \kern-0em} 4} - {{4b} \mathord{\left/ {\vphantom {{4b} {16}}} \right. \kern-0em} {16}}} \right) \times \\ \times \,\,{\text{exp}}\left( {{{ - a} \mathord{\left/ {\vphantom {{ - a} 4}} \right. \kern-0em} 4} - {b \mathord{\left/ {\vphantom {b {16}}} \right. \kern-0em} {16}}} \right) = 0. \\ \end{gathered} $

Из системы уравнений (15)–(16) следует:

(17)

$~a = - 2 - 8~{\text{ln}}\left( {2{{R}_{1}}} \right),~$

(18)

$~b = 8 + 16~{\text{ln}}\left( {2{{R}_{1}}} \right).$

Уравнение (15) означает, что при подстановке $v$ вместо $~x$ в полином $L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{x}^{2}}} \right)$ получим функцию $L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{v}^{2}}} \right)$, равную нулю, в граничных точках интервала $ - 0.5 \leqslant x \leqslant 0.5$. Уравнение (16) означает, что на границах интервала первая производная полинома также равна нулю:

(19)

$\begin{gathered} {{\left( {L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{v}^{2}}} \right)} \right)}^{'}} = ~\,\,\frac{d}{{dx}}L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{v}^{2}}} \right) = \\ = \frac{d}{{dv}}L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( {4{{r}^{2}}{{v}^{2}}} \right)\frac{{dv}}{{dx}} = 0. \\ \end{gathered} $

Эксперименты показали, что подстановка нелинейного времени $v$ вместо x в обобщенный полином Лагерра уменьшает боковые лепестки спектра, но этого не происходит при подстановке времени $v$ вместо x в экспоненту. Поэтому следует либо записывать экспоненту в виде ${\text{exp}}\left( { - 4{{r}^{2}}{{x}^{2}}} \right)~$, либо попытаться подобрать другое время $\tau ,$ с которым боковые лепестки спектра меньше, чем при времени x. Экспериментально удалось подобрать для некоторых значений параметра N (а именно для N = 3, 4, 5, 6 и 12) нелинейное время

(20)

$\tau = x(1 + 2{{x}^{4}} + 1.5{{x}^{6}}),$

которое приводит к положительному эффекту при подстановке в экспоненту вместо x. Для N = 7 и 9 подобраны другие выражения для $\tau $, уменьшающие боковые лепестки спектра.

С учетом сказанного выше из выражений (11) и (13) получаем модифицированное окно Гаусса–Тейлора:

(21)

$\begin{gathered} u\left( x \right) = {\text{exp}}~\left( { - 4{{r}^{2}}{{\tau }^{2}}} \right)~\,\, \times \\ \times \,L_{N}^{{\left( {\frac{1}{2}} \right)}}\,{{\left[ {4{{r}^{2}}{{x}^{2}}{\text{\;exp}}\left( { - 2a{{x}^{2}} - 2b{{x}^{4}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {4{{r}^{2}}{{x}^{2}}{\text{\;exp}}\left( { - 2a{{x}^{2}} - 2b{{x}^{4}}} \right)} \right]} {L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( 0 \right)}}} \right. \kern-0em} {L_{N}^{{\left( {\frac{1}{2}} \right)}}\left( 0 \right)}},~ \\ \left| x \right| \leqslant 0.5;\,\,\,\,\,u(x) = 0,\,\,\,\,\left| x \right| \geqslant 0.5, \\ \end{gathered} $

при этом a и b определяются равенствами (17) и (18).

На основании теоретических результатов были выполнены расчеты и построены графики для конкретных случаев окна Гаусса–Тейлора и модифицированного окна Гаусса–Тейлора и их спектров, которые могут быть использованы на практике.

Коэффициенты $r$, $a$, $b$ и экспериментально подобранная формула для нелинейного времени $\tau $ представлены в табл. 1.

Таблица 1.

Коэффициенты окна GTM и время$~\tau ~$при различных значениях N

N	r	a	b	$\tau $
3	2.65195	0.84147	0.3170639	x(1 + 2${{x}^{4}} + 1.5{{x}^{6}}$)
4	2.26658	0.736	0.52805	x(1 + 2${{x}^{4}} + 1.5{{x}^{6}}$)
5	2.78329	0.2703885	1.459223	x(1 + 2${{x}^{4}} + 1.5{{x}^{6}}$)
6	2.51975	0.229167	1.541665	x(1 + 2${{x}^{4}} + 1.5{{x}^{6}}$)
7	2.32575	0.206886	1.586228	x(1 – 0.41377${{x}^{2}}$ + 4${{x}^{4}}$)
9	2.04925	0.1840505	1.6318985	$x\left( {1 - 0.368{{x}^{2}} + 4.5{{x}^{4}}} \right)$
12	2.7053	0.678897	0.6422055	x(1 + 2${{x}^{4}} + 1.5{{x}^{6}}$)

В табл. 2 сравниваются параметры предложенного в статье окна GTM с параметрами известного окна FT [1].

Таблица 2.

Параметры окна GTM при различных значениях N и окна FT

Оконные функции	N	${{K}_{{\text{п}}}}$	${{W}_{{{\text{max}}}}},~\,{\text{дБ}}$	$\Delta W,\,\,~{\text{дБ}}$ на октаву	CG	$\Delta {{F}_{{\text{ш}}}}$	SL, дБ	MPL, дБ
GMT	3	0.639	–143	–12	0.153	5.59	0.0158	7.49
	4	0.671	–119	–12	0.160	5.44	0.0446	7.40
	5	0.695	–130	–12	0.118	7.53	–0.00857	8.76
	6	0.713	–117	–12	0.120	7.47	–0.0180	8.73
	7	0.729	–115	–12	0.121	7.46	–0.0294	8.70
	9	0.754	–111	–12	0.122	7.50	–0.0549	8.70
	12	0.780	–143	–12	0.081	11.35	–0.00742	10.54
FT	–	0.56	–82.6	–6	0.22	3.77	0.01	5.78

Примечание: ${{K}_{{\text{п}}}}$ – коэффициент прямоугольности; ${{W}_{{{\text{max}}}}}$ – максимальный уровень боковых лепестков относительно главного лепестка; $\Delta W - $ скорость спада боковых лепестков, CG – когерентное усиление; $\Delta {{F}_{{\text{ш}}}}$ – эквивалентная шумовая полоса; SL – паразитная амплитудная модуляция; MPL – максимальные потери преобразования.

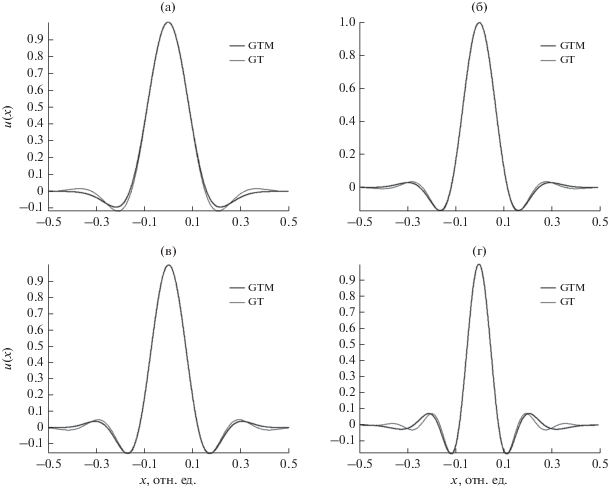
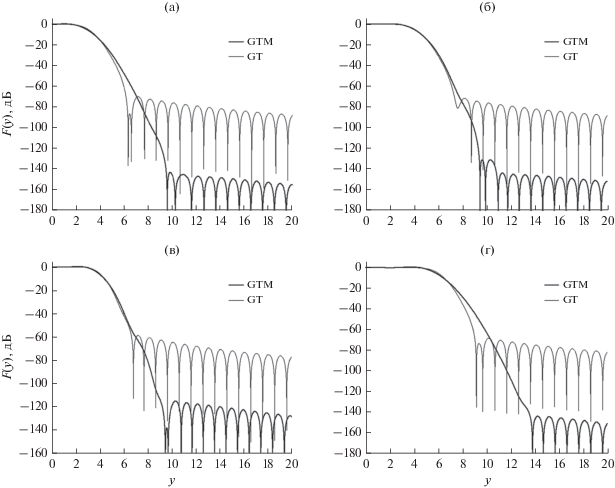
Часть экспериментального материала представлена на рис. 6, 7 . Это окна GTM и GT для случаев N = 3 (рис. 6а), 5 (рис. 6б), 7 (рис. 6в) и 12 (рис. 6г) и их спектры (рис. 7а, 7б, 7в и 7г соответственно).

Рис. 6.

Сравнение окон GTM и GT для N = 3 (а), 5 (б), 7 (в) и 12 (г).

Рис. 7.

Сравнение спектров окон GTM и GT для N = 3 (а), 5 (б), 7 (в) и 12 (г).

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Из равенств (6) следует, что окно Гаусса–Тейлора при $N \geqslant 3$ превосходит известное окно с плоской вершиной FT по коэффициенту прямоугольности ${{K}_{{\text{п}}}}$. Из рис. 7а–7г видно, что участки спектров от F(y) = 0 до F(y) = –20 дБ модифицированного окна Гаусса–Тейлора и окна Гаусса–Тейлора при одинаковых значениях параметра $N~$ практически совпадают. Таким образом, значения коэффициента ${{K}_{{\text{п}}}}$ при заданном значении параметра $N$ у этих окон одинаковы.

Отличительной особенностью окон GT и GTM является наличие боковых лепестков не только у спектров, но и у собственно окон. В разд. 2 отмечалось, что график функции (8) имеет N – 1 пар боковых лепестков. Однако количество пар боковых лепестков на рис. 6а–6г меньше. Это обусловлено, во-первых, ограничением окон GT и GTM по времени интервалом (9) и, во-вторых, использованием нелинейного времени для окна GTM.

Достоинства окна GTM (табл. 2): высокий коэффициент прямоугольности и малый уровень боковых лепестков спектра. Недостатки, обусловленные широкополосностью окна, $ - $ большая эквивалентная шумовая полоса, малое когерентное усиление и большие потери преобразования.

ЗАКЛЮЧЕНИЕ

Предложено модифицированное окно Гаусса–Тейлора, которое превосходит известное окно с плоской вершиной и по коэффициенту прямоугольности, и по уровню боковых лепестков спектра. Предложен способ, позволяющий уменьшить уровень боковых лепестков спектра. Материал статьи может быть использован в таких радиотехнических дисциплинах, как синтез сигналов и синтез фильтров.

Список литературы

Дворкович В.П., Дворкович А.В. Оконные функции для гармонического анализа сигналов. М.: Техносфера, 2016.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматлит, 1963.
Смирнов В.И. Курс высшей математики. Т. 3. Ч. 2. СПб.: БХВ–Петербург, 2010.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал