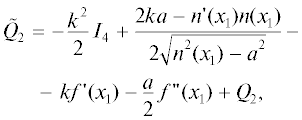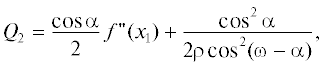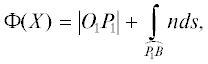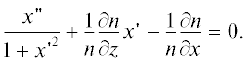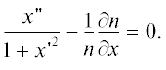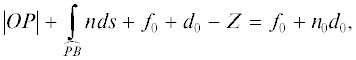Радиотехника и электроника, 2020, T. 65, № 9, стр. 872-880

ВВЕДЕНИЕ

Цилиндрические линзы из плавно неоднородного (градиентного) диэлектрика используются как в оптическом, так и в радиодиапазоне электромагнитных волн. Впервые цилиндрические линзы такого типа с плоскими поверхностями и квадратичным законом изменения коэффициента преломления вдоль декартовой координаты были изготовлены из желатина и исследованы в оптическом диапазоне [1]. В работах по оптике их часто называют линзами Вуда [2]. Точное решение задачи геометрооптического синтеза частного случая градиентной линзы – плоской линзы с первым фокусом на поверхности линзы, а вторым на бесконечности – было получено в работе [3] в виде зависимости коэффициента преломления от декартовой координаты в декартовой системе координат или радиальной координаты в цилиндрической системе координат. Эта линза получила название линза Микаэляна [4]. В работе [5] решение [3] было обобщено на случай линзы из анизотропного диэлектрика.

Теория геометрооптического синтеза градиентных линз с плоскими входной и выходной поверхностями и внешним фокусом, использующая классическую оптическую теорию аберраций, описана в работе [2]. Теория синтеза, использующая разложение коэффициента преломления по четным степеням расстояния от оси линзы, развита в работе [6], а с криволинейными поверхностями – в работах [7, 8]. Рекуррентный метод синтеза таких линз, основанный на использовании модели слоистой линзы с постоянными коэффициентами преломления внутри слоев, развит в работе [9].

Исследование эйконала (оптического пути) и его аберраций в градиентных линзах при смещении источника из фокуса усложняется из-за криволинейной формы лучей. Классическая оптическая теория аберраций таких линз описывает лучевую аберрацию в виде двумерного ряда (разложения по степеням угла зрения и апертуры линзы) [2]. В работах [10–12] развита новая теория аберраций для однородных диэлектрических линз с использованием разложения эйконала по одному параметру – величине смещения источника. В работе [13] теория обобщается для описания эйконала и его аберрации на выходной поверхности двумерной линзы с градиентом диэлектрической проницаемости вдоль декартовой координаты. Однако формула для эйконала, полученная в работе [13], неудобна для использования вблизи оси симметрии линзы, поскольку имеет на оси особенность.

Цель данной работы – получить формулу для эйконала, справедливую в параксиальной области, а также формулу, в которой используется приближение прямых лучей.

1. ЭЙКОНАЛ НА ВЫХОДНОЙ ПОВЕРХНОСТИ ЛИНЗЫ В ПАРАКСИАЛЬНОМ ПРИБЛИЖЕНИИ ПРИ СМЕЩЕННОМ ИЗ ФОКУСА ИСТОЧНИКЕ

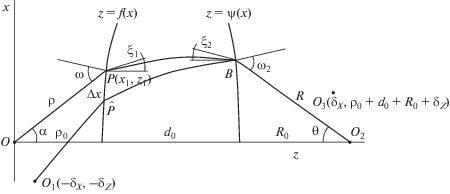
Рассмотрим цилиндрическую градиентную линзу, преобразующую цилиндрический фронт в цилиндрический (или плоский) с показателем преломления n, зависящим от декартовой координаты х (рис. 1). Пусть источник смещается из фокуса в точке О в точку О₁ с координатами $( - {{\delta }_{X}}, - {{\delta }_{Z}})$. Эйконал луча, выходящего из О₁, в произвольной точке $B({{x}_{2}},{{z}_{2}})$ на выходной апертуре линзы имеет вид [13]

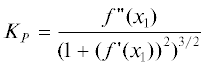Здесь J – оптический путь невозмущенного луча от точки Р до точки В, где $a = n({{x}_{1}})\cos {{\xi }_{1}}$ – лучевой параметр невозмущенного луча, – кривизна поверхности линзы в точке Р.

Кроме того, φ = 0 при х₂ > 0, φ = π при х₂ < 0, $J = {{\rho }_{0}} + {{n}_{0}}{{d}_{0}} + {{R}_{0}} - \rho - R,$ $\lambda = \frac{\Omega }{{{{\Omega }_{2}}}}\frac{{d\theta }}{{d\alpha }},$ $\theta = \theta (\alpha )$ – функция отображения при фокусировке на конечном расстоянии, $J = {{n}_{0}}{{d}_{0}} - {{d}_{0}} - \rho + {{Z}_{B}},$ $\lambda = \Omega \frac{{d{{x}_{2}}}}{{d\alpha }},$ ${{x}_{2}} = {{x}_{2}}(\alpha )$ – функция отображения при фокусировке на бесконечности (при формировании плоского фронта), $\Omega = \frac{{\cos \omega }}{{\rho \cos (\omega - \alpha )}},$ ${{\Omega }_{2}} = \frac{{\cos {{\omega }_{2}}}}{{R\cos ({{\omega }_{2}} - \theta )}}.$

Величина эйконала (1) зависит от первых производных функций, описывающих левую и правую поверхности линзы, от кривизны левой поверхности, углов входа и выхода невозмущенного луча, производной функции отображения, значения коэффициента преломления в точке входа и выхода невозмущенного луча, производной коэффициента преломления в точке входа невозмущенного луча. При этом выражение (1) справедливо как для монотонных лучей, так и немонотонных.

Формула (1) справедлива для любой точки В на правой поверхности линзы, кроме точки на оси z, потому что при х = 0 в формуле имеется особенность в выражении ${{\tilde {Q}}_{2}}$. Раскроем эту особенность. Из закона преломления в точках Р и В следует, что

(углы ξ₁, ξ₂, ω, ω₂ показаны на рис. 1). Раскладывая эти выражения в ряды по х₁ и х₂ и оставляя члены не выше первого порядка, получаем где ${{g}_{1}} = 2{{f}_{2}}({{n}_{0}} - 1) - \frac{1}{{{{\rho }_{0}}}},$ ${{h}_{1}} = 2{{\psi }_{2}}({{n}_{0}} - 1) + \frac{1}{{{{R}_{0}}}},$ ${{g}_{2}} = g_{1}^{2},$ f₂ и ψ₂ – коэффициенты разложения уравнения поверхностей ($z = {{\rho }_{0}} + {{f}_{2}}{{x}^{2}} + ...$ и z = $ = {{\rho }_{0}} + {{d}_{0}} + {{\psi }_{2}}{{x}^{2}} + ...$).

Разложим закон отображения для фокусировки на конечном расстоянии в ряд Тэйлора по нечетным степеням α: $\theta = {{m}_{1}}\alpha + {{m}_{3}}{{\alpha }^{3}} + ....$ Пусть при фокусировке в плоскую волну аналогичный ряд имеет вид ${{x}_{2}} = {{f}_{e}}\alpha + {{f}_{3}}{{\alpha }^{3}} + ...$ . При $\alpha \to 0$ и фокусировке на конечном расстоянии имеем

а при фокусировке в плоскую волну – При этом из соотношений ${{x}_{1}} = \alpha {{\rho }_{0}},$ ${{x}_{2}} = {{R}_{0}}\theta $ следует: где с₂ – коэффициент разложения ${{n}^{2}}(x) = n_{0}^{2} - {{c}_{2}}{{x}^{2}}.$

С учетом найденных соотношений получаем

тогда выражение для эйконала луча из смещенного фокуса можно представить в виде

(выражение для величины ${{\tilde {Q}}_{1}}$ было приведено выше).

Формула (2) определяет эйконал луча из смещенного источника в параксиальной области.

2. ФОРМУЛА ДЛЯ ЭЙКОНАЛА НА ВЫХОДНОЙ ПОВЕРХНОСТИ ЛИНЗЫ В ПРИБЛИЖЕНИИ ПРЯМЫХ ЛУЧЕЙ

Формула (1) описывает эйконал в точке В с погрешностью порядка $\delta _{X}^{3}$. Как показано в работе [12], для линзы из однородного диэлектрика можно получить приближенную формулу для эйконала путем прямого суммирования двух оптических путей:

где точка $\hat {P}$ имеет координаты (x + Δxcos φ, $f(x + \Delta x\cos \varphi ),$ Δх вычисляется по формуле

В параксиальной области формула (4) переходит в формулу

При этом ошибка формулы (3), зависящая от смещения, пропорциональна $\delta _{X}^{4}$. Первый член формулы (3) есть длина отрезка ${{O}_{1}}\hat {P}$, второй член представляется криволинейным интегралом по траектории луча, соединяющего точки $\hat {P}$ и В:

Вычислим эйконал луча в среде с показателем преломления, меняющимся по закону ${{n}^{2}}(x) = n_{0}^{2} - {{c}_{2}}{{x}^{2}}$. Уравнение монотонного луча в такой среде имеет вид

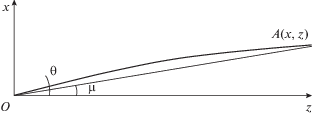
Здесь $a = {{n}_{0}}\cos \theta ,$ ${{p}^{2}} = \frac{{n_{0}^{2} - {{a}^{2}}}}{{{{c}_{2}}}} = \frac{{n_{0}^{2}{{{\sin }}^{2}}\theta }}{{{{c}_{2}}}}$, θ – угол касательной к лучу в точке О (рис. 2).

Эйконал луча в точке А представим в виде

Разлагая этот эйконал в ряд по степеням х и оставляя члены не выше второго порядка, получаем

Легко показать, что полученное выражение для эйконала справедливо и для немонотонного луча, т.е. имеющего экстремум внутри линзы. Вычислим эйконал на прямом отрезке, соединяющем точки О и А (см. рис. 2):

где L₂ и ${{\bar {L}}_{2}}$ – значение коэффициента разложения точного и приближенного эйконала соответственно. Этот отрезок тем ближе к истинному лучу в линзе, чем меньше величина градиента показателя преломления среды и тоньше линза. Численное сравнение коэффициентов L₂ и ${{\bar {L}}_{2}}$ показывает, что при n₀ = 1.6, c₂ = 1 и z = 0.5 получаем $\left| {{{L}_{2}} - {{{\bar {L}}}_{2}}} \right| = 3.4 \times {{10}^{{ - 4}}}$, а при n₀ = 1.6, c₂ = 3 и z = 1 имеем $\left| {{{L}_{2}} - {{{\bar {L}}}_{2}}} \right| = 2.75 \times {{10}^{{ - 2}}}$. Если при указанных параметрах заменить эйконал реального луча на эйконал спрямленного луча, то ошибка будет порядка $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{O} ({{x}^{4}})$.

С учетом полученных результатов эйконал в точке В на выходной поверхности можно записать в виде

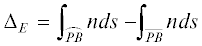где – разность криволинейного и прямолинейного интегралов для невозмущенного луча. Интегрирование в формуле (5) проводится по прямой, соединяющей точки Р₁ и В, а точка Р₁ имеет координаты ${{x}_{1}} = x + \Delta x\cos \varphi $, ${{z}_{1}} = f({{x}_{1}})$, где х – координата невозмущенной точки Р, а Δх выражается формулой (4).

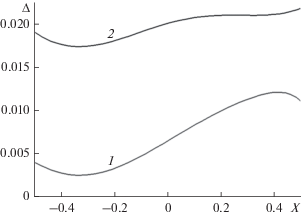
На рис. 3 приведены зависимости от координаты вдоль апертуры ошибки вычисления эйконала апланатической градиентной линзы с параболическим законом изменения диэлектрической проницаемости и параметрами ${{\rho }_{0}} = 1$, ${{d}_{0}} = 0.5$, ${{n}_{0}} = 1.6$, ${{f}_{e}} = 1.35$, ${{c}_{2}} = 1.5$. Величины смещения источника ${{\delta }_{X}} = 0.39904$, ${{\delta }_{Z}} = - 0.25024$ соответствуют отклонению луча на 20 град. Величины δ_X, δ_Z, ρ₀, d₀, R₀, f_e здесь и далее нормированы на величину апертуры линзы. Кривой 2 представлена разность точного эйконала и эйконала, вычисленного по формуле (1), а кривой 1 – разность точного эйконала и вычисленного по формуле (5). Как видно из рисунка, при данном наборе параметров точность формулы (5) выше, чем формулы (1).

3. ФОКАЛЬНЫЕ КРИВЫЕ

При выводе уравнения фокальной кривой, на которой эйконал имеет минимальную аберрацию (отклонение от эйконала центрального луча), рассмотрим три случая – один общий и два частных:

1) оба фокуса находятся на конечном расстоянии от линзы,

2) два фокальных расстояния равны,

3) второй фокус находится на бесконечности.

Начнем с частного случая 3. Найдем эйконал в точке В с координатами (Х, Z), лежащей на краю апертуры линзы, и добавим оптический путь до плоскости наклонного фронта. Для вывода уравнения используем формулы (1), (2) для эйконала на выходной поверхности линзы. Обозначим полученный в результате эйконал Ф(Х):

где θ – угол между лучом на выходе линзы и осью Z, $Z = \psi (X)$, а величина L(О₁,B) определяется формулой (1) или (на оси) формулой (2).

Эйконал Ф(Х) можно представить в виде суммы Ф(Х) = Ф₁(Х) + Ф₂(Х), где Ф₂(X) – четная, а Ф₁(X) – нечетная функции.

Используя соотношения $\sin \theta = {{{{\delta }_{X}}} \mathord{\left/ {\vphantom {{{{\delta }_{X}}} {{{f}_{e}}}}} \right. \kern-0em} {{{f}_{e}}}}$, cos θ = $ = 1 - {{\delta _{X}^{2}} \mathord{\left/ {\vphantom {{\delta _{X}^{2}} {(2f_{e}^{2})}}} \right. \kern-0em} {(2f_{e}^{2})}}$ и введя обозначения ${{q}_{2}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} {(4{{{\tilde {Q}}}_{2}})}}} \right. \kern-0em} {(4{{{\tilde {Q}}}_{2}})}}$, ${{q}_{{20}}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} {(4{{{\tilde {Q}}}_{{20}}})}}} \right. \kern-0em} {(4{{{\tilde {Q}}}_{{20}}})}},$ можно получить

где ${{L}_{0}} = {{\rho }_{0}} + {{n}_{0}}{{d}_{0}}$.

Приравнивая ${{\Phi }_{2}}(X) = {{\Phi }_{2}}(0)$, получаем уравнение фокальной кривой, определяющую зависимость ${{\delta }_{Z}}$(${{\delta }_{X}}$):

Теперь выведем уравнение фокальной кривой для частного случая 2, когда фокальные расстояния равны, т.е. ρ₀ = R₀. В этом случае линза имеет две плоскости симметрии и α = θ для любого луча. Найдем эйконал в точке В, лежащей на оси, т.е. при Х = 0 и α = 0. Из симметрии линзы можно получить, что ${{h}_{1}} = - {{g}_{1}}$, и из формулы (2) следует:

Прибавляя к полученному значению эйконала в точке В расстояние от В до О₃: $\left| {B{{O}_{3}}} \right| = $ $ = \sqrt {\delta _{X}^{2} + {{{({{\rho }_{0}} + {{\delta }_{Z}})}}^{2}}} $ = ${{\rho }_{0}} + {{\delta }_{Z}} + \frac{{\delta _{X}^{2}}}{{2{{\rho }_{0}}}}$,

получим эйконал от точки О₁ до О₃:

Приравнивая к нулю сумму членов с δ_Х и δ_Z, получаем уравнение фокальной кривой слева от линзы:

В силу симметрии линзы фокальная кривая справа от линзы симметрична кривой (7) относительно оси X.

И наконец, найдем уравнение фокальной кривой в общем случае 1, когда фокусные расстояния разные и конечные. При этом одна из фокальных кривых (например, правая) может быть задана в виде

где $({{\Delta }_{X}},{{\Delta }_{Z}})$ – координаты смещенного фокуса О₃. Ограничимся случаем апланатической линзы. По формуле (1) найдем эйконал в произвольной точке $B(X,Z)$ на правой поверхности и прибавим к нему расстояние $\left| {B{{O}_{3}}} \right|$:

Ограничиваясь линейными членами по δ_Х, Δ_Х, можно записать

Приведенная сумма в силу фокусировки есть константа, поэтому можно записать

где $m = {{\sin \theta } \mathord{\left/ {\vphantom {{\sin \theta } {\sin \alpha }}} \right. \kern-0em} {\sin \alpha }}$ – константа (параметр апланатизма).

По формуле (2) найдем эйконал в точке В, лежащей на оси, т.е. при Х = 0 и α = 0:

Прибавляя к полученному значению эйконала в точке В расстояние от В до O₃:

получим эйконал по лучу от точки О₁ до О₃:

где ${{L}_{0}} = {{\rho }_{0}} + {{n}_{0}}{{d}_{0}} + {{R}_{0}}$ – эйконал центрального луча. Выражая Δ_Х через δ_Х по формуле (9), а Δ_Z через Δ_Х по формуле (8) и требуя выполнения равенства $L({{O}_{1}},{{O}_{3}}) = {{L}_{0}}$, получаем уравнение фокальной кривой:

4. ИССЛЕДОВАНИЕ ТОЧНОСТИ ФОРМУЛ ДЛЯ ЭЙКОНАЛА И ЕГО АБЕРРАЦИЙ

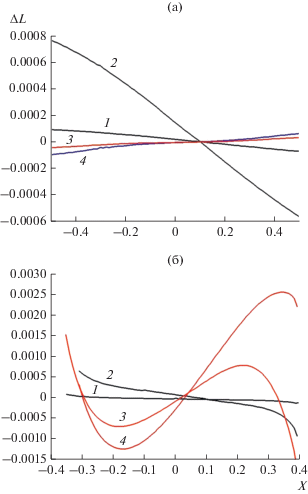
Была найдена разность эйконалов, вычисленных методом геометрической оптики и с помощью формул (1), (2) и (5) на выходной поверхности линзы с параболическим законом изменения диэлектрической проницаемости. Полученные данные приведены на рис. 4. На рис. 4а представлено распределение погрешности формул для эйконала на выходной поверхности линзы, которая преобразует цилиндрический фронт источника в плоский, а на рис. 4б – распределение погрешности для симметричной линзы. Кривые 1, 2 рассчитаны с использованием формулы (1), кривые 3, 4 – с использованием формулы (5). Из данных, представленных на рис. 4а, видно, что формула (5) почти на порядок точнее формулы (1), а из данных на рис. 4б – наоборот, на порядок хуже. Также видно, что погрешность формулы (1) обусловлена главным образом линейной составляющей, которая сдвигает точку фокусировки вдоль фокальной кривой и не влияет на величину аберрации, а зависимость на рис. 4б, определенная формулой (5), содержит существенную нелинейную погрешность.

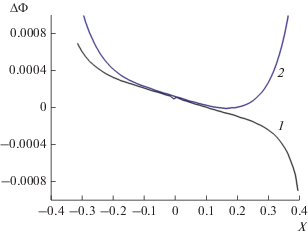
Для этой же линзы была определена разность эйконалов, вычисленных методом геометрической оптики и с помощью формул (1) или (2). На рис. 5 приведены полученные результаты, и видно, что в области $\left| X \right| \leqslant 0.25$ погрешности формул примерно равны.

Далее была исследована погрешность формулы (1) при вычислении аберрации в линзе с двумя плоскостями симметрии и параметрами ρ₀ = 1, R₀ = 1, d₀ = 1, n₀ = 1.6, c₂ = 2.9. Добавим к величине эйконала в точке В выходной апертуры линзы для луча из источника, расположенного в точке ${{O}_{1}}( - {{\delta }_{X}}, - {{\delta }_{Z}})$, расстояние до симметричной ей точки ${{O}_{3}}({{\delta }_{X}},{{\rho }_{0}} + {{d}_{0}} + {{R}_{0}} + {{\delta }_{Z}})$ и вычтем константу и линейную составляющую. В результате получаем

где Ф₀ – эйконал центрального луча несмещенного источника.

Эйконал $\Phi (X)$ будем вычислять двумя способами: по формуле (1) и методом геометрической оптики с использованием формулы

пределы интегрирования в которой находятся из уравнения луча для среды с квадратичной зависимостью диэлектрической проницаемости [4] для двух случаев:

1) если луч монотонный –

2) если луч имеет максимум –

Координаты точки пересечения луча (Z₂, X₂) с поверхностью находятся из системы двух уравнений, одно из которых – приведенное уравнение луча, а второе – уравнение образующей поверхности линзы $Z = \Psi (X)$.

Координата z для смещенного на δ_X = 0.2 источника на фокальной кривой, вычисленная по формуле (7), равна δ_Z = 0.01486, а на оптимальной фокальной кривой, найденной путем минимизации аберрации – δ_Z = 0.02686. Зависимости величины аберрации эйконала от координаты точки на выходной поверхности линзы приведены на рис. 6а для фокальной кривой (7) и на рис. 6б для оптимальной фокальной кривой.

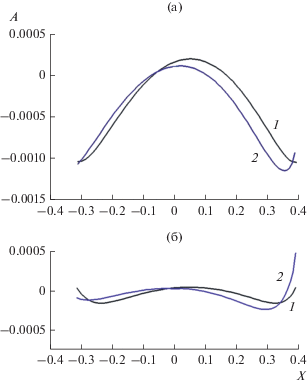
Следует отметить, что кривые на рис. 6а имеют значительные квадратичные составляющие. Это объясняется приближенным характером фокальной кривой, определенной формулой (7). Как видно из рис. 6б, оставшиеся квадратичные составляющие сопоставимы с составляющими более высоких четных степеней. Нечетные степени практически отсутствуют из-за апланатизма системы.

Введем величину среднеквадратической аберрации (СА) по формуле

где N = 100 – число лучей, прошедших через апертуру линзы от источника на фокальной кривой. Когда эйконал Ф(Х) вычисляется по формуле (1), то S_A = 0.9 × 10^–4, а когда эйконал Ф(Х) вычисляется методом геометрической оптики, то S_A = 0.87 × 10^–4. Разность этих значений составляет 3 × 10^–6 и определяет в данном случае погрешность вычисления СА эйконала с использованием формулы (1). Сравнивая эту разность с погрешностью вычисления эйконала (см. рис. 4б, кривая 2), можно убедиться, что последняя из них почти на три порядка больше.

Используя результаты работы [8], можно найти разложения поверхностей апланатической линзы с квадратичным законом изменения диэлектрической проницаемости ${{n}^{2}}(x) = n_{0}^{2} - {{c}_{2}}{{x}^{2}}$:

где ${{f}_{0}} = {{\rho }_{0}},$

Линза преобразует сферический фронт во фронт, близкий к плоскому, и при этом приближенно выполняется условие апланатизма: $X = {{f}_{e}}\sin \alpha $, где α – угол выхода луча из источника, а Х – координата точки выхода луча из линзы. Для более точного синтеза поверхностей линзы используем следующий алгоритм. Представим первую поверхность полиномом 8-й степени:

где ${{f}_{6}} = {{f}_{8}} = 0$ (${{f}_{2}},{{f}_{4}}$ определены выше). На первом этапе алгоритма рассмотрим лучи, падающие на левую поверхность, заданную формулой (12). Из закона преломления можно найти угол преломленного луча: где ω – угол между лучом и нормалью в точке х_Р определяется соотношением $\omega = {\text{arctg}}[f{\kern 1pt} '({{x}_{P}})] + \alpha .$ Траектория преломленного луча x(z) в среде описывается уравнением Эйлера [14]:

В силу того, что n не зависит от z, т.е. $\frac{{\partial n}}{{\partial z}} = 0$, это уравнение упрощается:

Запишем начальные условия для интегрирования дифференциального уравнения второго порядка: $x({{z}_{P}}) = {{x}_{P}},$ $x{\kern 1pt} '({{z}_{P}}) = {\text{tg}}\xi .$ Уравнение (13) решается методом Рунге–Кутты до точки В(X, Z), на которой выполняется условие равенства эйконала луча эйконалу центрального луча:

где интеграл вычисляется вдоль траектории луча. То есть для каждой точки Р на левой поверхности по приведенному алгоритму находится точка В на правой поверхности, которая обеспечивает идеальную фокусировку. Таким образом, массиву точек на левой поверхности соответствует массив точек правой поверхности. Для интерполяции поверхности между точками массива используется кубический сплайн.

Приведенная процедура исправляет ошибку фокусировки. Для уточнения условия апланатизма при нахождении точек на правой поверхности введем сумму:

где α – угол выхода луча из источника, Х – координата точки выхода луча из линзы, суммирование идет по всем N_P точкам. Далее минимизируем величину σ, варьируя коэффициенты ${{f}_{2}},{{f}_{4}},{{f}_{6}},{{f}_{8}}$. В результате проведенной процедуры было получено значение σ = 2 ×10^–4.

При смещении источника из фокуса градиентной линзовой антенны происходят искажения эйконала, которые можно охарактеризовать введенной выше величиной СА. В случае бесконечно удаленного фокуса эта величина описывает отклонение фронта от плоского и выражается формулой

где Х_i, Z_i – координаты точки луча на выходной апертуре линзы, Ф(Х_i ) – величина эйконала в этих точках, N = 100 – число рассмотренных лучей.

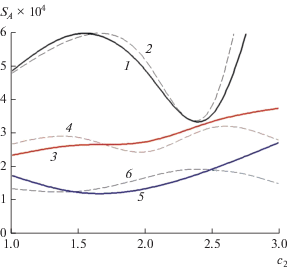
Для линз с параметрами ${{f}_{0}} = 1$, ${{d}_{0}} = 0.5$, ${{n}_{0}} = 1.6$ была найдена зависимость СА от ${{c}_{2}}$ (коэффициенты разложения ${{n}^{2}}(x) = n_{0}^{2} - {{c}_{2}}{{x}^{2}}$) при переменной ${{f}_{e}}$ (фокальный параметр) и угле наклона луча 15 град. Результаты приведены на рис. 7: кривые 1, 2 соответствуют линзе с фокальным радиусом f_e = 1.1, кривые 3, 4 соответствуют линзе с f_e = 1.2, кривые 5, 6 – с f_e = 1.35. Штриховые кривые соответствуют СА, рассчитанным с использованием геометрической оптики, сплошные кривые – с использованием приближенной формулы (5). Как показали расчеты, значения фокального радиуса большие чем 1.35, не приводят к уменьшению СА. Видно, что для фиксированного фокального радиуса и значений с₂ < 2.5 разность СА, вычисленной по формуле (5) и точной СА, не превосходит 0.3 × 10^–4, а при 2.5 < c₂ < 3 эта разность возрастает до 10^–4.

ЗАКЛЮЧЕНИЕ

На основе полученных результатов можно сделать следующие выводы:

– полученная приближенная формула для эйконала (13) не требует вычисления траекторий лучей в градиентной среде и определяется степенным рядом 2-й степени по смещению источника δ_Х;

– на основе полученной формулы выведены приближенные уравнения фокальных кривых;

– показана возможность использования приближенной формулы для вычисления аберраций в градиентных цилиндрических линзах и оптимизации их параметров.