Радиотехника и электроника, 2020, T. 65, № 9, стр. 919-926
Инжекционная неравновесная спиновая поляризация в магнитном переходе с учетом спиновой подвижности электронов
Е. А. Вилков a, *, С. А. Никитов a, О. А. Бышевский-Конопко a, А. Р. Сафин b, Л. А. Фомин c, С. Г. Чигарев a
a Институт радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация
b Национальный исследовательский университет “МЭИ”
111250 Москва, ул. Красноказарменная, 14, Российская Федерация
c Институт проблем технологии микроэлектроники и особо чистых материалов РАН
142432 Черноголовка, Московской обл., ул. Институтская, 6, Российская Федерация
* E-mail: e-vilkov@yandex.ru
Поступила в редакцию 29.10.2019
После доработки 29.10.2019
Принята к публикации 25.11.2019
Аннотация
С учетом спиновой подвижности электронов рассмотрено численное решение уравнения для неравновесной спиновой поляризации на границе магнитного контакта с током, образованного двумя ферромагнетиками. Рассчитаны частоты спин-инжекционного излучения. Показано, что при определенной плотности тока, превышающей пороговое значение, эти частоты лежат в терагерцовом диапазоне частот. При этом установлено, что для одного и того же терагерцового диапазона частот даже при небольших значениях разности подвижности электронов со спином вверх и вниз плотность тока может быть на два порядка меньше, чем плотность тока при одинаковой подвижности.
ВВЕДЕНИЕ
В настоящее время магнитные нанопереходы между двумя магнетиками с протекающим по ним спин-поляризованным током являются одними из интересных объектов исследований [1–11], что cвязано с перспективами их применений в терагерцовой спинтронике [12], в трехмерных наномагнитных устройствах [13], в запоминающих устройствах и сенсорах [14]. Спиновая инжекция током через наноконтакт двух магнетиков может приводить к значительному неравновесному накоплению спина в области непосредственно вблизи контакта. В частности, может возникать инверсная заселенность спиновых подзон ферромагнетика, в который инжектируются неравновесные по спину горячие электроны. При этом возможны излучательные спин-флип-переходы электронов проводимости, которые стимулированы опосредованно через s‒d-обменное взаимодействие с электромагнитной волной [15, 16]. Частота излучения при таких переходах определяется энергией эффективного обменного расщепления спиновых подзон и лежит в терагерцовом диапазоне [15], который весьма привлекателен для практического применения.
Сравнительно недавно нами [15] было получено уравнение для неравновесной спиновой поляризации на границе магнитного контакта с током, образованного двумя ферромагнетиками, и оценена частота спин-флип-перехода между неравновесными квазиуровнями Ферми с учетом непрямых электронных переходов. Показано, что при определенной плотности тока, превышающей пороговое значение, эта частота лежит в терагерцовом диапазоне частот. Однако в этой и других работах [17–19] всегда полагалось, что подвижности электронов с противоположным направлением спина равные, хотя известно, что в ферромагнетиках, как правило, подвижности отличаются друг от друга [3, 4]. Это приближение, возможно, является причиной несоответствия теоретических и экспериментальных значений порогового тока при регистрации терагерцового излучения [15].
Цель данной работы – проверить это предположение. Для этого было получено и решено численно уравнение для неравновесной спиновой поляризации в магнитном переходе с учетом разной подвижности электронов проводимости. Решение данной задачи важно как с теоретической, так и с практической точек зрения, поскольку оно позволяет более корректно описывать спиновую инжекцию в магнитных металлических переходах и определять частоту спин-инжекционного излучения с учетом непрямых межподзонных излучательных переходов электронов.
2. РЕШЕНИЕ УРАВНЕНИЯ ДЛЯ НЕРАВНОВЕСНОЙ СПИНОВОЙ ПОЛЯРИЗАЦИИ
Рассмотрим случай, когда электрический ток протекает через границу однородных ферромагнетиков, векторы намагниченности которых (они же соответствуют осям квантования в разных средах) образуют некоторый угол рассогласования $\varphi $. Будем считать, что между слоями ферромагнетиков нанесен сверхтонкий буферный слой (диэлектрик или немагнитный металл), устраняющий обменную связь между ними. Введем обозначения: ${{P}_{1}}$ – равновесная спиновая поляризация инжектора (ферромагнетик, из которого инжектируются спин-поляризованные электроны), ${{P}_{2}}$ – равновесная спиновая поляризация рабочей области (ферромагнетик, в который инжектируются спин-поляризованные электроны). Пусть электрический ток протекает вдоль оси х через границу ферромагнетиков. Для упрощения будем считать, что плотность электрического тока не меняется ($j = const$) как по поперечному сечению магнитного контакта, так и вдоль оси х, нормальной к его плоскости. Предположим также, что в обоих спиновых подзонах носители тока рабочей области имеют разные подвижности и коэффициенты диффузии:
где знаки “+” и “–” означают, что направление спина электрона проводимости сонаправленно или противоположно направлению намагниченности рабочей области соответственно.Из уравнения движения магнитного момента ${\vec {\mu }}$ неравновесных электронов [20] в стационарных условиях (${{\partial {\vec {\mu }}} \mathord{\left/ {\vphantom {{\partial {\vec {\mu }}} {\partial {\kern 1pt} t}}} \right. \kern-0em} {\partial {\kern 1pt} t}} = 0$) можно получить следующее уравнение [21]:
где $\tau $ – время продольной спиновой релаксации, ${{\mu }_{{\text{B}}}}$ – магнетон Бора, – плотность спинового потока ($e$ – заряд электрона, $n$ – концентрация электронов проводимости, ${{j}_{ \pm }}$ – парциальные плотности электрического (зарядового) тока).При наличии электрического поля E(x) и градиентов парциальных концентраций возникают парциальные плотности электрического (зарядового) тока, определяемые соотношением
(4)
${{j}_{ \pm }} = e{{\mu }_{ \pm }}{{n}_{ \pm }}(x)E(x) - e{{D}_{ \pm }}\frac{{d{{n}_{ \pm }}}}{{dx}},$Полная плотность тока $j = {{j}_{ + }}(x) + {{j}_{ - }}(x)$ в стационарном состоянии не зависит от $x$. Выражая $E(x)$ через $j$, получим с учетом (1), (2) для плотности спинового потока
(5)
${{J}_{s}}(x) = ({{{{\mu }_{{\text{B}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{\text{B}}}}} {en}}} \right. \kern-0em} {en}})\left\{ {Q\left( P \right)j - enD\left( P \right)\nabla P} \right\},$(6)
$\begin{gathered} Q\left( P \right) = \frac{{{{\mu }_{ + }} - {{\mu }_{--}} + \left( {{{\mu }_{ + }} + {{\mu }_{ - }}} \right)P}}{{{{\mu }_{ + }} + {{\mu }_{ - }} + \left( {{{\mu }_{ + }} - {{\mu }_{ - }}} \right)P}}, \\ D\left( P \right) = \frac{{{{\mu }_{ + }}{{D}_{ - }} + {{\mu }_{ - }}{{D}_{ + }} + \left( {{{\mu }_{ + }}{{D}_{ - }} - {{\mu }_{ - }}{{D}_{ + }}} \right)P}}{{{{\mu }_{ + }} + {{\mu }_{ - }} + \left( {{{\mu }_{ + }} - {{\mu }_{ - }}} \right)P}}. \\ \end{gathered} $Подстановка (5), (6) в (2) с учетом условия сохранения электрического заряда $\nabla \vec {j} = 0$ дает уравнение, описывающее неравновесную спиновую поляризацию в магнитном переходе:
(7)
$\begin{gathered} - \frac{{{{d}^{2}}P}}{{d{{x}^{2}}}}\left\{ {({{\mu }_{ + }}{{D}_{ - }} + {{\mu }_{ - }}{{D}_{ + }})({{\mu }_{ + }} + {{\mu }_{ - }})} \right. + \\ \left. { + \,\,2P(\mu _{ + }^{2}{{D}_{ - }} - \mu _{ - }^{2}{{D}_{ + }}) + ({{\mu }_{ + }} - {{\mu }_{ - }})({{\mu }_{ + }}{{D}_{ - }} - {{\mu }_{ - }}{{D}_{ + }}){{P}^{2}}} \right\} + \\ + \,\,\frac{{dP}}{{dx}}\frac{j}{{en}}2({{\mu }_{ + }} + {{\mu }_{ - }}) + 2{{\mu }_{ + }}{{\mu }_{ - }}({{D}_{ + }} - {{D}_{ - }}){{\left( {\frac{{dP}}{{dx}}} \right)}^{2}} + \\ + \,\,{{({{\mu }_{ + }} + {{\mu }_{ - }})}^{2}}\frac{{(P - {{P}_{2}})}}{\tau } + 2(\mu _{ + }^{2} - \mu _{ - }^{2}) \times \\ \times \,\,\frac{{({{P}^{2}} - {{P}_{2}}P)}}{\tau } + {{(\mu _{ + }^{{}} - \mu _{ - }^{{}})}^{2}}\frac{{({{P}^{3}} - {{P}_{2}}{{P}^{2}})}}{\tau } = 0, \\ \end{gathered} $Проводимость и коэффициент диффузии свободных электронов в металле связаны соотношением ${{\sigma }_{ \pm }} = {{e}^{2}}{{D}_{ \pm }}{{g}_{ \pm }}$ [22], согласно которому коэффициент диффузии запишем в виде
(8)
${{D}_{ \pm }} = {{{{\sigma }_{ \pm }}} \mathord{\left/ {\vphantom {{{{\sigma }_{ \pm }}} {{{e}^{2}}{{g}_{ \pm }}}}} \right. \kern-0em} {{{e}^{2}}{{g}_{ \pm }}}},$(9)
${{D}_{ \pm }} = {{{{n}_{ \pm }}{{\mu }_{ \pm }}} \mathord{\left/ {\vphantom {{{{n}_{ \pm }}{{\mu }_{ \pm }}} {e{{g}_{ \pm }}}}} \right. \kern-0em} {e{{g}_{ \pm }}}}.$В дальнейших преобразованиях примем, что разница в коэффициентах диффузии для электронов с разным направлением спинов определяется только разностью подвижностей, т.е. мы принимаем следующее равенство:
(10)
${{{{n}_{ + }}} \mathord{\left/ {\vphantom {{{{n}_{ + }}} {{{g}_{ + }}}}} \right. \kern-0em} {{{g}_{ + }}}} = {{{{n}_{ - }}} \mathord{\left/ {\vphantom {{{{n}_{ - }}} {{{g}_{ - }}}}} \right. \kern-0em} {{{g}_{ - }}}}.$Равенство (10) вполне допустимо, учитывая, что плотность состояний на уровне Ферми определяется по формулам
(11)
$\begin{gathered} {{g}_{ + }}(E) = \frac{{\sqrt 2 {{m}^{{3/2}}}}}{{{{\pi }^{2}}{{\hbar }^{3}}}}V\sqrt {{{E}_{f}}} , \\ {{g}_{ - }}(E) = \frac{{\sqrt 2 {{m}^{{3/2}}}}}{{{{\pi }^{2}}{{\hbar }^{3}}}}V\sqrt {{{E}_{f}} + 2{{I}_{2}}} . \\ \end{gathered} $Поскольку энергия Ферми много больше, чем обменная энергия ${{E}_{f}} \gg 2{{I}_{2}}$, то из (11) следует, что ${{g}_{ - }}(E) \approx {{g}_{ + }}(E)$. Соответственно, число электронов с разным направлением спина, участвующих в процессах переноса (вблизи уровня Ферми) и определяемых через (11) как ${{n}_{ + }} \approx g({{\varepsilon }_{{F + }}})\Delta \varepsilon ,$ ${{n}_{ - }} \approx g({{\varepsilon }_{{F - }}} + 2{{I}_{2}})\Delta \varepsilon ,$ приблизительно равно (различно, но не существенно). Вводим обозначение b – константы отношения подвижностей b = $ = {{{{\mu }_{ - }}} \mathord{\left/ {\vphantom {{{{\mu }_{ - }}} {{{\mu }_{ + }}}}} \right. \kern-0em} {{{\mu }_{ + }}}}.$ Тогда исходное уравнение (7) можно переписать в виде
(12)
$\begin{gathered} \frac{{{{d}^{2}}P}}{{d{{x}^{2}}}}\left\{ {b(1 + b) + ( - b + 1)P)} \right\} - \frac{{dP}}{{dx}}\frac{j}{{{{j}_{D}}l}}b - \\ - \,\,{{\left( {\frac{{dP}}{{dx}}} \right)}^{2}}b(1 - {{b}^{2}}) - \frac{{(P - {{P}_{2}})}}{{2{{l}^{2}}}}{{(1 + b)}^{2}} - \\ - \,\,(1 - {{b}^{2}})\frac{{({{P}^{2}} - {{P}_{2}}P)}}{{{{l}^{2}}}} - {{(1 - b)}^{2}}\frac{{({{P}^{3}} - {{P}_{2}}{{P}^{2}})}}{{{{l}^{2}}}} = 0, \\ \end{gathered} $Предположим теперь, что в обоих спиновых подзонах носители тока имеют одинаковые подвижности и коэффициенты диффузии, μ– = $ = {{\mu }_{ + }} = \mu $, ${{D}_{ - }} = {{D}_{ + }} = D$, т.е. b = 1. В этом случае уравнение (12), описывающее неравновесную спиновую поляризацию, значительно упрощается и имеет вид [15]
(13)
$\frac{{{{d}^{2}}P}}{{d{{x}^{2}}}} - \frac{j}{{j_{D}^{*}l}}\frac{{dP}}{{dx}} - \frac{{P - {{P}_{2}}}}{{{{l}^{2}}}} = 0.$Из условия непрерывности спинового потока (6) на границе между двумя ферромагнетиками [15] запишем граничное условие:
(14)
$\begin{gathered} {{J}_{s}}\left( 0 \right) = \frac{{{{\mu }_{B}}}}{{en}}\left\{ {{{{\left. {jQ\left( P \right)} \right|}}_{{x = 0}}} - e{{{\left. {nD\left( P \right)\nabla P} \right|}}_{{x = 0}}}} \right\} = \\ = \frac{{{{\mu }_{B}}}}{{en}}{{P}_{1}}j\cos \varphi . \\ \end{gathered} $Равенство (14) записано для случая, когда спиновая поляризация инжектора остается неизменной величиной или возмущается крайне слабо. Как показано в работе [15], данное условие выполняется при подборе соответствующих материалов. При этом, влиянием отраженного от границы потока электронов на спиновую поляризацию прошедших в рабочую область электронов можно пренебречь. Из формулы (14) с учетом формул (8)–(11) получим выражение
(15)
$\begin{gathered} P(0) = \\ = \frac{{(b - 1) + {{P}_{1}}(1 + b)\cos \varphi + 2bl({{{{j}_{D}}} \mathord{\left/ {\vphantom {{{{j}_{D}}} j}} \right. \kern-0em} j})({{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial x}}} \right. \kern-0em} {\partial x}}{{{\left. ) \right|}}_{{x = 0}}}}}{{(1 + b) + (b - 1){{P}_{1}}\cos \varphi }}. \\ \end{gathered} $Для получения в явном виде выражения для $P(0)$ примем следующее приближение:
(16)
$({{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial x}}} \right. \kern-0em} {\partial x}}{{\left. ) \right|}_{{x = 0,\,b \ne 1}}} \approx ({{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial x}}} \right. \kern-0em} {\partial x}}{{\left. ) \right|}_{{x = 0,\,b = 1}}}.$Такое допущение в первом приближении позволяет оценить граничные значения спиновой поляризации в зависимости от соотношения подвижностей. Таким образом, учитывая, что [15]
получим первое граничное условие в виде
(17)
$\begin{gathered} P(0) = \frac{{(b - 1) + {{P}_{1}}(1 + b)\cos \varphi + 2bld}}{{(1 + b) + (b - 1){{P}_{1}}\cos \varphi }}, \\ d = \frac{{{{P}_{1}}\cos \varphi - {{P}_{2}}}}{{({j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}}) - {{\lambda }_{1}}l}}{{\lambda }_{1}}. \\ \end{gathered} $Второе граничное условие очевидно:
Кроме того, при расчете мы предполагали, что в области магнитного перехода (определяется длиной спиновой релаксации) подвижность электронов с направлением спина вдоль намагниченности выше, чем подвижность электронов с противоположным направлением спина. Это предположение основано на хорошо известном явлении – магнитосопротивлении [4], когда электроны с направлением спина против направления намагниченности ферромагнетика испытывают дополнительное сопротивление их движению через контакт магнитного перехода, т.е. их подвижность значительно меньше. Таким образом, число неравновесных электронов в рабочей области около контакта слоев магнитного перехода должно расти за счет неравенства подвижностей. Это подтверждается результатами численного расчета уравнения (12), показанных на рис. 1 и 2.
Рис. 1.
Пространственное распределение спиновой поляризации (отнесенной к равновесному значению) вблизи границы двух ферромагнетиков, угол между направлениями намагниченностей 60°, P1/P2= 2 (а) и 5 (б), j/jD = 0.1 при различных значениях отношения подвижностей: $b$ = 1 (1), 0.9 (2), 0.8 (3), 0.7 (4).
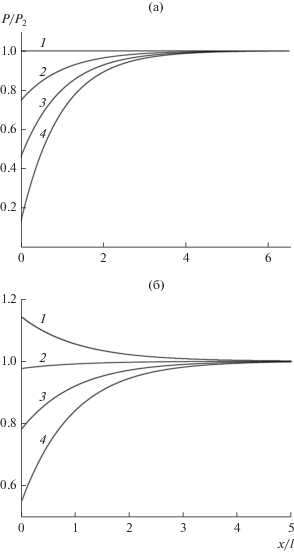
Рис. 2.
Пространственное распределение спиновой поляризации (отнесенной к равновесному значению) вблизи границы двух ферромагнетиков, угол между направлениями намагниченностей 120°, P1/P2= 5 и j/jD = 0.1 (а) и P1/P2= 2 и j/jD = 5 (б) при различных значениях отношения подвижностей: $b$ = 1 (1), 0.9 (2), 0.8 (3), 0.7 (4).
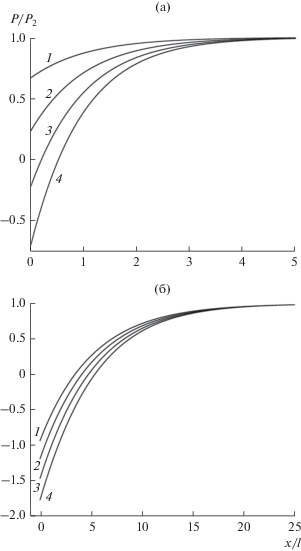
Из рис. 1 и 2 видно, что при различных углах $\varphi $ между намагниченностями слоев и отношений спиновой поляризации инжектора и рабочей области P1/P2 неравновесное значение спиновой поляризации Р вблизи границы $x = 0$ тем больше, чем больше значение $b$. Кроме того, при малых значениях плотностей токов, определяемых через j/jD (см. рис. 1, 2а) кривые быстрее выходят на полку асимптоты (примерно $x \approx 5\,l$), соответствующей равновесному значению спиновой поляризации, чем при большем отношении плотностей тока (рис. 2б) рабочей области. При больших отношениях j/jD (см. рис. 2б) выход на полку асимптоты происходит на расстояниях на порядок больше $x \approx 25\,l$.
Также согласно рис. 1, 2, для того чтобы возникла инверсная заселенность спиновых подзон, т.е. неравновесная спиновая поляризация была отрицательной $\Delta P < 0$, необходимо согласно формуле (14) наличие неравенства ${{P}_{1}}\cos \varphi < {{P}_{2}}$, что выполняется всегда при $\varphi > {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Но для $\varphi < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ инверсия возможна только при определенном соотношении ${{P}_{1}}$ и ${{P}_{2}}$. Неравенство $\Delta P > 0$ выполняется при условии, что ${{P}_{1}}\cos \varphi > {{P}_{2}}$. Согласно данным, приведенным на рис. 1а (кривая 1) и рис. 1б (кривая 2), можно подобрать два различных ферромагнетика с разной равновесной спиновой поляризацией, когда при протекании через них тока равновесная спиновая поляризация в рабочей области не нарушается и выполняется соотношение ${{{{P}_{{}}}} \mathord{\left/ {\vphantom {{{{P}_{{}}}} {{{P}_{2}}}}} \right. \kern-0em} {{{P}_{2}}}}$ = 1 для любого $x$. Для выполнения этого условия, согласно формуле (14), необходимо равенство нулю выражения ${{P}_{1}}\,\,\cos \varphi - {{P}_{2}} = 0\;$ и значения $b$, равного единице. Очевидно, что в этом случае неравновесные электроны заселяют энергетические подзоны электронов с разным направлением спина в рабочем слое в такой пропорции, что не нарушают равновесную спиновую поляризацию P2. Однако при тех же условиях, но с учетом разности подвижностей электронов происходит нарушение равновесной спиновой поляризации P2 тем больше, чем больше значение $b$ (см. рис. 1, кривые 2–4). При достаточно больших значениях $b$ и углах $\varphi > {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (см. рис. 2б) можно добиться инверсной заселенности спиновых подзон ${{{{P}_{{}}}} \mathord{\left/ {\vphantom {{{{P}_{{}}}} {{{P}_{2}}}}} \right. \kern-0em} {{{P}_{2}}}}$ < 0 со спиновой поляризацией больше, чем равновесная спиновая поляризация рабочей области (см. рис. 2б, область 0 < ${x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}$ < ~2) .
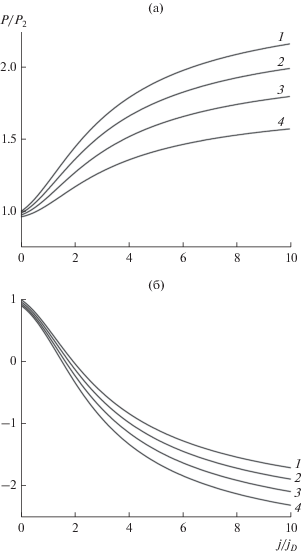
На рис. 3 показана зависимость спиновой поляризации (при $x \approx 0.2\,l$), отнесенной к ее равновесному значению${P \mathord{\left/ {\vphantom {P {{{P}_{2}}}}} \right. \kern-0em} {{{P}_{2}}}}$, от ${j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}}$ при различных углах $\varphi $ и отношениях подвижностей $b$ . Видно, что спиновая поляризация при малых токах близка к линейной зависимости от отношения ${j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}}$, но при увеличении плотности тока она стремится к предельному значению и все зависимости выходят на горизонтальные асимптоты. Для $b = 1$ максимальное значение неравновесной поляризации определяется выражением $P = {{P}_{1}}\,\,\cos \varphi $ [15]. Как и в случае пространственной зависимости (см. рис. 1, 2), при $\varphi > {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ для большей разности подвижностей электронов ($b < 1$) бóльшие по модулю значения неравновесной спиновой поляризации достигаются при меньших значениях плотности тока. При $\varphi < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ увеличение разностей подвижностей, наоборот, уменьшает неравновесное значение поляризации при одинаковом значении плотности тока. Это связано с тем, что при одинаковом направлении продольных компонент намагниченностей инжектора и рабочей области увеличение числа инжектированных электронов со спином по направлению намагниченности компенсируется более быстрым их уходом из рабочей области за счет их большей подвижности.
Рис. 3.
Спиновая поляризация на границе двух ферромагнетиков (отнесенной к равновесному значению) в зависимости от (безразмерной) плотности тока ${j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}}$ при $\varphi = 60^\circ $ (а) и 120° (б) для отношения ${{{{{{P}_{1}}} \mathord{\left/ {\vphantom {{{{P}_{1}}} P}} \right. \kern-0em} P}}_{2}}$ = 5 при различных значениях отношения подвижности: $b$ = 1 (1), 0.9 (2), 0.8 (3), 0.7 (4).
3. ЧАСТОТЫ СПИН-ИНЖЕКЦИОННОГО ИЗЛУЧЕНИЯ В МАГНИТНЫХ КОНТАКТНЫХ ПЕРЕХОДАХ
Как уже было показано ранее, инжекция спин-поляризованных электронов током приводит к нарушению равновесного спинового состояния в одном из слоев магнитного контакта. Следствием этого может быть как изменение магнитного состояния рабочей области, пронизываемой спиновым потоком (например, изменение направления ее намагниченности [4]), так и создание неравновесных по спину условий. В результате последнего одним из каналов релаксации неравновесной системы электронов могут быть их излучательные (прямые и непрямые) переходы между спиновыми подзонами (с переворотом спина) из занятых состояний в свободные, которые определяются неравновесными квазиуровнями Ферми. Предположим теперь, что в результате инжекции спинов в рабочую область магнитного контакта не происходит перемагничивание рабочей области и основным процессом спиновой релаксации являются излучательные электронные переходы.
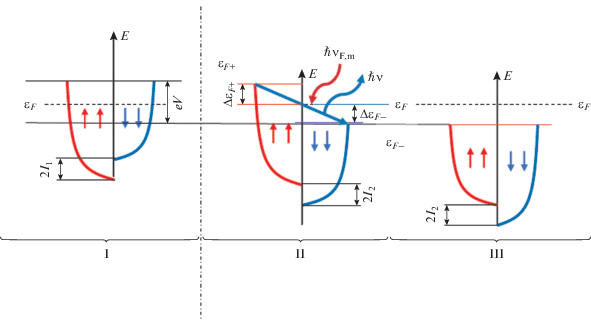
Неравновесные электроны имеют соответствующие им неравновесные квазиуровни Ферми ${{\varepsilon }_{{F + }}}$ и ${{\varepsilon }_{{F - }}}$, отсчитываемые от дна нижней спиновой подзоны (рис. 4). В неравновесных условиях возможны электронные переходы из занятых состояний, расположенных ниже квазиуровня Ферми ${{\varepsilon }_{{F + }}}$ для минорной спиновой подзоны, в свободные электронные состояния, расположенные выше квазиуровня Ферми ${{\varepsilon }_{{F - }}}$ для мажорной спиновой подзоны (см. рис. 4). Если квазиуровень Ферми ${{\varepsilon }_{{F + }}}$ смещен выше относительно равновесного значения уровня Ферми рабочей области на величину $\Delta {{\varepsilon }_{{F + }}} = {{\varepsilon }_{{F + }}} - ({{\varepsilon }_{{F0 + }}} - {{eV} \mathord{\left/ {\vphantom {{eV} 2}} \right. \kern-0em} 2})$, а квазиуровень Ферми ${{\varepsilon }_{{F - }}}$ – ниже на величину ΔεF– = (εF0– –eV/2) – ${{\varepsilon }_{{F - }}}$, то максимальную частоту излучения можно также представить в виде суммы величин $\Delta {{\varepsilon }_{{F + }}}$ и $\Delta {{\varepsilon }_{{F - }}}$, деленной на постоянную Планка $\hbar $ [15]:
(19)
$\begin{gathered} \nu \equiv \frac{{\Delta {{\varepsilon }_{{F + }}} + \Delta {{\varepsilon }_{{F - }}}}}{{2\pi \hbar }} = \\ = \frac{{\left| {{{\varepsilon }_{{F + }}} - {{\varepsilon }_{{F0 + }}}} \right| + \left| {{{\varepsilon }_{{F - }}} - {{\varepsilon }_{{F0 - }}}} \right|}}{{2\pi \hbar }}. \\ \end{gathered} $Рис. 4.
Схема энергетических электронных зон и квазиуровней Ферми: I – в первом ферромагнетике, II – для неравновесных электронов во втором ферромагнетике, III – для равновесных электронов во втором ферромагнетике вне области инжекции.
Мы ввели здесь знаки модуля, чтобы эта формула соответствовала любому знаку ΔP.
Значения квазиуровней подзон зависят от неравновесной спиновой поляризации ΔР и энергетического обменного расщепления I2:
Здесь было использовано предположение, что на один электрон приходится фазовый объем ${{(2\pi \hbar )}^{3}}$ и количество электронов с одним направлением спина ${{n}_{{ - , + }}} = {{n(1 \pm P)} \mathord{\left/ {\vphantom {{n(1 \pm P)} 2}} \right. \kern-0em} 2}$ равно объему сферы с радиусом, равным импульсу Ферми деленному на ${{(2\pi \hbar )}^{3}}$. Далее удобнее выразить изменение квазиуровней через равновесное значение ${{P}_{2}}$ и неравновесную добавку $\Delta P$ следующим образом:
(20)
$\Delta {{\varepsilon }_{{F + }}} = \frac{{{{\hbar }^{2}}}}{{2m}}{{\left( {3{{\pi }^{2}}n} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\left| {{{{\left( {\frac{{1 - {{P}_{2}} - \Delta P}}{2}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} - {{{\left( {\frac{{1 - {{P}_{2}}}}{2}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right|,$(21)
$\begin{gathered} \Delta {{\varepsilon }_{{F - }}} = \frac{{{{\hbar }^{2}}}}{{2m}}{{\left( {3{{\pi }^{2}}n} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \times \\ \times \,\,\left| {{{{\left( {\frac{{1 + {{P}_{2}}}}{2}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} - {{{\left( {\frac{{1 + {{P}_{2}} + \Delta P}}{2}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right|, \\ \end{gathered} $где $m$ – масса электрона, $n$ – концентрация электронов проводимости в металле. В формулах (19)–(21) знак изменений квазиуровней зависит от знака неравновесной спиновой добавки и может быть как положительным, так и отрицательным.
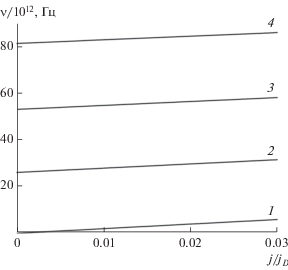
На рис. 5 представлена зависимость частоты излучения $\nu $ от тока, рассчитанная по формулам (19)–(21) для нескольких значений $b$. Видно, что учет разности проводимости и коэффициентов диффузии электронов в разных спиновых подзонах понижает теоретическое значение плотности тока для нижней и верхней границ терагерцового излучения на порядок для $b = 0.9$ и на два порядка для $b = 0.7$. Это позволяет объяснить существенное различие диапазонов (примерно на два порядка) пусковых плотностей тока, соответствующих терагерцовому диапазону между теоретической оценкой [15] и измерениями в эксперименте [19]. Согласно рис. 5 диапазону частот спин-инжекционного излучения 5…40 ТГц соответствуют плотности тока, примерно на три-четыре порядка меньшие (при $b = 0.85 - 0.95$) чем плотность тока диффузии. Исходя из оценки тока диффузии ${{j}_{D}}\sim {{10}^{{10}}}{{...10}^{{11}}}$ А/см2 получаем плотности тока в магнитном переходе ${{j}_{{}}}\sim {{10}^{6}}{{...10}^{7}}$ А/см2, что вполне достижимо экспериментально без теплового пробоя магнитного контакта. Более низкие частоты соответствуют меньшим плотностям тока. Однако при этом необходимо учитывать затухание электромагнитных волн, возникающее главным образом благодаря поглощению этих волны в слоях магнитного контакта. Как показано в работе [16], для того чтобы превысить уровень мощности, соответствующий потерям в слоях магнитного контакта и уровню тепловых шумов, необходимо превысить некоторое пусковое значение плотности тока, обеспечивающее необходимый уровень мощности излучения. Это может служить объяснением, почему в эксперименте спин-инжекционное излучение появляется, лишь с некоторого порогового значения плотности тока.
Рис. 5.
Зависимость частоты спин-инжекционного излучения от (безразмерной) плотности тока ${j \mathord{\left/ {\vphantom {j {{{j}_{D}}}}} \right. \kern-0em} {{{j}_{D}}}}$ при $\varphi = 120^\circ $ и для отношения ${{{{{{P}_{1}}} \mathord{\left/ {\vphantom {{{{P}_{1}}} P}} \right. \kern-0em} P}}_{2}}$ = 5 при различных значениях отношения подвижностей: $b$ = 1 (1), 0.9 (2), 0.8 (3), 0.7 (4).
ЗАКЛЮЧЕНИЕ
С учетом спиновой зависимости подвижности электронов рассмотрено численное решение уравнения для неравновесной спиновой поляризации на границе магнитного контакта с током, образованного двумя ферромагнетиками. Показано, что при различных углах между намагниченностями и отношениях спиновой поляризации инжектора и рабочей области неравновесное значение спиновой поляризации вблизи границы $x = 0$ тем больше, чем больше разность подвижностей электронов с противоположным направлением спина. Расчет частот спин-инжекционного излучения показал, что при определенной плотности тока, превышающей пороговое значения, эта частота лежит в терагерцовом диапазоне частот. При этом установлено, что для одного и того же диапазона частот даже при небольших значениях разности подвижности электронов со спином вверх и вниз плотность тока может быть на два порядка меньше, чем плотность тока при одинаковой подвижности. Это позволяет объяснить существенную разность, примерно на два порядка, между теоретической оценкой [15] и измерениями в эксперименте [19] плотностей тока, соответствующих терагерцовому диапазону частот.
Список литературы
Fert A., George J.-M., Jaffrès H. et al. // Europhys. News. 2003. V. 34. P. 227.
Gregg J.F., Petej I., Jouguelet E., Dennis C. // J. Phys. D: Appl. Phys. 2002. V. 35. P. R121.
Zutic I., Fabian J., Das Sarma S. // Rev. Mod. Phys. 2004. V. 76. P. 323.
Concepts in Spin Electronics / Ed. S. Maekawa. N.-Y.: Oxford Univ. Press, 2006.
Fert A. // Rev. Mod. Phys. 2008. V. 80. P. 1517.
Baltz V. , Manchon A. , Tsoi M. et al. // Rev. Mod. Phys. 2018. V. 90. № 1. P. 015005.
Grunberg P. A. // Rev. Mod. Phys. 2008. V. 80. P. 1531.
Гуляев Ю.В., Зильберман П.Е., Панас А.И., Эпштейн Э.М. // Успехи физ. наук. 2009. Т. 179. С. 359.
Звездин А.К., Звездин К.А., Хвальковский А.В. // Успехи физ. наук. 2008. Т. 178. С. 436.
Yu G., Upadhyaya P., Fan Y. et al. // Nature Nanotechnology. 2014. V. 9. P. 548.
Lau Y.-C., Betto D., Rode K. et al. // Nature Nanotechnology. 2016. V. 11. P. 758.
Walowski J., Munzenberg M. // J. Appl. Phys. 2016. V. 120. P. 140901.
Fernandez-Pacheco A., Streubel R., Fruchart O. et al. // Nature Commun. 2017. V. 8. P. 15756.
Dhillon S.S., Vitiell M.S., Linfield E.H., et al. // J. Phys. D: Appl. Phys. 2017 V. 50. P. 363001.
Вилков Е.А., Михайлов Г.М., Чигарев С.Г. и др. // РЭ. 2016. Т. 61. № 9. С. 844.
Kadigrobov A., Ivanov Z., Claeson T. et al. // Europhys. Lett. 2004. V. 67. P. 948.
Гуляев Ю.В., Зильберман П.Е., Эллиотт Р.Дж. // РЭ. 2003. Т. 48. № 9. С. 1030.
Гуляев Ю.В., Зильберман П.Е., Крикунов А.И. и др. // Письма в ЖЭТФ. 2007. Т. 85. С. 192.
Гуляев Ю.В., Зильберман П.Е., Маликов И.В. и др. // Письма в ЖЭТФ. 2011. Т. 93. С. 289.
Вилков Е.А., Михайлов Г.М., Никитов С.А. и др. // ЖЭТФ. 2018. Т. 154. С. 1108.
Вилков Е.А., Никитов С.А., Логунов М.В. и др. // РЭ. 2019. Т. 64. № 12. С. 105.
Абрикосов А.А. Основы теории металлов. М.: Наука, 1988.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


