Радиотехника и электроника, 2020, T. 65, № 9, стр. 864-871

Применение метода продолженных граничных условий к решению задачи дифракции волн на магнитодиэлектрических рассеивателях сложной геометрии

Д. В. Крысанов^a, *, А. Г. Кюркчан^a, b, c, С. А. Маненков^a

^a Московский технический университет связи и информатики
111024 Москва, ул. Авиамоторная, 8а, Российская Федерация

^b Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация

^c Центральный научно-исследовательский институт связи
111141 Москва, 1-й проезд Перова поля, Российская Федерация

^* E-mail: dimok1993@mail.ru

Поступила в редакцию 31.10.2019
После доработки 31.10.2019
Принята к публикации 27.11.2019

DOI: 10.31857/S003384942008015X

Полный текст (PDF)

Аннотация

На основе метода продолженных граничных условий предложена методика, позволяющая моделировать характеристики рассеяния, в том числе усредненные по углам ориентации, для тел произвольной геометрии. Рассмотрена двумерная задача дифракции плоской волны на диэлектрических телах со сложной геометрией сечения, в частности – на фракталоподобных телах. Проведено сравнение численных алгоритмов решения задачи дифракции на основе систем интегральных уравнений 1-го и 2-го рода. Корректность метода подтверждена при помощи проверки выполнения оптической теоремы для различных тел и путем сравнения с результатами расчетов, полученных модифицированным методом дискретных источников.

ВВЕДЕНИЕ

Задача дифракции волн на диэлектрическом теле сложной геометрии является весьма актуальной и остается сравнительно мало исследованной ввиду сложности ее решения. Результаты моделирования характеристик рассеяния волн диэлектрическими телами представляют большой интерес в таких, например, областях, как оптика неоднородных сред, лазерная дефектоскопия, проектирование поглощающих покрытий и др. [1–3]. Несмотря на то что на данный момент разработан ряд аналитических и численных методов решения этих задач (наиболее распространенными из которых являются метод Т-матриц [4] и метод дискретных источников [5]), потребности в моделировании дифракционных процессов возрастают довольно быстро, в связи с чем вопрос разработки более универсальных методов решения задач дифракции все еще остается актуальным. Широкая популярность метода Т-матриц объясняется во многом тем, что с использованием этого метода можно сравнительно легко выполнять такую важную, например в астрофизике, процедуру, как усреднение характеристик рассеяния тела по углам его ориентации относительно падающей плоской волны. Однако традиционный (классический) вариант метода Т-матриц [4], как и некоторые его недавно разработанные модифицированные варианты [5, 6], применимы к решению задач дифракции лишь на рассеивателях с аналитической границей.

В работах [7, 8] было предложено обобщение метода Т-матриц на основе метода продолженных граничных условий (МПГУ) для решения задачи дифракции с условием Дирихле на границе в двумерном и трехмерном случаях. Двумерный случай был также рассмотрен для импедансного краевого условия [9]. Идея МПГУ заключается в переносе граничного условия с поверхности $S$ рассеивателя на некоторую вспомогательную поверхность ${{S}_{\delta }}$, которая располагается вне рассеивателя на некотором достаточно малом расстоянии $\delta $ от его границы. К главным достоинствам МПГУ можно отнести отсутствие ограничений на геометрию рассеивателя (в том числе он применим и для рассеивателей, имеющих изломы границы, и для тонких экранов). Кроме того, МПГУ предлагает единый подход к решению краевых задач, не зависящий от их типа, размерности, геометрии поверхности рассеивателя и характера рассеиваемого поля. Отметим также, что в рамках МПГУ задача дифракции может быть сведена к решению системы интегральных уравнений 1-го или 2-го рода, что невозможно, например, при решении задачи методом поверхностных интегральных уравнений.

В данной статье предлагается обобщение описанной выше методики для решения двумерной задачи дифракции электромагнитных волн на диэлектрическом теле. Рассмотрены примеры моделирования характеристик рассеяния волн телами с поперечным сечением сложной геометрии и фракталоподобными телами. Рассчитаны такие характеристики, как диаграмма рассеяния и усредненная по углам ориентации диаграмма.

1. ВЫВОД ОСНОВНЫХ СООТНОШЕНИЙ

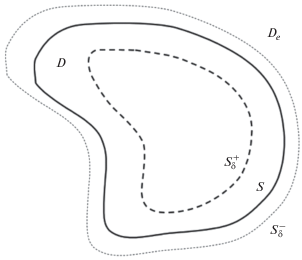
Пусть на бесконечно длинный магнитодиэлектрический цилиндр с образующей, параллельной оси $Oz$, и с направляющей $S$ падает первичное электромагнитное поле ${{\vec {E}}^{0}},{{\vec {H}}^{0}}.$ Геометрия задачи изображена на рис. 1. Рассмотрим случай Е-поляризации, когда вектор напряженности электрического поля $\vec {E}$ имеет только одну составляющую${{E}_{z}}$ (далее – ${{U}_{ - }}$ или ${{U}_{ + }}$), параллельную образующей цилиндрического тела. Тогда на границе рассеивателя будут иметь место следующие условия сопряжения:

(1)

${{\left. {{{U}_{ + }}} \right|}_{S}} = {{\left. {{{U}_{ - }}} \right|}_{S}},\,\,\,\,{{\left. {\frac{{\partial {{U}_{ + }}}}{{\partial n}}} \right|}_{S}} = {{\left. {\kappa \frac{{\partial {{U}_{ - }}}}{{\partial n}}} \right|}_{S}},$

Рис. 1.

Геометрия задачи.

где ${{U}_{ + }}$ – поле внутри цилиндра, ${{U}_{ - }} = {{U}^{0}} + {{U}^{1}}$ – полное поле вне тела, причем ${{U}^{0}}$ – падающее, а ${{U}^{1}}$ – рассеянное (вторичное) поле, ${\partial \mathord{\left/ {\vphantom {\partial {\partial n}}} \right. \kern-0em} {\partial n}}$ – дифференцирование по направлению внешней к $S$ нормали, $\kappa = {{{{\mu }_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{i}}} {{{\mu }_{e}}}}} \right. \kern-0em} {{{\mu }_{e}}}}$, ${{\mu }_{i}}$ и ${{\mu }_{e}}$ – абсолютные магнитные проницаемости сред внутри и вне тела соответственно. Внешняя среда (${{D}_{e}} = {{\mathbb{R}}^{2}}{\kern 1pt} \backslash {\kern 1pt} \bar {D},$ $\bar {D} = D \cup S$, $D$ – область, ограниченная кривой $S$) и среда внутри цилиндра полагаются однородными, линейными и изотропными. На бесконечности предполагаются выполненными стандартные условия излучения для рассеянного поля.

Воспользуемся следующими представлениями для решения уравнения Гельмгольца в областях $D$ и ${{D}_{e}}$ соответственно [5]:

(2)

$\begin{gathered} {{U}_{ - }}(\vec {r}) = {{U}^{0}}(\vec {r}) + \\ + \,\,\int\limits_S {\left\{ {{{U}_{ - }}(\vec {r}{\kern 1pt} ')\frac{{\partial {{G}_{ - }}(\vec {r},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} - \frac{{\partial {{U}_{ - }}(\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}{{G}_{ - }}(\vec {r},\vec {r}{\kern 1pt} ')} \right\}ds{\kern 1pt} '} , \\ {{U}_{ + }}(\vec {r}) = - \int\limits_S {\left\{ {{{U}_{ + }}(\vec {r}{\kern 1pt} ')\frac{{\partial {{G}_{ + }}(\vec {r},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} - \frac{{\partial {{U}_{ + }}(\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}{{G}_{ + }}(\vec {r},\vec {r}{\kern 1pt} ')} \right\}ds{\kern 1pt} '} , \\ \end{gathered} $

в которых ${{G}_{ \pm }}(\vec {r};\vec {r}{\kern 1pt} ') = \frac{1}{{4i}}H_{0}^{{(2)}}\left( {{{k}_{ \pm }}\left| {\vec {r} - \vec {r}{\kern 1pt} '} \right|} \right)$ – это фундаментальные решения скалярного уравнения Гельмгольца в ${{\mathbb{R}}^{2}}$ с материальными параметрами сред ${{D}_{e}}$ и $D$ соответственно, причем ${{k}_{ + }}$ и ${{k}_{ - }}$ – волновые числа среды внутри и вне рассеивателя. Потребовав в соответствии с МПГУ выполнения условий (1) на контуре $S_{\delta }^{ - }$, расположенном в ${{\mathbb{R}}^{2}}{\kern 1pt} {\kern 1pt} \backslash {\kern 1pt} \bar {D}$, и на контуре $S_{\delta }^{ + }$, расположенном в области $D$ (см. рис. 1) с использованием соотношений (2) получим следующие системы интегральных уравнений (СИУ) Фредгольма 1-го или 2-го рода соответственно:

(3)

$\begin{gathered} \int\limits_S {\left\{ {U(\vec {r}{\kern 1pt} ')\left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} + \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)} \right.} - \\ \left. { - \,\,\frac{{\partial U(\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\left( {{{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ') + \kappa {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')} \right)} \right\}ds{\kern 1pt} ' = - {{U}^{0}}({{{\vec {r}}}_{ - }}), \\ \int\limits_S {\left\{ {U(\vec {r}{\kern 1pt} ')\left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}} + \frac{1}{\kappa }\frac{{{{\partial }^{2}}{{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}} \right)} \right.} - \\ \left. { - \,\,\frac{{\partial U(\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n}} + \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n}}} \right)} \right\}ds{\kern 1pt} ' = - \frac{{\partial {{U}^{0}}({{{\vec {r}}}_{ - }})}}{{\partial n}}, \\ \end{gathered} $

(4)

$\begin{gathered} U(\vec {r}) = \frac{1}{2}{{U}^{0}}({{{\vec {r}}}_{ - }}) + \\ + \,\,\frac{1}{2}\int\limits_S {\left\{ {U(\vec {r}{\kern 1pt} ')\left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} - \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)} \right.} - \\ \left. { - \,\,\frac{{\partial U(\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\left( {{{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ') - \kappa {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')} \right)} \right\}ds{\kern 1pt} ',{\kern 1pt} \\ \frac{{\partial U(\vec {r})}}{{\partial n}} = \frac{1}{{1 + \kappa }}\frac{{\partial {{U}^{0}}({{{\vec {r}}}_{ - }})}}{{\partial n}} + \frac{1}{{1 + \kappa }} \times \\ \times \,\,\int\limits_S {\left\{ {U(\vec {r}')\left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}} - \frac{{{{\partial }^{2}}{{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}} \right) - \frac{{\partial U(\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right.} \times \\ \left. {\left. { \times \,\,\left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n}} - } \right.\kappa \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n}}} \right)} \right\}ds{\kern 1pt} ', \\ \end{gathered} $

где точки наблюдения $M({{\vec {r}}_{ \pm }})$ принадлежат контурам $S_{\delta }^{ \pm }$, а точка $M(\vec {r}) \in S$ и обозначено $U = {{U}_{ - }}$. Отметим, что чаще всего в качестве $S_{\delta }^{ \pm }$ [5, 10] выбирают контуры, отстоящие от S на некоторое достаточно малое расстояние $\delta $, т.е. рассматривают эквидистантные контуры. Пусть уравнение границы S задается в параметрическом виде

(5)

$\left\{ \begin{gathered} x = x{\kern 1pt} '(t), \hfill \\ y = y{\kern 1pt} '(t),\,\,\,\,t \in [0,{{t}_{{\max }}}]. \hfill \\ \end{gathered} \right.$

Тогда уравнения смещенных контуров $S_{\delta }^{ \mp }$ записываются следующим образом:

(6)

$\left\{ \begin{gathered} x(t) = x{\kern 1pt} '(t) \pm {{n}_{x}}(t)\delta , \hfill \\ y(t) = y{\kern 1pt} '(t) \pm {{n}_{y}}(t)\delta , \hfill \\ \end{gathered} \right.$

где ${{n}_{x}}$ и ${{n}_{y}}$ – координаты нормали к границе тела S. Для решения систем (3) и (4) используем метод Крылова–Боголюбова. Для этого запишем системы уравнений (3) и (4) в виде

(7)

$\begin{gathered} \int\limits_0^{{{t}_{{\max }}}} {\left( {{{K}_{{11}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{K}_{{12}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} ')} \right)dt{\kern 1pt} ' = {{b}_{1}}(t)} , \\ \int\limits_0^{{{t}_{{\max }}}} {\left( {{{K}_{{21}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{K}_{{22}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} ')} \right)dt{\kern 1pt} ' = {{b}_{2}}(t)} , \\ \end{gathered} $

(8)

$\begin{gathered} {{I}_{1}}(t) + \int\limits_0^{{{t}_{{\max }}}} {\left( {{{{\tilde {K}}}_{{11}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{{\tilde {K}}}_{{12}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} ')} \right)dt{\kern 1pt} ' = {{{\tilde {b}}}_{1}}(t)} , \\ {{I}_{2}}(t) + \int\limits_0^{{{t}_{{\max }}}} {\left( {{{{\tilde {K}}}_{{21}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{{\tilde {K}}}_{{22}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} ')} \right)dt{\kern 1pt} ' = {{{\tilde {b}}}_{2}}(t)} , \\ \end{gathered} $

в которых введены обозначения:

(9)

$\begin{gathered} {{I}_{1}}(t{\kern 1pt} ') = U(\vec {r}{\kern 1pt} '(t{\kern 1pt} ')),\,\,\,\,{{I}_{2}}(t{\kern 1pt} ') = \frac{{\partial U(\vec {r}{\kern 1pt} '(t{\kern 1pt} '))}}{{\partial n{\kern 1pt} '}}, \\ \xi (t{\kern 1pt} ') = \sqrt {\dot {x}{\kern 1pt} '{{{(t{\kern 1pt} ')}}^{2}} + \dot {y}{\kern 1pt} '{{{(t{\kern 1pt} ')}}^{2}}} , \\ {{K}_{{11}}} = \left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} + \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)\xi (t{\kern 1pt} '), \\ {{K}_{{12}}} = - \left( {{{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ') + \kappa {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')} \right)\xi (t{\kern 1pt} '), \\ {{K}_{{21}}} = \left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n\partial n'}} + \frac{1}{\kappa }\frac{{{{\partial }^{2}}{{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n\partial n'}}} \right)\xi (t{\kern 1pt} '), \\ {{K}_{{22}}} = - \left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }},\vec {r}{\kern 1pt} ')}}{{\partial n}} + \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }},\vec {r}{\kern 1pt} ')}}{{\partial n}}} \right)\xi (t{\kern 1pt} '), \\ {{b}_{1}}(t) = - {{U}^{0}}({{{\vec {r}}}_{ - }}(t)),\,\,\,\,{{b}_{2}}(t) = - \frac{{\partial {{U}^{0}}({{{\vec {r}}}_{ - }}(t))}}{{\partial n}}, \\ \end{gathered} $

(10)

$\begin{gathered} {{{\tilde {K}}}_{{11}}} = - \frac{1}{2}\left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }};\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} - \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }};\vec {r}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)\xi (t{\kern 1pt} '), \\ {{{\tilde {K}}}_{{12}}} = \frac{1}{2}\left( {{{G}_{ - }}({{{\vec {r}}}_{ - }};\vec {r}{\kern 1pt} ') - \kappa {{G}_{ + }}({{{\vec {r}}}_{ + }};\vec {r}{\kern 1pt} ')} \right)\xi (t{\kern 1pt} '), \\ {{{\tilde {K}}}_{{21}}} = - \frac{1}{{1 + \kappa }}\left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\vec {r}}}_{ - }};\vec {r}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}} - \frac{{{{\partial }^{2}}{{G}_{ + }}({{{\vec {r}}}_{ + }};\vec {r}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}} \right)\xi (t{\kern 1pt} '), \\ {{{\tilde {K}}}_{{22}}} = \frac{1}{{1 + \kappa }}\left( {\frac{{\partial {{G}_{ - }}({{{\vec {r}}}_{ - }};\vec {r}{\kern 1pt} ')}}{{\partial n}} - \kappa \frac{{\partial {{G}_{ + }}({{{\vec {r}}}_{ + }};\vec {r}{\kern 1pt} ')}}{{\partial n}}} \right)\xi (t{\kern 1pt} '), \\ {{{\tilde {b}}}_{1}}(t) = \frac{1}{2}{{U}^{0}}({{{\vec {r}}}_{ - }}(t)),\,\,\,\,{{{\tilde {b}}}_{2}}(t) = \frac{1}{{1 + \kappa }}\frac{{\partial {{U}^{0}}({{{\vec {r}}}_{ - }}(t))}}{{\partial n}}. \\ \end{gathered} $

Точка в (9) означает производную по $t$. Представим далее неизвестные функции ${{I}_{{1,2}}}(t{\kern 1pt} ')$ в виде сумм

(11)

${{I}_{q}}(t{\kern 1pt} ') \cong \sum\limits_{n = 1}^N {c_{n}^{q}{{\Phi }_{n}}(t{\kern 1pt} ')} ,\,\,\,\,q = 1,2,$

где ${{\Phi }_{n}}(t{\kern 1pt} ')$ – импульсные функции:

(12)

${{\Phi }_{n}}(t{\kern 1pt} ') = \left\{ \begin{gathered} 1,\,\,\,\,t \in [{{t}_{n}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2},{{t}_{n}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}], \hfill \\ 0,\,\,\,\,t \notin [{{t}_{n}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2},{{t}_{n}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}]. \hfill \\ \end{gathered} \right.$

Здесь ${{t}_{n}} = \frac{{{{t}_{{\max }}}}}{N}\left( {n - \frac{1}{2}} \right),$ $n = \overline {1,N} $, Δ = t_max/N – шаг сетки ($N$ – число базисных функций). Далее, подставив (11) в системы интегральных уравнений (7) и (8) и приравняв левую и правую части в выбранных на кривых $S_{\delta }^{ \pm }$ точках коллокации с координатами $(x({{t}_{n}}),y({{t}_{n}}))$, получим следующие системы алгебраических уравнений относительно величин $c_{n}^{q}$:

(13)

$\begin{gathered} \sum\limits_{n = 1}^N {\left( {K_{{mn}}^{{11}}c_{n}^{1} + K_{{mn}}^{{12}}c_{n}^{2}} \right)} = b_{m}^{1}, \\ \sum\limits_{n = 1}^N {\left( {K_{{mn}}^{{21}}c_{n}^{1} + K_{{mn}}^{{22}}c_{n}^{2}} \right)} = b_{m}^{2},\,\,\,\,m = \overline {1,N} , \\ \end{gathered} $

или

(14)

$\begin{gathered} c_{m}^{1} + \sum\limits_{n = 1}^N {\left( {\tilde {K}_{{mn}}^{{11}}c_{n}^{1} + \tilde {K}_{{mn}}^{{12}}c_{n}^{2}} \right)} = \tilde {b}_{m}^{1}, \\ c_{m}^{2} + \sum\limits_{n = 1}^N {\left( {\tilde {K}_{{mn}}^{{21}}c_{n}^{1} + \tilde {K}_{{mn}}^{{22}}c_{n}^{2}} \right)} = \tilde {b}_{m}^{2},\,\,\,\,m = \overline {1,N} , \\ \end{gathered} $

где матричные элементы и правые части вычисляются по формулам

(15)

$K_{{mn}}^{{pq}} = \int\limits_{{{t}_{n}} - \Delta /2}^{{{t}_{n}} + \Delta /2} {{{K}_{{pq}}}({{t}_{m}},t)dt} ,\,\,\,\,b_{m}^{p} = b_{p}^{{}}({{t}_{m}}),$

(16)

$\tilde {K}_{{mn}}^{{pq}} = \int\limits_{{{t}_{n}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{{{t}_{n}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {{{{\tilde {K}}}_{{pq}}}({{t}_{m}},t)dt} ,\,\,\,\tilde {b}_{m}^{p} = \tilde {b}_{p}^{{}}({{t}_{m}}),\,\,\,p,q = 1,2.$

Переходя к асимптотике рассеянного волнового поля при $r \to \infty $ с учетом формул (2), (5), (11) и (12) получим следующее выражение для диаграммы рассеяния:

(17)

$\begin{gathered} g(\varphi ) = \frac{{i\Delta }}{4} \times \\ \times \,\,\sum\limits_{n = 1}^N {\left( {c_{n}^{2} - c_{n}^{1}i{{k}_{ - }}(n_{x}^{'}({{t}_{n}})\cos \varphi + n_{y}^{'}({{t}_{n}})\sin \varphi )} \right)} \times \\ \times \,\,\xi ({{t}_{n}})\exp \left( {i{{k}_{ - }}\left[ {x{\kern 1pt} '({{t}_{n}})\cos \varphi + y{\kern 1pt} '({{t}_{n}})\sin \varphi } \right]} \right). \\ \end{gathered} $

Формулы (13)–(17) дают два численных алгоритма (основанных на системах уравнений 1-го и 2‑го рода) для решения сформулированной задачи дифракции.

Пусть тело облучается плоской волной

(18)

${{U}^{0}}(\vec {r}) = \exp ( - ikr\cos (\varphi - {{\varphi }_{0}})),$

где ${{\varphi }_{0}}$ – угол падения, $k \equiv {{k}_{ - }}$. Тогда для усредненной диаграммы, в случае если ориентация частицы по отношению к углам облучения ${{\varphi }_{0}}$ равновероятна, получим (при фиксированных углах падения и наблюдения плоской волны)

(19)

$\left\langle {\left| {g(\alpha )} \right|} \right\rangle = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left| {g(\alpha + {{\varphi }_{0}},{{\varphi }_{0}})} \right|d{{\varphi }_{0}}} .$

Одним из критериев правильности полученных результатов является оптическая теорема, которая записывается в виде [11]

(20)

$\sigma = - \operatorname{Re} (g(\varphi = {{\varphi }_{0}})),$

где

(21)

$\sigma = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{{\left| {g(\varphi )} \right|}}^{2}}d\varphi } .$

В качестве оценки точности выполнения оптической теоремы будем рассчитывать величину, которая представляет собой относительную разность левой и правой частей в формуле (20):

(22)

${{\Delta }_{{{\text{отн}}}}} \equiv \frac{{\left| {\sigma + \operatorname{Re} (g({{\varphi }_{0}}))} \right|}}{\sigma }.$

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Рассмотрим результаты численного моделирования. Всюду в дальнейшем будем предполагать, что тело облучается плоской волной (18). В качестве примера рассмотрим сначала задачу дифракции на эллиптическом цилиндре, цилиндре с сечением в виде четырехлистника и цилиндре с прямоугольным сечением. Уравнение контура тела с сечением в виде четырехлистника имеет вид (в полярных координатах)

(23)

$r = a(1 + \tau \cos 4\varphi ),\,\,\,0 < \tau < 1.$

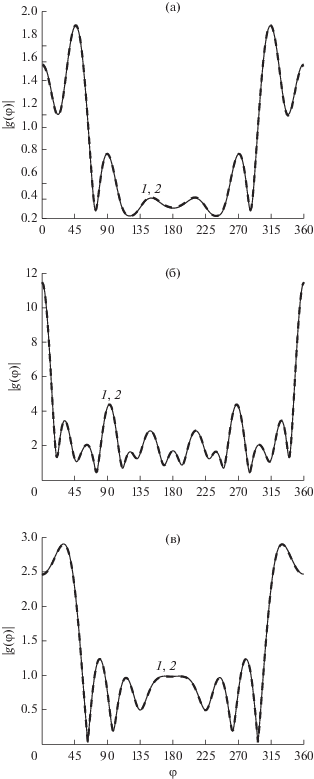
На рис. 2а–2в приведены угловые зависимости диаграммы рассеяния для соответствующих геометрий, полученные для следующих значений параметров задачи: $k\delta = {{10}^{{ - 4}}},$ ${{\varphi }_{0}} = 0,$ ${{\mu }_{i}} = 1,$ ${{\varepsilon }_{i}} = 4$ (материальные параметры внешней среды всюду ${{\mu }_{e}} = 1,$ ${{\varepsilon }_{e}} = 1$). Размеры тел имели следующие значения: полуоси эллипса или половины длин сторон прямоугольника $ka = 5,$ $kb = 1$, параметры $ka = 5$ и $\tau = 0.5$ для тела с сечением в виде четырехлистника. Результаты сравнивались с диаграммами, построенными при помощи модифицированного метода дискретных источников (ММДИ) [5, 12]. Отметим, что ММДИ не может быть непосредственно применен к задаче дифракции на телах, имеющих изломы границы, поэтому для решения задачи при помощи ММДИ проводилась аппроксимация контура осевого сечения тела гладким контуром [12]. Отметим также, что ММДИ обеспечивает высокую точность расчета для тел с гладкой границей, таких как эллипс, многолистник и т.д.

Рис. 2.

Угловые зависимости диаграмм рассеяния эллиптического цилиндра (а), тела с сечением в виде четырехлистника (б) и тела с прямоугольным сечением (в), рассчитанные методами ММДИ (кривые 1) и МПГУ (кривые 2).

В табл. 1 приведены разности модуля диаграммы рассеяния для указанных геометрий, полученные двумя методами: ММДИ и МПГУ. Как видно из табл. 1, разность результатов при увеличении числа используемых базисных функций уменьшается. Из приведенных данных также следует, что для тел с гладкой границей использование уравнений 1-го рода является более предпочтительным, в силу более быстрой сходимости. В случае тела с прямоугольным сечением использование уравнений 2-го рода дает лучшие результаты.

Таблица 1.

Абсолютная и относительная погрешности вычисления диаграммы рассеяния, полученной при помощи ММДИ и МПГУ

N	СИУ 1-го рода		СИУ 2-го рода
N	абсолютная погрешность	относительная погрешность, %	абсолютная погрешность	относительная погрешность, %
Дифракция на эллиптическом цилиндре
48	1.295 × 10^–2	2.038	1.453 × 10^–1	24.297
96	1.904 × 10^–3	0.230	4.183 × 10^–2	7.238
192	6.096 × 10^–4	0.067	1.144 × 10^–2	2.003
288	5.834 × 10^–4	0.075	5.539 × 10^–3	0.977
384	5.607 × 10^–4	0.075	3.450 × 10^–3	0.612
Дифракция на теле с сечением в виде четырехлистника
48	1.643 × 10^–1	10.411	3.836 × 10^–1	21.169
96	2.499 × 10^–2	1.442	9.462 × 10^–2	5.125
192	5.802 × 10^–3	0.325	2.534 × 10^–2	1.370
288	2.984 × 10^–3	0.166	1.143 × 10^–2	0.619
384	2.176 × 10^–3	0.121	6.474 × 10^–3	0.351
Дифракция на теле с прямоугольным сечением
48	3.498 × 10^–2	4.781	5.035 × 10^–2	6.795
96	1.466 × 10^–2	1.956	1.417 × 10^–2	1.715
192	7.358 × 10^–3	0.879	4.773 × 10^–3	0.466
288	5.229 × 10^–3	0.561	3.122 × 10^–3	0.248
384	4.219 × 10^–3	0.429	2.641 × 10^–3	0.208

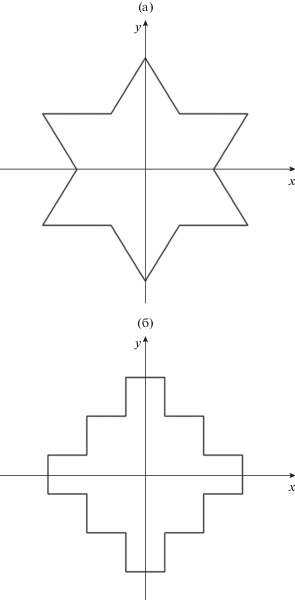
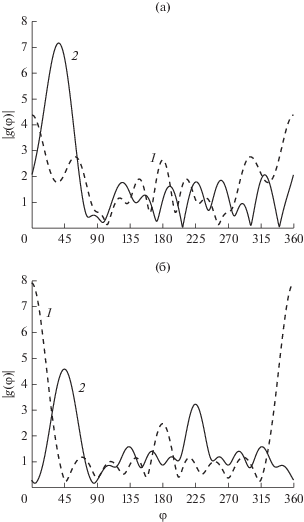
На рис. 3 приведены геометрии фракталоподобных цилиндров с сечением в виде снежинки Коха и кривой Серпинского (первая итерация) [13]. Рисунки 4а и 4б иллюстрируют угловые зависимости диаграммы рассеяния для указанных цилиндров для следующих параметров задачи: $k\delta = {{10}^{{ - 4}}},$ ${{\mu }_{i}} = 1,$ ${{\varepsilon }_{i}} = 4$. Максимальный поперечный размер тела с сечением в виде снежинки Коха и тела с сечением в виде кривой Серпинского по оси x составлял $kd = 10$. Рассматривалось два различных угла падения ${{\varphi }_{0}} = 0$ и 45°. Как следует из рисунков, для исследуемых геометрий точки максимума угловых зависимостей диаграммы рассеяния примерно совпадают с углами падения плоской волны. Видно также, что зависимость диаграммы как для тела с сечением в виде снежинки Коха, так и для тела с сечением в виде кривой Серпинского имеет достаточно большие боковые лепестки.

Рис. 3.

Геометрия тела с сечением в виде снежинки Коха (а) и кривой Серпинского (б).

Рис. 4.

Угловые зависимости диаграмм рассеяния тела с сечением в виде снежинки Коха (а) и кривой Серпинского (б) при двух углах: ${{\varphi }_{0}} = 0$ (кривые 1) и 45° (кривые 2).

Была также проведена проверка точности выполнения оптической теоремы для рассмотренных выше геометрий рассеивателей. Во всех случаях мы выбирали число базисных функций так, что число точек коллокации на одной длине волны составляло ${{N}_{\lambda }} = 25$. При этом относительная диэлектрическая проницаемость среды тела ${{\varepsilon }_{i}}$ варьировалась в пределах 4…10³, а относительная магнитная проницаемость выбиралась равной единице. В результате расчетов получили, что относительная разность правой и левой частей равенства (20) – величина ${{\Delta }_{{{\text{отн}}}}}$ – не превосходит $5 \times {{10}^{{ - 3}}}$, т.е. мала.

Для рассмотренных тел была также проверена точность выполнения теоремы Уфимцева [14], согласно которой интегральный поперечник рассеяния черного тела ровно в два раза меньше интегрального поперечника рассеяния идеально проводящего тела, имеющего тот же теневой контур (т.е. границу между освещенной и теневой частями поверхности тела). Это утверждение справедливо для всех выпуклых тел, линейные размеры и минимальный радиус кривизны которых много больше длины волны. Отметим, что в работах [15, 16] была рассчитана точность выполнения теоремы Уфимцева в зависимости от размеров рассеивателя. Были рассмотрены тела следующих геометрий: сфероид, круговой цилиндр, конус-сфера (конус с основанием в виде полусферы). Установлено, что при радиусе основания рассмотренных тел вращения ka > 4 (для сфероида ka – это волновой размер малой полуоси) точность выполнения теоремы достаточно высокая. Представляет интерес выяснить, с какой точностью выполняется эта теорема для тел сложной геометрии. В табл. 2 приведены результаты проверки теоремы Уфимцева для рассмотренных выше геометрий рассеивателей. Как видно из таблицы, теорема Уфимцева приближенно выполняется только для тел с сечением в виде снежинки Коха и шестиугольника.

Таблица 2.

Результат проверки теоремы Уфимцева

Геометрия рассеивателя	Интегральный поперечник рассеяния идеально проводящего тела	Интегральный поперечник рассеяния черного тела	Отношение поперечников
Эллипс	2.406448	1.088509	2.210774
Четырехлистник	7.876322	3.651952	2.156743
Четырехугольник	2.716768	1.251197	2.171335
Шестиугольник	5.928531	2.934776	2.020096
Первая итерация снежинки Коха	5.398117	2.612487	2.066275
Первая итерация кривой Серпинского	5.402070	2.498518	2.162109

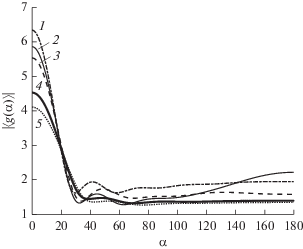
На рис. 5 приведены усредненные по углам ориентации диаграммы рассеяния для рассмотренных выше геометрий тела. Из рисунка видно, что максимумы всех зависимостей соответствуют углу $\alpha $, равному нулю. Видно также, что в случае тела с сечением в форме кривой Серпинского, шестиугольника и снежинки Коха, усредненные диаграммы имеют большие значения для углов $\alpha $, больших 90°, чем соответствующие диаграммы для эллиптического и прямоугольного цилиндров.

Рис. 5.

Усредненная по углам ориентации диаграмма рассеяния в зависимости от угла $\alpha $: кривая 1 – тело с сечением в виде правильного шестиугольника, кривая 2 – тело с сечением в виде снежинки Коха, кривая 3 – тело с сечением в виде кривой Серпинского, кривая 4 – цилиндр с прямоугольным сечением, кривая 5 – эллиптический цилиндр.

ЗАКЛЮЧЕНИЕ

При помощи МПГУ разработаны два численных алгоритма на основе СИУ 1-го и 2-го рода, позволяющие рассчитывать характеристики рассеяния магнитодиэлектрических тел произвольной геометрии. Получены результаты расчета диаграммы рассеяния для большого набора тел разной геометрии, в том числе фракталоподобных рассеивателей. Проведено сравнение методов на основе МПГУ с результатами, полученными при помощи ММДИ. Показано, что МПГУ позволяет получать результаты расчета диаграммы рассеяния с достаточно высокой точностью. Проиллюстрировано, что в случае гладкой границы тела метод на основе уравнений 1-го рода позволяет получать результаты с большей точностью. Проведена проверка точности выполнения оптической теоремы для рассматриваемых геометрий. Показано, что точность выполнения оптической теоремы составляет 5 × 10^–3. Получены угловые зависимости усредненной диаграммы рассеяния для различных геометрий рассеивателей.

Список литературы

Борен К., Хафмен Д. Поглощение и рассеяние света малыми частицами. М.: Мир, 1986.
Захарьев Л.Н., Леманский А.А. Рассеяние волн “черными” телами. М.: Сов. радио, 1972.
Mishchenko M.I., Zakharova N.T., Khlebtsov N.G. et al. // J. Quant. Spectr. Rad. Trans. 2017. V. 202. P. 240.
Waterman P.C. // Proc. IEEE. 1965. V. 53. P. 805.
Кюркчан А.Г., Смирнова Н.И. Математическое моделирование в теории дифракции с использованием априорной информации об аналитических свойствах решения. М.: ИД Медиа Паблишер, 2014.
Кюркчан А.Г., Смирнова Н.И., Чиркова А.П. // РЭ. 2015. Т. 60. № 3. С. 247.
Кюркчан А.Г., Смирнова Н.И. // РЭ. 2017. Т. 62. № 5. С. 476.
Кюркчан А.Г., Маненков С.А., Смирнова Н.И. // Оптика и спектроскопия. 2019. Т. 126. № 5. С. 547.
Крысанов Д.В., Кюркчан А.Г. // T-Comm. Телекоммуникации и транспорт. 2017. Т. 11. № 7. С. 17.
Кюркчан А.Г., Анютин А.П. // ДАН. 2002. Т. 385. № 3. С. 309.
Шендеров Е.Л. Излучение и рассеяние звука. Л.: Судостроение, 1989.
Kyurkchan A.G., Manenkov S.A. // J. Quant. Spectrosc. Radiat. Transfer. 2012. V. 113. P. 2368.
Кроновер Р.М. Фракталы и хаос в динамических системах. Основы теории. М.: Постмаркет, 2000.
Уфимцев П.Я. Теория дифракционных краевых волн в электродинамике. М.: Бином, 2007.
Кюркчан А.Г., Демин Д.Б. // Журн. техн. физики. 2004. Т. 74. № 2. С. 24.
Кюркчан А.Г., Демин Д.Б. // РЭ. 2004. Т. 49. № 11. С. 1218.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал