Радиотехника и электроника, 2020, T. 65, № 9, стр. 835-851

ВВЕДЕНИЕ

Развитие инфокоммуникационных систем требует постоянного совершенствования характеристик основных элементов и устройств приемо-передающих узлов, таких как излучающие элементы, фильтры, направленные ответвители, мультиплексоры, фазовращатели. Хорошо известно, что применение волноводоной техники позволяет заметно увеличить передаваемую мощность, уменьшить потери, повысить добротности частотно-селективных элементов, а также позволяет эффективно работать на более высоких, чем микрополосковые и коаксиальные линии, частотах вплоть до терагерцового диапазона. Для обеспечения большей компактности и широкополосности волноводным элементам требуется переход от волноводов с простым сечением к волноводам с поперечным сечением сложной формы, а включение диэлектрических элементов позволяет дополнительно получить уникальные частотно-селективные и поляризационные свойства. Так, наибольшую популярность как в отечественной, так и в зарубежной СВЧ-технике, приобрели прямоугольные и круглые волноводы с металлическими гребнями и кусочно-слоистым диэлектрическим заполнением. Однако несмотря на ряд значительных преимуществ, элементная база на круглых волноводах с металлическими гребнями не получила столь широкого распространения, как на прямоугольных волноводах. Несмотря на значительное количество публикаций о различных круглых волноводах, методах их расчета и возможности применения, имеющиеся данные носят несистематический характер и в полной мере не позволяют судить о развитии данных структур, алгоритмах, использующихся для их анализа и новых областях применения.

В работе приведена информация о различных типах круглых волноводов, проанализированы методы для расчета электродинамических параметров и показаны области применения данных структур.

1. ТИПЫ КРУГЛЫХ ВОЛНОВОДОВ

В самом простом случае круглый волновод представляет собой металлическую трубу с внутренним воздушным заполнением. Электродинамические свойства таких волноводов широко известны и подробно описаны во многих работах, например, [1, 2]. Однако развитие прикладной электродинамики, освоение новых диапазонов электромагнитных волн и развитие СВЧ-техники приводит к тому, что элементная база СВЧ-устройств усложняется. Поэтому наибольший интерес для изучения с точки зрения практического применения представляют круглые регулярные волноводы сложного поперечного сечения, круглые волноводы с неоднородным диэлектрическим заполнением, а также сложные металлодиэлектрические неоднородности в круглом волноводе.

Прежде всего рассмотрим круглые волноводы сложного поперечного сечения [3–13]. Данный вид волноводов хорошо известен благодаря расширению полосы одномодового режима работы. В качестве неоднородностей могут выступать регулярный продольный металлический гребень или несколько металлических гребней различной формы поперечного сечения, расположенные в круглом волноводе с определенным периодом или в определенном порядке по перечному сечению.

В литературе встречается описание круглых волноводов с различной формой и конфигурацией продольных регулярных металлических гребней. Известны круглые волноводы с одним прямоугольным гребнем, с двумя, с четырьмя, с восемью и с гребнями с угловым срезом (рис. 1а–1е).

Рис. 1.

Поперечные сечения круглого волновода с различным количеством гребней: с одним (а), с двумя (б), с четырьмя (в), с четырьмя гребнями и с повернутой плоскостью симметрии (г); с восемью гребнями (д), с двумя гребнями с угловым срезом (е).

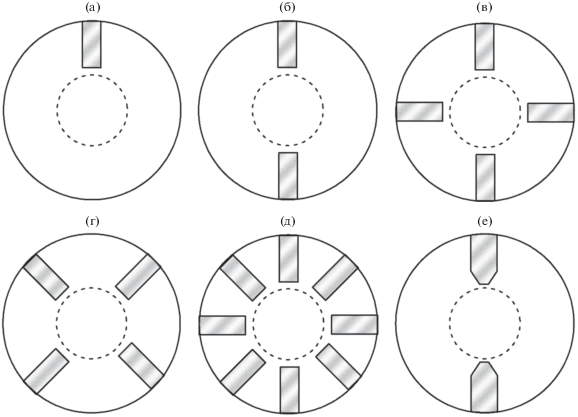
Исследования круглых волноводов со сложным поперечным сечением начались со структуры, изображенной на рис. 1а [3], так как данная структура обладала интересными свойствами, а именно низкими значениями критической частоты основной моды и низким волновым сопротивлением.

В структуре, приведенной на рис. 1б, было введен еще один дополнительный гребень, расположенный симметрично, относительно центра. Подобное симметричное расположение удобно использовать при расчетах и анализе, так как это позволяет рассматривать не всю структуру волновода, а только ее часть.

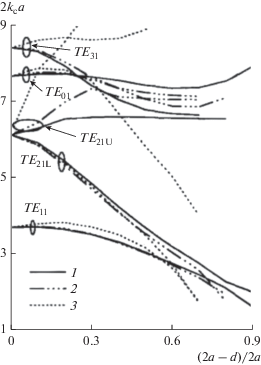
Авторы некоторых работ подробно изучали свойства четырехгребневого круглого волновода (см. рис. 1в), применяя различные методы для расчета характеристик [4–6]. В отличие от одно- или двухгребневого волновода основная мода в волноводе с четырьмя гребнями имеет критическую частоту, очень близкую к критической частоте второй моды. Таким образом, ширина полосы одномодового режима работы оказывается очень мала. Однако, когда удается подавить или не возбудить вторую моду, величина одномодового режима может быть очень широкой (рис. 2). Благодаря этому уникальному свойству, а также возможности двойной поляризации и низкого сопротивления волноводы с четырьмя гребнями широко используются в антеннах и СВЧ-устройствах [4]. Сравнение четырехгребневого круглого волновода с аналогичным волноводом прямоугольного сечения показывает, что такие его характеристики, как затухание и допустимая мощность, значительно лучше [5].

Рис. 2.

Зависимость нормированных критических волновых чисел от геометрии гребня TE₁₁-, TE_21L-, TE₀₁-, TE_21U- и TE₃₁-мод в круглом четырехгребневом волноводе для s/2a = 0.06 (1), 0.12 (2) и 0.30 (3) [4, рис. 1с].

Также в данной работе [5] отмечается, что за счет изменения геометрических параметров гребней, таких как ширина и высота, можно добиться наиболее широкой полосы одномодового режима. Как видно из рис. 1в, четырехгребневый волновод имеет две плоскости симметрии, поэтому для его анализа можно рассматривать 1/4 часть поперечного сечения.

Кроме того, поворачивая плоскость симметрии на 45°, четырехгребневый волновод может выглядеть как показано на рис. 1г, и в этом случае его можно рассматривать как щелевой круглый волновод [6].

Интересный подход к рассмотрению гребневого волновода описан в работе [7], где проведено исследование и сравнение двух-, четырех- и восьмигребневых волноводов (рис. 1д). При этом отмечено, что восьмигребневый волновод может быть представлен как два четырехгребневых волновода в одной структуре.

Проведенные исследования зависимости критических волновых чисел от геометрических параметров гребней и визуализации электромагнитного поля показали, что в восьмигребневых волноводах невозможно глубокое расположение гребней, так как при определенных соотношениях высоты гребня и радиуса структуры возникают ограничения в оптимизации ширины одномодового режима работы. Фактически оптимальная ширина одномодового режима работы достигается при соотношении h/R = 0.21, где h – высота гребня, а R – радиус волновода (рис. 3).

Рис. 3.

Четырехгребневый волновод с параметрами R, h, w, где R – радиус волновода, h – высота гребня, w – ширина гребня [7].

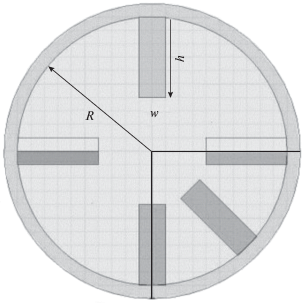
Как видно, описанные выше работы по исследованиям гребневых волноводов фокусировались на структурах с гребнями одной и той же геометрической формы, изменялось лишь количество гребней и период их расположения.

Следующим этапом развития круглых волноводов с гребнями стало изменение самой формы гребня. В результате появились гребни Т-образной формы [8, 9], гребни с угловым срезом [10, 11], радиальные гребни [12] и радиальные гребни со сложной формой [13].

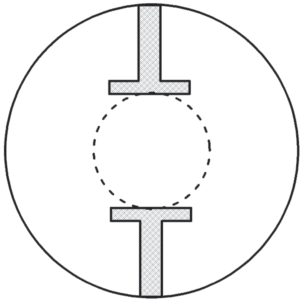
Впервые Т-образные гребни (рис. 4) были изучены в структурах волноводов с прямоугольной формой поперечного сечения [14–16]. Данные структуры показали, что благодаря наличию гребней Т-образной формы происходит значительное увеличение полосы одномодового режима работы по сравнению с волноводами с прямоугольными гребнями.

Рис. 4.

Круглый волновод с Т-образными гребнями.

Аналогичным образом для улучшения ширины полосы одномодового режима был исследован круглый волновод с двумя Т-образными гребнями [8, 9]. В работах проведены исследования распределения электрического поля первых четырех H-мод, рассчитаны нормированные значения критических волновых чисел и проведено сравнение с круглым двухгребневым волноводом.

Ряд авторов предложили использовать ребра не прямоугольного поперечного сечения, а с заострением конца ребра. Благодаря гребням с угловым срезом (рис. 1е) удается достичь не только более широкой полосы одномодового режима, но и увеличить допустимую мощность устройства.

Впервые данное свойство экспериментально было показано в работе [10]. Позже круглый волновод с четырьмя подобными гребнями был исследован в [11].

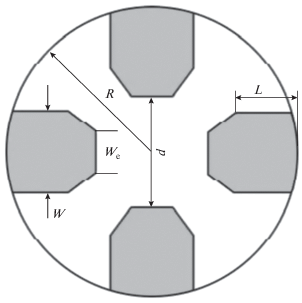
Для круглого волновода с гребнями с угловым срезом толщина гребня W не обязательно должна быть меньше зазора между гребнями (рис. 5), что является обязательным условием в четырехгребневом круглом волноводе с гребнями прямоугольной формы. Отсутствие такого ограничения позволяет варьировать эти параметры для еще большего увеличения полосы одномодового режима.

Рис. 5.

Поперечное сечение четырехгребневого круглого волновода с ребрами с угловым срезом [11].

В работе [12] исследована структура, изображенная на рис. 6а. Визуализация электромагнитного поля позволяет увидеть области с более плотным расположением силовых линий для H- и E-волн, что может быть важным при проектировании частотно-селективных устройств.

Рис. 6.

Поперечное сечение круглого волновода с гребнями конечной толщины (а) и со сложными радиальными гребнями конечной толщины (б).

Следует отметить, что чем более точно задана геометрия гребня в поперечном сечении круглого волновода, тем более успешно будет осуществлен процесс создания устройств на основе данных структур. В указанных выше работах был рассмотрен круглый волновод с гребнями, описанными в прямоугольной системе координат. Однако если гребням соответствует цилиндрическая система координат, это позволяет избежать в рамках строгого анализа смешанных систем координат, которые возникают при использовании прямоугольных выступов в цилиндрическом волноводе. К тому же гребни конической формы более просты в практической реализации, нежели прямоугольные.

Подобные радиальные гребни (рис. 6б) рассмотрены в работе [13], в которой проведены исследования зависимости критических волновых чисел от геометрических параметров гребня, например от угла раскрыва гребня. Данное исследование показало, что при увеличении раскрыва гребня ширина одномодового режима увеличивается.

Структуры с одним, двум, тремя и четырьмя радиальными гребнями проанализированы в работе [17]. В ней приведены зависимости критических волновых чисел для разных параметров гребней, а именно для разной ширины гребня и разной глубины.

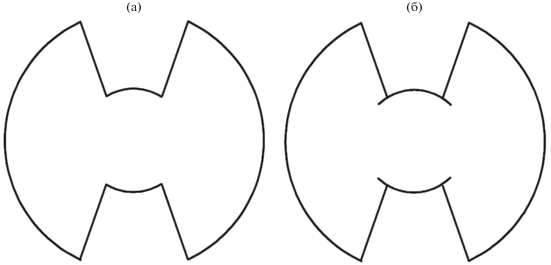
Круглые коаксиальные волноводы были исследованы в работе [18]. Рассматривались две волноводные структуры: в первой из них центральный проводник имеет остроконечную винтовую форму, во второй – внешний проводник лопастной формы (рис. 7). Для данных структур приведено подробное описание метода и рассчитаны критические волновые числа для разных геометрических параметров.

Рис. 7.

Поперечное сечение коаксиального волновода с гребневым центральным проводником (а) и с проводником винтовой формы (б).

Кроме волноводов с металлическими гребнями особый интерес представляют волноводы с диэлектрическим заполнением. Одним из основных преимуществ диэлектрически заполненного волновода является уменьшение его размеров, что может быть очень полезно в практических применениях [19].

Как видно, существует огромное количество разнообразных структур, каждая из которых имеет свои преимущества и недостатки. При этом в настоящее время данные структуры активно исследуются и создаются новые. Однако надо отметить, что исследования связаны не только с усложнением или изменением самих структур, но и с созданием новых методов или усовершенствованием существующих для расчета характеристик и электродинамического анализа волноводных цилиндрических структур со сложной формой поперечного сечения. При этом необходимо отметить, что количество методов, применяемых для исследования характеристик и параметров, огромно, так как каждая структура имеет свои особенности, накладывающие определенные условия и ограничения при проведении расчетов.

2. МЕТОДЫ РАСЧЕТА

Методы, используемые для расчета электродинамических параметров волноводных структур, можно разделить на три группы: аналитические, численные и численно-аналитические. Аналитические методы позволяют решить краевую задачу в явном виде. Однако их применение ограничено простейшими конфигурациями, и они практически не используются для решения современных задач компьютерного моделирования. При использовании численных методов решение задачи получают в виде числовых значений в конечном наборе пространственных точек. К численным методам относятся метод конечных элементов, метод конечных разностей, метод граничного элемента. В случае численно-аналитических методов решение задачи выражается с помощью некоторых функций, а удовлетворение граничным условиям производится численно. К численно-аналитическим методам относятся метод конечных элементов с масштабированными границами, метод частичных областей. Широкое распространение получили также метод согласования мод, метод связанных интегральных уравнений и метод R-функций.

Среди этих методов метод конечных элементов является одним из наиболее широко распространенных [20]. Данный метод основан на представлении и приближенном решении краевых задач с помощью решения дифференциальных уравнений в частных производных. При использовании данного метода поперечное сечение круглого волновода разбивается на несколько областей (рис. 8), в каждой из которых выбирается функция, значение которой на границах областей является решением заданной задачи.

Рис. 8.

Координатное представление метода конечных элементов с масштабированными границами [20].

Долгое время данный метод применялся для анализа структур только в прямоугольной системе координат [21]. Однако для цилиндрических волноводов невозможно с помощью декартового элемента полностью заполнить их поперечное сечение. В декартовой геометрии конечный элемент разбиваемой области представляет собой треугольник. В круговой полярной геометрии новый конечный элемент снова является треугольником, контуры которого, как правило, представляют собой круговые спирали. В таком случае данный метод может быть применен для анализа круглых, эллиптических волноводов, а также неоднородностей, имеющих конусообразную форму. Преимуществом данного метода является его универсальность при решении задач с различной геометрией, различными материалами и различными граничными условиями [22]. Однако при наличии открытой области, возникновении особенности электромагнитного поля на острых углах в исследуемой области, состоящей из нескольких материалов, данный метод имеет недостатки. При наличии бесконечной области можно предположить, что на достаточно далекой границе характеристика будет равна нулю. Но при таком подходе ухудшается точность расчетов и в вычислительном отношении для моделирования распространения волн данный метод оказывается невыгодным [23, 24]. Для второй проблемы, связанной с наличием сингулярности в краевой задаче, возникает ухудшение характеристик численного решения. Это связано с тем, что вблизи сингулярной точки с особенностью электромагнитного поля получаемые решения являются большими или неограниченными, поэтому оно не может быть точно аппроксимировано локально кусочно-полиномиальной функцией на нормальной сетке. В результате было предложено несколько специальных методов конечных элементов, которые подходят для конкретного вида особенности электромагнитного поля. Эти методы обычно основаны на некотором знании формы сингулярности и могут быть классифицированы следующим образом.

Первый метод – это добавление сингулярной функции в пространство конечных элементов, что позволяет ей приближаться к решению вблизи сингулярности.

Второй метод – специальные сингулярные элементы используются для аппроксимации сингулярного решения.

Третий метод – это локальное уточнение сетки, благодаря чему контролируется распределение вычислительной ошибки.

Метод конечных элементов дает точные результаты, однако требует большого времени вычисления. Недавно созданный гибридный метод, состоящий из мультимодального вариационного метода и метода конечных элементов, успешно применяется для анализа неоднородностей в различных структурах, улучшая время вычисления и использование оперативной памяти компьютера [25].

По сравнению с другими модальными методами, такими как метод согласования мод и анализ обобщенной матрицы рассеяния, мультимодальный вариационный метод использует матрицу рассеяния с меньшим размером, что сводит к минимуму использование необходимых вычислительных ресурсов и время расчета [26].

Одним из первых методов для решения краевых задач был метод конечных разностей. Данный метод основан на решении дифференциальных уравнений, сводящихся к разностным схемам.

При использовании данного метода на поперечное сечение волновода накладывается квадратная или прямоугольная сетка, разбивающая сечение волновода на квадратные или прямоугольные области соответственно [27, 28] (рис. 9). В узлах, образовавшихся областей, в соответствие дифференциальным уравнениям ставятся разностные схемы. И далее, задавая граничные условия, можно найти решения задачи в узлах области.

Рис. 9.

Стандартное наложение сетки на волноводную структуру [27].

Однако с помощью данного метода можно рассчитать электродинамические параметры не только для основной моды круглого волновода, но и для мод высшего порядка (рис. 10) [29]. Разновидностью метода конечных разностей являются метод конечных разностей во временной и частотной областях, отличие которых состоит в представлении уравнений Максвелла соответственно во временной области и в частотной областях [30].

Рис. 10.

Критические нормированные числа различных мод и при разных размерах сетки для круглого волновода с параметрами h = 0.6, a = 3.0 [29].

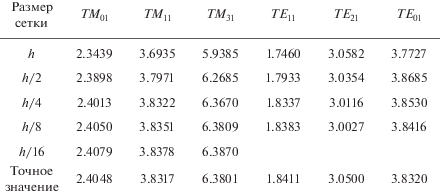
Метод граничного элемента является альтернативой методу конечных элементов. Он основан на решении интегральных уравнений. В отличие от метода конечных элементов производится разбиение не всей области, а только границ областей, так как имеющиеся дифференциальные уравнения в области сводятся к интегральным уравнениям на границе с помощью функции Грина. Это значительно упрощает процесс вычисления характеристик. Кроме того, данный метод можно применять к задачам с бесконечными границами. Но и он имеет определенные недостатки: метод применяется только для границ, не имеющих углов, так как в данных местах отсутствует решение интегрального уравнения и к тому же матрицы, получаемые для расчета неизвестных параметров, являются полными, что требует большой вычислительной мощности. Метод граничного элемента использовался для анализа круглого волновода с одним гребнем в работе [31]. Точность нахождения критических волновых чисел варьировалась с помощью количества членов в ряду функции Грина.

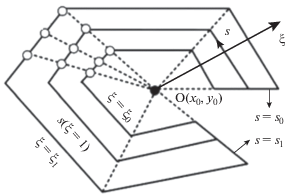
Одной из разновидности метода конечных элементов является метод конечных элементов с масштабированными границами. Данный метод – это сочетание метода конечных элементов и метода граничного элемента. Его универсальность, точность и эффективность не только равны, но и потенциально лучше, чем метод конечных элементов и метод граничных элементов для определенных задач. Впервые данный метод был предложен в работе [32]. Для того чтобы удобно задать граничные условия, вводятся масштабированные граничные координаты, которые состоят из так называемой радиальной координаты и двух окружных координат, определяемых конечной дискретизацией граничного элемента (рис. 11). Тогда радиальная координата постоянна на границе.

Рис. 11.

Секция с масштабированными границами [32].

Применение метода конечных элементов с масштабированными границами в двух окружных направлениях, параллельных границе, дает линейные обыкновенные дифференциальные уравнения второго порядка с радиальной координатой в качестве независимой переменной. Таким образом, сила метода конечных элементов с масштабированной границей состоит в преобразовании дифференциальных уравнений в частных производных в обычные дифференциальные уравнения, которые могут быть решены аналитически. В этом случае только граница дискретизируется конечными элементами с криволинейной поверхностью. Данный метод применялся в работе [33] для расчета характеристик четырехгребневого круглого волновода со срезанными углами.

Для решения краевых задач можно использовать метод R-функций. [34]. Теория R-функций позволяет рассматривать различные области сложной формы, используя булевую алгебру и аналитическую геометрию. В данном методе уравнения границ области выражаются в неявном виде, подбирается такая функция, у которой ее значение во внутренней области является положительным, а за пределами области – отрицательным. Далее подбираются такие аналитические функции, которые удовлетворяют граничным условиям.

Широкое распространение при расчете электродинамических характеристик волноводных структур получил метод частичных областей. Данный метод предполагает разбиение поперечного сечения волновода на несколько областей с определенными граничными условиями. Далее в каждой частичной области задаются компоненты полей, а на границе раздела происходит их сшивание. Авторы разработанного метода отмечают, что при наличии острых углов, которые характерны для волноводов со сложной формой поперечного сечения, сходимость данного метода ухудшается [35]. Однако вводя дополнительные функции на границе сшивания, учитывающие данные особенности, можно значительно улучшить сходимость. Такой метод получил название метод частичных областей с учетом особенности электромагнитного поля на ребре и активно использовался авторами данного обзора для решения многих электродинамических задач [36‒39]. Так, в работе [39] критические волновые числа и их зависимость от параметров гребней приведены для случаев круглого волновода с тонкими металлическими гребнями, рассмотрен случай дифракции волн при их падении на протяженную неоднородность.

В случае многослойного диэлектрического заполнения волновода при использовании метода частичных областей количество линейных алгебраических уравнений увеличивается, что значительно затрудняет процесс расчета характеристик. Авторы работы [40] предлагают использовать функции Грина и теорию длинных линий для анализа многослойных структур. С помощью данного метода рассчитан круглый волновод с многослойным заполнением.

Для расчета дисперсионных характеристик и затухания диэлектрически заполненных волноводов существуют общепринятые методы: энергетический метод, метод возмущений и метод комплексных параметров. Однако они являются приближенными. А метод расчета, при котором функции действительного аргумента продолжаются на комплексную плоскость, является строгим [41]. Однако при использовании данного метода необходимо добавлять дополнительные частичные области, что значительно усложняет задачу. К тому же диэлектрическая проницаемость в этом случае является постоянной величиной.

Если диэлектрическая проницаемость меняется ступенчато, то можно воспользоваться модификацией метода Галеркина для расчета двухслойного экранированного волновода и волновода с градиентным заполнением [42]. Сравнение с результатами, получаемыми из расчета с помощью метода частичных областей, доказало эффективность и корректность предложенного метода. К тому же он обладает более высокой скоростью расчета.

Также в случае неоднородно заполненного диэлектрического волновода (рис. 12) для расчета постоянных распространения можно воспользоваться методом задачи Коши [43].

Рис. 12.

Исследуемая структура по методу задач Коши [43].

Предложенная методика расчета приближенного собственного значения оказывается работоспособной в случае дискретных собственных значений. К тому же расчеты, производимые по данной разработанной методике, производятся значительно быстрее, нежели с помощью интегральных дисперсионных уравнений, а также с любой задаваемой точностью.

Актуальным исследованием является также изучение открытых диэлектрических волноводов с различным поперечным сечением.

При решении данной задачи существует несколько особенностей и сложностей методов, применяемых для расчетов. В первую очередь одной из особенностей является слабонаправляемость структуры. Чтобы решить данную проблему, в работе [44] применен гибридный метод на основе метода интеграла Фурье и модифицированного метода Галеркина. С помощью данного подхода были рассчитаны диэлектрические круглые волноводы разного сечения, а именно: круглый волновод простого сечения, открытый трубчатый диэлектрический волновод (рис. 13), открытый трубчатый диэлектрический волновод с крестообразным сечением и открытый трубчатый диэлектрический волновод со звездообразным поперечным сечением.

Рис. 13.

Дисперсионные характеристики первых четырех (1–4) несимметричных волн трубчатого диэлектрического волновода: r₀ = 1.7 мм, ε = 20 [44], на вставке – конфигурация трубчатого диэлектрического волновода.

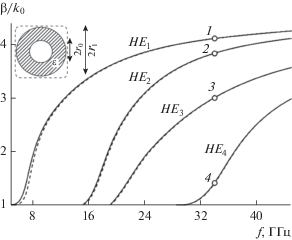
Также для открытых круглых волноводов может быть применим модифицированный метод дискретных источников [45]. Однако из-за специфики данного метода, при расчете постоянных распространения могут возникать дополнительные корни, не имеющие физического смысла. Чтобы избежать этого, авторами работы предложено решать дополнительную задачу дифракции.

Очень часто для расчета круглых открытых диэлектрических волноводов используют спектральный метод, предложенный в работе [46]. Во-первых, он обладает универсальностью, так как с его помощью можно рассчитывать открытые диэлектрические волноводы с любой геометрической формой поперечного сечения и высокими значениями диэлектрической проницаемости. А во-вторых, он позволяет найти весь спектр волн для заданного частотного диапазона для открытых диэлектрических волноводов с произвольным поперечным сечением.

Метод согласования мод [47] является одним из наиболее эффективных и точных методов моделирования волноводных структур. Ключевая идея этого метода состоит в разделении анализируемой структуры на отдельные волноводные подобласти. Электромагнитное поле в каждой из этих областей может быть выражено как суперпозиция волноводных мод. Конкретная амплитуда каждой моды учитывает граничные условия между соседними областями, а также возбуждение и нагрузку всей структуры. Метод наиболее эффективен, когда моды каждой подобласти известны аналитически. Метод согласования мод был использован в работе [48] для вычисления матрицы рассеяния на стыке простого круглого волновода и двух- или четырехгребневого волновода. Полученный алгоритм обладал хорошей точностью и использовался для проектирования и оптимизации пятизвенного фильтра на основе двухгребневого круглого волновода и четырехгребневого волноводного трансформатора.

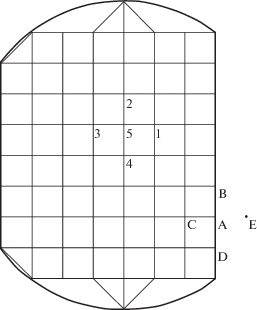
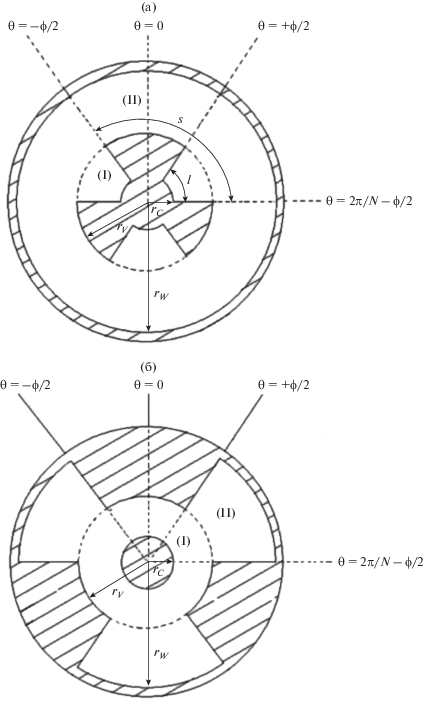
В работе [49] для расчета критических волновых чисел четырехгребневого круглого волновода с гребнями с угловым срезом использовался гибридный метод: сочетание метода согласования мод и метода граничного элемента. Как известно, метод граничного элемента использовался для анализа круглого волновода с одним гребнем. Теоретически, используя данный метод, можно рассчитать характеристики для любого поперечного сечения волновода. Однако в случае четырехгребневого круглого волновода с гребнями с угловым срезом контур поперечного сечения оказывается очень сложным для расчета. Поэтому, используя симметрию структуры, сечение волновода разделили на четыре идентичные области (рис. 14). Затем одна из этих областей была поделена еще на три подобласти: I, II области с простой геометрией рассчитываются методом согласования мод, III область со сложной геометрией сечения рассчитывается методом граничного элемента.

Рис. 14.

Одна четвертая область поперечного сечения волновода: I, II, III – частичные области, E.W. – граничное условие типа электрической стенки, M.W. – граничное условие типа магнитной стенки [49].

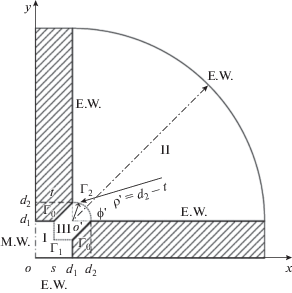
Подробное описание метода связанных интегральных уравнений дано в работе [50]. Данный метод применен для анализа гребневого круглого волновода. С помощью него можно задать условия для ребер, улучшить сходимость и рассчитать как симметричные, так и асимметричные структуры.

Многообразие методов, используемых для расчета и анализа электродинамических параметров круглых волноводов со сложной формой поперечного сечения и неоднородным диэлектрическим заполнением, обусловлено не только огромным разнообразием самих структур, но также и широкой областью их применения. Следует отметить, что большинство существующих методов не являются универсальными, так как с их помощью можно рассчитать ограниченное количество структур по форме. Поэтому задача о разработке высокоскоростных универсальных методов и алгоритмов расчета остается актуальной.

3. ПРИМЕНЕНИЯ ДАННЫХ СТРУКТУР

Волноводы со сложной геометрической формой поперечного сечения находят широкое применение в современных устройствах [51–69 ]. Они используются в приемных и передающих антеннах, в устройствах, предназначенных для получения круговой поляризации, в делителях мощности. Кроме того, такие волноводные структуры обладают частотно-селективными свойствами, поэтому применяются для построения различных типов фильтров: полосно-пропускающих, полосно-запирающих, нижних и верхних частот.

Как известно, фильтры, построенные на запредельных волноводах, имеют меньшие размеры и лучшее затухание в полосе заграждения [51]. Для таких фильтров используются круглые волноводы с произвольно расположенными гребнями. В работе [51] в качестве примеров рассмотрены четыре конструкции фильтров: на двухгребневом круглом волноводе, на круглом волноводе с одним Т-образным гребнем, на круглом волноводе с гребнями в виде “ключа” и на круглом волноводе с двумя Т‑образными гребнями (рис. 15). Расчеты проводились с помощью комбинации двух методов: метода сшивания мод и спектрального анализа мод собственных значений. Для каждой из структур полученные результаты сравнивались с характеристиками из CST Microwave Studio.

Рис. 15.

Амплитудно-частотные характеристики полосно-пропускающих фильтров на круглых волноводах с металлическими гребнями различной конфигурации [51]: кривые – результаты моделирования, звездочки (а) и пунктир (б) – эксперимент.

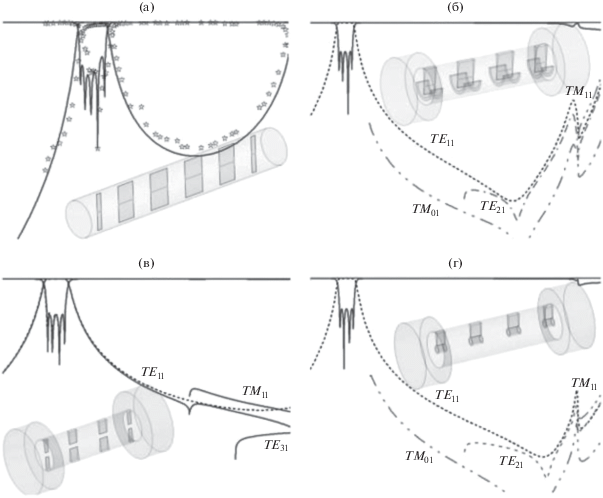
Используя подобный подход, были также проанализированы фильтры на круглом волноводе с диафрагмами, на круглом двухгребневом волноводе, на круглом трехгребневом волноводе, на круглом четырехгребневом волноводе, на круглом волноводе с радиальным Т-образным гребнем [9, 52].

Аналогичная структура (рис. 16) была использована в работе [9] для проектирования полосно-пропускающего фильтра на запредельных волноводах. Авторам удалось показать, что данный круглый волновод со сложной формой поперечного сечения можно использовать не только как линию передачи или излучающий элемент, но и в качестве базовой структуры для создания различных частотно-селективных устройств.

Рис. 16.

Конструкция фильтра на круглом волноводе с Т-образными гребнями: 1 – коаксиально-волноводный переход, 2 – прототип фильтра [9].

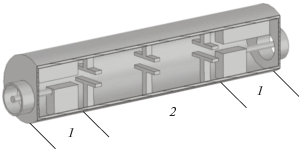
Для равномерного распределения электромагнитной волны в мобильной связи в условиях ограниченной среды, например железная дорога, метро или тоннели, использовался негерметичный коаксиальный кабель. Однако потери в таком кабеле сильно возрастают с увеличением рабочей частоты. Поэтому вместо такого кабеля используется круглый волновод, но у данной волноводной структуры существует вращение плоскости поляризации доминирующей моды. Чтобы нарушить симметрию плоскости поляризации, необходимо использовать круглые волноводы с различными металлическими гребнями и вставками для работы с более высокими частотами [53]. Изменяя параметры гребней и вставок, можно добиться разного уровня потерь.

Круглые волноводы применяются и в качестве многолучевых облучателей, когда необходимо сформировать многолучевую характеристику направленности, в которой лучи отстоят друг от друга на минимальное угловое расстояние [54]. Данное свойство используется в случае космической связи для покрытия территории сложной конфигурации, так как при этом требуется формирование многолучевой диаграммы направленности.

В последнее время появились работы, в которых круглые волноводы используются для бесконтактного зондирования и для получения изображений внутреннего строения объектов. Прямоугольные волноводы широко используются в качестве зондирующих антенн в системах ближнего поля во многих промышленных приложениях. Это связано с тем, что они просты в изготовлении и относительно недороги. Известно, что сужение прямоугольного волновода существенно улучшает пространственное разрешение полученных изображений, в отличие от стандартных волноводов, работающих на той же частоте. Особое внимание к использованию конических прямоугольных волноводов для изображений в ближней зоне уделено в работе [55]. Эффективность конического зонда была продемонстрирована путем количественного сравнения как распределения реальной мощности, так и теоретических изображений, полученных с использованием конических и стандартных зондов. Было показано, что конический волновод способен значительно увеличить разрешение без изменения частоты работы.

Как правило, стандартные прямоугольные волноводы использовались в качестве зондов для формирования изображений внутренних дефектов в различных диэлектрических средах. В работе [56] авторы предлагают использовать конические волноводы для достижения более высокого разрешения при сохранении приемлемой чувствительности. Данное исследование было весьма актуальным, так как методы визуализации и контроля с использованием СВЧ не носили разрушающего характера для исследуемого объекта, что позволяло использовать их в промышленных и медицинских целях [56].

Было установлено, что в ближнем поле боковое разрешение, достигаемое с помощью таких зондов, обратно пропорционально площади апертуры волновода [57]. К тому же при уменьшении размера диафрагмы область зондирования зонда уменьшается и, следовательно, возможность распознать мелкие включения и дефекты в изображении значительно возрастает.

Безапертурные зонды и зонды с резонансной диафрагмой находят свое применение в рефлектометрии для оценки и характеристики искусственных и естественных материалов, например, диэлектрических и металлических структур биологических образцов и критических частей зданий и сооружений [58]. Преимуществом микроволновой рефлектометрии является возможность бесконтактной работы в реальном времени при малых мощностях в условии сохранения высокой разрешающей способности получаемого изображения.

Сравнение излучения из круглого волновода с излучением из волновода прямоугольной формы показало, что наиболее эффективными являются первые [59, 60]. Основное преимущество заключается в том, что боковые лепестки круглого волновода имеют более низкий уровень (рис. 17).

Рис. 17.

Излучение в ближнем поле (нормированная напряженность) вдоль оси y на расстоянии 1 мм от отверстия для TE₁₁ в круглом зонде (а) и TE₁₀ в прямоугольном зонде (б) [59].

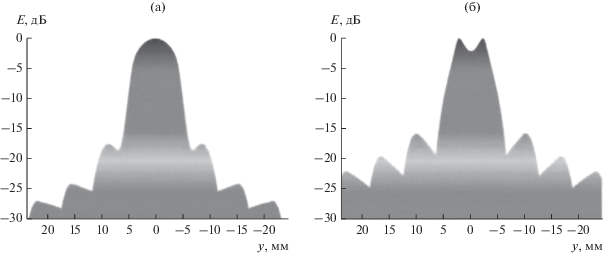
К тому же круглые волноводы обладают лучшей чувствительностью и более высоким разрешением (рис. 18). Данные преимущества могут быть использованы в промышленности для контроля многокомпонентных материалов, оценки коррозии, контроля толщины краски и характеристик материала, для обнаружения трещин в металле, а также в системах наблюдения и проверки в аэропортах.

Рис. 18.

Y-скан рентгеновского изображения с кругового зонда (а), Y-скан рентгеновского изображения с прямоугольного зонда (б), настройка рентгеновского сканирования (в), X-скан круглого зондового изображения (г) и X-скан прямоугольного зондового изображения (д) [59].

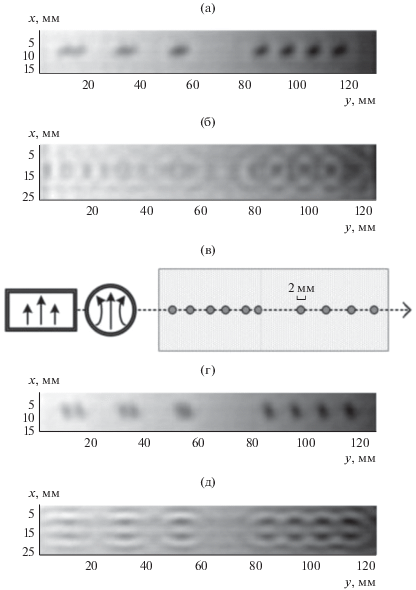
Характеристики круглых и прямоугольных волноводов сравнивали с помощью численного моделирования, а также экспериментальным путем, используя образцы с коррозией. Процесс формирования изображения основан на взаимодействии между мишенью и электромагнитным полем. С точки зрения моделирования цель может быть представлена в виде геометрического/материального пространственного распределения. Электрическое поле, излучаемое зондом, также является функцией пространственных переменных (оно имеет определенное пространственное распределение).

Существует много методов, таких как рентгенография, компьютерная томография, двухфотонная рентгеновская абсорбциометрия, магнитно-резонансная томография, которые применяют для неинвазивного наблюдения при детском краниосиностозе. Однако такие методы, основанные на радиации, вредны для младенцев и не являются целесообразными с медицинской точки зрения [61]. Из-за этого интервал проведения процедур составляет целый год, но в течение года необходимо профилактическое наблюдение развития черепа младенца для выявления возможности рецидива или нормализации состояния.

Альтернативным методом оценки костной ткани являются микрохирургия и неинвазивные методы на основе ультразвука. Ультразвук использует неионизирующее излучение, что позволяет производить частые измерения.

Последние исследования показали, что использование излучения круглых волноводов для наблюдения пациентов после черепной операции является самым оптимальным вариантом в силу их свойств. Так, в работе [62] рассматривается вопрос о возможности использования круглого волновода для наблюдения процесса заживления костей путем моделирования и создания диэлектрической заполненной волноводной системы с открытым контуром в полосе частот 1…3 ГГц, способным определять одну из трех стадий развития болезни.

Известно, что объемные резонаторы широко используются в устройствах электронного парамагнитного резонанса. При этом одним из ключевых свойств таких устройств является обеспечение однородного поля вдоль осей резонатора. Так, в работе [63] предложено использовать круглый волновод с прямоугольными металлическими гребнями для решения данной задачи. Показано, что использование четырехгребневого круглого волновода, зажимающего диэлектрический образец в пространстве между гребнями, позволяет существенно улучшить характеристики конечного устройства.

Цилиндрические структуры могут быть использованы как проходные резонаторы при конструировании фильтров [64]. Как известно, нули функции передачи обычно используются, чтобы увеличить селективные возможности полосовых фильтров. В настоящее время существуют два способа практической реализации нулей передаточной функции. Первый из них через многолучевое распространение, которое создается в самой структуре фильтра, что в свою очередь создает ослабляющую интерференцию на некоторых нужных частотах, называемых нулевыми частотами передачи. Обычно это достигается с помощью перекрестной связи между несмежными узлами или резонаторами в структуре фильтра. Второй способ предполагает создание элементов, генерирующих нуль передачи, которые затем включаются последовательно в цепи более высокого порядка или соединяются с другими элементами.

Однако эти методы часто приводят к громоздким фильтрам из-за большого числа требуемых элементов и иногда из-за неудобных топологий. Чтобы создать полосовой резонанс с определенными конечными частотными нулями передачи использованы входные резонаторы, на основе цилиндрических структур. Общее представление такой входной линии было впервые введено Кохом при проектировании ответвителей, и позднее подобные конфигурации применяли при создании полосно-пропускающих и полосно-запирающих фильтров.

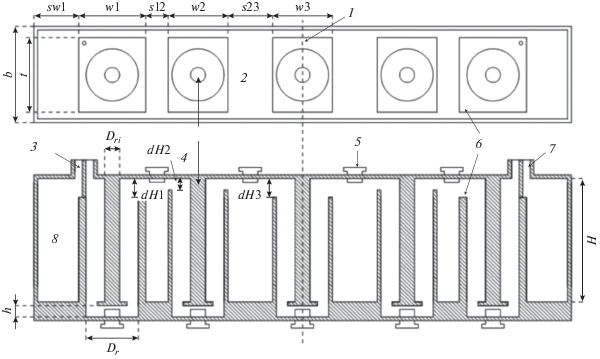
Исследуемая конструкция (рис. 19) предлагает простую и легкую реализацию псевдоэллиптических фильтров, в которых требуется более высокий уровень затухания в верхней части полосы пропускания, чем тот уровень, который обеспечивают коаксиальные фильтры. Этот тип фильтров полезен для подавления помех в сотовых базовых станциях.

Рис. 19.

Схема расположения повторяющихся резонаторов (вид сверху и поперечное сечение вида сбоку) [64]: 1 – линия симметрии; 2, 8 – воздушное заполнение; 3 – вход; 4 – внутренний проводник; 5 – подстрочные винты; 6 – средний проводник; 7 – выход.

В последние годы метаматериалы и их потенциальные применения, такие как антенны [65] и поглощающие материалы [66], широко изучаются. Метаматериалы, состоящие из металлического кольцевого резонатора, нанесенного на поверхность диэлектрической пластины, были детально изучены, чтобы получить их дисперсионные характеристики внутри круглого волновода.

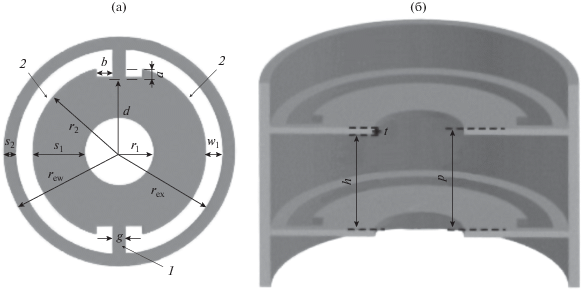
Кроме того, наблюдалось интересное явление распространения обратной волны ниже критической частоты волновода, заполненного элементарными ячейками метаматериала [67]. Поэтому замедляющая волновая структура метаматериала, состоящая из волновода с периодическими кольцевыми диафрагмами (рис. 20) имеет определенные преимущества перед стандартными замедляющими структурами, в частности по габаритным размерам. Подобные структуры могут быть использованы при создании частотно-селективных СВЧ-устройств [68].

Рис. 20.

Вид элементарной ячейки метаматериала, состоящей из кольцевых резонаторов (а), и замедляющая структура метаматериала (б) [68]: 1 – металл; 2 – вакуум.

ЗАКЛЮЧЕНИЕ

Широкое разнообразие структур и их различное применение требует разработки численно-аналитических методов и алгоритмов электродинамического анализа и синтеза. Несмотря на то что уже существует много методов расчета характеристик, эти методы не являются универсальными. Таким образом, для эффективного проектирования устройств на основе круглых волноводов сложного сечения необходимо создание и постоянное совершенствование алгоритмов, так как перспектива использования круглых волноводов как элементной базы огромна.