Радиотехника и электроника, 2021, T. 66, № 10, стр. 974-979

Трехфокальная трехслойная волноводно-щелевая антенная решетка

В. А. Калошин^a, *, Д. Т. Ле^b

^a Институт радиотехники и электроники им. В.А. Котельникова РАН
125007 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

^b Московский физико-технический институт (национальный исследовательский университет)
141700 Долгопрудный, Московской обл., Институтский пер., 9, Российская Федерация

^* E-mail: vak@cplire.ru

Поступила в редакцию 22.08.2019
После доработки 21.11.2019
Принята к публикации 15.12.2019

DOI: 10.31857/S0033849421100077

Полный текст (PDF)

Аннотация

Предложена и исследована трехфокальная планарная волноводно-щелевая антенная решетка, состоящая из трех слоев, первые два из которых представляют собой планарные волноводы, а третий – решетку прямоугольных металлических волноводов с парными продольными или поперечными щелями на широких стенках. В результате решения задачи синтеза найдена форма зеркал и положения щелей в прямоугольных волноводах, которые обеспечивают излучение плоской волны при трех положениях источника цилиндрической волны (облучателя) в планарном волноводе. Проведено исследование величины среднеквадратической аберрации антенной решетки, оптимизированной в угле зрения 40 и 80 град при перемещении облучателя по фокальной кривой и показано, что эта величина в 4.5…11 раз меньше, чем у трехслойной двухзеркальной и двухслойной однозеркальной бифокальных антенных решеток.

ВВЕДЕНИЕ

Планарные многолучевые волноводно-щелевые антенные решетки (АР) с квазиоптическим формированием лучей рассматривалась в ряде работ [1–7]. В простейшем случае такая АР содержит два слоя, которые связаны между собой параболической щелью или системой отверстий и замкнуты параболическим зеркалом [2, 3]. В первом слое решетки расположены облучатели. Однако из-за фазовых аберраций при сдвиге облучателя из фокуса параболического зеркала параболы такая антенна не может обеспечить широкоугольную многолучевую диаграмму направленности. Для уменьшения аберраций в работе [1] в качестве диаграммо-образующей системы (ДОС) использована бифокальная волноводная зеркально-линзовая система, в работах [4–7] – трехфокальная система на основе микрополосковой линзы Ротмана. В работах [8–10] синтезирована и оптимизирована, а в работе [11] экспериментально исследована двухзеркальная апланатическая планарная ДОС, в работе [12] синтезирована и исследована двухзеркальная бифокальная ДОС, в работе [13] – трехзеркальная апланатическая ДОС, а в работе [14] – трехфокальная волноводная зеркально-линзовая планарная ДОС с одинаковыми длинами волноводов. Однако применение линзовых и зеркально-линзовых систем с принудительным преломлением приводит к усложнению конструкции и увеличению потерь ДОС. В работе [15] предложена и исследована бифокальная волноводно-щелевая АР на основе простой двухслойной конструкции с эллиптическим зеркалом. Показана возможность формирования многолучевой диаграммы в угле зрения 80°. Дальнейшее расширение угла зрения и числа лучей ограничивается аберрациями бифокальной системы.

В данной работе ставится и решается задача синтеза формы двух зеркал и положения щелей, обеспечивающих точную фокусировку при трех положениях облучателя на фокальной кривой в первом слое трехслойной волноводно-щелевой АР и оптимизации этих положений (фокусов) с целью минимизации среднеквадратической аберрации (СКА) в углах зрения 80° и 40°. Также проводится анализ СКА синтезированных и оптимизированных антенн, результаты которого сопоставлены с соответствующими результатами для двухслойной однозеркальной бифокальной АР и трехслойной двухзеркальной бифокальной АР с прямыми линиями расположения щелей в соседних волноводах.

1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА

Синтезируемая АР (рис. 1) состоит из трех слоев: первого – в виде планарного волновода 1 с расположенными на фокальной линии облучателями 2, второго – в виде планарного волновода 3, связанного через криволинейные щели 5 и 6 с первым и третьим, и третьего – в виде решетки заполненных диэлектриком прямоугольных волноводов 4, которые возбуждаются через криволинейную щель связи 6 между вторым и третьим слоями. Щели связи 5 и 6 находятся на краях планарных волноводов, которые замыкается конфокальными щелям зеркалами. В широкой стенке каждого прямоугольного волновода 4 периодически расположены парные продольные или поперечные щели 7.

Рис. 1.

Конструкция трехслойной волноводно-щелевой антенной решетки: 1 – планарный волновод первого слоя, 2 – облучатель, 3 – планарный волновод второго слоя, 4 – прямоугольный волновод третьего слоя, 5–7 – щели связи, 8, 9 – зеркала.

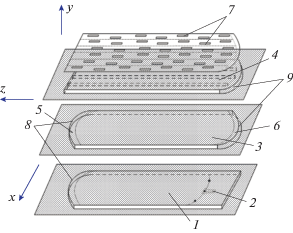
Цилиндрическая волна, излученная облучающим рупором на первом этаже, распространяется по планарному волноводу 1, отражается от первого зеркала 8 и через щель связи 5 попадает в планарный волновод 3 на втором слое. Далее она распространяется по планарному волноводу 3, отражается от второго зеркала 9 и через щель связи 6 возбуждает решетку прямоугольных волноводов 4. В каждом из прямоугольных волноводов возбуждается основная мода, которая, распространяясь вдоль волновода, излучает энергию через щели в его широкой стенке, в результате чего при условии синфазного излучения всех щелей антенной решетки формируется узкий луч с высоким усилением. При перемещении облучателя вдоль фокальной кривой изменяются фазовые соотношения между модами прямоугольных волноводов и в результате осуществляется сканирование луча антенны. При расположении на фокальной кривой нескольких облучателей реализуется многолучевой режим излучения АР.

Задача синтеза АР заключается в определении формы зеркал (щелей связи) и расположения щелей в волноводах, которые обеспечивают излучение плоской волны в трех направлениях при расположении облучателей в трех фокусах.

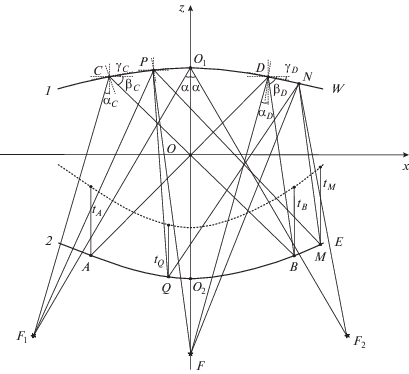
Нетрудно убедиться, что эта задача эквивалентна трехмерной задаче синтеза двухмерной трехзеркальной системы, с одной стороны которой расположены два симметричных относительно оси z фокуса (точки F₁ и F₂), третий лежит на этой оси (точка F), а второе и третье зеркало соединены линиями передачи (волноводами), параллельными этой оси (рис. 2). Потребуем, чтобы после последовательного отражения от двух зеркал цилиндрической волны источника, расположенного в фокусе F₁, F₂ или F, после прохождения через линии передачи эйконалы полей в точках пересечения этих линий с третьим зеркалом удовлетворяли соответственно условиям:

(1)

$\begin{gathered} {{F}_{1}}C + CB + {{t}_{B}} + ({{x}_{M}} - {{x}_{B}})\sin \alpha + \\ + \,\,\left| {{{z}_{M}} - {{z}_{B}}} \right|\cos \beta - \left| {{{t}_{M}} - {{t}_{B}}} \right|\cos \beta = \\ = {{F}_{1}}P + PM + {{t}_{M}}, \\ \end{gathered} $

(2)

$\begin{gathered} {{F}_{2}}D + DA + {{t}_{A}} = {{F}_{2}}N + NQ + {{t}_{Q}} + \\ + \,\,({{x}_{Q}} - {{x}_{A}})\sin \alpha + \left| {{{z}_{A}} - {{z}_{Q}}} \right|\cos \beta - \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta , \\ \end{gathered} $

(3)

$FP + PQ + {{t}_{Q}} - \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta = FD + DB + {{t}_{B}},$

Рис. 2.

К синтезу формы зеркал и положения щелей (пояснения в тексте).

где

$\begin{gathered} FP = \sqrt {{{{({{x}_{F}} - {{x}_{P}})}}^{2}} + {{{({{z}_{F}} - {{z}_{P}})}}^{2}}} , \\ FD = \sqrt {{{{({{x}_{F}} - {{x}_{D}})}}^{2}} + {{{({{z}_{F}} - {{z}_{D}})}}^{2}}} , \\ PQ = \sqrt {{{{({{x}_{P}} - {{x}_{Q}})}}^{2}} + {{{({{z}_{P}} - {{z}_{Q}})}}^{2}}} , \\ DB = \sqrt {{{{({{x}_{D}} - {{x}_{B}})}}^{2}} + {{{({{z}_{D}} - {{z}_{B}})}}^{2}}} , \\ \end{gathered} $

$\begin{gathered} {{F}_{2}}D = \sqrt {{{{({{x}_{{F2}}} - {{x}_{D}})}}^{2}} + {{{({{z}_{{F2}}} - {{z}_{D}})}}^{2}}} , \\ DA = \sqrt {{{{({{x}_{D}} - {{x}_{A}})}}^{2}} + {{{({{z}_{D}} - {{z}_{A}})}}^{2}}} , \\ {{F}_{2}}N = \sqrt {{{{({{x}_{{F2}}} - {{x}_{N}})}}^{2}} + {{{({{z}_{{F2}}} - {{z}_{N}})}}^{2}}} , \\ NQ = \sqrt {{{{({{x}_{N}} - {{x}_{Q}})}}^{2}} + {{{({{z}_{N}} - {{z}_{Q}})}}^{2}}} , \\ \end{gathered} $

$\begin{gathered} {{F}_{1}}C = \sqrt {{{{({{x}_{C}} - {{x}_{{F1}}})}}^{2}} + {{{({{z}_{C}} - {{z}_{{F1}}})}}^{2}}} , \\ CB = \sqrt {{{{({{x}_{B}} - {{x}_{C}})}}^{2}} + {{{({{z}_{B}} - {{z}_{C}})}}^{2}}} , \\ {{F}_{1}}P = \sqrt {{{{({{x}_{P}} - {{x}_{{F1}}})}}^{2}} + {{{({{z}_{P}} - {{z}_{{F1}}})}}^{2}}} , \\ PM = \sqrt {{{{({{x}_{M}} - {{x}_{P}})}}^{2}} + {{{({{z}_{M}} - {{z}_{P}})}}^{2}}} , \\ \end{gathered} $

$\alpha $ – угол между осью z и лучами F₁O₁, F₂O₁; t_A, t_Q, t_B, t_M расстояния от соответствующих точек до линии размещения центров щелей, β угол излучения –1 пространственной гармоники вытекающей волны относительно оси волновода (Oz), $\cos \beta = \frac{{\gamma p - 2\pi }}{{kp}}$, постоянная распространения вытекающей волноводной моды; p – период размещения щелей вдоль волновода (оси Oz); k – постоянная распространения в свободном пространстве, остальные обозначения понятны из рис. 2.

В случае расположения щелей в точках пересечения линий с третьим зеркалом и выполнения уравнений (1)–(3) величины эйконалов лучей из фокусов в этих точках плюс расстояния этих точек до плоскости с нормалью, расположенной под углом β к линиям передачи, будут равны.

Таким образом, задача синтеза сводится к определению функций z₁(x), z₂(x) и t(x), удовлетворяющих системе уравнений (1)–(3).

2. СИНТЕЗ ТРЕХФОКАЛЬНОЙ ТРЕХЗЕРКАЛЬНОЙ СИСТЕМЫ

Предположим, что луч цилиндрической волны из первой точки идеальной фокусировки (первого фокуса) F₁ (см. рис. 2) отражается от первого зеркала в точке C (x_C, z_C) и падает на второе зеркало в точке B(x_B, z_B). А луч цилиндрической волны из второго фокуса F отражается от первого зеркала в точке D(x_D, z_D) и тоже падает на второе зеркало в точке B(x_B, z_B).

Зададим профиль центральной части первого зеркала (CD) в виде параболической функции z₁(x) = b₂x²+ b₀, второго зеркала (AB) – в виде параболической функции z₂(x) = a₂x² + a₀, а также определим положения точек F₁(x_F1, z_F1), F(x_F, z_F), F₂(x_F2, z_F2), C(x_C, z_C), О₂(x_O2, z_O2) и расстояние от точки B до линии размещения центров щелей t_B.

Из геометрии на рис. 2 следует:

$\alpha = arctg({{{{x}_{{F1}}}} \mathord{\left/ {\vphantom {{{{x}_{{F1}}}} {({{z}_{{F1}}} - {{z}_{{O1}}})}}} \right. \kern-0em} {({{z}_{{F1}}} - {{z}_{{O1}}})}}),$

угол между осью z и лучом F₁C в точке C равен

${{\alpha }_{C}} = arctg({{({{x}_{C}} - {{x}_{{F1}}})} \mathord{\left/ {\vphantom {{({{x}_{C}} - {{x}_{{F1}}})} {({{z}_{C}} - {{z}_{{F1}}})}}} \right. \kern-0em} {({{z}_{C}} - {{z}_{{F1}}})}}),$

угол между осью z и лучом FD в точке D –

${{\alpha }_{D}} = \operatorname{arctg} ({{({{x}_{D}} - {{x}_{F}})} \mathord{\left/ {\vphantom {{({{x}_{D}} - {{x}_{F}})} {({{z}_{D}} - {{z}_{F}})}}} \right. \kern-0em} {({{z}_{D}} - {{z}_{F}})}}),$

где ${{x}_{D}} = - {{x}_{C}},\,\,{{z}_{D}} = {{z}_{C}},$ ${{\gamma }_{C}} = {{(90^\circ - {{\alpha }_{C}} - {{\beta }_{C}})} \mathord{\left/ {\vphantom {{(90^\circ - {{\alpha }_{C}} - {{\beta }_{C}})} 2}} \right. \kern-0em} 2}$, ${{b}_{2}} = {{\operatorname{tg} {{\gamma }_{C}}} \mathord{\left/ {\vphantom {{\operatorname{tg} {{\gamma }_{C}}} {(2{{x}_{C}})}}} \right. \kern-0em} {(2{{x}_{C}})}}$, ${{b}_{0}} = {{y}_{C}} - {{b}_{2}}{{x}_{C}}^{2},$ ${{\gamma }_{D}} = - {{\gamma }_{C}}$, β_D = $ = {{\alpha }_{D}} + 2{{\gamma }_{D}} - 90^\circ $, ${{z}_{B}} = {{x}_{B}}\operatorname{tg} {{\beta }_{D}} + {{z}_{D}} - {{x}_{D}}\operatorname{tg} {{\beta }_{D}},$ x_B = $ = ({{z}_{D}} - {{x}_{D}}\operatorname{tg} {{\beta }_{D}} - {{z}_{C}} + $ ${{{{x}_{C}}\operatorname{tg} ( - {{\beta }_{C}}))} \mathord{\left/ {\vphantom {{{{x}_{C}}\operatorname{tg} ( - {{\beta }_{C}}))} {(\operatorname{tg} ( - {{\beta }_{C}})}}} \right. \kern-0em} {(\operatorname{tg} ( - {{\beta }_{C}})}} - \operatorname{tg} {{\beta }_{D}})$, ${{a}_{0}} = {{z}_{{O2}}}$; ${{a}_{2}} = {{({{z}_{B}} - {{a}_{0}})} \mathord{\left/ {\vphantom {{({{z}_{B}} - {{a}_{0}})} {x_{B}^{2}}}} \right. \kern-0em} {x_{B}^{2}}}$.

Предположим, что луч, выходящий из фокуса F, отражается от первого зеркала в некоторой точке P в интервале CD. Тогда угол между осью z и падающим лучом в точке P имеет вид

${{\alpha }_{{FP}}} = \operatorname{arctg} ({{({{x}_{P}} - {{x}_{F}})} \mathord{\left/ {\vphantom {{({{x}_{P}} - {{x}_{F}})} {({{z}_{P}} - {{z}_{F}})}}} \right. \kern-0em} {({{z}_{P}} - {{z}_{F}})}}),$

где z_P = z₁(x_P);

угол между осью x и касательной прямой первого зеркала в точке P –

${{\gamma }_{P}} = \operatorname{arctg} (z_{1}^{'}({{x}_{P}})),$

а угол между осью x и отраженным лучом в точке P –

${{\beta }_{{PQ}}} = 2{{\gamma }_{P}} + {{\alpha }_{{FP}}} - 90^\circ .$

Предположим, что отраженный луч падает на второе зеркало в точке Q. Из геометрии на рис. 2 можно получить систему уравнений:

$\left\{ \begin{gathered} {{z}_{Q}} = {{x}_{Q}}\operatorname{tg} {{\beta }_{{PQ}}} + {{z}_{P}} - {{x}_{P}}\operatorname{tg} {{\beta }_{{PQ}}} \hfill \\ {{z}_{Q}} = {{a}_{2}}{{x}_{Q}}^{2} + {{a}_{0}} \hfill \\ \end{gathered} \right.,$(4)

решение которой имеет вид

(5)

$\left\{ \begin{gathered} {{x}_{Q}} = \frac{{\operatorname{tg} {{\beta }_{{PQ}}} \pm \sqrt {\operatorname{tg} \beta _{{PQ}}^{2} - 4{{a}_{2}}{{a}_{0}} + 4{{a}_{2}}{{z}_{P}} - 4{{a}_{2}}{{x}_{P}}\operatorname{tg} {{\beta }_{{PQ}}}} }}{{2{{a}_{2}}}} \hfill \\ {{z}_{Q}} = {{a}_{2}}x_{Q}^{2} + {{a}_{0}} \hfill \\ \end{gathered} \right..$

Знак перед корнем выбирается так, чтобы значение x_Q было положительным числом.

Из уравнения (3), получаем

(6)

${{t}_{Q}} = FD + DB + {{t}_{B}} - FP - PQ + \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta .$

Для определения нового участка первого зеркала предположим, что луч из фокуса F₂, падающий на первое зеркало и отражающийся от него в некоторой точке N в интервале DW, попадет в точку Q во втором зеркале. Из уравнения (2) следует:

(7)

${{z}_{N}} = \frac{{{{A}_{1}} \pm A\sqrt {{{A}_{2}}{{A}_{3}}} + {{A}_{4}}}}{{{{A}_{5}}}},$

где

$\begin{gathered} A = {{F}_{2}}D + DA + {{t}_{A}} - {{t}_{Q}} - ({{x}_{Q}} - {{x}_{A}}) \times \\ \times \,\,\sin \alpha - \left| {{{z}_{A}} - {{z}_{Q}}} \right|\cos \beta + \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta , \\ \end{gathered} $

$\begin{gathered} {{A}_{1}} = {{A}^{2}}({{z}_{{F2}}} + {{y}_{Q}}) - (x_{{F2}}^{2} - x_{Q}^{2})({{z}_{{F2}}} - {{z}_{Q}}) + \\ + \,\,{{z}_{{F2}}}z_{Q}^{2} + z_{{F2}}^{2}{{z}_{Q}} - z_{{F2}}^{3} - z_{Q}^{3}, \\ \end{gathered} $

${{A}_{2}} = - {{A}^{2}} + x_{{F2}}^{2} - 2{{x}_{{F2}}}{{x}_{Q}} + x_{Q}^{2} + z_{{F2}}^{2} - 2{{z}_{{F2}}}{{z}_{Q}} + z_{Q}^{2},$

$\begin{gathered} {{A}_{3}} = - {{A}^{2}} + x_{{F2}}^{2} - 4{{x}_{N}}({{x}_{{F2}}} + {{x}_{Q}}) + 2{{x}_{{F2}}}({{x}_{Q}} - {{z}_{Q}}) + \\ + \,\,4x_{N}^{2} + x_{Q}^{2} + z_{{F2}}^{2} + z_{Q}^{2}, \\ \end{gathered} $

${{A}_{4}} = 2{{x}_{{F2}}}{{x}_{N}}{{z}_{{F2}}} - 2{{x}_{{F2}}}{{x}_{N}}{{z}_{Q}} - 2{{x}_{N}}{{x}_{Q}}{{z}_{{F2}}} + 2{{x}_{N}}{{x}_{Q}}{{z}_{Q}},$

${{A}_{5}} = 2{{A}^{2}} - 2z_{{F2}}^{2} + 4{{z}_{{F2}}}{{z}_{Q}} - 2z_{Q}^{2},$

а знак перед корнем в (7) выбирается так, чтобы значение z_N было положительным. Отсюда имеем угол между осью z и лучом F₂N –

${{\alpha }_{{F2N}}} = \operatorname{arctg} ({{({{x}_{{F2}}} - {{x}_{N}})} \mathord{\left/ {\vphantom {{({{x}_{{F2}}} - {{x}_{N}})} {({{z}_{N}} - {{z}_{{F2}}})}}} \right. \kern-0em} {({{z}_{N}} - {{z}_{{F2}}})}})$

и угол между осью z и лучом NQ в точке N –

${{\beta }_{{NQ}}} = \operatorname{arctg} ({{({{x}_{N}} - {{x}_{Q}})} \mathord{\left/ {\vphantom {{({{x}_{N}} - {{x}_{Q}})} {({{z}_{N}} - {{z}_{Q}})}}} \right. \kern-0em} {({{z}_{N}} - {{z}_{Q}})}}).$

Из геометрии на рис. 2 следует, что угол между осью x и касательной прямой первого зеркала в точке N имеет вид

(8)

${{\gamma }_{N}} = \frac{{{{\alpha }_{{F2N}}} - {{\beta }_{{NQ}}}}}{2}.$

Для определения нового участка второго зеркала предположим, что луч из фокуса F₁, падающий на первое зеркало и отражающийся от него в некоторой точке P в интервале CD, попадет в точку M в интервале BE второго зеркала. При этом луч из фокуса F, отражающийся от первого зеркала в точке N, тоже попадет в точку M в интервале BE второго зеркала. Отсюда угол между осью z и лучом F₁P имеет вид

${{\alpha }_{{F1P}}} = \operatorname{arctg} ({{({{x}_{P}} - {{x}_{{F1}}})} \mathord{\left/ {\vphantom {{({{x}_{P}} - {{x}_{{F1}}})} {({{z}_{P}} - {{z}_{{F1}}})}}} \right. \kern-0em} {({{z}_{P}} - {{z}_{{F1}}})}}),$

угол между осью x и лучом PM в точке P –

${{\beta }_{{PM}}} = 2{{\gamma }_{P}} + {{\alpha }_{{F1P}}} - 90^\circ ,$

угол между осью z и лучом FN –

${{\alpha }_{{FN}}} = \operatorname{arctg} (({{x}_{N}} - {{x}_{F}})/({{z}_{N}} - {{z}_{F}}))$,

угол между осью x и лучом NM в точке N –

${{\beta }_{{NM}}} = 2{{\gamma }_{N}} + {{\alpha }_{{FN}}} - 90^\circ .$

Из геометрии на рис. 2 находим координаты точки M:

(9)

${{x}_{M}} = \frac{{{{z}_{P}} - {{x}_{P}}\operatorname{tg} {{\beta }_{{PM}}} - {{z}_{N}} + {{x}_{N}}\operatorname{tg} {{\beta }_{{NM}}}}}{{\operatorname{tg} {{\beta }_{{NM}}} - \operatorname{tg} {{\beta }_{{PM}}}}},$

(10)

${{z}_{M}} = {{x}_{M}}\operatorname{tg} {{\beta }_{{PM}}} + {{z}_{P}} - {{x}_{P}}\operatorname{tg} {{\beta }_{{PM}}}.$

Из уравнения (1) для всех лучей, выходящих из фокуса F₁, отражающихся от первого зеркала в интервале CD и от второго зеркала в интервале BE, и лучей, выходящих из фокуса F, отражающихся от первого зеркала в интервале DW и от второго зеркала в интервале BE, следует:

(11)

$\begin{gathered} FD + DB + {{t}_{B}} - \left| {{{t}_{M}} - {{t}_{B}}} \right|\cos \beta = \\ = FN + NM + {{t}_{M}}, \\ \end{gathered} $

где

$\begin{gathered} FD = \sqrt {{{{({{x}_{D}} - {{x}_{F}})}}^{2}} + {{{({{z}_{D}} - {{z}_{F}})}}^{2}}} , \\ DB = \sqrt {{{{({{x}_{B}} - {{x}_{D}})}}^{2}} + {{{({{z}_{B}} - {{z}_{D}})}}^{2}}} , \\ FN = \sqrt {{{{({{x}_{N}} - {{x}_{F}})}}^{2}} + {{{({{z}_{N}} - {{z}_{F}})}}^{2}}} , \\ NM = \sqrt {{{{({{x}_{M}} - {{x}_{N}})}}^{2}} + {{{({{z}_{M}} - {{z}_{N}})}}^{2}}} . \\ \end{gathered} $

Вычитая уравнение (11) из уравнения (1), получаем

(12)

$B + FN + NM = 0,$

где

$\begin{gathered} B = {{F}_{1}}C + CB + ({{x}_{M}} - {{x}_{B}})\sin \alpha - \\ - \,\,{{F}_{1}}P - PM - FD - DB + \left| {{{z}_{M}} - {{z}_{B}}} \right|\cos \beta . \\ \end{gathered} $

Решение уравнения (12) имеет вид

(13)

${{x}_{N}} = \frac{{ \pm B\sqrt {{{B}_{1}}{{B}_{2}}} + {{B}_{3}} + {{B}_{4}}}}{{{{B}_{5}}}},$

где

${{B}_{1}} = - {{B}^{2}} + x_{F}^{2} - 2{{x}_{F}}{{x}_{M}} + x_{M}^{2} + z_{F}^{2} - 2{{z}_{F}}{{z}_{M}} + z_{M}^{2},$

$\begin{gathered} {{B}_{2}} = - {{B}^{2}} + x_{F}^{2} - 2{{x}_{F}}{{x}_{M}} + 2{{z}_{F}}{{z}_{M}} + \\ + \,\,x_{M}^{2} + z_{F}^{2} - 4{{z}_{N}}({{z}_{F}} + {{z}_{M}}) + z_{M}^{2} + z_{N}^{2}, \\ \end{gathered} $

$\begin{gathered} {{B}_{3}} = {{B}^{2}}({{x}_{F}} + {{x}_{M}}) + {{x}_{F}}(x_{M}^{2} - x_{F}^{2} + z_{M}^{2}) + \\ + \,\,{{x}_{M}}(x_{F}^{2} + z_{F}^{2} - z_{M}^{2}), \\ \end{gathered} $

$\begin{gathered} {{B}_{4}} = 2{{y}_{N}}({{x}_{F}} - {{z}_{M}})({{z}_{F}} - {{z}_{M}}); \\ {{B}_{5}} = 2{{B}^{2}} - 2x_{F}^{2} + 4{{x}_{F}}{{x}_{M}} - 2x_{M}^{2}, \\ \end{gathered} $

а знак корня выбирается из условия положительной величины x_N.

Из уравнения (7) находим z_N, из уравнений (8)–(10) находим x_M и z_M, из уравнения (12) находим t_M. При перемещении точки P в интервале CD и перемещении точки Q в интервале AB соответственно находим участок DW первого зеркала, участок BE второго зеркала и расстояние t от второго зеркала в интервале BE до линии размещения центра щелей.

Повторяя аналогичную процедуру, получаем следующие участки зеркал и положения щелей.

3. АНАЛИЗ АБЕРРАЦИИ ТРЕХФОКАЛЬНОЙ ПЛАНАРНОЙ ВОЛНОВОДНО-ЩЕЛЕВОЙ АНТЕННОЙ РЕШЕТКИ

Для анализа нормированной СКА эйконала в апертуре трехфокальной планарной волноводно-щелевой АР при излучении вытекающей волны по нормали к волноводу (β = 90°) синтезируем два варианта решетки (для углов зрения 80° и 40°). Величину СКА определим по формуле

$\sigma = \sqrt {{{\sum\limits_{i = 1}^n {{{{\left( {{{L}_{i}} - {{L}_{о}}} \right)}}^{2}}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^n {{{{\left( {{{L}_{i}} - {{L}_{о}}} \right)}}^{2}}} } N}} \right. \kern-0em} N}} ,$

где L_i – длина оптического пути луча с номером i от источника до точки фокусировки; L₀ – длина центрального луча; N = 50 – число учтенных лучей.

При синтезе положения точек F₁(x_F1, z_F1), F(x_F, z_F), F₂(x_F2, z_F2), C(x_C, z_C), О₂(x_O2, z_O2) и расстояние от точки B до линии размещения центров щелей t_B оптимизируются так, чтобы величина СКА в заданных углах зрения была наименьшей. В результате оптимизации получаем следующие величины параметров:

– для угла зрения 80°

$\begin{gathered} {{x}_{F}}_{1} = - 0.25,\,\,\,\,{{z}_{{F1}}} = - 0.23,\,\,\,\,{{x}_{F}} = 0, \\ {{z}_{F}} = - 0.25,\,\,\,\,{{x}_{{F2}}} = - 0.25,\,\,\,\,{{z}_{{F2}}} = - 0.23, \\ {{x}_{C}} = - 0.08,\,\,\,\,{{z}_{C}} = 0.25,\,\,\,\,{{x}_{{O2}}} = 0, \\ {{z}_{{O2}}} = - 1.02;\,\,\,\,{{t}_{B}} = 0.25; \\ \end{gathered} $

– для угла зрения 40°:

$\begin{gathered} {{x}_{{F1}}} = - 0.25,\,\,\,\,{{z}_{{F1}}} = - 0.68,\,\,\,\,{{x}_{F}} = 0, \\ {{z}_{F}} = - 0.707,\,\,\,\,{{x}_{{F2}}} = - 0.25, \\ {{z}_{{F2}}} = - 0.68,\,\,\,\,{{x}_{C}} = - 0.05, \\ {{z}_{C}} = 0.25,\,\,\,\,{{x}_{{O2}}} = 0,\,\,\,\,{{z}_{{O2}}} = - 0.52,\,\,\,\,~{{t}_{B}} = 0.25. \\ \end{gathered} $

На рис. 3а, 3б показаны зависимости величины СКА от угла зрения соответственно для первого и второго вариантов синтезированной трехфокальной планарной волноводно-щелевой АР, а также аналогичные зависимости двухзеркальной трехслойной бифокальной АР с прямолинейными линиями расположения щелей в соседних волноводах и формой зеркал, синтезированных в [12], и однозеркальной однослойной бифокальной АР [15].

Рис. 3.

Зависимость величины СКА от угла зрения: а) синтез для угла зрения 80°; б) синтез для угла зрения 40°; 1 – трехфокальная трехслойная АР, 2 – бифокальная трехслойная АР, 3 – бифокальная двухслойная АР.

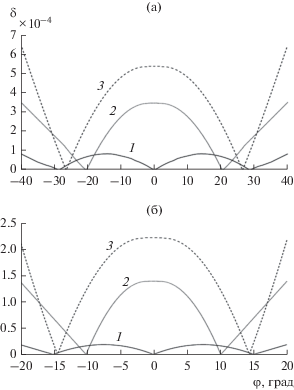
Как видно из рис. 3, с уменьшением угла зрения в два раза СКА трехфокальной АР падает на порядок, а бифокальных решеток – в два-три раза. При этом в угле зрения 80° значение СКА трехфокальной трехслойной АРс двухзеркальной ДОС (0.8 × 10^–4) в семь раз меньше, чем двухслойной с однозеркальной ДОС (5.6 × 10^–4), и в 4.5 раза меньше, чем трехслойной с двухзеркальной ДОС (3.4× 10^–4), а в угле 40° СКА трехфокальной трехслойой АР с двухзеркальной ДОС (0.2 × 10^–5) в 11 раз меньше, чем двухслойной с однозеркальной ДОС (2.2 × 10^–4) и в семь раз меньше, чем трехслойной с двухзеркальной ДОС (1.4 × 10^–4).

ЗАКЛЮЧЕНИЕ

На основании полученных результатов можно сделать следующие выводы.

1. Для обеих исследованных в работе углов зрения минимальной величиной СКА обладает трехфокальная трехслойная антенная решетка, а максимальной – бифокальная двухслойная.

2. СКА бифокальной трехслойной антенной решетки с двухзеркальной ДОС в 1.5–2 раза меньше, чем двухслойной с однозеркальной ДОС, но в 5–7 раз больше, чем трехфокальной трехслойной антенной решетки с двухзеркальной ДОС.

3. Расположение щелей трехслойной трехфокальной и однослойной бифокальной антенной решетки зависит от угла излучения волновода вытекающей волны β, т.е. от частоты. Поэтому при изменении частоты возникают дополнительные аберрации, что ограничивает полосу рабочих частот этих антенн.

ФИНАНСИРОВАНИЕ РАБОТЫ

Работа выполнена за счет бюджетного финансирования в рамках государственного задания по теме № 0030-2019-006.

Список литературы

Калошин В.А. // Тр. 13-й Междунар. Крымской конф. “СВЧ техника и телекоммуникационные технологии” (КрыМиКо-2003). Севастополь, 8–12 сент. Севастополь: Вебер, 2003. С. 383.
Ettorre M., Gandini E., Sauleau R. // Proc. 5th Europ Conf. on Antennas and Propagation (EUCAP). Rome. 11–15 Apr. 2011. N.Y.: IEEE, 2011. P. 2947.
Банков С.Е., Грачев Г.Г., Дупленкова М.Д., Фролова Е.В. // РЭ. 2014. Т. 59. № 6. С. 552.
Tekkouk K., Ettorre M., Le Coq L., Sauleau R. // IEEE Trans. 2016. V. AP-64. № 2. P. 504.
Tekkouk K., Ettorre M., Sauleau R., Casaletti M. //Proc. IEEE Antennas and Propagation Int. Simp. (APSURSI) Chicago. 8–14 Jul. 2012. N.Y.: IEEE, 2012. P. 361.
Toan Vo Dai, Tuan Nguzen, Ozlem Kilic // Proc. IEEE Int. Simp. Antennas and Propagation & USNC/URSI National Radio Science Meeting. San Diego. 9–14 Jul. 2017. N.Y.: IEEE, 2017. P. 2129.
Yi Liu, Hu Yang, Zusheng Jin, Jiang Zhu // IET Microwave Antennas Propagation. 2018. V. 12. № 15. P. 2307.
Калошин В.А., Фролова Е.В. // Журн. радиоэлектроники. 2014. № 1. http://jre.cplire.ru/jre/jan14/ 16/text.pdf.
Венецкий А.С., Калошин В.А. // РЭ. 2014. Т. 59. № 11. С. 1102.
Банков С.Е., Калошин В.А., Фролова Е.А. // РЭ. 2014. Т. 59. № 11.
Банков С.Е., Фролова Е.В. // РЭ. 2017. Т. 62. № 5. С. 463.
Калошин В.А., Ле Д.Т. // Журн. радиоэлектроники. 2018. № 9. http://jre.cplire.ru/jre/sep18/13/text.pdf.
Венецкий А.С., Калошин В.А., Нгуен К.Т., Фролова Е.В. // Журн. радиоэлектроники. 2018. № 1. http://jre.cplire.ru/jre/jan18/4/text.pdf.
Калошин В.А., Нгием Х.Д., Фролова Е.В. // Журн. радиоэлектроники. 2018. № 1. http://jre.cplire.ru/jre/jan18/3/text.pdf.
Калошин В.А., Ле Д.Т., Фролова Е.В. // РЭ. 2019. Т. 64. № 8. С. 768.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал