Радиотехника и электроника, 2021, T. 66, № 2, стр. 105-121
Многоканальная фильтрация микроволн с дипольными и киральными элементами в мета-интерферометре с резонатором Фабри–Перо
Г. А. Крафтмахер a, *, В. С. Бутылкин a, Ю. Н. Казанцев a, В. П. Мальцев a, И. П. Никитин a
a Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация
* E-mail: gkraft@ms.ire.rssi.ru
Поступила в редакцию 14.06.2020
После доработки 14.06.2020
Принята к публикации 29.07.2020
Аннотация
Экспериментально показано в диапазоне 3…6 ГГц новое применение дипольных и киральных элементов и структур на их основе в качестве одного из отражателей резонатора Фабри–Перо, расположенного в метаинтерферометре, которое позволяет управлять многоканальной фильтрацией микроволн. Продемонстрировано влияние управляемых резонансных эффектов в элементах на спектр резонатора и динамику интерферограммы. Исследованы особенности, связанные с применением разных элементов и структур: нагруженного варактором или стационарной емкостью диполя “бабочка”, ряда из трех одинарных колец с двумя разрывами, нагруженными двумя варакторами, а также решеток из спиральных элементов в 1.5 оборота и двойных разомкнутых колец. Теоретическое исследование проводили на примере метаинтерферометра с метаструктурой в виде бианизотропно-волноводного слоя с учетом возможности реализации режимов как прямой, так и обратной волны.
ВВЕДЕНИЕ
Интерес к метаструктурам, метаповерхностям и метаатомам сохраняется благодаря новым применениям и разработке новых оригинальных структур. На микроволнах известны магнитоэлектрические материалы, метаструктуры, метаповерхности и метаатомы, содержащие разомкнутые проводящие резонансные элементы, совместимые с элементами управления. Большое развитие получили работы, инициированные публикациями, связанными с исследованием киральных и бианизотропных сред [1–7] и предложениями возможных применений (“левые среды” [3, 4], микроволновые фильтры [5], радиопоглотители [6, 7]).
Обзору современных теоретических исследований киральных сред и метаматериалов посвящена работа [8]. Практическая значимость микроволновых фильтров благодаря возможности управления отмечается в [9]. Комбинации с ферритом позволяют усиливать невзаимные эффекты и управлять ими электрическим напряжением наряду с магнитостатическим полем [10, 11]. Новое применение метаматериалы нашли в резонаторах Фабри–Перо [12–15] и микроволновой интерферометрии [16, 17]. В [16] были обнаружены оригинальные функциональные возможности микроволновой интерферометрии при использовании метаструктуры в качестве управляемого разделителя пучка. Было показано, что применение ферритовой пластины приводит к специфическому проявлению невзаимных эффектов и возможности селективного магнитного управления. Структуры на основе феррита и диполя позволяют достичь магнитное и электрическое управление при воздействии ферромагнитного и дипольного резонансов на дисперсионные характеристики – селективно управляемую невзаимность прохождения микроволн в интерференционных полосах запрета, т.е. управление интерферограммой как внешним магнитостатическим полем, так и электрическим напряжением на варакторе. Особенности микроволновой интерферометрии с метаструктурами можно использовать при разработке селективно управляемых многополосных фильтров.
В [18] предложено применение метаструктуры на основе линейных резонансных проводов в качестве одного из отражателей резонатора Фабри–Перо, расположенного в метаинтерферомере, и обнаружена возможность селективного управления интерферограммой в диапазоне 3…6 ГГц.
В данной работе исследуем влияние других метаструктур и связанные с ними особенности в аналогичной ситуации. Это нагруженный варактором или конденсатором диполь “бабочка”, ряд из трех одинарных колец с двумя разрывами в каждом кольце, нагруженными двумя варакторами, а также решетка киральных планарных спиралей в 1.5 оборота и решетка двойных разомкнутых колец. Привлечение разнообразных метаструктур как в принципе известных, так и оригинальных, представляет интерес, поскольку наблюдаемые эффекты связаны с их резонансными свойствами, которые зависят от их вида и геометрии.
1. МЕТОДЫ И РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ
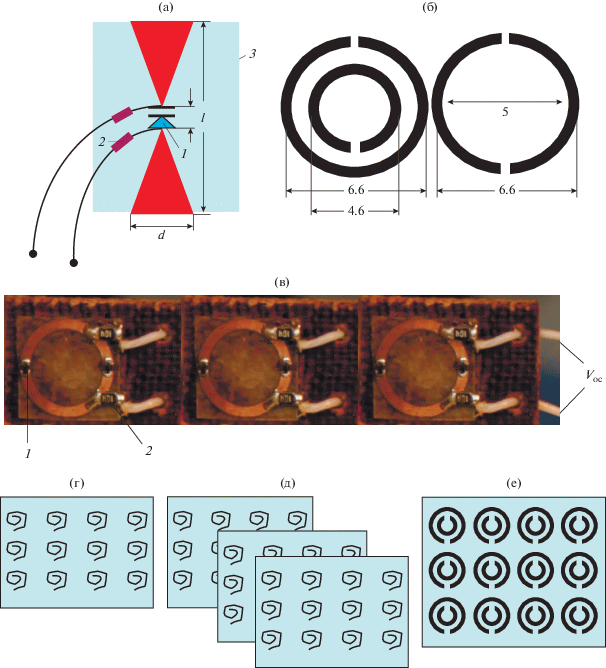
Исследуемые элементы и метаструктуры схематически представлены на рис. 1а–1е. Они выполнены методами фотолитографии на фольгированной полиамидной пленке.
Рис. 1.
Схемы исследованных элементов и метаструктур на их основе в качестве отражателя резонатора Фабри–Перо в тройниковом интерферометре: (а) нагруженный варактором диполь “бабочка” (d – ширина, l – высота, 1 – варактор, 2 – резистор RL, 3 – подложка); (б) двойное разомкнутое кольцо ПДРК и одинарное дважды разомкнутое кольцо ОК (размеры в мм); (в) ряд из трех нагруженных варакторами ОК (фото) (1 – варактор, 2 – резистор, 3 – подложка); (г, д) решетка и система из трех параллельно расположенных решеток из планарных спиралей ПС в полтора оборота; (ж) решетка ПДРК.
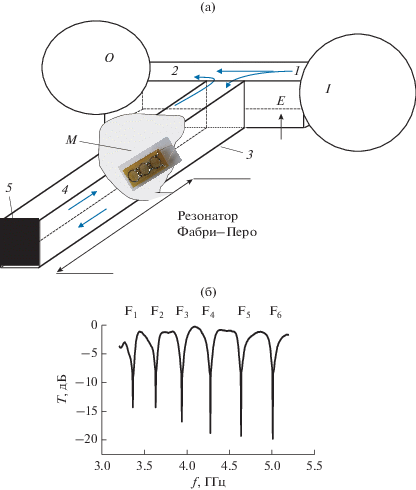
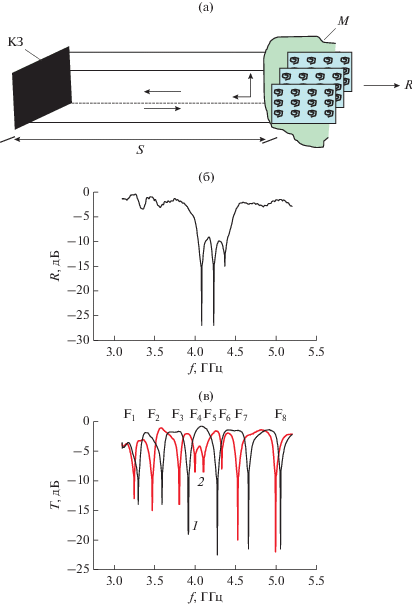
На рис. 2а показана схема волноводного тройникового интерферометра с метаструктурой M в виде ряда нагруженных варакторами одинарных колец. Метаструктура помещена вдоль направления распространения волны в закороченное h-плечо 3 (длина плеча равна 290 мм), на расстоянии s = = 110 мм от короткозамыкателя, образуя конфигурацию управляемого резонатора Фабри–Перо 4 отражательного типа между передней границей метаструктуры и короткозамыкателем. В отсутствие метаструктуры тройник трансформируется в интерферометр и обладает свойствами многополосного фильтра, измеренные частотные зависимости коэффициента прохождения T представлены на рис. 2б. Увеличивая длину плеча, можно увеличить число интерференционных полос.
Рис. 2.
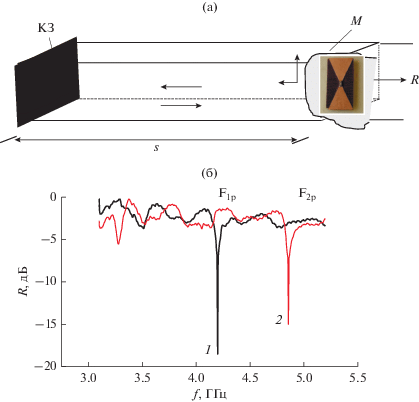
Схема метаинтерферометра (а): I – вход, O – выход, 1 – входной, 2 – выходной, 3 – закороченный волновод, М – метаструктура, 4 – резонатор Фабри–Перо между передней границей метаструктуры и короткозамыкателем, 5 – короткозамыкатель (КЗ); а также измеренные частотные зависимости (б) коэффициента прохождения T в метаинтерферометре в отсутствие метаструктуры.
Состояние интерферограммы характеризуем положением и глубиной полос запрета. Измеряем динамику частотной зависимости коэффициентов прохождения T = S21 на выходе O интерферометра при использовании разных метаструктур и при внешнем воздействии напряжения обратного смещения Vос на варакторе. Проводим сравнительный анализ с поведением резонанса в метаструктуре, измеряя коэффициенты прохождения T и отражения R = S11 в прямоугольном волноводе 48 × 24 мм. Измеряем коэффициент отражения R от резонатора Фабри–Перо, в котором в качестве отражателя используется та или другая метаструктура. Анализируем связь с динамикой R от резонатора Фабри–Перо.
Для электрического управления в разрывы диполя впаиваем варактор MA46H120, а в два разрыва одинарного кольца два варактора MA46H120. При Vос от 0 до 29 В емкость варактора меняется в пределах 6.5…0.55 пФ. К выходам варактора подключаем резисторы RL = 100 кОм, чтобы уменьшить влияние наведенных постоянных токов и, соответственно, паразитных резонансных эффектов. Размеры структур выбираем так, чтобы в диапазоне 3…6 ГГц панорамного измерителя КСВН возбуждался резонанс в элементах.
1.2. Диполь “бабочка” с варактором
Нагруженный варактором MA46H120 диполь “бабочка” (длина l = 22 мм, ширина у основания d = 10 мм) изготовлен из фольгированной полиамидной пленки толщиной 0.15 мм на 1.0-миллиметровой текстолитовой подложке (схема – рис. 1а, фото – рис. 3а).
Рис. 3.
Фото диполя “бабочка” с варактором (а) и измеренные частотные зависимости Т (1–4) и R (5, 6) в волноводе (б) при Vос = 0 (1, 5), 1.5 (2), 3 (3), 10 (4) и 20 В (6); и T в интерферометре (в) при Vос = 0 (1), 2 (2), 10 В (3).
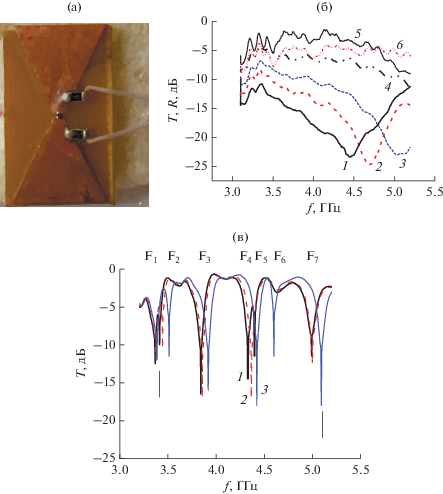
Частотные зависимости T и R от диполя в прямоугольном волноводе при разных величинах Vос представлены на рис. 3б. В отсутствие Vос на кривой T видим резонансный минимум $T_{{{\text{min}}}}^{{{\text{0В}}}}$ = –23 дБ и на кривой R соответствующий ему резонансный максимум отражения Rmax = –1.5 дБ, связанные с широким дипольным резонансом (ДР), который при изменении Vос от 0 до 3 В плавно смещается на 0.7 ГГц, от 4.4 до 5.1 ГГц. Резонанс охватывает практически весь заданный частотный диапазон 3…6 ГГц.
Проявление влияния резонанса в диполе на интерферограмму в интерферометре показано на рис. 3в, где представлены измеренные на выходе интерферометра частотные зависимости прохождения T при трех величинах Vос – 0, 2 и 10 В. Сравнивая их с интерферограммой пустого интерферометра (см. рис. 1б), видим изменение интерферограммы, нарушение периодичности интерференционных полос, изменение вида, ширины, глубины. При Vос = 0 В интерферограмма представляет собой интерференционную зависимость T от частоты с полосами запрета:
${\text{F}}_{1}^{{{\text{0В}}}}$ (частота $f_{1}^{{{\text{0V}}}}$ = 3.4 ГГц, глубина $T_{{{\text{1}}\,\,{\text{min}}}}^{{{\text{0В}}}}$ = = ‒12.5 дБ),
${\text{F}}_{2}^{{{\text{0В}}}}$ (3.4 ГГц, –10 дБ),
${\text{F}}_{3}^{{{\text{0В}}}}$ (3.84 ГГц, –16.5 дБ),
${\text{F}}_{4}^{{{\text{0В}}}}$ (4.32 ГГц, –14.5 дБ),
${\text{F}}_{5}^{{{\text{0В}}}}$ (4.4 ГГц, –11.5 дБ),
${\text{F}}_{6}^{{{\text{0В}}}}$ (5 ГГц, –11.5 дБ).
Наглядное представление о состоянии интерферограммы в случае Vос = 2 и 10 В дает табл. 1. При подаче Vос = 2 В происходит небольшое изменение интерферограммы. С увеличением Vос до 10 В в интерферограмме проявляются дополнительные резонансы, изменяется положение и глубина ряда полос запрета. Полосы ${\text{F}}_{4}^{{{\text{10В}}}}$ и ${\text{F}}_{5}^{{{\text{10В}}}}$ сливаются, проявляются полосы ${\text{F}}_{2}^{{{\text{10В}}}}$ и ${\text{F}}_{6}^{{{\text{10В}}}}$. Видим, что с диполем “бабочка” при изменении Vос происходит специфическое управление (синхронное, но неодинаковое изменение частоты, ширины и глубины разных полос). Это связано с тем, что для ДР характерна довольно широкая полоса, его влияние охватывает несколько интерференционных полос, при этом разные полосы подвергаются разному влиянию ДР.
Таблица 1.
Состояние интерферограммы с диполем, нагруженным варактором, при различных Vос
| Параметр | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|---|
| Vос = 0 В | |||||||
| f, ГГц Tmin, дБ |
3.4 –12.5 |
3.6 –2 |
3.84 –16.5 |
4.32 –14.5 |
4.4 –11.5 |
4.6 –3 |
5 –11.5 |
| Vос = 2 В | |||||||
| f, ГГц Tmin, дБ |
3.37 –12 |
3.44 –10.5 |
3.85 –17 |
4.36 –17 |
4.36 –17 |
4.63 –2.75 |
5.0 –12.5 |
| Vос = 10 В | |||||||
| f, ГГц Tmin, дБ |
3.4 –12 |
3.5 –11.5 |
3.9 –16 |
4.4 –18 |
4.4 –18 |
4.6 –11.5 |
5.1 –18 |
1.2 . Диполь “бабочка” с конденсатором
Рассмотрим, как меняются функциональные свойства интерферометра, когда в разрыв диполя вместо варактора впаиваем конденсатор с необходимым номиналом емкости, обеспечивающей возбуждение резонанса в заданном диапазоне. Подобрав соответствующую емкость и меняя конденсаторы, можно смещать резонанс в диполе, так же как и в случае с варактором при изменении напряжения. Необходимые исследования были проведены с тремя диполями, нагруженными разными емкостями C (C1 = 0.8 пФ, C2 = 0.5 пФ, C3 = 0.1 пФ). Диполь выполнен из фольгированной полиамидной пленки толщиной 0.15 мм на 0.5-миллиметровой подложке из гетинакса (рис. 4а).
Рис. 4.
Фото диполя с конденсатором (а) и измеренные частотные зависимости Т (кривые 1–3) и R (4, 5) в волноводе (б) при C = 0.8 (1, 4), 0.5 (2), 0.1 пФ (3, 5); и T в интерферометре (в) при C = 0.8 (1), 0.1 пФ (2).
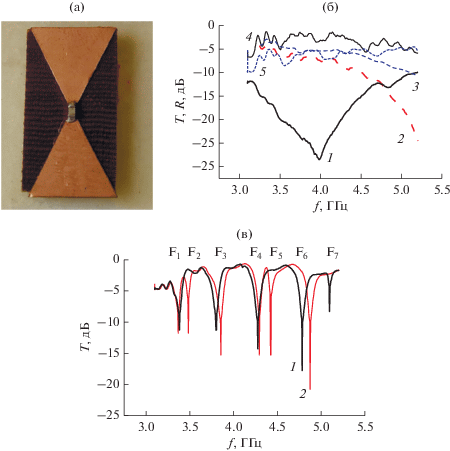
Результаты исследований приведены на рис. 4 и 5. Они получены измерениями по изложенной выше схеме: динамика дипольного резонанса ДР, измеренная в прямоугольном волноводе с диполем, состояние интерферограммы, полученное измерениями в интерферометре с диполем, и свойства резонатора Фабри–Перо с диполем в качестве одного из отражателей.
Рис. 5.
Схема резонатора Фабри–Перо с диполем в качестве отражателя (а) и измеренные частотные зависимости отражения R (б) при C = 0.8 (1) и 0.5 пФ (2).
Динамика управляемого ДР в прямоугольном волноводе продемонстрирована на частотных зависимостях T, изменяющихся при изменении емкости (рис. 4б). Легко видеть, что ДР, который проявляется как резонансный Tmin, наблюдается на разных частотах с разными диполями в зависимости от величины C. С уменьшением C резонанс смещается к высоким частотам, как и в случае с варактором. С диполем, нагруженным емкостью 0.8 пФ, широкий ДР наблюдаем на частоте f0.8 пФ = = 4 ГГц с резонансным Tmin = –29 дБ и Rmах = = ‒1.7 дБ. Измерения с другими диполями показывают, что при уменьшении емкости (это соответствует уменьшению емкости при увеличении Vос в случае диполя с варактором) ДР смещается к высоким частотам, уходя за пределы исследуемого диапазона 3…6 ГГц, при этом величина R уменьшается до –6 дБ. Видим, что поведение ДР для диполя с варактором и диполей с конденсаторами качественно идентичны.
При исследовании интерферограммы, измеряя частотную зависимость T на выходе интерферометра при разных величинах C (рис. 4в) и используя разные диполи, видим, что состояние интерферограммы с диполем 0.8 пФ отличается от интерферограммы с диполем 0.1 пФ. Изменения охватывают несколько полос (см. также табл. 2) подобно тому, как меняется интерферограмма с диполем, нагруженным варактором. Отметим, сравнивая с интерферограммой пустого интерферометра, уменьшение величин $T_{{{\text{2min}}}}^{{{\text{0}}{\text{.8}}\,\,{\text{пФ}}}}$ и $T_{{{\text{5min}}}}^{{{\text{0}}{\text{.8}}\,\,{\text{пФ}}}}$ в частотной области полос F2 и F5, соответствующей области возбуждения ДР.
Таблица 2.
Состояние интерферограммы при С1 = 0.8 и С2 = 0.1 пФ
| Параметр | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
| С1= 0.8 пФ | |||||||
| f, ГГц | 3.38 | 3.56 | 3.8 | 4.27 | 4.45 | 4.78 | 5.1 |
| Tmin, дБ | –11.3 | –2.2 | –11.3 | –14.3 | –1.7 | –17.8 | –8.3 |
| С2 = 0.1 пФ | |||||||
| f, ГГц | 3.37 | 3.48 | 3.85 | 4.29 | 4.42 | 4.87 | – |
| Tmin, дБ | –11.8 | –11.8 | –15.3 | –15.3 | –15.3 | –20.8 | – |
Схема и результаты измерений R от резонатора Фабри–Перо в случае C1 = 0.8 пФ и C2 = 0.5 пФ приведены на рис. 5. Частотная зависимость R представляет собой резонансный спектр с резонансными минимумами отражения в полосах F1р, F2р. При этом в зависимости от C резонансные эффекты эффективно проявляются на разных частотах. Так, при C1 = 0.8 пФ наблюдается полоса ${\text{F}}_{{{\text{1р}}}}^{{{\text{0}}{\text{.8}}\,\,{\text{пФ}}}}$ (частота $f_{{{\text{1р}}}}^{{{\text{0}}{\text{.8}}\,\,{\text{пФ}}}}$ = 4.2 ГГц, глубина $R_{{{\text{1р}}\,\,{\text{min}}}}^{{{\text{0}}{\text{.8}}\,\,{\text{пФ}}}}$ = = – 18.5 дБ), полоса ${\text{F}}_{{{\text{2р}}}}^{{{\text{0}}{\text{.8}}\,\,{\text{пФ}}}}$ имеет небольшую глубину и слабо проявляется.
С уменьшением величины C (C2 = 0.5 пФ) $R_{{{\text{1р}}\,\,{\text{min}}}}^{{{\text{0}}{\text{.5}}\,\,{\text{пФ}}}}$ = –3 дБ без изменения частоты, полоса же ${\text{F}}_{{{\text{2р}}}}^{{{\text{0}}{\text{.5}}\,\,{\text{пФ}}}}$ углубляется и наблюдается на более высоких частотах ($R_{{{\text{2р}}\,\,{\text{min}}}}^{{{\text{0}}{\text{.5}}\,\,{\text{пФ}}}}$ = –15 дБ, $f_{{{\text{2р}}}}^{{{\text{0}}{\text{.5}}\,\,{\text{пФ}}}}$ = 4.86 ГГц). Видим, что в зависимости от величины C резонансные эффекты (ДР в волноводе и в резонаторе) наблюдаются на разных частотах. При этом частоты полос ${\text{F}}_{{{\text{1р}}}}^{{{\text{0}}{\text{.8}}\,\,{\text{пФ}}}}$ и ${\text{F}}_{{{\text{2р}}}}^{{{\text{0}}{\text{.5}}\,\,{\text{пФ}}}}$ резонатора соответствует частотам ДР в волноводе.
Таким образом, наблюдается влияние резонанса в диполе, который перестраивается с изменением емкости конденсатора, на спектр резонатора Фабри–Перо и интерферограмму при сближении резонансных частот диполя и интерференционной полосы.
2. РЯД ИЗ ТРЕХ ОДИНАРНЫХ ДВАЖДЫ РАЗОМКНУТЫХ КОЛЕЦ, НАГРУЖЕННЫХ ДВУМЯ ВАРАКТОРАМИ MA46H120
Одинарные дважды разомкнутые кольцевые резонаторы (одинарные кольца ОК, их диаметр 6.6 мм) выполнены методом фотолитографии на фольгированной полиамидной пленке. В каждое кольцо впаиваем два варактора MA46H120. Ряд из трех ОК, расположенный на 1-миллиметровой текстолитовой подложке (${\text{см}}{\text{.}}$ рис. 1в и 6а), помещаем вдоль оси закороченного h-плеча интерферометра на расстоянии s = 110 мм так, что микроволновое магнитное поле пронизывает ось кольца. В этом случае в ОК возбуждается магнитный резонанс МР, обусловленный наведением резонансных кольцевых токов микроволновым магнитным полем h [19]. Особенности МР проявляются на частотных кривых отражения. В [19] было показано, что для проводящих киральных кольцевых элементов наряду с резонансным максимумом отражения наблюдается связанный с ним резонансный минимум, положение которого зависит от ориентации элемента (типа возбуждения). Так, при электрическом возбуждении резонансный минимум имеет место на более высоких частотах относительно резонансного максимума. При магнитном возбуждении резонансный минимум наблюдается на более низких частотах, при этом со стороны высоких частот относительно максимума коэффициент отражения медленно спадает, сохраняя довольно большую величину в некотором диапазоне частот.
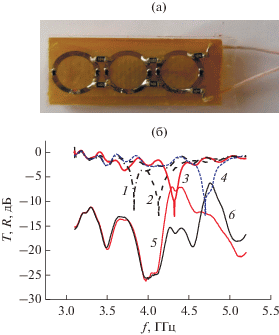
Исследуем динамику МР при наложении Vос в прямоугольном волноводе, как и в случае ДР диполя. Результаты измерений T и R приведены на рис. 6б. Видим, что МР, который проявляется в виде резонансного Tmin = –13 дБ плавно смещается к высоким частотам с увеличением Vос, при этом резонансный $R_{{{\text{mах}}}}^{{{\text{10В}}}}$ = –7 дБ, $R_{{{\text{mах}}}}^{{{\text{20В}}}}$ = –6 дБ. Наряду с резонансными максимумами R видим характерные для МР резонансные минимумы: $R_{{{\text{min}}}}^{{{\text{10В}}}}$ = –25 дБ, $f_{{R\,{\text{min}}}}^{{{\text{10В}}}}$ = 4 ГГц; $R_{{{\text{min}}}}^{{{\text{15В}}}}$ = –20 дБ, $f_{{R\,{\text{min}}}}^{{{\text{15В}}}}$ = 4.5 ГГц). С изменением Vос в пределах 7…15 В видим смещение МР на 0.88 ГГц, от 3.82 до 4.7 ГГц, с сохранением интенсивности резонанса.
Рис. 6.
Фото ряда из трех одинарных дважды разомкнутых колец ОК, нагруженных варакторами (а) и измеренные в прямоугольном волноводе частотные зависимости (б) прохождения T (1–4) и отражения R (5, 6) при Vос = 7 (1), 8 (2), 10 (3, 5), 15 В (4, 6).
Динамику интерферограммы интерферометра при изменении Vос можно оценить, измеряя частотную зависимость T на выходе интерферометра (рис. 7). В отсутствие Vос (см. рис. 7а) наблюдаем зависимость T со следующими интерференционными полосами запрета:
Рис. 7.
Измеренные частотные зависимости коэффициента прохождения T в интерферометре с ОК при Vос: 0 (а), 5.5 (б), 7.5 (в), 10.5 (г) и 12.5 В (д).
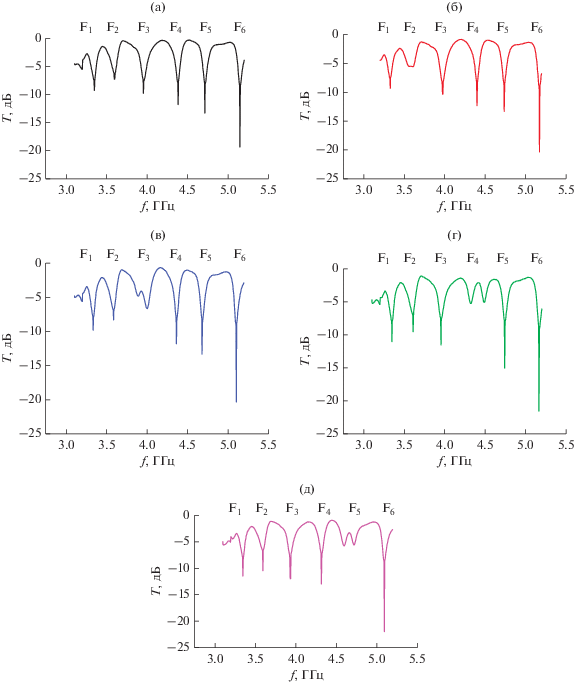
${\text{F}}_{1}^{{{\text{0В}}}}$ (частота $f_{1}^{{{\text{0В}}}}$ = 3.35 ГГц, глубина $T_{{1{\text{min}}}}^{{{\text{0В}}}}$ = = ‒9.3 дБ),
${\text{F}}_{2}^{{{\text{0В}}}}$ (3.6 ГГц, –7.3 дБ),
${\text{F}}_{3}^{{{\text{0В}}}}$ (3.95 ГГц, –9.8 дБ),
${\text{F}}_{4}^{{{\text{0В}}}}$ (4.38 ГГц, –12 дБ),
${\text{F}}_{5}^{{{\text{0В}}}}$ (4.71 ГГц, –13 дБ),
${\text{F}}_{6}^{{{\text{0В}}}}$ (5.14 ГГц, –19.3 дБ).
При Vос = 5.5 В (см. рис. 7б) подвергается воздействию полоса ${\text{F}}_{2}^{{{\text{5}}{\text{.5В}}}}$ (существенно меняется ее вид, глубина и ширина при сохранении вида и положения остальных полос). Интерферограмма имеет вид
${\text{F}}_{1}^{{{\text{5}}{\text{.5В}}}}$ (f15.5В= 3.35 ГГц, $T_{{{\text{1min}}}}^{{{\text{5}}{\text{.5В}}}}$ = –9.3 дБ ),
${\text{F}}_{2}^{{{\text{5}}{\text{.5В}}}}$ (3.59 ГГц, –5.4 дБ),
${\text{F}}_{3}^{{{\text{5}}{\text{.5V}}}}$ (3.97 ГГц, –10.3 дБ),
${\text{F}}_{4}^{{{\text{5}}{\text{.5V}}}}$ (4.4 ГГц, –12.3 дБ),
${\text{F}}_{5}^{{{\text{5}}{\text{.5V}}}}$ (4.73 ГГц, –13 дБ),
${\text{F}}_{6}^{{{\text{5}}{\text{.5V}}}}$ (5.17 ГГц, –20.3 дБ).
Полоса F3 подвергается воздействию при Vос = = 7.5 В (см. рис. 7в). Для изменения формы и ширины F4 необходимо приложить Vос = 10.5 В (см. рис. 7г); изменение в полосе F5 происходят при Vос = 12.5 В (рис. 7д).
При Vос = 7.5 В интерферограмма имеет вид
${\text{F}}_{1}^{{{\text{7}}{\text{.5В}}}}$ ($f_{1}^{{{\text{7}}{\text{.5В}}}}$ = 3.33 ГГц, $T_{{{\text{1min}}}}^{{{\text{7}}{\text{.5В}}}}$ = –9.8 дБ ),
${\text{F}}_{2}^{{{\text{7}}{\text{.5В}}}}$ (3.58 ГГц, –8.3 дБ),
${\text{F}}_{3}^{{{\text{7}}{\text{.5В}}}}$ (3.9 ГГц, –6.5 дБ),
${\text{F}}_{4}^{{{\text{7}}{\text{.5В}}}}$ (4.36 ГГц, –11.8 дБ),
${\text{F}}_{5}^{{{\text{7}}{\text{.5В}}}}$ (4.68 ГГц, –13 дБ),
${\text{F}}_{6}^{{{\text{7}}{\text{.5В}}}}$ (5.1 ГГц, –20.3 дБ).
При Vос = 10.5 В имеет вид
${\text{F}}_{1}^{{{\text{10}}{\text{.5В}}}}$ (3.35 ГГц, –11 дБ),
${\text{F}}_{2}^{{{\text{10}}{\text{.5В}}}}$ (3.6 ГГц, –9.5 дБ),
${\text{F}}_{3}^{{{\text{10}}{\text{.5В}}}}$ (3.95 ГГц, –11.5 дБ),
${\text{F}}_{4}^{{{\text{10}}{\text{.5В}}}}$ (4.4 ГГц, –5 дБ),
${\text{F}}_{5}^{{{\text{10}}{\text{.5В}}}}$ (4.74 ГГц, –15 дБ),
${\text{F}}_{6}^{{{\text{10}}{\text{.5В}}}}$ (5.16 ГГц, –21.5 дБ).
При Vос = 12.5 В – следующий вид:
${\text{F}}_{1}^{{{\text{12}}{\text{.5В}}}}$ (3.35 ГГц, –11.5 дБ),
${\text{F}}_{2}^{{{\text{12}}{\text{.5В}}}}$ (3.59 ГГц, –10.5 дБ),
${\text{F}}_{3}^{{{\text{12}}{\text{.5В}}}}$ (3.93 ГГц, –12 дБ),
${\text{F}}_{4}^{{{\text{12}}{\text{.5В}}}}$ (4.32 ГГц, –13 дБ) ,
${\text{F}}_{5}^{{{\text{12}}{\text{.5В}}}}$ (4.7 ГГц, –5.5 дБ),
${\text{F}}_{6}^{{{\text{12}}{\text{.5В}}}}$ (5.1 ГГц, –22 дБ).
Как видим, с изменением Vос уменьшается поочередно глубина интерференционной полосы (увеличивается Tmin) и одновременно увеличивается ее ширина с изменением формы, при этом могут наблюдаться раздвоенные резонансы. Полагаем, что эти эффекты связаны с проявлением связанных резонансов: МР в кольцах и резонанса в полосе, обусловленного переотражениями, при приближении управляемого МР к частоте полосы.
Таким образом, с ОК в интерферометре появляется возможность селективного электрического управления каждой полосой поочередно. Это можно объяснить тем, что в ОК возбуждается довольно узкий МР, который воздействует на отдельную полосу. При подаче Vос может меняться поочередно форма и ширина отдельной полосы запрета без изменения практически спектра других полос.
3. РЕШЕТКИ КИРАЛЬНЫХ ЭЛЕМЕНТОВ
Рассмотрим, как влияют на интерферограмму решетки (20 × 30 мм) киральных планарных спиралей (ПС) в 1.5 оборота и планарных двойных разомкнутых колец (ПДРК), см. схемы на рис. 1г, 1д, 1ж.
Резонансные эффекты в решетках, обусловленные наведением резонансных кольцевых токов в элементах, проявляются в волноводе на частотных зависимостях T. Результаты измерений представлены на рис. 8. Резонанс в ПС наблюдаем на частоте 4.5 ГГц, а в ПДРК вблизи 5.5 ГГц почти за пределами заданного диапазона длин волн (рис. 8б).
Рис. 8.
Вид решеток на основе планарных спиралей ПС и дважды разомкнутых колец ПДРК (а) и измеренные частотные зависимости T: б) в волноводе для ПС (1) и ПДРК (2); в) в метаинтерферометре в отсутствие решетки (1), для ПС (2); г) в метаинтерферометре в отсутствие решетки (1), для ПДРК (2).
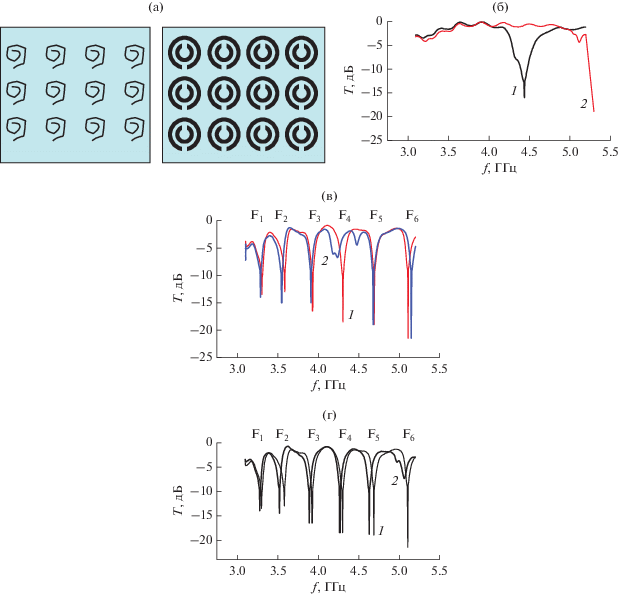
Исследуем интерферограмму с решетками в метаинтерферометре. Как видим из рис. 8в (для ПС) и 8г (для ПДРК), изменяется вид (форма, глубина, ширина) отдельной полосы в сравнении с пустым интерферометром. Для ПС изменения наблюдаются в полосе F4 на частоте 4.3 ГГц. С ПДРК воздействию подвергается полоса F6 (меняется форма, уменьшается глубина, увеличивается ширина) на частоте 5.1 ГГц. Видим, что изменения происходят с теми полосами, частоты которых близки к частотам резонанса в элементах решетки.
Результаты исследований при использовании трех решеток с ПС представлены на рис. 9.
Рис. 9.
Схема резонатора Фабри–Перо с системой из трех решеток ПС (а) и измеренные частотные зависимости: (б) R от резонатора; (в) T в метаинтерферометре в отсутствие решеток (1), для ПС (2).
Измерения в резонаторе Фабри–Перо (см. рис. 9б) демонстрируют трехгорбый резонанс с расщеплением резонансной кривой в диапазоне 4…4.5 ГГц, который, как показано ниже, соответствует диапазону особенностей в интерферограмме интерферометра.
На рис. 9в представлены частотные зависимости T на выходе интерферометра с тремя решетками ПС (расстояние между решетками равно 10 мм) в сравнении с пустым интерферометром.
Интерферограмма интерферометра в отсутствие решеток содержит шесть полос запрета с плавным увеличением глубины в направлении высоких частот.
Интерферограмма интерферометра с тремя решетками содержит восемь полос запрета:
F1ПС (3.24 ГГц, –13 дБ),
F2ПС (3.47 ГГц, –15 дБ),
F3ПС (3.8 ГГц, –14 дБ),
F4ПС (4.0 ГГц, –8.5 дБ),
F5ПС (4.1 ГГц, – 8.5 дБ),
F6ПС (4.3 ГГц, – 8 дБ),
F7ПС (4.5 ГГц, –20 дБ),
F8ПС (5.0 ГГц, –22 дБ).
По сравнению с пустым интерферометром интерферограмма перестроилась, изменилось количество и частоты полос. Внутри интерферограммы наблюдаются особенности в области трех полос запрета F4ПС, F5ПС и F6ПС в диапазоне 4…4.5 ГГц, в котором нарушается закономерность в частотной зависимости Tmin с ростом частоты, видим, что глубина и ширина этих полос существенно меньше, чем у остальных.
Очевидно, что особенности в интерферограмме с тремя решетками, отличающиеся от случая с одной решеткой, обусловлены влиянием резонансных эффектов, которые связаны не только с коллективным вкладом элементов в каждой решетке, но и с взаимовлиянием решеток друг на друга.
4. К ТЕОРИИ МЕТАИНТЕРФЕРОМЕТРА. ПРИМЕР БИАНИЗОТРОПНО- ВОЛНОВОДНОГО СЛОЯ КАК МЕТАСТРУКТУРЫ
Формирование интерферограммы в метаинтерферометре можно описывать, развивая подход работы [18], на примере интерферометра с резонатором Фабри–Перо, одним из отражателей которого служит отрезок волновода с метаматериальным заполнением.
Схема метаинтерферометра представлена на рис. 10а. Следуя [18], введем S-матрицу с элементами ${{S}_{{ml}}} = {{s}_{{ml}}}exp\left( {{\text{i}}{{\varphi }_{{ml}}}} \right)$. Индексы m и l относятся к соответствующим участкам интерферометра. Интерферограмма представляет собой частотную зависимость коэффициента передачи со входа I на выход O излучения по мощности $T(\omega ) = {{\left| {{{S}_{{OI}}}} \right|}^{2}}$. Здесь
(1)
$\begin{gathered} {{S}_{{OI}}} = \left\{ {{{S}_{{21}}} + {{S}_{{23}}}{{r}^{{(FP)}}}{{S}_{{31}}}} \right. \times \\ \times \,\,\left. {{{exp\left( { - {\text{2}}i{{k}_{3}}{{L}_{3}})} \right)} \mathord{\left/ {\vphantom {{exp\left( { - {\text{2}}i{{k}_{3}}{{L}_{3}})} \right)} {\left[ {1 - {{r}^{{(FP)}}}{{S}_{{33}}}exp\left( { - 2i{{k}_{3}}{{L}_{3}}} \right)} \right]}}} \right. \kern-0em} {\left[ {1 - {{r}^{{(FP)}}}{{S}_{{33}}}exp\left( { - 2i{{k}_{3}}{{L}_{3}}} \right)} \right]}}} \right\} \times \\ \times \,\,exp\left( { - i{\text{(}}{{k}_{1}}{{L}_{1}} + {{k}_{2}}{{L}_{2}})} \right) \\ \end{gathered} $(2)
$\begin{gathered} {{r}^{{(FP)}}} = r_{{33}}^{{(M)}} + t_{{43}}^{{(M)}}{{r}_{5}}t_{{34}}^{{(M)}} \times \\ \times \,\,exp{{\left( { - 2i{{k}_{4}}{{L}_{4}}} \right)} \mathord{\left/ {\vphantom {{\left( { - 2i{{k}_{4}}{{L}_{4}}} \right)} {\left[ {1 - r_{{44}}^{{(M)}}{{r}_{5}}exp\left( { - 2i{{k}_{4}}{{L}_{4}}} \right)} \right]}}} \right. \kern-0em} {\left[ {1 - r_{{44}}^{{(M)}}{{r}_{5}}exp\left( { - 2i{{k}_{4}}{{L}_{4}}} \right)} \right]}} \\ \end{gathered} $Рис. 10.
Схема метаинтерферометра (а): I – вход, O – выход, 1 и 2 – входной и выходной волноводы, 3 и 4 – полые волноводные отрезки, М – метаструктура, 5 – КЗ; б) фрагмент с метаструктурой (с бианизотропным слоем), LM – длина метаструктуры.
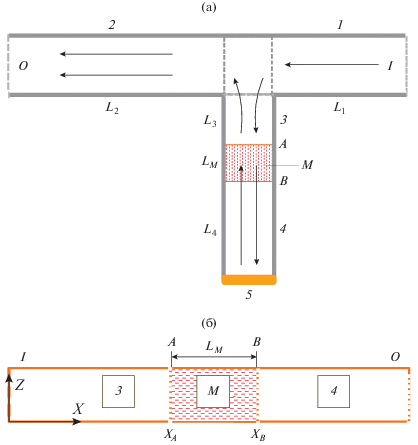
На рис. 10б изображен волновод, в котором имеется секция, заполненная метаматериалом. Эта секция с учетом переотражений между границами слоя сама является резонатором Фабри–Перо. Таким образом, отражателем резонатора в интерферометре (переотражения в системе отражатель–короткозамыкатель) является резонатор Фабри–Перо, представляющий собой слой метаматериала. В наших обозначениях его амплитудные коэффициенты отражения и пропускания имеют вид
(3a)
$\begin{gathered} r_{{33}}^{{(M)}} = r_{{33}}^{{(A)}} + t_{{M3}}^{{(A)}}r_{{MM}}^{{(B)}}t_{{3M}}^{{(A)}} \times \\ \times \,\,{{exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \mathord{\left/ {\vphantom {{exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}} \right. \kern-0em} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}; \\ \end{gathered} $(3б)
$\begin{gathered} r_{{44}}^{{(M)}} = r_{{44}}^{{(B)}} + t_{{3M}}^{{(B)}}r_{{MM}}^{{(A)}}t_{{M4}}^{{(B)}} \times \\ \times \,\,{{exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \mathord{\left/ {\vphantom {{exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}} \right. \kern-0em} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}; \\ \end{gathered} $(3в)
$\begin{gathered} t_{{43}}^{{(M)}} = t_{{M3}}^{{(A)}}t_{{4M}}^{{(B)}} \times \\ \times \,\,{{exp\left( { - i{{k}_{M}}{{L}_{M}}} \right)} \mathord{\left/ {\vphantom {{exp\left( { - i{{k}_{M}}{{L}_{M}}} \right)} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}} \right. \kern-0em} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}; \\ \end{gathered} $(3г)
$t_{{34}}^{{(M)}} = {{t_{{M4}}^{{(B)}}t_{{3M}}^{{(A)}}exp\left( { - i{{k}_{M}}{{L}_{M}}} \right)} \mathord{\left/ {\vphantom {{t_{{M4}}^{{(B)}}t_{{3M}}^{{(A)}}exp\left( { - i{{k}_{M}}{{L}_{M}}} \right)} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}} \right. \kern-0em} {\left[ {1 - r_{{MM}}^{{(A)}}r_{{MM}}^{{(B)}}exp\left( { - 2i{{k}_{M}}{{L}_{M}}} \right)} \right]}}.$Здесь ${{L}_{M}}$ – длина отрезка волновода с метаматериалом, ${{k}_{M}} = {{\omega {{n}_{M}}} \mathord{\left/ {\vphantom {{\omega {{n}_{M}}} c}} \right. \kern-0em} c}$ и ${{n}_{M}}$ – постоянная распространения и коэффициент замедления такого волновода, $t_{{ml}}^{{(A,B)}}$ – амплитудный коэффициент пропускания сигнала через границу A (или B) в область m из области l, $r_{{mm}}^{{(A,B)}}$ – амплитудный коэффициент отражения от границы A (или B) сигнала, пришедшего со стороны области m.
Рассмотрим электромагнитные волны
(4)
$\begin{gathered} \vec {\mathcal{E}} = 2Re\left\{ {\vec {E}\exp \left[ {i\left( {\omega t - \vec {k}\vec {R}} \right)} \right]} \right\}; \\ \vec {\mathcal{H}} = 2Re\left\{ {\vec {H}exp\left[ {i\left( {\omega t - \vec {k}\vec {R}} \right)} \right]} \right\}. \\ \end{gathered} $Волновой вектор $\vec {k}$ представляется проекциями
Как известно [21], проекции полей волн H10 незаполненного волновода равны
(5a)
${{E}_{x}} = {{E}_{z}} = 0;\,\,\,\,{{E}_{y}} = i{{({{\varepsilon }_{0}})}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}A\frac{{{{\lambda }_{c}}}}{\lambda }\sin \frac{{2\pi }}{{{{\lambda }_{c}}}}z;$(5б)
$\begin{gathered} {{H}_{x}} = {{\left( {{{\mu }_{0}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}Acos\frac{{2\pi }}{{{{\lambda }_{c}}}}z;\,\,\,\,{{H}_{y}} = 0; \\ {{H}_{z}} = iA{{({{\mu }_{0}})}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\gamma }_{x}}\frac{{{{\lambda }_{c}}}}{\lambda }\sin \frac{{2\pi }}{{{{\lambda }_{c}}}}z. \\ \end{gathered} $Здесь ${{\lambda }_{c}} = 2a$ – критическая длина волны (критическая частота ${{\omega }_{c}} = {{2\pi c} \mathord{\left/ {\vphantom {{2\pi c} {{{\lambda }_{c}}}}} \right. \kern-0em} {{{\lambda }_{c}}}}$). Величина
(6)
${{\gamma }_{x}} = n_{{{\text{пол}}}}^{ \pm } = \pm \sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} $определяет эффективные показатели замедления бегущих навстречу друг другу волн в пустом (полом) волноводе. Импедансы этих волн
(7)
$Z_{ \pm }^{{{\text{пол}}}} = \frac{{{{E}_{y}}}}{{{{H}_{z}}}} = \frac{{{{{\left( {{{\mu }_{0}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{{\left( {{{\varepsilon }_{0}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( { \pm \sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} } \right)}}.$Средние по времени векторы Пойнтинга направлены по/против оси X и равны
(8)
$\begin{gathered} \Pi _{{{\text{пол}}}}^{ \pm } = 2{{\left| {E_{y}^{ \pm }} \right|}^{2}}\operatorname{Re} {{\left( {Z_{{{\text{пол}}}}^{ \pm }} \right)}^{{ - 1}}} = \\ = 2{{\left| {{{A}^{ \pm }}} \right|}^{2}}\lambda _{c}^{2}{{\lambda }^{{ - 2}}}\operatorname{Re} n_{{{\text{пол}}}}^{ \pm }si{{n}^{2}}\left( {{{2\pi z} \mathord{\left/ {\vphantom {{2\pi z} {{{\lambda }_{c}}}}} \right. \kern-0em} {{{\lambda }_{c}}}}} \right) \times \\ \times \,\,exp\left( {2{{k}_{0}}x\operatorname{Im} n_{{{\text{пол}}}}^{ \pm }} \right). \\ \end{gathered} $Для волны, бегущей в направлении оси X, выбирается “+”, а для встречной волны “–”.
Остановимся в качестве примера на заполнении бианизотропным метаматериалом с эффективными параметрами вида [22]
(9)
$\begin{gathered} \varepsilon = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{x}}}&0&0 \\ 0&{{{\varepsilon }_{y}}}&0 \\ 0&0&1 \end{array}} \right),\,\,\,\,\mu = \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&1&0 \\ 0&0&{{{\mu }_{z}}} \end{array}} \right), \\ \kappa = \left( {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&0 \\ 0&\kappa &0 \end{array}} \right),\,\,\,\,{{\kappa }^{T}} = \left( {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&\kappa \\ 0&0&0 \end{array}} \right). \\ \end{gathered} $Исследования диэлектрической и магнитной проницаемостей и киральности метаматериалов с планарными дважды разомкнутыми кольцами в свободном пространстве ${\text{cм}}{\text{.}}$ также в [23–25], с бескиральными конфигурациями в [26, 27].
Проекции полей H10-волны в волноводе с этим заполнением равны [22]
(10a)
${{E}_{x}} = {{E}_{z}} = 0,\,\,\,\,{{E}_{y}} = i{{\left( {{{\varepsilon }_{0}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{A}_{{MM}}}\frac{{{{\lambda }_{c}}}}{\lambda }sin\frac{{2\pi }}{{{{\lambda }_{c}}}}z;$(10б)
$\begin{gathered} {{H}_{x}} = {{\left( {{{\mu }_{0}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{A}_{{MM}}}cos\frac{{2\pi }}{{{{\lambda }_{c}}}}z;\,\,\,\,{{H}_{y}} = 0; \\ {{H}_{z}} = i{{\left( {{{\mu }_{0}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{A}_{{MM}}}\left( {{{\gamma }_{x}} - i\kappa } \right)\frac{{{{\lambda }_{c}}}}{{\lambda {{\mu }_{z}}}}sin\frac{{2\pi }}{{{{\lambda }_{c}}}}z. \\ \end{gathered} $Здесь ${{A}_{{MM}}}$ – амплитуда волны в метаматериальной области, показатель замедления ${{\gamma }_{x}}$ волны определяется соотношением
(11)
${{\gamma }_{x}} = n_{{MM}}^{ \pm } = \pm \sqrt {{{\varepsilon }_{y}}{{\mu }_{z}} - {{\kappa }^{2}} - {{{{\mu }_{z}}{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{z}}{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} .$Импедансы волн
(12)
$\begin{gathered} Z_{{MM}}^{ \pm } = \frac{{{{E}_{y}}}}{{{{H}_{z}}}} = \frac{{{{{\left( {{{\mu }_{0}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\mu }_{z}}}}{{{{{\left( {{{\varepsilon }_{0}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( {n_{{MM}}^{ \pm } - i\kappa } \right)}} = \\ = \frac{{{{{\left( {{{\mu }_{0}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\mu }_{z}}}}{{{{{\left( {{{\varepsilon }_{0}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( { \pm \sqrt {{{\varepsilon }_{y}}{{\mu }_{z}} - {{\kappa }^{2}} - {{{{\mu }_{z}}{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{z}}{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - i\kappa } \right)}}. \\ \end{gathered} $Средние по времени векторы Пойнтинга направлены по/против оси X и равны
(13)
$\begin{gathered} {{\Pi }_{ \pm }} = 2{{\left| {E_{у}^{ \pm }} \right|}^{2}}\operatorname{Re} {{\left( {Z_{{MM}}^{ \pm }} \right)}^{{ - 1}}} = \\ = 2{{\left| {A_{{MM}}^{ \pm }} \right|}^{2}}c\lambda _{c}^{2}{{\lambda }^{{ - 2}}}\mu _{z}^{{ - 1}}\operatorname{Re} n_{{MM}}^{ \pm } \times \\ \times \,\,si{{n}^{2}}\left( {{{2\pi z} \mathord{\left/ {\vphantom {{2\pi z} {{{\lambda }_{c}}}}} \right. \kern-0em} {{{\lambda }_{c}}}}} \right)exp\left( {2{{k}_{0}}x\operatorname{Im} n_{{MM}}^{ \pm }} \right). \\ \end{gathered} $Ситуации, в которых волны в волноводе с метаматериалом являются “прямыми” и “обратными”, существенно различаются. У прямых волн направления распространения фазы и энергии совпадают, у обратных – противоположны [28]. Здесь специально отметим, что коэффициент замедления, определяющий в (3) постоянную распространения ${{k}_{M}}$, надо брать со знаком “плюс” (т.е. ${{n}_{M}} = n_{{MM}}^{ + }$, см. (11)), когда волна в метаматериально-заполненном волноводе прямая, и со знаком “минус” (т.е. ${{n}_{M}} = n_{{MM}}^{ - }$), если волна в метаматериально-заполненном волноводе обратная.
Определим коэффициенты прохождения и отражения от границ слоя. На любой границе (например, ${{X}_{A}}$ в случае отсутствия незаполненного волновода 3 при полубесконечности заполненного волновода 2) из условия непрерывности тангенциальных компонент полей падающей, отраженной и прошедшей волн
(14)
$\begin{gathered} E_{y}^{{{\text{пад}}}}({{X}_{A}}) + E_{y}^{{{\text{отр}}}}({{X}_{A}}) = E_{y}^{{{\text{прош}}}}({{X}_{A}}), \\ H_{z}^{{{\text{пад}}}}({{X}_{A}}) + H_{z}^{{{\text{отр}}}}({{X}_{A}}) = H_{z}^{{{\text{прош}}}}({{X}_{A}}) \\ \end{gathered} $для коэффициентов прохождения $t = {{E_{y}^{{{\text{прош}}}}} \mathord{\left/ {\vphantom {{E_{y}^{{{\text{прош}}}}} {E_{y}^{{{\text{пад}}}}}}} \right. \kern-0em} {E_{y}^{{{\text{пад}}}}}}$ и отражения $r = {{E_{y}^{{{\text{отр}}}}} \mathord{\left/ {\vphantom {{E_{y}^{{{\text{отр}}}}} {E_{y}^{{{\text{пад}}}}}}} \right. \kern-0em} {E_{y}^{{{\text{пад}}}}}}$ имеем систему уравнений
(15)
$\left\{ \begin{gathered} t - r = 1 \hfill \\ t\rho _{{{\text{прош}}}}^{{{\text{пад}}}} - r\rho _{{{\text{отр}}}}^{{{\text{пад}}}} = 1 \hfill \\ \end{gathered} \right.,$где использованы отношения импеданса падающей волны к импедансам прошедшей и отраженной волн $\rho _{{{\text{прош}}}}^{{{\text{пад}}}} = {{Z_{{MM}}^{{{\text{пад}}}}} \mathord{\left/ {\vphantom {{Z_{{MM}}^{{{\text{пад}}}}} {Z_{{MM}}^{{{\text{прош}}}}}}} \right. \kern-0em} {Z_{{MM}}^{{{\text{прош}}}}}}$, $\rho _{{{\text{отр}}}}^{{{\text{пад}}}} = {{Z_{{MM}}^{{{\text{пад}}}}} \mathord{\left/ {\vphantom {{Z_{{MM}}^{{{\text{пад}}}}} {Z_{{MM}}^{{{\text{отр}}}}}}} \right. \kern-0em} {Z_{{MM}}^{{{\text{отр}}}}}}$. Решения этих уравнений имеют вид
(16)
$\begin{gathered} t = {{\left( {1 - \rho _{{{\text{отр}}}}^{{{\text{пад}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \rho _{{{\text{отр}}}}^{{{\text{пад}}}}} \right)} {\left( {\rho _{{{\text{прош}}}}^{{{\text{пад}}}} - \rho _{{{\text{отр}}}}^{{{\text{пад}}}}} \right)}}} \right. \kern-0em} {\left( {\rho _{{{\text{прош}}}}^{{{\text{пад}}}} - \rho _{{{\text{отр}}}}^{{{\text{пад}}}}} \right)}}, \\ r = {{\left( {1 - \rho _{{{\text{прош}}}}^{{{\text{пад}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \rho _{{{\text{прош}}}}^{{{\text{пад}}}}} \right)} {\left( {\rho _{{{\text{прош}}}}^{{{\text{пад}}}} - \rho _{{{\text{отр}}}}^{{{\text{пад}}}}} \right)}}} \right. \kern-0em} {\left( {\rho _{{{\text{прош}}}}^{{{\text{пад}}}} - \rho _{{{\text{отр}}}}^{{{\text{пад}}}}} \right)}}. \\ \end{gathered} $В соответствии с принципом причинности падающей является волна, несущая энергию к рассматриваемой границе, отраженной – волна, несущая энергию от границы в том же волноводе, а прошедшей – волна, несущая энергию от границы в примыкающем волноводе. Направления потоков энергии определяются знаком векторов Пойнтинга этих волн.
4.1. Коэффициенты отражения и прохождения уединенных границ
Из (10) видно, что условием существования обратных волн является отрицательность ${{\mu }_{z}}$. В связи с этим сгруппируем результаты по знаку ${{\mu }_{z}}$.
I. Случай ${{\mu }_{z}} > 0$.
Падение волны на границу A со стороны незаполненного волновода $(3 \to M)$
(17a)
$r_{{33}}^{{(A)}} = \frac{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right)}}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right)}},$(17б)
$t_{{M{\text{3}}}}^{{(A)}} = \frac{{2{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right)}}.$Падение на границу A с метаматериально заполненной стороны $({\text{3}} \leftarrow M)$
(18a)
$r_{{MM}}^{{(A)}} = \frac{{\left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa } \right) - {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right)}},$(18б)
$t_{{{\text{3}}M}}^{{(A)}} = \frac{{2\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa }}.$Падение на границу B со стороны незаполненного волновода $(M \leftarrow 4)$
(19a)
$r_{{44}}^{{(B)}} = \frac{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa } \right)}}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa } \right)}},$(19б)
$t_{{M{\text{4}}}}^{{(B)}} = \frac{{2{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa } \right)}}.$Падение на границу B с метаматериально-заполненной стороны $(M \to 4)$
(20a)
$r_{{MM}}^{{(B)}} = \frac{{\left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right) - {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa } \right)}},$(20б)
$t_{{4M}}^{{(B)}} = \frac{{2\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa }}.$II. Случай ${{\mu }_{z}} < 0$.
Падение волны на границу A со стороны незаполненного волновода $(3 \to M)$
(21a)
$r_{{33}}^{{(A)}} = \frac{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa } \right)}},$(21б)
$t_{{M{\text{3}}}}^{{(A)}} = \frac{{2{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + i\kappa } \right)}}.$Падение волн на границу A с метаматериально-заполненной стороны $(3 \leftarrow M)$
(22a)
$r_{{MM}}^{{(A)}} = \frac{{\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} + {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - i\kappa }}{{\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + i\kappa }},$(22б)
$t_{{{\text{3}}M}}^{{(A)}} = \frac{{2\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} }}{{\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + i\kappa }}.$Падение волны на границу B со стороны незаполненного волновода $(M \leftarrow 4)$
(23a)
$r_{{44}}^{{(B)}} = \frac{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right)}}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right)}},$(23б)
$t_{{M{\text{4}}}}^{{(B)}} = \frac{{2{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{{{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - \left( {\sqrt {\left( {{{\varepsilon }_{y}} - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} \right){{\mu }_{z}} - {{\kappa }^{2}}} - i\kappa } \right)}}.$Падение волн на границу B с метаматериально-заполненной стороны $(M \to 4)$
(24a)
$r_{{MM}}^{{(B)}} = \frac{{\sqrt {{{\varepsilon }_{y}}{{\mu }_{z}} - {{\kappa }^{2}} - {{{{\mu }_{z}}{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{z}}{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} + i\kappa + {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{\sqrt {{{\varepsilon }_{y}}{{\mu }_{z}} - {{\kappa }^{2}} - {{{{\mu }_{z}}{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{z}}{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - i\kappa - {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }},$(24б)
$t_{{{\text{4}}M}}^{{(B)}} = \frac{{2\sqrt {{{\varepsilon }_{y}}{{\mu }_{z}} - {{\kappa }^{2}} - {{{{\mu }_{z}}{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{z}}{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}{{\sqrt {{{\varepsilon }_{y}}{{\mu }_{z}} - {{\kappa }^{2}} - {{{{\mu }_{z}}{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{z}}{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} - i\kappa - {{\mu }_{z}}\sqrt {1 - {{{{\lambda }^{2}}} \mathord{\left/ {\vphantom {{{{\lambda }^{2}}} {\lambda _{c}^{2}}}} \right. \kern-0em} {\lambda _{c}^{2}}}} }}.$Опираясь на приведенные выше соотношения, можно выявить парциальные, относительно независимые механизмы, которые, действуя совместно, определяют вид интерферограммы как частотной зависимости коэффициента пропускания метаинтерферометра. Это:
1) отстройка частоты от критической частоты волновода (через ${\lambda \mathord{\left/ {\vphantom {\lambda {{{\lambda }_{c}}}}} \right. \kern-0em} {{{\lambda }_{c}}}}$);
2) частотное различие набегов фазы при прохождении между отражателями резонаторов, разное в резонаторах разной длины (L3, LM, L4), включая различие их кратностей $2\pi $;
3) частотная дисперсия элементов S-матрицы волноводного разветвления;
4) частотная дисперсия элементов тензоров диэлектрической и магнитной проницаемостей и киральности (через дисперсию коэффициента замедления ${{n}_{{\text{M}}}}$ в заполненном волноводе и коэффициентов отражения и пропускания границ между заполненным и незаполненными волноводами). Здесь важны резонансы, частоты которых определяются электрической емкостью метаатомов, составляющих метаматериал. Подключение конденсаторов [29], варакторов и PIN-диодов [5, 30] позволит производить дискретную и плавную перестройку интерферограмм.
Наличие нескольких парциальных механизмов, определяющих интерферограммы, предоставляет более широкие и разнообразные возможности формирования интерферограмм подходящего вида. Это дополняет продемонстрированный в экспериментах потенциал, связанный с выбором метаструктуры. Возбуждение плазменно-поляритонных волн или высших волноводных мод может предоставить новые возможности (хотя многоволновость и осложнит теоретический анализ [31]).
Таким образом, получены аналитически результаты прохождения и отражения на границах бианизотропного слоя, рассматриваемого как своеобразный резонатор Фабри–Перо метаструктуры, который является одним из отражателей резонатора Фабри–Перо в интерферометре, т.е. метаинтерферометр содержит резонатор в резонаторе. Теоретические результаты свидетельствуют о существенном влиянии тензорных параметров киральности, диэлектрической и магнитной проницаемости и подтверждают разнообразные возможности, связанные с выбором метаструктуры, что и наблюдается экспериментально.
ЗАКЛЮЧЕНИЕ
Получены экспериментальные результаты, открывающие пути для новых методов и подходов в разработке переключаемых и управляемых многополосных микроволновых фильтров, востребованных в многофункциональных многоканальных телекоммуникационных системах.
Предложено новое применение метаструктуры с проводящими резонансными дипольными и киральными элементами в качестве отражателя резонатора Фабри–Перо в интерферометре. Резонатор формируется при расположении метаструктуры в закороченном плече волноводного тройникового интерферометра на некотором расстоянии от короткозамыкателя. Исследованы функциональные возможности интерферометра при использовании разных метаструктур. Использовались метаструктуры в виде диполя “бабочка”; кольцевых элементов, меньших длины волны (ряда ОК из трех одинарных колец с двумя разрывами, нагруженными двумя варактором в каждом кольце; решетки ПС из спиральных элементов в 1.5 оборота, решетки ПДРК из двойных разомкнутых колец, а также системы из трех решеток ПС).
Измерена динамика интерферограммы с метаструктрами в диапазоне 3…6 ГГц. Проведен сравнительный анализ с результатами измерений в волноводе и резонаторе Фабри–Перо.
Продемонстрировано воздействие дипольного резонанса ДР, возбуждаемого в диполе микроволновым электрическим полем, на полосы запрета интерферограммы при изменениях напряжения обратного смещения Vос на варакторе или емкости C конденсатора.
Показано воздействие магнитного резонанса, возбуждаемого микроволновым магнитным полем в ОК, на отдельную полосу запрета в интерферограмме с изменением формы, глубины и ширины полосы. С изменением Vос и смещением МР воздействию подвергается поочередно каждая полоса запрета.
Показано воздействие резонансных эффектов с решетками ПС и ПДРК. Продемонстрированы особенности в интерферограмме в диапазоне, соответствующем диапазону возбуждения резонанса. С одной решеткой практически не нарушается интерференционный спектр в интерферограмме, воздействию подвергается одна полоса (меняется форма, уменьшается глубина, увеличивается ширина). С тремя решетками меняется вид резонанса (расщепление на три пика), в интерферограмме наблюдается увеличение числа полос запрета и особенности в трех полосах в диапазоне возбуждения резонанса.
Показано, что ДР в диполе оказывает воздействие на несколько полос, что можно объяснить тем, что в диполе возбуждается довольно широкий резонанс, тогда как узкий МР в ОК позволяет обеспечить селективное воздействие на одну полосу запрета.
Показано, что для всех метаструктур особенности в интерферограмме наблюдаются в полосах запрета, частоты которых близки к частотам резонанса в элементах. При смещении резонансов подачей электрического напряжения на варакторе или заменой элемента изменяется интерферограмма в зависимости от свойств резонанса, разных для разных метаструктур.
Получены аналитические соотношения, которые выявляют механизмы, определяющие вид интерферограммы.
Список литературы
Lindell I.V., Sihvola A.H., Tretyakov S.A., Viitanen A.J. // Electromagnetic Waves in Chiral and Bi-isotropic Media. Norwood, MA: Artech House. 1994.
Костин М.В., Шевченко В.В. // РЭ. 1998. Т. 43. № 8. С. 921.
Smith D.R., Padilla W.J., Vier D.C. et al. // Phys. Rev. Lett. 2000. V. 84. № 18. P. 4184.
Pendry J., Holden A., Robbins D., Stewart W. // IEEE Trans. 1999. V. MTT-47. № 11. P. 2075.
Gil I., Garcia-Garcia J., Bonache J. et al. // Electron. Lett. 2004. V.40. № 21. P. 1347.
Varadan V.K., Varadan V.V., Lakhtakia A. // J. Wave-Material Interaction. 1987. V. 2. № 1. P. 71.
Bohren C.F., Luebbers R., Langdon H.S., Hunsberger F. // Appl. Opt. 1992. V. 31. № 30. P. 6403.
Tretyakov S.A. // J. Opt. 2017. V. 19. № 1. P. 013002.
Cameron R., Kudsia C., Mansour R. // Microwave Filters for Communication Systems: Fundamentals, Design, and Applications. John Wiley & Sons, Inc. 2018.
Крафтмахер Г.А., Бутылкин В.С., Казанцев Ю.Н. // Письма в ЖТФ. 2013. Т. 39. № 6. С. 505.
Kraftmakher G., Butylkin V., Kazantsev Y., Maltsev V. // Electron. Lett. 2017. V. 53. № 18. P. 1264.
Antonenko J.V., Gribovsky A.V., Kuzmichev I.K. // Telecommunications and Radio Engineering (English translation of Elektrosvyaz and Radiotekhnika). 2018. V. 77. № 12. P. 1029.
Банков С.Е., Дупленкова М.Д., Фролова Е.В. // Журн. радиоэлектроники. 2013. № 7. С. 8. https://elibrary.ru/item.asp?id=20362390.
Krupka J., Cwikla A., Mrozowski M. et al. // IEEE Trans. 2005. V. UFFC-52. № 9. P. 1443.
Liu Z.G., Zhang W.X., Fu D.L. et al. // Microwave and Optical Technology Lett. 2008. V. 50. № 6. P. 1623.
Крафтмахер Г.А., Бутылкин В.С., Казанцев Ю.Н., Мальцев В.П. // Письма в ЖЭТФ. 2019. Т. 109. № 4. С. 224.
Крафтмахер Г.А., Бутылкин В.С., Казанцев Ю.Н., Мальцев В.П. // РЭ. 2019. Т. 64. № 11. С. 1070.
Крафтмахер Г.А., Бутылкин В.С., Казанцев Ю.Н. и др. // РЭ. 2021. Т. 66. № 1. С. 3.
Kraftmakher G.A., Butylkin V.S., Kazantsev Yu.N. et al. // Appl. Phys. A. 2017. V.123. № 1. P. 56.
Stone J.M. // Radiation and Optics: An Introduction to the Classical Theory. N.Y.: McGraw-Hill, 1963.
Вайнштейн Л.А. // Электромагнитные волны. М.: АСТ, 1988.
Бутылкин В.С., Крафтмахер Г.А. // РЭ. 2008. Т. 53. № 1. С. 5.
Marqu’es R., Medina F., Rafii-El-Idrissi R. // Phys. Rev. B. 2002. V. 65. № 14. P. 144440.
Sauviac B., Simovski C., Tretyakov S. // Electromagnetics. 2004. V. 24. № 5. P. 317.
Бутылкин В.С., Крафтмахер Г.А. // РЭ. 2006. Т. 51. № 5. С. 518.
Simovski C.R., Belov P.A., He S. // IEEE Trans. 2003. V. AP-51. № 10. P. 2582.
Бутылкин В.С., Крафтмахер Г.А. // РЭ. 2008. Т. 53. № 7. С. 800.
Шевченко В.В. // Успехи физ. наук. 2007. Т. 177. № 3. С. 301.
Aydin K., Ozbay E. // J. Appl. Phys. 2007. V. 101. № 2. P. 024911.
Kholodnyak D., Serebryakova E., Vendik I., Vendik O. // IEEE Microw. Wireless Comp. Lett. 2006. V. 16. № 5. P. 258.
Банков С.Е. // Электромагнитные кристаллы. М.: Физматлит, 2010.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


