Радиотехника и электроника, 2021, T. 66, № 2, стр. 145-154
Вероятностные характеристики бестестовых методов адаптивной коррекции сигналов
М. Л. Маслаков *
Российский институт мощного радиостроения
199178 Санкт-Петербург, 11-я линия В.О., 66, Российская Федерация
* E-mail: maslakovml@gmail.com
Поступила в редакцию 27.08.2019
После доработки 25.06.2020
Принята к публикации 06.07.2020
Аннотация
Разработана модель и выведены выражения для оценки вероятностных характеристик бестестовых методов адаптивной коррекции сигналов, а именно вероятности устойчивой работы системы связи за заданное время и среднего времени устойчивой работы. Показаны зависимости вероятности нахождения сегмента сигнала и расчета новых (обновления) коэффициентов корректирующего фильтра, а также вероятности срыва процедуры бестестовой адаптивной коррекции. Проведенный анализ демонстрирует работоспособность методов бестестовой адаптивной коррекции сигналов при использовании их в каналах с межсимвольной интерференцией при относительно невысоких значениях отношения сигнал-шум, порядка 8…15 дБ.
ВВЕДЕНИЕ
При передаче данных по каналам связи, характеризующимися нестационарностью характеристик и многолучевым распространением, таких как, например, коротковолновый (КВ) канал, обычно применяют методы адаптивной коррекции сигналов [1]. Сущность адаптивной коррекции заключается в построении корректирующего фильтра (КФ) или эквалайзера, компенсирующего искажения сигнала, внесенные радиоканалом. Так, для расчета коэффициентов КФ в известных одночастотных КВ-модемах передачи данных [2] в передаваемый сигнал осуществляют периодические вставки тестовых сигналов. При этом функционирование такого модема предполагает оперативное изменение коэффициентов КФ при изменении состояния радиоканала, поэтому на передачу тестовых сигналов затрачивается от 30 до 50% временного ресурса [2].
В настоящее время тенденции развития современных систем передачи данных характеризуются повышающимися требованиями к максимально эффективному использованию выделенного частотно-временно́го ресурса радиоканала [1]. Поэтому большой интерес приобретает концепция построения бестестовых систем передачи данных. При этом расчет коэффициентов КФ осуществляется по принимаемым информационным сигналам. Построению бестестовых методов адаптивной коррекции посвящены работы [3–5].
Однако при использовании таких методов существует вероятность так называемого “срыва” процедуры коррекции [6], схожего с эффектом размножения ошибок, возникающим при использовании в процедуре адаптивной коррекции алгоритма обратной связи по решению [7]. Данный эффект вызван возможным использованием ошибочного сегмента, вследствие ошибок демодуляции, а также невозможностью своевременно найти соответствующий сегмент, в результате чего коэффициенты КФ, найденные на предыдущем шаге, могут “устареть”. Поэтому в работе [8] автором предложено ввести такие показатели как вероятность устойчивой работы за заданное время и среднее время устойчивой работы.
Цель данной работы – оценка вероятностных характеристик бестестовых методов адаптивной коррекции сигналов.
1. МОДЕЛЬ СИСТЕМЫ ПЕРЕДАЧИ ДАННЫХ С БЕСТЕСТОВОЙ АДАПТИВНОЙ КОРРЕКЦИЕЙ
Методы бестестовой адаптивной коррекции [3–5] предполагают использование сегмента информационного сигнала для расчета импульсной характеристики (ИмХ) канала связи и соответствующих коэффициентов КФ. В основе метода лежит гипотеза, что информационная последовательность представляет собой случайный набор символов (бит), обычно равновероятных. Кроме того, к кодированным символам кодового блока часто [2] добавляют скремблирующую последовательность, цель которой сделать поток случайным набором бит без длинных сегментов повторяющихся “0” или “1”.
Таким образом, среди уже демодулированных информационных символов необходимо найти сегмент, который может быть использован в качестве тестового сигнала. Данный сегмент должен обладать “хорошими” спектральными свойствами, т.е. равномерно занимать всю используемую полосу частот и не иметь нулей в этой полосе. Для контроля достоверности используемого информационного сегмента необходимо провести анализ результатов декодирования, при этом поиск сегментов производится только в тех кодовых блоках, в которых используемым кодом было обнаружено число ошибок не более заданного.
Рассмотрим подробнее процесс приема информационного закодированного помехоустойчивым кодом сообщения в системе связи с бестестовой адаптивной коррекцией сигнала. На рис. 1 представлена упрощенная модель передачи и приема сигнала с использованием метода бестестовой адаптивной коррекции сигналов на основе анализа результатов декодирования. Для определенности рассматриваем КВ-систему передачи данных, использующую сигналы с когерентной фазовой модуляцией [2, 3, 8].
Рис. 1.
Модель передачи и приема сигнала при использовании бестестовой адаптивной коррекцией сигналов, МСИ – межсимвольная интерференция.
Введем индекс $m$, которым обозначим номер шага, соответствующий также номеру передаваемого кодового блока. Информационный сигнал, соответствующий $m$-му кодовому блоку, обозначим как ${{s}^{m}}(t)$. При этом полагаем, что ИмХ канала изменяется дискретно и постоянна на длительности сигнала ${{s}^{m}}(t)$ – ${{T}_{s}}$. На вход приемника поступает искаженный зашумленный сигнал ${{u}^{m}}(t)$, определяемый выражениями
где $h_{{\text{к}}}^{m}(t)$ – соответствующая данному интервалу ИмХ канала связи; ${{\bar {u}}^{m}}(t)$ – искаженный принимаемый сигнал, соответствующий $m$-му кодовому блоку; ${{\xi }^{m}}(t)$ – аддитивный шум.
На выходе КФ получаем откорректированный сигнал ${{\hat {s}}^{m}}(t)$, определяемый из выражения
где $h_{{{\text{КФ}}}}^{m}(t)$ – ИмХ КФ.
При этом полагая, что
где $\delta (t)$ – дельта-функция, имеет место
Пределы интегрирования в (1а), (1б) и (2) умышленно опускаем, так как длительности сигналов ${{s}^{m}}(t)$ и ${{u}^{m}}(t)$ отличны (в основном из-за наличия многолучевости). При этом не берем во внимание наличие наложения “хвостов” сигналов, соответствующих $m - 1$ и $m$ кодовым блокам. Таким образом, условие (4) имеет место лишь на длительности ${{T}_{s}}$.
Допустим, что коррекция, осуществляемая КФ, коэффициенты которого найдены на текущем шаге, идеальная, т.е. межсимвольная интерференция (МСИ) на выходе КФ полностью компенсирована. Тогда можно полагать, что сигнал ${{\hat {s}}^{m}}(t)$, определяемый из выражения (2) и передаваемый на вход демодулятора, по сути, поступает из канала с аддитивным шумом, т.е.
где ${{\eta }^{m}}(t)$ – аддитивный шум.
При этом отметим, что если ${{\xi }^{m}}(t)$ белый шум, то ${{\eta }^{m}}(t)$ не обязательно является белым. Напротив, если ${{\xi }^{m}}(t)$ небелый шум, то $h_{{{\text{КФ}}}}^{m}(t)$ потенциально может являться обеляющим фильтром.
Для удобства последующих рассуждений будем полагать, что для любого $m$ шумовые составляющие ${{\xi }^{m}}(t)$ и ${{\eta }^{m}}(t)$ являются белым гауссовским шумом. Это допустимо в рамках линейной фильтрации, если считать, как оговорено выше, что МСИ на выходе КФ полностью компенсирована [9].
Данное допущение позволит использовать известное выражение для оценки вероятности ошибки на бит. Так, в случае когерентной двухпозиционной фазовой модуляции вероятность ошибки на бит на выходе демодулятора можно определить по формуле [10]
(6)
${{P}_{0}} = \frac{1}{2}{\text{erfc}}\left( {\sqrt {{\text{SN}}{{{\text{R}}}_{{{\text{КФ}}}}}} } \right),$где ${\text{erfc}}\left( x \right) = \frac{2}{{\sqrt \pi }}\int_x^\infty {\exp ( - {{y}^{2}})dy} $ – функция ошибки; SNRКФ – значение отношения сигнал/шум (ОСШ) на выходе КФ.
В соответствии с [3, 4] ИмХ КФ, найденная на некотором шаге $m$, используется для коррекции последующего информационного сигнала ${{u}^{{m + 1}}}(t)$, соответствующего следующему $\left( {m + 1} \right)$-му кодовому блоку. Тогда откорректированный сигнал ${{\hat {s}}^{{m + 1}}}(t)$ будет определяться из выражения
(7)
$\int {{{u}^{{m + 1}}}(\tau )h_{{{\text{КФ}}}}^{m}(t - \tau )d\tau } = {{\hat {s}}^{{m + 1}}}(t).$При этом ${{\hat {s}}^{{m + 1}}}(t)$ по аналогии с (5) можно представить в виде
(8)
${{\hat {s}}^{{m + 1}}}(t) = {{s}^{{m + 1}}}(t) + {{\eta }^{{m + 1}}}(t) + {{\mu }^{{m + 1}}}(t),$где ${{\mu }^{{m + 1}}}(t)$ – ошибка вычисления, связанная с неполной компенсацией МСИ.
Допустим, что на $\left( {m + 1} \right)$-м шаге подходящий сегмент не был найден и, соответственно, вычислить новые коэффициенты КФ не удалось. В этом случае для коррекции информационного сигнала ${{u}^{{m + 2}}}(t)$, соответствующего следующему $\left( {m + 2} \right)$-му кодовому блоку, будет использован КФ с ИмХ, полученной ранее на шаге $m$, т.е. $h_{{{\text{КФ}}}}^{m}(t)$. В общем случае новый сегмент может быть найден на некотором шаге $\left( {m + {{m}_{0}}} \right)$, поэтому для удобства последующих рассуждений примем $m = 0$ и введем индекс $m{\kern 1pt} ' = 1,2,...,{{m}_{0}}$. Тогда
(9)
$\int {{{u}^{{m{\kern 1pt} '}}}(\tau )h_{{{\text{КФ}}}}^{{\left\{ 0 \right\}}}(t - \tau )d\tau } = {{\hat {s}}^{{m{\kern 1pt} '}}}(t),$где
(10)
${{\hat {s}}^{{m{\kern 1pt} '}}}(t) = {{s}^{{m{\kern 1pt} '}}}(t) + {{\eta }^{{m{\kern 1pt} '}}}(t) + {{\mu }^{{m{\kern 1pt} '}}}(t).$То есть при коррекции принимаемых информационных сигналов ${{u}^{{m{\kern 1pt} '}}}(t)$ с использованием ИмХ КФ $h_{{{\text{КФ}}}}^{{\left\{ 0 \right\}}}(t)$ из выражения (9) будем получать сигналы ${{\hat {s}}^{{m{\kern 1pt} '}}}(t)$ в форме (10) до тех пор, пока на некотором шаге $m{\kern 1pt} ' = {{m}_{0}}$ не будет найден подходящий сегмент и рассчитаны новые коэффициенты КФ, после чего вновь примем $m{\kern 1pt} ' = 1$.
При этом будем полагать, что для любого $m{\kern 1pt} '$ ошибка вычисления ${{\mu }^{{m{\kern 1pt} '}}}(t)$ также является гауссовским процессом с дисперсией $\sigma _{\mu }^{2}(m{\kern 1pt} ')$. Отметим, что это допустимо лишь для небольших значений $m{\kern 1pt} '$, так как ${{\mu }^{{m{\kern 1pt} '}}}(t)$ связано с неполной компенсацией МСИ, т.е. с “неидеальностью” коэффициентов КФ. С увеличением значения шага $m{\kern 1pt} '$ величина $\sigma _{\mu }^{2}(m{\kern 1pt} ')$ будет быстро расти, а откорректированный сигнал ${{\hat {s}}^{{m{\kern 1pt} '}}}(t)$ будет “сколь угодно много” отличаться от ${{s}^{{m{\kern 1pt} '}}}(t)$. Однако с учетом характерных для КВ-канала значений длительности интервала корреляции (порядка нескольких сотен миллисекунд) это вполне допустимо для значений шага, соответствующих половине интервала корреляции.
Данное допущение позволяет использовать формулу (6) для оценки вероятности ошибки на бит. Таким образом, ОСШ на выходе КФ будет являться функцией, зависящей от $m{\kern 1pt} '$, и определяться из выражения
(11)
${\text{SN}}{{{\text{R}}}_{{{\text{КФ}}}}}(m{\kern 1pt} ') = \frac{{{{W}_{{{\text{симв}}}}}}}{{2\left( {{{\sigma }^{2}} + \sigma _{\mu }^{2}(m{\kern 1pt} ')} \right)}},$где ${{W}_{{{\text{симв}}}}}$ – мощность элементарного символа передаваемого сигнала.
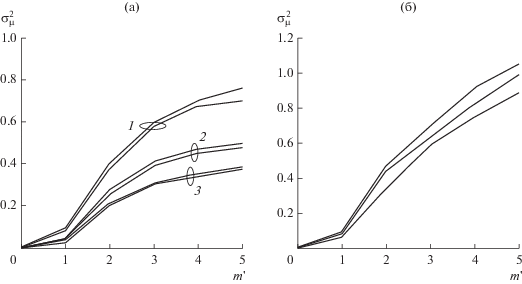
Было проведено моделирование и получены зависимости $\sigma _{\mu }^{2}(m{\kern 1pt} ')$ для двухлучевой модели канала Ваттерсона [11] с замираниями по закону Релея, а также для канала с замираниями по закону Накагами [12] (при параметре распределения ${{m}_{{{\text{Нак}}}}} = 2$ и $5$) для значений ОСШ на входе КФ 10 и 15 дБ. Результаты моделирования приведены на рис. 2а. Кроме того, на рис. 2б приведены аналогичные зависимости $\sigma _{\mu }^{2}(m{\kern 1pt} ')$, полученные по результатам обработки трассовых испытаний [8] для трех выборок усредненных на длительности 1 мин, сделанных в течение 3 мин.
Рис. 2.
Зависимости дисперсии ошибки $\sigma _{\mu }^{2}(m{\kern 1pt} ')$: (а) для имитационной модели при ОСШ 10 и 15 дБ с замираниями по закону Релея (кривые 1), с замираниями по закону Накагами при параметре распределения mНак = 2 (2) и 5 (3); (б) реальные измерения.
Отметим, что значение ОСШ на входе КФ (см. рис. 1) – постоянная величина, определяемая следующим образом:
2. ВЫВОД ВЫРАЖЕНИЙ ДЛЯ ОЦЕНКИ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК БЕСТЕСТОВЫХ МЕТОДОВ АДАПТИВНОЙ КОРРЕКЦИИ
2.1. Некоторые вспомогательные величины
Вероятность нахождения сегмента, используемого в качестве тестового сигнала, как показано в [3], вычислить аналитически не представляется возможным, поэтому там же приведены значения, полученные путем моделирования. При этом длительность сегмента может быть различной с ограничением снизу (не менее интервала многолучевости), что повышает вероятность нахождения такого сегмента. Вычисленное экспериментально значение вероятности нахождения такого сегмента для кодовой последовательности длиной 127 бит составляет величину Pтест = 0.98 [3].
Вероятность правильного декодирования кодового блока для кода с параметрами $\left( {n,k,d} \right)$ определяется из выражения [13]
(13)
${{P}_{{{\text{дек}}}}}(m{\kern 1pt} ') = \sum\limits_{l = 0}^{{{q}_{{{\text{ош}}}}}} {C_{n}^{l}{{P}_{0}}{{{(m{\kern 1pt} ')}}^{l}}{{{\left( {1 - {{P}_{0}}(m{\kern 1pt} ')} \right)}}^{{n - l}}}} ,$где ${{q}_{{{\text{ош}}}}} = \left\lfloor {\frac{{d - 1}}{2}} \right\rfloor $ – число ошибок, исправляемых кодом; $\left\lfloor {} \right\rfloor $ – округление в меньшую сторону; ${{P}_{0}}(m{\kern 1pt} ')$ – вероятность ошибки на бит, вычисляемая по формуле (6), с учетом значения ОСШ на выходе КФ, определяемого из (11).
Тогда вероятность того, что в очередном кодовом блоке на шаге $m{\kern 1pt} '$ будет найден сегмент, на основе которого будут вычислены новые коэффициенты ИмХ КФ, определяется следующим образом:
(14)
${{P}_{{\text{н}}}}(m{\kern 1pt} ') = {{P}_{{{\text{дек}}}}}(m{\kern 1pt} '){{P}_{{{\text{тест}}}}}.$Предположим, что новые коэффициенты ИмХ КФ не были найдены на шаге $m{\kern 1pt} ' = 1$, т.е. данная “попытка” оказалась неудачной. Это возможно в случае, если кодовый блок был декодирован, но не был найден сегмент – вероятность данного события определяется как ${{P}_{{{\text{дек}}}}}(1)\left( {1 - {{P}_{{{\text{тест}}}}}} \right)$, либо кодовый блок с вероятностью $\left( {1 - {{P}_{{{\text{дек}}}}}(1)} \right)$ не был декодирован. При этом имеет место очевидное тождество
(15)
${{P}_{{{\text{дек}}}}}(1)\left( {1 - {{P}_{{{\text{тест}}}}}} \right) + \left( {1 - {{P}_{{{\text{дек}}}}}(1)} \right) \equiv 1 - {{P}_{{\text{н}}}}(1).$В результате можно получить выражения для вероятностей следующих событий:
– вероятность найти подходящий сегмент и обновить коэффициенты ИмХ КФ на шаге $m{\kern 1pt} '$ при условии, что все прошлые $\left( {m{\kern 1pt} '\,\, - 1} \right)$ попыток неудачные, есть
(16)
${{P}_{1}}(m{\kern 1pt} ') = {{P}_{{\text{н}}}}(m{\kern 1pt} ')\prod\limits_{l = 1}^{m{\kern 1pt} '\,\, - 1} {\left( {1 - {{P}_{{\text{н}}}}(l)} \right)} ;$– вероятность найти подходящий сегмент и обновить коэффициенты ИмХ КФ за $m{\kern 1pt} '$ шагов есть
2.2. Вероятность срыва процедуры бестестовой адаптивной коррекции
Для заданных параметров модели канала и значения ОСШ на входе КФ существует некоторое значение $m{\kern 1pt} ' = m{\text{*}}$, при котором вероятность ошибки на бит ${{P}_{0}}(m{\kern 1pt} ' = m*)$ увеличится настолько, что соответствующая вероятность декодирования кодового блока ${{P}_{{{\text{дек}}}}}(m{\kern 1pt} ' = m*)$ станет крайне мала, а значит, найти сегмент и обновить коэффициенты КФ станет маловероятно. Кроме того, передача сообщений с заданной достоверностью также станет невозможной. В этом случае произойдет срыв процедуры бестестовой адаптивной коррекции.
Очевидно, что при передаче сообщения, состоящего из $N$ кодовых блоков, при $N \leqslant m{\text{*}}$ срыв процедуры бестестовой адаптивной коррекции невозможен.
Пусть
Тогда, при $j = 1$ вероятность срыва будет определяться как вероятность того, что сегмент для расчета коэффициентов ИмХ КФ не будет найден за $m{\text{*}}$ шагов, т.е.
Допустим $j = 2$, тогда срыв процедуры коррекции может произойти на шаге $j = 1$ с вероятностью (19), либо на шаге $j = 2$ с вероятностью ${{P}_{1}}(1)\left( {1 - {{P}_{2}}(m*)} \right)$, т.е.
(20)
$\begin{gathered} {{P}_{{{\text{ср}}}}}(2) = 1 - {{P}_{2}}(m*) + {{P}_{1}}(1)\left( {1 - {{P}_{2}}(m*)} \right) = \\ = {{P}_{{{\text{ср}}}}}(1) + {{P}_{1}}(1)\left( {1 - {{P}_{2}}(m*)} \right). \\ \end{gathered} $Аналогично, при $j = 3$ вероятность срыва будет определяться из выражения
(21)
${{P}_{{{\text{ср}}}}}(3) = {{P}_{{{\text{ср}}}}}(2) + \left( {{{P}_{1}}^{2}(1) + {{P}_{1}}(2)} \right)\left( {1 - {{P}_{2}}(m*)} \right).$Таким образом, в общем случае вероятность срыва есть
(22)
${{P}_{{{\text{ср}}}}}(j) = {{P}_{{{\text{ср}}}}}(j - 1) + Q\left( {j,m{\text{*}}} \right)\left( {1 - {{P}_{2}}(m*)} \right),$где $Q\left( {j,m{\text{*}}} \right)$ – функционал, определяющий вероятность всех комбинаций вероятностей P1(l), $l = 1,\,\, \ldots ,\,\,m{\text{*}}$, при которых срыва процедуры коррекции не происходит.
Вид функционала $Q\left( {j,m{\text{*}}} \right)$ для различных значений $j$ и $m{\text{*}}$ приведен в табл. 1.
Таблица 1.
Вид функционала $Q\left( {j,m{\text{*}}} \right)$ для различных значений $j$ и $m{\text{*}}$
| $j$ | $Q\left( {j,m{\text{*}}} \right)$ | Номер формулы |
|---|---|---|
| $m* = 2$ | ||
| 2 | ${{P}_{1}}(1)$ | Iа |
| 3 | $P_{1}^{2}(1) + {{P}_{1}}(2)$ | Iб |
| 4 | $P_{1}^{3}(1) + 2{{P}_{1}}(1){{P}_{1}}(2)$ | Iв |
| 5 | $P_{1}^{4}(1) + 3P_{1}^{2}(1){{P}_{1}}(2) + P_{1}^{2}(2)$ | Iг |
| 6 | $P_{1}^{5}(1) + 4P_{1}^{3}(1){{P}_{1}}(2) + 3P1(1)P_{1}^{2}(2)$ | Iд |
| $m* = 3$ | ||
| 2 | ${{P}_{1}}(1)$ | Iа |
| 3 | $P_{1}^{2}(1) + {{P}_{1}}(2)$ | Iб |
| 4 | $P_{1}^{3}(1) + 2{{P}_{1}}(1){{P}_{1}}(2) + {{P}_{1}}(3)$ | IIв |
| 5 | $P_{1}^{4}(1) + 3P_{1}^{2}(1){{P}_{1}}(2) + 2{{P}_{1}}(1){{P}_{1}}(3) + P_{1}^{2}(2)$ | IIг |
| 6 | $P_{1}^{4}(1) + 4P_{1}^{3}(1){{P}_{1}}(2) + 3P_{1}^{2}(1){{P}_{1}}(3) + 3{{P}_{1}}(1)P_{1}^{2}(2) + 2{{P}_{1}}(2){{P}_{1}}(3)$ | IIд |
| $m* = 4$ | ||
| 2 | ${{P}_{1}}(1)$ | Iа |
| 3 | $P_{1}^{2}(1) + {{P}_{1}}(2)$ | Iб |
| 4 | $P_{1}^{3}(1) + 2{{P}_{1}}(1){{P}_{1}}(2) + {{P}_{1}}(3)$ | IIв |
| 5 | $P_{1}^{4}(1) + 3P_{1}^{2}(1){{P}_{1}}(2) + 2{{P}_{1}}(1){{P}_{1}}(3) + P_{1}^{2}(2) + {{P}_{1}}(4)$ | IIIг |
| 6 | $P_{1}^{5}(1) + 4P_{1}^{3}(1){{P}_{1}}(2) + 3P_{1}^{2}(1){{P}_{1}}(3) + 3{{P}_{1}}(1)P_{1}^{2}(2) + 2{{P}_{1}}(2){{P}_{1}}(3) + 2{{P}_{1}}(1){{P}_{1}}(4)$ | IIIд |
| $m* = 5$ | ||
| 2 | ${{P}_{1}}(1)$ | Iа |
| 3 | $P_{1}^{2}(1) + {{P}_{1}}(2)$ | Iб |
| 4 | $P_{1}^{3}(1) + 2{{P}_{1}}(1){{P}_{1}}(2) + {{P}_{1}}(3)$ | IIв |
| 5 | $P_{1}^{4}(1) + 3P_{1}^{2}(1){{P}_{1}}(2) + 2{{P}_{1}}(1){{P}_{1}}(3) + P_{1}^{2}(2) + {{P}_{1}}(4)$ | IIIг |
| 6 | $P_{1}^{5}(1) + 4P_{1}^{3}(1){{P}_{1}}(2) + 3P_{1}^{2}(1){{P}_{1}}(3) + 3{{P}_{1}}(1)P_{1}^{2}(2) + 2{{P}_{1}}(2){{P}_{1}}(3) + 2{{P}_{1}}(1){{P}_{1}}(4) + {{P}_{1}}(5)$ | IVд |
Для больших значений $j$ и $m{\text{*}}$ вид функционала $Q\left( {j,m{\text{*}}} \right)$ достаточно громоздкий, а его вывод весьма затруднителен. Однако с учетом роли данного функционала можно заменить его на $\left( {1 - {{P}_{{{\text{ср}}}}}(j - 1)} \right)$, т.е. вероятность с которой срыва процедуры коррекции не происходит, и тогда от (22) приходим к следующему выражению
(23)
${{P}_{{{\text{ср}}}}}(j) = {{P}_{{{\text{ср}}}}}(j - 1) + \left( {1 - {{P}_{{{\text{ср}}}}}(j - 1)} \right)\left( {1 - {{P}_{2}}(m*)} \right).$Кроме того, поскольку вероятность нахождения сегмента за заданное число шагов в основном определяется вероятностью ${{P}_{1}}(1) \equiv {{P}_{2}}(1)$, то для более простой оценки вероятности срыва можно также воспользоваться формулой
2.3. Среднее время устойчивой работы
Длительность сеанса связи определяется длиной передаваемого сообщения, которая кратна количеству передаваемых кодовых блоков. С учетом выражения (23) и определения из [14] функция распределения длительности сеанса связи есть
Как известно [14], математическое ожидание длительности сеанса, определяется из выражения
Тогда среднее время устойчивой работы с учетом (18) есть
3. ПОСТРОЕНИЕ ВЕРОЯТНОСТНЫХ КРИВЫХ И АНАЛИЗ РЕЗУЛЬТАТОВ
Рассмотрим систему связи, описанную в [3] и использующую помехоустойчивый код с параметрами $\left( {127,85,13} \right)$, а также циклический код CRC [12] длиной 8 бит, служащий для контроля правильного декодирования.
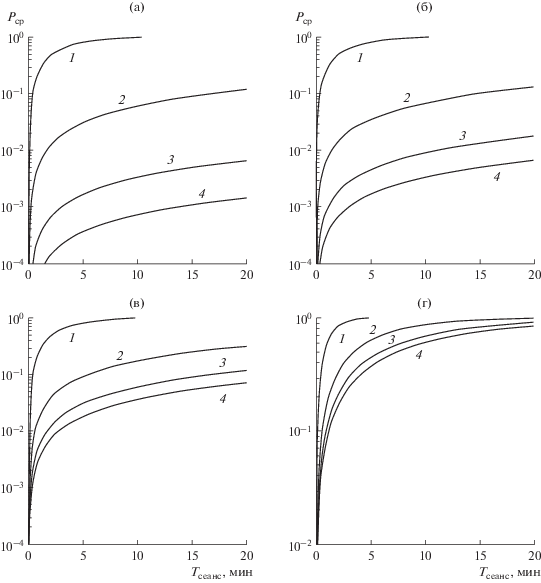
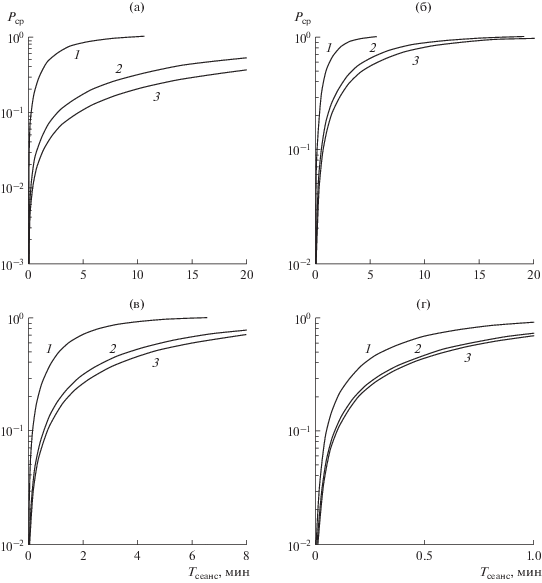
На рис. 3 приведены зависимости вероятности срыва процедуры бестестовой адаптивной коррекции от длительности сеанса ${{T}_{{{\text{сеанс}}}}}$ для различных значений ОСШ на входе КФ и различных значений $m{\text{*}}$. Под сеансом понимается передача некоторого числа кодовых блоков. При этом $j$ соответствует передаче одного кодового блока с параметрами $\left( {127,85,13} \right)$. Длительность сигнала, соответствующего одному такому кодовому блоку, при частоте следования символов 1600 симв/с составляет ${{T}_{s}} = 79.4$ мс. В качестве $\sigma _{\mu }^{2}$ взяты значения, полученные в ходе испытаний на реальной трассе (см. рис. 2б).
Рис. 3.
Вероятность срыва процедуры бестестовой адаптивной коррекции сигналов в зависимости от длительности сеанса связи для $m{\text{*}}$ = 2 (1), 3 (2), 4 (3) и 5 (4) и ОСШ на входе КФ: 15 (а), 10 (б), 7 (в), 5 дБ (г).
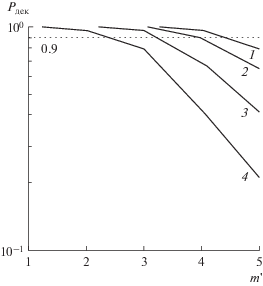
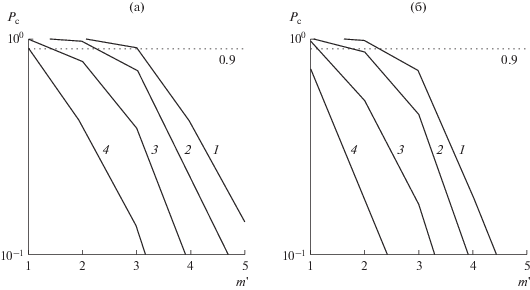
Следует отметить, что выбор значения $m{\text{*}}$ должен исходить из задаваемой (требуемой) вероятности декодирования кодового блока. Для большинства известных КВ-систем передачи данных это значение задают $ > 0.9$ [1, 2, 14]. Зависимости вероятности декодирования кодового блока ${{P}_{{{\text{дек}}}}}$ от номера шага $m{\kern 1pt} '$, вычисленные по формуле (13) с учетом устаревания ИмХ КФ, приведены на рис. 4, там же показана граница вероятности декодирования 0.9.
Рис. 4.
Зависимости вероятности декодирования кодового блока ${{P}_{{{\text{дек}}}}}$ от номера шага $m{\kern 1pt} '$ для различных значений ОСШ на входе КФ: 15 (1), 10 (2), 7 (3) и 5 дБ (4), пунктирная линия – граница вероятности декодирования 0.9.
Вычисленные значения для среднего времени устойчивой работы ${{M}_{{{\text{УР}}}}}$ для значений $m{\text{*}}$, выбираемых с учетом порога ${{P}_{{{\text{дек}}}}} > 0.9$ приведены в табл. 2.
Таблица 2.
Рассчитанные значения среднего времени устойчивой работы
| ОСШ, дБ | $m*$ | ${{M}_{{{\text{УР}}}}}$, мин |
|---|---|---|
| 15 | 2 | 3.3 |
| 3 | 165 | |
| 4 | 1772 | |
| 10 | 2 | 3.3 |
| 3 | 146 | |
| 7 | 2 | 3.13 |
| 3 | 51 | |
| 5 | 2 | 1.14 |
На рис. 5а–5г представлены аналогичные зависимости вероятности срыва процедуры бестестовой адаптивной коррекции от длительности сеанса при использовании анализа результатов синдромного декодирования [4]. В качестве надежных кодовых блоков, в которых осуществляется поиск сегмента, полагаем блоки с синдромами, соответствующим не более ${{q}_{{\text{с}}}} = 2$ (рис. 5а, 5б) и ${{q}_{{\text{с}}}} = 1$ (рис. 5в, 5г) ошибкам.
Рис. 5.
Зависимости вероятности срыва процедуры бестестовой адаптивной коррекции сигналов в зависимости от длительности сеанса связи при ${{q}_{{\text{с}}}} = 2$ (а, б) и ${{q}_{{\text{с}}}} = 1$ (в, г) для $m{\text{*}}$ = 2 (1), 3 (2) и 4 (3) и ОСШ на входе КФ: 15 (а, в) и 10 дБ (б, г).
Зависимости вероятности появления синдрома ${{P}_{{\text{с}}}}$, соответствующего не более ${{q}_{{\text{с}}}} = 2$ и ${{q}_{{\text{с}}}} = 1$ ошибкам, от номера шага $m{\kern 1pt} '$ с учетом устаревания ИмХ КФ, рассчитаны по формуле (13) с заменой верхнего предела в сумме на значение ${{q}_{{\text{с}}}}$ и приведены на рис. 6.
Рис. 6.
Зависимости вероятности появления синдрома, соответствующего не более ${{q}_{{\text{с}}}} = 2$ (а) и ${{q}_{{\text{с}}}} = 1$ (б) ошибкам, от номера шага $m{\kern 1pt} '$ для различных значений ОСШ на входе КФ: 15 (1), 10 (2), 7 (3) и 5 дБ (4), пунктирная линия – граница вероятности декодирования 0.9.
Вычисленные значения для среднего времени устойчивой работы ${{M}_{{{\text{УР}}}}}$ для значений ОСШ на входе КФ 15 и 10 дБ и заданных значениях допустимого количества ошибок ${{q}_{{\text{с}}}} = 2$ и ${{q}_{{\text{с}}}} = 1$ при различных значениях $m{\text{*}}$ приведены в табл. 3.
Таблица 3.
Рассчитанные значения среднего времени устойчивой работы при поиске сегмента в надежных кодовых блоках
| ОСШ, дБ | ${{q}_{{\text{с}}}}$ | $m{\text{*}}$ | ${{M}_{{{\text{УР}}}}}$, мин |
|---|---|---|---|
| 15 | 2 | 2 | 3.13 |
| 3 | 27.5 | ||
| 1 | 2 | 1.7 | |
| 3 | 5.5 | ||
| 10 | 2 | 2 | 1.5 |
| 3 | 5 | ||
| 1 | 2 | 0.45 | |
| 3 | 0.81 |
Из представленных результатов можно сделать следующие выводы.
1. Вероятность найти соответствующий сегмент, на основе которого будет вычислены новые коэффициенты ИмХ КФ, определяется главным образом исправляющей способностью используемого помехоустойчивого кода, либо числом допустимых ошибок в соответствующем синдроме при декодировании.
2. Вероятность устойчивой работы за заданное время во многом зависит от ${{P}_{{\text{н}}}}(m{\kern 1pt} ')$ на начальных шагах (при $m{\kern 1pt} ' \leqslant 2$). При этом вычисление новых коэффициентов и обновление ИмХ КФ с вероятностью, близкой к 1, будет осуществлено на первом шаге алгоритма поиска сегмента.
Таким образом, вероятность “срыва” процедуры коррекции для методов бестестовой адаптивной коррекции невелика, а среднее время устойчивой работы достаточно для непрерывной передачи сообщений в течение нескольких минут. Это также подтверждается трассовыми испытаниями, проведенными автором, результаты которых приведены в [8].
ЗАКЛЮЧЕНИЕ
Приведем некоторые замечания, связанные с использованными допущениями при выводе аналитических выражений.
Использование модели канала, в котором изменение ИмХ происходит с шагом, меньшим длительности кодового блока (т.е. меньше шага алгоритма поиска сегмента), эквивалентно увеличению дисперсии ошибки вычисления. Это следует из приведенных зависимостей для $\sigma _{\mu }^{2}(m{\kern 1pt} ')$, приведенных на рис. 2а для моделей каналов с различным законом замираний.
Случайные процессы ${{\eta }^{{m{\kern 1pt} '}}}(t)$ и ${{\mu }^{{m{\kern 1pt} '}}}(t)$ в общем случае не являются гауссовскими процессами, а значит, вероятность ошибки на бит на выходе демодулятора будет несколько выше, так как процедуру демодуляции в этом случае нельзя считать оптимальной. Данное допущение было сделано лишь для того, чтобы воспользоваться известным выражением (6) для оценки вероятности ошибки на бит.
Для учета данных допущений можно, например, использовать эквивалентное ОСШ, значение которого будет меньше, чем для случая гауссовского шума.
Таким образом, разработанная автором модель, а также результаты имитационного моделирования и трассовых испытаний, приведенные в работах [3–5, 8], подтверждают работоспособность и устойчивость методов бестестовой адаптивной коррекции сигналов.
Список литературы
Березовский В.А., Дулькейт И.В., Савицкий О.К. Современная декаметровая радиосвязь: оборудование, системы и комплексы. М.: Радиотехника, 2011.
Johnson E.E., Koski E., Furman W.N. et al. Third-Generation and Wideband HF Radio Communications. Norwood: Artech House, 2013.
Егоров В.В., Маслаков М.Л., Мингалёв А.Н. // Электросвязь. 2011. № 11. С. 32.
Егоров В.В., Зайченко К.В., Маслаков М.Л., Михайлов В.Ф. // Радиотехника. 2017. № 5. С. 10.
Маслаков М.Л., Смаль М.С. // Изв. вузов России. Радиоэлектроника. 2018. № 4. С. 32.
Зяблов В.В., Коробков Д.Л., Портной С.Л. Высокоскоростная передача сообщений в реальных каналах. М.: Радио и связь, 1991.
Николаев Б.И. Последовательная передача дискретных сообщений по непрерывным каналам с памятью. М.: Радио и связь, 1988.
Маслаков М.Л. // Электросвязь. 2014. № 7. С. 40.
Грант П.М., Коуэн К.Ф.Н., Фридлендер Б. и др. Адаптивные фильтры. М.: Мир, 1988.
Финк Л.М. Теория передачи дискретных сообщений М.: Сов. радио, 1970.
Watteson C.C., Juroshek J.R., Bensema W.D. // IEEE Trans. 1970. V. COM-18. № 6. P. 792.
Тихонов В.И. Статистическая радиотехника М.: Сов. радио, 1966.
Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. М.: Высш. школа, 1973.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


