Радиотехника и электроника, 2021, T. 66, № 2, стр. 162-173
Пространственно-неоднородное распределение плотности квантово-механического тока при подбарьерном отражении электронной волны от потенциальной ступеньки в 2D-наноструктуре
В. А. Петров a, *, А. В. Никитин a
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, Моховая ул., 7, корп. 11, Российская Федерация
* E-mail: vicanpet@mail.ru
Поступила в редакцию 25.05.2020
После доработки 25.05.2020
Принята к публикации 05.06.2020
Аннотация
Теоретически исследовано влияние интерференции электронных волн при их отражении от прямоугольного полубесконечного потенциального барьера на пространственное распределение плотности квантово-механического тока еjx(x, z) (e – заряд электрона, jx(x, z) – плотность потока вероятности) в полупроводниковой 2D-наноструктуре. Структура представляет собой последовательно расположенные в направлении распространения электронной волны узкую и широкую прямоугольные квантовые ямы (КЯ). Предполагается, что волна падает из узкой КЯ1 на потенциальный барьер высоты V0 в широкой КЯ2. Показано, что при падении на барьер волны с энергией, меньше V0, при определенных условиях в КЯ1 существует осциллирующее сложным образом пространственно-неоднородное распределение $еj_{x}^{{\left( 1 \right)}}(x,z)$. При этом в КЯ2 возможно экспоненциально затухающее и имеющее координатную зависимость просачивание $еj_{x}^{{\left( 2 \right)}}(x,z)$ под барьер. Показано, что такое поведение $еj_{x}^{{\left( 1 \right)}}(x,z)$ и $еj_{x}^{{\left( 2 \right)}}(x,z)$ обусловлено интерференцией электронных волн, распространяющихся по разным квантово-размерным подзонам в рассматриваемой наноструктуре.
ВВЕДЕНИЕ
В настоящее время успехи нанотехнологии позволяют создавать полупроводниковые наноструктуры, в которых линейные размеры 1D- или 2D-проводящего канала в направлении распространения электронной волны меньше длины свободного пробега электрона. В таком канале частицы движутся в баллистическом режиме, что позволяет экспериментально исследовать в данных структурах эффекты баллистического переноса, в частности, различные электронные интерференционные эффекты. Теоретические основы этих эффектов, а также анализ основных экспериментальных результатов в этой области, приведены в ряде монографий [1–3]. Существует большое число теоретических работ, посвященных исследованию баллистического переноса электронов в 1D- и 2D-наноструктурах, общей особенностью которых является наличие в квантовых каналах участков резкого (неадиабатического) изменения либо геометрии канала, либо потенциального рельефа в нем. Например, квантовый транспорт был теоретически исследован в 1D-каналах прямоугольного [4] и параболического [5] профилей, соединяющих два 2D-электронных резервуара, а также в квантовых точечных контактах различного типа, соединяющих такие резервуары [6], Т-образных каналах [7, 8], каналах с резкими изломами и каналах изогнутой формы [9–11], каналах с δ-образным рассеивающим центром внутри [12], скрещенных каналах [13], одиночных геометрически неоднородных каналах с участками разной ширины [14–17], геометрически однородных 1D- и 2D-наноструктурах с участками резкого изменения потенциального рельефа, управляемого поперечным постоянным электрическим полем [18]. Роль затухающих мод в квантовых точечных контактах была рассмотрена в [12, 19, 20]. Во всех этих работах принципиальным моментом является рассеяние электронных волн на какой-либо неоднородности наноструктуры, что, в свою очередь, приводит к рассеянию электронной волны по всем квантоворазмерным подзонам структуры и, как следствие, к возникновению электронных интерференционных эффектов. Во всех этих работах (а также в ряде других аналогичных по тематике) конечной целью являлось вычисление либо квантовомеханического коэффициента прохождения структуры, либо ее кондактанса. Так как при нахождении этих величин необходимо вычислить полный ток частиц в квантовом канале, что достигается интегрированием зависящей от координат плотности квантовомеханического тока по поперечному сечению канала, то пространственно-неоднородные эффекты для плотности квантовомеханического тока в таких работах не рассматривались. Возможность существования пространственно-неоднородных эффектов для плотности потока вероятности jх(x, z) в полупроводниковой 2D-наноструктуре кратко обсуждалась ранее [21]. В дальнейшем мы более детально исследовали теоретически такие пространственно-неоднородные эффекты в полупроводниковых 1D- и 2D-наноструктурах различного типа. Мы показали, что в 1D- [22] и 2D-наноструктурах [23, 24], представляющих собой последовательно расположенные в направлении распространения электронной волны узкую и широкую по оси z квантовые ямы (КЯ), возможны эффекты пространственного повторения и мультипликации для jх(x, z) (или квантовомеханической плотности тока ejх(x, z)). Было показано, что для КЯ прямоугольного сечения (ось z – ось размерного квантования) поперечное распределение jх(0, z), существующее на входе широкой КЯ, с определенной точностью воспроизводится на расстоянии Х1 от входа (повторяемость) и расщепляется внутри каждого повторяющегося отрезка длины Х1 в симметричной по оси z наноструктуре на q идентичных пиков в q раз меньшей интенсивности на расстоянии Х1/q (мультипликация). При этом исходное распределение jх(0, z) периодически воспроизводится в сечениях Хp = pХ1 (q и р – целые числа). Эти эффекты в широкой КЯ возникают из-за интерференции электронных волн, распространяющихся в ней одновременно по разным квантоворазмерным подзонам. В наноструктурах, состоящих из последовательно расположенных узкой прямоугольной КЯ и широкой КЯ параболического профиля в 1D- [25] и 2D-наноструктурах [26] эффекты повторяемости также присутствуют, но эффекты мультипликации выражены гораздо слабее по сравнению с широкой прямоугольной КЯ. Мы также исследовали влияние постоянного поперечного электрического поля в области широкой КЯ на эффекты повторяемости и мультипликации в таких наноструктурах и показали, что электрическое поле позволяет кардинально менять пространственное распределение jх(x, z) [27‒31].
Основная цель данной работы – всестороннее теоретическое исследование влияния интерференции электронных волн на их отражение от прямоугольного полубесконечного потенциального барьера в полупроводниковой 2D-наноструктуре в случае, когда энергия падающей волны меньше высоты барьера. Полученные в этой работе результаты были частично и очень кратко изложены ранее в [32].
1. МОДЕЛЬ ГЕОМЕТРИЧЕСКИ-НЕОДНОРОДНОЙ 2D-НАНОСТРУКТУРЫ
Структура состоит из последовательно расположенных в направлении распространения электронной волны прямоугольных узкой (x < 0, КЯ1) и широкой (x > 0, КЯ2) квантовых ям. Потенциальный барьер высоты V0 находится в широкой КЯ2 при x > 0 (рис. 1). Как известно [32], в обычной ситуации, когда в трехмерном случае электронная волна с энергией Е < V0 падает на барьер по оси х, а движение по осям y и z свободно, квантовомеханические плотности тока $ej_{х}^{{\left( 1 \right)}}(x,y,z)$ при x < 0 и $ej_{х}^{{\left( 2 \right)}}(x,y,z)~$ под барьером при x > 0 равны нулю. Плотность вероятности нахождения частицы под барьером при этом отлична от нуля и экспоненциально спадает при х → ∞, а равенство нулю тока следует из действительности волновой функции частицы под барьером. Мы покажем, что в геометрически–неоднородных наноструктурах, в которых существуют квантово-размерные подзоны (КРП), ситуация кардинально меняется. Интерференция электронных волн, распространяющихся по этим подзонам, при определенных условиях может приводить к возникновению в таких наноструктурах пространственно-неоднородного распределения квантовомеханического тока.
Рис. 1.
Схематичный вид потенциального рельефа симметричной 2D-наноструктуры на основе последовательности двух прямоугольных квантовых ям: узкой (КЯ1) и широкой (КЯ2), ширина которых соответственно а и А. В области КЯ2 при х ≥ 0 существует полубесконечный прямоугольный потенциальный барьер высотой V0; $E_{c}^{{(1)}}$ и $E_{c}^{{(2)}}$ – энергетические положения доньев зон проводимости в КЯ1 и КЯ2 соответственно.
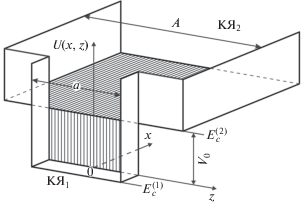
В данной работе дано полное теоретическое описание эффекта отражения электронной волны от прямоугольного полубесконечного потенциального барьера в 2D-наноструктуре. Представлены результаты аналитического расчета для двух ситуаций. В первой ситуации предполагалось, что в КЯ1 падение и отражение волны с действительным квазиимпульсом происходит только по одной (нижней) КРП. Во всех вышележащих КРП в КЯ1, а также во всех подзонах в КЯ2 квазиимпульсы мнимые. Вторая ситуация отличалась от первой только возможностью незатухающего отражения волны в КЯ1 от барьера по второй подзоне с действительными квазиимпульсами. Мы показали, что в ситуации 1, когда электронная волна падает по первой (нижней) КРП в КЯ1 и ее продольная энергия Еx меньше энергетического положения дна второй подзоны в КЯ1 (т.е. незатухающее распространение отраженной от барьера волны возможно только по этой же нижней подзоне в КЯ1) квантовомеханические плотности тока $ej_{х}^{{\left( 1 \right)}}(x,z)$ при x < 0 в КЯ1 и $ej_{х}^{{\left( 2 \right)}}(x,z)$ под барьером в КЯ2 при x > 0 равны нулю. Однако в ситуации 2, когда энергия частицы, распространяющейся по нижней подзоне в КЯ1, больше энергетического положения дна второй подзоны, из-за интерференции отраженных волн картина кардинально меняется. Возможность отражения волны при х → –∞ по второй подзоне приводит к возникновению в КЯ1 осциллирующего сложным образом пространственно-неоднородного распределения $ej_{х}^{{\left( 1 \right)}}(x,z)$, а под барьером в КЯ2 экспоненциально затухающего при х → ∞ и имеющего координатную зависимость $ej_{х}^{{\left( 2 \right)}}(x,z)$. Далее, мы приводим результаты численного расчета $ej_{х}^{{\left( 1 \right)}}(x,z)$ и $ej_{х}^{{\left( 2 \right)}}(x,z)$ для симметричной по оси z структуры (рис. 1) конкретными параметрами, полностью подтверждающие результаты аналитического рассмотрения.
2. ОБЩАЯ СХЕМА РАСЧЕТА ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ПЛОТНОСТИ ПОТОКА ВЕРОЯТНОСТИ jx(x, z)
Рассмотрим 2D-наноструктуру, состоящую из двух последовательно расположенных вдоль оси x квантовых ям: КЯ1 с потенциалом U1(z) (х < 0) и КЯ2 c потенциалом U2(z) (x > 0), локализующими частицу по оси z (нормаль к плоскостям ям). Будем также считать, что движение по оси y отделяется и является свободным, а потенциальная энергия частицы в пределах каждой из областей не зависит от x, меняясь скачком в точке сочленения ям (x = 0). Эффективные массы частиц m* будем считать изотропными и одинаковыми в обеих областях. Тогда уравнения Шредингера, описывающие движения частицы по оси z в каждой из областей, имеют вид
(1)
$ - \frac{{{{\hbar }^{2}}}}{{2m{\text{*}}}}\frac{{{{d}^{2}}{{\chi }_{j}}(z)}}{{d{{z}^{2}}}} + {{U}_{1}}(z){{\chi }_{j}}(z) = {{E}_{j}}{{\chi }_{j}}(z).$(2)
$ - \frac{{{{\hbar }^{2}}}}{{2m{\text{*}}}}\frac{{{{d}^{2}}{{\varphi }_{n}}(z)}}{{d{{z}^{2}}}} + {{U}_{2}}(z){{\varphi }_{n}}(z) = {{E}_{n}}{{\varphi }_{n}}(z).$Здесь Еj и Еn – собственные значения, а χj(z) и φn(z) – собственные функции уравнений (1) и (2) соответственно в КЯ1 и КЯ2. Полная энергия частицы E = Ex,z + Ey, где Ey = ${{{{\hbar }^{2}}k_{y}^{2}} \mathord{\left/ {\vphantom {{{{\hbar }^{2}}k_{y}^{2}} {2m{\text{*}}~}}} \right. \kern-0em} {2m{\text{*}}~}}$ – энергия, соответствующая свободному движению по оси y. Рассмотрим ситуацию, когда слева направо, из КЯ1 по квантовой подзоне m в КЯ2 распространяется монохроматическая электронная волна единичной амплитуды с действительным квазиимпульсом km. Будем считать, что квантовые ямы, локализующие частицу по оси z, имеют бесконечно высокие потенциальные барьеры, т.е. спектры энергий в обеих ямах в этом направлении полностью дискретны. В такой 2D-наноструктуре с произвольными U1(z) и U2(z) нас будет интересовать ситуация, когда энергия падающего электрона в КЯ1 удовлетворяет условию Ех < ΔU = U2(z) – U1(z), причем U2(z) включает и дополнительный встроенный потенциал V0. В этом случае в КЯ1 существует конечное число М нижних подзон с действительными k, а все лежащие выше подзоны имеют мнимые волновые векторы. Тогда волновые функции частицы μ(1)(x, z) и μ(2)(x, z) в каждой из областей по отдельности имеют вид
(3)
$\begin{gathered} {{\mu }^{{\left( 1 \right)}}}\left( {x,z} \right) = {{\chi }_{m}}\left( z \right){\text{exp}}\left( {i{{k}_{m}}x} \right) + \\ + \,\,\sum\limits_j {{{В}_{j}}{{\chi }_{j}}\left( z \right)} {\text{ exp}}\left( { - i{{k}_{j}}x} \right),~ \\ \end{gathered} $(4)
${{\mu }^{{\left( 2 \right)}}}\left( {x,z} \right) = \sum\limits_n {{{C}_{n}}{{j}_{n}}} \left( z \right){\text{exp}}\left( {ik_{n}^{'}x} \right).~$Здесь Вj и Сn – постоянные коэффициенты, определяющие соответственно амплитуды волн, отраженных в КЯ1 по подзонам Еj и прошедших в КЯ2 по подзонам Еn; kj,m и $k_{n}^{'}$ – волновые числа, соответствующие движению частицы по оси х в этих областях:
Отражение и трансформация электронных волн в такой структуре происходят из-за скачкообразного изменения потенциала ΔU = U2(z) – U1(z) в точке х = 0. Отметим, что если Е – Ey > Еj, Еn, то kj и $k_{n}^{'}$ действительны и соответствующие им волны являются распространяющимися; при обратном неравенстве – kj и $k_{n}^{'}$ мнимые и волны являются затухающими, с характерными длинами затухания lj = |kj|–1 и ln = |$k_{n}^{'}$|–1. Для рассматриваемых нами структур со ступенчатым переходом между КЯ1 и КЯ2 коэффициенты Вj и Cn определяются из системы уравнений, которая вытекает из граничных условий для волновых функций и их производных в точке x = 0:
(5)
$\begin{gathered} {{\mu }^{{(1)}}}\left( {х = 0,z} \right) = {{\mu }^{{(2)}}}\left( {x = 0,z} \right); \\ {{\nabla }_{x}}{{\mu }^{{(1)}}}\left( {х = 0,z} \right) = {{\nabla }_{x}}{{\mu }^{{(2)}}}\left( {x = 0,z} \right); \\ {{\chi }_{m}}(z) + \sum\limits_j {{{В}_{j}}{{\chi }_{j}}(z)} = \sum\limits_n {{{C}_{n}}{{\varphi }_{n}}(z);} \\ \end{gathered} $(6)
${{k}_{m}}{{\chi }_{m}}(z) - \sum\limits_j {{{k}_{j}}{{В}_{j}}{{\chi }_{j}}(z)} = \sum\limits_n {k_{n}^{'}{{C}_{n}}{{\varphi }_{n}}(z).} $Умножая слева уравнение (5) на $\varphi _{p}^{*}(z)$, а (6) на $\chi _{p}^{*}(z)$ (звездочка (*) – знак комплексного сопряжения) и интегрируя полученные выражения по z, получим систему линейных алгебраических уравнений для определения коэффициентов Вj и Cn:
(7б)
${{k}_{m}}{{\delta }_{{pm}}}~\,\, - \,\,{{k}_{p}}{{В}_{p}} = \sum\limits_n {k_{n}^{'}{{C}_{n}}{{f}_{p}}_{{,n}}.~} $Здесь tp,m = $\int {\varphi _{p}^{*}(} z){{\chi }_{m}}(z)dz$ и fp,n = $\int {\chi _{p}^{*}} (z){{\varphi }_{n}}(z)dz$ – коэффициенты неортогональности собственных функций в КЯ1 и КЯ2. Отметим, что fpm = $t_{{mp}}^{*},~$ а если собственные функции, как в нашем случае, вещественны, то fpm = tmp . Перепишем (7а) и (7б) с учетом этого обстоятельства:
(8б)
$k_{p}^{{}}{{B}_{p}} + \sum\limits_n {k_{n}^{'}{{C}_{n}}{{f}_{{p,n}}}} = k_{m}^{{}}{{\delta }_{{p,m}}}.$Отметим, что в симметричных по оси z структурах, когда локализующие частицу потенциалы U1(z) и U2(z) в КЯ1 и КЯ2 удовлетворяют условиям U1(z) = U1(–z) и U2(z) = U2(–z) (точка z = 0 находится на оси симметрии структуры), собственные функции χi(z) и φn(z) в КЯ1 и КЯ2 можно классифицировать по четности. В этом случае коэффициенты неортогональности равны нулю для функций разной четности.
Расширенная матрица системы (8а), (8б) при учете N уровней, имеющая порядок 2 N (j, p = 1, ..., N; m принимает одно из значений от 1 до N), имеет вид
(9)
$\left( {\begin{array}{*{20}{c}} {{{f}_{{1,1}}}}&{{{f}_{{2,1}}}}& \cdots &{ - 1}&0& \cdots \\ {{{f}_{{1,2}}}}&{{{f}_{{2,2}}}}& \cdots &0&{ - 1}& \cdots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots \\ {k_{1}^{{}}}&0& \cdots &{k_{1}^{'}{{f}_{{1,1}}}}&{k_{2}^{'}{{f}_{{1,2}}}}& \cdots \\ 0&{k_{2}^{{}}}& \cdots &{k_{1}^{'}{{f}_{{2,1}}}}&{k_{2}^{'}{{f}_{{2,2}}}}& \cdots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots \end{array}\left| {\begin{array}{*{20}{c}} { - {{f}_{{1,1}}}} \\ { - {{f}_{{1,2}}}} \\ \vdots \\ {k_{m}^{{}}{{\delta }_{{1,m}}}} \\ {k_{m}^{{}}{{\delta }_{{2,m}}}} \\ \vdots \end{array}} \right.} \right).$Решение системы (8а), (8б) для N учтенных уровней, как известно, имеет вид
Здесь D – определитель матрицы (9), а ${{D}_{j}}$ – определители, получающиеся из D после замены в нем j-столбца столбцом из свободных членов системы (8а), (8б).
В дальнейшем нас будут интересовать координатные зависимости $j_{x}^{{(1)}}(x,z)$ и $j_{x}^{{(2)}}(x,z)$ – плотности потока вероятности вдоль оси х соответственно в КЯ1 и КЯ2 (или $еj_{x}^{{(1)}}(x,z)$ и $еj_{x}^{{(2)}}(x,z)$ – компоненты плотности квантовомеханического тока вдоль оси х). Плотность потока вероятности [33] имеет вид
(11)
$\begin{gathered} j_{x}^{{}}(x,{\text{ }}z) = \frac{{i\hbar }}{{2m{\text{*}}}} \times \\ \times \,\,\left[ {\mu \left( {x,z} \right){{\nabla }_{x}}\mu {\text{*}}\left( {x,z} \right) - \mu {\text{*}}\left( {x,z} \right){{\nabla }_{x}}\mu \left( {x,z} \right)} \right]{\text{ }}. \\ \end{gathered} $Подставляя волновые функции частицы (3)–(4) в (11), получим
(12)
$\begin{gathered} j_{x}^{{(1)}}(x,z) = \,\,~\frac{\hbar }{{2m{\text{*}}}}\left[ {2\left( {{{k}_{m}}\chi _{m}^{2} - \sum\limits_{i = j = 1}^M {{{k}_{i}}\chi _{i}^{2}{{{\left| {{{B}_{i}}} \right|}}^{2}}} } \right)} \right. - \\ - \,\,\sum\limits_{i \ne j} {{{B}_{j}}B_{i}^{*}{{\chi }_{i}}{{\chi }_{j}}({{k}_{j}} + k_{i}^{*})\exp (i(k_{i}^{*} - {{k}_{j}})x)} + \\ \left. {\frac{{^{{}}}}{{}} + \,\,{{\chi }_{m}}\exp ( - i{{k}_{m}}x)\sum\limits_{j \ne m} {{{\chi }_{j}}{{B}_{j}}({{k}_{m}} - {{k}_{j}})\exp ( - i{{k}_{j}}x)} } \right] + \\ + \,\,{{\chi }_{m}}\exp (i{{k}_{m}}x)\sum\limits_{i \ne m} {B_{i}^{*}{{\chi }_{i}}({{k}_{m}} - k_{i}^{*})\exp (ik_{i}^{*}x)} . \\ \end{gathered} $В (12) мы оставили только члены, отличные от нуля и выделили в отдельную сумму члены с i = j, где эти индексы пробегают значения от 1 до М по всем подзонам с действительными квазиимпульсами. При этом очевидно, что члены с чисто мнимыми квазиимпульсами при i = j равны нулю. Также равны нулю члены в последних двух суммах при i = m и j = m. Таким образом, во второй сумме остаются только перекрестные члены. Выражение для $j_{x}^{{(2)}}(x,z),$ в котором суммирование ведется по индексам, соответствующим только мнимым $k_{n}^{'}$, имеет вид
(13)
${\text{ }}j_{x}^{{(2)}}(x,z) = \frac{\hbar }{{m{\text{*}}}}\left[ {\sum\limits_{n = 1}^N {{{\varphi }_{n}}(z)\left( {\sum\limits_{t = n + 1}^N {{{\varphi }_{t}}(z)\exp ( - (p_{n}^{'} + p_{t}^{'})x)(p_{n}^{'} - p_{t}^{'})({{C}_{{n1}}}{{C}_{{t2}}} - {{C}_{{t1}}}{{C}_{{n2}}})} } \right)} } \right].$При записи (12) и (13) мы сменили индексы суммирования j для (μ(1)(x, z))* и n для (μ(2)(x, z))* на i и t соответственно и учли, что в рассматриваемой нами задаче волновые функции φn(z) и χj(z) действительны, что позволяет представить в (13) чисто мнимые $k_{n}^{'}$ в виде $k_{n}^{'} = ip_{n}^{'}$, где $p_{n}^{'} = \operatorname{Im} (k_{n}^{'})$, а комплексные коэффициенты Cn в виде ${{C}_{n}} = {{C}_{{n1}}} + i{{C}_{{n2}}}$, где ${{C}_{{n1}}} = \operatorname{Re} \left( {{{C}_{n}}} \right)$, ${{C}_{{n2}}} = \operatorname{Im} \left( {{{C}_{n}}} \right)$. Здесь Re(Cn), Im(Cn) и Im($k_{n}^{'}$) – реальная часть Cn и мнимые части Cn и $k_{n}^{'}$, соответственно. В (13) отсутствуют члены с n = t, которые равны нулю. Если в системе уравнений (8а), (8б) для определения коэффициентов Bi,j и Cn,t будут присутствовать при расчете подзоны с мнимыми ki,j и $k_{{n,t}}^{'},$ то коэффициенты Bi,j и Cn,t будут комплексными. Таким образом, выражения (12), (13) совместно с найденными из решения уравнений (1), (2) собственными функциями χi(z) и φn(z), а также определенными из решения системы (8а), (8б) коэффициентами Вj и Cn дают полное решение задачи о распределении плотностей потоков вероятности $j_{x}^{{(1)}}(x,z)$ и $j_{x}^{{\left( 2 \right)}}(x,z)$ (или квантовомеханических плотностей токов) в рассматриваемой наноструктуре.
Отметим, что полный поток плотности вероятности вдоль оси x в КЯ1$J_{x}^{{(1)}} = \int {j_{x}^{{(1)}}(x,z)dz} $ (а значит, и полный квантовомеханический ток) вследствие ортонормированности функций {χi(z)}, как следует из (12), не имеет координатной зависимости от х и равен
(14)
$J_{x}^{{(1)}} = \int {j_{x}^{{(1)}}(x,z)dz{\text{ }} = \frac{\hbar }{{m{\text{*}}}}} \left[ {\left( {{{k}_{m}} - \sum\limits_{i = j = 1}^M {{{k}_{i}}{{{\left| {{{B}_{i}}} \right|}}^{2}}} } \right)} \right].$В (14) суммирование проводится по всем подзонам в КЯ1 с действительными ki, по которым происходит незатухающее распространение электронных волн. Отметим, что кондактанс структуры G также не зависит от х.
Из (13) вследствие ортонормированности функций {φn(z)} следует также, что в КЯ2
Далее рассмотрим две ситуации.
Ситуация 1. Кинетическая энергия частицы Eх в КЯ1 находится в интервале $E_{1}^{{(1)}} < {{E}_{x}} < E_{2}^{{(1)}}$ и меньше величины барьера Vэф в КЯ2, т.е. Eх < Vэф (верхние индексы (1) означают принадлежность подзон к КЯ1). При этом предполагается, что электронная волна падает по нижней квантоворазмерной подзоне в КЯ1 (m = 1) и может отражаться от барьера без затухания только по этой же подзоне с действительным квазиимпульсом k1, и в режиме затухания по всем остальным лежащим выше подзонам с энергиями $E_{i}^{{(1)}} > E_{1}^{{(1)}}~$ с чисто мнимыми квазиимпульсами. В КЯ2 существуют только подзоны с чисто мнимыми квазиимпульсами. Покажем теперь, что в ситуации 1 под барьером в КЯ2$j_{x}^{{\left( 2 \right)}}(x,z)$ = 0. Представим в (13) комплексные коэффициенты ${{C}_{t}}$ в виде ${{C}_{t}} = {{r}_{t}}\exp \left( {i{{\theta }_{t}}} \right)$.
(15)
$j_{x}^{{(2)}}{\text{(}}x,z{\text{) = }} - \frac{\hbar }{{m{\text{*}}}}\left[ {\sum\limits_{n = 1}^N {{{r}_{n}}{{\varphi }_{n}}(z)\left( {\sum\limits_{t = n + 1}^N {{{\varphi }_{t}}(z)\,\exp ( - (p_{n}^{'}\, + \,p_{t}^{'})x)(p_{n}^{'}\, - \,p_{t}^{'}){{r}_{t}}\sin \left( {{{\theta }_{n}}\, - \,{{\theta }_{t}}} \right)} } \right)} } \right].$Рассмотрим отношение
(16)
$\begin{gathered} {{\sigma }_{{n,t}}} = \frac{{{{C}_{n}}}}{{{{C}_{t}}}} = \frac{{{{r}_{n}}\exp \left( {i{{\theta }_{n}}} \right)}}{{{{r}_{t}}\exp \left( {i{{\theta }_{t}}} \right)}} = \frac{{{{r}_{n}}}}{{{{r}_{t}}}}\exp \left( {i\left( {{{\theta }_{n}} - {{\theta }_{t}}} \right)} \right) = \\ = \frac{{{{r}_{n}}}}{{{{r}_{t}}}}\left( {\cos \left( {{{\theta }_{n}} - {{\theta }_{t}}} \right) + i\sin \left( {{{\theta }_{n}} - {{\theta }_{t}}} \right)} \right). \\ \end{gathered} $Так как ${{C}_{t}} = {{{{D}_{t}}} \mathord{\left/ {\vphantom {{{{D}_{t}}} D}} \right. \kern-0em} D}$, то отношение ${{{{C}_{n}}} \mathord{\left/ {\vphantom {{{{C}_{n}}} {{{C}_{t}}}}} \right. \kern-0em} {{{C}_{t}}}}$ = ${{{{D}_{n}}} \mathord{\left/ {\vphantom {{{{D}_{n}}} {{{D}_{t}}}}} \right. \kern-0em} {{{D}_{t}}}}$. Вычисляя определители ${{D}_{n}}$ получим
(17)
$\begin{gathered} D_{{N + n}}^{{}} = {{( - 1)}^{{(N + n) + (N + 1)}}} \times \\ \times \,\,2k_{1}^{{}}\left( {\begin{array}{*{20}{c}} {{{f}_{{1,1}}}}&{{{f}_{{2,1}}}}&{...}&{ - 1}&0&{...} \\ {{{f}_{{1,2}}}}&{{{f}_{{2,1}}}}&{...}&0&{ - 1}&{...} \\ \vdots & \vdots & \ddots & \vdots & \vdots &{...} \\ {{{f}_{{1,N}}}}&{{{f}_{{2,N}}}}&{...}&0&0&{...} \\ 0&{ip_{2}^{{}}}&{...}&{ip_{1}^{'}{{f}_{{2,1}}}}&{ip_{2}^{'}{{f}_{{2,2}}}}&{...} \\ {...}&{...}&{...}&{...}&{...}&{...} \end{array}} \right) = \\ = {{( - 1)}^{{(N + n) + (N + 1)}}}2{{k}_{1}}{{d}_{{N + n,N + 1}}}. \\ \end{gathered} $В (17) мы ввели обозначения $k_{{N + n}}^{'} = ip_{{N + n}}^{'}$, где $p_{{N + n}}^{'} = \operatorname{Im} \left( {k_{{N + n}}^{'}} \right).$Здесь ${{d}_{{N + n,N + 1}}}$ – минор элемента ${{a}_{{N + n,N + 1}}}$ в определителе (17), имеющий порядок (N – 1). В (17) все нижние (N – 1) строки определителя содержат только чисто мнимые квазиимпульсы. Поэтому из каждой строки можно вынести (i), так что ${{d}_{{N + n,N + 1}}} = {{(i)}^{{(N - 1)}}}{{c}_{n}}$, где ${{c}_{n}}$ – действительное число, т.е.
Так как ${{c}_{n}}$ – действительные числа, то отношение
также вещественное число. Поэтому, как следует из (16), разность фаз ${{C}_{n}} - {{C}_{t}} = \pi m$, где $m = 0, \pm 1,...$ Так как такие соотношения выполняются для любых пар коэффициентов ${{C}_{n}}$ и ${{C}_{t}}$ в (13) и (15), то в ситуации 1 в КЯ2$j_{x}^{{(2)}}(x,z) = 0$. Мы вычислили также $j_{x}^{{(1)}}{\text{(}}x,{\text{ }}z{\text{)}}$ в ситуации 1 по формуле (12), представив коэффициенты ${{B}_{{i,j}}}$ в виде ${{B}_{{i,j}}} = \left| {{{B}_{{i,j}}}} \right|\exp (i{{\theta }_{{i,j}}})$, и показали, что в этой ситуации $j_{x}^{{(1)}}{\text{(}}x,{\text{ }}z{\text{) = 0}}$.
Ситуация 2. В этом случае ситуация кардинально меняется. Кинетическая энергия частицы в КЯ1 находится в интервале $E_{2}^{{(1)}} < {{E}_{x}} < E_{3}^{{(1)}}$ и, как и в ситуации 1, меньше величины потенциального барьера Vэф в КЯ2. В этом случае незатухающее распространение отраженной от барьера электронной волны возможно как по нижней, так и по второй подзоне в КЯ1.
Рассмотрим сначала поведение в ситуации 2 плотности потока вероятности $j_{x}^{{(2)}}(x,z)$ в КЯ2. Выражение для $j_{x}^{{(2)}}(x,z)$ в этом случае будет иметь такой же вид (13), (15), как и в ситуации 1. Ранее, при рассмотрении ситуации 1 мы, получая выражения (19) для определителей ${{D}_{{N + n}}},$ на последнем этапе расчета вынесли из миноров ${{d}_{{(N + n),(N + 1)}}}$ множители ${{(i)}^{{(N - 1)}}}$, так как квазиимпульс ${{k}_{2}}$ был чисто мнимым числом. В рассматриваемой сейчас ситуации 2 квазиимпульс ${{k}_{2}}$ – действительное число. Найдем в этой ситуации определитель${{D}_{{N + n}}}$ порядка 2N, разбив его на сумму двух определителей:
(19)
$\begin{gathered} {{D}_{{N + n}}} = D_{{N + n}}^{{(1)}} + D_{{N + n}}^{{(2)}} = {{( - 1)}^{{(n + 1)}}}2{{k}_{1}}\left[ {d_{{_{{(N + n),(N + 1)}}}}^{{(1)}} + d_{{_{{(N + n),(N + 1)}}}}^{{(2)}}} \right] = \\ = {{(i)}^{{N - 2}}}{{( - 1)}^{{(n + 1)}}}2{{k}_{1}}\left\{ \begin{gathered} \left( {\begin{array}{*{20}{c}} {{{f}_{{1,1}}}}&{{{f}_{{2,1}}}}&{...}&{ - 1}&{...}&0&0&{...} \\ {{{f}_{{1,2}}}}&{{{f}_{{2,1}}}}&{...}&0&{...}& \vdots & \vdots &{...} \\ \vdots & \vdots & \ddots & \vdots & \vdots &0& \vdots &{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots &{ - 1}&0&{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots &0&{ - 1}&{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots &{...} \\ {{{f}_{{1,N}}}}&{{{f}_{{2,N}}}}&{...}&{...}&{...}&0&0&{...} \\ 0&{k_{2}^{{}}}&{...}&{...}&{...}&0&0&{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ldots \end{array}} \right) \hfill \\ + i\left( {\begin{array}{*{20}{c}} {{{f}_{{1,1}}}}&{{{f}_{{2,1}}}}&{...}&{ - 1}&{...}&0&0&{...} \\ {{{f}_{{1,2}}}}&{{{f}_{{2,1}}}}&{...}&0&{...}& \vdots & \vdots &{...} \\ \vdots & \vdots & \ddots & \vdots & \vdots &0& \vdots &{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots &{ - 1}&0&{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots &0&{ - 1}&{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots &{...} \\ {{{f}_{{1,N}}}}&{{{f}_{{2,N}}}}&{...}&0&{...}&0&0&{...} \\ 0&0&{...}&{p_{1}^{'}{{f}_{{2,1}}}}&{...}&{p_{{\bar {n} - 1}}^{'}{{f}_{{2,\bar {n} - 1}}}}&{p_{{\overline n + 1}}^{'}{{f}_{{2,\bar {n} + 1}}}}&{...} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ldots \end{array}} \right) \hfill \\ \end{gathered} \right\}. \\ \end{gathered} $Во втором миноре в (19) введено обозначение $\bar {n} = N + n$. Так как в первом миноре $d_{{N + n,N + 1}}^{{(1)}}$ нижние (N – 2) строк, а во втором $d_{{N + n,N + 1}}^{{(2)}}$ нижние (N – 1) строк содержат чисто мнимые квазиимпульсы $k_{n}^{'} = i{\text{Im(}}k_{n}^{'}{\text{) = }}ip_{n}^{'}$, то в (19) мы вынесли общий множитель ${{(i)}^{{N - 2}}}$. В (19) все элементы определителей, а значит, и сами определители, вещественны, но детерминант DN + n – комплексное число. Таким образом, в ситуации 2 отношение
(20)
$\frac{{{{C}_{n}}}}{{{{C}_{t}}}} = {{( - 1)}^{{n + t}}}\frac{{\left[ {d_{{(N + n),(N + 1)}}^{{(1)}} + d_{{(N + n),(N + 1)}}^{{(2)}}} \right]}}{{\left[ {d_{{(N + t),(N + 1)}}^{{(1)}} + d_{{(N + t),(N + 1)}}^{{(2)}}} \right]}}$является комплексным числом. Запишем (20) в виде
(21)
$\frac{{{{C}_{n}}}}{{{{C}_{t}}}} = \frac{{{{a}_{n}} + i{{b}_{n}}}}{{{{a}_{t}} + i{{b}_{t}}}} = \frac{{{{a}_{n}}{{a}_{t}} + {{b}_{n}}{{b}_{t}}}}{{a_{t}^{2} + b_{t}^{2}}} + i\frac{{{{b}_{n}}{{a}_{t}} - {{a}_{n}}{{b}_{t}}}}{{a_{t}^{2} + b_{t}^{2}}}.$Представим (21) в виде (16):
(22)
$\begin{gathered} \frac{{{{r}_{n}}}}{{{{r}_{t}}}}\left( {\cos \left( {{{\theta }_{n}} - {{\theta }_{t}}} \right) + i\sin \left( {{{\theta }_{n}} - {{\theta }_{t}}} \right)} \right) = \\ = \frac{{{{a}_{n}}{{a}_{t}} + {{b}_{n}}{{b}_{t}}}}{{a_{t}^{2} + b_{t}^{2}}} + i\frac{{{{b}_{n}}{{a}_{t}} - {{a}_{n}}{{b}_{t}}}}{{a_{t}^{2} + b_{t}^{2}}}. \\ \end{gathered} $Из (22) получаем
(23)
${\text{tg}}\left( {{{\theta }_{n}} - {{\theta }_{t}}} \right) = \frac{{{{b}_{n}}{{a}_{t}} - {{a}_{n}}{{b}_{t}}}}{{{{a}_{n}}{{a}_{t}} + {{b}_{n}}{{b}_{t}}}}.$Таким образом, при наличии в КЯ1 более чем одного уровня с действительными квазиимпульсами разность фаз в каждом из членов в суммах (13), (15) в КЯ2 отлична от нуля, т.е. ${\text{в}}$ ситуации 2 под барьером в КЯ2 плотность потока вероятности имеет вид $j_{x}^{{(2)}}(x,z) \ne 0$ и экспоненциально затухает при $x \to \infty $. В рассматриваемой ситуации каждой паре коэффициентов ${{C}_{n}},{{C}_{t}}$ в (13), (15) соответствует своя разность фаз ${{\Delta }_{{n,t}}} = \left( {{{\theta }_{n}} - {{\theta }_{t}}} \right)$. Поэтому при вычислении явного вида $j_{x}^{{(2)}}(x,z)$ в сумме по n,t суммируются члены с разными амплитудами и разными ${{\Delta }_{{n,t}}}$, отличными от нуля, для всех различных пар ${{C}_{n}},{{C}_{t}}$. Из полученного выше доказательства отличия от нуля $j_{x}^{{(2)}}(x,z)$ под барьером в КЯ2 следует, что в КЯ1 в ситуации 2 также $j_{x}^{{(1)}}(x,z) \ne 0$. В противном случае (при равенстве нулю $j_{x}^{{(1)}}(x,z)$) было бы невозможно существование отличного от нуля $j_{x}^{{(2)}}(x,z)$ в КЯ2 .
Запишем выражение для $j_{x}^{{(1)}}(x,z)$ в ситуации 2. Тогда квазиимпульсы $k_{1}^{{}}$ и $k_{2}^{{}}$ в КЯ1 – вещественные, а все остальные – мнимые. Все квазиимпульсы в КЯ2 – мнимые. Введя, как и раньше, обозначения ${{k}_{i}} = i{{p}_{i}}$, где ${{p}_{i}} = \operatorname{Im} ({{k}_{i}})$, и записав коэффициенты Bi в виде ${{B}_{i}} = {{r}_{i}}{\text{exp}}(i{{\theta }_{i}})$, можно представить в этой ситуации выражение для $j_{x}^{{(1)}}(x,z)$ в виде
(24)
$\begin{gathered} j_{x}^{{(1)}}(x,z) = \frac{\hbar }{{m{\text{*}}}}\left\{ {\left[ {{{k}_{1}}\chi _{1}^{2}(z)(1 - r_{1}^{2}) - {{k}_{2}}\chi _{2}^{2}(z)r_{2}^{2} - } \right.} \right. \\ - \,\,{{r}_{2}}\chi _{1}^{{}}(z){{\chi }_{2}}(z)\left[ {{{r}_{1}}({{k}_{1}} + k_{2}^{{}})\cos (({{\theta }_{1}} - {{\theta }_{2}} + (k_{2}^{{}} - {{k}_{1}})x)} \right. + \\ \left. {\left. { + \,\,({{k}_{1}} - {{k}_{2}})\cos (({{k}_{1}} + {{k}_{2}})x - {{\theta }_{2}})} \right]} \right] + 2\sum\limits_{i = 3}^N {{{r}_{i}}{{\chi }_{i}}(z)} \times \\ \times \,\,\left( {\sum\limits_{j = i + 1}^N {{{r}_{j}}{{\chi }_{j}}(z)\exp (({{p}_{i}} + {{p}_{j}})x)({{p}_{i}} - {{p}_{j}})\sin ({{\theta }_{i}} - {{\theta }_{j}})} } \right) - \\ - \,\,\sum\limits_{i = 3}^N {{{r}_{i}}{{\chi }_{i}}(z)({{p}_{i}} + {{p}_{j}})\exp ({{p}_{i}}x)} \left[ {{{r}_{1}}{{\chi }_{1}}(z){{q}_{1}}\sin ({{\theta }_{1}} - {{\theta }_{i}} - {{k}_{1}}x + {{\varphi }_{1}})} \right. + \\ + \,\,{{r}_{2}}{{\chi }_{2}}(z){{q}_{2}}\sin ({{\theta }_{1}} - {{\theta }_{i}} - {{k}_{2}}x + {{\varphi }_{2}})) - \\ \left. {\frac{{}}{{}} - \,\,{{\chi }_{1}}(z){{q}_{1}}\left. {\sin ({{\theta }_{i}} - {{k}_{1}}{{x}_{i}} + {{\varphi }_{1}}))} \right]} \right\}, \\ \end{gathered} $где ${{q}_{{1,2}}} = \sqrt {k_{{1,2}}^{2} + p_{i}^{2}} $ и $\sin {{\varphi }_{{1,2}}} = {{{{k}_{{1,2}}}} \mathord{\left/ {\vphantom {{{{k}_{{1,2}}}} {{{p}_{i}}}}} \right. \kern-0em} {{{p}_{i}}}}$.
Отметим разное поведение членов в выражении (24) при $x \to - \infty $. Так, первый и второй члены в фигурных скобках не зависят от х. Члены, содержащие суммы по i, при $x \to - \infty $ осциллируют, экспоненциально затухая, а третий член в (24) имеет осцилляторный незатухающий характер при всех отрицательных значениях координаты х. Таким образом, в ситуации 2 $j_{x}^{{(1)}}(x,z)$ сложным образом осциллирует в КЯ1. Причиной этого является интерференция электронных волн, отражающихся от барьера по двум нижним подзонам с действительными квазиимпульсами. Детальные распределения $j_{x}^{{(1)}}(x,z)$ и $j_{x}^{{(2)}}(x,z)$ можно получить только в результате численных расчетов. Результаты таких расчетов приведены ниже. Подчеркнем еще раз отличие фазовых соотношений для любых пар комплексных коэффициентов ${{B}_{i}},{{B}_{j}}$ и ${{C}_{n}},{{C}_{t}}$ в ситуации 1 от ситуации 2. При учете в ситуации 1 только одной подзоны с вещественным квазиимпульсом k1 разности фаз для всех различных пар коэффициентов ${{C}_{n}},{{C}_{t}}$ в (15) одинаковы и имеют вид ${{\Delta }_{{n,t}}} = {{\theta }_{n}} - {{\theta }_{t}} = \pi m$, где $m = 0, \pm 1.$ Однако в ситуации 2 учет второй подзоны с вещественными $k_{2}^{{}}$ приводит к появлению в выражении (24) для $j_{x}^{{(1)}}(x,z)$ дополнительных членов, возникающих из-за интерференции электронных волн с вещественными $k_{1}^{{}}$и $k_{2}^{{}}$. Вследствие этого, у каждой пары коэффициентов ${{C}_{n}},{{C}_{t}}$ появляется своя, отличная от нуля, разность фаз ${{\Delta }_{{n,t}}}$, причем ${{\Delta }_{{n,t}}}$ для всех пар в КЯ2 различны. В результате плотности потоков вероятности $j_{x}^{{(1)}}(x,z)$ в КЯ1 и $j_{x}^{{(2)}}(x,z)$ в КЯ2 становятся отличными от нуля.
3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РАСЧЕТА
Очевидно, что полностью реализовать схему расчета $j_{x}^{{(1)}}(x,z)$ и $j_{x}^{{(2)}}(x,z)$, изложенную в предыдущем разделе, при учете большого числа квантоворазмерных подзон в КЯ1 и КЯ2 можно только с помощью численных методов. В этом разделе мы приводим результаты численного расчета влияния электронной интерференции на отражение электронной волны от полубесконечного прямоугольного потенциального барьера в полупроводниковой 2D-наноструктуре с конкретными параметрами. Мы рассмотрели задачу о рассеянии монохроматической электронной волны единичной амплитуды, распространяющейся по нижней квантоворазмерной подзоне (m = 1) из узкой прямоугольной КЯ1 (x < 0; а = 150 Å) в широкую прямоугольную КЯ2 (x > 0; А = 500 Å) в симметричной по оси z 2D-наноструктуре с параметрами GaAs (m* = 0.067m0, m0 – масса свободного электрона). Так как в таких симметричных структурах локализующие частицу потенциалы U1(z) и U2(z) в КЯ1 и КЯ2 удовлетворяют условиям U1(z) = U1(–z) и U2(z) = U2(–z) (точка z = 0 находится на оси симметрии структуры), то собственные функции χj(z) и φn(z) в КЯ1 и КЯ2 можно классифицировать по четности. В этом случае коэффициенты неортогональности этих функций ${{f}_{j}}_{{,n}} = \int {\chi _{j}^{*}(z){{\varphi }_{n}}(z)dz} $ равны нулю для функций разной четности. Это приводит к разбиению системы (8а), (8б) на две независимые подсистемы:
1) подсистему неоднородных линейных уравнений, содержащую только коэффициенты Вj и Cn с индексами той же четности, что и номер подзоны m, по которой волна падает из КЯ1 на барьер в КЯ2,
2) подсистему однородных линейных уравнений для коэффициентов Вj и Cn с индексами противоположной m четности.
Так как в определителе системы однородных уравнений нет линейно зависимых строк или столбцов, то этот определитель отличен от нуля, т.е. для рассматриваемого нами случая с m = 1 все коэффициенты Вj и Cn с четными j и n равны нулю. Это обстоятельство существенно уменьшает объем численных расчетов. При расчете предполагалось, что высота потенциального барьера в КЯ2V0 = 243 мэВ (рис. 1). Наличие такого барьера приводило фактически к изменению энергетического положения дна зоны проводимости в КЯ2 до энергии $E_{c}^{{(2)}}$. Энергетическая диаграмма структуры приведена на рис. 2. Энергия частицы отсчитывается от дна зоны проводимости $E_{c}^{{(1)}}$ в КЯ1. Минимумы энергий четырех нижних квантоворазмерных подзон находились в КЯ1 при значении энергии
Рис. 2.
Энергетическая схема 2D-наноструктуры, изображенной на рис. 1. $E_{1}^{{(1)}}{\kern 1pt} - {\kern 1pt} E_{4}^{{(1)}}$ и $E_{1}^{{(2)}}{\kern 1pt} - {\kern 1pt} Е_{4}^{{(2)}}$ – энергетические положения доньев четырех нижних квантово-размерных подзон соответственно в КЯ1 и КЯ2; $E_{{1,2,3,4}}^{{(1)}}\left( {{{k}_{x}}} \right)$ и $E_{{1,2,3,4}}^{{(2)}}\left( {k_{x}^{{'(2)}}} \right)$ – законы дисперсии электронов для этих подзон в КЯ1 и КЯ2; $E_{c}^{{(1)}}$ и $E_{c}^{{(2)}}$ – энергетические положения доньев зон проводимости в КЯ1 и КЯ2 соответственно; $E_{x}^{{(1)}}$ или $E_{x}^{{(2)}}$ – энергии инжектированного электрона с волновым вектором $k_{{1x}}^{{(1)}}$ или $k_{{1x}}^{{(2)}}$ в КЯ1. Энергия частицы отсчитывается от дна зоны проводимости $E_{c}^{{(1)}}$ в КЯ1.
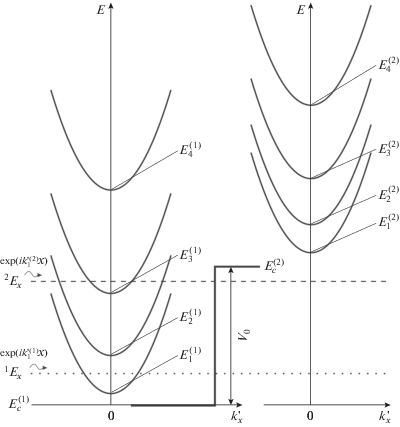
и в КЯ2 при –
где $E_{{1 - 4}}^{{(A)}}$ – энергии четырех нижних уровней размерного квантования в КЯ2, ширина которых А равнялась 2.25, 8.98, 20.21 и 35.92 мэВ соответственно. При этом эффективная высота потенциального барьера для частицы, падающей на барьер из КЯ1, была равна Vэф = $E_{1}^{{\left( A \right)}}$ + V0. Расчет был сделан для КЯ с бесконечно высокими потенциальными стенками. В рассматриваемом нами случае, когда энергия продольного движения падающей из КЯ1 на барьер частицы Ex < Vэф, необходимо при расчете $j_{x}^{{\left( 2 \right)}}(x,z)$ использовать выражение (13), так как в КЯ2 при таких Ex существуют только члены с мнимыми волновыми векторами $k_{{n,t}}^{'}$. Мы исследовали численно две рассмотренные выше ситуации, учитывая при расчете в каждой квантовой яме по 31-й подзоне.
Ситуация 1. Кинетическая энергия частицы Ex в КЯ1 находилась в интервале $E_{1}^{{(1)}} < {{E}_{x}} < E_{2}^{{(1)}}$ и была меньше эффективной высоты барьера Vэф в КЯ2, т.е. Ex < Vэф. В этой ситуации электронная волна падала по нижней квантоворазмерной подзоне в КЯ1 (m = 1) и могла отражаться от барьера без затухания только по этой же подзоне с реальным kх1, а в режиме затухания - по подзонам с мнимыми kхj. Расчет подтвердил результаты проведенного выше теоретического анализа, что в ситуации 1 $j_{x}^{{(1)}}(x,z)$ = 0 и $j_{x}^{{(2)}}(x,z)$ = 0.
Ситуация 2. В этом случае ситуация кардинально меняется. Кинетическая энергия частицы в КЯ1Ex = 245 мэВ находилась в интервале $E_{3}^{{(1)}} < {{E}_{x}} < E_{5}^{{(1)}}$ и, как и в ситуации 1, была меньше высоты эффективного потенциального барьера Vэф в КЯ2 на 10.25 мэВ. В этом случае незатухающее распространение отраженной от барьера электронной волны было возможно как по нижней, так и по третьей подзоне в КЯ1 (отражение по второй подзоне в КЯ1 для рассматриваемой нами симметричной по оси z наноструктуры было запрещено правилами отбора). На рис. 3 приведен общий вид пространственно-неоднородного распределения плотностей потоков вероятностей $j_{x}^{{(1)}}(x,z)$ и $j_{x}^{{(2)}}(x,z)$ в рассматриваемой 2D-наноструктуре в интервале от х = 15 нм до х = –49 нм (рис. 3). На нем отчетливо видно, что в КЯ1$j_{x}^{{(1)}}(x,z)$ имеет сложную осцилляторную структуру, состоящую из пиков, в которых $j_{x}^{{(1)}}(x,z)$ > 0, и провалов, в которых $j_{x}^{{(1)}}(x,z)$ < 0. Проекции амплитуд $j_{x}^{{(1)}}(x,z)$ на плоскость (х,z = 0) в интервале от х = 0 до х = –49 нм приведены на рис. 4а и на плоскость (х = 0, z) в интервале z = ±a/2 – на рис. 4б. На рис. 5 приведен общий вид пространственно-неоднородного распределения плотности потока вероятности $j_{x}^{{(2)}}(x,z)$ в КЯ2 в интервале от х = 15 нм до х = 0. Видно, что в ситуации 2 под барьером в КЯ2 плотность потока вероятности $j_{x}^{{(2)}}(x,z)$ отлична от нуля и в КЯ2 существуют три области, в которых квантовомеханический ток $еj_{x}^{{\left( 2 \right)}}\left( {x,z} \right)$ имеет координатную зависимость от x и z. Это центральная область, расположенная зеркально симметрично относительно плоскости (z–x), в которой ток $еj_{x}^{{\left( 2 \right)}}\left( {x,z} \right)$ направлен в положительном направлении оси х. И две симметрично расположенные по оси z боковые области, в которых ток $еj_{x}^{{\left( 2 \right)}}\left( {x,z} \right)$ направлен в противоположную сторону, в отрицательном направлении оси х. Очевидно, что наличие боковых областей с обратным направлением тока необходимо для обеспечения оттока заряда из-под барьера. Отсутствие таких областей привело бы к накоплению заряда под барьером. В этих трех областях амплитуда $еj_{x}^{{\left( 2 \right)}}\left( {x,z} \right)$ экспоненциально затухает при х → ∞. Разумеется, полный ток под барьером, полученный интегрированием по z выражения для $еj_{x}^{{\left( 2 \right)}}\left( {x,z} \right)$ (13), из-за ортогональности поперечных волновых функций для разных квантоворазмерных подзон в КЯ2 равен нулю. На рис. 4 приведены кривые, демонстрирующие распределение по оси z под барьером в широкой КЯ2 с параметрами GaAs нормированной плотности потока вероятности jx(x, z)/jx(0, 0) для шести поперечных сечений, последовательно расположенных по оси х в шести точках: X1,2,3,4,5,6 = 0, 5, 10, 15, 20 и 30 Å. На рис. 5а представлена топограмма пространственного распределения под барьером в широкой КЯ2 в плоскости (x-z) нормированной плотности потока вероятности ${{j_{x}^{ + }\left( {x,z} \right)} \mathord{\left/ {\vphantom {{j_{x}^{ + }\left( {x,z} \right)} {{{j}_{x}}\left( {0,0} \right)}}} \right. \kern-0em} {{{j}_{x}}\left( {0,0} \right)}}$ (область 2) и (области 1 и 3).
Рис. 3.
Общий вид пространственно-неоднородного распределения плотностей потоков вероятностей $j_{x}^{{(1)}}(x,z)$ и $j_{x}^{{(2)}}(x,z)$ в рассматриваемой 2D-наноструктуре в интервале х = 15…–49 нм.
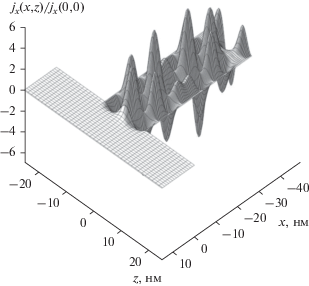
Рис. 4.
Распределение по оси z под барьером в широкой КЯ2 с параметрами GaAs нормированной плотности потока вероятности jx(x, z)/jx(0,0) для шести поперечных сечений, последовательно расположенных по оси х в шести точках: X = 0 (1), 5 (2), 10 (3), 15 (4), 20 (5) и 30 Å (6). Положительные значения jx(x, z)/jx(0,0) соответствуют плотности квантово-механического тока вдоль положительного направления оси x; отрицательные – в противоположном направлении; (Цифры в квадратах – нумерация кривых.) Кинетическая энергия частицы $E_{x}^{{(2)}}$ в КЯ1 равнялась 245 мэВ и была меньше полной эффективной высоты потенциального барьера в КЯ2Vэфф= = $E_{1}^{A} + {{V}_{0}}$ на 10.25 мэВ (V0 = 243 мэВ).
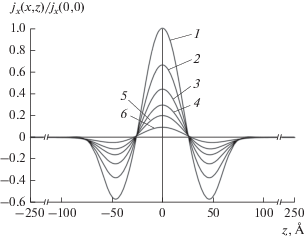
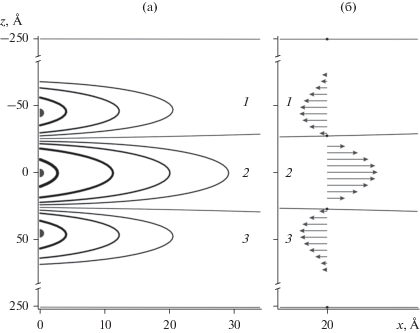
Рис. 5.
Топограмма (а) пространственного распределения под барьером в широкой КЯ2 в плоскости (x–z) нормированной плотности потока вероятности $j_{x}^{ + }$(x, z)/jx (0,0) (область 2) и $j_{x}^{ - }$(x z)/jx (0,0) (области 1 и 3). Амплитуды пиков представлены в отн.ед. Линии, уменьшающиеся по толщине в области 2, – сечения пика $j_{x}^{ + }$(x,z)/jx(0,0) на высотах 1.0, 0.8, 0.4, 0.2, 0.1. Линии, уменьшающиеся по толщине в областях 1 и 3, соответствуют сечениям пиков $j_{x}^{ - }$(x,z)/jx(0,0) высотой –0.57 в точках $j_{x}^{ - }$(0 ± 46 Å)/jx (0,0) при высотах –0.4, –0.2, –0.1. Зависимости (б) от z нормированных подбарьерных плотностей потоков вероятностей $j_{x}^{ + }$(x, z)/jx (0,0) (область 2) и $j_{x}^{ - }$(x, z)/jx (0,0) (области 1 и 3) в широкой КЯ2 при х = 20 Å. Направления стрелок указывают направления токов, их длины соответствуют различным значениям нормированной амплитуды по оси z в каждой из трех областей. Положительные $j_{x}^{ + }$(x, z) и отрицательные $j_{x}^{ - }$(x, z) соответствуют положительному и отрицательному направлениям вдоль оси х.
Таким образом, в работе показано, что при энергии частицы меньше высоты потенциального барьера в рассмотренных 2D-наноструктурах интерференция электронных волн при определенных условиях приводит к подбарьерному просачиванию плотности квантовомеханического тока.
Очевидно, что если в наноструктуре в области x < 0 с помощью боковых электродов приложить по оси z постоянное электрическое поле, меняющее потенциальный профиль КЯ1, то можно непрерывно перейти от ситуации 1, когда $j_{x}^{{(1)}}(x,z)$ = 0, к ситуации 2, когда $j_{x}^{{(1)}}(x,z)$ ≠ 0. Такой переход может быть обусловлен как понижением симметрии (включение второго уровня с действительным квазиимпульсом) при включении поля, так и изменением расстояния между размерными подзонами в КЯ1.
В данной работе рассмотрена 2D-наноструктура с квантовыми ямами прямоугольного сечения и прямоугольным потенциальным барьером. Однако необходимо отметить, что рассмотренные эффекты носят общий характер и должны проявляться как в неоднородных по оси х 2D-наноструктурах с другими потенциальными профилями квантовых ям и потенциальных барьеров, так и в аналогичных 1D-наноструктурах. При этом единственным необходимым условием появления интерференционных эффектов является существование в КЯ1, откуда на барьер падает электронная волна, как минимум двух квантоворазмерных подзон с действительными квазиимпульсами, что обеспечивает возникновение интерференции отражающихся от барьера волн.
В настоящее время существуют способы инжекции квазимоноэнергетических пучков электронов в 2D-наноструктурах. Так, например, в [34] был исследован баллистический электронный транспорт по минизонам в сверхрешетке на основе системы GaAlAs–GaAs путем инжекции в сверхрешетку пучков горячих электронов.
ЗАКЛЮЧЕНИЕ
Проведенные в работе теоретический анализ и численный расчет показывают, что в полупроводниковых 2D-наноструктурах, геометрия и потенциальный рельеф которых обеспечивают существование в таких структурах электронных интерференционных эффектов, возможен новый эффект – возникновение пространственно-неоднородного распределения плотности квантовомеханического тока еjx(x, z). Рассмотрена наноструктура, состоящая из последовательно расположенных в направлении распространения электронной волны узкой и широкой прямоугольных квантовых ям. Показано, что при энергии частицы меньше высоты потенциального барьера в такой наноструктуре при определенных условиях возможно возникновение осциллирующего пространственно-неоднородного распределения еjx(x, z) в узкой квантовой яме и экспоненциально затухающее и имеющее координатную зависимость просачивание еjx(x, z) под полубесконечный прямоугольный потенциальный барьер высотой V0, созданный в широкой квантовой яме. Этот эффект обусловлен интерференцией электронных волн, распространяющихся по разным квантово-размерным подзонам в такой наноструктуре.
Список литературы
Имри Й. Введение в мезоскопическую физику. М.: Физматлит, 2002.
Ferry D.K., Goodnick. S.M. Transport in Nanostructures. Cambridge: Cambridge Univ. Press, 1997.
Datta S. Electronic Transport in Mesoscopic Systems. Cambridge: Cambridge Univ. Press, 1995.
Kircenow G. // Phys. Rev. B. 1989. V. 39. № 14. P. 10452.
Kircenow G. // Sol. St. Com. 1988. V. 68. № 8. P. 715.
Tekman E., Ciraci S. // Phys. Rev. B. 1991. V. 43. № 9. P. 7145.
Sols F., Macucci M., Ravaioli U., Hess K. J. // J. Appl. Phys. 1989. V. 66. № 8. P. 3892.
Tachibana H., Totsuji H. // J. Appl. Phys. 1996. V. 79. № 9. P. 7021.
Wu H., Sprung D.W.L., Martorell J. // J. Appl. Phys. 1992. V. 72. № 1. P. 151.
Namiranian A., Khajehpour M.R.H., Kolesnichenko Yu.A., Shevchenko S.N. // Physica E. 2001. V. 10. № 4. P. 549.
Olendski O., Mikhailovska L. // Phys. Rev. B. 2002. V. 66. № 3. P. 035331.
Bagwell P.F. // Phys. Rev. B. 1990. V. 41. № 15. P. 10354.
Takagaki Y., Ferry D.K. // Phys. Rev. B. 1991. V. 44. № 15. P. 8399.
Itoh T., Nobuyuki Sano N., Yoshii A. // Phys. Rev. B. 1992. V. 45. № 24. P. 14131.
Singha Deo P., Gupta B.C., Jayannavar A.M., Peeters F.M. // Phys. Rev. B. 1998. V. 58. № 16. P.10784.
Nicolic K., Sordan R. // Phys. Rev. B. 1998. V. 58. № 15. P. 9631.
Jin G.J., Wang Z.D., Hu A., Jiang S.S. // J. Appl. Phys. 1999. V. 85. № 3. P. 1597
Петров В.А., Сандлер И.М. // Микроэлектроника. 1994. Т. 23. № 4. С. 3.
Berggrenn K.F., Ji Z.-L. // Phys. Rev. B. 1991. V. 43. № 6. P. 4760.
Ji Z.-L., Berggrenn K.-F. // Phys. Rev. B. 1992. V. 45. № 12. P. 6652.
Petrov V.A., Bratman V.L. // Phys. Stat. Sol.(b). 2000. V. 221. № 1. P. 459.
Petrov V.A., Nikitin A.V. // Proc. SPIE. 2004. V. 5401. P. 377.
Петров В.А., Никитин А.В. // РЭ. 2007. Т. 52. № 11. С. 1387.
Petrov V.A., Nikitin A.V. // Physics, chemistry and application of nanostructures. Proc. Int. Conf. on Nanomeeting. Minsk, Belarus, 22–25 May 2007. P. 109.
Petrov V.A., Nikitin A.V. // Proc. SPIE. 2008. V. 7025. P. 70250O-1.
Петров В.А., Никитин А.В. // Физика и техника полупроводников. 2005. Т. 39. № 4. С. 436.
Petrov V.A., Nikitin A.V. // Phys. Stat. Sol. (c). 2006. V. 3. № 7. P. 2423.
Петров В.А., Никитин А.В. // Физика и техника полупроводников. 2006. Т.40. № 8. С. 977.
Petrov V.A., Nikitin A.V. // Proc. SPIE. 2006. V. 6260. P. 62600N-1.
Петров В.А., Никитин А.В. // РЭ. 2009. Т. 54. № 2. С. 220.
Petrov V.A., Nikitin A.V. // Proc. 17th Int. Symp. “Nanostructures: Physics and Technology”, Minsk, Belarus, 22–26 Jun. 2009. P. 254.
Petrov V.A., Nikitin A.V. // Proc. 11th IEEE Nanotechnology Materials and Devices Conf. (NMDC 2016), 9‒12 October, Toulouse, France. https://doi.org/10.1109/NMDC.2016.7777168
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. М.: Наука, 1989.
Rauch C., Strasser G., Unterrainer K. et al. // Physica E. 1998. V. 2. № 1–4. P. 282.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


