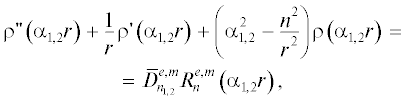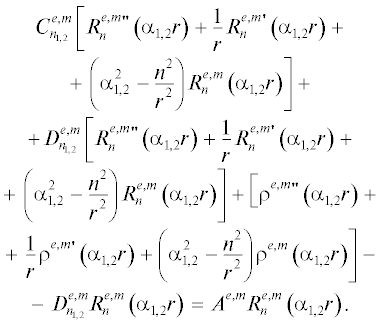Радиотехника и электроника, 2021, T. 66, № 2, стр. 133-140

ВВЕДЕНИЕ

Как известно [1–3], наиболее общим решениям несамосопряженных краевых задач соответствуют комплексные собственные значения. В электродинамических задачах комплексность собственных значений определяет комплексность волновых чисел. Комплексные волновые числа в направляющих структурах без диссипации энергии соответствуют комплексным волнам [4, 5]. Парное возбуждение комплексных волн (КВ) с комплексно сопряженными амплитудами и волновыми числами приводит к возникновению комплексного резонанса [6–9]. Особенностью его является [6–8] существование во всем диапазоне КВ. Отрезок волновода, в котором могут существовать КВ, включенный “на проход” или “на отражение”, обнаруживает резонансные свойства во всем диапазоне существования пары комплексных волн. Это замечательное свойство электродинамических структур, направляющих КВ, может быть использовано при построении различных частотно-избирательных устройств.

Поскольку колебание, соответствующее комплексному резонансу (КР), может существовать только в присутствии источника, возбуждающего указанную пару КВ, его не следует считать собственным. Его будем называть колебанием, “присоединенным” к источнику [10–13]. Собственные колебания описываются решениями однородных краевых задач. В случае КР присутствие источника делает краевую задачу неоднородной, а колебание, соответствующее КР, несобственным.

В данной работе на примере круглого двуслойного экранированного волновода (КДЭВ) рассматриваются вопросы теории КВ и КР, приводятся результаты их экспериментального исследования.

1. ВОЗБУЖДЕНИЕ КОМПЛЕКСНЫХ ВОЛН. ОБРАЗОВАНИЕ ПРИСОЕДИНЕННОГО КОЛЕБАНИЯ

Поскольку комплексные волны описываются собственными функциями несамосопряженного дифференциального оператора второго порядка, “порождаемого” [14] системой однородных уравнений Максвелла, их поля должны удовлетворять условию

где ${{S}_{i}}$ – произвольное поперечное сечение исследуемого волновода, n и k – номера собственных волн.

Это условие может выполняться только либо при отсутствии у подынтегрального выражения зависимости от продольной координаты, либо при тождественном равенстве интеграла нулю. Объединяя эти два варианта, записываем

Равенство (1) является записью условия ортогональности собственных волн экранированного волновода в энергетическом смысле. При его использовании амплитуду прямой комплексной волны I, распространяющейся справа от источника, записываем в виде

амплитуду обратной комплексной волны II, также распространяющейся справа от источника, –

В соотношениях (2) и (3): ${{\vec {E}}^{{\left( - \right)}}}$ и ${{\vec {H}}^{{\left( - \right)}}}$ – поля комплексной волны с продольным волновым числом ${{\beta }^{{\left( - \right)}}} = - \beta $ ($\beta $ – продольное волновое число прямой волны I); ${{\bar {\vec {E}}}^{{\left( - \right)}}}$ и ${{\bar {\vec {H}}}^{{\left( - \right)}}}$ – поля комплексной волны с продольным волновым числом ${{\bar {\beta }}^{{\left( - \right)}}} = - \bar {\beta }$ ($\bar {\beta }$ – продольное волновое число обратной комплексной волны II).

Вводя обозначения

и учитывая связи между амплитудными коэффициентами потенциальных функций $\psi _{{1,2}}^{{e,h}}$ во внутреннем и внешнем слоях волновода, записываем

Как видно из (4), поля прямой и обратной комплексных волн связаны равенствами

В выражениях (4), (5) знак (*) обозначает комплексную сопряженность волновых чисел и полей.

Полагая, что поля в волноводе возбуждаются токами ${{\vec {I}}^{e}} = {{\vec {j}}^{e}}$ и ${{I}^{m}} = i{{\vec {j}}^{m}}$, являющимися действительными функциями координат, из выражений (2), (3) с учетом (4) и (5) получаем

Видно, что при выбранных источниках амплитуды прямой и обратной комплексных волн, распространяющихся справа от источника, связаны равенством $\vec {A} = A{\text{*}}$, из которого следует, что обе указанные волны возбуждаются совместно с комплексно сопряженными амплитудами. Совместное существование двух волн приводит к образованию поля стоячей волны, локализованного вблизи источника.

Это поле, ввиду его неразрывной связи с источником, должно описываться неоднородной краевой задачей на уравнении Гельмгольца, в правой части которого стоит решение однородной краевой задачи. Такое уравнение будем называть присоединенным. В случае КДЭВ однородная краевая задача является [1–3] несамосопряженной.

При возбуждении поля стоячей волны, затухающего при удалении от источника, можно говорить о возникновении в двуслойном волноводе, в области существования комплексных волн, резонанса, который называем [6] комплексным. Зададим источники в виде

где $\beta $ совпадает с продольным волновым числом комплексной волны I, $j_{0}^{e}$ и $j_{0}^{m}$ – действительные величины.

Подставив (6) в выражения (2) и (3) и выполнив интегрирование по продольной координате, с учетом соотношений (4) получаем

где S – поперечное сечение волновода, $\left[ {{{z}_{1}}{\kern 1pt} - {\kern 1pt} {{z}_{2}}} \right]$ – интервал, в котором заключены источники.

Из (8) видим, что, если

то амплитуда обратной комплексной волны II равна нулю, в то время как амплитуда прямой волны I, в соответствии с (7), отлична от нуля. В соотношении (9) ${{\lambda }_{{\text{в}}}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\beta }_{1}}}}} \right. \kern-0em} {{{\beta }_{1}}}}$; n = 1, 2, 3…. Таким образом, взяв источники поля типа антенны бегущей волны (6), подбором интервалов, по продольной оси волновода, в которых заключены эти источники, можно добиться возбуждения только одной комплексной волны. Это свидетельствует о том, что рассматриваемые комплексные волны (как собственные) могут существовать независимо.

Реально в направляющих структурах существуют лишь те волны, которые можно возбудить соответствующим источником. В частности, как показано выше, для возбуждения одной собственной КВ требуется источник типа антенны бегущей волны. В этом случае в правой части присоединенного уравнения Гельмгольца должна стоять функция, описывающая бегущую собственную волну. При возбуждении указанной выше пары сопряженных КВ в правой части присоединенного уравнения Гельмгольца должна стоять функция, описывающая экспоненциально затухающую при удалении от источника стоячую волну. Это является признаком самосогласованности краевой задачи [10–13].

Таким образом, краевая задача, описывающая КР, состоит из уравнения

которое называем присоединенным уравнением Гельмгольца, и граничных условий

где ${\text{П}}_{z}^{{e,m}}$ – продольные компоненты электрического и магнитного векторов Герца; a и b – радиусы внутреннего слоя и экрана КДЭВ; $\beta = {{\beta }_{1}} + i{{\beta }_{2}}$ – продольное волновое число.

Функции в правой части уравнения (10) имеют вид

где ${{J}_{n}}\left( {{{\alpha }_{{1.2}}}r} \right)$, ${{Y}_{n}}\left( {{{\alpha }_{2}}r} \right)$ – цилиндрические функции первого и второго рода; ${{\alpha }_{{1,2}}}$ – поперечные волновые числа [1].

Поля в неоднородных электродинамических структурах в общем случае описываются несамосопряженными краевыми задачами [1–3]. Для экранированных структур эти задачи, будучи однородными, определяют спектры собственных волн (колебаний). Для открытых структур несамосопряженные краевые задачи, являясь полуоднородными, наряду с собственными волнами могут [14] описывать несобственные волны дискретного спектра [1‒3, 14]. Понятие “несобственные волны” впервые, по-видимому, введено в работе В.В. Шевченко [14]. В экранированных волноводах с неоднородным заполнением наряду с собственными волнами могут [10, 11] существовать присоединенные к источнику несобственные волны, описываемые присоединенным уравнением Гельмгольца, под которым здесь понимаем уравнение (10) с правой частью, являющейся решением однородной краевой задачи, т.е. задачи на однородном уравнении Гельмгольца. Как показано в [6] и отмечено выше, собственные КВ слоистых экранированных волноводов возбуждаются источниками, описываемыми действительными функциями пространственных координат, в виде комплексно-сопряженных парами [1–3, 6], приводя к возникновению явления комплексного резонанса (КР). Резонансным признаком явления служит факт увеличения запасенной энергии в указанной выше полосе частот, что позволяет ввести понятие добротности (в энергетической формулировке), вычислить ее и измерить косвенным методом. Понятие КР было введено в работе [6]. В неоднородных направляющих структурах (например, в КДЭВ) КР, отличающийся от обычного резонанса своим существованием не в точке, а во всем диапазоне существования КВ, имеет место [8] только при наличии источника, через который замыкаются прямой и обратный потоки мощности [15]. Таким образом, две взаимодействующие между собой КВ оказываются “привязанными” к источнику, а поле КР можно назвать “присоединенным” к источнику электромагнитным колебанием. Задача о возбуждении КР является самосогласованной – источник создает пару КВ, образующих замкнутые через этот источник потоки мощности.

Поля двух комплексных волн с комплексно сопряженными амплитудами образуют “присоединенное” к источнику колебание, которое в силу обязательного присутствия источника не является собственным. Соответствующий этому колебанию КР образуется полем, локализованным вблизи источника, т.е. имеющим вид стоячей волны с амплитудой, экспоненциально убывающей при удалении от источника в соответствии с продольной зависимостью поля КВ.

Термин “колебание, присоединенное к источнику”, введен для того, чтобы приблизить математическое понятие “присоединенное решение” к его физическому (в данной конкретной ситуации) смыслу. Присоединенное решение связывается с возбуждением колебания источником особого вида, соответствующего присоединенной краевой задаче. Функцию в правой части уравнения (10) можно рассматривать как функцию источника, создающего КР.

Запишем решение сформулированной краевой задачи в виде

где функции ρ^e,m(α^1,2r) удовлетворяют уравнениям

которые можно рассматривать как присоединенные уравнения Бесселя, и граничным условиям Дирихле и Неймана на поверхности r = b, определяющим значения ${{\alpha }_{{1,2}}}$. Подставляя решение (12) в уравнение (10), получаем

Из соотношения (14) видно, что решение (12) с учетом уравнения (13) удовлетворяет присоединенному уравнению Гельмгольца (10) при условии

Как и должно быть, характер возбуждаемой заданным источником волны определяется амплитудой $A_{{}}^{{e,m}}$ этого источника – условием, накладываемым на эту амплитуду.

В том случае, когда

решения (12) удовлетворяют обычному (однородному) уравнению Гельмгольца и соответствуют точке жордановой кратности волновых чисел [16], обеспечивая полноту системы волн направляющей структуры [17, 18].

Условия (15), (16) являются естественными дополнительными условиями, накладываемыми на источник, поскольку от последнего зависит вид возбуждаемого им поля: несобственного колебания, в частности, соответствующего (при возбуждении пары сопряженных КВ) комплексному резонансу.

Сформулированная задача о возбуждении КР является самосогласованной, а колебание, соответствующее КР, следует называть колебанием, присоединенным к источнику. Самосогласованность задачи следует из совпадения волновых чисел в правой части уравнения (10) с волновыми числами КВ, образующих колебание, соответствующее КВ.

Таким образом, источники, описываемые действительными функциями координат, возбуждают в КДЭВ по обе стороны от себя по две комплексные волны с противоположно направленными фазовыми скоростями. Это приводит к возникновению стоячей волны, поле которой локализовано вблизи источника. При этом отрезок волновода, включаемый “на проход” или “на отражение” (в первом случае в плоскости симметрии, перпендикулярной оси волновода, располагаются возбуждающий и воспринимающий электроды, во втором – лишь один возбуждающий электрод) во всем диапазоне комплексных волн ведет себя как резонатор и имеет при этом фильтрующие свойства. Поскольку в отличие от обычного резонанса отмеченное явление, возникающее в двуслойном экранированном волноводе, обнаруживает резонансные свойства (возрастание выходного сигнала в схеме “на проход” и резкое падение коэффициента стоячей волны по напряжению ${{K}_{{{\text{ст}}U}}}$ в схеме “на отражение”) во всем частотном диапазоне комплексных волн, оно классифицировано [6] как “комплексный резонанс”.

Резонансным признаком рассматриваемого явления служит факт увеличения запасенной энергии в указанной выше полосе частот, что позволяет ввести понятие добротности (в энергетической формулировке), вычислить ее и измерить косвенным методом. Поскольку КР существует только в присутствии источника, возбуждающего пару КВ, и описывается присоединенной краевой задачей, соответствующее ему колебание следует называть присоединенным, а краевую задачу полагать самосогласованной.

3. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ КР В КДЭВ

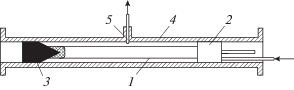
Продольное сечение исследуемой волноводной структуры показано на рис. 1. Диэлектрический стержень 1 и возбуждающий электрод 2 жестко соединены между собой, так что они могут перемещаться вдоль металлического волновода 4 одновременно. На конце диэлектрического стержня размещен поглощающий конус 3 с впрессованными в него резистивными пленками. Устройство для отбора мощности 5 (воспринимающее устройство), состоящее из петли связи, предельной трубки, отрезка коаксиальной линии и детектора, выполнено неподвижным. Перемещение диэлектрического стержня вместе с возбуждающим электродом относительно воспринимающего позволяет проводить исследование продольного распределения поля вдоль описанной волноводной структуры. При этом исключается необходимость в прорезании продольной щели в стенке волновода (как в обычной измерительной линии), которая могла бы существенно исказить структуру поля исследуемой волны, а также внести дополнительное затухание.

Возбуждающее устройство было спроектировано так, чтобы оно обеспечивало фильтрацию волны ${{E}_{{01}}}$. Последняя при известных параметрах заполнения (режим комплексных волн соответствует этим параметрам) является основной и в области существования КВ может оказаться распространяющейся, что, естественно, затруднит проведение измерений. Отсутствие поля волны ${{E}_{{01}}}$ проверялось экспериментально путем поворота возбуждающего устройства на 90°. Диаметр волновода, на котором проводились измерения, D = 25 мм; диаметр диэлектрического стержня, изготовленного из материала ПЭНДТ (полиэтилен низкого давления с двуокисью титана, $\varepsilon = 15$, ${\text{tg}}\delta = {{10}^{{ - 4}}}$), d =15 мм.

Проведение измерений начинают с диапазона распространения основной волны НЕ₁₁. При этом связь воспринимающего электрода с полем в волноводе устанавливают достаточно слабой, так чтобы сигнал на осциллографе не более чем на порядок превышал уровень шумов. Промодулированный сигнал СВЧ-генератора подают через ферритовый вентиль на возбуждающее устройство. При перемещении диэлектрического стержня и возбуждающего устройства относительно зонда 5 уровень сигнала на осциллографе фиксировали. При этом из-за неполного согласования, а также вносимого затухания, он изменялся в пределах ±10%. Установленный уровень сигнала на осциллографе сохраняли при уменьшении частоты вплоть до значения f₀ = 4435 МГц. При переходе через указанное значение наблюдали резкое (примерно на два порядка) возрастание сигнала на осциллографе, что свидетельствовало о возникновении резонанса. При этом продольное распределение поля, фиксируемое воспринимающим электродом, приобретало характер затухающей по мере удаления от возбуждающего электрода стоячей волны. Частота f₀ с точностью не хуже 1% совпадала с верхней границей диапазона существования комплексных волн.

Для определения фазовой постоянной $\beta $ и коэффициента затухания $\alpha $ КВ многократно измеряли продольное распределение поля на различных фиксированных частотах. Измеренные значения фазовой постоянной отличаются от расчетных не более чем на 10%, а коэффициента затухания – не более чем на 1.5%.

На частотах f < f₀ наблюдали КР; распределение поля при этом соответствовало полю затухающей стоячей волны. Измерить добротность резонанса обычными частотными методами невозможно, поскольку резонанс имеет место во всей полосе частот, соответствующей диапазону существования КВ. Временнóй метод потребовал бы создания специального переключающего устройства с длительностью фронта импульса порядка 5 нс (при постоянной времени экспоненты порядка 30 нс), поэтому использовали подход, основанный на сравнении двух резонансов: эталонного, для которого добротность известна, и исследуемого комплексного.

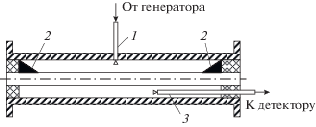
Исследуемый резонатор, который представлял собой отрезок круглого двуслойного волновода длиной L = 240 мм с диаметром экрана D = 31.5 мм; диаметром диэлектрического стержня d = 14.4 мм и его относительной диэлектрической проницаемостью $\varepsilon = 20$, изображен на рис. 2. Здесь 1 − петля связи, 2 − поглощающие клинья, 3 − зонд). Возбуждались резонансы двух типов: обычный (при замкнутых концах волновода) и комплексный (при согласованных концах). Согласование в последнем случае проверяли по отсутствию обычного резонанса на частоте f = 3579 МГц. Средняя по диапазону существования КВ частота КР f = 3520 МГц. Тонким зондом, вводимым в резонатор через отверстие в его торце, исследовали распределение поля в резонаторе при возбуждении резонансов того и другого типов.

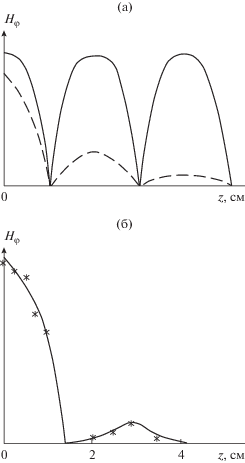
Качественный характер продольного распределения поля в этих случаях представлен на рис. 3а, где сплошной линией показано теоретическое распределение амплитуды поля обычной стоячей волны, штриховой линией – стоячей волны, соответствующей комплексному резонансу. На рис. 3б показано полученное экспериментально (крестики) распределение амплитуды поля стоячей волны, соответствующей комплексному резонансу. С помощью зонда определяли уровень поля в случае обычного резонанса и КР. Отношение этих уровней определялось как $q = \sqrt {{{{{I}_{{{\text{КР}}}}}} \mathord{\left/ {\vphantom {{{{I}_{{{\text{КР}}}}}} {{{I}_{{\text{0}}}}}}} \right. \kern-0em} {{{I}_{{\text{0}}}}}}} $, где ${{I}_{{{\text{КР}}}}}$ и ${{I}_{{\text{0}}}}$ – токи квадратичного детектора для случаев КР и обычного резонанса. По продольному распределению поля в случае КР определены фазовая постоянная $\beta = 1.1$ см^–1 и коэффициент затухания $\alpha = 0.79$ см^–1. Используя эти результаты, определяли значения добротности обоих резонансов. Для обычного резонанса – по ширине резонансной кривой на уровне 0.5 – она составила Q₀ = 325. Невысокое значение добротности объясняется использованием латунной трубы с относительно низким классом обработки внутренней поверхности. Добротность КР Q_КР измеряли на специальной установке. При проведении эксперимента основную линию направленного ответвителя замыкали на конце при частоте КР и определяли отраженную мощность P_КР измерителем мощности, подключенным к вспомогательной линии направленного ответвителя. Затем вместо замыкающего устройства к основной линии направленного ответвителя подключали испытуемый резонатор и измеряли отраженную мощность. При измерениях в обоих случаях подстройкой фазовращателя и возбуждающего устройства достигался максимальный уровень отраженной мощности (P_КР)_max. Поглощаемую в резонаторе мощность $\Delta $P_КР определяли по разности двух измерений. Наличие КР фиксировали на осциллографе, к вертикальным пластинам которого подавали продетектированный сигнал с резонатора (генератор работал в режиме “меандр”).

Результаты измерений в центре полосы существования КР: P_КР = 35 мкВт, (P_КР)_max = 32 мкВт, $\Delta $P_КР = 3 мкВт. В случае замкнутого на концах резонатора поглощаемая им мощность в режиме обычного резонанса равна P₀ = 52 мкВт, (P₀)_max = = 15 мкВт, $\Delta $P₀ = 37 мкВт.

Таким образом, мощность, поглощаемая резонатором при КР, в р = $\Delta $P₀/$\Delta $P_КР раз меньше, чем в обычном. Поскольку добротность обычного резонанса известна, остается найти соотношение запасенных в резонаторе мощностей в обоих случаях. Численные результаты показали, что в волноводе, на основе которого выполнен рассматриваемый резонатор, на частоте комплексного резонанса f = 3520 МГц поперечное волновое число в области диэлектрика равно k_КР = (2.5 + i0.12) см^–1, на частоте обычного резонанса f = 3579 МГц оно равно k_КР = 2.7 см^–1. Учитывая, что мнимая часть поперечного волнового числа в случае КР значительно меньше действительной, которая, в свою очередь, достаточно близка к величине поперечного волнового числа в случае обычного резонанса, полагаем, что структуры полей в области диэлектрика при резонансах обоих типов также достаточно близки.

Остается определить величину q. Величину q измеряли в области максимумов стоячих волн при фиксированном по радиусу (см. рис. 2) положении зонда в промежутке между экраном и диэлектриком. Исследования показали, что $q \approx 1,2$.

С учетом уровня подводимой в том и другом случаях мощности и экспоненциального уменьшения поля при удалении от возбуждающего электрода при КР для отношения запасенных мощностей можно записать

где

Установив соотношения между запасенными и поглощенными мощностями для резонансов обоих типов, окончательно получаем

Экспериментальное значение добротности ${{Q}_{{{\text{КР}}}}} \approx 294$. Расчетное значение собственной добротности комплексного резонанса, вычисляемое на основе ее энергетического определения, получается выше и может достигать значения ~10³.

Теоретически собственная добротность КР рассчитывали по следующей схеме.

Выразив компоненты поля через векторы Герца:

где функции ${{\chi }_{{11}}}\left( {{{\alpha }_{2}}r} \right)$, ${{\chi }_{{21}}}\left( {{{\alpha }_{2}}r} \right)$ – комбинации цилиндрических функций, обеспечивающие выполнение на экранирующей поверхности граничных условий Дирихле и Неймана соответственно, подставим их и решения дисперсионного уравнения в формулу

учитывающую потери в диэлектрике и в экранирующей поверхности волновода.

В (18) индексы “1”, “2” соответствуют внутренней и внешней областям двуслойного волновода; S – экранирующая поверхность, $\sigma $ – проводимость ее материала; f – частота КР. Формула (18) записана в гауссовой системе единиц. Значительное отличие теоретического результата от экспериментального объясняется влиянием внешних цепей резонатора (при эксперименте измеряли нагруженную добротность). Кроме того, при определении добротности по формуле (17) полагали, что распределения полей в области, заполненной диэлектриком, при комплексном и эталонном резонансах совпадают, однако в действительности это выполняется лишь приближенно.

Исследования показали, что добротность КР в волноводных структурах рассмотренного типа имеет порядок $Q = 300{\kern 1pt} - {\kern 1pt} 1000$ (${{Q}_{{{\text{эксп}}}}} \approx 300$; ${{Q}_{{{\text{теор}}}}} \approx 1000$) и уменьшается с приближением к нижней частотной границе диапазона существования КВ.

ЗАКЛЮЧЕНИЕ

Показано, что в диапазоне существования комплексных волн при условии их парного возбуждения в круглом двуслойном экранированном волноводе возникает резонансное явление, получившее название “комплексный резонанс” [6]. Рассмотрены вопросы теории комплексного резонанса, установлено его соответствие самосогласованной краевой задаче, описаны его характерные особенности, приведены результаты экспериментального исследования явления. Сформулирован подход к определению добротности комплексного резонанса, определен ее порядок. На основе проведенных теоретических и экспериментальных исследований разработан макет полосового фильтра. Колебание, соответствующее комплексному резонансу, предлагается классифицировать как присоединенное к источнику, поскольку теоретически оно описывается краевой задачей на присоединенном уравнении Гельмгольца, в правой части которого стоит функция, являющаяся решением однородной краевой задачи. Такая задача (на присоединенном уравнении Гельмгольца) является самосогласованной.